2019-2020学年冀教版七年级数学下册期末测试卷(含答案)
冀教版七年级下册数学期末测试卷及含答案
冀教版七年级下册数学期末测试卷及含答案一、单选题(共15题，共计45分)1、不等式的解集为x＞2，则m的值为（）A.4B.2C.D.2、不等式组的解集在数轴上表示正确的是（）A. B. C.D.3、如图，在正方形ABCD中，对角线AC，BD交于点O，折叠正方形ABCD，使AB边落在AC上，点B落在点H处，折痕AE分别交BC于点E，交BO于点F，连结FH，则下列结论正确的有几个（）⑴AD=DF；（2）= ；（3）= ﹣1；（4）四边形BEHF为菱形．A.1个B.2个C.3个D.4个4、如果关于 x、y 的二元一次方程组的解是则a-b的值为（）A.0B.1C.2D.35、下列能组成三角形的线段是（）A.3cm、3cm、6cmB.3cm、4cm、5cmC.2cm、4cm、6cm D.3cm、5cm、9cm6、把一根长11cm的绳子截成1cm和3cm两种规格的绳子，要求每种规格的绳子至少1根，且无浪费．下面有四种说法：①规格为1cm的绳子可能截出8根；②规格为1cm的绳子可能截出5根；③规格为1cm的绳子可能截出2根；④规格为1cm的绳子可能截出1根．则所有符合题意说法的序号是（）A.①②③④B.①②③C.①②④D.②③④7、下列计算中，正确的有（）①；②；③；④。
A.0个B.1个C.2个D.3个8、下列计算正确的是（）.A. B. C. D.9、已知某等腰三角形三边长分别为5，a，11，则a的值为( )A.5B.5.5C.11D.5或1110、下列命题是假命题的是（）A.互补的两个角不能都是锐角B.两直线平行，同位角相等C.若a ∥b，a∥c，则b∥cD.同一平面内，若a⊥b，a⊥c，则b⊥c11、如图，过x轴正半轴上的任意一点P，作y轴的平行线，分别与反比例函数y＝﹣和y＝的图象交于A，B两点．若点C是y轴上任意一点，连接AC、BC，则△ABC的面积为（）A.3B.4C.5D.1012、在平面直角坐标系中，将点A（﹣1，﹣2）向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为（）A.（﹣3，﹣2）B.（2，2）C.（﹣2，2）D.（2，﹣2）13、三角形ABC的三条内角平分线为AE，BF，CG，下面的说法中正确的个数有（）①△ABC的内角平分线上的点到三边距离相等②三角形的三条内角平分线交于一点③三角形的内角平分线位于三角形的内部④三角形的任一内角平分线将三角形分成面积相等的两部分．A.1个B.2个C.3个D.4个14、不等式组的解集在数轴上表示正确的是（）A. B. C. D.15、下列运算中，正确的是 ( )A.2x-x=1B.x+x=2xC.(x 3) 3=x 6D.二、填空题(共10题，共计30分)16、如图，A、B是直线m上两个定点，C是直线n上一个动点，且m∥n．以下说法：①△ABC的周长不变；②△ABC的面积不变；③△ABC中，AB边上的中线长不变．④∠C的度数不变；⑤点C到直线m的距离不变．其中正确的有________ （填序号）．17、一个四边形的边长依次为a、b、c、d，且a2+b2+c2+d2﹣2ac﹣2bd=0，则这个四边形的形状是________18、若，，则________．19、如图，把△ABC沿AB边平移到△A’B’C’的位置，它们的重叠部分(即图中阴影部分)的面积是△ABC面积的一半．若AB= ，则此三角形平移的距离AA’是________．20、如图，FE∥ON，OE平分∠MON，∠FEO=28°，则∠MFE=________度．21、如图，AB∥CD，BE平分∠ABD，DE平分∠BDC，且BE与DE相交于点E，求证∠E=90°证明：∵AB∥CD（________）∴∠ABD+∠BDC=180°（________）∵BE平分∠ABD（________）∴∠EBD= ________（________）又∵DE平分∠BDC∴∠BDE= ________（________）∴∠EBD+∠EDB= ∠ABD+ ∠BDC（________）= （∠ABD+∠BDC）=90°∴∠E=90°．22、三角形有两条边的长度分别是5和7，则第三边a的取值范围是________．23、若方程组的解x、y互为相反数，则a=________．24、如图,双曲线经过点A(2,2)与点B(4, ),则△AOB的面积为________.25、如图，有两个正方形夹在AB与CD中，且AB∥CD，若∠FEC＝10°，两个正方形临边夹角为150°，则∠1的度数为________度（正方形的每个内角为90°）三、解答题(共5题，共计25分)26、解不等式组：．27、解不等式组：，并将解集在数轴上表示出来，且写出它的整数解.28、计算：(-3x2y)2·(-6xy3)÷(-9x4y2).29、如图，在中，，若，，则上的高是多少？30、已知：如图，直线AB∥CD，直线EF与直线AB、CD分别交于点M、N，MG 平分∠AMF，NH平分∠END.求证：MG∥NH.参考答案一、单选题(共15题，共计45分)1、B2、C3、D4、A5、B6、B8、B9、C10、D11、C12、B13、B14、B15、B二、填空题(共10题，共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、30、。
冀教版七年级数学下册第9章达标测试卷附答案
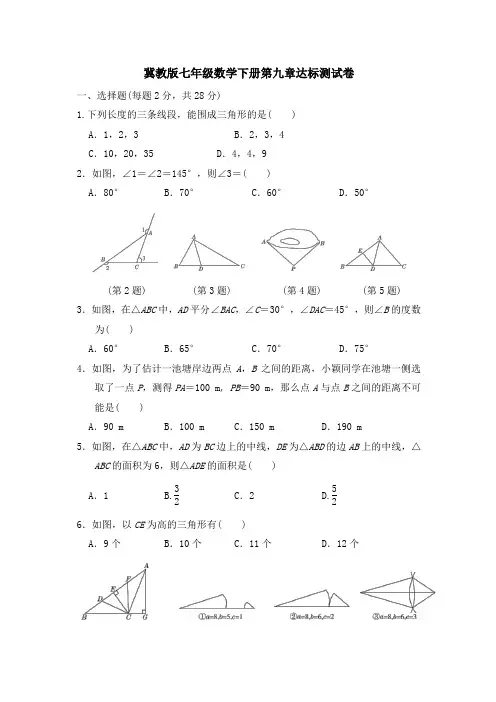
冀教版七年级数学下册第九章达标测试卷一、选择题(每题2分，共28分)1.下列长度的三条线段，能围成三角形的是( )A．1，2，3 B．2，3，4C．10，20，35 D．4，4，92．如图，∠1＝∠2＝145°，则∠3＝( )A．80°B．70°C．60°D．50°(第2题) (第3题) (第4题) (第5题) 3．如图，在△ABC中，AD平分∠BAC，∠C＝30°，∠DAC＝45°，则∠B的度数为( )A．60°B．65°C．70°D．75°4．如图，为了估计一池塘岸边两点A，B之间的距离，小颖同学在池塘一侧选取了一点P，测得PA＝100 m, PB＝90 m，那么点A与点B之间的距离不可能是( )A．90 m B．100 m C．150 m D．190 m5．如图，在△ABC中，AD为BC边上的中线，DE为△ABD的边AB上的中线，△ABC的面积为6，则△ADE的面积是( )A．1 B.32C．2 D.526．如图，以CE为高的三角形有( )A．9个B．10个C．11个D．12个(第6题) (第7题)7．在一次数学课上，老师让学生作出了如图所示的3个图，你觉得学生可能会发现的结论是( )A．三条线段首尾顺次相接能构成三角形B．三角形的内角和是180°C．三角形的任意一个外角大于和它不相邻的内角D．三角形任意两边之和大于第三边8．将一副直角三角尺按如图所示方式放置，使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一直线上，则∠1的度数为( ) A．45°B．65°C．70°D．75°(第8题) (第9题) (第10题)9．如图，五角星的五个角的度数和是( )A．360°B．180°C．90°D．60°10．如图，在△ABC中，∠B＝90°，∠A＝55°，含45°角的直角三角板DEF 的顶点D在AC上，DE∥BC，则∠FDC的度数为( )A．10°B．15°C．20°D．25°11．如图，D，E，F分别是BC，AD，AC的中点，若阴影部分的面积为3，则△ABC的面积是( )A．5 B．6 C．7 D．8(第11题) (第12题) (第13题) (第14题)12．如图，在△ABC中，∠C＝90°，将△ABC沿DE折叠，使得点B落在AC边上的点F处，若∠CFD＝60°且△AEF中有两个内角相等，则∠A的度数为( )A．30°或40°B．40°或50°C．50°或60°D．30°或60°13．如图，AB∥DC，ED∥BC，AE∥BD，那么图中与△ABD面积相等的三角形有( ) A．1个B．2个C．3个D．4个14．如图，△ABC的角平分线CD，BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG 于G，下列结论：①∠CEG＝2∠DCB；②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝12∠CGE.其中正确的有( )A．1个B．2个C．3个D．4个二、填空题(每题3分，共12分)15．如图，∠CBD＝100°，∠A＝20°，则∠C＝________°.(第15题) (第16题) (第17题) (第18题)16．如图，在△ABC中，∠ABC，∠ACB的平分线BO，CO交于点O，CE为△ABC 的外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC＝∠1，∠BEC＝∠2＝α，则∠1＝______，∠BOC＝______．(用含α的式子表示)17．如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线，….若∠A1＝α，则∠A2 023＝________.18．如图，在△ABC中，∠C＝90°，BC＝8 cm，AC＝6 cm，点E是BC的中点，动点P从A点出发，先以每秒2 cm的速度沿A→C运动，然后以每秒1 cm 的速度沿C→B运动．设点P运动的时间是t s，那么当t＝________时，△APE的面积等于6 cm2.三、解答题(19～22题每题9分，23，24题每题12分，共60分)19．如图，在△ABC中，∠BAC＝90°，BE是角平分线，AD是高，BE，AD相交于点F，试说明：∠1＝∠2.(第19题)20．在△ABC中，∠A＋∠B＝∠C，∠B－∠A＝30°.(1)求∠A，∠B，∠C的度数；(2)按角分类，△ABC是什么三角形？按边分类，△ABC是什么三角形？21．如图，在△ABC中，∠B＜∠ACB，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E.(1)若∠B＝35°，∠ACB＝85°，求∠E的度数；(2)试说明：∠E＝12(∠ACB－∠B)．(第21题)22．如图，直线AE∥CD，点P是射线EA上的一个动点(不与点E重合)，将△EPF 沿PF折叠，使顶点E落在点Q处．(1)若∠PEF＝48°，点Q恰好落在其中的一条平行线上，请直接写出∠EFP的度数；(2)若∠PEF＝75°，2∠CFQ＝∠PFC，求∠EFP的度数．(第22题)23．【荣德原创】某教辅书中有如下题目：如图①，∠BDC＝96°，∠C＝36°，∠A＝35°，求∠B的度数．参考答案如下：解：如图②，延长CD交AB于点E，∵∠1＝∠C＋∠A，∠C＝36°，∠A＝35°，∴∠1＝36°＋35°＝71°.∵∠BDC＝∠1＋∠B，∠BDC＝96°，∴∠B＝∠BDC－∠1＝96°－71°＝25°.(1)小丽解此题时所作辅助线与参考答案不同：连接AD并延长，如图③.请根据小丽所作辅助线解此题；(2)请用不同于上述两种方法的方法解此题．(第23题)24．在△ABC中，∠A＝70°，点D，E分别是边AC，AB上的点(不与点A，B，C 重合)，点P是平面内一动点(P与D，E不在同一直线上)，设∠PEB＝∠1，∠DPE＝∠2，∠PDC＝∠3.(1)若点P在BC上运动(不与点B，C重合)，如图①所示，则∠2＝________________(用含有∠1，∠3的代数式表示)；(2)若点P在△ABC的外部，如图②所示，则∠1，∠2，∠3之间有何数量关系？写出你的结论，并说明理由．(3)若点P在CB的延长线上运动，试画出相应图形，标注有关字母与数字，并写出对应的∠1，∠2，∠3之间的数量关系(不需要说明理由)．(第24题)答案一、1.B 2.B 3.A 4.D 5.B 6.B 7．D 8.D 9.B 10.A 11.D 12．B 提示：∵∠CFD ＝60°， ∴∠AFD ＝∠AFE ＋∠EFD ＝120°. ∵∠C ＝90°，∴∠A ＋∠B ＝90°.由折叠知∠EFD ＝∠B ，∴∠EFD ＝90°－∠A . ①当∠AFE ＝∠AEF 时，可得∠AFE ＝12(180°－∠A )，∴12(180°－∠A )＋90°－∠A ＝120°， ∴∠A ＝40°.②当∠A ＝∠FEA 时，可得∠AFE ＝180°－2∠A ， ∴180°－2∠A ＋90°－∠A ＝120°， ∴∠A ＝50°.③当∠A ＝∠AFE 时，易得点F 与点C 重合，不符合题意． 综上所述，∠A 的度数为40°或50°. 故选B. 13．C14．C 提示：①因为EG ∥BC ， 所以∠CEG ＝∠ACB .因为CD 是△ABC 的角平分线， 所以∠ACD ＝∠BCD ，∠ACB ＝2∠DCB ， 所以∠CEG ＝2∠DCB ，故①正确； ②根据已知条件无法推出∠GCE ＝∠ACB ， 所以CA 不一定平分∠BCG ，故②错误； ③因为∠A ＝90°， 所以∠ADC ＋∠ACD ＝90°. 所以∠ADC ＋∠BCD ＝90°.因为EG ∥BC ，CG ⊥EG ，所以CG ⊥BC . 所以∠GCB ＝90°，即∠GCD ＋∠BCD ＝90°， 所以∠ADC ＝∠GCD ，故③正确；④因为∠A ＝90°，所以∠ABC ＋∠ACB ＝90°.因为BE 平分∠ABC ，CD 平分∠ACB ，所以∠EBC ＝12∠ABC ，∠DCB ＝12∠ACB ，所以∠DFB ＝∠EBC ＋∠DCB ＝12(∠ABC ＋∠ACB )＝45°.因为CG ⊥EG ， 所以∠CGE ＝90°， 所以∠DFB ＝12∠CGE ，故④正确．故选C.二、15.80 16.2α；90°＋α 17.α22 022提示：∵BA 1是∠ABC 的平分线，CA 1是∠ACD 的平分线， ∴∠A 1BC ＝12∠ABC ，∠A 1CD ＝12∠ACD .又∵∠ACD ＝∠A ＋∠ABC ，∠A 1CD ＝∠A 1BC ＋∠A 1， ∴12(∠A ＋∠ABC )＝12∠ABC ＋∠A 1， ∴∠A 1＝12∠A ，同理可得∠A 2＝12∠A 1，∠A 3＝12∠A 2，….∵∠A 1＝α，∴∠A 2＝12α，∠A 3＝⎝ ⎛⎭⎪⎫122α，…，∴∠A 2 023＝α22 022. 18．1.5或5或9 提示：∵点E 为BC 的中点，BC ＝8 cm ，∴CE ＝4 cm .当点P在AC 上时，由题意得AP ＝2t cm .易知S △APE ＝12AP ·CE ，∴12×2t ×4＝6.∴t ＝1.5.当点P 在BC 上时，易得t ＞3，S △APE ＝12EP ·AC .由题意得CP ＝(t －3)cm .当点P在点E 左侧时，PE ＝CE －CP ＝(7－t )cm ，∴12(7－t )×6＝6，∴t ＝5.当点P 在点E 右侧时，PE ＝CP －CE ＝(t －7)cm ，∴12(t －7)×6＝6.∴t ＝9.综上，t ＝1.5或5或9.三、19.解：∵∠BAC ＝90°，∠BAC ＋∠2＋∠ABE ＝180°， ∴∠2＋∠ABE ＝90°. ∵AD 是高， ∴∠ADB ＝90°.∵∠BFD ＋∠ADB ＋∠DBF ＝180°， ∴∠BFD ＋∠DBF ＝90°. ∵BE 是角平分线， ∴∠ABE ＝∠DBF ， ∴∠2＝∠BFD . ∵∠BFD ＝∠1， ∴∠1＝∠2.20．解：(1)由题意得⎩⎨⎧∠A ＋∠B ＝∠C ，∠B －∠A ＝30°，∠A ＋∠B ＋∠C ＝180°，解得⎩⎨⎧∠A ＝30°，∠B ＝60°，∠C ＝90°.(2)按角分类，△ABC 是直角三角形．按边分类，△ABC 是不等边三角形． 21．解：(1)因为∠B ＝35°，∠ACB ＝85°， 所以∠BAC ＝180°－∠B －∠ACB ＝60°. 因为AD 平分∠BAC ，所以∠BAD＝30°.所以∠ADC＝∠B＋∠BAD＝65°.因为PE⊥PD，所以∠DPE＝90°，所以∠E＝180°－∠DPE－∠ADC＝25° .(2)因为∠B＋∠BAC＋∠ACB＝180°，所以∠BAC＝180°－(∠B＋∠ACB)．因为AD平分∠BAC，所以∠BAD＝12∠BAC＝90°－12(∠B＋∠ACB)．所以∠ADC＝∠B＋∠BAD＝90°－12(∠ACB－∠B)．因为PE⊥AD，所以∠DPE＝90°.所以∠ADC＋∠E＝180°－90°＝90°. 所以∠E＝90°－∠ADC，即∠E＝12(∠ACB－∠B).22．解：(1)∠EFP的度数为42°或66°. (2)因为AE∥CD，所以∠EFD＝∠PEF＝75°.所以∠CFE＝105°.①当点Q在AE，CD之间时，设∠EFP＝x°，由折叠可知∠PFQ＝∠EFP＝x°，因为2∠CFQ＝∠CFP，所以∠CFQ＝∠PFQ＝x°，所以∠CFE＝3x°＝75°，所以x＝35，所以∠EFP＝35°.②当点Q在CD下方时，设∠EFP＝y°，由折叠可知∠PFQ＝∠EFP＝y°，因为2∠CFQ＝∠CFP，所以∠PFQ＝32∠CFP.所以∠CFP＝23y°，所以∠CFE＝23y°＋y°＝105°，解得y＝63，所以∠EFP＝63°.综上所述，∠EFP的度数为35°或63°.23．解：(1)∵∠CDF＝∠C＋∠CAD，∠BDF＝∠B＋∠BAF，∴∠BDC＝∠CDF＋∠BDF＝∠C＋∠CAD＋∠B＋∠BAF＝∠C＋∠BAC＋∠B.又∵∠BDC＝96°，∠C＝36°，∠BAC＝35°，∴∠B＝25°.(2)如图，连接BC.∵∠A＋∠ACB＋∠ABC＝180°，∠BCD＋∠DBC＋∠BDC＝180°，∴∠A＋∠ACB＋∠ABC＝∠BCD＋∠DBC＋∠BDC.∵∠ABC＝∠ABD＋∠CBD，∠ACB＝∠ACD＋∠BCD，∴∠BDC＝∠ABD＋∠ACD＋∠A.又∵∠BDC＝96°，∠ACD＝36°，∠A＝35°，∴∠ABD＝96°－35°－36°＝25°.提示：(2)方法不唯一．(第23题)24．解：(1)∠1＋∠3－70°提示：∵∠AEP＝180°－∠1，∠ADP＝180°－∠3，∠AEP＋∠ADP＋∠2＋∠A ＝360°，∴180°－∠1＋180°－∠3＋∠2＋70°＝360°，∴∠2＝∠1＋∠3－70°.(2)∠3＝∠1＋∠2－70°.如图①，∵∠1＝∠4＋∠A，∠3＝∠2＋∠5，∠4＝∠5，∴∠3＝∠1＋∠2－∠A，∴∠3＝∠1＋∠2－70°.(3)画出图形如图②，此时∠1＝∠3＋∠2－70°，画出图形如图③，此时∠3＝∠1＋∠2＋70°.提示：在图②中，∵∠1＝∠2＋∠5，∠3＝∠4＋∠A，∠4＝∠5，∴∠1＝∠3＋∠2－∠A.∴∠1＝∠3＋∠2－70°.在图③中，∵∠5＝∠1＋∠2，∠3＝∠4＋∠A，∠5＝∠4，∴∠3＝∠1＋∠2＋∠A，∴∠3＝∠1＋∠2＋70°.(第24题)。
冀教版2020七年级数学下册第八章整式的乘法自主学习基础达标测试题3(附答案)
B． a2 3 a6 ，故选项 B 符合题意；
C． a2a3 a5 ，故选项 C 不合题意；
D． 4x2 与 x 不是同类项，故不能合并，所以选项 D 不合题意．
故选：B． 【点睛】 此题考查了合并同类项、同底数幂的乘法、积的乘方以及幂的乘方的性质．此题比较简单， 注意掌握指数的变化是解此题的关键． 11．1 【解析】 【分析】 先根据多项式乘以多项式的方法计算(x－2)(x +3)，得到 x 2 +x－6，再结合题意即可得到答案. 【详解】 因为(x－2)(x +3)= x 2 + 3x -2x－6= x 2 +x－6，且(x－2)(x +3)= x 2 + ax－6 ，所以 a =1. 【点睛】 本题考查多项式乘以多项式，解题的关键是掌握多项式乘以多项式的方法.
得结果作为系数，字母和字母的指数不变．幂的乘方法则：底数不变，指数相乘．积的乘方
法则：把每一个因式分别乘方，再把所得的幂相乘．
【详解】
解：A． a2 a3 ，不是同类项，不能合并，A 错误；
B． a2 a4 a6 ，B 错误；
C． a2 a a ，C 正确；
D． (a2b)3 a6b3 ，D 错误；
13．利用乘法公式计算： 982 _________=___________；
14．水星和太阳的平均距离为 57900000000 米，57900000000 米用科学计数法表示为 ______米
15．已知 a b 3，代数式 a2 b2 5 ，则 ab 的值是_____________．
的形式，其中
， 为整数，能正确确定 的值以及 的值是解题关键．
5．D
冀教版2019-2020学年七年级下学期数学期末考试试卷新版
冀教版2019-2020学年七年级下学期数学期末考试试卷新版一、选择题 (共10题；共20分)1. （2分）下列说法正确的是（）A . 了解飞行员视力的达标率应使用抽样调查B . 一组数据3，6，6，7，9的中位数是6C . 从2000名学生中选200名学生进行抽样调查，样本容量为2000D . 掷一枚质地均匀的硬币，正面朝上是必然事件2. （2分）若3a＞3b，则有（）A . a＞bB . a＜bC . a≥bD . a≤b3. （2分）下面的计算中，错误的是（）A .B .C .D .4. （2分）如图，在方格纸中，线段a，b，c，d的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有（）A . 3种B . 6种C . 8种D . 12种5. （2分）为了了解2013年昆明市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩．下列说法正确的是（）A . 2013年昆明市九年级学生是总体B . 每一名九年级学生是个体C . 1000名九年级学生是总体的一个样本D . 样本容量是10006. （2分）若点P（2m+4，m﹣3）在第四象限内，则m的取值范围是（）A . m＞3B . m＜﹣2C . ﹣2＜m＜3D . 无解7. （2分）下列实数中，无理数是（）A . 3.14B . 2.12122C .D .8. （2分）如图，小手盖住的点的坐标可能为（）A . （-4，-5）B . （-4，5）C . （4，5）D . （4，-5）9. （2分）下列说法正确的是（）A . x=4是不等式2x＞－8的一个解B . x=－4是不等式2x＞－8的解集C . 不等式2x＞－8的解集是x＞4D . 2x＞－8的解集是x＜－410. （2分）某市举办花展，如图，在长为14m，宽为10m的长方形展厅，划出三个形状、大小完全一样的小长方形摆放水仙花，则每个小长方形的周长为（）A . 8B . 13C . 16D . 20二、填空题 (共6题；共14分)11. （1分）若是方程ax﹣y=0的解，则a=________．12. （2分）如图，直线AB是某天然气公司的主输气管道，点C、D是在AB异侧的两个小区，现在主输气管道上寻找支管道连接点，向两个小区铺设管道。
冀教版七年级下册期末测试数学
期末测试卷一、单选题（共20题；共40分）1.一个盒子中装有四X完全相同的卡片，分别写着2cm，3cm，4cm和5cm，盒子外有两X卡片，分别写着3cm和5cm，现随机从盒中取出一X卡片，与盒子外的两X卡片放在一起，以卡片上的数量分别作为三条线段的长度，那么这三条线段能构成三角形的概率是（）A.B.C.D.2.计算：m6m3的结果（）18A.m9B.m3C.m2D.m3.甲在集市上先买了3只羊，平均每只a元，稍后又买了2只，平均每只羊b元，后来他以每只元的价格把羊全卖给了乙，结果发现赔了钱，赔钱的原因是（）A.a＞bB.a=bC.a＜bD.与a、b大小无关4.（2017?XX）“双11”促销活动中，小芳的妈妈计划用1000元在唯品会购买价格分别为80元和120元的两种商品，则可供小芳妈妈选择的购买方案有（）A.4种B.种5C.种6D.种75.方程3x+y=9在正整数X围内的解的个数是（）A.1个B.2个C.个3D有.无数个6.下列各式正确的是（）A.（a+b）2=a2+b2B（.x+6）（x﹣6）=x2﹣6C.（2x+3）2=2x2﹣12x+9D（.2x﹣1）2=4x2﹣4x+17.如图，直线AB∥CD，EF⊥CE，垂足为E，EF交CD于点F，∠1=48°，则∠2的度数是（）A.42°B.48C.52°D.58°°8.如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（）A.42、°138°B.都是10°C.42、138°或10°、°10°D.以上都不对9.关于x的方程mx﹣1=2x的解为正实数，则m的取值X围是（）A.m≥2B m.≤2C.＞m2D.m＜210.下列计算，正确的是（）22=6a2B（.2x﹣1）?3x2y=6x3y﹣1A.3a×2a32b2D.（）0×3=0C.（﹣a b）÷（﹣a b）=a11.若a＞b，则下列不等式中正确的是（）A.a﹣b＜0B.﹣5a＜﹣5bC.a+8＜b﹣8D.12.下列分解因式正确的是（）1/10期末测试卷22+2xy﹣y=﹣y（xy﹣2x）﹣xy=2x（x﹣y）B.﹣xyA.2x22D.x2﹣x﹣3=x（x﹣1）﹣3﹣8x+8=2（x﹣2）C.2x13.如图，将完全相同的四个矩形纸片拼成一个正方形，则可得出一个等式为（）A.（a+b）2=a2+2ab+b2B.（a﹣b）2=a2﹣2ab+b22﹣b2=（a+b）（a﹣b）D.（a+b）2=（a﹣b）2+4abC.a14.下列乘法中，不能运用平方差公式进行运算的是（）A.（x+a）（x﹣a）B（.﹣x﹣b）（x﹣b）C.（a+b）（﹣a﹣b）D.（b+m）（m﹣b）15.（2015?XX）XX红星大市场某种高端品牌的家用电器，若按标价打八折销售该电器一件，则可获利润500元，其利润率为20%．现如果按同一标价打九折销售该电器一件，那么获得的纯利润为（）A.562.5元B.875元C.550元D.750元16.不等式组的解集在数轴上表示正确的是（）A.B.C.D.17.如果是方程2x+y=0的一个解（m≠0），那么（）A.m≠0，n=0B.m，n异号C.m，n同号D.m，n可能同号，也可能异号18.下列说法中，正确的有（）①有一个角为60°的等腰三角形是等边三角形.②三边分别是1，，3的三角形是直角三角形.③一边上的中线等于这条边的一半的三角形是直角三角形.④三个角之比为3：4：5的三角形是直角三角形.A.1个B.个2C.个3D.个419.若a<0关于x的不等式ax+1>0的解集是（）A.x>B.x<C.x>-D.x<-20.如图，在平行四边形ABCD中，对角线AC,BD的长度分别为10和6，则AB长度的最大整数值是（）A.8B.5C.6D.7二、填空题（共8题；共8分）2/10期末测试卷21.若，那么k的值是________.22.因式分解：________；23.在解关于，的方程组时，老师告诉同学们正确的解是，小明由于看错了系数，因而得到的解为，则的值________。
相交线与平行线 冀教版七年级下册数学达标测试卷(含答案)
第七章达标测试卷一、选择题(1～10题每题3分，11～16题每题2分，共42分)1．下列生活现象中，属于平移变换的是()A．推拉抽屉B．汽车雨刮器的运动C．荡秋千D．投影片的文字经投影到大屏幕2．如图，两只手的食指和拇指在同一个平面内，它们构成的一对角可看成是()A．同位角B．内错角C．对顶角D．同旁内角(第2题)(第3题)3．如图，a∥b，AB∥CD，CE⊥b，FG⊥b，点E，G为垂足，则下列说法中错误的是()A．AB＝CDB．CE＝FGC．A，B两点之间的距离就是线段AB的长D．直线a，b之间的距离就是线段CD的长4．下列正确的选项是()A．命题“同旁内角互补”是真命题B．“作线段AC”这句话是命题C．“对顶角相等”是定义D．说明命题“若x＞y，则a2x＞a2y”是假命题，只能举反例a＝05．如图，给出下列说法：①∠B和∠1是同位角；②∠1和∠3是对顶角；③∠2和∠4是内错角；④∠A和∠BCD是同旁内角．其中说法正确的有() A．0个B．1个C．2个D．3个(第5题)(第6题)6．如图，将木条a，b与c钉在一起，∠1＝80°，∠2＝50°.要使木条a与b平行，木条a旋转的度数至少是()A．10°B．20°C．30°D．50°7．能说明“锐角α，锐角β的和是锐角”是假命题的例证图是()8．如图，给出下列条件：①∠1＝∠3；②∠2＝∠3；③∠2＝∠4；④∠5＋∠4＝180°.其中不能判定a∥b的是()A．①B．②C．③D．④(第8题)(第10题)9．下列命题，其中为真命题的是()①经过直线外一点，有且只有一条直线与已知直线平行；②同位角相等；③同一平面内，过一点有且只有一条直线与已知直线垂直；④对顶角相等．A．①②B．①③④C．①④D．②③④10．如图，在三角形ABC中，∠BAC＝90°，且AD⊥BC于点D，∠B＝35°，那么下列结论中错误的是()A．∠BAD＝55°B．∠CAD＝55°C．∠B＝∠CAD D．∠BAD＝∠C11．如图，点A在直线l1上，点B，C在直线l2上，AB⊥l2，AC⊥l1，AB＝4，BC＝3，AC＝5，则下列说法正确的是()A．点B到直线l1的距离等于4 B．点C到直线l1的距离等于5 C．点C到AB的距离等于4 D．点B到AC的距离等于5(第11题)(第12题)12．如图，一块直角三角尺的60°角的顶点A与直角顶点C分别在两平行线FD，GH上，斜边AB平分∠CAD，交直线GH于点E，则∠ECB的大小为() A．60°B．45°C．30°D．25°13．一个小区大门的栏杆如图所示，BA垂直地面AE于A，CD平行于地面AE，那么∠ABC＋∠BCD是()A．180°B．245°C．270°D．360°(第13题(第14题)14．如图，已知直线a∥b，则∠1，∠2，∠3的关系是()A．∠1＋∠2＋∠3＝360°B．∠1＋∠2－∠3＝180°C．∠1－∠2＋∠3＝180°D．∠1＋∠2＋∠3＝180°15．将一副三角尺按如图所示放置，下列结论中不正确的是() A．若∠2＝30°，则有AC∥DEB．∠BAE＋∠CAD＝180°C．若BC∥AD，则有∠2＝30°D．若∠CAD＝150°，则有∠4＝∠C(第15题)(第16题)16．如图，已知AB∥EG，BC∥DE，CD∥EF，则x，y，z三者之间的关系是()A．x＋y＋z＝180°B．x－z＝yC．y－x＝z D．y－x＝x－z二、填空题(17题3分，其余每空2分，共11分)17．为了便于游客领略“人从桥上过，如在景中游”的美好意境，某景区拟在如图所示的长方形水池上架设景观桥．若长方形水池的周长为300 m，景观桥宽忽略不计，则小桥总长为________m.(第17题)(第18题)(第19题)18．如图，∠1＝∠2，∠3＝∠B，则图中两组平行线分别为________________；若∠C＝80°，则∠AED＝________．19．如图，AE∥CF，∠ACF的平分线交AE于点B，G是CF上的一点，∠GBE 的平分线交CF于点D，且BD⊥BC，若∠A＝α，则与∠DBE互余的角有______________，∠BDF＝________(用含α的式子表示)．三、解答题(20题8分，21～23题每题9分，24～25题每题10分，26题12分，共67分)20．运动会中裁判员使用的某品牌遮阳伞的剖面图如图，若AG平分∠BAC，DG 平分∠EDF，点A，D，G在同一直线上，AB∥ED，试说明AC∥DF.请将横线上的证明过程和依据补充完整．解：∵AB∥DE，∴∠____＝∠____(________________)．∵AG平分∠BAC，DG平分∠EDF(已知)，∴∠DAC＝∠DAB，∠GDE＝∠GDF(________________)．∴∠____＝∠____(________________)．∴AC∥DF(________________)．(第20题)21．如图，点G在射线BC上，射线DE与AB，AG分别交于点H，M.若DF∥AB，∠B＝75°，∠D＝105°.试说明：∠AME＝∠AGC.(第21题)22．如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，空白的部分种上各种花草．(1)请利用平移的知识求出种花草的面积．(2)若空白的部分种植花草共花费了4 620元，则每平方米种植花草的费用是多少元？(3)若正方形土地的边长为a米，3条道路宽都是b米，则种花草的面积用a，b可表示为________________平方米．(只列式，不化简)(第22题)23．如图，AB∥CD，∠ABE＝40°，若CF平分∠ECD，且满足CF∥BE，求∠ECD的度数．(第23题)24．在正方形网格中，每个小正方形的边长都为1个单位长度，三角形ABC的三个顶点的位置如图所示，现将三角形ABC平移后得三角形DEF，使点A 的对应点为点D，点B的对应点为点E.(1)画出三角形DEF；(2)连接AD，BE，判断线段AD与BE的关系；(3)求三角形DEF的面积．(第24题)25．如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2，试说明：CD⊥AB.(第25题)26．如图，已知AB∥DE，CM平分∠BCE交AB于M，CN⊥CM，且射线CN 在直线ED的上方．(1)作图，将图形补充完整；(2)猜想∠B和∠DCN的数量关系，并说明理由．(第26题)答案一、1.A 2.B 3.D 4.D 5.B 6.C7．C8.B9.B10.B11.B12.C13．C14.B15.C16．B点拨：如图所示，延长AB交DE于H.因为BC∥DE，所以∠ABC＝∠AHE＝x，因为CD∥EF，AB∥EG，所以∠D＝∠DEF＝z，∠AHE＝∠DEG＝z＋y，所以∠ABC＝∠DEG，即x＝z＋y.所以x－z＝y，故选B.(第16题)二、17.15018.EF∥AB，DE∥BC；80°19．∠ABC，∠CBG，∠ACB，∠BCG；180°－α2三、20.DAB；GDE；两直线平行，同位角相等；角平分线的定义；DAC；GDF；等量代换；同位角相等，两直线平行21．解：因为∠B＝75°，∠D＝105°，所以∠B＋∠D＝180°.因为DF∥AB，所以∠D＝∠BHE，所以∠B＋∠BHE＝180°，所以DE∥BC，所以∠AME＝∠AGC.22．解：(1)(8－2)×(8－1)＝6×7＝42(平方米)．答：种花草的面积为42平方米.(2)4 620÷42＝110(元)．答：每平方米种植花草的费用是110元.(3)(a－2b)(a－b)23．解：如图，延长BE交DC的延长线于G.(第23题)因为AB∥CD，所以∠ABE＝∠G，因为CF∥BE，所以∠FCD＝∠G，所以∠FCD＝∠ABE＝40°.因为CF平分∠ECD，所以∠ECD＝2∠FCD＝80°.24．解：(1)如图所示，三角形DEF即为所求．(第24题)(2)如图，线段AD与BE的关系是平行且相等．(3)S三角形DEF＝3×3－12×2×3－12×1×2－12×1×3＝72.25．解：因为DG⊥BC，AC⊥BC，所以∠DGC＝∠ACB＝90°.所以∠DGC＋∠ACB＝180°，所以DG∥AC，所以∠2＝∠ACD.因为∠1＝∠2，所以∠1＝∠ACD.所以EF∥CD，所以∠AEF＝∠ADC.因为EF⊥AB，所以∠AEF＝90°，所以∠ADC＝90°，所以CD⊥AB.26．解：(1)如图．(第26题)(2)猜想：∠B＝2∠DCN.理由：因为CM平分∠BCE交AB于M，CN⊥CM，所以∠MCB＝12∠ECB，∠MCN＝∠MCB＋∠NCB＝90°.因为∠ECB＋∠BCD＝180°，所以12∠ECB＋12∠BCD＝90°，即∠MCB＋12∠BCD＝90°.所以∠NCB＝12∠BCD.所以∠DCN＝12∠BCD.因为AB∥ED，所以∠B＝∠BCD＝2∠DCN.。
冀教版七年级下册数学第9章 三角形 三角形两条角平分线的交角与第三角关系的三种模型、六种应用
∴∠A＝∠ACM－∠ABC＝60°， ∠ACB＝180°－∠ACM＝80°， ∴∠BCP＝∠ACB＋∠ACP＝130°. ∵∠ABP＝∠PBC＝20°， ∴∠P＝180°－∠PBC－∠BCP＝30°， ∴∠A＋∠P＝90°.
7．如图，∠ABD，∠ACD 的角平分线交于点 P，若∠A＝60°， ∠D＝20°，求∠P 的度数．
解：∠A＝180°－2∠D，理由如下： ∵BD，CD 分别是∠EBC 和∠FCB 的平分线， ∴∠EBC＝2∠DBC，∠FCB＝2∠DCB. ∵∠A＋∠ABC＋∠ACB＝180°， ∴∠ABC＝180°－(∠A＋∠ACB)＝180°－2∠DBC， ∠ACB＝180°－(∠A＋∠ABC)＝180°－2∠DCB， ∴∠A＋180°－2∠DBC＋180°－2∠DCB＝180°，
C．在△ADC 中，∠ADC＋∠CAD＋∠ACD＝180°， ∵CD 是△ABC 的外角∠ACF 的平分线，∴∠ACD＝∠DCF. ∵AD∥BC，∴∠ADC＝∠DCF，∠CAD＝∠ACB， ∴∠ACD＝∠ADC，∠CAD＝∠ACB＝∠ABC＝2∠ABD， ∴∠ADC＋∠CAD＋∠ACD＝∠ADC＋2∠ABD＋∠ADC＝ 2∠ADC＋2∠ABD＝180°，∴∠ADC＋∠ABD＝90°， ∴∠ADC＝90°－∠ABD，故 C 正确；D.根据已知条件无法判定 DB 平分∠ADC，∴D 错误．故选 D. 【答案】D
5．如图①，点 A，B 分别在射线 OM，ON 上运动(不与点 O 重 合)，AC，BC 分别是∠BAO 和∠ABO 的平分线，BC 的延长 线交 OM 于点 G.
(1)若∠MON＝60°，则∠ACG＝__6_0_°____；若∠MON＝90°，则 ∠ACG＝___45_°____；
(2)若∠MON＝n°，请求出∠ACG 的度数；(用含 n 的代数式表示) 解：∵∠MON＝n°，∴∠OAB＋∠OBA＝180°－n°. ∵AC，BC 分别平分∠OAB，∠OBA， ∴∠ABC＝12∠OBA，∠BAC＝12∠BAO. ∴∠ABC＋∠BAC＝12(∠OAB＋∠OBA)＝90°－12n°， ∴∠ACG＝∠ABC＋∠BAC＝90°－12n°.
冀教版七年级数学期末试卷(附答案)
2019—2020学年度第二学期期末教学质量检测七年级数 学 试 卷（B ）(冀教版)题号一二三总分2122 23 24 25 26 得分一、选择题（每小题3分，共48分。
在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确选项的代码填在下面的表格内） 题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 答案1.如图，直线m 、n 相交，则∠1与∠2的位置关系为（ ） A. 邻补角 B. 内错角C. 同旁内角D. 对顶角2. 下列方程中,是二元一次方程的是( ) A. 324x y z -= B. 244y x -=C. 146y x+= D. 690xy += 3. 下列各式中，计算正确的是（ ） A. 235x y xy += B. 623x x x ÷=C. ()33926xx -=-D. 325a a a ⋅=4.若(m －3)0＝1，则m 的取值为( ) A. m ＜3B. m ＞3C. m ＝3D. m ≠35. 计算2(2)a -的结果是（ ） A. 24a -B. 224a a -+C. 244a a -+D.24a +6. 在△ABC 中，∠A=20°，∠B=60°，则△ABC 的形状是（ ） A. 等边三角形 B. 锐角三角形 C. 直角三角形D. 钝角三角形7. 肥皂泡的泡壁厚度大约是0.0007mm ，0.0007用科学记数法表示为（ ） A. 0.7×10﹣3 B. 7×10﹣3C. 7×10﹣4D. 7×10﹣5得分 评卷人8. 如图，已知直线a 、b 被直线c 所截，那么∠1的同位角是( ) A. ∠2 B. ∠3 C. ∠4 D. ∠5 9. 下列命题中是假命题的是（ ） A. 对顶角相等 B. 同旁内角互补C. 两点确定一条直线D. 垂线段最短第8题图 第10题图10. 如图，点E 在CD 延长线上，下列条件中不能判定AC ∥BD 的是( ) A. ∠1=∠2 B. ∠3=∠4 C. ∠5=∠C D. ∠C+∠BDC=018011. 已知11x y =⎧⎨=-⎩是方程23x ay b -=的一个解，那么3a b -的值是（ ）A. 2B. 0C. ﹣2D. 112.不等式组21217x x -≥⎧⎨->-⎩的解集在数轴上表示正确的是( )A ．B ．C ．D ．13. 如果一个等腰三角形两边的长分别是1，5，那么它的周长是( ) A. 11 B. 7 C. 7或11 D. 以上选项都不对 14. 已知二元一次方程组23825x y x y -=⎧⎨-=⎩，则x y -的值为( )A ．14B ．3C ．377D ．515.多项式2mx m -与多项式221x x -+的公因式是（ ） A. 1x - B. 1x +C. 21x -D. ()21x -16.不等式组0321x a x -<⎧⎨-≤-⎩的整数解共有3个，则a 的取值范围是（ ）A ．45a <<B ．45a <≤C ．45a ≤<D ．45a ≤≤二、填空题（每小题3分，共12分，把答案写在题中横线上）17.写出一个能使不等式1202x -<成立的x 的值 ； 18.计算()22a = ；19. 分解因式：33a b ab -=___________．20.在△ABC 中，已知∠A ＝60°，∠B ＝80°，则∠C 的外角的度数是________．三、解答题（本大题共6个小题，共60分。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020学年七年级数学下册期末测试卷一、选择题（本大题共14个小题，每小题3分，满分42分，在每小题给出的四个选项中，只有一项是符合要求的）1. 计算 ，下列结论正确的是（ ）A. B. C. D.2. 下列命题中，是假命题的是（ ）A. 两点之间，线段最短B. 同旁内角互补C. 直角的补交仍然是直角D. 对顶角相等3. 已知直线AB ，CB ，l 在同一个平面内，若AB ⊥l ，垂足为B ，BC ⊥l ，垂足也为B ，则符合题意的图形可以是（ ）D.4. 对于任意的底数a ，b ，当n 是正整数时，n n b n a n ab n n b a b b b a a a ab ab ab ab =⨯⨯⨯⨯⨯=⨯⨯= 个个个)()()()()()(第一步变形 第二步变形其中，第二步变形的依据是（ ）A. 乘法交换律与结合律B. 乘法交换律C. 乘法结合律D. 乘方的定义5. 在数轴上表示不等式01≥-x 的解集，正确的是（ ）A. B. C. D.6. 据报道，人类首张黑洞照片于北京时间2019年4月10日全球六地同步发布，该黑洞位于 室女座一个巨椭圆星系M87的中心，距离地球5500万光年，其中5500万用科学计数法表示为（ ）A. B. C. D.7. 方程组⎩⎨⎧=--=835y x x y 用代入法消去y 后所得到的方程，不正确．．．的是（ ） A. 853=--x x B. 583-=-x xC. 8)5(3=--x xD. 853=+-x x8. 如图所示，△ABC 中AC 边上的高线是（ ）A. 线段DAB. 线段BAC. 线段BDD. 线段BC9. 若y x >，且y a x a )3()3(-<-，则a 的值可能是（ ） A. 0 B. 3 C. 4 D. 510. 下列图形中，能通过其中一个三角形平移得到的是（ ）l l l a 25a 5a 6a 5a a ⨯41055⨯4105.5⨯71055.0⨯7105.5⨯A. B. C. D.11. 下列等式从左到右的变形，属于因式分解的是（ ）A. ay ax y x a -=-)(B. )1)(1(3-+=-x x x x xC. 34)3)(1(2++=++x x x xD. 1)2(122++=++x x x x12. 已知三角形三边长分别为3，x ，10，若x 为正整数，则这样的三角形个数为（ ）A. 2B. 3C. 5D. 713. 对不等式18321>+--x x ，给出了以下解答： ①去分母，得8)3()1(4>+--x x ；②去括号，得8344>+--x x ；③移项、合并同类项，得93>x ；④两边都除以3，得3>x其中错误开始的一步是（ ）A. ①B. ②C. ③D. ④14. 如图，P 是∠ABC 内一点，点Q 在BC 上，过点P 画 直线a ∥BC ，过点Q 画直线b ∥AB ，若∠ABC=115°，则直线a 与b 相交所成的锐角的度数为（ ）A. 25°B. 45°C. 65°D. 85°二、填空题（本大题满分12分，其中15、16题每小题3分，17题两个空，每个空3分） 15. 若⎩⎨⎧==21y x 是方程3=+y ax 的解，则=a 。
16. 计算：=-22)21(b a 。
17. 已知关于x 的不等式013>+-m x ，若1=m ，则不等式的解集为 ；若不等式的最小整数解为2，则实数m 的取值范围是 。
三、解答题（本大题共7个小题，共66分，解答应写出文字说明、演算步骤或证明过程）18.（本小题满分8分）如图，AB 、CD 相交于点O ，OE 是∠AOD 的平分线，∠AOC=30°，求∠BOE 的度数。
19.（本小题满分9分）A C EDB O已知：1232-=x A ，332105xy y x B +=，1)3)(1(+++=x x C 。
问多项式A ，B ，C 是否有公因式？若有，求出其公因式；若没有，请说明理由。
20.（本小题满分9分）如图，在△ABC 中，∠C=45°，∠A=55°，BE 是△ABC 的角平分线，点D 在AB 上，且DE ∥BC ，求∠DEB 的度数。
21.（本小题满分9分）如图1，长方形的两边长分别为3+m ，13+m ；如图2的长方形的两边长分别为5+m ，7+m 。
（其中m 为正整数） （1）用m 的代表式分别表示图1的面积1S 、图2的面积2S ，并比较1S ，2S 的大小；（2）现有一个正方形的周长与图1中的长方形的周长相等，试探究该正方形的面积与图1中的长方形的面积的差是否是一个常数，如果是，求出这个常数；如果不是，说明理由。
22.（本小题满分10分）3+m 13+m 5+1图2图已知关于x 、y 的二元一次方程组⎩⎨⎧+=++=-②25①42m y x m y x 。
（1）若1=m ，求方程组的解；（2）若方程组的解中，x 的值为正数，y 的值为负数，求m 的范围。
23.（本小题满分10分）【发现】任意三个连续偶数的平方和是4的倍数。
【验证】（1）222642++的结果是4的几倍？（2）设三个连续偶数的中间一个为n 2，写出它们的平方和，并说明是4的倍数。
【延伸】（3）设三个连续奇数的中间一个数为12+n ，写出它们的平方和，它是12的倍 数吗？若是，说明理由，若不是，写出被12除余数是多少？24、（本小题满分11分）某商场计划经销A 、售价如下表所示。
（1）若该商场购进这批台灯共用去2500元，问这两种台灯各购进多少盏？（2）在每种台灯销售利润不变的情况下，若该商场销售这批台灯的总利润不少于1400 元，问至少需购进B 种台灯多少盏？七年级期末考试数学试题参考答案1-5 DBCAC 6-10 DACAC 11-14 BCBC15. 1 16. 2441b a 17. 0>x ，74<≤m18. 解：∵∠AOC=30°，∴∠AOD=180°﹣∠AOC=150°，……………………………3分∵OE 是∠AOD 的平分线，∴∠DOE=21∠AOD=75°，……………………………………6分 ∵∠DOB=∠AOC=30°，∴∠BOE=∠DOB+∠DOE=105° ………………………………8分19. 解：多项式A 、B 、C 有公因式，…………………………………………………………2分 ∵A=)2)(2(3)4(312322-+=-=-x x x x ，……………………………………………………4分 B=)2(51053332+=+x xy xy y x ，……………………………………………………………6分 C=222)2(441341)3)(1(+=++=+++=+++x x x x x x x …………………………………8分 ∴多项式A 、B 、C 的公因式是：)2(+x ，……………………………………………………9分20. 解：∵∠C=45°，∠A=55°，∴∠ABC=80°，…………………………………………3分 又∵BE 平分∠ABC ，∴∠CBE=40°，…………………………………………………………6分 ∵DE ∥BC ，∴∠DEB=∠CBE=40°，…………………………………………………………9分21. 解：（1）∵3916)3)(13(21++=++=m m m m S ，3512)5)(7(22++=++=m m m m S ………3分 ∴04421>+=-m S S ，∴21S S >，……………………………………………………………5分（2）∵一个正方形的周长与图1中的长方形的周长相等，∴正方形的边长为8+m ，正方形的面积=64162++m m ，…………………………………………………………………………7分 ∴25)3916(641622=++-++m m m m ，∴该正方形的面积与长方形的面积的差是一个常数；…………………………………………9分22. 解：（1）当1=m ，方程组为⎩⎨⎧=+=-②7①52y x y x ………………………………………………1分①+②得，123=x ，解得，4=x ………………………………………………………………3分把4=x 代入②得，3=y ，∴方程组的解为⎩⎨⎧==34y x …………………………………………5分 （2）①+②得，933+=m x ，解得，3+=m x ………………………………………………7分 把3+=m x 代入②得，m y m 253+=++，解得，2+=m y ………………………………8分由题意得。
⎩⎨⎧<+>+0203m m ，解得，23-<<-m …………………………………………………7分23. 解：（1）∵1445636164642222⨯==++=++，∴222642++的结果是4的14倍；……2分（2）设三个连续偶数分别为22-n ，n 2，22+n ，（其中n 是整数）……………………3分 则222)22()2()22(+++-n n n4844484222+++++-=n n n n n8122+=n)23(42+=n ，∴三个连续偶数的平方和是4的倍数；……………………………………6分（3）设三个连续奇数分别为12-n ，12+n ，32+n ，（其中n 是整数）…………………7分 则222)32()12()12(++++-n n n9124144144222+++++++-=n n n n n n1112122++=n n11)(122++=n n ，∴222)32()12()12(++++-n n n 不能被12整除，被12除余数是11，……………………10分24. 解：（1）设购进A 种新型节能台灯x 盏，B 种新型节能台灯y 盏，由题意得⎩⎨⎧=+=+2500654050y x y x ，……………………………………………………………………………3分 解得：⎩⎨⎧==2030y x ，…………………………………………………………………………………5分 答：购进A 型节能台灯30盏，B 型节能台灯20盏；………………………………………6分（2）设购进B 种新型节能台灯a 盏，则购进A 种新型节能台灯)50(a -盏，由题意得： 1400)50)(4060()65100(≥--+-a a ，…………………………………………………8分 解得：3226≥a ，………………………………………………………………………………10分 ∵a 表示整数，∴至少需购进B 种台灯27盏，答：至少需购进B 种台灯27盏，……………………………………………………………11分1、只要朝着一个方向努力，一切都会变得得心应手。