中国剩余定理问题的解题技巧
高考数学冲刺中 国剩余定理考点精讲

高考数学冲刺中国剩余定理考点精讲在高考数学的冲刺阶段,国剩余定理作为一个重要的考点,需要我们深入理解和掌握。
国剩余定理,又称中国余数定理,是数论中的一个重要定理,对于解决一些特定类型的数学问题具有关键作用。
首先,让我们来了解一下国剩余定理的基本概念。
国剩余定理主要用于解决这样一类问题:已知一个数除以几个不同的数所得的余数,求这个数。
比如说,有一个数除以 3 余 2,除以 5 余 3,除以 7 余 2,求这个数。
这就是一个典型的可以用国剩余定理来解决的问题。
为了更好地理解国剩余定理,我们需要先引入一些相关的概念。
比如,同余的概念。
如果两个整数 a 和 b 除以正整数 m 所得的余数相同,我们就说 a 和 b 对模 m 同余,记作a ≡ b (mod m)。
接下来,我们来看国剩余定理的具体表述。
设 m1, m2,, mk 是两两互质的正整数,M = m1m2mk,Mi = M/mi (i = 1, 2,, k),则同余方程组:x ≡ a1 (mod m1)x ≡ a2 (mod m2)x ≡ ak (mod mk)在模 M 下的解为:x ≡ M1' M1a1 + M2' M2a2 ++ Mk' Mkak(mod M),其中 Mi' 为 Mi 模 mi 的逆元。
可能这一段表述看起来有些复杂,但其实通过具体的例子来理解就会变得清晰很多。
比如,我们有这样一个同余方程组:x ≡ 2 (mod 3)x ≡ 3 (mod 5)x ≡ 2 (mod 7)首先,我们计算 M = 3×5×7 = 105。
然后,M1 = 105÷3 = 35,M2 = 105÷5 = 21,M3 = 105÷7 = 15。
接着,我们要找到 M1 模 3 的逆元,M2 模 5 的逆元,M3 模 7 的逆元。
对于 M1 模 3 的逆元,因为35 ≡ 2 (mod 3),2×2 ≡ 1 (mod 3),所以 M1 的逆元为 2。
中国剩余定理(孙子定理)详解

中国剩余定理(孙⼦定理)详解问题:今有物不知其数,三三数之剩⼆,五五数之剩三,七七数之剩⼆。
问物⼏何?简单点说就是,存在⼀个数x,除以3余2,除以5余三,除以7余⼆,然后求这个数。
上⾯给出了解法。
再明⽩这个解法的原理之前,需要先知道⼀下两个定理。
定理1:两个数相加,如果存在⼀个加数,不能被整数a整除,那么它们的和,就不能被整数a整除。
定理2:两数不能整除,若除数扩⼤(或缩⼩)了⼏倍,⽽被除数不变,则其商和余数也同时扩⼤(或缩⼩)相同的倍数(余数必⼩于除数)。
以上两个定理随便个例⼦即可证明!现给出求解该问题的具体步骤:1、求出最⼩公倍数lcm=3*5*7=1052、求各个数所对应的基础数(1)105÷3=3535÷3=11......2 //基础数35(2)105÷5=2121÷5=4 (1)定理2把1扩⼤3倍得到3,那么被除数也扩⼤3倍,得到21*3=63//基础数633、105÷7=1515÷7=2 (1)定理2把1扩⼤2倍得到2,那么被除数也扩⼤2倍,得到15*2=30//基础数30把得到的基础数加和(注意:基础数不⼀定就是正数)35+63+30=1284、减去最⼩公倍数lcm(在⽐最⼩公倍数⼤的情况下)x=128-105=23那么满⾜题意得最⼩的数就是23了。
⼀共有四个步骤。
下⾯详细解释每⼀步的原因。
(1)最⼩公倍数就不解释了,跳过(记住,这⾥讨论的都是两两互质的情况)(2)观察求每个数对应的基础数时候的步骤,⽐如第⼀个。
105÷3=35。
显然这个35是除了当前这个数不能整除以外都能够被其他数整除,就是其他数的最⼩公倍数。
相当于找到了最⼩的起始值,⽤它去除以3发现正好余2。
那么这个基础数就是35。
记住35的特征,可以整除其他数但是不能被3整除,并且余数是2。
体现的还不够明显,再看下5对应的基础数。
21是其他数的最⼩公倍数,但是不能被5整除,⽤21除以5得到的余数是1,⽽要求的数除以5应该是余1的。
中国剩余定理问题的解题技巧

中国剩余定理问题的解题技巧中国剩余定理问题的解题技巧【问题】有1个数,除以7余2.除以8余4,除以9余3,这个数至少是多少?这种问题称为“中国剩余定理”问题。
我一般用两种方法解决这类问题。
第一种是逐步满足法,方法麻烦一点,但适合所有这类题目。
第二种是最小共倍法,方法简单,但只适合特殊类型的题目。
还有“中国剩余定理”的方法,但它不完善且解法较为复杂,普及应用有一定难度,还不稳定。
所以一般不用。
下面分别介绍一下常用的两种方法。
通用的方法:逐步满足法【问题】一个数,除以5余1,除以3余2。
问这个数最小是多少?把除以5余1的数从小到大排列:1,6,11,16,21,26,……然后从小到大找除以3余2的,发现最小的是11。
所以11就是所求的数。
先满足一个条件,再满足另一个条件,所以称之为“逐步满足法”。
好多数学题目都可以用逐步满足的思想解决。
特殊的`方法:最小公倍法情况一【问题】一个数除以5余1,除以3也余1。
问这个数最小是多少?(1除外)除以5余1:说明这个数减去1后是5的倍数。
除以3余1:说明这个数减去1后也是3的倍数。
所以,这个数减去1后是3和5的公倍数。
要求最小,所以这个数减去1后就是3和5的最小公倍数。
即这个数减去1后是15,所以这个数是15+1=16。
情况二【问题】一个数除以5余4,除以3余2。
问这个数最小是多少?这种情况也可以用特殊法。
数除以5余4,说明这个数加上1后是5的倍数。
数除以3余2,说明这个数加上1后也是3的倍数。
所以,这个数加上1后是3和5的公倍数。
要求最小,所以这个数加上1后就是3和5的最小公倍数。
即这个数加上1后是15,所以这个数是15-1=14。
多个数的,比如3个数的,有时候其中两个可以用特殊法,那就先用特殊法,用特殊法求出满足两个条件的数后再用通用的方法求满足最后一个条件的数。
所以有时候特殊法和通用法混合使用。
在使用的过程中如果能灵活运用余数问题的技巧,会非常有利于解题。
谈“中国剩余定理”小学解法

谈“中国剩余定理”小学解法谈“中国剩余定理”小学解法前问题解答中所涉题目属于“中国剩余定理”,也称为鬼谷算,还叫隔墙算,或称为韩信点兵等。
“中国剩余定理”是公元5-6世纪、我国南北朝时期的一部著名算术著作《孙子算经》中的一个“物不知数”的解法问题:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。
问物几何?答曰:二十三。
解法后来归结为口诀诗:三人同行七十稀,五树梅花廿一枝,七子团圆月正半,除百零五便得知。
这诗的口诀的解法是:用3除所得的余数乘上70,加上用5除所得余数乘以21,再加上用7除所得的余数乘上15,结果大于105就减去105的倍数,这样就得到所求的数。
如上题解:70×2+21×3+15×2=233, 233-105×2=23但这种解法比较局限,只能是除以3,5,7的,其它的就无法解。
“中国剩余定理”实质是初等数论解一元一次同余式方程组,按小学培优是不定方程组,这对于小学生来讲,无疑过于深奥和复杂。
所以小学涉及到的题目往往比较特殊,因而可以分类使用特殊简单的方法解答。
当然一般复杂的也可使用稍复杂的通解,现整理如下:第一类:余数相同或除数与余数的差相同,那么解答的方法是:除数的公倍数加上相同余数或除数的公倍数减去相同的除数与余数的差。
再根据要求加,减公倍数。
如:题1,一个数在100到200之间,除以3余2,除以5余2,除以7余2,这个数是几?解,最小是2,加上(3,5,7)的公倍数105得2+105=107.题2,一个数一个数在100到200之间,除以3余2,除以5余4,除以7余6,这个数是几?解,3-2,5-4,7-6的差是1,所以(3,5,7)的公倍数105减去1得105-1=104昨天问题解答题:一列队伍中的人数比20多,比30少。
按1,2,3,4报数,最后一个人报3,按1,2,3报数,最后一个人报2。
这列队伍的人数是多少?解,差是1,在20到30之间,4和3的公倍数24减1 得24-1=23第二类,部分同第一类,分两步,先按第一类解答出第一步,在试算出第二步。
中国剩余定理求解同余方程组

中国剩余定理求解同余方程组
中国剩余定理是一种求解同余方程组的方法,它可以将一个方程组转化为一个等价的方程,从而简化计算。
具体来说,如果我们有以下同余方程组:
x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
…
x ≡ an (mod mn)
其中m1、m2、…、mn是两两互质的正整数,那么中国剩余定理告诉我们,存在一个唯一的解x,满足0 ≤ x < M = m1 × m2 ×…× mn,并且这个解可以通过以下方式求出:
1. 计算M1 = M/m1, M2 = M/m2, …, Mn = M/mn。
2. 对于每个i,计算Mi的逆元ti(即满足Mi ti ≡ 1 (mod mi)的ti),可以使用扩展欧几里得算法求出。
3. 计算x = a1 M1 t1 + a2 M2 t2 + … + an Mn tn (mod M)。
这个方法的时间复杂度为O(nlogM),其中logM是M的位数。
因此,当n较小而M较大时,中国剩余定理比较适用。
需要注意的是,如果m1、m2、…、mn不两两互质,那么这个方程组可能无解,或者有多个解。
此时,我们需要先对方程组进行合并,得到一个两两互质的方程组,再使用中国剩余定理求解。
- 1 -。
中国剩余定理的算术解法

中国剩余定理的算术解法中国剩余定理是一个重要的数论概念,它可以用来解决线性同余方程。
它指出了一些模数之间的问题,它可以使用算术方法来解决。
它的原理是,假设有一个整数的线性关系,其中的系数和常数均为非负整数,那么可以利用中国剩余定理来解决这一问题。
中国剩余定理是中国古代数学家张丘建提出的,它有着源远流长的历史。
用中文说,中国剩余定理是求模n个同余方程组的解法。
它与求解一般方程的方法是不同的,它可以将一般方程转化为一个模n 意义上的线性同余方程组。
系数和常数均为非负整数,然后求解该方程,可以求出这个线性方程的整数解。
用中国剩余定理解决线性同余方程的算术解法,有三个基本步骤:1、将原线性方程转化为模n意义上的线性同余方程组。
2、使用中国剩余定理,求出该同余方程组的解。
3、将解代入原方程,求出原方程的解。
下面将详细说明如何使用中国剩余定理来解决线性同余方程。
首先,将原线性方程转化为模n意义上的线性同余方程组。
假设原方程为:a1x1 + a2x2 + a3x3 + ... + anxn = b (mod n)首先,我们必须取一个大于等于m的n,使得ai和b都为n的整数倍数。
然后再将原方程化为:(a1/n)x1 + (a2/n)x2 + (a3/n)x3 + ... + (an/n)xn = b/n (mod n)将原方程转换为模n的同余方程组,就完成了第一步。
第二步,使用中国剩余定理来求出该同余方程组的解。
中国剩余定理的公式如下:x1 = (a1b1 + a2b2 + a3b3 + ... + anbn) mod n因此,模n的同余方程组的解为:x1 = (a1b1 + a2b2 + a3b3 + ... + anbn) mod nx2 = (a1b2 + a2b3 + a3b4 + ... + anbn-1) mod nx3 = (a1b3 + a2b4 + a3b5 + ... + anbn-2) mod n......xn = (a1bn + a2bn-1 + a3bn-2 + ... + ann-1) mod n 完成了第二步。
中国剩余定理例题讲解2
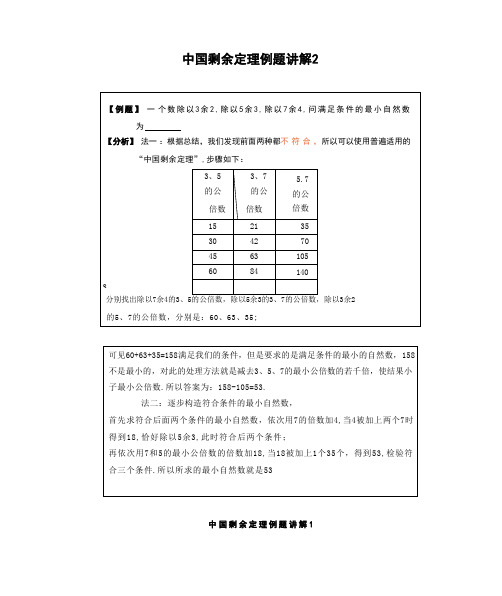
【例题】一个数除以3余2,除以5余3,除以7余4,问满足条件的最小自然数
为
【分析】法一:根据总结,我们发现前面两种都不符合,所以可以使用普遍适用的
“中国剩余定理”,步骤如下:
Q
3、5
的公
倍数
3、7
的公
倍数
5.7的公
倍数
15
21
35
30
42
70
45
63
105
60
84
140
分别找出除以7余4的3、5的公倍数,除以5余3的3、7的公倍数,除以3余2
代,数学家程大位把这个问题的算法编成了四句歌诀:
三人同行七十稀,
五树梅花廿一枝;
O
七子团圆正半月,
除百零五便得知,
用现在的话来说就是:一个数用3除,除得的余数乘70;用5除,除得的余数乘21;用7除,除得的余数乘15.最后把这些乘积加起来再减去105的倍数,算法是;
11除余7,由于[3,5,11]=165,所以这个数最小是165+7=172.
法二:事实上,如果没有“大于10”这个条件,7即可符合条件,所以只需要在7的
基础上加上3、5、11的最小公倍数,得到172即为所求的数.
什么是中国剩余定理?
“物不知数问题”一般解题步骤:
o
①凑“多”相同,即把余数处理成相同条件;余数与除数的和相同
不相互影响各自被对应除数除后所得的余数,
即70a+213+15c是被3除余a,被5除余b,被7除余c的数,
得到18,恰好除以5余3,此时符合后两个条件;
再依次用7和5的最小公倍数的倍数加18,当18被加上1个35个,得到53,检验符
江苏事业单位考试:数量关系之中国剩余定理

江苏事业单位考试:数量关系之中国剩余定理在事业单位备考到来之季,中公事业单位考试网为帮助考生更好的备考行测考试,特意准备了2016年行测答题技巧《数量关系之中国剩余定理》,助力考生顺利通过事业单位行测考试。
近期各省事业单位招聘进行得轰轰烈烈,在事业单位行测考试中,数量关系部分一直是考试中考生认为最难的一个部分,通常把它放在最后去做,或者干脆全蒙B,然而,数量关系部分分值较高,要想在行测拿到不错的分数,数量关系的分数是必不可少的。
因此,对于数量部分比较容易能够拿分的题目我们依然要尽可能学会,保证数量不拉分。
我们今天就来给大家分享一个较为简单的题型,关于我们的中国剩余定理。
一、题型特征已知X÷A……a,X÷B……b,X÷C……c,……求X是多少?二、求解方法(1) 余同加余X÷3......2 X÷4 (2)余数相同,则X=除数公倍数+余数,即X=12N+2(2) 和同加和X÷3......2 X÷4 (1)除数和余数的和相同(都是5),则X=除数公倍数+和(除数与余数的和),即X=12N+5(3) 差同减差X÷3......2 X÷4 (3)除数与余数的差相同(都是1),则X=除数公倍数-差(除数和余数的差),即X=12N-1(4) 逐步满足当余数、和、差都不相同,需要逐个尝试,从除数最大的开始满足。
X÷3……1 × √X÷4……2 6 10即符合条件的最小整数是10,则X=除数公倍数+最小满足数,即X=12N+10三、真题演练【真题演练】幼儿园组织小朋友列队,每列三每列五人也多2人,且幼儿园小朋友有不到50人,求小朋友最多有多少个?A.32B.49C.47D.45【答案】C。
根据题干分析可知,幼儿园小朋友人数除以3余2,除以5余2,属于中国剩余定理考核,而且余数相同,则考虑余同加余,所以人数=15n+2,由于不到50人,又要尽可能大,则最大是n=3,即共有47人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【问题】有1个数,除以7余2.除以8余4,除以9余3,这个数至少是多少?
这种问题称为“中国剩余定理”问题。
我一般用两种方法解决这类问题。
第一种是逐步满足法,方法麻烦一点,但适合所有这类题目。
第二种是最小共倍法,方法简单,但只适合特殊类型的题目。
还有“中国剩余定理”的方法,但它不完善且解法较为复杂,普及应用有一定难度,还不稳定。
所以一般不用。
下面分别介绍一下常用的两种方法。
通用的方法:逐步满足法
【问题】一个数,除以5余1,除以3余2。
问这个数最小是多少?
把除以5余1的数从小到大排列:1,6,11,16,21,26,……
然后从小到大找除以3余2的,发现最小的是11.
所以11就是所求的数。
先满足一个条件,再满足另一个条件,所以称之为“逐步满足法”。
好多数学题目都可以用逐步满足的思想解决。
特殊的方法:最小公倍法
情况一
【问题】一个数除以5余1,除以3也余1。
问这个数最小是多少?(1除外)
除以5余1:说明这个数减去1后是5的倍数。
除以3余1:说明这个数减去1后也是3的倍数。
所以,这个数减去1后是3和5的公倍数。
要求最小,所以这个数减去1后就是3和5的最小公倍数。
即这个数减去1后是15,所以这个数是15+1=16.
情况二
【问题】一个数除以5余4,除以3余2。
问这个数最小是多少?
这种情况也可以用特殊法。
数除以5余4,说明这个数加上1后是5的倍数。
数除以3余2,说明这个数加上1后也是3的倍数。
所以,这个数加上1后是3和5的公倍数。
要求最小,所以这个数加上1后就是3和5的最小公倍数。
即这个数加上1后是15,所以这个数是15-1=14.
多个数的,比如3个数的,有时候其中两个可以用特殊法,那就先用特殊法,用特殊法求出满足两个条件的数后再用通用的方法求满足最后一个条件的数。
所以有时候特殊法和通用法混合使用。
在使用的过程中如果能灵活运用余数问题的技巧,会非常有利于解题。
我们接下来分析最开始的那个问题。
【问题】有1个数,除以7余2.除以8余4,除以9余3,这个数至少是多少?
这道题目不能用特殊法,我们用通用法,解题过程中注意余数知识的运用。
除以7余2的数可以写成7n+2。
7n+2这样的数除以8余4,由于2除以8余2,所以要求7n除以8余2。
(余数知识)
7n除以8余2,7除以8余7,要求n除以8余6(余数知识),则n最小取6。
所以满足“除以7余2,除以8余4”的最小的数是7×6+2=44.
所有满足“除以7余2,除以8余4”的数都可以写成44+56×m。
(想想为什么?)
要求44+56×m除以9余3,由于44除以9余8,所以要求56×m除以9余4。
(余数知识)
56×m除以9余4,由于56除以9余2,所以要求m除以9余2(余数知识),则m最小取2。
所以满足“除以7余2,除以8余4,除以9余3”的最小的数是44+56×2=156.。
