神奇万能截位法破解资料分析计算难题
公务员考试“行测“考试技巧《资料分析—截位直除》

公务员考试“申论”考试技巧《资料分析-截位直除》
在计算比值型,具体数值的时候,截位直除是最强大的办法,只是不适用计算增量,要算太多数据了,在大小比较中,截位直除是最笨的办法,完全用不到。
要点1:分子不截位,分母截三位,已经能保证千分级的误差,在99.9%的题型中都适用,还有一种不适用的是:选项误差大概在3%以内,而且分母是4位数,这种题型明显是在考除法。
要点2,3256/3568,中写成3256/357,在3256/3657中,写成3256/365,正确的思维是后面的不管什么数都截掉,看到8 9就给它进一位,在“考虑要不要进一位”这是思维,本身就是浪费思维。
公务员备考:资料分析技巧之加减截位法

国家公务员| 事业单位 | 村官 | 选调生 | 教师招聘 | 银行招聘 | 信用社 | 乡镇公务员| 各省公务员|政法干警 | 招警 | 军转干 | 党政公选 | 法检系统 | 路转税 | 社会工作师 公务员备考: 资料分析技巧之加减截位法奇偶特性,好多考生应该在数学运算中听说过,其实在数字推理中,有时候遇到无从下手的题目时,也可以利用奇偶法来巧妙的猜答案,幸运的话可能直接猜对,即便不幸运,也可以排除掉两个选项,提高猜对的概率。
【例1】1,8,21,40,( ),96A. 55B.60C.65D.70【常规解析】本题属于没有明显特征,且数据相差不大的题目,可以考虑做差,两两做差得:7,13,19,是公差为6的等差数列,故下一项的差为19+6=25,因此括号中卫40+25=65,因此,本题答案为C 。
【提分小技巧】因为数列的奇偶规律比较明显,奇偶相间,故()中应为奇数,可以排除B 和D 。
剩下两个选项,代入看大致的趋势,代入A.55,则原数列变为1,8,21,40,(55),96,此时明显55影响了整个数列的趋势,21与40相差19,40与55只相差15,而55又与96相差太多,故排除A ,因此本题答案为C 。
【例2】(2011河北)2,3,4,9,32,( )A. 47B.83C.128D.279【常规解析】整体趋势递增,且后面增长的比较快,考虑递推积,4*9-4=32,验证前者,3*4-3=9.故可以推出()=9*32-9=279,因此本题答案为D 选项。
【提分小技巧】因为数列奇偶规律比较明显,偶奇相间,故()中应该为奇数,排除选项C ,剩下A 、B 、D 。
再根据数列整体趋势,从9直接到32,后面变化比较快,故答案不可能为47与83,因此本题答案为D 选项。
最后,唐山华图提示大家,要想获得更多资料和考试信息,关注唐山华图官网(/)。
行政职业能力测试 资料分析截位法在资料分析中的巧妙应用

截位法在资料分析中的应用(一)16927*55.6%/1237 A.6.7 B.7.0 C.7.6 D.12.7计算详析:16927 * 5/9 *8 = 4 * 16927/9=4*17/9=68/9=7又5/9=7555 ( 5*8=40 这里0就忽略了。
) 把556 看成5555,即5/9 把1237 看成1250 即1/8 除以1/8 就是乘以8了。
把16927 看成17000 算出来的结果是7555。
我们看选项,ABC都是从第二位开始变化,且变化幅度较小,(尤其跟算出结果相近的BC 选项差得比较大),D差得更大。
而我们的取值是从第三位变化,且变化很小。
不可能对第二位产生多到那么大的差距。
所以我们可以大胆地选C7.6 整个过程口算可以搞定。
关键是要记住一些常见的分数,比如1/8=0。
125 1/9=0。
111 而5/9=0。
555(2007年天津上半年资料第二大题)3.2004年中环企业利润减幅比2005年多几个百分点? A.2.12个百分点 B.1.86个百分点C.1.59个百分点 D.1.38个百分点列式为:(38.6-35.6)/38.6 -(35.6-33.4)/35.63/386 - 2.2/356 求其差。
其接算的话是很麻烦的。
7772-6179=1593 这是用计算机算出来的结果。
手算的话显得有点繁琐。
如果用截位法该怎么算呢?3/386 - 2.2/356=356 386 只第二位不同,用截位法原理很好统一分母。
以小一点的数为基准,变化:22/356= ?/386分母左二加3,356 约是22的1.5倍多一点,(22+11=33)那么分子左二应该加3/1.5多=2小一点,为方便计算就取2,因此:22/356=24/3563/386-2.4/386=6/386=3/192>3/2=1.5提示:在除法过程中不断进行约分,是一个好办法,可以简化计算,如果约为1-11 的分母,就非常好算了。
行测技巧:直除-截位法

行测技巧:直除-截位法资料分析题目一直是公务员考试里面的重点,分值较大,题目简单,但是资料分析也是令大部分人头疼的题目:数据繁多,计算复杂。
而资料分析中的计算题绝大多数是不需要精算的,只要能够在四个备选答案中选出正确的答案即可。
所以,合理地运用计算技巧,对于提高计算速度、快速完成资料分析意义重大。
在这里,华图教育资深专家给大家讲解三种常用到的速算技巧。
【速算技巧二:直除-截位法】“直除法”是指在比较或者计算较复杂分数时,通过“直接相除”的方式得到商的首位(首一位或首两位),从而得出正确答案的速算方式。
“直除法”在资料分析的速算当中有非常广泛的用途,并且由于其“方式简单”而具有“极易操作”性。
“直除法”从题型上一般包括两种形式:一、比较多个分数时,在量级相当的情况下,首位最大/小的数为最大/小数;二、计算一个分数时,在选项首位不同的情况下,通过计算首位便可选出正确答案。
截位标准:首位不同,截两位;首位相同,第二位不同截两到三位(特别提示:被除数保持不变,除数四舍五入取前两位,结果取前两位)“直除法”从难度深浅上来讲一般分为三种梯度:一、简单直接能看出商的首位;二、通过动手计算能看出商的首位;三、某些比较复杂的分数,需要计算分数的“倒数”的首位来判定答案。
【例1】“十一五”期间,我国农村居民人均纯收入由2005年的3255元提高到2010年的5919元,增加2664元。
2010年农村居民的工资性收入人均2431元,比2005年增加1257元,增长1.1倍,年均增长15.7%。
”“十一五”期间,我国农村居民人均工资性收入的增加值对农村居民人均纯收入增加的贡献率约为:( )A.37.1%B.43.6%C.47.2%D.50.4%【解析】本题是部分增长贡献率的考查。
部分增长贡献率=该部分的量/总量的增量,列式子是1257/2664,通过直除法可以判定首位商4,观察四个选项,只有C选项首位数字是4,故答案是C 选项。
截位法原理 与 在资料分析中的巧妙应用

本帖作者zhouming801221(神算老周)于2012.12.14日修正。
纠正了原作中因为文字编辑问题而产生的两处位置没有对齐的错误.老周更多力作陆续发布,敬请关注QZZN行测各版。
所谓截位法,就是把多位数乘除法截成个位,或较少位的乘除,从而达到简化计算目的的一种方法。
在公务员考试的资料分析中大有用武之地!截位法具体如何计算,以前我曾发过帖作过详细的截位示例说明(本论坛帖名:神奇截位法解决资料分析计算难题),但一直未将截位法的原理作一个解释,让一些朋友心里没底,不知道这样算可不可以,准不准?那么今天我就将截位法的原理,和在资料分析中的一些应用作一个说明,希望能给大家带来一点有益的启示。
我们先从简单说起:比如:804/402=我们把分母402 变成400;然后804相应地调整,变成800,这样就变成800/400=8/4=2 ,这样分母变成个位数,计算起来就简单了。
当然,这个式子是很简单的,我们一眼就能看出是2。
资料分析的题目一般不会这么简单。
我们试举一例:8432.16/4196.38=选项:2108 2019 2009 2003我们可用截位法4196.38 变成4200,这样分母只有二位(不包括0),计算起来就简单多了。
对除法而言,分母位数越少,计算越简单。
因此,除法我们尽量把分母变短。
经过可口算的截位处理,我们把原式可变为:844/42=422/21=20095 跟C选项很相近,故选C。
(截位法的误差分析以后我有机会再跟大家交流。
)那具体我们是如何截位处理的呢?资料分析题,在计算前一定要看一下选项,不要一上来就列式计算,要根据选项的差别大少,决定是估算,还是截位粗算,截位精算,或者是精度要求十分高,选择直接算。
此题我们看选项,CD,差得近,差别到左边第四位了,那么我们截位取值至少要截到左四,有的要截到左五。
这题的话结果首位2,比分子分母4,8都要少,截到四位就够了。
(具体如何这样,以后有机会跟大家详解,这里只略说一下)8432.16/4196.38=第一步:四舍五入取左四位变为:8432/4196第二步:计算分子分母大致倍数。
神奇万能截位法破解资料分析计算难题

神奇万能截位法破解资料分析计算难题(原创)相信很多朋友跟我一样,对资料分析多位数的乘除法很感头痛。
我通过学习,研究在李委明老师介绍的截位法的基础上,总结出一种能够大大简化计算的截位方法,相信大家熟练掌握,在做题中多次运用后,一定会加快计算速度,不再对资料分析计算题望而生畏。
通过截位法,把多位数除法变为多位/二位甚至一位的除法,通过简单口算就得到结果,避免了繁琐的除法计算。
我先介绍多位数除法化为多位/二位的方法。
然后再深一步介绍把多位数除法,变为多位/一位的方法。
比如:45869/1236 -》36669/1000 到此可直接口算出结果先介绍截成二位的乘除法。
比如8422.15/2122.36 变为:8340/2100=3.9714万能截位法(一般可精确到左数第二位。
)一,计算倍数二,截分母:确定先截哪个。
除法要截分母。
先把多位数分母,四舍五入取左三位,然后截去左数第三位,分母变为2位。
分母位数减少可大大简化计算过程。
三,根据倍数关系和开始所截的数确定另一个数的截位数先计算二数的倍数,然后根据倍数确定同时加或减的数.比如8422.15/2122.36 二者倍数约是4分母四舍五入取左三位得212,然后把左三位的2截去,变为210如果分子变为21,那么分母的左三位应该减2*4 即83408340/2100=3.9714如果分母变为8400 那么分子减2/4,不到1忽略不计. 这里834后面的215,也可照写。
分子后面为0,或其它数字对计算难度影响不大。
8400/2120=3.9623实际结果为84122.15/2122.36=3.9636误差很少.如果二数首位差很近,比如3412/2658 就可同时截位.如:345/27 第三位同时加4本质跟李委明老师讲的是一样的。
根据倍数同时加减,比如是二数相除,就是使分子分母扩大或缩少的的百分比相近。
如4512/1124 分子大约是分母的4倍。
如果把分母变为1100 分母就应在同位减去4×2=8 变为443分母缩小了:2/112=178/10000分子缩小了:8/451 =177/10000可知这样做误差很少。
国家公务员考试资料分析速算技巧

1、什么是截位?资料分析中,做题的最后一步就是要进行计算。
一般资料分析中的数据都比较大,如果按照常规方法计算,将会消耗大量的时间,因此如何提高资料分析的计算速度就成为拿下资料分析的关键,下面简单梳理一下资料分析中常用的速算技巧。
一、截位直除例:58724国家公务员考试资料分析速算技巧截位就是从左往右四舍五入保留若干位有效数字。
5①截2位:59②截3位:5872、何为有效数字?从左往右的第一位非0的数字。
例:0.34287①截2位:34②截3位:343例3、如何截位?看选项:选项差距大截2位;选项差距小截3位。
4、如何判断选项差距大小?(1)选项差距大:a.选项首位各不相同;b.选项首位有相同,最接近两项的次位差>首位。
(2)选项差距小:选项首位有相同,最接近两项的次位差≤首位。
:1 A.11 B.21 C.31 D.41(选项首位各不相同,选项差距大)②A.11 B.21 C.25 D.41(B 、C 首位相同,次位差=5-1=4>2,次位差>首位,选项差距大)③A.11 B.21 C.23 D.41(B 、C 首位相同,次位差=3-1=2,次位差=首位,选项差距小)④A.21 B.22 C.25 D.29(四项首位相同,A 、B 次位最接近,次位差=2-1=1<2,次位差<首位,选项差距小。
)5、截谁?(1)一步除法(A B 例:3617.211+19.3),分子不动,只截分母;%,若选项差距大且位数相同,则分母截取2位,此式可以直接看成3617.2112,如果只有一个3开头的选项,则直接选该选项;若有两个3开头的选项,继续除看第2位商几,最接近的选项即为正确答案。
(2)多步计算(A B÷C、A B×C、A B÷C D、A B×C D),分子、分母都截位。
例:177781+18.9%÷512002.451+51.8%,若选项差距大且位数相同,此式可以直接看成1812÷5115 1812×1551,分子分母先约分:1812×1551 32×517 1534,再结合选项首位或次位进一步计算得出正确选项。
2018.09.29 2019国考资料分析:大数求和的技巧
2019国考资料分析:大数求和的技巧京佳教育在资料分析的各类型考题中,涉及到大数求和的题目屡有出现,对于该类试题我们只有掌握了其速算技巧才能既快又稳地解题。
在此,京佳教育崔老师就资料分析命题中的大数求和考点进行剖析,望能够给予广大考生以帮助。
一、基本概念阐述大数求和,即命题让求多个数据的和;由于数据较多,如果直接相加则计算繁琐,此时我们可以采取以下两个方法来解决:(1)截位法,即对所有数据进行截位处理,从个位数开始截掉相同的位数,并且四舍五入,将剩余部分进行处理,如:14033+20918,可以处理为(14+21),这样计算就比较便捷;(2)若涉及求平均数,可结合选项折中处理,具体见后面例题解析。
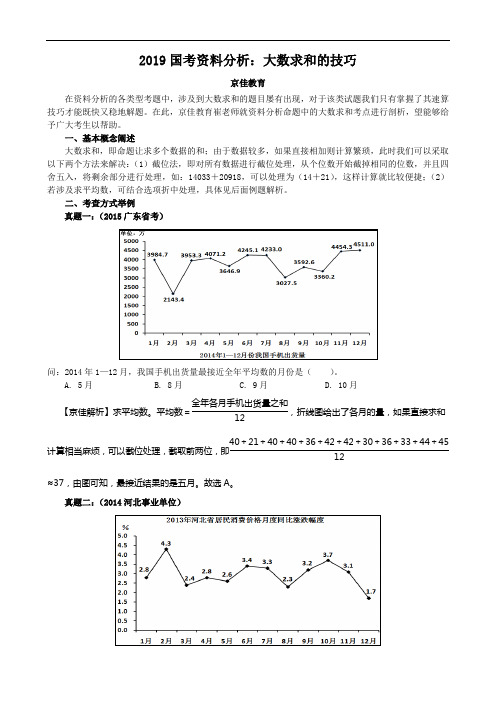
二、考查方式举例真题一:(2015广东省考)问:2014年1—12月,我国手机出货量最接近全年平均数的月份是( )。
A. 5月B. 8月C. 9月D. 10月【京佳解析】求平均数。
平均数=全年各月手机出货量之和12,折线图给出了各月的量,如果直接求和计算相当麻烦,可以截位处理,截取前两位,即40+21+40+40+36+42+42+30+36+33+44+4512≈37,由图可知,最接近结果的是五月。
故选A 。
真题二:(2014河北事业单位)问:2013年河北省居民消费价格月度同比平均涨跌幅度是( )。
A. 2.97%B. 3.02%C. 3.17%D. 3.2%【京佳解析】常规解法:求平均数。
锁定图形数据,先将12个月的同比涨幅求和,再除以12,得出平均涨跌幅度,即:(2.8+4.3+2.4+2.8+2.6+3.4+3.3+2.3+3.2+3.7+3.1+1.7)÷12≈2.97%。
故选A。
折中处理:上述解法计算过程较为复杂,我们可以通过借助选项的办法快速求解;选项中只有A项小于3%,我们将12个月的同比涨幅按照大小顺序排序得:4.3、3.7、3.4、3.3、3.2、3.1、2.8、2.8、2.6、2.4、2.3、1.7,第一项和倒数第一项相加(第二项和倒数第二项相加,依次类推),要么等于6,要么小于6,即平均后的值一定小于3,只能选择A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神奇万能截位法破解资料分析计算难题(原创)
相信很多朋友跟我一样,对资料分析多位数的乘除法很感头痛。
我通过学习,研究在李委明老师介绍的截位法的基础上,总结出一种能够大大简化计算的截位方法,相信大家熟练掌握,在做题中多次运用后,一定会加快计算速度,不再对资料分析计算题望而生畏。
通过截位法,把多位数除法变为多位/二位甚至一位的除法,通过简单口算就得到结果,避免了繁琐的除法计算。
我先介绍多位数除法化为多位/二位的方法。
然后再深一步介绍把多位数除法,变为多位/一位的方法。
比如:45869/1236 -》36669/1000 到此可直接口算出结果
先介绍截成二位的乘除法。
比如8422.15/2122.36 变为:8340/2100=3.9714
万能截位法(一般可精确到左数第二位。
)
一,计算倍数
二,截分母:确定先截哪个。
除法要截分母。
先把多位数分母,四舍五入取左三位,然后截去左数第三位,分母变为2位。
分母位数减少可大大简化计算过程。
三,根据倍数关系和开始所截的数确定另一个数的截位数
先计算二数的倍数,然后根据倍数确定同时加或减的数.
比如8422.15/2122.36 二者倍数约是4
分母四舍五入取左三位得212,然后把左三位的2截去,变为210
如果分子变为21,那么分母的左三位应该减2*4 即8340
8340/2100=3.9714
如果分母变为8400 那么分子减2/4,不到1忽略不计. 这里834后面的215,也可照写。
分子后面为0,或其它数字对计算难度影响不大。
8400/2120=3.9623
实际结果为84122.15/2122.36=3.9636
误差很少.
如果二数首位差很近,比如3412/2658 就可同时截位.
如:345/27 第三位同时加4
本质跟李委明老师讲的是一样的。
根据倍数同时加减,比如是二数相除,就是使分子分母扩大或缩少的的百分比相近。
如4512/1124 分子大约是分母的4倍。
如果把分母变为1100 分母就应在同位减去4×2=8 变为443
分母缩小了:2/112=178/10000
分子缩小了:8/451 =177/10000
可知这样做误差很少。
关键在于准确计算倍数。
本质原理就是使分子分母缩少的百分比是一样的。
例如:8562/3276 =2.614
倍数是2倍多一点,3倍少一点。
这种情况可估计为2.5倍
分母变为33 00 左边第三位加3
分子变为: 左边第三位加3×2.5=约等于7 即8630/33=2.615
能有效减少误差。
•博主回复:2010-08-22 20:57:21
你理解得非常到位!建议你以后计算就按这
•李大师,您说的zhouming19801221这位同学的思路,是否也可以用在乘法上面呢?
比如:123.5*251.6
25/12约为2
第三位变化
123.5251.6
↓3↑3*2=6
估算为:120*257
与除法区别在于,乘法一个升,另一个就按一定幅度降
可行么?
博主回复:2010-09-01 16:45:24
非常可行!
•李老师,前段时间我恰好也在考虑截位法的问题,如何才能计算更
精确?我发现,如果二个数最高位差不多大少,比如4871.12/34.25 3和4相差不大,那同时从左边三位开始截位,误差很少.4850/34.0=142.647
实际结果为:142.222
但是如果二数相差较大,那就需要一个数加倍或者减倍
比如:8256.25/2015.32
二数的首位数相差3倍,
如果2015.32截为200,那么8256.25缩少的数就要扩大四倍,即821 821/200=4.105
实际结果为4.097
比同时截一样的数:4.12更精确.
如果截大数的话,就可如此截:
8256.25/2015.32 820/200=4.1 即少数应该截5/4,这里就截1
与实际结果4.097误差很少.
李老师,对这种二数首位相差大的数,我觉得从大数截起,比较好算一点.大数最大可以是截5, 少数则只要截5/4 即1左右.
如果相差倍数较大,少数要截位的数可以保持不变.只要截大数就行了. 比如:9265.23/2215.76=4.1815 截为927/221 =4.1945 少数不变,误差也不大.
当然如果更精确一点,少数加4/4=1 927/222=4.1757
李老师,不知道我对截位法的这种理解对不对?资料分析题中如果用这种方法减少误差,能不能正确地确定选项.
博主回复:2010-08-17 10:40:25
你的理解非常的正确,但建议你好好把我的这几篇文章读一下,读完之后就会发现里面的理论根据了。
(以上文字从我发的帖中复制过来,未再加整理,有不理解的请问我。
)
化解除法难题的截位法
截位法应用:把任意二个多位数相除,化为:多位数/个位数的形式步骤:
一,计算分子分母倍数关系。
二,四舍五入取分母左三位,然后把分母左二三位截去
三,按照倍数关系相应地变化分子
四,口算出结果
五,根据分母四舍五入时的误差,相应地调整结果。
比如:45869/1236
我们这里说的倍数关系不看位数,比如这里分子五位,分母四位,计算出来的倍数不是40倍,而是4倍。
1. 计算倍数的方法:分子分母都四舍五入取左二位,比如这里取46/12
那么我们计算倍数关系就是4倍,少4*12-46/12=1/6 .因为我们截位的幅度较大,所以一定要准确计算倍数,这个1/6一定要算出来,这样才能准确控制误差。
2.分母四舍五入取左三位,得124。
我们把24截掉,分母变为1000
3.分母减少24,那么分子相应的倍数应该减少24*4-24*1/6=92.也就是分母的左二三位送去92,458-92=366 把后面的69添到后面,得36669
4.口算出结果:36669/1000=36.669
5.不可忽略的一步:对结果左三位做调整。
我们刚才分母1236变为1240时,把分母变大了。
尤其要注意的是当分母是1,2开头的数,尤其是1开头的数时,截位时产生的误差相应较大。
为什么呢?比如1236 变为1240 增多了4/1236,而如果是9236变为9240 增多仅4/9236。
所以我们这里把1236截成3位时相应地产生了一些误差。
那么计算出结果后,就可在结果的左三位加一个数字。
结果开头的数越大,加减的幅度越大,比如这里36669以3开关,那么就应该比结果是16669开头,调整的幅度要大。
我们在这里给它左三位加3或4,变成36969,或37069。
这就是最后结果
这里有一句口诀:
分母实际取数,比原数取得大,所得结果要增加;
分母实际取数,比原数取得小,所得结果要减少。
比如:1240比实际的1236取得要大,结果要加。
截位法结果:36.969
实际结果 37.11
实际上我们这样算出的结果,只是左三位比实际结果差不到2,这个误差是很小的。
在资料分析题中完全够用了。
这还是因为分母是1开关的数,如果分母的基数较大,误差会控制得更少。
再举一例:
28459/65328
这里跟上题不一样,分母基数6比分子基数2要大,那还是一样的计算倍数,只是变化分子时,要用除法。
1. 28 和65 28*2+11=65 2倍,多11/28 ,变为1/N的形式,即1/2,稍大。
即分母是分子的
2.5倍稍大一点
2. 取653 ,比实际减少一点。
53+47=100,所以分母左二三位加47,变为70000
3.变化分子53/2.5多=20 。
53/2.5>50/2.5=20 可知结果要比20稍大。
如果这里分母看作2.5,比原数少一点,那结果要减少一点,那么20多
点,再减少一点,我们就取20。
分母左二三位加20,得30459
4.30459/7=4351
5.分母6530比原分母6533减少了3/6533左右,这个误差对结果的影响是很少的。
那么我们可以忽略不计。
还取原结果:
截位结果:4351
实际结果:4356
我们看到结果精确到了左三位,相当准确了。
应当注意的一点:当分母是1开关的数时,截位时要分外小心,严格控制误差。
比如刚才1236,变为1240 开关的基数小,后面要加的4又相对较大一点,那么就要适当调整算出后的结果。
