七年级数学竞赛试题精选(七)
初一数学奥数竞赛题

初一数学奥数竞赛题近年来,数学奥数竞赛在中小学生中越来越受欢迎。
这些竞赛要求学生具备扎实的数学基础知识和灵活的解题能力,提高他们的逻辑思维和问题解决能力。
今天,我们来看几个适合初一学生的数学奥数竞赛题。
题目1:小美在她家门口卖冰淇淋,一支冰淇淋卖5元,两支冰淇淋卖9元。
小美今天一共卖出了30支冰淇淋,她一共赚了多少钱?解析:我们可以设冰淇淋的单价为x元,因为一支冰淇淋卖5元,所以我们可以得到一个方程:5 = x。
两支冰淇淋卖9元,所以我们可以得到另一个方程:9 = 2x。
解这个方程组,我们可以得到x = 4.5。
小美一共卖出30支冰淇淋,所以她赚的总钱数为30 * 4.5 = 135元。
题目2:小明的爸爸今年40岁,小明今年12岁。
假设小明的爸爸每年的年龄都是相同的增长,他几年后的年龄和小明的年龄之和是100岁。
请问那时小明的年龄是多少岁?解析:设小明的爸爸从现在开始每年的年龄增长为x岁。
那么,小明几年后的年龄就是12 + x岁,小明的爸爸几年后的年龄就是40 + x岁。
根据题意,小明几年后的年龄和小明的爸爸几年后的年龄之和是100岁,所以我们可以得到一个方程:(12 + x)+(40 + x)= 100。
解这个方程,我们可以得到x = 18。
所以,几年后小明的年龄就是12 + 18 = 30岁。
题目3:一个长方形花坛周长是20米,其中一条边的长度是4米。
我们要在长方形花坛的周围建一道宽度相等的砖墙,这道砖墙的长度是花坛周长的一半。
问这道砖墙的长度是多少米?解析:设砖墙的宽度为x米,花坛的长度为L米,宽度为W米。
花坛周长是20米,所以我们可以得到一个方程:2L + 2W = 20。
其中一条边的长度是4米,所以我们可以得到另一个方程:2L + W = 4。
将两个方程联立,我们可以解得L = 4,W = 6。
砖墙的长度是花坛周长的一半,所以砖墙的长度是20 / 2 = 10米。
通过解这些数学奥数竞赛题,可以让初一学生锻炼他们的数学思维和解题能力。
七年级数学竞赛试题及答案

七年级数学竞赛试题一、选择题(每小题4分,共40分)1、如果m 是大于1的偶数,那么m 一定小于它的……………………( )A 、相反数B 、倒数C 、绝对值D 、平方2、当x=-2时,37ax bx +-的值为9,则当x=2时,37ax bx +-的值是( )A 、-23B 、-17C 、23D 、17 3、255,344,533,622这四个数中最小的数是………………………( )A. 255B. 344C. 533D. 6224、把14个棱长为1的正方体,在地面上堆叠成如图1所示的立体,然后将露出的表面部分染成红色.那么红色部分的面积为 …………………………….. ( ).A 、21B 、24C 、33D 、375、有理数的大小关系如图2所示,则下列式子中一定成立的是……( )A 、c b a ++>0B 、c b a <+C 、c a c a +=-D 、a c c b ->-6、某商场国庆期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100元(100元可以是现金,也可以是购物券,或二者合计)就送20元购物券,满200元就送40元购物券,依次类推,现有一位顾客第一次就用了16000元购物,并用所得购物券继续购物,那么他购回的商品大约相当于打 ( )A 、9折B 、8.5折C 、8折D 、7.5折7、如果有2005名学生排成一列,按1、2、3、4、3、2、1、2、3、4、3、2、1……的规律报数,那么第2005名学生所报的数是……………………………………………………………… ( )图1 图2A 、1B 、2C 、3D 、48、方程 |x|=ax+1有一负根而无正根, 则a 的取值范围…………( )A. a>-1B. a>1C. a ≥-1D. a ≥19、122-+-++x x x 的最小值是…………………………………( )A. 5B.4C.3D. 210、某动物园有老虎和狮子,老虎的数量是狮子的2倍。
七年级数学竞赛试题(含答案)
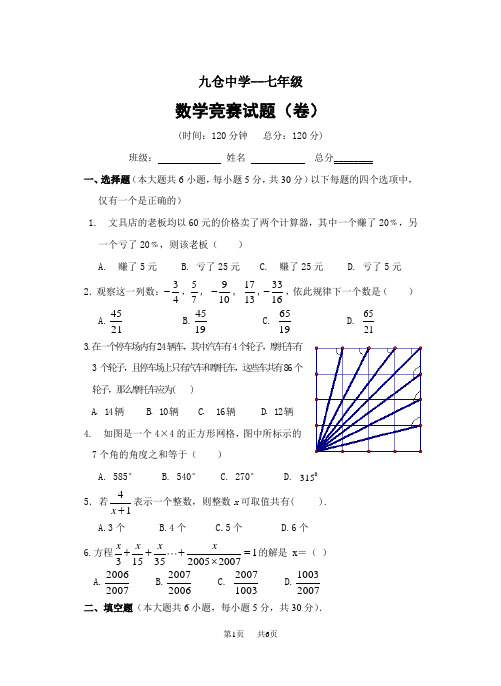
九仓中学--七年级数学竞赛试题(卷)(时间:120分钟 总分:120分)班级: 姓名 总分________一、选择题(本大题共6小题,每小题5分,共30分)以下每题的四个选项中,仅有一个是正确的)1. 文具店的老板均以60元的价格卖了两个计算器,其中一个赚了20﹪,另一个亏了20﹪,则该老板( )A. 赚了5元B. 亏了25元C. 赚了25元D. 亏了5元 2.观察这一列数:34-,57, 910-, 1713,3316-,依此规律下一个数是( ) A.4521 B.4519 C. 6519 D. 65213.在一个停车场内有24辆车,其中汽车有4个轮子,摩托车有3 个轮子,且停车场上只有汽车和摩托车,这些车共有86个轮子,那么摩托车应为( )A . 14辆B . 10辆C . 16辆D . 12辆 4. 如图是一个4×4的正方形网格,图中所标示的7个角的角度之和等于( )A. 585°B. 540°C. 270°D. 0315 5.若14+x 表示一个整数,则整数x 可取值共有( ). A.3个 B.4个 C.5个 D.6个 6.方程13153520052007x x x x +++=⨯的解是 x =( ) A.20072006 B.20062007 C. 10032007 D.10032007二、填空题(本大题共6小题,每小题5分,共30分).7.若|x-y+3|+()21999-+y x =0,则yx yx -+2= . 8. 等腰三角形的一个外角等于0140, 则这个等腰三角形的顶角为___ ____. 9.有一个正方体,在它的各个面上分别标上字母A 、B 、C 、D 、E 、F ,甲、乙、丙三位同学从不同方向去观察其正方体,观察结果如图所示.问:F 的对面是 .10. 用三种边长相等的正多边形铺地面,已选了正方形和正五边形两种,还应选正___边形.11.北京到兰州的铁路之间有25个站台(含北京和兰州),设制 种票才能满足票务需求. 12.设c b a ,,为有理数,则由abcabcc c b b a a +++ 构成的各种数值是 . 三、解答题(本大题共4小题,每小题15分,共60分) 要求:写出推算过程. 13.岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州.据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守.请问,兵力应如何调整?14. 对于有理数x ,y ,定义新运算:x*y=2ax +bx+c ,其中a 、b 、c 是常数,等式右边是通常的加法与乘法运算.已知1*2=9,(-3)*3=6,0*1=2,求2*(-7)的值.5 1 5151 5 115.小明和哥哥在环形跑道上练习长跑。
七年级数学竞赛试题及答案

七年级数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. 2D. -12. 如果一个数的3倍加上5等于这个数的5倍减去9,那么这个数是:A. 3B. 4C. 5D. 63. 一个长方形的长是14厘米,宽是10厘米,那么它的周长是多少厘米?A. 24B. 28C. 48D. 564. 下列哪个分数是最接近0.5的?A. 1/2B. 3/5C. 4/7D. 5/95. 一个数的75%是60,那么这个数是多少?A. 80B. 120C. 160D. 2006. 一个班级有48名学生,其中2/3是男生,那么这个班级有多少名女生?A. 16B. 24C. 32D. 407. 一个数除以3的商加上2等于这个数除以4的商,这个数是多少?A. 6B. 9C. 12D. 158. 下列哪个数是质数?A. 2B. 4C. 6D. 89. 一个长方体的体积是120立方厘米,长是10厘米,宽是6厘米,那么它的高是多少厘米?A. 1B. 2C. 3D. 410. 下列哪个表达式的结果是一个整数?A. (1/2) + (1/3)B. (1/2) + (1/4)C. (1/3) + (1/6)D. (1/4) + (1/5)二、填空题(每题4分,共40分)11. 一个数的1/4加上它的1/2等于______。
12. 如果5个连续的整数的和是45,那么中间的数是______。
13. 一个数的2倍与7的和是35,那么这个数是______。
14. 一个等腰三角形的两个底角都是70度,那么它的顶角是______度。
15. 一本书的价格是35元,如果打8折出售,那么现价是______元。
16. 一辆汽车以每小时60公里的速度行驶,2小时后它行驶了______公里。
17. 一个数的3/4加上它的1/2等于5,那么这个数是______。
18. 一个长方体的长、宽、高分别是8厘米、6厘米和5厘米,那么它的表面积是______平方厘米。
胶州市七年级数学竞赛试题

胶州市七年级数学竞赛试题一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. -1B. 0C. 1D. 22. 如果一个数的平方等于它本身,那么这个数可能是:A. 1B. -1C. 0D. 1或-13. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 零D. 正数或零4. 以下哪个是完全平方数?A. 24B. 25C. 26D. 275. 一个数的立方等于它本身,这个数可能是:A. 1B. 0C. -1D. 1或-16. 一个分数的分子和分母同时乘以或除以同一个不为零的数,分数的值:A. 变大B. 变小C. 不变D. 无法确定7. 一个数的倒数是它本身,这个数只能是:A. 1B. -1C. 0D. 1或-18. 以下哪个数不是有理数?A. πB. √2C. 0.3333...D. 1/39. 若a > b > 0,且c < 0,则下列不等式正确的是:A. ac > bcB. ac < bcC. 不能确定D. 以上都不是10. 一个多项式减去一个单项式,结果可能是:A. 多项式B. 单项式C. 常数D. 多项式或单项式二、填空题(每题4分,共20分)11. 一个数的相反数是-5,这个数是 _______。
12. 如果一个三角形的内角和为180°,那么一个四边形的内角和为_______。
13. 一个数的平方根是4,那么这个数是 _______。
14. 一个数的立方根是-2,那么这个数是 _______。
15. 如果一个分数的分子分母都乘以2,那么这个分数的大小 _______。
三、解答题(每题10分,共50分)16. 计算下列各题,并写出计算过程:a) (-2) × (-3)b) √25c) (-1)^317. 解释什么是有理数和无理数,并给出一个有理数和一个无理数的例子。
18. 说明什么是同类项,并给出一个包含同类项的多项式的例子。
七年级数学竞赛试题(含答案)

七年级数学竞赛试题一、选择题(本大题共5小题,每小题4分,共20分)1.下面四个所给的选项中,能折成如图给定的图形的是( )A .B .C .D . 2.若定义“⊙”:a ⊙b=b a ,如3⊙2=23=8,则3⊙等于( )A .B .8C .D .3.已知x+y=7,xy=10,则3x 2+3y 2=( )A .207B .147C .117D .874.一天有个年轻人来到李老板的店里买了一件礼物,这件礼物成本是18元,标价是21元.结果是这个年轻人掏出100元要买这件礼物.李老板当时没有零钱,用那100元向街坊换了100元的零钱,找给年轻人79元.但是街坊后来发现那100元是假钞,李老板无奈还了街坊100元.现在问题是:李老板在这次交易中到底损失( )A .179元B .97C .100元D .118元5.如图,直线a ∥b ,那么∠x 的度数是( )A .72°B .78°C .108°D .90°二、填空题(本大题共8小题,每小题4分,共32分) 6.若()()1532-+=++mx x n x x ,则m 的值为___________。
7.已知4433553,5,2===c b a ,则a ,b ,c 的大小关系(从小到大排列,用“<”连接)__________________。
8.如果代数式535-++cx bx ax ,当x=﹣2时该式的值是7,那么当x=2时该式的值是__________。
9.若()0862=+++-y y x ,则xy=__________。
10. 如图的号码是由14位数字组成的,每一位数字写在下面的方格中,若任何相邻的三个数字之和都等于14,则x 的值等于__________。
11. 已知多项式162++px x 是完全平方式,则p 的值为___________。
12.己如,△ABC 的面积为1,分别延长AB 、BC 、CA 到D 、E 、F ,使AB=BD ,BC=CE ,CA=AF ,连DE 、EF 、FD ,则△DEF 的面积为___________。
七年级数学竞赛试题(含详细答案)

1.三个质数p ,q ,r 满足p+q=r ,且p<q ,那么p 等于( )A 、2B 、3C 、7D 、132.数a ,b ,c ,d 所对应的点A 、B 、C 、D 在数轴上的位置如图所示,那么a+c与b+d 的大小关系是( )A 、a+c<b+dB 、a+c=b+dC 、a+c>b+dD 、不能确定3.如果有2003名学生排成一列,按1,2,3,4,3,2,1,2,3,4,3,2,。
的规律报数,那么第2003名学生所报的数是( )A 、1B 、2C 、3D 、44.画两条线段,它们除有一个公共点外不再有重叠的部分,在所得图中,设以所画线段的端点以及它们的公共点为端点的线段条数为n ,那么对于各种可能的图形,不同的n 值有( )A 、2个B 、3个C 、4个D 、多于4个5.已知2n -1表示“任意正奇数”,那么表示不大于零的偶数的是( )A 、-2nB 、2(n -1)C 、-2(n+1)D 、-2(n -1)6.用一根长度为11的铅丝折成三段,再首尾相接围成一个等腰三角形,如果要求所围成的等腰三角形的边长都是整数,那么其底边可取的不同长度有( ) A 、2个 B 、3个 C 、4个 D 、5个7.如图,在一个正方体的两个面上画了两条对角线AB ,AC ,那么这两条对角线的夹角等于 度8.小王出门时看了一下家里的时钟是晚上7时多,且时针与分针成直角,过了一段时间回家看了一下时钟仍是晚上7时多,且时针与分针仍成直角,那么小王在外面过了的时间是_______分.9.用写有数字的四张卡片可以排出不同的四位数,其中能被22整除的四位数的和是_____________10.把一根绳子对折后再对折,然后在其一个三等分处剪断,这样变成了________根绳子,其中最长的是最短的长度的________倍11.有31个盒子,每个盒子最多能放5只乒乒球,现取若干只乒乒球往盒里放,那么这些盒子中至少有____________个盒子里的球数相同12.如图,一个大正方形被两条线段分割成两个小正方形和两个长方形,如果S 1=75cm 2,S 2=15cm 2,那么大正方形的面积是S =_____________cm 2. A . D . B . C . O 1 2 3 4 S 4S 1 S 2S 3 第12题13.(本题满分12分)如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.(1) 28和2 012这两个数是神秘数吗?为什么?(2) 设两个连续偶数为2k +2和2k (其中k 取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?(3) 两个连续奇数的平方差(取正数)是神秘数吗?为什么?14.(本题满分14分)将正整数按右表所示的规律排列,并把排在左起第m 列,上起第n行的数记为以a mn ,(1)试用m 表示a m1,用n 表示a 1n 。
七年级(初一)数学竞赛试题及答案

1.若四边形ABCD中,∠A:∠B:∠C:∠D=1:3:5:6,则∠A,∠D的度数分别为()24°,144°2.已知a=255,b=344,c=533,d=622,那么a、b、c、d从小到大的顺序是解:∵a=255=(25)11,b=344=(34)11,c=533=(53)11,53>34>62>25,∴(53)11>(34)11>(62)11>(25)11,即a<d<b<c,3.7..对于有理数x,y,定义一种新的运算“*”:x*y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法与乘法运算,已知3*5=15,4*7=28,求1*1的值.9.已知|a|=3,|b|=2,且|a-b|=b-a,则a+b= -1或-5解:∵|a-b|=b-a,∴知b>a,∵|a|=3,|b|=2,∴a=-3,b=2或-2,当a=-3,b=2时,a+b=-1,当a=-3,b=-2时,a+b=-5,∴a+b=-1或-5,故答案为-1或-5.10.设m2+m-1=0,则m3+2m2+2010=2011∵m2+m-1=0,①∴①×m得,m3+m2-m=0,②∴①+②得,m3+2m2-1=0,即m3+2m2=1,则m3+2m2+2010=1+2010=2011.15.把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内如图,一个啤酒瓶的高度为30cm,瓶中装有高度12cm的水,将瓶盖盖好后倒置,解:设瓶的底面积为Scm,则左图V水=12Scm3,右图V空=10Scm3,∵V瓶=V水+V空=22Scm3,∴V水:V瓶=6:11.如图,长方形ABCD 被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学竞赛试题精选(七)
一、拆分法及应用 例1、 计算:
991
63135115131+
+++。
(第三届华杯赛) 练习:(1)208
1
130170128141+
+++。
(2)
)
2(1641531421311+⨯+⋅⋅⋅⋅⋅⋅+⨯+⨯+⨯+⨯n n 。
(60年上海) (3)2003减去它的
21,再减去(第一次)余下的3
1
,再减去(第二次)余下的41,、、、、、、,依次类推,一直到减去(第2001次)余下的2003
1,问最后余下的是多少?(第六届华杯赛)
(4)计算20022002200320003200032002⨯-⨯。
(第四届迎春杯)
二、错位相减法 例2、比较1234248162
n n n
S =
++++⋅⋅⋅⋅⋅⋅+(n 为任意自然数)与2的大小。
练习:(1)
1231001121311001
2222----+++⋅⋅⋅⋅⋅⋅+。
(2)2
1
512412562561451212102411++⋅⋅⋅⋅⋅⋅+++。
三、观察归纳法 例 3 计算:⎪⎭
⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛+⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝
⎛+9115113111011611411211 (第六届华杯赛)
例4 计算:355
133********
1--
-
-
-
练习:90
1177211556113421113019201712156131++++++++。
(第四届华杯赛)
五、放缩法 例5、已知1991
1
198311982119811198011
+⋅⋅⋅++++=
S ,求 S 的整数部分。
例6、已知下式,求a 的整数部分:
10069
15681467136612651170
156914681367126611⨯⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯+⨯=
a ,问a 的整数部分是
多少? (第二届华杯赛)
六、换元法 例7、计算:
1
1112111311431411958
1958
+++++++
+++
练习:已知2000
19992001
1998,2001199920001998,2001200019991998⨯⨯-
=⨯⨯-=⨯⨯-=C B A 试比较C B A ,,的大小。
七、公式法 例8、计算:⎪⎭
⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛
-
22222200311200211411311211 练习:计算:
.2
20012001
20011999200120002
22
-+
例9、计算:
1993
321993
321543254321432432132321221+⋅⋅⋅+++⋅⋅⋅+++⨯
⋅⋅⋅⨯+++++++⨯+++++⨯+++⨯+。
八、单一数字整数的表示法
例10、已知存在正整数n ,能使数
1
111个n ⋅⋅⋅⋅⋅⋅被1987整除,求证: 7
8
9
1
777888999111个个个个n n n n p ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=,和
7
18
19
11
1777888999111个个个个++++⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n n n n q ,能被1987整除。
