教材所用附录
教材里面的附录 一维黎曼问题的求解编程代码 - 副本

E[2]=(U[2]+p)*u; } /*------------------------------------------------------一维 MacCormack 差分格式求解器 入口: U, 上一时刻的 U 矢量,Uf、Ef,临时变量, dx,网格宽度,dt, 时间步长; 出口: U, 计算得到的当前时刻 U 矢量。 ---------------------------------------------------------*/ void MacCormack_1DSolver(double U[J+2][3],double Uf[J+2][3],double Ef[J+2][3],double dx,double dt) { int i,k; double r,nu,q; r=dt/dx; nu=0.25; for(i=1;i<=J;i++) { q=fabs(fabs(U[i+1][0]-U[i][0])-fabs(U[i][0]-U[i-1][0])) /(fabs(U[i+1][0]-U[i][0])+fabs(U[i][0]-U[i-1][0])+1e-100); //开关函数 for(k=0;k<3;k++) Ef[i][k]=U[i][k]+0.5*nu*q*(U[i+1][k]-2*U[i][k]+U[i-1][k]);//人工黏性项 } for(k=0;k<3;k++) for(i=1;i<=J;i++)U[i][k]=Ef[i][k]; for(i=0;i<=J+1;i++)U2E(U[i],Ef[i]); for(i=0;i<=J;i++) for(k=0;k<3;k++) Uf[i][k]=U[i][k]-r*(Ef[i+1][k]-Ef[i][k]); //U(n+1/2)(i+1/2) for(i=0;i<=J;i++)U2E(Uf[i],Ef[i]); //E(n+1/2)(i+1/2) for(i=1;i<=J;i++) for(k=0;k<3;k++) U[i][k]=0.5*(U[i][k]+Uf[i][k])-0.5*r*(Ef[i][k]-Ef[i-1][k]); //U(n+1)(i) } /*------------------------------------------------------输出结果, 用 Origin 数据格式画图
高等数学教材附录部分内容

高等数学教材附录部分内容附:常用数学符号表本附录为高等数学教材的附带部分,旨在为读者提供常用的数学符号表,方便理解和应用高等数学中的概念和表达方式。
以下是一些常见的数学符号及其含义:1. 数学符号① Σ(Sigma): 表示求和,常用于表示一系列数的和。
例子:1 + 2 + 3 + ... + n可用Σ表示为∑(i=1 to n) i。
② ∫(Integral): 表示积分,常用于表示求函数在某一区间上的面积或变化率。
例子:对于函数f(x),在区间[a,b]上的积分可以表示为∫(a to b) f(x) dx。
③ Δ(Delta): 表示差分或增量,常用于表示两个数或量之间的变化。
例子:△x表示x的增量,△y表示y的增量。
④ θ(Theta): 表示角度,常用于表示平面或空间中的角。
例子:在三角函数中,sinθ和cosθ表示角度θ的正弦和余弦值。
⑤ π(Pi): 表示圆周率,常用于表示圆的周长与直径的比值。
例子:π≈3.14159,是一个无理数。
2. 数学运算符① +(加号): 表示加法运算,用于表示两个数相加。
例子:a + b表示a和b的和。
② -(减号): 表示减法运算,用于表示两个数相减。
例子:a - b表示a和b的差。
③ ×(乘号): 表示乘法运算,用于表示两个数相乘。
例子:a × b表示a和b的积。
④ ÷(除号): 表示除法运算,用于表示一个数除以另一个数。
例子:a ÷ b表示a除以b的商。
⑤ =(等号): 表示相等关系,用于表示两个数或表达式相等。
例子:a = b表示a等于b。
以上是常见的数学符号和运算符,它们在高等数学中发挥着重要的作用,帮助我们准确地表达和计算数学问题。
熟练掌握这些符号和运算符的含义和用法,对于理解和应用高等数学知识将起到积极的推动作用。
附录部分的内容至此结束,希望读者能够通过对常用数学符号和运算符的学习,提升对高等数学教材的理解和掌握。
供热教材附录表格
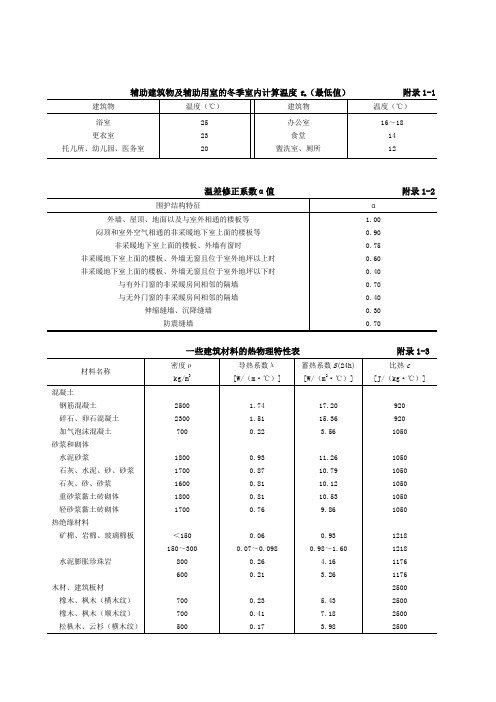
辅助建筑物及辅助用室的冬季室内计算温度t n(最低值)附录1-1温差修正系数α值附录1-2常用围护结构的传热系数K值[W/(m2·℃)] 附录1-4注:本表摘自《暖通规范》(部分城市)允许温差△t y值(℃)附录1-6注:1.表中t n——室内计算温度,℃;t1——在室内计算温度和相对湿度状况下的露点温度,℃;2.与室内空气相通的楼板和非采暖地下室上面的楼板,其允许温差△t y值,可采用2.5℃。
一些铸铁散热器规格及其传热系数K值附录2-1注:1.本表前四项由哈尔滨建筑工程学院ISO散热器实验台测试,其余柱型由清华大学ISO散热器试验台测试。
2.散热器表面喷银粉漆、明装、同侧连接上进下出。
3.圆翼型散热器因无实验公式,暂按以前一些手册数据采用。
4.此为密闭试验台测试数据,在实际情况下,散热器的K和Q值,约比表中数值增大10%左右。
一些钢制散热器规格及其传热系数K值附录2-2散热器组装片数修正系数β 1 附录2-3注:上表仅适用于各种柱型散热器,长翼型和圆翼型不修正。
其他散热器需要修正时,见产品说明。
散热器连接形式修正系数β 2 附录2-4注:1.本表数值由哈尔滨建筑工程学院供热研究室提供,该值是在标准状态下测定的。
2.其他散热器可近似套用上表数据。
散热器安装形式修正系数β 3 附录2-5注:散热器明装,敞开布置,β3=1.0。
PE-X管单位地面面积的散热量和向下传热损失附录2-61.当地面层为水泥或陶瓷、热阻R=0.02(m2·K/W)时,单位地面面积的散热量和向下传热损失可按附录2-6-1取值注:计算条件:加热管公称外径为20mm、填充层厚度为50mm、聚苯乙烯泡沫塑料绝热层厚度20mm、供回水温差10℃。
PE-X管单位地面面积的散热量和向下传热损失(W / m2)附录2-6-12.当地面层为塑料类材料、热阻R=0.075(m2·K/W)时,单位地面面积的散热量和向下传热损失可按附录2-6-2取值。
高等数学A2教材附录

高等数学A2教材附录附录一:数学符号表在高等数学中,有许多常用的符号和记号。
以下是一些常见数学符号及其含义的表格:符号含义π 圆周率e 自然对数的底数∑ 求和∫ 积分∂ 偏导数∞ 无穷大⇒导致/蕴含⊂包含于≅全等于附录二:常用函数表高等数学中,有一些常用的函数,它们在各种数学问题中具有重要的作用。
下面是一些常见函数及其定义和性质:函数定义性质幂函数 y = x^n n为常数,x为自变量指数函数 y = a^x a>0,a≠1,x为自变量对数函数y = logₐ(x) a>0,a≠1,x为自变量三角函数 sin, cos, tan 角度为自变量反三角函数 arcsin, arccos, arctan 以数值为自变量指数和对数函数、三角函数和反三角函数等在数学分析、微积分、微分方程等领域中广泛应用。
附录三:常用的数学公式1. 三角函数的和差公式:sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)tan(x ± y) = (tan(x) ± tan(y)) / (1 ∓ tan(x)tan(y))2. 指数与对数函数的基本性质:a^x * a^y = a^(x+y)(a^x)^y = a^(xy)logₐ(xy) = logₐ(x) + logₐ(y)logₐ(x/y) = logₐ(x) - logₐ(y)3. 微积分中的基本公式:导数公式:(1)常数函数导数为0(2)幂函数的导数:(x^n)' = nx^(n-1)(3)指数函数的导数:(a^x)' = a^x * ln(a)(4)对数函数的导数:(logₐ(x))' = 1 / (x * ln(a))积分公式:(1)幂函数的积分:∫(x^n)dx = (1/(n+1)) * x^(n+1) + C(2)指数函数的积分:∫a^xdx = (1/ln(a)) * a^x + C(3)对数函数的积分:∫(1/x)dx = ln|x| + C以上是高等数学中一些常见的函数和公式,希望对你的学习有所帮助。
高一英语北师大版必修1 附录——教材课文译文

晚上 10 点我才能到家。 到家后还要浏览带回的文件, 为第二天的工作做准 备。我一般半夜才上床睡觉。那时妻子和孩子们都早已进入梦乡。 我很少有时间娱乐或和家人一起活动。妻子和孩子们总是抱怨,但我得拼 命工作,为他们赚更多的钱。再者,要没事可做我会觉得非常无聊。我真的喜 欢忙忙碌碌。”
Lesson 4 黛比是伦敦市中心一家大公司的会计。 我通常每天 7 点起床,9 点前赶到办公室。我乘地铁上班。那就是人们所 称的伦敦地下铁系统。乘地铁大约需要 50 分钟。通常地铁很拥挤,很难找到座 位,我只好站着。到办公室前,我总是已感到很疲惫。我不喜欢乘地铁。 每天上午我要核对数字。午饭总是很简单,我通常在附近的三明治店买三 个三明治,或吃些饼干,喝杯咖啡。然后下午我回到办公室处理文字资料。 星期一晚上我去上舞蹈课。星期三晚上去健身房。我需要做这些运动,因 为我其他时间的运动量不够。星期二和星期四晚上我去上法语课。我在一家法 国公司上班,所以我认为学法语对我的工作有帮助。
农场上每天都有很多事情要做。我们的工作时间和在城市办公室工作的人 们不同,我们的工作是依需要而定,可能是在一大早,也可能在半夜。我的农 场里有牛、羊、猪、鸡, 得确保它们不得病。我也种麦子、蔬菜,所以我有很 多事情需要料理。 晚上我喜欢和孩子们一块儿玩。我有两个孩子,一男一女,一个 6 岁,一 个 8 岁。我也喜欢学习。眼下我正在通过远程教育学习汉语。我对中国很感兴 趣。我一直梦想着有一天能亲眼看到长城。
我喜欢看电影。妻子称我为“影迷”。但是我们村里没有电影院,所以我 没机会经常去看电影。 我一年只能看两次电影, 通常是在和家人去伦敦的时候。 只要农场上的活不太多,我们会在那儿度周末。我妻子喜欢逛服装店;我喜欢 看看人群、听听城市的嘈杂声。我还喜欢买几支雪茄烟。遗憾的是,我妻子不 像我那样喜欢雪茄。我儿子和女儿喜欢乘伦敦的红色公共汽车浏览观光。他们 特别喜欢乘地铁!
高等数学教材附录

高等数学教材附录附录一:数学符号在高等数学中,有许多特定的数学符号被广泛使用。
下面列举了一些常见的数学符号及其含义:1. 基本运算符号加法:$+$,减法:$-$,乘法:$\times$,除法:$\div$2. 常用运算符号等于:$=$,不等于:$\neq$,小于:$<$,大于:$>$,小于等于:$\leq$,大于等于:$\geq$3. 集合符号属于:$\in$,不属于:$\notin$,子集:$\subset$,包含:$\supset$,真子集:$\subsetneq$,真包含:$\supsetneq$,并集:$\cup$,交集:$\cap$,空集:$\emptyset$4. 指数和根号上标:$a^b$,下标:$a_b$,指数:$a^{bc}$,根号:$\sqrt{a}$5. 极限极限:$\lim$,导数:$\frac{d}{dx}$,偏导数:$\frac{\partial}{\partial x}$6. 微积分符号积分:$\int$,定积分:$\int_a^b$,不定积分:$\int dx$,微分:$dx$7. 求和求和:$\sum$,无穷求和:$\sum_{n=1}^{\infty}$,乘积符号:$\prod$8. 向量和矩阵符号向量:$\vec{a}$,矩阵:$\mathbf{A}$,转置:$^T$,内积:$\cdot$,叉乘:$\times$9. 特殊函数符号绝对值:$|x|$,自然对数:$\ln$,常用对数:$\log$,三角函数:$\sin, \cos, \tan$,反三角函数:$\arcsin, \arccos, \arctan$,指数函数:$e^x$此外,还有许多其他的数学符号和表达方式,在具体的数学领域中有特定的使用方法。
熟练运用这些数学符号,将有助于更好地理解和表达高等数学的概念和原理。
附录二:常用公式以下为一些常见的高等数学公式,在学习过程中可以作为参考和复习之用:1. 三角函数公式$\sin^2x + \cos^2x = 1$$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$$\tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$2. 指数与对数公式$a^m \cdot a^n = a^{m + n}$$\frac{a^m}{a^n} = a^{m - n}$$(a^m)^n = a^{mn}$$\log_a (mn) = \log_a m + \log_a n$$\log_a \frac{m}{n} = \log_a m - \log_a n$3. 微分与积分公式导数公式:$\frac{d(u \pm v)}{dx} = \frac{du}{dx} \pm \frac{dv}{dx}$$\frac{d(uv)}{dx} = u\frac{dv}{dx} + v\frac{du}{dx}$$\frac{d(\frac{u}{v})}{dx} = \frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}$$\frac{d(e^x)}{dx} = e^x$$\frac{d(\ln x)}{dx} = \frac{1}{x}$$\frac{d(\sin x)}{dx} = \cos x$$\frac{d(\cos x)}{dx} = -\sin x$积分公式:$\int x^n dx = \frac{1}{n+1}x^{n+1} + C$$\int e^x dx = e^x + C$$\int \sin x dx = -\cos x + C$$\int \cos x dx = \sin x + C$$\int \frac{1}{x} dx = \ln |x| + C$4. 三角函数的导数与积分公式$\frac{d(\sin x)}{dx} = \cos x$$\frac{d(\cos x)}{dx} = -\sin x$$\frac{d(\tan x)}{dx} = \sec^2 x$$\int \sin x dx = -\cos x + C$$\int \cos x dx = \sin x + C$$\int \tan x dx = -\ln |\cos x| + C$附录三:参考书目以下是一些优秀的高等数学教材供您进一步学习和参考:1. 《高等数学》(同济大学版)作者:郭家著、刘畅、杨健编出版社:高等教育出版社2. 《高等数学》(科学出版社版)作者:郭家著、邓约威、史钟智编出版社:科学出版社3. 《高等数学》(清华大学版)作者:陈纪修、李荣华、李维善编出版社:高等教育出版社4. 《高等数学教程》(第7版)作者:冯震、陈建中、貌涌臣编出版社:高等教育出版社这些教材内容丰富、结构清晰,适合高等数学的学习和教学使用。
人教版初中地理八年级下册 附录二:本书常用地图图例(区一等奖)
《图例》教学设计六合区竹镇民族中学史道山一、教学目标1、了解图例的定义并能依据图例的形状进行准确分类。
2、识记基本的图例,并能在教材配图中迅速的寻找图例,熟练运用图例。
3、能够根据题意自主设计简单图例。
二、教学重点识记基本的图例形状,在解题中熟练运用三、教学难点自主设计简单图例四、教学准备1、教学设计2、地理填充图册3、教学设计1、结合图例,说出该地区的种植的农作物2、结合图例,比较甲、乙两地发展的农业类型并说明理由3、尝试指出该地区河流的流向合作学习3:各小组迅速在本册教材中寻找以下图例。
(公路、街区街道、高速公路)要求标出页码,并说出地图名称。
合作学习4:各小组迅速在本册教材中寻找以下图例。
(机场、港口、铁路及车站、香港特别行政区界)要求标出页码,并说出地图名称。
合作学习5:各小组迅速在本册教材中寻找以下图例。
(常年湖、常年河、沼泽、省、自治区、直辖市界)要求标出页码,并说出地图名称。
教师:视频介绍塔里木河(内流河)。
设计图例:在下图中画出塔里木盆地、准格尔盆地、天山山脉、昆仑山山脉、阿尔泰山图册P33练习2:1、结合图例归纳西北地区降水分布特征2、请将甲、乙、丙三地与照片A、B、C连线练习3:1、东北地区主要有哪些矿产资源学生:认真观看视频,体会军事分界线。
学生:反馈练习。
在课堂上完成。
及时对所完成的练习题进行点评学生:图北京的市区交通学生:图香港和澳门特别行政区的地形学生:图东北三省的地形学生:欣赏塔里木河学生:准确的进行连线学生:在音乐中熟记天气案的能力及时巩固知识,增强学生对知识的掌握。
训练学生综合思维,归纳能力培养学生寻找解决对策,解决问题能力。
培养学生动手操作的能力,自主设计图例。
及时巩固所学知识,强化对新授课的理解。
课后反思:在教学活动中,要想上一节好课,备课是关键,特别是备学生,本节课属于地理八下的附录二内容,在知识体系上属于地图三要素的范畴。
由于学生在七年级就学过地图,因此,我在导入新课使用了荆轲刺秦王这一历史故事,希望调动学生学习的积极性。
教材组织结构
教材组织结构
教材的组织结构非常重要,它影响着学习者对知识的理解和掌握。
以下是一个常见的教材组织结构:
引言和目的:教材通常以引言开始,介绍教材的目的和主题,以
及学习者可以期望从中获得的知识。
概览:教材的概览部分提供了对整个教材内容的概括,让学习者
了解教材的整体结构和组织方式。
章节划分:教材通常被划分为不同的章节。
每个章节可能包含一
个特定的主题或概念,这将有助于学习者逐步理解知识。
每章概述:每个章节通常都有一个概述部分,介绍该章节将要学
习的主题和内容。
主要内容:每个章节的主要内容提供了详细的知识和信息,以便
学习者深入了解主题。
示例和案例:为了帮助学习者更好地理解和应用所学的知识,教
材通常会提供一些实际的示例和案例。
练习和习题:学习者需要通过练习和习题来巩固所学的知识。
教
材通常会提供一些练习和习题,以帮助学习者加深理解和提高应用能力。
总结和复习:每个章节或教材的结尾通常会提供一个总结部分,
概括重要知识点和关键概念,以方便学习者进行复习和回顾。
附录和参考资料:教材的附录部分通常包含一些额外的资料,如
词汇表、图表、表格等。
参考资料则提供了教材中所引用的其他书籍、文章或研究报告的详细信息。
通过以上的组织结构,教材能够合理有序地呈现知识,使学习者
更好地理解和掌握所学内容。
附录11国内化学专业教材信息
2
2008
浙大
分析化学
华东理工+川大
高等教育
5
71
浙大
物理化学
天津大学物理化学教研室
高等教育
浙大
复旦
有机化学
莫里森
科学
2
1993
复旦
复旦
复旦
复旦
有机化学实验
谷珉珉,贾韵仪,姚子鹏
复旦大学
1991
复旦
生物化学教程
复旦大学生物化学系编
自编
1993
复旦
生物化学
沈同等编
自编
1991
复旦
物理化学
邓景发、范康年
高等教育
1993
复旦
物质结构
徐光宪,王祥之
高等教育
1987
复旦
物质结构
汪元生
高等教育
1997
复旦
2001
南大
物理化学(上、中、下)
胡英主编
高等教育
4
1999
南大
。
7
2002
南大
物理化学
朱文涛
清华大学
1
1995
清华
分析化学
薛华
清华大学
2
1994
清华
基础无机化学实验
崔爱莉
高等教育
1
2007
67
清华
基础有机化学实验
阴金香
清华大学
1
2010
清华
无机及分析化学
浙江大学
高等教育
2
浙大
有机化学
王彦广、吕萍、张殊佳、吴军
化学动力学基础
韩德刚
北京大学
1987
单片机课程设计附录
单片机课程设计附录一、课程目标知识目标:1. 理解单片机的硬件结构及其工作原理,掌握相关术语和概念;2. 学会使用单片机编程软件,掌握基本的编程语法和指令;3. 掌握单片机外围电路的设计与搭建,了解常见传感器的应用。
技能目标:1. 能够运用所学知识,独立完成单片机的编程与调试;2. 能够分析实际问题,设计简单的单片机控制系统;3. 培养学生的动手实践能力和团队协作能力。
情感态度价值观目标:1. 培养学生对单片机技术的兴趣,激发创新意识;2. 培养学生严谨、踏实的科学态度,注重实践与理论相结合;3. 增强学生的自信心,培养克服困难、解决问题的决心。
课程性质分析:本课程为单片机技术相关课程,旨在让学生掌握单片机的基本原理、编程及应用。
课程强调实践性与实用性,注重培养学生的动手能力和实际操作技能。
学生特点分析:本课程针对的学生群体为具有一定电子基础知识和编程能力的初中或高中学生。
他们对新技术充满好奇,具备一定的自学能力和探索精神。
教学要求:1. 结合教材内容,注重理论与实践相结合,提高学生的实际操作能力;2. 采用案例教学,激发学生的兴趣,培养学生的创新思维;3. 强化团队合作,提高学生的沟通与协作能力;4. 注重过程评价,及时反馈学生的学习成果,调整教学策略。
二、教学内容1. 单片机硬件结构:介绍单片机的内部组成,包括CPU、存储器、输入输出接口等,结合教材第一章内容,让学生了解单片机的基本构成和工作原理。
2. 编程语言与开发环境:学习单片机编程所需的基础知识,包括汇编语言和C 语言,使用教材第二章推荐的编程软件,如Keil uVision,进行实践操作。
- 汇编语言基础- C语言基础- Keil uVision使用方法3. 基本编程指令与语法:学习单片机编程中的常用指令,如逻辑运算、跳转、循环等,结合教材第三章内容,让学生掌握编程的基本技巧。
4. 外围电路设计与传感器应用:介绍单片机与其他电子元件的连接方法,学习传感器的工作原理及应用,参照教材第四章,进行外围电路设计和搭建。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
break;
case'+':
case'-': while(gettop_r()!='('&&tr.top>0)
附录A 课程设计指导
/* 若是加法或减法运算符,则只要算符栈中有运算符,并
已不是'(' 运算符。*/
count();
/*则去计算原来栈中的运算*/
qq=sp;
push_r(ch); /*保存这次的运算符*/
附录A 课程设计指导
3. 程序实现 #include <stdio.h> #include <stdlib.h> #include <io.h> #include <string.h> #define MAX 20 struct st_optr
/*算符栈的描述*/
附录A 课程设计指导
{ char elem[MAX+1]; int top;
附录A 课程设计指导
附录A 课程设计指导
附录A 课程设计指导
问题1:设计一程序,要求从键盘上输入一个只含加、减、 乘、除等四种运算符的算术表达式,便可计算表达式的结果。
解:本题的求解如下。 1. 相关知识 要对一个表达式求值,首先要了解算术四则运算的规则。 即: (1) 先乘除,后加减。 (2) 同级运算,从左到右。 (3) 先括号内,后括号外。
char pop_r() {
char e; if (tr.top>0) { e=tr.elem[tr.top]; tr.top=tr.top-1; return e; } else return NULL; }
/*算符出栈函数*/
附录A 课程设计指导
char gettop_r()
/*取算符栈栈顶元素的函数*/
sp++ ;
} /*while*/
if(yy= =1)
/*如果刚处理的是数字字符串*/
{
附录A 课程设计指导
qq=sp; sp--; push_d(atoi(bb));
/*将数字字符串转换为数值后进操作数栈*/ bb[0] ='\0'; if (test(qq))
/*测试表达式是否扫描完毕*/ continue; }
附录A 课程设计指导
case'/': while(gettop_r()=='*'||gettop_r()=='/')
/*若栈中有乘或除运算符 */
count();
/*则先去计算栈中的乘法或除法*/
qq=sp; push_r(ch);
/*将这次扫描得到的运算符进 栈,以便下次运算*/
test(qq);
附录A 课程设计指导
任何一个表达式都是由操作数、算符组成的。一般地, 操作数既可以是常数也可以是被说明为变量或常量的标识 符。算符包括运算符和界符两种,其中运算符又可以分为 算术运算符、关系运算符和逻辑运算符等三类,基本界符 有左右括号和表达式结束符等。为了叙述的简洁,我们仅 讨论简单算术表达式的求值问题。这种表达式只含加、减、 乘、除等四种运算符。
附录A 课程设计指导
(5)有关算法中的变量设置:可将上述讨论中所提 及的变量k、v作为参数(仅提供值而不返回值),将g作 为地址传送型参数(虽然不会改变其值,但这种形式更 节省时间和空间),将数组B和visited作为全程变量,以 便各调用层能共享,并节省时间、空间,同时使程序 更清晰。
2. 算法分析 为实现算符优先算法,使用两个工作栈。一个称做算符 栈tr,用以存放算符;另一个称做操作数栈 nd,用以存放操 作数或运算结果。 (1) 首先置操作数栈和算符栈为空栈。 (2) 读入表达式,用一个指针指向该表达式的每个字符, 若是操作数,则进nd栈,若是算符,则与tr栈的栈顶算符比 较优先级后做相应操作,直到整个表达式求值完毕(即tr栈为 空)。
② 若不成功,则应恢复w的有关信息,以使w在试 探其它路径时成为可选顶点。
附录A 课程设计指导
为了能求出解以及所有可能的解,需要做如下两方面 的工作:
① 选择起点:应以每个顶点为起点进行搜索。 ② 搜索路径:在从v往下搜索时,应依次选择v的所有 不在当前试探路径中的邻接点往下搜索。 为此,需要有这方面的保证:应在试探某顶点w后并 在换下一个试探顶点前恢复w的有关状态,以使其仍为可 选择的顶点。
附录A 课程设计指导
default: printf("输入错误!\n");
exit(-1);
/*中断程序的执行*/
} /* switch */
} /* for */
} /* main */
附录A 课程设计指导
问题2:在有n个选手P1,P2,P3,…,Pn参加的单循环 赛中,每对选手之间非胜即负。现要求求出一个选手序 列,,,…,,,使其满足胜(i = 1,…,n-1)。
附录A 课程设计指导
根据上述的三条运算规则,我们可以把算符的优先级从 高到低排列出来为:左括号→乘、除→加、减→右括号。因 此,在运算的每一步中,任意两个相继出现的算符a和b,至 多是下面三种关系之一:
a<b a的优先级低于b a=b a的优先级等于b a>b a的优先级高于b
附录A 课程设计指导
}; struct st_opnd {
float elem [2*MAX]; int top; }; struct st_optr tr; struct st_opnd nd;
/*操作数栈的描述*/
附录A 课程设计指导
char aa[30];
/*定义一个全程变量,用以存放输入的
表达式*/
int flag=1;
break;
case'-': n1=n1-n2;
break;
case'*': n1=n1*n2;
break;
case'/': n1=n1/n2;
break;
}
push_d(n1);
/*将运算的中间结果进栈保存*/
}
附录A 课程设计指导
void stch(char *bb,char item) /*数值型字符串形成函数*/
附录A 课程设计指导
(4)本算法的基本思想: ① 若k = n,则说明已经求得一解,因此可输出结果, 并结束本次调用。 ② 若k<n,则依次选择v的所有不在当前试探路径中 的邻接点w往下搜索,这包括以下的操作: 试探:将w放到B[k + 1]中,并置visited[w]为1,然后 以w为起点往下搜索。 恢复:将w恢复为不在当前路径中,以使其在试探其 它路径时可用。
/*返回1,表示应继续扫描*/
while(tr.top!=0)
/*若表达式已全部扫描完,并
且算符栈中还有运算符*/
count();
/*则执行最后一次运算*/
printf("数学表达式 %s= =%f\n",aa,nd.elem[1]);
/*显示最后的计算结果*/
flag=0;
/*修改标志变量,以结束程序
/*操作数出栈函数*/
附录A 课程设计指导
void count()
/*运算函数*/
{
float n1,n2;
char op;
/*取得两操作数*/
n2=pop_d();
n1=pop_d();
op=pop_r();
/*取得运算符*/
switch(op){
附录A 课程设计指导
case'+': n1=n1+n2;
附录A 课程设计指导
解:本题的求解如下: 1. 模型表示 由于仅涉及到n个选手,并且这些选手之间的关系仅是 胜负关系,因此可用图来表示。 (1) 用顶点表示选手。 (2) 用弧表示选手之间的胜负关系:当且仅当Pi胜Pj时, 有从顶点i到j的一条弧。 在这种表示下,本题变成了在有向图中求解出一条包 含所有顶点的简单路径的问题。 附图1所示为一个有8个选手的问题的一个示例,其中 的一个解为1,2,3,4,8,6,5,7。
test(qq);
break;
附录A 课程设计指导
case')': while( gettop_r()!='(' ) /*若扫描到的是')',且算符栈中有其他运算符*/ count(); /*则去计算原来栈中的运算*/ pop_r(); /*消去一对括号*/ qq=sp+1; test(qq); break;
}
void push_d(float m) {
/*操作数进栈函数*/
附录A 课程设计指导
if (nd.top==2*MAX-1) { printf("内存不够! \n"); exit(-2); } else { nd.top=nd.top+1; nd.elem[nd.top]=m; }
}
附录A 课程设计指导
附录A 课程设计指导
(3) 可能情况的处理:既然是试探型求解,则需对当 前顶点v的每个邻接点(不妨用w表示)进行试探,试探由v 经w往下是否可以得到解。每个w都可能有成功(指现在 可以将该顶点放在路径上,这包括暂时的和最终的)与失 败(指此路不通)两种情况,对此应分别作不同的处理:
① 若试探成功,则应将w放入路径中,并置相应的 状态值。然后再由w往下求解。
附录A 课程设计指导
附图1 8个选手比赛情况示例
附录A 课程设计指导
2. 算法设计 (1) 设计本题算法的构思:为搜索出符合条件的简
单路径,需按深度优先搜索方式进行遍历。因此求解算 法应是深度遍历算法的变形形式,也应是递归形式的算 法。
