七年级数学《线段的大小比较》课件
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第三章“平面几何初步”中的第二节“线段的大小比较”。
具体内容包括:线段的定义、线段长度的度量方法、以及线段大小比较的方法。
二、教学目标1. 理解并掌握线段的概念及其性质。
2. 学会使用工具测量线段的长度,并能准确进行比较。
3. 能够运用线段大小比较的方法解决实际问题。
三、教学难点与重点教学难点:线段大小比较的方法在实际问题中的应用。
教学重点:线段的定义、测量及大小比较。
四、教具与学具准备教具:尺子、直尺、圆规、多媒体课件。
学具:尺子、直尺、练习本。
五、教学过程1. 实践情景引入通过展示一些日常生活中的实例,如操场的跑道、书本的尺寸等,引导学生理解线段的概念及其在生活中的应用。
2. 知识讲解(1)线段的定义:线段是由两个端点及这两个端点之间的所有点组成的图形。
(2)线段长度的测量:使用尺子、直尺等工具,按照一定的比例进行测量。
(3)线段大小比较:通过比较线段的长度,判断线段的大小。
3. 例题讲解例题1:比较下列线段的长度,指出较长的线段。
解答:通过直接测量或比较,得出结论。
例题2:在下列图形中,找出最长的线段。
解答:观察图形,比较各线段的长度,找出最长的线段。
4. 随堂练习发放练习题,让学生独立完成,巩固所学知识。
六、板书设计1. 线段的定义2. 线段长度的测量3. 线段大小比较4. 例题及解答5. 随堂练习七、作业设计1. 作业题目线段AB:________ 线段CD:________(2)找出下列图形中最长的线段:答案:________2. 答案(1)线段AB:________ 线段CD:________(2)最长的线段:________八、课后反思及拓展延伸1. 反思:本节课学生掌握了线段的概念、测量及大小比较,但在解决实际问题时,还需加强练习。
2. 拓展延伸:引导学生了解线段的性质,如线段的垂直平分线、线段的中点等,为后续学习打下基础。
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第五章“平面几何中的基本元素”中第二节“线段的大小比较”。
具体内容包括:线段的定义、线段长度的度量方法、线段大小比较的方法,以及线段等分的概念。
二、教学目标1. 理解线段的定义,掌握线段长度的度量方法。
2. 学会线段大小比较的方法,并能应用于实际问题。
3. 了解线段等分的概念,能够运用等分线段的方法解决相关问题。
三、教学难点与重点教学难点:线段大小比较的方法,线段等分的实际应用。
教学重点:线段的定义,线段长度的度量方法,线段大小比较的方法。
四、教具与学具准备1. 教具:黑板、粉笔、尺子、圆规、直角三角板。
2. 学具:练习本、铅笔、直尺、圆规。
五、教学过程1. 导入:通过展示生活中常见的线段,如跳绳的长度、书桌的长度等,引导学生认识到线段在生活中的广泛应用。
2. 新课导入:(1)讲解线段的定义,强调线段是有限长的直线部分。
(2)介绍线段长度的度量方法,演示如何使用尺子测量线段长度。
(3)引导学生发现,当线段长度相等时,线段大小相同;当线段长度不等时,可以通过比较长度来判断线段的大小。
3. 实践操作:(1)让学生分组讨论,如何比较两条线段的大小。
4. 例题讲解:(1)给出两条线段,让学生比较大小。
(2)通过分析题目,引导学生运用所学知识解决问题。
5. 随堂练习:(1)让学生完成教材第5页的练习题1。
(2)教师挑选部分题目进行讲解,分析解题思路。
6. 知识拓展:(1)介绍线段等分的概念。
(2)演示如何使用尺子和圆规进行线段等分。
(1)回顾本节课所学内容,强调线段大小比较的方法。
(2)提醒学生注意线段等分在实际问题中的应用。
六、板书设计1. 板书线段的大小比较2. 主要内容:(1)线段的定义(2)线段长度的度量方法(3)线段大小比较的方法(4)线段等分的概念及方法七、作业设计1. 作业题目:(1)教材第5页的练习题2。
(2)自编题目:给出两条线段,让学生比较大小,并说明理由。
线段的大小的比较ppt课件
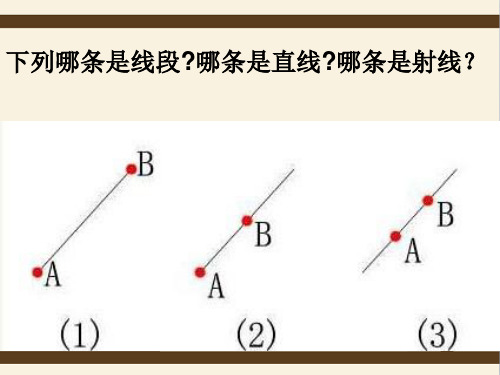
如图,已知线段a,画出线段AB ,使得AB=a.
a
解: 方法二: 1.画一条射线AC;
用直尺和圆
2.在射线AC上截取线段AB=a.
规
A
B
C
以点A为圆心,a
为半径画弧,交射
∴线段AB就是所要画的线段.
线AC于点B.
例题:先观察估计图中线段a,b的大小,然后用比较
线段大小的方法验证你的估计,并用“<”符号连结.
活动室
联结两点的线段的 长度叫做两点之间 的距离.
教学楼
两点之间,线段最短.
练习:下列叙述正确的是( D )
A.联结两点的直线叫做两点之间的距离. B.联结两点的线段叫做两点之间的距离. C.联结两点的直线的长度叫做两点之间的距离. D.联结两点的线段的长度叫做两点之间的距离.
线段是几何图形,两点 之间的距离是一个数量.
下列哪条是线段?哪条是直线?哪条是射线?
讨论:说一说直线、射线、线段之间的区别与联系.
名称
直线AB 射线AB 线段AB
图形 端点个数 延伸方向 能否度量
AB
AB
A
B
无 一个 两个
向两方无限 延伸
向一方无限 延伸
不向任何一 方延伸
不能 不能
能
线段和射线是直线的一部分.
线段的表示方式
(1)用表示端点的两个大写英文字母表示:
思考:如图为正方体和圆柱体实心木块,小老鼠从表面 爬过,走什么线路,吃到汉堡时爬过的路程最短?
A
自主小结:
1.线段的两种表示方法:
A 两个大写英文字母;
B 记作线段AB
一个小写英文字母.
a
记作线段a
2.线段大小的比较的一般方法:目测法;度量法;叠合法.
人教版线段的比较大小教学PPT课件

a
2、你能用直尺和圆规画出一条线段c,使它等于已知线段a的2倍。
尺规作图注意事项: 1、只要求作出图形,说明结果; 2、保留作图痕迹。
请说说你的画法
O
P
B
线段OB就是所求做的线段c
A
直尺只用来画线,不用来量距离;
已知:线段a,b(如图),用直尺和圆规画一条线段c,使得它的长度等于两条已知线段的长度的和。
=8-5=3cm
l
A
B
C
l
A
B
C
1、有A、B、C三个城市,已知A、B两城市的距离 为50千米,B、C两城市的距离为 30 千米,那么 A、C两城市的距离是( ) A、80千米 B、20千米 C、40千米 D、处于20千米到80千米间
数学小趣闻—尺规作图
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
比较线段长短的两种方法: 1、度量法——从“数值”的角度比较 2、叠合法——从“形”的角度比较
起点对齐,看终点
1) 用刻度尺量出图中的三角形 三条边的长: AC=__cm; BC=__cm; AB=__cm.
2) 用“=”、“<”或“>”号填入 下面的空格: AC___BC, AC___AB, AB___BC.
A
B
C
1.0
2.0
>
<
>
1.8
2、用圆规比较下列各组线段的长短。
>
<
=
1、已知线段a,用直尺和圆规画一条线段b,使它等于已知线段a。
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第五章“几何初步”中的第二节“线段的大小比较”。
详细内容包括线段的定义、线段长度的测量方法,以及如何直观和准确地比较两条线段的大小。
二、教学目标1. 理解线段的定义,掌握线段长度的测量方法。
2. 学会直观和准确地比较两条线段的大小,并运用到实际问题中。
3. 培养学生的观察能力、逻辑思维能力和实际操作能力。
三、教学难点与重点教学难点:线段大小的准确比较。
教学重点:线段的定义、长度测量方法,以及线段大小比较的方法。
四、教具与学具准备1. 教具:多媒体课件、直尺、三角板、圆规等。
2. 学具:直尺、三角板、练习本等。
五、教学过程1. 实践情景引入:展示一张地图,提出问题:“如何比较地图上两个城市之间的距离?”引导学生思考线段大小比较的实际意义。
2. 知识讲解:a. 线段的定义及性质。
b. 线段长度的测量方法。
c. 线段大小比较的方法。
3. 例题讲解:a. 通过实际操作,比较两条线段的大小。
b. 讲解如何利用工具(如直尺)进行线段长度的测量和比较。
4. 随堂练习:a. 让学生测量并比较教室内不同物品的长度。
b. 在练习本上完成线段大小比较的题目。
六、板书设计1. 线段的定义及性质2. 线段长度的测量方法3. 线段大小比较的方法a. 直观比较b. 工具测量比较七、作业设计1. 作业题目:AB = 5cm,CD = 8cm;EF = 12cm,GH = 15cm。
课本的长度、宽度;笔的长度;课桌的高度。
2. 答案:a. CD > AB,GH > EF。
b. 略。
八、课后反思及拓展延伸1. 反思:本节课学生对线段大小比较的方法掌握程度,以及在实际操作中的表现。
2. 拓展延伸:a. 探讨线段长度与距离的关系。
b. 研究线段大小比较在生活中的应用,如测量地图上的距离、比较物品长度等。
重点和难点解析1. 线段大小比较的方法。
2. 实际操作中测量线段长度的准确性。
线段的大小比较和画法PPT课件
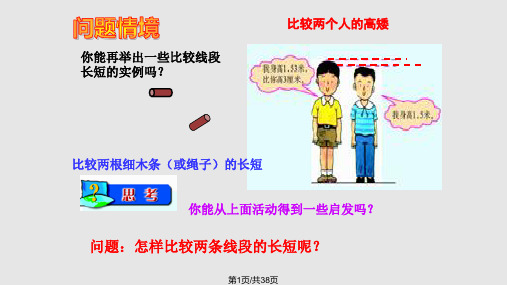
A
BC
(1) AB<AC
(2) AC-AB=BC AC-BC=AB BC+AB=AC
第12页/共38页
再来测测眼力吧!
在刚才的活动中我们知道了AB<CD,你知道 AB比CD少多少吗?你能用线段表示吗?
C A
BD
AB+BD=CD
CD-AB=BD
你知道如何画线段的和与差吗?
第13页/共38页
二、概念延伸,思维提升
(1)如果点P是AB的中点,
则AP=
_
1
2_
AB
A
CPD B
(2)如果点C,1D三等分AB,则 AC=CD= D_ B_ = _3_ AB
(3)CP可以表示成哪两条线段的差?你有几种不 同的表示?
(4)现在告诉你CP=1.5cm,求线段AB的长。
第23页/共38页
试一试
• 1.已知线段AB=80cm,M为AB的中点,P在MB上,N为PB的中点,且 NB=14cm。
连接两点间的线段的长度,叫做这两点的距离。
①
② ③
第25页/共38页
安全 地带
练一练
1. 判 断 : 两 点 之 间 的 距 离 是 指 两 点 之 间 的 线 段 。
( 错)
2.如图:这是A、B两地之间的公路,在公路工程改造 计划时,为使A、B两地行程最短,应如何设计线路? 在图中画出。你的理由是
AC
所以AB=a+b.
B
l
a
b
第15页/共38页
想一想
问题三:已知线段a,b(b>a)画一条线段
AC,使AC=b-a。
a
b
画法:①先用直尺画一条直线l;
②在直线l上截取AD = b;
初中数学七年级上册 4.2 2 线段的大小比较 课件

单击输入您的封面副标题
君子看人背后,小人背后看人。远离那些背后说别人坏话的人,请记住,他(她)能说别人坏话,就能在暗地说你坏话!这就是俗话说的, 不怕真小人,就怕伪君子! 人不能创造时机,但是它可以抓住那些已经出现的时机。 我们每一个人都应该有更多的同情,更多的爱,比维持我们生存需要的多得多,我们应该把它分散给别人,追求是生命之光。 没有情感,道德就会变成枯燥无味的空话,只能培养出伪君子。——苏霍姆林斯基 我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯 才须学也。非学无以广才,非志无以成学。——孔明 只要你确信自己正确就去做。做了有人说不好,不做还是有人说不好,不要逃避批判。 当你知道迷惑时并不可怜,当你不知道迷惑时,才最可怜。 为了照亮夜空,星星才站在天空的高处。 要纠正别人之前,先反省自己有没有犯错。 己欲立而立人,己欲达而达人。——《论语·雍也》 谁不向前看,谁就会面临许多困难。 我的努力求学没有得到别的好处,只不过是愈来愈发觉
6.3 线段的长短比较 教学课件 (共28张PPT)
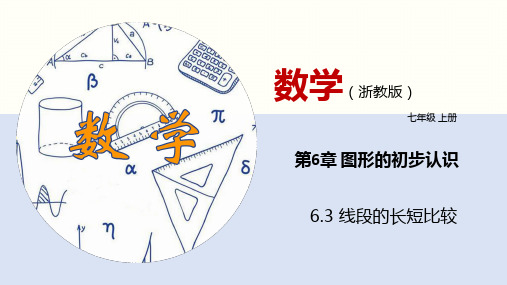
讲授新课
作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF; 第二步:用圆规在射线 AF 上截取 AB = a. 所以线段 AB 为所求线段.
a Aa B F
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
讲授新课
尺规作图的要点: 1.直尺只能用来画线,不能量距; 2.尺规作图要求作出图形,说明结果,并保留作图痕迹.
生活中我们常常会比较两个物体的长短。如图两支铅笔 谁长?
我们可以把两支铅笔看成两条线段,这样我们就把实际 问题转化为了几何问题.
讲授新课
思考:怎样比较两条线段的长短??
Aa B
(1)度量法 用刻度尺量出它们的 长度,再进行比较.
Cb
D
(2) 叠合法 将其中一条线段“移动”, 使其一端点与另一线段的 一端点重合,两线段的另 一端点均在同一射线上.
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射个
C.3个
D.4个
当堂检测
2.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银
杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(
)
A.两点之间线段最短 C.垂线段最短
解:作图步骤如下:
aa b
(1)作射线 AM;
A B1 B2
BM
(2)在 AM 上顺次截取 AB1=a,B1B2=a,
B2B=b,则线段 AB=2a+b.
讲授新课 知识点三 有关线段的基本事实
探究
我要去书店 怎么走呀?
商场
礼堂
书店
讲授新课
根据生活经验,容易发现: 两点之间的所有连线中,线段最短
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当直线a上标出n个点时,可得到 2n条射线,
n(n-1)
2
条线段。
如何比较线段AB 与线段CD的长短?
A
B
C
D
线段的比较方法
❖ 度量法。(刻度尺) ❖ 叠合法。(一端对齐,在同一侧)
如图,线段AC,点B把AC
分成相等的两条线段.
A
B
C
点B叫做线段AC的中点
想一想
那么AC=
2 AB=
2BC;AB= BC=
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
三.拓展
一个点与其余三个点可组成三条线段
共有4×3条
·· · ·
AO
B
C
这儿为什 么写“6”? a
1、当直线a上标出一个点时,可得到 2 条射线, 0 条线段; 2、当直线a上标出二个点时,可得到 4 条射线, 1 条线段;
3、当直线a上标出三个点时,可得到 6 条射线, 3 条线段; 4、当直线a上标出四个点时,可得到 8 条射线, 6 条线段;
1. 用符号表示线段、射线、直线。 2. 两点间的距离。 3. 两点之间的所有连线中,线段最短。 4. 经过两点有一条直线,并且只有一条直 线。(两点确定一条直线)。 5. 线段中点的概念。
一个人看不到自己的远方是很可怕的, 有了远方也就有了人生追求的高度, ---而人一旦有了追求, ---远方也就不再遥远。
如图,要从甲地到乙地去,有3
条路线,请你选择一条相对近一
些的路?
①
②
乙地
③
甲地
从甲地到乙地能否修一条最近的路? 如果能,你认为这条路应该怎样修?
①
②
乙地
③
甲地
生活常识告诉我们:
结论 两点之间的所有连线中,线段最短。
定义 两点之间线段的长度叫做两点之间的距离
请你做裁判
❖ 过A、B、C三个点中的任两 点作直线,小明说有三条;小林 说有一条;小王说不是一条,就 是三条;你认为他们三人谁的说 法对?为什么?
课题: 线段 射线 直线
第二课时
一.选择题
1、如图下列说法错误的是( B )
A、点A在直线m上 B、点B在直线 l 上 C、点A在直线 l 上
D、直线m不经过B点
l
A B
m
2、如图,射线PA与PB是同一条射线,则 符合题意的图为(C )
A
P B
A PB
A AP
B P
PB
A
B
C
D
3、下列说法正确的是( C) A、两点确定两条直线 B、三点确定一条直线 C、过一点能作无数条直线 D、过一点可以作一条直线
比一比,看谁更优秀
❖ 判断题:
❖ 1、一条直线长100米。………… ( )
❖ 2、手电筒照在墙上,从灯泡到墙上光线是射
线。……………
()
❖ 3、线段是直线的一部分。……… ( )
❖ 4、直线比射线长。……………… ( )
❖ 5、在射线上可以截取2厘米长的线段( )
❖ 6、过一个点只可以画一条射线。……( )
4.下列图形能相交的是( D )
A
B
C
D
5、在平面内有4个点,过2个点画一条直线,则直线
的条数是(D )
A . 1条 B . 4条 C . 6条 D . 1条或4条或6条
二.观察下图,图中共有多少条线段?分别有
哪些?
A
答:6条线段.
B
D
分别是线段AB、线段AC、 线段AD、线段BD、线段BC、 C 线段DC.
2 、 点C是AB延长线上的一点,点D是AB中点, 如果点B 恰好是DC的中点,设AB=2cm,则 AC=__3____cm
例:如图,线段AB=8cm,点C是AB的中点, 点D在CB上且DB=1.5cm,求线段CD的长度。
A
C
DB
解:CB=
1 2
AB=4cm,
CD=CB-DB
=4-1.5
=2.5(cm)
1 2 AC
1、如图,点C是线段AB的中点
(1)若AB=6cm,则AC= 3 cm。 (2)若AC=6cm,Leabharlann AB= 12 cm。AC B
2、已知:AD=4cm,BD=2cm,C为
AB的中点,则BC=__3___cm.
A CD B
1 、 在同一条直线上依次有A、B、C三点, 取AB中点 M,取BC中点N,如果AC=6cm,则 MN=___3___cm
