菲涅耳衍射数字模拟仿真与实验
菲涅耳衍射实验的模拟与仿真

光 学 试 验 仿 真 的 首 要 问 题 是 光 束 传 播 的 仿 真 . 波 的 传 播 、 射 、 像 等 现 象 都 可 以 光 衍 成
看 作 是 线 性 和 空 间 不 变 的 . 以 可 以 用 线 性 系 统 分 析 的 典 型 方 法 , 别 是 傅 里 叶 分 析 法 所 特
[ 中图分类号】 N 7 . T 2 15 [ 文献标 识码 ] A ( 文章编号]0 4— 07 20 )5— 0 0— 5 10 7 7 (0 8 0 04 0
1 引 言
“ 学 ” 物 理 学 专 业 的 重 要 基 础 课 . 是 大 部 分 光 学 内 容 比较 抽 象 , 不 借 助 实 验 , 光 是 但 如
距 光 源 和 接 收 屏 均 为 有 限 远 , 者 其 中之 一 为 有 限 远 , 一 种 是 夫 琅 和 费 衍 射 , 缝 距 光 或 另 单 源 和接 收 屏 均 为 无 限远 或 相 当于 无 限远 .
本 文 主 要 讨 论 菲 涅 耳 圆 孔 衍 射 和 单 缝 衍 射 .它 也 是 光 学 试 验 中 比 较 重 要 的 试 验 之
Ed ( ) = Eo (
r ) x j2 -d ) x [ qA f + e p( q e p 一j' d( ̄ )] r
涉 及 的 大 多数 现 象 展 示 在学 生 面前 , 加 深对 光 学 内容 的理解 . 以
Malb是 Mah r s 司 于 1 8 年 推 出 的 一 套 高 性 能 的 数 值 计 算 和 可 视 化 软 件 . t a twok 公 92 它
集 数 值 分 析 、 阵 运 算 、 号 处 理 和 图 形 显 示 于 一 体 , 成 了 一 个 方 便 、 面 友 好 的 ,l 矩 信 构 界 E户 E 环境. MATI 语 言 的 图 形 用 户 界 面 (GUI AB )可 以 使 程 序 变 成 通 用 化 的 应 用 软 件 , 导 用 引 户进行计3 g ̄ 5 析 , 户 可 以 利 用 事 先 设 计 的 用 户 界 面 通 过 其 上 的 按 钮 和 菜 单 与 计 算 机 } - 用 直 接 进 行 信 息 交 流 , 择 所 需要 的功 能 完 成 各 种计 算 和 分 析 . 选 本 文 根 据 M ATL AB 的 GUI界 面 , 作 了 菲 涅 耳 圆 孑L 单 缝 衍 射 仿 真 试 验 , 后 给 出 制 和 最
基于半波带法菲涅耳声透镜的仿真与实验研究

月10
期
大 学 物 理
COLLEGE PHYSICS
Vol.37 No.10 Oct.2018
基于半波带法菲涅耳声透镜的仿真与实验研究
陈冰心1,朱浩宇2,涂宏业1,李金华1,张 烨1,金光勇1
(1.长春理工大学 理学院,吉林 长春 130022;2.长春理工大学 光电工程学院,吉林 长春 ) 130022
Li 等人[10,11]设计了具有空气排孔通道的复合法布 里-珀罗共振声学结构的声透镜,实现了在空气中 对可闻声波的放大,并进行了有限元数值仿真.由于 低频声源在空气中声聚焦与超声波在水下环境中的 声聚焦相比,其声速大大降低,介质也有很大不同, 从而声透镜的设计结构也会有很大的区别(列如前 面两人设计的声透镜结构就与水中聚焦的凹型声透 镜有很大不同).因此,对期望得到空气环境下声聚 焦的效果,空气中声透镜结构的设计和研究是非常 有意义和必要的.
+
-1
a N+ 1 N
(1)
同样的原理可以运用于声学上.
图 2 菲涅耳声透镜几何结构图
声压公式[13]:
(,) ( ) p r t = p0 cos ωt-kr
(2)
r
p
0
为初 以
始压强,ω 为角频率,k 为波矢量. S 为点声源,B 为聚焦点.若只露出
奇
数
个
半
波带,在 B 点处的总声压为
但
考
虑
到
; 收稿日期: 修回日期:
2018 - 12 - 19
2018 - 05 - 08
基金项目:吉林省教育科学“十三五”规划课题( )、吉 GH170178 林省教育厅高等教育教学改革研究课题(重点)资助
菲涅耳衍射仿真
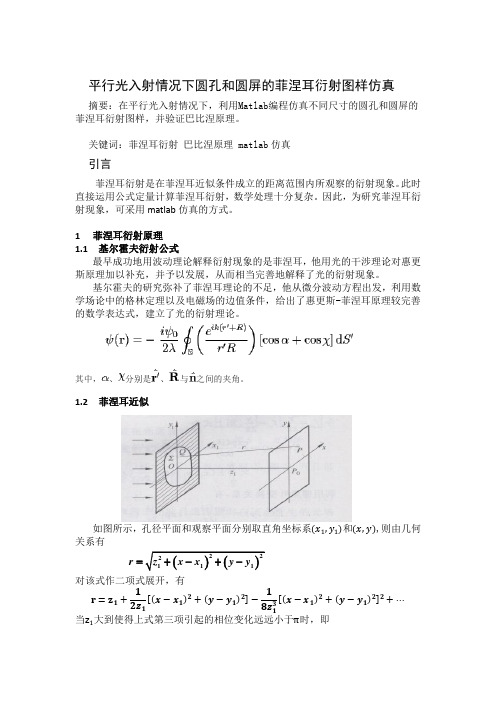
屏上 P 点的光场复振幅,������0 ������ 表示无衍射屏时 P 点的光场复振幅,根据惠更斯菲涅耳原理,������1 ������ 和������2 ������ 可表示成对
1
和
2
开孔部分的积分,而两个屏
的开孔部分加起来就相当于屏不存在,因此 ������0 ������ = ������1 ������ + ������2 ������ 该式说明,互补屏在衍射某点产生的复振幅之和等于光波自由传播时在该点 产生的光场复振幅。 2 matlab 仿真程序设计 2.1 菲涅耳衍射的实现 在菲涅耳近似下,P点的光场复振幅可表示为 ������ ������, ������ = ������������ ������1 , ������1 ∗ ℎ(������, ������) 其中
总结与展望
利用所学知识基本完成了菲涅耳衍射的仿真。但在完成课程设计的过程中深 深的感受到自身各方面的不足。还需更为努力。对于该仿真,因为使用了卷积, 当采样数过大时,运算速度会变得很慢。该仿真还有更好的实现方式,是基于傅 里叶变换的,可大大降低时间复杂度,无奈能力,精力有限,就不去实现了。
参考文献
【1】 奥本海姆., Oppenheim A, 刘树棠. 信号与系统[M].西安: 西安交通大学出 版社, 1998.
E3 (������)图样
E3 (������)分布图
E3 ������ 与对应正方形衍射屏中央剖面光强分布对比图 可见巴比涅定理成立。
3.4 夫琅禾费衍射
菲涅耳数F ≪ 1时,衍射图样为夫琅禾费衍射。 选取F=0.1,n=400,p=2
F=0.1时圆孔衍射图样
F=0.1时圆孔衍射光强分布图
圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

工程光学综合练习-----圆孔、矩孔的菲涅尔衍射模拟圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布,为倾斜因子。
根据基尔霍夫对此公式的完善,有设衍射屏上点的坐标为(x1, y1),接收屏上点的坐标为(x, y),衍射屏与接收屏间距离为z1,当满足菲涅尔近似条件时,即此时可得到菲涅尔衍射的计算公式把上式指数项中的二次项展开,并改写成傅里叶变换的形式,可以写成上式为菲涅尔衍射的傅里叶变换表达式,它表明除了积分号前面的一个与x1、y1无关的振幅和相位因子外,菲涅尔衍射的复振幅分布是孔径平面的复振幅分布和一个二次相位因子乘积的傅里叶变换。
相对于夫琅和费衍射而言,菲涅尔衍射的观察屏距衍射屏不太远。
在菲涅尔衍射中,输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场以及光强分布,考虑到这三个量都是二维分布,而且Matlab主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x, y)以及(x1, y1)。
二、圆孔菲涅尔衍射用MATLAB分别构造表示衍射屏和接收屏的二维矩阵。
注意使两矩阵阶次相同,考虑到运算量的要求,采样点数不能过多,所以每个屏的x和y方向各取200到300点进行运算。
根据式(4),选取合适的衍射屏和接收屏尺寸和相距的距离,模拟结果如下:取典型的He-Ne激光器波长λ=632.8nm,固定衍射屏和接收屏尺寸和相距的距离,分别取不同的圆孔半径,得到以下三组衍射图样,其圆孔半径分别为12mm,20mm,50mm图1(r=12mm)图2(r=20mm)图3(r=50mm) 三、矩孔的菲涅尔衍射步骤与上述相同,仅需改变与衍射屏形状对应的矩阵。
这里选择矩孔的长宽相等,分别为15mm,20mm,30mm,其衍射图样及强度分布如图4、5、6图4(a=b=15mm)图5(a=b=20mm)图 6(a=b=30mm)四、MATLAB 程序%所有长度单位为毫米lamda=632.8e-6; k=2*pi/lamda;z=1000000;%先确定衍射屏N=300; %圆屏采样点数a=15;b=15;[m,n]=meshgrid(linspace(-N/2,N/2-1,N));I=rect(m/(2*a)).*rect(n/(2*b));q=exp(j*k*(m.^2+n.^2)/2/z);subplot(2,2,1); %圆孔图像画在2行2列的第一个位置 imagesc(I) %画衍射屏的形状colormap([0 0 0; 1 1 1]) %颜色以黑白区分axis imagetitle('衍射屏形状')L=300;M=300; %取相同点数用于矩阵运算若为圆孔,方框内替换为以下程序 r=12;a=1;b=1; I=zeros(N,N); [m,n]=meshgrid(linspace(-N/2,N/2-1,N)); D=((m-a).^2+(n-b).^2).^(1/2); i=find(D<=r); I(i)=1; %孔半径范围内透射系数为1[x,y]=meshgrid(linspace(-L/2,L/2,M));h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z);%接收屏H =fftshift(fft2(h));B=fftshift(fft2(I)); %圆孔频谱G=H.*B; %公式中为卷积,空间域中相卷相当于频域中相乘U= fftshift(ifft2(G)); %求逆变换,得到复振幅分布矩阵Br=(U/max(U)); %归一化subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)% figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U)); %画三维图形subplot(2,2,4);plot(abs(Br))。
经典实验讲义-菲涅尔单缝衍射 (演示实验)
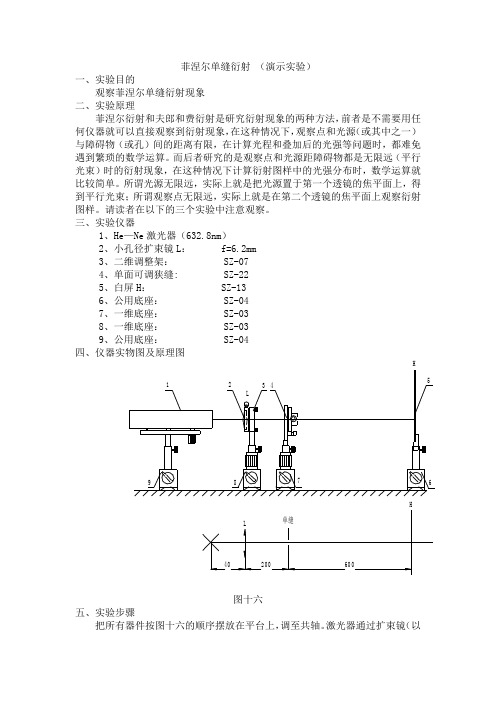
菲涅尔单缝衍射(演示实验)一、实验目的观察菲涅尔单缝衍射现象二、实验原理菲涅尔衍射和夫郎和费衍射是研究衍射现象的两种方法,前者是不需要用任何仪器就可以直接观察到衍射现象,在这种情况下,观察点和光源(或其中之一)与障碍物(或孔)间的距离有限,在计算光程和叠加后的光强等问题时,都难免遇到繁琐的数学运算。
而后者研究的是观察点和光源距障碍物都是无限远(平行光束)时的衍射现象,在这种情况下计算衍射图样中的光强分布时,数学运算就比较简单。
所谓光源无限远,实际上就是把光源置于第一个透镜的焦平面上,得到平行光束;所谓观察点无限远,实际上就是在第二个透镜的焦平面上观察衍射图样。
请读者在以下的三个实验中注意观察。
三、实验仪器1、He—Ne激光器(632.8nm)2、小孔径扩束镜L: f=6.2mm3、二维调整架: SZ-074、单面可调狭缝: SZ-225、白屏H: SZ-136、公用底座: SZ-047、一维底座: SZ-038、一维底座: SZ-039、公用底座: SZ-04四、仪器实物图及原理图图十六五、实验步骤把所有器件按图十六的顺序摆放在平台上,调至共轴。
激光器通过扩束镜(以不满足远场条件)投射到单缝上,如图十六所示,即可在屏幕上出现衍射条纹,缓慢地连续地将单缝由窄变宽,同时注意屏幕上的图样,即可观察到与理论分析结果一致的由夫郎和费单缝衍射图样过渡到菲涅尔单缝衍射图样。
也可不加扩束镜。
(图中数据均为参考数据)实验十七 菲涅尔圆孔衍射(演示实验)一、实验目的观察菲涅尔圆孔衍射现象二、实验原理附图13如附图13所示:S —单色光源P —光场中任一点S 与P 之间有一带圆孔的光屏M ,圆孔中心在SP 连线上。
这时S 对P 的作用就只是内露出的一部分波面∑上的那些次波源在P 点所产生的光振动的叠加。
按照波带法,分别以P 为中心,r+2/λ,r+λ…为半径将露出的波面分成若干个波带,各波带在P 点产生振动的振幅为: 122i j a a A =± 当圆孔露出奇数个波带时,P 点的光强度是约等于21a 亮点,而当圆孔露出偶数个波带时,P 点是光强度接近于零的暗点。
具有光栅结构方孔的菲涅耳衍射仿真与分析

收稿日期:2008209206 修改日期:2008210217基金项目江苏省教育厅自然科学研究项目基金资助(K D )作者简介高玲,女,南京晓庄学院物理与电子工程学院副教授,主要从事光信息方面的研究2008年11月第6期南京晓庄学院学报JOURNAL OF NANJ I NG X I A OZ HUANG U N I V ERS ITY Nov .2008No .6具有光栅结构方孔的菲涅耳衍射仿真与分析高 玲,林继成,何龙庆(南京晓庄学院物理与电子工程学院,江苏南京210017)摘 要:运用数值计算方法对具有光栅结构的方孔的菲涅耳衍射场的光强分布进行分析和仿真,基于菲涅耳衍射积分和子波相干叠加概念设计了数值算法,给出了相应的MAT LAB 程序以及仿真结果.从数值分析结果可以直观而明确的看到,具有正弦振幅光栅结构的方孔的菲涅耳衍射花样是带有明显方孔衍射特征的光栅的像,像的清晰度以及与原光栅的相似度由方孔衍射的菲涅耳数以及光栅条纹数决定.与无穷大正弦振幅光栅的菲涅耳衍射类似,当满足一定的条件时也会出现像的频率加倍的现象.关键词:光学;光栅;菲涅耳衍射;数值模拟中图分类号:O436.1 文献标识码:A 文章编号:100927902(2008)06200112040 引言当衍射物的尺寸比光波长大得多时,标量衍射理论是有效的.在光学系统设计、光信息处理和传输等众多领域,标量衍射理论有着重要的应用.然而,基于惠更斯2菲涅耳原理的衍射积分的计算通常是很困难的,为此需要对衍射积分进行近似处理并采用数值计算方法.当所研究的衍射场局限在旁轴区域时,菲涅耳近似在大多数情况下可以达到满意的精度[1].近年来,在菲涅耳近似下的衍射场数值计算问题人们已经进行了大量的研究[227],但未见有对有限大小光栅衍射的仿真算法的介绍.本文以MAT LA B 为计算平台,以菲涅耳衍射积分为基础,采用子波叠加概念,针对带有正弦振幅光栅结构的菲涅耳衍射,设计了数值仿真算法并给出了相应的程序,并对仿真结果进行了分析.1 光栅衍射的标量理论波长λ单位振幅的单色平面波,垂直照射带有宽度为2L 方形孔径的衍射屏,孔径上贴有一片振幅型薄透射光栅,衍射屏位于xy 平面,坐标原点取在孔径中心,x 轴和y 轴分别与孔径两边平行,z 轴沿入射光方向,光栅的刻线与y 轴平行.当满足旁轴近似条件时,衍射场复振幅可由菲涅耳衍射积分确定[1].U (x O ,y O )=exp (jkz )j λz exp j k 2z (x 2O +y 2O )κ∞-∞t (x,y)exp j k 2z (x 2+y 2)exp -j k z(x O x +y O y )d x d y (1)其中,t (x,y )是衍射屏透过率函数t (x,y)=12[1+m cos (2πx /d)](-L ≤x ≤L,-L ≤y ≤L )(2)则衍射复场分布可表为U (x O ,y O )=e jkz j λz exp j k 2z (x 2O +y 2O )I x I y (3):07J 140122.:.其中I x =∫L-L 12[1+m cos (2πx /d )]e j k 2z (x 2-2x O x)d x I y =∫L -Le j k 2z (y 2-2y O y)d y(4)观察屏上衍射光强的分布为I(x O ,y O )=1λz 2|I x I y |2(5)2 仿真算法将光栅孔径沿平行于长度和高度方向分割成N ×N 个微小单元,当N 足够大时,每个单元可视为一个次级点源.所有点源在观察屏上P (x O ,y O )点合成复振幅可由(4)和(5)式将积分改为求和得到I x =2L N ∑N /2i =-N /212[1+m cos (2πx i /d )e jk(x 2i -2x O x i )/2z ]I y =2L N ∑N /2i =-N /2e jk(y 2i -2y O y i )/2z(6)其中x i =i 2LN ,y i =i 2LN (7)以MATLAB 为计算平台,在观察屏上取适当大小的正方形区域,并进行M ×M 采样,采样点阵的坐标用二维数组X O 和Y O 存储,由于Y O =X T O ,实际只需一个数组.用二维数组I x 和I y 存储输出面上各采样点对应的经由(7)式算得的I x 和I y 值.即I x =2L N ∑N /2i =-N /212[1+m cos (2πx i /d )e jk (x 2i -2x i X O )/2z ]I y =2L N ∑N /2i =-N /2e j k (y 2i -2y i X T O )/2z(8)3 仿真结果分析3.1 沿z 轴的衍射光强分布对于无穷大正弦振幅光栅,其菲涅耳衍射光强沿z 轴是呈正弦分布的[1],对于没有光栅结构的方孔菲涅耳衍射沿z 轴的光强分布如图1(a )所示,而方形正弦振幅光栅孔径的菲涅耳衍射光强沿z 轴的分布如图1(b )所示.图1(c )是图1(b )在靠近纵轴的局部放大图形,图1(d )是图1(c )前三个波形的进一步放大的图形.可见在距离衍射屏较近的区域内与无穷大正弦振幅光栅菲涅耳衍射的光强分布相似,只是在正弦分布之上叠加了频率逐渐减小的快速小幅波动,表明在该区域内以光栅衍射作用为主;右侧光强的分布规律,除了振荡幅度有所减小外与没有光栅结构的方孔菲涅耳衍射几乎完全相同,表明在该区域内以方孔衍射作用为主.3.2 与z 轴垂直平面上的衍射光强分布图2为取λ=7×10-7m ,L =1.4×10-2m ,孔径内光栅总线数α=30时的两幅衍射仿真图和沿x 轴光强分布图.由图2可见,方形正弦振幅光栅孔径的菲涅耳衍射场的光强分布是无穷大正弦振幅光栅光栅的衍射和方孔衍射的共同结果,衍射花样是带有明显方孔衍射特征的光栅的像.当菲涅耳数较大时,除了边缘部分之外,能够得到光栅的较清晰的像;菲涅耳数较小时像发生变形和模糊;菲涅耳数小于某一值时,光栅像将完全消失.对于无穷大正弦振幅光栅衍射,当满足一定的条件[1]时将得到光栅理想的像(Talbot 像).由于方孔衍射作用不可忽略,这里不可能产生光栅理想的像.对仿真结果的分析发现,只有当d 2/8λ<z <2αd 2/λ时才有可能出现光栅的像,这恰对应图()的区域当孔径内光栅条纹总数给定时,像的清晰度和与原光栅的相似度由方孔衍射菲涅耳数决定,通常菲涅耳数越大像越清晰相似度越高1c ..图1 正弦振幅光栅菲涅耳衍射场沿z轴的光强分布图2 仿真图和沿x 轴的光强分布图,α=30,L =0.014m对于无穷大正弦振幅光栅的衍射,当满足条件zλ/d 2=n -1/2时,光栅像的频率是原光栅频率的两倍[1].对于方形光栅孔径的衍射,计算发现当满足下式N F =α24n -2 (n =1,2,……).(9)时,也会出现像的频率加倍的现象.图3是取光栅条纹总数α=30,N F =450时的仿真图和相应的光强分布图.因满足条件(9),将其与图2(a )比较即可看出,像的频率是原光栅频率的两倍,而像的可见度明显降低. 结论通过对大量仿真结果的分析,发现具有正弦振幅光栅透射率的方孔的菲涅耳衍射场的光强分布是无穷4图3 当满足条件(12)时像的频率加倍且亮度和对比度降低大正弦振幅光栅的衍射和方孔衍射的共同结果,衍射花样是带有明显方孔衍射特征的光栅的像,而不能产生光栅的理想的像,光栅像的清晰度以及与原光栅的相似度由方孔衍射的菲涅耳数以及孔径内光栅条纹数决定.当满足条件(9)时会出现像的频率加倍的现象.本文给出的算法不仅能够对具有正弦振幅光栅透射率函数的方孔的菲涅耳衍射进行仿真,而且适用于具有任何透射率函数的矩形孔衍射计算和分析,只要该透射率函数可表为分离变量形式.参考文献:[1]G ood man J W.Introduc ti on t o Fourie r Opti c s(s econd editi on)[M].M cGraw2Hill Co mpanies,1998,57281.[2]侯红方,钟丽云.矩孔菲涅耳衍射的一种数值计算方法[J].光电技术应用,2006,21(6):59261.[3]柴晓冬,韦穗.菲涅耳衍射光场分布的数值计算与数字重构[J].量子电子学报,2003,20(4):4352438.[4]喻力华,赵维义.圆孔衍射光强分布的数值计算[J].大学物理,2001,20(1):16219.[5]钱晓凡,胡涛,张晔.基于MAT LAB的衍射场模拟计算[J].昆明理工大学报(理工版),2004,29(3):1322134.[6]陈聪,李定国.基于快速傅里叶变换的衍射现象的数值仿真[J].大学物理,2004,23(9):46249.[7]吕百达,季小玲,陶向阳,赵光普,肖希.硬边衍射光束的计算模拟[J].红外与激光工程,2005,34(03):3012305.[8]Kraus H G.Huygens2Fresne l2Kirchhoff wave2front diffracti on for m ulati on:s pherical waves[J].J Op t Soc Am A,1989,6(8):119621205.(责任编辑:王海军) Num er i ca l S im ul a ti on of Fr esnel D i ffra cti on bya Squa r e Aper tur e with Gra ti ng Str uctur eGAO Ling,L I N J i2cheng,HE Long2qing(School of Physi c s and El ec tronic Engineering,Nanjing Xi aozhuangUnive rsity,N anjing210017,China)Abstrac t:The intensity distribution of the Fr e snel diffrac ti on field f or square aperture with grating structure is ana2 lyzed and si m ulated by a nume rical m ethod.A n algorithm of nu m erica l ca lcula tions of Fr e snel diffraction by a square a pe rture with grating structure is presented alongw ith the corres pondingMA T LA B p r ogr a m s and si mulations. The results indica te that the F r e snel diffrac tion pattern of a square apertur e with sinus oida l amplitude gr a ting struc2 ture is an i mage of gr a ting w ith fea tur e s of diffraction by squa r e apertur e,and the i mage definition is decided by F resnel num ber and the number of s patial peri ods of the grating contained in the ape rture.Si m ilar t o the F r e snel diffraction by a boundle ss sinusoidal a mp litude gr ating,the i m age has t wice the fr equency that the original gr a ting doe s and ha s reduced the contrast when certain conditi ons a r e sa tisfied.Key wor ds:optics;gr a ting;F r e snel diffracti on;nu m erica l si m ulati on。
圆孔矩孔的菲涅尔衍射模拟(matlab实现)-工程光学

圆孔矩孔的菲涅尔衍射模拟(m a t l a b实现)-工程光学-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII工程光学综合练习-----圆孔、矩孔的菲涅尔衍射模拟圆孔和矩孔的菲涅尔衍射模拟一、原理由惠更斯-菲涅尔原理可知接收屏上的P点的复振幅可以表示为其中为衍射屏上的复振幅分布,为倾斜因子。
根据基尔霍夫对此公式的完善,有设衍射屏上点的坐标为(x1, y1),接收屏上点的坐标为(x, y),衍射屏与接收屏间距离为z1,当满足菲涅尔近似条件时,即此时可得到菲涅尔衍射的计算公式把上式指数项中的二次项展开,并改写成傅里叶变换的形式,可以写成上式为菲涅尔衍射的傅里叶变换表达式,它表明除了积分号前面的一个与x1、y1无关的振幅和相位因子外,菲涅尔衍射的复振幅分布是孔径平面的复振幅分布和一个二次相位因子乘积的傅里叶变换。
相对于夫琅和费衍射而言,菲涅尔衍射的观察屏距衍射屏不太远。
在菲涅尔衍射中,输入变量和输出变量分别为衍射孔径平面的光场分布和观察平面的光场以及光强分布,考虑到这三个量都是二维分布,而且Matlab主要应用于矩阵数值运算,所以本程序选择用二维矩阵来存储衍射孔径平面和观察平面的场分布,并分别以矩阵的列数和行数来对应平面的直角坐标值(x, y)以及(x1, y1)。
二、圆孔菲涅尔衍射用MATLAB分别构造表示衍射屏和接收屏的二维矩阵。
注意使两矩阵阶次相同,考虑到运算量的要求,采样点数不能过多,所以每个屏的x和y方向各取200到300点进行运算。
根据式(4),选取合适的衍射屏和接收屏尺寸和相距的距离,模拟结果如下:取典型的He-Ne激光器波长λ=,固定衍射屏和接收屏尺寸和相距的距离,分别取不同的圆孔半径,得到以下三组衍射图样,其圆孔半径分别为12mm,20mm,50mm图 1(r=12mm)图 2(r=20mm)图 3(r=50mm)三、矩孔的菲涅尔衍射步骤与上述相同,仅需改变与衍射屏形状对应的矩阵。
Fraunhofer衍射实验

F r a u n h o f e r..............衍射实验一,实验目的调试程序仿真F r a u n h o f e r单缝衍射实验,观察光的衍射现象;认识F r a u n h o f e r 衍射是实现F o u r i e r变换运算的物理方法,这是对光学图像作频谱分析的基础;调整仿真程序中的可控参数,加深对远场衍射的理解。
二,实验原理三实验内容1、仿真F r a u n h o f e r单缝衍射实验;2、改变可调的实验参数,观察衍射现象的变化,分析影响衍射光强分布变化的因素。
3、分析F r a u n h o f e r衍射与F o u r i e r变换的关系。
clear;Lambda=input('输入光的波长(单位为nm):取500)');Lambda=Lambda*1e-9;aWidth=input('输入缝的间距(单位为mm):(取2)');aWidth = aWidth *0.001;Z=input('输入缝到屏的距离(单位为m):(取1)');ymax=3*Lambda*Z/ aWidth;Ny=51;ys=linspace(-ymax,ymax,Ny);NPoints=51;yPoint=linspace(-aWidth/2, aWidth/2,NPoints);for j=1:NyL=sqrt((ys(j)-yPoint).^2+Z^2);Phi=2*pi.*(L-Z)./Lambda;SumCos=sum(cos(Phi));SumSin=sum(sin(Phi));B(j)=(SumCos^2+SumSin^2)/NPoints^2;endplot(ys,B,'*',ys,B);gridaxis([-ymax,ymax,0.0,1.0]);set(gcf,'color','w')输入光的波长(单位为nm):取500)500输入缝的间距(单位为mm):(取0.2)0.2输入缝到屏的距离(单位为m):(取1)>> 1clearlam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam; sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2; endN=255;Br=(B/max(B))*N;subplot(1,2,1);image(ym,ys,Br);colormap(gray(N));subplot(1,2,2);plot(B,ys);2、改变可调的实验参数,观察衍射现象的变化,分析影响衍射光强分布变化的因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验注意事项(必读)
1. 提前预习,没有弄清楚实验内容者,禁止接触 实验仪器。 2. 注意激光安全。绝对不可用眼直视激光束,或 借助有聚光性的光学组件观察激光束,以免损 伤眼睛。 3. 注意用电安全。He-Ne 激光器电源有高压输出, 严禁接触电源输出和激光头的输入端,避免触 电。 4. 注意保持卫生。严禁用手或其他物品接触所有 光学元件(透镜、反射镜、分光镜等)的光学 表面;特别是在调整光路中,要避免手指碰到 光学表面。 5. 光学支架上的调整螺丝,只可微量调整。过度 的调整,不仅损坏器材,且使防震功能大减。 6. 实验完成后,将实验所用仪器摆放整齐,清理 一下卫生。
2.2 菲涅耳衍射算法讨论 A. 菲涅耳脉冲响应(IR)算法: (Fresnel Impulse Response)
(5)
根据公式(4)则观察平面的菲涅耳衍射场的分布可以表示为两个傅里叶变 化乘积的逆变换形式,即
U 0 ( x, y ) = F −1 F {U1 ( x, y )} F {h ( x, y )}
图 4. 十字形窄缝物体 (5) 模拟十字型窄缝在衍射距离分别为 200mm 和 2m 时的光场分布。 将结果保 存在电脑中。 (6) 菲涅耳衍射的实验观察:
透镜
激光器
扩束镜 衍射物体 观察屏
图 5. 实验光路示意图 按光路示意图 5 调整光路,调节共轴,调出平行光,使小孔屏或十字狭 缝(本实验使用光阑和十字狭缝)处于扩束的光斑中心。
λz
L
时,传递函数算法(TF)准确;当抽样间
λz
L
时,脉冲响应函数算法(IR)准确。根据以上判据条件,选择
合适的算法,模拟光场分布大小为 5cm*5cm,波长为 0.532um,矩形孔半 宽度 1cm 的情况下,在衍射距离 z=200mm,和 z=200m 时的菲涅耳光场分 布,将所得结果保存在电脑中。 (4) 自己设计十字型窄缝物体(参考以前的实验一内容) ,如下图,物体大小 3cm*3cm,十字形窄缝的宽度为 1mm,长度为 1cm。
k i [( x0 − x1 ) 2 + ( y0 − y1 ) 2 ] 1 ikz 2z = e U1 ( x1 , y1 )e dx1dy1 iλ z ∫∫ −∞
(1)
菲涅耳衍射系统是线性空不变系统。如果令
1 ikz i 2kz [( x − x0 )2 +( y − y0 )2 ] =h( x0 − x1 , y0 − y1 ) (2) h( x0 , y0 ; x1 , y1 ) = e e iλ z
思考题
(1)圆孔的菲涅耳衍射的 matlab 模拟? (2)设计利用 matlab 条件程序,整合两种算法,使菲涅耳衍射可模拟任意 衍射距离的光场分布。
6 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
k=2*pi/lamda; %波数 w=0.005; %物体的半宽度 z=50000e-3;%衍射距离 %%%%----------矩形物体--------------[X1,Y1]=meshgrid(x1,y1); u1=rect(X1/(2*w)).*rect(Y1/(2*w)); %矩形物体光场分布 I1=abs(u1.^2); figure(1) imagesc(x1,y1,I1); axis square; axis xy; colormap('gray'); xlabel('x(m)'); ylabel('y(m)'); title('z= 0 m'); %%%-----------------衍射场的分布计算-----------% u2=profTF(u1,L1,lamda,z);% dx >= lamda*z/L 时准确 u2=profIR(u1,L1,lamda,z);% dx <= lamda*z/L 时准确 x2=x1; y2=y1; I2=abs(u2.^2); figure(2) imagesc(x2,y2,I2); axis square; axis xy; colormap('gray'); xlabel('x(m)'); ylabel('y(m)'); text_buffer = strcat( '传播距离为 z= ',num2str(z),'m'); title(text_buffer);
{
}
(8)
2.3 菲涅耳衍射算法的 Matlab 代码(我们编写新的 Matlab 的函数,以后可以 直接调用) A. 菲涅耳脉冲响应(IR)算法的 Matlab 函数代码: (将以下代码输入,新建一 个 M 文件,保存名字为 propIR) function [ u2 ] = profIR( u1,L,lamda,z ) % 传播-脉冲响应函数方法 % 假设 x 和 y 方向具有相同的长度和相同的抽样 % u1-输入场函数 % L-输入和观察平面的长度 % lamda-波长 % z-传播距离 % u2-观察场
5 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
2.4 举例-矩形孔的菲涅耳衍射场分布计算:
x 10
-3
z= 0 m
8 6 4 2
y(m)
0 -2 -4 -6 -8 -10 -10
-5
0 x(m)
5 x 10
-3
图 3. 矩形孔物体 (矩形孔的制作,可参考实验一的内容,这里我们用函数 matlab 代码(实验一 中的附录有源代码 rect.m) )讲一下代码新建一 M 文件文件名为 rect.m function [ out ] = rect( x ) %矩形孔函数 out=abs(x)<=1/2; end
ikz x y = H ( f x , f y ) e= eikz e − iπλ z 1−( λ f )2 −( λ f )2 ( f x2 + f y2 )
(7)
则观察平面的菲涅耳衍射场的分布可以表示为
U 0 ( x, y ) = F −1 F {U1 ( x, y )} H ( f x , f y )
8 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专接收白屏先远后近地移动,观察圆孔和 十字窄缝的强度交替变化的规律。
五、实验报告要求:
(1) 简述菲涅耳衍射的基本原理。 (2) 讨论菲涅耳衍射不同算法的模拟结果, 给出模拟结果的总结、 说明和讨论。 (3) 讨论实验观察到的小孔和十字孔的菲涅耳衍射图像。
(4)
= U1 ( x0 , y0 ) * h( x0 , y0 )
其中,U1 ( x0 , y0 ) 为透过物体后得透过率函数,h( x0 , y0 )
3 鲁东大学物理与光电工程学院
为脉冲相应函数
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
eikz i 2kz ( x 2 + y 2 ) h( x0 , y0 )= e iλ z
4 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
[M,N]=size(u1); %获取入射场的阵列大小 dx=L/M; %抽样间隔 k=2*pi/lamda; %波数 x=-L/2:dx:L/2-dx;%频率域坐标 [X,Y]=meshgrid(x,x); h=1/(j*lamda*z)*exp(j*k/(2*z)*(X.^2+Y.^2)); %脉冲响应函数公式 5,我们忽略了 eikz 因一相位常数,不影响光场分布 H=fft2(fftshift(h))*dx.^2; %创建传递函数 U1=fft2(fftshift(u1)); % 入射场 u1 的傅里叶变换 U2=H.*U1;%两个函数的乘积 u2=ifftshift(ifft2(U2));% 逆傅里叶变换,公式 6 end
实验过程中要切记以上注意事项。如 有违犯,将严重影响你的实验成绩!
1 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
菲涅耳衍射数字模拟仿真与实验
一、实验目的:
1. 2. 3. 掌握菲涅耳衍射的基本原理及其 Matlab 编程语言; 利用 Matlab 数值模拟几种典型物体的菲涅耳衍射光场分布; 利用现有激光实验系统自己动手搭建衍射光路,观察几种物体的菲涅耳衍射 场的空间分布,加深对光的衍射现象和理论的理解。
三、实验仪器:
电脑、导轨、氦氖激光器、扩束镜、透镜、反射镜、衍射元器件、一维位移 架、导轨滑块。
7 鲁东大学物理与光电工程学院
2015 年光电信息科学与工程专业综合实验-信息光学专题实验
四、实验内容
(1) 掌握菲涅耳衍射的基本理论,熟悉菲涅耳衍射的 matlab 编程方法。 (2) 根据讲义上的实例,改变不同参数观察在不同衍射距离处,两种算法的模 拟结果。 (3) 判据条件:当抽样间隔 ∆x ≥ 隔 ∆x ≤
其中, F {} , F
−1
{
}
(6)
{} 分别表示为傅里叶变化与逆傅里叶变换。
B. 菲涅耳传递函数(TF)算法: (Fresnel Transfer Function) 菲涅耳衍射的卷积积分表达式表明:若把菲涅耳衍射看作是一个系统,则这 个系统等效为一个线性空不变系统, 因此这个衍射过程存在一个相应的传递函数 如下:
以下为矩形孔物体的菲涅耳衍射的 matlab 代码: 模拟光场大小为 2cm*2 厘米,波长 0.6328um,孔大小,半宽度 5mm,衍射距离 50m。 clear all close all clc %%%%%%%%%----参数设定--L1=0.02; % 光场边长的长度,单位 m M=300; %抽样点数 dx1=L1/M; %抽样间隔 x1=-L1/2:dx1:L1/2-dx1; %抽样坐标 y1=x1; % x 与 y 方向相等 lamda=0.6328e-6; %波长
