概念设计阶段曲轴强度计算规范

合集下载

概念设计阶段连杆强度计算规范

CAE 规范第1部分：概念设计阶段连杆强度计算1 范围本部分规定了连杆强度的校核方法。

本部分适用于概念设计阶段连杆强度的校核，以安全系数表示连杆在发动机产品生命周期内的安全裕度。

对船用发动机，需同时采用船检规范进行校核。

2 名称、符号图1 连杆杆身最小截面模型示意图表-1 连杆强度计算参数序号名称符号单位 1连杆质量rod m kg2 活塞组质量 pst mkg 3 连杆长度 Lmm 4 缸套内径 D mm 5连杆大头轴瓦宽度ps Lmm6 连杆主轴瓦宽度js Lmm7 杆身最小截面积 A2mm 8 极惯性矩（z 轴） z I 4mm 9极惯性矩（y 轴）y I4mmσMPa10 材料的屈服极限sL mm11 连杆大小头孔中心距y12 连杆杆身长z L mm13 材料的抗拉强度bσMPaσMPa13 材料的疲劳极限1-14 转速n rpm15 最大爆压g p MPa 3 计算流程图2 流程图4 计算原理连杆的设计基于对高应力区域的疲劳安全进行评估。

本规范中的计算基于以下假定：●连杆小头内侧、杆身过渡圆角处、大头盖螺栓台阶面是高应力区域；●活塞组往复惯性力以轴向抛物线、径向120°余弦分布作用在小头衬套和连杆轴瓦上；●爆发压力以轴向抛物线、径向120°余弦分布作用在小头衬套和连杆轴瓦上；●活塞组往复惯性力、爆发压力是引起连杆破坏的主要因素，连杆旋转惯性力产生的影响很小，可以忽略不计。

5 计算工况对长期稳定工作于额定转速的发动机，以全负荷工况为计算工况；对在大转速范围内工作的发动机，以额定转速为计算工况；对船用发动机，以超负荷（110%负荷）工况为计算工况。

通常，一个工作周期内，由燃气压力和惯性力引起的作用在连杆上的径向载荷对所有曲柄位置都应计算。

简单起见，径向力可以采用简化计算，并只计算一个工作周期内的最大受拉和最大受压两种状态。

6 连杆载荷6.1 压杆稳定时连杆载荷连杆属于细长杆件类的柴油机零件，在承受较大爆发压力的工况下须做杆件的稳定性校核：临界载荷由Rankine Gordan 公式计算：p zz F pn = py yF p n =6.2 连杆受到惯性载荷连杆载荷以大小头孔轴向抛物线、径向120°余弦分布的分布力作用在衬套和连杆轴瓦上，作用范围为连杆大头轴瓦宽度（见图3-b ），其大小按以下公式计算：θθ23cos )41(25),(22psps p p p L x L D F x q -⋅=p F ：作用在衬套和连杆轴瓦上的径向载荷，N ；对于连杆小头p F 可按曲柄连杆动力学或多体动力学计算得到，对V 型机，p F 应考虑不同的相位和连杆设计（分叉连杆、连接连杆、并列连杆等）分别计算与合成。

轴强度计算公式(机械设计)

M 21H M 21V 829400Nmm M1
2 2 M1 M 1H M 1V 717300Nmm
3.求作扭矩图：
4..求作当量弯矩图：
M 1ca M 1 (T ) 2 1.376106 Nmm ca M 1 (T ) 2 M 1 7.173105 Nmm M1
三. 转轴→弯矩＋转矩→按弯扭合成强度计算
1.受力分析：M + T 由┌Ｍ→ σb→ r =－1 └Ｔ→ τ →┌单向→
T
合成弯矩Ｍ r =0 r =－ 1
M M H 2 MV 2
└双向→ 2.转轴的强度计算 ⑴ 按弯扭合成强度计算当量弯矩Ｍca：
M ca M 2 (T ) 2
Ⅱ
B Ⅰ
2
M Bca (T ) 2 T 1.098106 Nmm
5 .求轴的直径：Ⅰ-Ⅰ; Ⅱ-Ⅱ
危险截面？
Ⅰ-Ⅰ截面： d1 3 M1 ca /(0.1 1 ) 65.93mm
Ⅱ-Ⅱ截面: d 2 3 M Bca /(0.1 1 ) 61.16mm
轴功率计算公式抗拉强度计算公式光照强度计算公式屈服强度计算公式抗弯强度计算公式弯曲强度计算公式钢筋强度计算公式暴雨强度计算公式强度计算公式抗压强度计算公式
§15—3 轴的强度计算 (一) 轴的受力分析及强度计算
一. 心轴－只受弯矩→按弯曲强度计算 1.受力分析：由Ｍ→ b ①固定心轴－轴不转动
A
10500 tg20o / cos12o15 3900N Fa Ft tg 10500 tg12o15 2280N
c
2 .求作支反力及弯矩图 H面：
RBH=FtC/(b+C)=10500×180/(110+180) =6520N RCH=Ft－RBH=10500-6520=3980N

轴的强度计算

例：试设计图示斜齿圆柱齿轮轮减速器的低速袖。已知轴的转速n＝ 140r/min．传递功率P＝5kw。轴上齿轮的参数为：齿数Z＝58，法面模数mn＝3mm，分度圆螺旋角β＝11°17′ 3 ″齿宽及轮毂宽b＝70mm。
解：1)选择轴的材料
减速器功率不大．又无特殊要求，改选最常用的45号钢，并作正火处
对于受重载，尺寸受限制和重要场合工作的轴，应采用安全系数法校核。并进行刚度、稳定性等方面的校核计算。
一、按扭转强度计算
已知条件：传递功率P（KW），转速n（r/min）
由于跨距不知——M不知T
T WT
9.55 106 0.2d 3
p n
[ ]T
二、按弯扭合成强度计算
对于一般钢制轴，第三强度理论
e b2 4 2 [b ]
b

M W
,
T
WT
T 2W
e
( M )2 4( T )2 1
W
2W W
M 2 T 2 [ b ]
对于一般转轴，弯曲应力为对称循环变应力，而切应力的循环特性往往与弯曲应力不同，所以应对上式中的转矩T乘以一个系数α，以考虑两者循环特性不同的影响，
三、提高轴的强度及刚度一些措施
减小应力集中内凹圆角
适当加大截面变化处的过渡圆角半径。或采用：
过渡肩环（隔离环）
减载槽
a)端铣刀加工的键槽
b)盘铣刀加工的键槽
改善轴的受力状况
a. 改变轴上零件的结构，使受载减小。
b.合理安排轴上载荷的传递路线
输入
T1
T2
T1 +T2
输入
T1 T1 +T2
T2
T1 扭矩图

曲轴强度计算

JX4D30曲轴强度计算发动机开发部汪恩波曲轴的强度直接影响发动机寿命，因此曲轴强度计算是发动机设计的重要环节。

最近几年来，随着计算机及其软件技术的发展，出现了许多先进的曲轴强度计算方法，但在设计的初始阶段，目前普遍采用上午还是曲轴强度估算法。

RICARDO 计算方法该计算方法有两点假定：（一）曲轴的每一个曲拐是相互独立的，不受其轴其他部分受力的影响，并以简支梁的形式支撑在主轴承上。

（二）曲轴所受力是以点负荷的形式作用在曲轴上。

已知条件连杆轴颈 d=53 宽l=33主轴颈 D=70 宽l=31曲臂厚 h=19.5 宽B=110重叠度 A=9.05连杆长L=158mm曲柄半径52.45mm活塞行程 S=104.9mm圆角半径 R=3.5mm缸径d=95.4mm发动机转速额定转速 n=3600,r/min;发动机最高转速 n=4200r/min最高燃烧压力max p =160bar;最大平均有效压力me p =12.222bar;活塞连杆组往复质量 m1=1.3195,kg;活塞连杆组旋转质量m2=0.8925kg.曲轴材料 S53C 屈服强度 δs=588 Mpa抗拉强度 δb=660 Mpa重叠度的定义：重叠度2P J D D S A +-=的定义（P D 为连杆轴颈直径，J D 为主轴径直径，S 为活塞行程）弯曲应力计算1．曲轴受力计算压缩上止点时的曲轴作用力max max max 2p jL R F F F F F +===式中，j F 为活塞连杆组往复惯性力；p F 为燃气作用力（N ）;max L F 、max R F 为左右两侧主轴承支撑力的最大值（N ）22521225[1]101823600104.9104.9[0.8925 1.31951]1019734.1182158j j n S F S m m LF ππ--=-++⨯=-⨯++⨯=⨯（）（） 2max 22max max 495.41611431044114310197346702222p p p j F d p F d p N F F F N πππ===⨯⨯=++===排气上止点时的曲轴作用力min min 29867.52j jF F F F N=== 2、单个曲拐三个危险截面（A-A 、B-B 、C-C ）上的弯矩经过计算a=19.25mm b=32.5mm c=40.5mm l=58mm曲柄臂中央处（A-A ）max max A M F a ==67022x19.25=1290173.5Nmmmin min A M F a ==9867.5x19.25=189939.75Nmm连杆轴颈圆角处（B-B ）max max B M F b ==67022x32.5=2178215Nmmmin min B M F b ==9867.5x32.5=314827.5Nmm连杆轴颈中央处（C-C ）max max C M F c ==67022x32.5=67022x40.5=2714391 Nmmmin min C M F c ==9867.5x40.5=399633.75Nmm式中，max A M 、min A M 、max B M 、min B M 、max C M 、min C M 分别为曲拐三个危险截面上的最大和最小弯矩（N.m ）a b c 为曲轴有关尺寸，如图所示。

轴的强度计算

轴的强度计算部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑轴的强度计算一、按扭转强度条件计算适用：①用于只受扭矩或主要承受扭矩的传动轴的强度计算；②结构设计前按扭矩初估轴的直径d min强度条件：Mpa (11-1>设计公式：<mm）轴上有键槽放大：3~5%一个键槽；7~10%二个键槽。

取标准植——许用扭转剪应力<N/mm2），表11-3 ——考虑了弯矩的影响A0——轴的材料系数，与轴的材料和载荷情况有关。

注意表11-3下面的说明对于空心轴：<mm）， d1—空心轴的内径<mm）注意：如轴上有键槽，则d放大：3~5%1个；7~10%2个取整。

二、按弯扭合成强度条件计算条件：已知支点、距距，M可求时步骤：如图11-17以斜齿轮轴为例1、作轴的空间受力简图<将分布看成集中力，）轴的支承看成简支梁，支点作用于轴承中点，将力分解为水平分力和垂直分力<图11-17a）b5E2RGbCAP2、求水平面支反力RH1、RH2作水平内弯矩图<图11-17b）3、求垂直平面内支反力RV1、RV2，作垂直平面内的弯矩图<图11-17c）4、作合成弯矩图<图11-17d）5、作扭矩图<图11-17e）6、作当量弯矩图——为将扭矩折算为等效弯矩的折算系数∵弯矩引起的弯曲应力为对称循环的变应力，而扭矩所产生的扭转剪应力往往为非对称循环变应力∴与扭矩变化情况有关——扭矩对称循环变化= ——扭矩脉动循环变化——不变的扭矩，，分别为对称循环、脉动循环及静应力状态下的许用弯曲应力。

7、校核轴的强度——Mcamax 处；Mca较大，轴径d较小处。

Mpa (11-6> W——抗弯截面模量 mm3，见表11-4不同截面的W。

设计公式：<mm）如果计算所得d大于轴的结构设计d结构，则应重新设计轴的结构，对于心轴：T=0，Mca=M：转动心轴，许用应力用；固定心轴，许用应力用——弯曲应力为脉动循环。

2019曲柄轴的强度设计、疲劳强度校核及刚度计算说明.doc

材料力学课程设计设计计算说明书设计题目：曲柄轴的强度设计、疲劳强度校核及刚度计算序号: 160题号: 10 - 16教学号:专业: 土木工程（路桥）姓名：指导教师：目录一、材料力学课程设计的目的—————————2二、材料力学课程设计的任务和要求——————3三、设计计算说明书的要求——————————3四、分析讨论及说明部分的要求————————4五、程序计算部分的要求———————————4六、设计题目————————————————5七、设计内容————————————————6 （一）画出曲柄轴的内力图------------------ 7 （二）设计曲柄颈直径d，主轴颈直径D------- 9 （三）校核曲柄臂的强度--------------------10 （四）校核主轴颈的疲劳强度--------------- 14 （五）用能量法计算A截面的转角----------- 15 （六）计算机程序------------------------- 17八、设计体会——————————————----21九、参考文献——————————————----21一、课程设计的目的材料力学课程设计的目的是在于系统学习材料力学后，能结合工程中的实际问题，运用材料力学的基本理论和计算方法，独立地计算工程中的典型零部件，以达到综合运用材料力学的知识解决工程实际问题之目的。

同时，可以使我们将材料力学的理论和现代计算方法及手段融为一体。

既从整体上掌握了基本理论和现代的计算方法，又提高了分析问题，解决问题的能力；既能对以前所学的知识（高等数学、工程图学、理论力学、算法语言、计算机和材料力学等）的综合应用，又为后继课程（机械设计、专业课等）得学习打下基础，并初步掌握工程中的设计思想和设计方法，对实际工作能力有所提高。

1、使所学的材料力学知识系统化，完整化。

2、在系统全面复习的基础上，运用材料力学知识解决工程实际问题。

机械设计-轴的强度计算

轴的强度校核
5 小结
轴的强度校核
传动轴的强度计算轴的强度计算方法心轴的强度计算
转轴的强度计算切应力计算传动轴切应力计算轴端直径计算
弯曲应力计算芯轴弯曲应力计算
轴端直径计算
当量弯曲应力计算转轴的当量弯曲应力计算
轴端直径计算
谢谢观看
d
3
Me 0.1 1
w
另外，需考虑键槽对轴强度的削弱，上式直径应增大4％～7％，单键槽时取较小
值，双键槽时取较大值。
T --轴的切应力 M--作用在轴上的弯矩 WT --轴的抗扭截面系数
σ W --轴的弯曲应力 W --轴的抗弯截面系数
M e--当量弯矩
[σ] W --轴的许用弯曲应力 T--轴传递的转矩
轴的强度校核
1 轴的强度计算方法 2 传动轴切应力计算 3 芯轴弯曲应力计算 4 转轴的当量弯曲应力计算 5 小结
CONTENTS
目录
轴的强度校核
1 轴的强度计算方法初步完成轴的结构设计之后进行轴的强度计算，对于不
同受载和应力性质的轴，应采用不同的计算方法。
1、传动轴的强度计算 2、心轴的强度计算 3、转轴的强度计算
轴的强度校核
4 转轴的当量弯曲应力计算
转轴在复合应力作用下危险截面的当量弯曲应力计算
ew
2 w
4
2 T
M W
2

4
T WT
2
w
WT
2W
ew
1 W
M 2 T 2 w
考虑弯曲应力与扭切应力循环特性的差异，将上式中的转矩T乘以应力校正系数α
ew
1 W
M
2
T
2
Me W

轴的强度计算

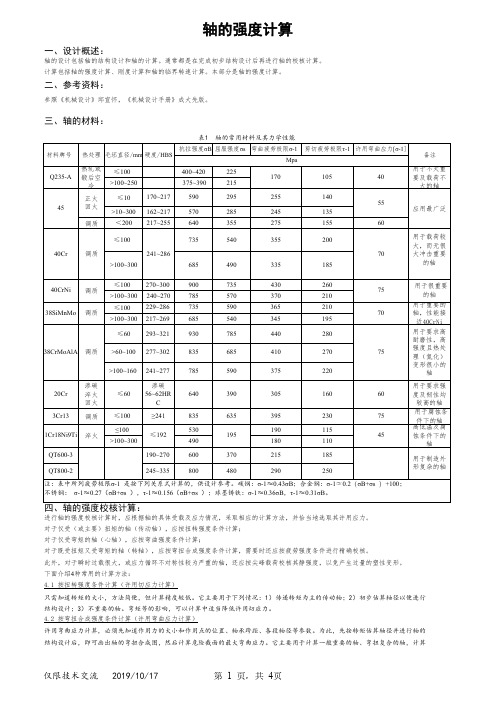
112-97
注：表中的许用扭转切应力是考虑了弯曲的影响而经过降低之后的取值。
应当指出，当轴截面上开有键槽时，应适当增大轴径以抵抗开键槽对轴强度的削弱影响。
对于d≤100，单键槽时，轴径增大5%-7%，双键槽时，轴径增大10%-15%。
对于d＞100，单键槽时，轴径增大3%，双键槽时，轴径增大7%。
表3 抗弯截面系数W和抗扭截面系数WT的计算公式
热处理毛坯直径/mm 硬度/HBS
热轧或 ≤100 锻后空
冷 >100~250
抗拉强度σB 屈服强度σs 弯曲疲劳极限σ-1 剪切疲劳极限τ-1
Mpa
400~420
225
170
105
375~390
215
许用弯曲应力[σ-1] 40
备注
用于不太重要及载荷不
大的轴
正火
≤10 170~217
590
从而改善各薄弱环节，有利于提高轴的疲劳强度。 4.4 按静强度条件进行校核
4.1 按扭转强度条件计算（许用切应力计算）
受扭矩T（N·mm)的实心圆轴，其切应力：
.× /
==
≤
.
MPa
写成设计公式，其最小直径（实心圆轴）：
式中：
扭转切应力
MPa
T
轴所受的扭矩
N·mm
W
轴抗扭截面系数
mm3
n
轴的转速
r/min
仅限技术交流 2019/10/17
第 1 页，共 4页
轴的强度计算
计算精度适中。 4.3 按疲劳强度条件进行精确计算（安全系数校核计算）
安全系数校核计算也是在轴的结构设计后进行，不仅要定出轴的各段直径，还要定出过渡圆角、轴毂配合、表面粗糙度等细节。它

曲轴计算的几种准则

柴油机曲轴的疲劳强度评定王民摘要：柴油机曲轴强度对保障船舶的安全性有着重要意义，本文首先介绍了柴油机曲轴疲劳强度评定方法，并给出柴油机动力计算中交变弯矩、交变压应力的计算方法。

本文探讨了IACS M53计算方法的合理性，指出强度评定中的常见错误并给出改进建议。

本文中部分意见已被船级社规范采纳，并用于实际曲轴强度校核。

关键词：曲轴强度评定、疲劳强度、IACS M531．前言曲轴是影响船舶柴油机可靠性最关键的零部件，柴油机的可靠性在很大程度上依靠曲轴的可靠性。

由于曲轴无法采用冗余设计，不得不提高自身的可靠性，因此国际船级社协会(IACS)制订了曲轴强度校核的统一要求(IACS UR M53)。

曲轴在工作时承受缸内的气体力、往复和旋转质量惯性力、扭转力等的作用。

施加在连杆轴颈上的径向力使曲轴承受弯曲作用，切向力使曲轴承受扭矩，同时轴系带来的扭转振动、纵向振动、曲轴形状弯曲等都影响曲轴强度。

曲轴承受的切向力和径向力都是随时间周期变化的量，曲轴各处的应力也具有周期变化的性质。

对曲轴断裂事故进行实际分析证明，大多数断轴事故是疲劳破坏，因此UR M53 采用了疲劳强度评价准则，主要评价曲轴圆根及油孔处的疲劳强度。

本文介绍根据M53及中国船级社规范进行柴油机曲轴强度分析的实用方法，研究实际计算中常见的问题。

通过对比几种曲轴疲劳强度计算方法，对船舶规范和M53提出修改建议。

由于大型低速机计算相对简单，所以本文以V型中速机为例。

2．IACS曲轴疲劳强度评定方法国际船级社协会IACS UR M53船舶柴油机曲轴疲劳强度校核准则，来源于国际内燃机学会（CIMAC）的通用计算方法，并被各船级社所采纳，广泛应用于船舶柴油机曲轴设计。

通过曲轴疲劳强度计算，可以计算出曲轴在主轴颈、曲柄销颈、油孔处的名义交变弯曲应力、名义压应力、名义交变扭转应力，然后乘以应力集中系数，并根据最大应变能强度理论，合成为一当量交变应力，然后同材料的疲劳强度值进行比较，M53要求该比值（即合格系数）不小于1.15，以评判曲轴强度是否满足要求。

轴结构设计和强度校核

轴结构设计和强度校核
在进行轴的结构设计时，首先需要计算轴的弯曲应力。

弯曲应力是由于轴在负载作用下会发生弯曲而产生的应力，可以通过以下公式计算：σ=(M*c)/(I*y)
其中，σ为轴的弯曲应力，M为轴端的扭矩，c为轴的断面形心距，I为轴截面的惯性矩，y为轴上其中一截面上的最大距离。

根据弯曲应力的计算结果，可以选择合适的材料和轴的几何形状，以满足强度要求。

常用的轴材料有碳钢、合金钢和不锈钢等。

此外，轴还需要考虑扭转应力。

扭转应力是由于轴在传递扭矩时会产生的应力，可以通过以下公式计算：
τ=(T*r)/(J)
其中，τ为轴的扭转应力，T为轴端的扭矩，r为轴的半径，J为轴截面的极惯性矩。

轴的强度校核主要是通过计算轴的弯曲和扭转应力与材料的抗弯和抗扭强度之间的比较来完成。

一般来说，轴的弯曲应力不应超过材料的抗弯强度，而扭转应力不应超过材料的抗扭强度。

如果轴的弯曲应力或扭转应力超过了材料的强度限制，需要重新设计轴的几何尺寸或者选择更高强度的材料。

轴结构设计和强度校核是机械设计中非常重要的一部分。

合理的轴设计可以确保机械设备的正常运行，并提高其工作效率和寿命。

同时，通过强度校核可以避免轴的失效和损坏，保证机械设备的安全性。

因此，在机械设计中，轴结构设计和强度校核是必不可少的工作环节之一。

曲柄轴的强度设计疲劳强度校核及刚度计算

目录1、设计目的2、设计任务和要求2.1、设计计算说明书的要求 2.2、分析讨论及说明书部分的要求 2.3、程序计算部分的要求3、设计题目3.1、画出曲轴的内力图3.2、设计主轴颈D 和曲轴颈直径d 3.4、校核主轴颈的疲劳强度3.5、用能量法计算A 端面的转角y θ ，z θ4、分析讨论及说明5、参考文献6、设计体会7、附录：计算机程序及结果一、设计目的本课程设计的目的是在于系统学完材料力学之后，能结合工程中的实际问题，运用材料力学的基本理论和计算方法，独立地计算工程中的典型零部件，以达到综合运用材料力学的知识解决工程实际问题之目的。

同时，可以使学生将材料力学的理论和现代计算方法及手段融为一体。

既从整体上掌握了基本理论和现代的计算方法，又提高了分析问题，解决问题的能力；既把以前所学的知识（高等数学、工程图学、理论力学、算法语言、计算机和材料力学等）综合运用，又为后继课程（机械设计、专业课等）打下基础，并初步掌握工程中的设计思想和设计方法，对实际工作能力有所提高。

具体的有以下六项：1、使学生的材料力学知识系统化、完整化；2、在系统全面复习的基础上，运用材料力学知识解决工程中的实际问题；3、由于选题力求结合专业实际，因而课程设计可以把材料力学知识和专业需要结合起来；4、综合运用了以前所学的个门课程的知识（高数、制图、理力、算法语言、计算机等等）使相关学科的知识有机地联系起来；5、初步了解和掌握工程实践中的设计思想和设计方法；6、为后继课程的教学打下基础。

二、材料力学课程设计的任务和要求要求参加设计者，要系统地复习材料力学的全部基本理论和方法，独立分析、判断、设计题目的已知条件和所求问题。

画出受力分析计算简图和内力图，列出理论依据和导出计算公式，独立编制计算程序，通过计算机给出计算结果，并完成设计计算说明书。

1、设计计算说明书的要求设计计算说明书是该题目设计思想、设计方法和设计结果的说明。

要求书写工整，语言简练，条理清晰、明确，表达完整。

曲轴强度计算..

JX4D30曲轴强度计算发动机开发部汪恩波曲轴的强度直接影响发动机寿命，因此曲轴强度计算是发动机设计的重要环节。

最近几年来，随着计算机及其软件技术的发展，出现了许多先进的曲轴强度计算方法，但在设计的初始阶段，目前普遍采用上午还是曲轴强度估算法。

RICARDO 计算方法该计算方法有两点假定：（一）曲轴的每一个曲拐是相互独立的，不受其轴其他部分受力的影响，并以简支梁的形式支撑在主轴承上。

（二）曲轴所受力是以点负荷的形式作用在曲轴上。

已知条件连杆轴颈 d=53 宽l=33主轴颈 D=70 宽l=31曲臂厚 h=19.5 宽B=110重叠度 A=9.05连杆长L=158mm曲柄半径52.45mm活塞行程 S=104.9mm圆角半径 R=3.5mm缸径d=95.4mm发动机转速额定转速 n=3600,r/min;发动机最高转速 n=4200r/min最高燃烧压力max p =160bar;最大平均有效压力me p =12.222bar;活塞连杆组往复质量 m1=1.3195,kg;活塞连杆组旋转质量m2=0.8925kg.曲轴材料 S53C 屈服强度 δs=588 Mpa抗拉强度 δb=660 Mpa重叠度的定义：重叠度2P J D D S A +-=的定义（P D 为连杆轴颈直径，J D 为主轴径直径，S 为活塞行程）弯曲应力计算1．曲轴受力计算压缩上止点时的曲轴作用力max max max 2p jL R F F F F F +===式中，j F 为活塞连杆组往复惯性力；p F 为燃气作用力（N ）;max L F 、max R F 为左右两侧主轴承支撑力的最大值（N ）22521225[1]101823600104.9104.9[0.8925 1.31951]1019734.1182158j j n S F S m m LF ππ--=-++⨯=-⨯++⨯=⨯（）（） 2max 22max max 495.41611431044114310197346702222p p p j F d p F d p N F F F N πππ===⨯⨯=++===排气上止点时的曲轴作用力min min 29867.52j j F F F F N=== 2、单个曲拐三个危险截面（A-A 、B-B 、C-C ）上的弯矩经过计算a=19.25mm b=32.5mm c=40.5mm l=58mm曲柄臂中央处（A-A ）max max A M F a ==67022x19.25=1290173.5Nmmmin min A M F a ==9867.5x19.25=189939.75Nmm连杆轴颈圆角处（B-B ）max max B M F b ==67022x32.5=2178215Nmmmin min B M F b ==9867.5x32.5=314827.5Nmm连杆轴颈中央处（C-C ）max max C M F c ==67022x32.5=67022x40.5=2714391 Nmmmin min C M F c ==9867.5x40.5=399633.75Nmm式中，max A M 、min A M 、max B M 、min B M 、max C M 、min C M 分别为曲拐三个危险截面上的最大和最小弯矩（N.m ）a b c 为曲轴有关尺寸，如图所示。

曲柄轴强度设计计算

曲柄轴强度设计计算曲柄轴强度设计计算是一项关键的工程设计任务，涉及到机械工程中重要的运动和力学原理，对于确保机械设备的稳定运转和安全性具有重要意义。

本文将介绍曲柄轴强度设计计算的一般流程、关键参数和注意事项，为相关工程设计人员提供指导和帮助。

一、设计计算流程曲柄轴强度设计计算的一般流程包括以下步骤：1.确定曲柄轴的类型和尺寸，包括轴的长度、直径、圆角半径等参数。

2.计算曲柄轴的受力情况，包括轴上的弯矩、剪力、轴向力等。

3.根据曲柄轴的材料和受力情况，计算轴的极限强度、疲劳强度等参数。

4.结合轴的工作条件和使用寿命要求，确定曲柄轴的安全余量和设计寿命。

5.进行轴的设计优化和材料选择，最终确定曲柄轴的结构参数和材料类型。

二、关键参数在进行曲柄轴强度设计计算时，需要注意以下关键参数：1.曲柄轴的材料类型和强度参数，包括抗拉强度、屈服强度、弹性模量等。

2.曲柄轴的受力情况，包括在旋转运动中承受的弯矩和剪力等。

3.曲柄轴的实际工作条件，包括转速、负载、温度等因素。

4.曲柄轴的设计寿命，包括使用寿命和寿命设计要求等。

三、注意事项在进行曲柄轴强度设计计算时，需要注意以下事项：1.根据实际情况选择合适的曲柄轴材料和强度参数，确保曲柄轴的强度和刚度满足设计要求。

2.根据曲柄轴的受力情况和实际工作条件，采用相应的受力分析方法和计算公式，有效地评估轴的受力情况。

3.注意曲柄轴的设计优化和材料选择，优化轴的结构参数和减少轴的重量，提高轴的运转效率和耐久性。

4.在进行曲柄轴强度设计计算时，需要考虑到轴的疲劳强度和使用寿命等重要参数，确保轴的可靠性和安全性。

总之，曲柄轴强度设计计算是机械工程中极为重要的一环，需要工程设计人员具备相应的力学和材料知识，以确保机械设备的稳定和安全运转。

希望本文能够为相关设计人员提供帮助和指导，提高工程设计质量和效率。

曲轴强度计算

JX4D30曲轴强度计算发动机开发部汪恩波曲轴的强度直接影响发动机寿命，因此曲轴强度计算是发动机设计的重要环节。

最近几年来，随着计算机及其软件技术的发展，出现了许多先进的曲轴强度计算方法，但在设计的初始阶段，目前普遍采用上午还是曲轴强度估算法。

RICARDO 计算方法该计算方法有两点假定：（一）曲轴的每一个曲拐是相互独立的，不受其轴其他部分受力的影响，并以简支梁的形式支撑在主轴承上。

（二）曲轴所受力是以点负荷的形式作用在曲轴上。

概念设计阶段曲轴强度计算规范

CAE规范第1部分：概念设计阶段曲轴强度计算1 范围m kg1 连杆质量rodm kg2 活塞组质量pst3 曲柄半径R mm4 连杆长度L mm5 缸套内径D mmD mm6 曲柄销直径p7 曲柄销长度p L mmD mm8 主轴颈直径j9 主轴颈长度j L mmL mm10 连杆大头轴瓦宽度psL mm11 曲轴主轴瓦宽度jsδmm12 曲柄销凸台厚度p13 主轴颈凸台厚度jδmm14 曲柄销圆角凹入深度p T mm15 主轴颈圆角凹入深度j T mm16 曲柄臂厚度h mm17 曲柄臂宽度B mm18 转速n rpm19 最大爆压g p MPa 3 计算流程图2 流程图4 计算原理曲轴的设计基于对高应力区域的疲劳安全进行评估。

本规范中的计算基于以下假定：●曲柄销圆角、主轴颈圆角为高应力区域；●曲拐简支在主轴颈上且各曲拐相互独立，可简化为截断简支梁模型；●曲柄销、主轴颈支反力以轴向抛物线、径向120°余弦分布作用在曲柄销、主轴颈上；●弯曲应力是引起曲轴破坏的主要因素，输出扭矩产生的影响很小，可以忽略不计。

5 计算工况对长期稳定工作于额定转速的发动机，以全负荷工况为计算工况；对在大转速范围内工作的发动机，以最大扭矩工况为计算工况；对船用发动机，以超负荷（110%负荷）工况为计算工况。

通常，一个工作周期内，由燃气压力和惯性力引起的作用在曲柄销上的径向载荷对所有曲柄位置都应计算。

简单起见，径向力可以采用简化计算，并只计算一个工作周期内的最大受拉和最大受压两种状态。

6 曲轴载荷 6.1 曲柄销载荷曲柄销载荷以轴向抛物线、径向120°余弦分布的分布力作用在曲柄销上，作用范围为连杆大头轴瓦宽度，其大小按以下公式计算：图3 曲柄销载荷θθ23cos )41(25),(22psps p p p L x L D F x q -⋅=式中：p F ：作用在曲柄销上的径向载荷，N ；p F 可按曲柄连杆动力学或多体动力学计算得到，对V 型机，p F 应考虑不同的相位和连杆设计（分叉连杆、连接连杆、并列连杆等）分别计算与合成。

曲轴的设计要求及基本参数设计原则

曲轴的设计要求及基本参数设计原则曲轴的设计要求及基本参数设计原则曲轴在不断周期性变化的气体压力下，产生强烈的扭转和弯曲，受到的巨大应力可能会导致曲轴发生断裂，在曲轴设计过程中，首先要充分考虑提高曲轴的强度和刚度，同时要综合考虑曲轴的重量、耐磨性和生产成本等因素。

在现实的生产中，它们是互为一体，却又相互矛盾的。

比如，要想提高曲轴的刚度就需要增大曲柄销和主轴颈的直径，这样的结果就是导致曲轴的重量增加，生产制造成本增加。

因此要想解决好这些问题，就要从曲轴的材料、结构、强化手段和生产加工工艺等方面综合考虑，这样才能生产出符合实际生产要求的产品。

在设计曲轴时，各部件生产的前后连贯性非常强，它们的尺寸不能孤立进行，必须综合考虑。

比如要增加各部件的强度，就势必要增大尺寸，重量增加，这在曲轴的设计要求中是互相矛盾的，如何生产出强度高、重量轻的优质曲轴，是在整个曲轴的设计过程中需要解决的重点问题。

CY4102的曲轴参数与4D型曲轴参数如下表表3.1－1 CY4102曲轴基本参数单位：毫米项目曲柄销直径d1 主轴颈直径d2 曲臂厚度h 曲拐半径R 表3.1－2 4D型曲轴基本参数单位：毫米项目曲柄销直径d1 主轴颈直径d2 曲臂厚度h 曲拐半径R 指标Φ73 Φ82 25 62.5 项目曲臂最大厚度平衡块半径RP 曲柄销长度L1 主轴颈长度L2 指标 151 105 41 38 指标Φ64 Φ80 23 59 项目曲臂最大厚度平衡块半径RP 曲柄销长度L1 主轴颈长度L2 指标 130 98 38 34 通过上表可以看出，原有的4D型曲轴是在4102曲轴的基础上进行改进设计的，各部件的尺寸都有所增加，这势必增加了曲轴的重量和运动负荷，降低曲轴的寿命，因此，我们需要进行深入细致的研究，生产出符合生产要求的更轻便，更坚固，寿命更长的曲轴。

感谢您的阅读，祝您生活愉快。

机械基础——轴的结构设计与强度计算

二、心轴的强度设计
心轴工作时承受弯矩，其抗弯强度条件为
计算心轴的直径时，设计公式为
三、转轴的强度计算
对于一般钢制的轴，可按第三强度理论进行校核计算，其强度条件为
计算轴的直径时，上式可以写成
当轴上有键槽时，应将求得的轴径增大3％～7％，单键槽取较小值，双键槽取较大值。
四、应用举例
作业
P386：12、13
四、避免或减少应力集中
为了提高轴的疲劳强度，在进行结构设计时，应考虑避免或减少应力集中。当应力集中不可避免时，应采取减少应力集中的措施。
第三节轴的强度计算
一、传动轴的强度计算
传动轴的抗扭强度条件为
轴的直径计算式为
按上式算出的轴径，如果上面开有键槽，还要考虑键槽对轴强度的削弱影响（按开一个键槽时将增大3~5%、开两个键槽时增大7~10%）。
课题
轴的结构设计与强度计算
教学目的
1、掌握轴结构设计的基ቤተ መጻሕፍቲ ባይዱ因素和基本方法；
2、掌握一般传动轴和心轴设计计算的基本技能。
教学安排
组织教学
讲述新课
三、改善轴的结构工艺性
1、装配工艺性轴端应有倒角45°；阶梯轴应制成两端小、中间大；一般轴头长度应稍短于装在上面的与之配合的轮毂轴向长度。
2、切削加工工艺性不同轴段均有键槽时，应布置在同一母线上；螺纹轴段要有退刀槽，磨削段要有越程槽，并均应符合有关规范；轴上的键槽、圆角、倒角、退刀槽、越程槽等，应尽可能分别采用同一尺寸以便加工和检验；

轴的强度计算与设计

轴的强度计算与设计发布者：环球轴承网来源：互联网发布日期：2007年12月28日9.3.1轴的扭转强度计算开始设计轴时，通常还不知道轴上零件的位置及支点位置，无法确定轴的受力情况，只有待轴的结构设计基本完成后，才能对轴进行受力分析及强度、刚度等校核计算。

因此，一般在进行轴的结构设计前先按纯扭转受力情况对轴的直径进行估算。

设轴在转矩T的作用下，产生剪应力τ。

对于圆截面的实心轴，其抗扭强度条件为：式中T为轴所传递的转矩，单位为N·mm；Wr为轴的抗扭截面系数，单位为mm3；P 为轴所传递的功率，单位为kW；n为轴的转速，单位为r/min；τ，［τ］分别为轴的剪应力，单位为MPa；d为轴的估算直径，单位为mm。

轴的设计计算公式为常用材料的［τ］值、C值可查表9.1。

［τ］值、C值的大小的材料及受载情况关。

当作用在轴上的弯矩比转矩小，或轴只受转矩时，［τ］值取较大值，C值取较小值，否则相反。

由式（9.2）求出的直径值，需圆整成标准直径，并作为轴的最小直径。

如轴上有一个键槽，可将算得的最小直径增大3%～5%，如有两个键槽可增大7%～10%。

9.3.2轴的弯扭合成强度计算完成轴的结构设计后，作用在轴上外载荷（转矩和弯矩）的大小、方向、作用点、载荷种类及支点反力等就已确定，可按弯扭合成的理论进行轴危险截面的强度校核。

进行强度计算时通常把轴当作置于铰链支座上的梁，作用于轴上零件的力作为集中力，其作用点取为零件轮毂宽度的中点。

支点反的作用点一般可近似地取在轴承宽度的中点上。

具体的计算步骤如下：（1）画出轴的空间力系图。

将轴上作用力分解为水平面和垂直面分力，并求出水平面和垂直面上的支点反力。

（2）分别作出水平面上的弯矩（M H）图和垂直面上的弯矩（Mv）图。

（3）计算出合成弯矩M＝M2H+M2v，绘出合成弯矩图。

（4）作出转矩（T）图。

（5）计算当量弯矩Me＝M2H+（aT)2，绘出当量弯矩图。

式中α为考虑弯曲应力与扭转剪力循环特性的不同而引入的修正系数。

轴的设计、计算、校核

如计算应力超出许用值，应增大轴危险断面的直径。如计算应力比许用值小很多，一般不改小轴的直径。因为轴的直径还受结构因素的影响。
一般的转轴，强度计算到此为止。对于重要的转轴还应按疲劳强度进行精确校核。此外，对于瞬时过载很大或应力循环不对称性较为严重的轴，还应按峰尖载荷校核其静强度，以免产生过量的塑性变形。
>10~18
>18~30
>30~50
>50~80
0.8
1.0
1.2 1.6
2.0
>80~120> 2.5
120~180 3.0
轴的材料
Q235
[] A0
12～20 160～135
表 3 轴常用几种材料的[ ]和 A0 值
1Cr18Ni9Ti
35
45
40Cr,35SiMn,2Cr13,20CrMnTi
12～25
20～30
30～40
40～52
148～125
135～118 118～107
107～98
-可编辑修改-
。
表 4 抗弯抗扭截面模量计算公式
-可编辑修改-
。
-可编辑修改-
。
THANKS !!!
致力为企业和个人提供合同协议，策划案计划书，学习课件等等打造全网一站式需求
欢迎您的下载，资料仅供参考
毛坯直径材料牌号热处理
（mm）
Q235A
热轧或锻后空
冷
≤100 >100~250
表 1 轴的常用材料及其主要力学性能
硬度 (HBS)
弯曲疲剪切疲许用弯曲抗拉强度极屈服强度
劳极限劳极限应力[σ 限σb 极限σs
σ-1 τ-1 -1]