(完整版)一年级数学上册重难点之等量代换
一年级等量代换

一年级等量代换在数学的世界里,有一个非常重要的概念叫做等量代换。
这是我们在学习加法和减法之后,进一步理解数学的基础之一。
这个概念对于我们理解更复杂的数学概念,如代数和几何,也是至关重要的。
等量代换是指用一种量来代替与其相等的另一种量。
例如,我们可以说10个苹果等于5个橙子。
在这个例子中,我们用10个苹果的重量来代替5个橙子的重量。
这就是等量代换。
在一年级的数学课程中,我们通常会学习如何使用等量代换。
我们会用数字来代替量,比如用10来代替10个苹果,用5来代替5个橙子。
然后我们可以通过简单的算术运算来找出两种量之间的关系。
例如,如果我们有10个苹果和5个橙子,我们可以通过等量代换来找出1个橙子等于多少个苹果。
如果我们设1个橙子等于x个苹果,那么我们可以建立如下方程:10 = 5x,解这个方程可以得到x=2。
所以,1个橙子等于2个苹果。
通过这样的学习,我们可以更好地理解数量的概念,掌握基本的算术运算,提高我们的数学素养。
我们也可以了解到数学在现实生活中的应用,比如在购物和做交易时如何进行数量的比较和转换。
等量代换是数学学习中一个非常基础但非常重要的概念。
通过学习等量代换,我们可以更好地理解数学的基础知识,为以后的学习打下坚实的基础。
在人生中,有些看似复杂的难题,其实可以用简单的等量代换来解答。
今天,我想和大家分享一个我在一年级时学到的重要概念——等量代换。
在一年级的数学课上,我们开始学习用数字来描述世界。
老师让我们认识数字,学习加减法,这都很有趣。
但最让我印象深刻的,是老师给我们讲的一个故事。
老师告诉我们,有一个古老的村庄,村子里的人们非常善良。
每当有外来人来到村子里,村民们都会给他们一些食物。
但这个村子的食物非常特别,它叫做“公平食”。
每份公平食都是用两个苹果和三个橘子做成的。
有一天,一个外来人来到了村子里,他非常饿。
村民们给了他一份公平食。
这个人吃了一半的公平食,发现自己已经饱了。
他看着剩下的食物,想把它们带走。
小学等量代换优秀教案

小学等量代换优秀教案年级学科:小学数学教学目标:1. 让学生理解等量代换的概念,能运用等量代换解决实际问题。
2. 培养学生逻辑思维能力和解决问题的能力。
3. 培养学生合作交流的能力,提高学生数学素养。
教学内容:1. 等量代换的概念及应用。
2. 等量代换在实际生活中的运用。
教学重点:1. 让学生掌握等量代换的方法。
2. 培养学生运用等量代换解决实际问题的能力。
教学难点:1. 理解等量代换的概念。
2. 运用等量代换解决实际问题。
教学过程:一、导入(5分钟)1. 教师通过生活中的实例引入等量代换的概念,如:“如果有2个苹果,我用1个橙子来换,我们还是有一个苹果的数量。
”2. 学生讨论,理解等量代换的含义。
二、新课讲解(15分钟)1. 教师讲解等量代换的定义和规则。
2. 学生跟随教师一起练习一些等量代换的题目,加深理解。
三、实例分析(15分钟)1. 教师提出一些实际问题,如:“小明有3个球,小华有5个球,他们一共有几个球?”引导学生运用等量代换的方法解决。
2. 学生分组讨论,交流解题思路,展示解题过程。
四、课堂练习(10分钟)1. 教师给出一些等量代换的练习题,让学生独立完成。
2. 教师选取部分学生的作业进行点评,总结解题技巧。
五、总结与拓展(5分钟)1. 教师引导学生总结等量代换的方法和应用。
2. 教师提出一些拓展问题,如:“等量代换在生活中的其他应用有哪些?”引导学生思考。
教学评价:1. 课后收集学生的课堂练习作业,评估学生对等量代换的掌握程度。
2. 在下一节课开始时,教师可以提出一些有关等量代换的问题,检查学生对课堂内容的复习情况。
以上是一篇关于小学等量代换教学设计的教案,希望能对你的教学有所帮助。
完整版等量代换一年级
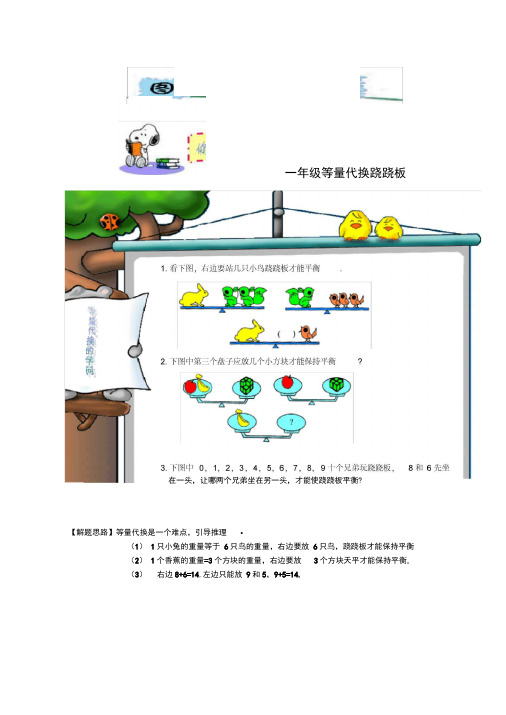
【解题思路】等量代换是一个难点,引导推理 •
(1) 1只小兔的重量等于 6只鸟的重量,右边要放 6只鸟,跷跷板才能保持平衡
(2) 1个香蕉的重量=3个方块的重量,右边要放
3个方块天平才能保持平衡. (3) 右边8+6=14,左边只能放 9和5,9+5=14.
一年级等量代换跷跷板
在一头,让哪两个兄弟坐在另一头,才能使跷跷板平衡?
£
有一天,小狗老师要在动物学校挑选队员参加数学竞赛,小松鼠很高兴也
跑来了•小狗老师说:“那我就来考考你!你把下面的题做对了就可以参加了
小松鼠看了半天说:“老师,你写的这是什么?”小狗老师说:“哈哈!看
心―———
哈哈!水果兄弟们也组成了各种不同的图文算式,它们各代表一个数,你能猜出它们各代表几吗?
20 ! 0=5 0 …
e 十€ - 6=15+10
8
=
H A +
F面的符号各代表一个数,相同的符号代表相同的数,它们各代表几呢?
F面这些由美丽花朵组成的算式,你能猜岀这些花朵都表示什么数吗
?
! - 矽+ ◎匸■
[△*△ + △}桃| 竇=14,
1* + ^iA + A=is f
[A = ( ) - ★=();'V/ R
I;6p
根F面的算式,你知
道冃、、Ml各代表数字几?
F面的符号各表示几?。
最新一年级数学上册重难点之等量代换

一年级数学上册重难点之等量代换
《等量代换》,分类,方法,技巧昨天,一位一年级的家长让我给她找几个数学题目,孩子平时考试,其它的题目都完成得很好,计算能力也不错,这周还去参加计算比赛.但是呢,有个题老是弄不好,如下图:
这是一个等量代换的题目,一年级的奥数里面也有这样的题型.
同时,这个题还会出现在试卷后面的较难的题中,属于需要动脑筋的题.
对于一年级的孩子来说,这个数学题目需要一定的理解力.因为涉及到推理能力!等量代换的关键是推理:
1个桃子等于4个苹果,那么右边的式子中,就把桃子换成4个苹果,这个时候,就知道右边是6个苹果啦.
所以答案是6.
这题属于形象化的,还是比较好理解的.例如:
练习1:
练习题来了(4道):。
《等量代换》 知识清单

《等量代换》知识清单一、什么是等量代换等量代换是数学中一种非常重要的思想方法,它指的是用一种量(或一种量的一部分)来代替和它相等的另一种量(或另一种量的一部分)。
简单来说,如果两个量是相等的,那么在一定的条件下,它们可以互相替换。
例如,我们知道 1 个苹果的重量等于 2 个橘子的重量,而 2 个橘子的重量又等于 3 个草莓的重量。
那么通过等量代换,我们就可以得出 1 个苹果的重量等于 3 个草莓的重量。
等量代换的核心在于找到相等的量,并利用这种相等关系进行转换和推理。
二、等量代换的重要性1、解决数学问题在数学学习中,等量代换常常被用于解决各种问题,比如求解方程、几何证明、计算图形的面积和体积等。
通过等量代换,可以将复杂的问题简化,找到解题的关键。
2、培养逻辑思维学会等量代换能够帮助我们锻炼逻辑推理能力,让我们更加有条理地思考问题,从已知条件中推导出未知的结论。
3、为后续学习打下基础等量代换是数学中的基础思想方法之一,对于后续学习更高级的数学知识,如代数、函数等,都有着重要的铺垫作用。
三、等量代换的应用场景1、等式计算在等式中,如果有多个量之间存在等量关系,我们可以通过等量代换来求解未知量。
例如:已知 a + b = 5,b + c = 7,a = 2,求 c 的值。
因为 a = 2,代入 a + b = 5 中,可得 2 + b = 5,b = 3。
再将 b = 3 代入 b + c = 7 中,可得 3 + c = 7,c = 4。
2、几何图形在计算几何图形的面积、周长等问题时,等量代换也经常被用到。
比如,两个三角形的高相等,底的长度存在倍数关系,那么它们的面积也存在相应的倍数关系。
3、实际生活在日常生活中,等量代换也有着广泛的应用。
例如,在购物时,如果知道不同商品之间的价格比例关系,就可以通过等量代换来比较哪种购买方式更划算。
四、等量代换的解题步骤1、分析题目仔细阅读题目,找出其中给出的等量关系和已知量、未知量。
小学数学解题方法6--等量代换

小学数学解题方法6--等量代换小朋友们一定都知道曹冲(曹操的小儿子)称大象的故事吧。
曹冲用一条船,让大象先上船,看船被河水水面淹没到什么位置,然后刻上记号。
把大象赶上岸,再把这条船装上石块,当船被水面淹没到记号的位置时,就可以判断:船上的石块共有多重,大象就有多重。
为什么大象的重量可以换成一船石块的重量呢?因为两次船下沉后被水面所淹没的深度一样,只有当大象与一船石头一样重(重量相等)时,才会淹没得一样深。
“曹冲称象”不是瞎称的,而是运用了“等量代换”的思考方法:两个完全相等的量,可以互相代换。
解数学题,经常会用到这种思考方法。
【例1】百货商店运来300双球鞋,分别装在2个木箱、6个纸箱里。
如果2个纸箱同1个木箱装的球鞋一样多,想一想:每个木箱和每个纸箱各装多少双球鞋?【分析与解】我们根据“2个纸箱同一个木箱装的球鞋一样多”,把木箱换成纸箱,也就是说,把300双球鞋全部用纸箱装,不用木箱装。
根据已知条件,2个木箱里的球鞋刚好装满4个纸箱,再加上原来已装好的6个纸箱,一共是10个纸箱。
这样,题目就变为“把300双球鞋平均装在10个纸箱里,平均每个纸箱装多少双球鞋?”可以求出每个纸箱装多少双球鞋。
也就能求出一个木箱装多少双球鞋。
300÷(2×2+6)=300÷10=30(双)30×2=60(双)答:每个纸箱里装30双球鞋,每个木箱里装60双球鞋。
想一想:如果把纸箱换成木箱,假如300双球鞋全部用木箱装,应该怎样解答?【例2】如图6-1:阴影部分是正方形,求出最大的长方形的周长。
【分析与解】因为中间是正方形,正方形的四边相等,所以DF=FE=BE=BD①长方形ABDC的周长为7×2=14(厘米),长方形EHGF的周长为5×2=10(厘米),又因为最大的长方形AHGC的周长等于:AB+AC+CD+DF+FG+GH+EH+BE ②根据①式对②式进行等量代换,就得到所求最大长方形的周长正好等于长方形ABDC的周长加上长方形EHGF的周长。
等量代换教学重难点

等量代换教学重难点以等量代换教学重难点为标题,我们来探讨一下等量代换在教学中的重要性和难点。
等量代换是数学中的一个重要概念,它在解题过程中经常被使用。
了解等量代换的重难点,有助于我们更好地掌握这个概念,并能够灵活运用于实际问题中。
一、等量代换的基本概念等量代换,顾名思义就是用等值的表达式替代原来的表达式,使得两者在数值上相等。
在数学中,等量代换是一种思维方式,通过将复杂的问题转化为简单的形式来解决。
等量代换的基本思想是将一个未知量或一个复杂的表达式用一个已知的等量进行替代,从而简化问题的求解过程。
二、等量代换的重要性等量代换在解决数学问题中起着重要的作用。
首先,等量代换可以帮助我们简化问题,将原先复杂的表达式转化为简单的形式,从而更容易解决。
其次,等量代换可以帮助我们发现问题中的隐藏规律,通过代换可以将问题转化为我们熟悉的形式,从而更好地理解问题的本质。
最后,等量代换可以帮助我们建立数学模型,将实际问题转化为数学问题,从而利用数学方法进行求解。
三、等量代换的常见应用等量代换在解决数学问题中有广泛的应用。
下面列举几个常见的应用场景。
1. 解方程在解方程的过程中,经常需要进行等量代换。
例如,对于一个复杂的方程,我们可以通过等量代换将其转化为简单的形式,从而更容易求解。
2. 求极限在求极限的过程中,等量代换也是常用的方法之一。
通过等量代换,我们可以将复杂的极限问题转化为简单的形式,从而更好地计算极限。
3. 求导数和积分在求导数和积分的过程中,等量代换也经常被使用。
通过等量代换,我们可以将复杂的函数转化为简单的形式,从而更方便地求导和积分。
四、等量代换的难点和注意事项虽然等量代换在解题过程中有很多优势,但也存在一些难点和需要注意的问题。
1. 选择合适的等量代换在进行等量代换时,需要选择合适的等量进行代换。
选择不当可能会导致问题更加复杂,甚至无法解决。
因此,在进行等量代换时,需要仔细观察问题,并选择合适的等量进行代换。
一年级等量代换数学题

一年级等量代换数学题
《一年级等量代换数学题,真有趣!》
哎呀,你们知道吗?我们一年级学的等量代换数学题可有意思啦!
就比如说,老师给我们出了一道这样的题:一个苹果等于两个橘子,一个橘子又等于三个草莓,那一个苹果等于几个草莓呀?这可把我们班的同学难住了,大家都皱着小眉头,苦思冥想。
我也在那想啊,这一个橘子是三个草莓,那两个橘子不就是六个草莓嘛,一个苹果等于两个橘子,那不就等于六个草莓嘛!我高兴地举起手,大声说:“老师,我知道啦,一个苹果等于六个草莓!”老师笑着点点头,说:“你真聪明!”
还有一次,老师又出了一道更难的。
她说:“一只小兔子加上一只小鸡等于三只小鸭子,一只小兔子等于两只小鸡,那一只小鸡等于几只小鸭子呀?”这可把我难住了,我看看同桌,他也一脸迷茫。
我就小声地跟他说:“这可咋办呀?”他摇摇头说:“我也不知道。
”我们俩就一起在那琢磨。
后来我想,一只小兔子等于两只小鸡,那把一只小兔子换成两只小鸡,不就变成三只小鸡等于三只小鸭子了嘛,那一只小鸡不就等于一只小鸭子嘛!我赶紧又举手告诉老师,老师夸我会动脑筋。
我们做等量代换数学题的时候,就好像在玩一个神秘的游戏。
每一道题都是一个小秘密,等着我们去解开。
这不就跟拼图一样嘛,一块一块地找,最后就能拼成一幅完整的画。
每次解开一道题,我都觉得自己像个小英雄,特别有成就感!我觉得这些数学题就像一个个小小的宝藏,等着我们去发现。
你们说,等量代换数学题是不是特别有趣呀?反正我是特别喜欢,我觉得通过做这些题,我的小脑袋变得越来越聪明啦!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一年级数学上册重难点之
《等量代换》,分类,方法,技巧昨天,一位一年级的家长让我给她找几个数学题目,孩子平时考试,其它的题目都完成得很好,计算能力也不错,这周还去参加计算比赛。
但是呢,有个题老是弄不好,如下图:
这是一个等量代换的题目,一年级的奥数里面也有这样的题型。
同时,这个题还会出现在试卷后面的较难的题中,属于需要动脑筋的题。
对于一年级的孩子来说,这个数学题目需要一定的理解力。
因为涉及到推理能力!等量代换的关键是推理:
1个桃子等于4个苹果,那么右边的式子中,就把桃子换成4个苹果,这个时候,就知道右边是6个苹果啦。
所以答案是6.
这题属于形象化的,还是比较好理解的。
例如:练习1:
练习题来了(4道):。
