有限长均匀带电导体直线的电场分布特点
大学物理作业学生新版答案

班级________学号_________姓名_________成绩_______
一、选择题
1.一质点在平面上作一般曲线运动,其瞬时速度为 ,瞬时速率为 ,某一段时间内的平均速度为 ,平均速率为 ,它们之间的关系有
[](A) (B)
(C) (D)
2.某物体的运动规律为 ,式中的k为大于零的常数。当t=0时,初速为 ,则速度v与t的函数关系是
(C)顶点a、c处是正电荷,b、d处是负电荷.
(D)顶点a、b、c、d处都是负电荷.
6、下面说法正确的是:
[](A)等势面上,各点场强的大小一定相等;
(B)在电势高处,电势能也一定高;
(C)场强大处,电势一定高;
(D)场强的方向总是从电势高处指向电势低处。
7、两个薄金属同心球壳,半径各为 和 ( ),分别带有电荷 和 ,两者电势分别为 和 (设无穷远处为电势零点),将两球壳用导线连起来,则它们的电势为:
[ ](A) (B)
(C) (D)
3.在带电量为-Q的点电荷A的静电场中,将另一带电量为q的点电荷B从a点移到b点,a、b两点距离点电荷A的距离分别为r1和r2,如图所示。则在电荷移动过程中电场力做的功为
[](A) ;(B) ;
(C) ;(D) 。
4.某电场的电力线分布情况如图所示,一负电荷从M点移到N点。有人根据这个图得出下列几点结论,其中哪点是正确的?
(A)1>2,S=q/0.
(B)1q/0.
(D)1<2,S=q/0
4、关于高斯定理的理解有下面几种说法,其中正确的是()
(A)如果高斯面上 处处为零,则该面内必无电荷;
(B)如果高斯面内无电荷,则高斯面上 处处为零;
高中物理电场中的电场线分布特点

高中物理电场中的电场线分布特点在高中物理的学习中,电场是一个非常重要的概念,而电场线则是描述电场的一种直观工具。
掌握电场线的分布特点,对于理解电场的性质、电场力的作用以及电荷的运动等方面都有着至关重要的作用。
首先,我们来了解一下什么是电场线。
电场线是为了形象地描述电场而人为引入的假想曲线。
电场线上每一点的切线方向都与该点的电场强度方向一致,而电场线的疏密程度则表示电场强度的大小。
正点电荷产生的电场中,电场线是以点电荷为中心,呈放射状向外分布的。
越靠近点电荷,电场线越密集,电场强度越大;离点电荷越远,电场线越稀疏,电场强度越小。
这就好像从一个光源发出的光线,离光源越近越亮,离光源越远越暗。
负点电荷产生的电场中,电场线是呈会聚状指向负点电荷。
同样,靠近负点电荷的地方电场线密集,电场强度大;远离负点电荷的地方电场线稀疏,电场强度小。
等量同种电荷产生的电场中,如果是正电荷,那么在两电荷连线的中点处电场强度为零,从连线的中点向两侧,电场强度先增大后减小,电场线的分布比较复杂,呈现出一些弯曲和不均匀的特点。
等量异种电荷产生的电场中,在两电荷连线的中垂线上,电场强度从中点向两侧逐渐减小,电场线与中垂线垂直。
匀强电场是一种比较特殊的电场,其电场线是相互平行且等间距的直线,电场强度的大小和方向处处相同。
比如两块平行金属板,分别带等量异种电荷时,它们之间的电场就是匀强电场。
在实际问题中,我们常常需要根据电场线的分布特点来判断电场强度的大小和方向,从而分析电荷在电场中的受力和运动情况。
例如,一个带正电的粒子在正点电荷产生的电场中运动。
由于电场线的方向是从正点电荷指向无穷远,所以正电荷受到的电场力是沿着电场线的方向向外的。
而且,粒子靠近点电荷时,受到的电场力较大,加速度也较大;远离点电荷时,受到的电场力逐渐减小,加速度也逐渐减小。
再比如,在匀强电场中,一个带电粒子受到的电场力大小和方向都是恒定的。
如果粒子的初速度为零,那么它将沿着电场线的方向做匀加速直线运动;如果粒子有初速度,且初速度方向与电场线方向平行,那么它将做匀变速直线运动;如果初速度方向与电场线方向垂直,那么它将做类平抛运动。
有限长均匀带电直线电场的分析

有限长均匀带电直线电场的分析金彪(浙江省上虞市春晖中学,浙江 上虞 312353)摘要:本文分析了有限长均匀带电直线周围的电场,用两种方法论述了有限长均匀带电直线电场的电场线为双曲线而等势面为旋转椭球面,并由此计算出导体旋转椭球面电容及面电荷密度分布。
关键词:有限长均匀带电直线;旋转椭球面;双曲线;等势面;电场线;电势;电场强度如图1所示线段AB 为真空中均匀带正电直线,长为2c ,线电荷密度为e η,求其产生的电场中任一点D 的电场强度D E 与电势D U 。
1 用等效替代法求电场过D 点作AB 的垂线段DE ,垂足为E ,以D 为圆心,DE 长为半径,作圆弧FEG ,点F 在线段AD 上,点G 在线段BD 上,当圆弧FEG 的线电荷密度也为e η时,圆弧FEG 与线段AB 在D 点产生的电场强度相等。
论证如下:过D 点作任一微小角θd ,在圆弧和线段上分别截得HI 、JK ,过K 作KN 垂直于DJ ,则有三角形相似可得:22DHDJHI DH DJ NK DE DJ NK JKL L L L L L L L L L ⋅=⋅=⋅= (1) 由点电荷电场求解公式可得:线电荷密度相等短线JK 和HI 在D 点产生的电场强度相等,故线段AB和圆弧FG 在D 点的电场也相等。
由此可以得到线段AB 在D 的电场强度E D 方向为沿ADB ∠的角平分线DC 反向延长线向外。
若沿电场线方向移动一段微小距离l d 到D /,如图3。
可得ADC l L L AD AD /∠⋅=-sin d ,BDC l L L BD BD /∠⋅=-sin d ,由于DC 是ADB ∠的角平分线,可得BD BD AD AD L L L L //-=-, BD AD BD AD L L L L //-=-。
即:当D 点始终沿电场强度方向运动时,D 点运动的轨迹为电场线,而D 点到A 、B 两点的距离差保持不变,即电场线为双曲线。
大学物理实验报告,静电场,无限长同轴圆柱面之间的电势分布关系

大学物理实验报告,静电场,无限长同轴圆柱面之间的电势分布关系静电场的模拟实验报告实验二静电场的描绘【目的与任务】1、理解用模拟法描绘静电场的原理和方法;2、学会用模拟法描绘静电场的等势线和电场线;3、定性说明同轴圆柱面和带电直导线电流场的特点及其应用。
【仪器与设备】静电场描绘仪(西安教学仪器厂生产),万用电表,坐标纸等。
仪器简介:1、交流电源交流电源输出电压在0~10V之间连续可调,最大输出电流l A。
实验时将输出电压调节到实验要求之值。
2、静电场描绘仪图1 静电场描绘仪静电场描绘仪如图1所示,支架采用双层式结构,下层放置水盘和电极,上层安放坐标纸。
P是测量探针,用于在水中测量各点的电势,P′是与P联动的记录探针,可将P在水中测得的各电势点通过按下指针P′在坐标纸上打出印迹,同步地记录在坐标纸上。
由于P、P′是固定在同一探针架上的,所以两者绘出的图形完全相同。
3、模拟电极可提供两点电荷(平行输电线),同轴柱面(同轴电缆),聚焦电极三种模拟电极。
【原理与方法】1、直接测量静电场的困难带电体在周围空间产生的静电场,可用电场强度E或电势U的空间分布来描述。
一般情况下,可从已知的电荷分布,用静电场方程求出其对应的电场分布,但对较复杂的电荷分布,如电子管、示波管、电子显微镜、加速器等电极系统,数学处理上十分困难,因而总是希望用实验方法直接测量。
但是,直接测量静电场往往很困难。
因为,首先静电场中无电流,不能使用磁电式仪表,而只能使用较复杂的静电仪表和相应的测量方法;其次,探测装置必须是导体或电介质,一旦放入静电场中,将会产生感应电荷或极化电荷,使原电场发生改变,影响测量结果的准确性。
若用相似的电流场来模拟静电场,则可从电流场得到对应的静电场的具体分布。
2、用稳恒电流场模拟静电场的可行性如果两种物理现象在一定条件下满足同一形式的数学规律,则可将对其中某一种物理现象的研究来代替对另一种物理现象的研究,这种研究方法称为模拟法。
高二物理竞赛无限长均匀带电直线的场强分布课件
对于电荷连续分布的带电体,
E
q
dq
40r2
er
6.
电通量:
Φe
EdS
S
7. 高斯定律: EdS 1
S
0
qin t
8. 典型静电场:
均匀带电球面: E = 0
(球面内)
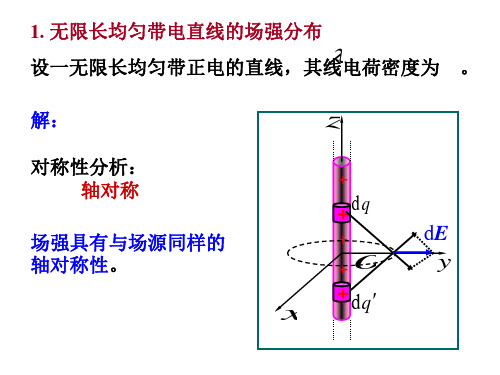
场强具有与场源同样的轴对称性。
电偶极子在电场中受到的力矩:
设一无限长均匀带正电的直线,其线电荷密度为 。
q 设一无限长均匀带正电的直线,其线电荷密度为 。
。
Φ EdS S’ 其解中:: 对q称0为性静分止析点:电E 垂荷e直于平面S
e 解:设通过该平面的电通量为
n
E
EdS EdS 设其面电荷密度为 。
++++++++++
S
S
EdSr2E0 S
EdSr2ESE
S
2
例4 设正方形平面边长为a ,点电荷 q 位于距平面中点 a/2处,求通过该平面的电通量。
er
(球体外)
均匀带电无限长直线: E 2 0r
方向垂直于带电直线
均匀带电无限大平面: E 2 0
方向垂直于带电平面
9. 电偶极子在电场中受到的力矩:
MpE
THE END
2. 电偶极子轴线的中垂线上一点的电场强度
E
1
4 0
q r2
e
E
1
40
q r2
e
r r r
y2(l)2 2
e( l/2iyj)r e(l/2iyj)r
又 qint S2x1
由高斯定律:
2ES1 0S2x1 E0x1
有限长直线电荷的电场分布

有限长直线电荷的电场分布江俊勤【摘要】用Mathematica-10.3强大的数值计算和数字绘图能力,特别是绘制等值线和流线图的卓越功能,研究和比较了有限长均匀带电直线和带电导体直线两种电场的分布, 绘制了电势和电场大小、等势线和电场线的分布图.这种方法绘制的等势线和电场线能满足"等势线疏密程度反映电势变化的快慢"和"电场线疏密程度反映电场强弱"的定性要求,避免了以往文献只能随意绘制的缺陷.%Using the famous software Mathematica-10.3, the distributions of two kinds of electric field in the uniformly charged finite length-straight line and the charged conductor finite length-straight line are studied and compared, the distribution maps of the electric field intensity and the isoelectric line well as well the electric field line are plotted.The equipotential lines and the electric field lines drawn by this method can meet the qualitative requirements that "the density of the equal potential line reflects the speed of the electric potential change" and "the density of the electric field lines reflects the electric field strength", which avoids the defects of previous literature.【期刊名称】《广东第二师范学院学报》【年(卷),期】2017(037)003【总页数】6页(P65-70)【关键词】均匀带电有限长直线;带电有限长直导线;电势;电场强度;等势线;电场线【作者】江俊勤【作者单位】广东第二师范学院物理与信息工程系, 广东广州 510303【正文语种】中文【中图分类】O441.1有限长直线电荷的电场,是电磁场的重要模型之一,是人们一直关注的问题[1-4].文[1-3]使用点电荷的电势或电场强度公式和叠加原理导出了均匀带电有限长直线的电势或电场强度,文[4]则用椭球面坐标系和高斯定理推导出均匀带电有限长直线的电场强度. 但现有文献存在两点不足:1)由于同种电荷相斥,有限长直线段上的电荷不会是均匀的,特别是有限长导体直线,其电荷分布必然是中间疏两头密.到目前为止,未见有资料详细研究带电有限长直导线的电势或电场强度分布问题;2)讨论均匀带电有限长直线的文献[2-4]没有给出定量的电场空间分布图, 都只是随意绘制了若干条等势线和电场线——未满足“等势线疏密程度反映电势变化的快慢”和“电场线疏密程度反映电场强弱”的定性要求.为了弥补现有文献的不足,本文用Mathematica-10.3强大的数值计算能力、卓越的数字绘图功能,统一研究和比较有限长均匀带电直线和带电导体直线两种电场的分布, 定量绘制电势和电场大小的空间分布图,并给出疏密程度符合物理要求的等势线和电场线分布图.设长度为2l的直线段上总带电荷量为Q ,以直线段中心为坐标原点,z轴在直线段上,研究该电场的空间分布.由于本问题具有轴对称性,只需研究P(x,0,z)点处电场的空间分布.设z=z′点处的电荷线密度为λ,则线元z′~z′+dz′上的电荷量为dQ=λdz′(点电荷)在P(x,0,z)点处产生的电势为dU==.对全直线段求积分,得U=.电场强度由电势的负梯度求得Ex=-,Ez=-.电势的计算依赖于电荷线密度λ,下面将分两种情况进行具体研究.先考虑最简单的模型,假设电荷Q均匀分布于直线段上,则λ为常数,λ=Q/2l,U=.以U0=Q/(4π2ε0l)为电势单位;相应地,电场强度以E0=Q/(4π2ε0l2)为单位, 由式(4)积分得U=U0ln[z+l+]-U0ln[z-l+].由式(3)得Ex=E0-E0,Ez=E0-E0.由式(5),令U==U0ln C1(C1≥1),得xoz平面内的等势线方程z+l+=C1[z-l+].对式(7)移项、等式两边平方,化简得(C2-1)x2+2(C-1)z2=2l2(C+1),式中 C= ;C1≥1,C≥1. 当C≠1,即C1≠1时,式(8)可改写为+=1,这是标准椭圆方程,半短轴为a=、半长轴为b=、半焦距为c==l.当C1→1,即C→1时,由式(8)得l→0或者x/l→∞或者z/l→∞, 直线分布电荷退化为点电荷(等势线是同心圆簇),或者对应于远场(此时电场分布接近于点电荷的电场).给定一个C1值,由式(7)或式(8)可绘制出相应的一条等势线,电磁学要求等势线疏密程度应定性地反映电势变化的快慢,所以C1值的选取必须考虑电势U(x,z)的分布情况,使用Mathematica绘制三维曲面图的命令Plot3D,以-10≤x/l≤10和-10≤z/l≤10为画图区域,由式(5)和式(6)容易绘制电势U(x,z)和电场强度大小E(x,z)=的分布图,如图1所示,在带电直线段上电势和电场强度都是无穷大,绘图时被截去顶部(下同).不同观测区域电势变化的快慢差别很大:在区域外围,电势分布接近于点电荷的电势,而且变化缓慢;在接近带电线段时,电势快速变化. 按照定义要求:等势线疏密程度应定性地反映电势变化的快慢,如果根据式(7)或式(8)使用隐函数绘图法绘制等势线分布图,需要取大量不同的C1值,而C1值集合的选取必须考虑图1所示电势的变化规律,这是一件十分繁琐的工作. 所幸的是,在Mathematica-10.3等版本中,内置了绘制等高线的命令,直接把式(5)代入ContourPlot之中就可以方便准确地绘制出等势线分布图,以-10≤x/l≤10和-10≤z/l≤10为画图区域,取250条等高线,结果如图2所示(对应于不带箭头的黑色闭合曲线).图2显示: xoz平面内的等势线的确是以线段两个端点z=±l为焦点的共焦椭圆簇(在三维空间里则是绕z轴旋转的共焦椭球面簇);在离带电线段较远的外围,等势线稀疏,代表电势变化缓慢、电场强度较小,而且椭圆形等势线的偏心率较小(接近于圆);越往中心区,等势线越密,椭圆的偏心率越大;在带电线段附近,等势线十分密集(以至于无法分开各条等势线而形成一个黑色阴影区),表示电势快速变化、电场强度很大.文[2]随意绘制出10条等势线(见该文中图2的虚线),文[2]没有说明决定10条等势线位置的10个C1常数具体取多少以及凭什么依据取值,其结果图显然不满足“等势线疏密程度定性地反映电势变化的快慢”的要求、不符合图1所示的电势变化规律,其主要问题有两方面:(a)内层的等势线密度反而比中间层等势线密度小;(b)电势快速变化的中心区完全没有等势线(文[3]的情况也类似, 文[4]则象征性地画出两条等势线草图).电场线由一阶微分方程确定=.把式(6)代入式(10),经化简和凑微分得 =.积分得电场线簇方程-=2C2(|C2|≤l).由式(11)移项、等式两边平方,化简得-+=1.式(12)是标准双曲线方程,其半焦距c==l,与C2无关,所以电场线是以z=±l为焦点的共焦双曲线簇,给定一个C2值就得到一条电场线. C2的值集如何选取才能使电场线疏密程度定性反映电场强弱?现有文献都没有妥善处理,文[2]和文[3]给出的电场线分布图都是在平行于带电直线方向上电场线十分稀疏,在垂直方向上电场线则密集得多(见文[2]的图2和文[3]的图3), 这与图1(b)所示的电场分布图不一致!C2值的选择是一个颇为复杂问题,在本文中我们将直接避开这个麻烦,方法是使用Mathematica-10.3等较高版本中一个十分有用的绘制流线图命令, 其格式为:StreamPlot[{Ex,Ez},其他选项]这样,可以直接从式(6)出发绘制电场线分布图,不用求解微分方程、不需要选择积分常数C2,这对于电场线微分方程没有解析解的情况更有意义!使用适当的“其他选项”后,得到电场线分布图,如图2中带箭头的射线簇所示, 电场线分布图较好地描述了电场的发布情况:在带电线段附近,x方向与z方向的分布明显不同,确保每条电场线都与大偏心率的椭圆形等势线正交(后面的近区放大图将更加清晰展现这一现象);在离带电线段较远的外围,电场线的分布趋于各项同性,即趋于点电荷的电场分布规律.美中不足的是:在接近带电线段处,有些电场线没有画至与带电直线段相接,这是因为在这些地方的电场线过于密集,软件系统自动省去一些线段,但这不是大问题,我们在读图时只需将它顺延画到带电直线上就可以了.正如上面提到的,在远离带电线段的外围,电场分布情况与点电荷的电场相近;在带电直线段附近区域,电场分布情况才具有特色. 下面,取画图区域为-0.5≤x/l≤0.5和-1.5≤z/l≤1.5,电势、电场强度大小以及等势线和电场线合并图分别如图3、图4和图5所示.图1~图5全面、形象和准确地描述了均匀带电有限长直线的电场空间分布.图1和图2显示了电场分布的整体概貌;图3和图4详细地描述在带电直线段附近电势和电场强度大小的空间分布;图5详细地描述在带电直线段附近等势线和电场线的分布及其相互关系. 这些图不但美观而且正确反映了物理规律,图2和图5中等势线和电场线疏密程度能定性地反映电势的变化快慢和电场强度的大小分布.相较于文献[2]和[3]随意绘制若干条等势线和电场线,本文的方法和结果是一次质的飞跃. 需要特别强度的是:本文中,只需将电势和电场强度计算式直接代入Mathematica-10.3的绘图命令就可快速获得这些精美图像,无需推导和处理等势线方程和电场线方程. 在研究更复杂电荷系统的电场分布时(通常没有解析解),这种方法尤其有用,下面用该方法研究有限长带电导体直线的电场分布.由于同种电荷相斥,有限长直线段上的电荷不会是均匀的,特别是有限长细导线,其电荷分布必然是中间疏两头密[5],导线上z′点处的电荷线密度为λ=.把式(13)代入式(2)和式(3), 得U=,Ex=,Ez=.式(14)~式(16)是复杂的积分,本文用Mathematic-10.3的标准数值积分法进行计算,其他的处理方法和步骤与均匀带电有限长直线段的方法相同.取研究区域在导线附近:-0.5≤x/l≤0.5和-1.5≤z/l≤1.5,根据式(14)~式(16), 用三维曲面画图命令Plot3D、等值线绘图命令ContourPlot和流线图绘制命令StreamPlot,就可绘制出电势、电场强度大小以及等势线和电场线合并图,分别如图6、图7和图8所示,他们从各个角度准确地描述了带电有限长导体直线的电场分布.有限长直线电荷的电场,是人们关注的重要问题之一. 由于数学的复杂性,到目前为止,未见有其他作者研究和绘制有限长带电导体直线的等势线和电场线分布图;已有的文献仅仅讨论了最简单的情形——均匀带电有限长直线——其等势线和电场线方程都有解析解,分别含有任意常数C1和C2;但是C1值集和C2值集的选择必须考虑电势和电场强度的分布规律而且数集的元素必须足够多,这是一件繁难的工作,已有的文献都没有处理好这个问题、所给出的等势线和电场线分布图都是随意地绘制——不符合“等势线疏密程度反映电势变化的快慢”和“电场线疏密程度反映电场强弱”的物理要求.【相关文献】[1] 郑开春. 电动力学解题指导[M]. 北京:北京大学出版社,2004:20-21.[2] 卢林芳, 胡先权, 周林, 等. 有限长直线电荷等电势线和电力线的求解与描绘[J]. 重庆师范大学学报,2008, 25(3):66-69.[3] 姜付锦. 有限长均匀带电直线的电场分布特点[J]. 物理通报,2013(5):32-33. [4] 王爱霞,高国棉,周九茹. 有限长均匀带电直线电场的对称性分析与计算[J]. 大学物理,2015,34(10):17-19.[5] 陈钢. 有限长带电导体直线的电荷分布[J]. 大学物理,2011, 30(10):28-29.。
均匀带电导体球,半径为a,带电量为q
均匀带电导体球,半径为a,带电量为q1. 概述均匀带电导体球是一种重要的物理模型,它在静电学中有着广泛的应用。
对于这种物体的研究不仅可以帮助我们理解带电体的电场分布特性,还可以为相关领域的研究提供基础和参考。
在本文中,我们将对均匀带电导体球的性质和特点进行详细的分析和讨论。
2. 带电体的基本特点带电体是指带有静电荷的物体。
当一物体带有电荷时,它将产生电场,并且在外部电场的作用下,带电体将受到电场力的影响。
在静电学中,我们通常关注的是带电体所产生的电场和在外部电场中所受到的作用力。
均匀带电导体球作为一种重要的带电体模型,其电场分布和电势分布具有一定的规律性和特点。
3. 均匀带电导体球的电场性质3.1 电场分布对于均匀带电导体球而言,其内部电场强度为零,而在球面上和球外的某一点P处的电场强度可根据库仑定律进行推导。
在球外某点P处,球的电场强度与点电荷的电场强度具有相同的形式,即E = kq/r^2,其中k为库仑常数,q为带电体的电量,r为点P到带电球的距离。
在球面上某一点P处,电场强度的大小同样满足E = kq/r^2,且方向沿着球面的法线方向,且大小大小随着点P到球心的距离r的变化而变化。
3.2 电势分布均匀带电导体球的电势分布也具有一定的规律性。
根据电势的定义,我们知道电势V与电场强度E满足V = -∫ E·dr,其中积分路径为从参考点到指定点的路径。
对于均匀带电导体球而言,我们可以利用球对称性以及电场处处垂直于等势面的性质进行推导,得到该球的电势分布。
4. 均匀带电导体球的作用力均匀带电导体球受到外部电场的作用力与其所带电荷量和外部电场的分布有着密切的关系。
根据静电学的基本原理,我们可以得到带电导体球受到的作用力大小与方向。
5. 结论在本文中,我们对均匀带电导体球的性质和特点进行了详细的分析和讨论。
通过对该物体的电场分布、电势分布和作用力进行分析,我们可以更好地理解带电体的静电学特性,并为相关领域的研究提供基础和参考。
大学物理第四章静电场课后习题概要
b
p
o
x
l
dx
x
kxdx dE 4 0 x b 2 kxdx k bl l E ln 2 0 4 4 0 b l b 0 x b
l
1
1
方向沿x轴的负方向。
练习题4-7 图为两个分别带有电荷的同心球壳系统。 设半径为 R1 和R2 的球壳上分别带有电荷 Q1 和 Q2 ,求: (1)I、II 、III三个区域中的场强;(2)若 Q1 Q2 , 各区域的电场强度又为多少?画出此时的电场强度分 布曲线。 q内 2 解: s E dS 4r E 0
0 r R1
E1 0
Q1
R1
R1 r R2
r R2
当 Q1 Q2 时
40 r Q1 Q2 E3 40 r 2
2
E2
Q1
Q2
Ⅲ Ⅱ
O Ⅰ
R2
0 r R1
E1 0
R1 r R2
r R2
当 Q1 Q2 时
0 r R1
当 Q1 Q2 时
Q1
R1
R2
O Ⅰ Ⅱ Ⅲ
Q2
r
练习题4-12 同轴电缆是由两个很长且彼此绝缘的同 轴金属圆柱体构成,如图所示。设内圆柱体的电势 为U1,半径为R1;外圆柱体的电势为U2 ,外圆柱体 的内半径为R2,两圆柱体之间为空气。求两个圆柱 体的空隙中离轴为r处(R1 < r <R2)的电势。
定理可知球外空间的场强E外
(3)因为球表面的场强 E表 变小。
q 4 0 r
2
。由此可知,球
外空间的场强与气球吹大过程无关。
微元法研究均匀带电体的电场分布
微元法研究均匀带电体的电场分布*阳喜元†,蔡新华,吴丹(湖南文理学院物理与电子科学学院,湖南常德415000)摘要:以均匀无限长带电直线的电场分布为基础,运用微元法和叠加原理研究了无限大均匀带电平面和无限长均匀带电圆柱面在其周围电场分布情况。
然后根据均匀带电圆环轴线上的电场分布,进一步讨论均匀圆柱面在其轴线上的电场和均匀带电球面在其周围产生的电场,所得结果与高斯定理完全符合。
关键词:微元法;电场分布;均匀带电体;叠加原理中图分类号:O441.1 文献标识码:A 文章编号:1003-7551(2008)03-0034-041 引言微元法在大学物理教学中有非常重要的作用。
在多年大学物理教学实践中,我们发现这样的问题,即由于学生对微积分知识掌握不够牢固,常使他们在解答有关大学物理问题时感到无从下手,更难以理解各物理量的真正含义乃至正确解答有关物理题。
因此,在教学过程中,教师不仅要把抽象物理知识讲透彻,还应将微元法传授给学生来解答物理问题,从而增强两者之间的联系,激发学生学习物理学兴趣。
目前,一般教材在讲授带电体电场分布时,都运用电场强度定义和叠加原理,以例题形式讲授无限长均匀带电直线和均匀带电圆环在其轴线上某一点的电场,而对对称性较高带电体的电场分布,则用高斯定理给予解决,而已有参考文献[1-3]计算方法又较复杂,对于非物理专业学生来说,是难以接受,也不利于学生对微元法基本思想的理解。
因此,为了使学生更好地理解和掌握电场强度的概念、叠加原理以及微积分的有关知识,本文以上面提到的两种带电体电场分布为基础,运用微元法,根据电场定义和叠加原理研究其他均匀带电体电场分布情况。
2 无限长带电直线电场分布应用无限长均匀带电直线的电场分布[4]:E = λ2πε0a(1)其中,λ 是均匀带电导线的线电荷密度,即单位长度导线带的电量,a 是点到导线的距离,电场强度的方向垂直于导线。
2.1 无限大带电平面的电场分布首先,建立一个坐标系,其圆点O 在选定无限长平面的中轴线上,x 轴垂直于带电面,y 轴在面内(如图1 所示)以(1)式为基础,运用微元法和叠加原理来求:宽为2L ,无限长的均匀带电平面(电荷密度为σ )在x 轴上一点P 的电场强度E 。
大学应用物理答案7
(b)
分析:在带电半圆环上任取一线元 dl = Rdθ ,其电荷为: dq =
Q dl ,此电荷元可视 πR
1
1 dq ,方向沿径向,如图 7 - 4πε 0 r 2 69(b)所示, 。因圆环上电荷对 y 轴呈对称性分布,所以电场分布也是轴对称的,即在 x
为点电荷,它在 O 点产生的电场强度大小为: dE = 轴上的电场强度 E x = 解:
ε0 当 r < R 时, E ⋅ 2π r ⋅ l = 0 , E = 0 ;
S
� ∫
E i dS =
∑q
i
,有:
3
当 r > R 时, E ⋅ 2π r ⋅ l =
σ i2π Ril σR r; ,E = ε0 ε 0r 2
7-15 求均匀带电球体内、外的场强分布,已知球体半径为 R,所带总电荷为 q。 分析:由题可知,电荷分布是球对称的,所以电场强度的分布也是球对称的。因此,在 电场强度的空间中任意点的电场强度的方向沿径矢, 大小则依赖于从球心到场点的距离。 即 在同一球面上的各点的电场强度的大小是相等的。 解:以球心到场点的距离为半径作一球面,则通过此球面的电通量为:
s1
s0
同理,由 s2 和以 R 为半径的大圆面 s0 。组成一个封闭曲面 s`,则可得:
2 Φ eS2 = − � ∫ E ids = ES = Eπ R
s0
7-13 如图 7-71(a)所示,电荷线密度为 λ1 的无限长均匀带电直线,其旁垂直放置电荷 线密度为 λ2 的有限长均匀带电直线 AB,两者位于同一平面内。则 AB 所受静电作用力的大 小为多少? 分析一: 由题意可知,两直线均匀带电。由于库仑定律只适用于点电荷系统。因此, 需将两带电直线分成许多电荷元;建立如图 7-71 (b) 所示的直角坐标系,有 dq1 = λ1dy ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限长均匀带电导体直线的电场分布特点
姜付锦
(武汉市黄陂区第一中学,湖北 武汉 430300)
摘要:通过库仑定律和麦克斯韦方程推导出有限长均匀带电导体直线的电场线方程和等 势线方程,并利用绘图软件WINPLOT 对电场线与等势线画出函数图像,直观表示了电场的特点。
关键词:有限长均匀带电导体直线;电场线方程;等势线方程
法拉第为形象地描绘静电场在空间的分布情况,引入了电场线的概念。
麦克斯韦通过对电场线特点的分析总结出了麦克斯韦方程组。
本文将通过库仑定律和麦克斯韦方程对有限长均匀带电导体直线的电场线方程与等势线方程进行推导,得出它们的分布规律,并利用绘图软件WINPLOT 对电场线与等势线画出函数图像,直观表示了电场的特点。
1 电场强度的计算
如图1所示,有一均匀带电导体直线,长度为a (0)a <<∞,总电量为q ,以直线的中点为坐标原点,并以直线为x 轴,建立平面直角坐标系xoy ,在x 轴上坐标为0x 处取一电荷元,其电量为0(
dq dx λλ==
根据库仑定律,它在(,)P x y 点激发的电场强度为0
3
k dx d E r r
λ= ,式中:r 是从0dx 指向P 点的矢量,r d E 与x 轴的夹角为θ,则d E 沿x 轴和y 轴的两个分量分别为cos ,sin x y dE dE dE dE θθ==[1],则
000
223/2223/2
00(),[()][()]x y
k x x dx k ydx dE dE y x x y x x λλ-=
=+-+-
图1 均匀带电导体直线外任一点处的场强
将上列两式积分,得
0022223/2
0220
22223/2
022()[()][()]a a a a x x a
a a a y y k x x dx k E dE y x x y
a a
x x
k ydx k E dE y x x y λλ
λλ-----===+--+===++-⎰⎰
⎰⎰
2 电场线方程的推导
根据麦克斯韦方程可知,电场线的微分方程为y
x
E dy dx E =
,将上式代入后得
dy dx
x x =-++
()()a a
x dx ydy x dx ydy
++-+=
2222[()][()]
a a
d y x d y x +++-=,两边同时积分得
C =(式中C 是一常量)
焦点相同的双曲线,式中a C -≤≤
3 等势线方程的推导
如图2所示,图中P 点的电势
a P ϕ=⎰
[2]
,
将上式整理后得,
图2 均匀带电导体直线外任一点处的电势
[ln(ln(
22
a
P
a a
k x x ϕλ
==-+---+
⎰
4 数值模拟
利用Winplot强大的绘图功能,对以上的电场线和等势线进行模拟,数值模拟中令1C/m,=1m
a
λ=,如图3所示
5 结语
通过对电场线与等势线数值模拟的分析可以发现:在原坐标系中,当,
x y
→∞→∞时有限长均匀带电导体直线相当于一个“点电荷”,它的电场线的反向延长线趋近于通过原点;等势面趋近于圆周。
以上的推导都是建立在电荷均匀分布的条件下,但是实际上有限长带电直线的电荷的分布不是均匀的,所以本文中的分析只是一种简化处理情形[3]。
进一步研究可以发现,均匀带电导体直线的电场线和等势线与波的干涉图样相似,干涉图样中的波面与本文中的等势线相似;干涉图样中的波线与本文中的电线线相似[4]。
参考文献:
[1] 徐斌富章可钦邹勇潘传芳大学基础物理(第一册)[M] 北京:科学出版社,2007:
8-9
[2] 郭硕鸿电动力学(第二版)[M] 北京:高等教育出版社1998:56-57
[3] 陈钢有限长带电导体直线的电荷分布[J] 大学物理,2010 10(30):28-29
[4] 陈敏数形结合剖析水波的干涉图样[J] 物理通报,2012 (5):89~92
The distribution characteristic of the electric field
of the uniformly charged conductor straight-line with finite length
JIANG Fujin
(The First High School of Huangpi District in Wuhan, Wuhan 430300, Hubei ) Abstract: In this paper, we derive the electric field line equation and the equipotential line equation of the uniformly charged conductor straight-line by Coulomb's law and the Maxwell Equation.Then we plot the image of the electric field and the equipotential line with the mapping software WINPLOT and give an intuitive presentation of the electric field.
图3 均匀带电导体直线的电场线和等势线
Key words: uniformly charged conductor straight-line with finite length, electric field line equation, equipotential line equation。
