2020年中考数学必考经典题讲练案-图形的变换综合问题

合集下载

2020年中考数学压轴解答题14 图形变换和类比探究类几何压轴综合问题 (学生版)

备战2020中考数学之解密压轴解答题命题规律专题14 图形变换和类比探究类几何压轴综合问题【类型综述】本节内容每年中考都会选择一种变换作为压轴题的背景素材,可以对函数图象进行平移,可以对几何图形进行平移、旋转,考查学生的数学综合应用能力．在选择、填空中也会涉及变换的概念和简单应用．只要抓住全等变换的特点,找到变与不变的量就可以解决问题．预计在2019年中考中仍会在压轴部分渗透变换,但是会有新情境的渗透．【方法揭秘】1.平移的性质(1)平移前后,对应线段平行、对应角相等；(2)各对应点所连接的线段平行（或在同一直线上）或相等；(3)平移前后的图形全等,注意：平移不改变图形的形状和大小.2.旋转的性质：(1)对应点到旋转中心的距离相等；(2)每对对应点与旋转中心所连线段的夹角等于旋转角；(3)旋转前后的图形全等.3.中心对称的性质：在成中心对称的两个图形中,对应点的连线都经过对称中心,并且被对称中心平分_．成中心对称的两个图形全等.【典例分析】【例1】操作与证明：如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF．取AF中点M,EF的中点N,连接MD、MN．（1）连接AE,求证：△AEF是等腰三角形；猜想与发现：（2）在（1）的条件下,请判断MD、MN的数量关系和位置关系,得出结论．结论1：DM、MN的数量关系是；结论2：DM、MN的位置关系是；拓展与探究：（3）如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则（2）中的两个结论还成立吗？若成立,请加以证明；若不成立,请说明理由．【例2】已知：如图1,OM是∠AOB的平分线,点C在OM上,OC＝5,且点C到OA的距离为3．过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论：OD+OE等于多少；（1）把图1中的∠DCE绕点C旋转,当CD与OA不垂直时（如图2）,上述结论是否成立？并说明理由；（2）把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时：①请在图3中画出图形；②上述结论还成立吗？若成立,请给出证明；若不成立,请直接写出线段OD、OE之间的数量关系,不需证明．【例3】两个三角板ABC,DEF按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内),其中,∠C＝∠DEF＝90°,∠ABC＝∠F＝30°,AC＝DE＝4 cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动．设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2)．(1)当点C落在边EF上时,x＝________cm；(2)求y关于x的函数表达式,并写出自变量x的取值范围；(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值．【例4】在△ABC中,∠ABC=90°,AB=BC=4,点M是线段BC的中点,点N在射线MB上,连接AN,平移△ABN,使点N移动到点M,得到△DEM（点D与点A对应,点E与点B对应）,DM交AC于点P．（1）若点N是线段MB的中点,如图1．①依题意补全图1；②求DP的长；（2）若点N在线段MB的延长线上,射线DM与射线AB交于点Q,若MQ=DP,求CE的长．【例5】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E（4,0）．（1）写出D的坐标和直线l的解析式；（2）P（x,y）是线段BD上的动点（不与B,D重合）,PF⊥x轴于F,设四边形OFPC的面积为S,求S与x 之间的函数关系式,并求S的最大值；（3）点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′．在图2中探究：是否存在点Q,使得M′恰好落在y轴上？若存在,请求出Q的坐标；若不存在,请说明理由．【例6】再读教材:宽与长的比是5-1(约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.第三步,折出内侧矩形的对角线AB,并把AB折到图③中所示的AD处,第四步,展平纸片,按照所得的点D折出DE,使DE⊥ND,则图④中就会出现黄金矩形,问题解决:（1）图③中AB=________(保留根号);（2）如图③,判断四边形BADQ的形状,并说明理由;（3）请写出图④中所有的黄金矩形,并选择其中一个说明理由.（4）结合图④.请在矩形BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.【变式训练】一、单选题1．如图,正方形ABCD 中,6AB =,E 为AB 的中点,将ADE ∆沿DE 翻折得到FDE ∆,延长EF 交BC 于G ,FH BC ⊥,垂足为H ,连接BF 、DG .结论:①BF DE P ；②DFG ∆≌DCG ∆；③FHB ∆∽EAD ∆；④43GEB ∠=；⑤ 2.6BFG S ∆=.其中的正确的个数是（）A ．2B ．3C ．4D ．52．如图所示,点P 是边长为2的正方形ABCD 的对角线BD 上的动点,过点P 分别作PE ⊥BC 于点E,PF ⊥DC 于点F,连接AP 并延长,交射线BC 于点H,交射线DC 于点M,连接EF 交AH 于点G ,当点P 在BD 上运动时（不包括B 、D 两点）,以下结论中：①MF ＝MC ；②AP ＝EF ；③AH ⊥EF ；④AP 2＝PM•PH ；⑤EF 的最小值是2．其中正确结论有（）A ．2个B ．3个C ．4个D ．5个3．如图,在平面直角坐标系中,菱形ABCD 的顶点C 的坐标为()1,0-,点B 的坐标为()0,2,点A 在第二象限,直线1y x 52=-+与x 轴、y 轴分别交于点N 、M ．将菱形ABCD 沿x 轴向右平移m 个单位,当点A 落在MN 上时,则m 为（）A ．1B ．2C ．3D ．44．如图,在平面直角坐标系中,A （1,2）,B （3,2）,连接AB ,点P 是x 轴上的一个动点,连接AP 、BP ,当△ABP 的周长最小时,对应的点P 的坐标和△ABP 的最小周长分别为（）A ．(10)224+，，B ．(30)224+，，C ．(20)25，，D ．(20)252+，，5．如图,将小正方形AEFG 绕大正方形ABCD 的顶点A 顺时针旋转一定的角度α（其中0°≤α≤90°）,连接BG 、DE 相交于点O ,再连接AO 、BE 、DG ．王凯同学在探究该图形的变化时,提出了四个结论： ①BG ＝DE ；②BG ⊥DE ；③∠DOA ＝∠GOA ；④S △ADG ＝S △ABE ,其中结论正确的个数有（）A ．1个B ．2个C ．3个D ．4个6．如图,点P 是等边三角形外一点,把BP 绕点B 顺时针旋转60°到BP ',已知AP B '∠=150°,:2:3P A P C ''=,则:PB P A '的值是（）A ．2 : 1B ．2 : 1C ．5 : 2D ．3 : 1二、填空题7．如图,在菱形ABCD 中,AB ＝2,∠BAD ＝60°,将菱形ABCD 绕点A 逆时针方向旋转,对应得到菱形AEFG,点E 在AC 上,EF 与CD 交于点P,则DP 的长是________.8．如图,在平面直角坐标系中,直线l :28y x =+与坐标轴分别交于A ,B 两点,点C 在x 正半轴上,且OC ＝O B ．点P 为线段AB （不含端点）上一动点,将线段OP 绕点O 顺时针旋转90°得线段OQ ,连接CQ ,则线段CQ 的最小值为___________．9．如图,直角三角形ABC 中,90ACB ∠=︒,10AB =,6BC =,在线段AB 上取一点D ,作DF AB ⊥交AC 于点F ,现将ADF ∆沿DF 折叠,使点A 落在线段DB 上,对应点记为1A ；AD 的中点E 的对应点记为1E .若111E FA E BF ∆∆:,则AD =______.10．如图,四边形ABCD 是矩形,AD ＝5,AB ＝163,点E 在CD 边上,DE ＝2,连接BE ,F 是BE 边上的一点,过点F 作FG ⊥AB 于G ,连接DG ,将△ADG 沿DG 翻折的△PDG ,设EF ＝x ,当P 落在△EBC 内部时（包括边界）,x 的取值范围是__．11．如图,将函数3(0)y x x=>的图象沿y 轴向下平移3个单位后交x 轴于点C ,若点D 是平移后函数图象上一点,且BCD ∆的面积是3,已知点(2,0)B -,则点D 的坐标__________.12．如图,有一条折线11223344A B A B A B A B ⋯,它是由过()10,0A ,()12,2B ,()24,0A 组成的折线依次平移4,8,12,⋯个单位得到的,直线2y kx =+与此折线恰有2(1n n ≥,且为整数)个交点,则k 的值为______．三、解答题13．如图,直线：y ＝﹣3x +4与x 轴、y 轴分别別交于点M 、点N ,等边△ABC 的高为3,边BC 在x 轴上,将△ABC 沿着x 轴的正方向平移,在平移过程中,得到△A 1B 1C 1,当点B 1与原点O 重合时,解答下列问题：（1）点A 1的坐标为．（2）求△A 1B 1C 1的边A 1C 1所在直线的解析式；（3）若以P 、A 1、C 1、M 为顶点的四边形是平行四边形,请直接写出P 点坐标．14．如图1,在△ABC 中,AB=BC=5,AC=6,△ABC 沿BC 方向向右平移得△DCE,A 、C 对应点分别是D 、E.AC 与BD 相交于点O.（1）将射线BD 绕B 点顺时针旋转,且与DC,DE 分别相交于F,G,CH ∥BG 交DE 于H,当DF=CF 时,求DG 的长；（2）如图2,将直线BD 绕点O 逆时针旋转,与线段AD,BC 分别相交于点Q,P.设OQ=x,四边形ABPQ 的周长为y,求y 与x 之间的函数关系式,并求y 的最小值.（3）在（2）中PQ 的旋转过程中,△AOQ 是否构成等腰三角形？若能构成等腰三角形,求出此时PQ 的长？若不能,请说明理由.15．在平面直角坐标系中,O 为原点,点A （6,0）,点B 在y 轴的正半轴上,ABO 30∠︒=．矩形CODE 的顶点D,E,C 分别在OA,AB,OB 上,OD=2.．（Ⅰ）如图①,求点E 的坐标；（Ⅱ）将矩形CODE 沿x 轴向右平移,得到矩形C O D E '''',点C,O,D,E 的对应点分别为C O D E ，，，''''．设OO t '=,矩形C O D E ''''与ΔABO 重叠部分的面积为S ．①如图②,当矩形C O D E ''''与ΔABO 重叠部分为五边形时,C E '',E D ''分别与AB 相交于点M,F,试用含有t 的式子表示S,并直接写出t 的取值范围；3S 53剟,求t 的取值范围（直接写出结果即可）．16．如图,将矩形OABC放在平面直角坐标系中,O为原点,点A在x轴的正半轴上,B（8,6）,点D是射线AO 上的一点,把△BAD沿直线BD折叠,点A的对应点为A′．（1）若点A′落在矩形的对角线OB上时,OA′的长=；（2）若点A′落在边AB的垂直平分线上时,求点D的坐标；（3）若点A′落在边AO的垂直平分线上时,求点D的坐标（直接写出结果即可）．17．在Rt△ABC中,∠ACB=90°,∠BAC=60°,BC=23,D是AB的中点,直线BM∥AC,E是边CA延长线上一点,将△EDC沿CD翻折得到△E′DC,射线DE′交直线BM于点F．（1）如图1,当点E′与点F重合时,求证：四边形ABE′C为平行四边形；（2）如图2,延长ED交线段BF于点G．①设BG=x,GF=y,求y与x的函数关系式；②若△DFG的面积为33,求AE的长．18．如图①,若直线l︰y=－2x+4交x轴于点A、交y轴于点B,将△AOB绕点O逆时针旋转90o得到△COD．过点A,B,D的抛物线h︰y=ax2+bx+4．（1）求抛物线h的表达式；（2）若与y轴平行的直线m以1秒钟一个单位长的速度从y轴向左平移,交线段CD于点M、交抛物线h 于点N,求线段MN的最大值；（3）如图②,点E为抛物线h的顶点,点P是抛物线h在第二象限的上一动点（不与点D、B重合）,连接PE,以PE 为边作图示一侧的正方形PEFG ．随着点P 的运动,正方形的大小、位置也随之改变,当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标．19．已知,正方形ABCD 的边长为4,点E 是对角线BD 延长线上一点,AE=BD ．将△ABE 绕点A 顺时针旋转α度（0°＜α＜360°）得到△AB′E′,点B 、E 的对应点分别为B′、E′．（1）如图1,当α=30°时,求证：B′C=DE ；（2）连接B′E 、DE′,当B′E=DE′时,请用图2求α的值；（3）如图3,点P 为AB 的中点,点Q 为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ 长度的取值范围为．20．如图,在菱形ABCD 中,对角线AC 、BD 交于点O ,已知4AC =,25AB =（1）求BD 的长；（2）点E 为直线AD 上的一个动点,连接CE ,将线段EC 绕点C 顺时针旋转BCD ∠的角度后得到对应的线段CF （即)ECF BCD ∠=∠,EF 交CD 于点P ．①当CE AD ⊥时,求EF 的长；②连接AF 、DF ,当DF 的长度最小时,求ACF ∆的面积．21．如图1,在Rt△ABC中,∠BAC＝90°,AB＝AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α．（1）问题发现：当α＝0°时,ADBE的值为；（2）拓展探究：当0°≤α＜360°时,若△EDC旋转到如图2的情况时,求出ADBE的值；（3）问题解决：当△EDC旋转至A,B,E三点共线时,若设CE＝5,AC＝4,直接写出线段BE的长．22．如图1,矩形ABCD中,AB＝8,AD＝6；点E是对角线BD上一动点,连接CE,作EF⊥CE交AB边于点F,以CE和EF为邻边作矩形CEFG,作其对角线相交于点H．（1）如图2,当点F与点B重合时,求CE和CG的长；（2）如图3,当点E是BD中点时,求CE和CG的长；（3）在图1,连接BG,当矩形CEFG随着点E的运动而变化时,猜想△EBG的形状？并加以证明．。

2020初中数学中考专题复习——图形变换旋转综合题解答题专项训练4(附答案详解)

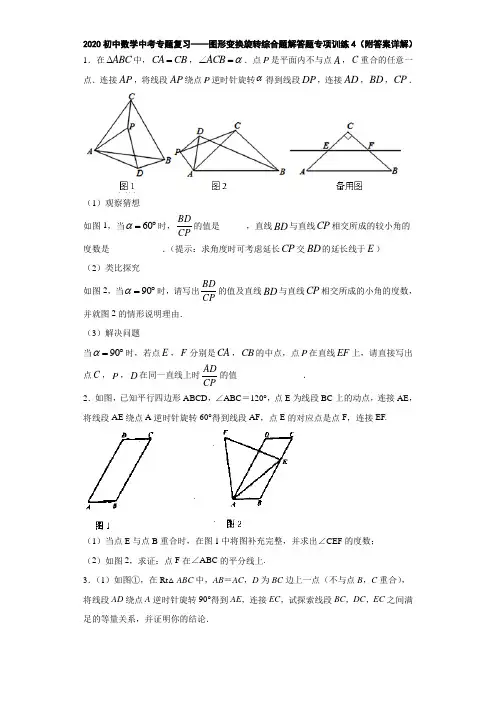
2020初中数学中考专题复习——图形变换旋转综合题解答题专项训练4（附答案详解） 1．在ABC ∆中，CA CB =，ACB α∠=．点P 是平面内不与点A ，C 重合的任意一点．连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，BD ，CP ．（1）观察猜想如图1，当60α=︒时，BD CP 的值是______，直线BD 与直线CP 相交所成的较小角的度数是____________．（提示：求角度时可考虑延长CP 交BD 的延长线于E ）（2）类比探究如图2，当90α=︒时，请写出BD CP 的值及直线BD 与直线CP 相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当90α=︒时，若点E ，F 分别是CA ，CB 的中点，点P 在直线EF 上，请直接写出点C ，P ，D 在同一直线上时AD CP的值_______________． 2．如图，已知平行四边形ABCD ，∠ABC ＝120°，点E 为线段BC 上的动点，连接AE ，将线段AE 绕点A 逆时针旋转60°得到线段AF ，点E 的对应点是点F ，连接EF.（1）当点E 与点B 重合时，在图1中将图补充完整，并求出∠CEF 的度数；（2）如图2，求证：点F 在∠ABC 的平分线上.3．（1）如图①，在Rt △ABC 中，AB ＝AC ，D 为BC 边上一点（不与点B ，C 重合），将线段AD 绕点A 逆时针旋转90°得到AE ，连接EC ，试探索线段BC ，DC ，EC 之间满足的等量关系，并证明你的结论．（2）如图②，在Rt △ABC 与Rt △ADE 中，AB ＝AC ，AD ＝AE ，将△ADE 绕点A 旋转，使点D 落在BC 边上，试探索线段AD ，BD ，CD 之间满足的等量关系，并证明你的结论．4．如图，四边形ABCD 是正方形，连接AC ，将ABC ∆绕点A 逆时针旋转α得AEF ∆，连接CF ，O 为CF 的中点，连接OE ，OD .（1）如图1，当45α︒=时，求证：OE OD =；（2）如图2，当4590α︒︒<<时，（1）OE OD =还成立吗？请说明理由.5．在ABC ∆中，90ACB ∠=o ，2AC BC ==，以点B 为圆心、1为半径作圆，设点M 为⊙B 上一点，线段CM 绕着点C 顺时针旋转90o ，得到线段CN ，连接BM 、AN ．（1）在图中，补全图形，并证明BM AN = .（2）连接MN ，若MN 与⊙B 相切，则BMC ∠的度数为 .（3）连接BN ，则BN 的最小值为；BN 的最大值为 . 6．如图，在等边△ABC 中，点D 是 AB 边上一点，连接CD ，将线段CD 绕点C 按顺时针方向旋转60°后得到CE ，连接AE ．求证：AE ∥BC ．7．如图，△ABC 和△ADE 是有公共顶点的等腰直角三角形，∠BAC ＝∠DAE ＝90°，点P 为直线BD ，CE 的交点．（1）如图，将△ADE 绕点A 旋转，当D 在线段CE 上时，连接BE ，下列给出两个结论：①BD ＝CD +2AD ；②BE 2＝2（AD 2+AB 2）．其中正确的是，并给出证明．（2）若AB ＝4，AD ＝2，把△ADE 绕点A 旋转，①当∠EAC ＝90°时，求PB 的长；②旋转过程中线段PB 长的最大值是．8．如图，在ABC V 中，90C ∠=︒，10AB =，8AC =，将线段AB 绕点A 按逆时针方向旋转90︒到线段AD .EFG V 由ABC V 沿CB 方向平移得到，且直线EF 过点D .（1）求1∠的大小；（2）求AE 的长.9．问题的提出:如果点P 是锐角△ABC 内一动点，如何确定一个位置，使点P 到△ABC 的三顶点的距离之和PA+PB+PC 的值为最小?问题的转化:(1)把ΔAPC 绕点A 逆时针旋转60度得到AP C V ，''连接PP '，这样就把确定PA+PB+PC 的最小值的问题转化成确定BP PP P C +'+''的最小值的问题了,请你利用如图证明: +PA PB PC BP PP P C +=+'+''；问题的解决:(2)当点P 到锐角△ABC 的三项点的距离之和PA+PB+PC 的值为最小时，请你用一定的数量关系刻画此时的点P 的位置:_____________________________；问题的延伸：(3)如图是有一个锐角为30°的直角三角形，如果斜边为2，点P 是这个三角形内一动点，请你利用以上方法，求点P 到这个三角形各顶点的距离之和的最小值.10．在矩形ABCD 中，点P 在AD 上，AB=2，AP=1.直角尺的直角顶点放在点P 处，直角尺的两边分别交AB 、BC 于点E 、F ，连接EF(如图1).(1)当点E 与点B 重合时，点F 恰好与点C 重合(如图2).①求证：△APB ∽△DCP ；②求PC 、BC 的长.(2)探究：将直角尺从图2中的位置开始，绕点P 顺时针旋转，当点E 和点A 重合时停止.在这个过程中(图1是该过程的某个时刻)，观察、猜想并解答：① tan ∠PEF 的值是否发生变化？请说明理由.② 设AE=x ，当△PBF 是等腰三角形时，请直接写出x 的值.11．如图1所示，点O 为直线AB 上一点，过点O 作射线OC ，使60AOC ︒∠=，将一块透明的三角尺的直角顶点放在点O 处，边OM 在射线OB 上，边ON 在直线AB 的下方.（1）将图1中的三角尺绕点O 逆时针旋转至如图2所示的位置，使边OM 在BOC ∠的内部，且恰好平分BOC ∠，求CON ∠的度数.（2）将图1中的三角尺绕点O 按每秒10︒的速度逆时针旋转一周，在旋转过程中，第t 秒时，直线ON 恰好平分锐角AOC ∠，则t 的值为________（直接写出结果）.（3）将图1中的三角尺绕点O 逆时针旋转至如图3所示的位置，使ON 在AOC ∠的内部，请探究AOM ∠与NOC ∠之间的关系，并说明理由.12．如图1，在平面直角坐标系，O 为坐标原点，点A （﹣2，0），点B （0，3．（1）直接写求∠BAO 的度数；（2）如图1，将△AOB 绕点O 顺时针得△A ′OB ′，当A ′恰好落在AB 边上时，设△AB ′O 的面积为S 1，△BA ′O 的面积为S 2，S 1与S 2有何关系？为什么？（3）若将△AOB 绕点O 顺时针旋转到如图2所示的位置，S 1与S 2的关系发生变化了吗？证明你的判断．13．已知平行四边形ABCD ．（1）如图1，将▱ABCD 绕点D 逆时针旋转一定角度得到▱A 1B 1C 1D ，延长B 1C 1，分别与BC 、AD 的延长线交于点M 、N ．①求证：∠BMB 1＝∠ADA 1；②求证：B 1N ＝AN +C 1M ；（2）如图2，将线段AD 绕点D 逆时针旋转，使点A 的对应点A 1落在BC 上，将线段CD 绕点D 逆时针旋转到C 1D 的位置，AC 1与A 1D 交于点H ．若H 为AC 1的中点，∠ADC 1+∠A 1DC ＝180°，A 1B ＝nA 1C ，试用含n 的式子表示1A H DH的值． 14．如图，将ABC ∆绕点A 逆时针旋转90︒得到ADE ∆.（1）观察猜想小明发现，将DAC ∆绕点A 逆时针旋转90︒，如图1，他发现ACD ∆的面积1S 与BAE ∆的面积2S 之间有一定的数量关系，请直接写出这个关系：______；（2）类比探究如图2，M 是CD 的中点，请写出AM 与BE 之间的数量关系和位置关系，并说明理由；（3）解决问题如图3，AB AD =，AB AD ⊥，AC AE =，AC AE ⊥，C 在线段BD 上，AH BE ⊥交CD 于H ，若2BC =，3CD =，请直接写出AH 的长.15．在△ABC 中，AB ＝AC ，∠BAC ＝90°，D 为平面内的一点．（1）如图1，当点D 在边BC 上时，且∠BAD ＝30°，求证：AD 2BD ．（2）如图2，当点D 在△ABC 的外部，且满足∠BDC ﹣∠ADC ＝45°，求证：BD 2AD ．（3）如图3，若AB ＝4，当D 、E 分别为AB 、AC 的中点，把△DAE 绕A 点顺时针旋转，设旋转角为α（0＜α≤180°），直线BD 与CE 的交点为P ，连接PA ，直接写出△PAC 面积的最大值．16．如图，△ABC 为等边三角形，点P 是线段AC 上一动点（点P 不与A ，C 重合），连接BP ，过点A 作直线BP 的垂线段，垂足为点D ，将线段AD 绕点A 逆时针旋转60°得到线段AE ，连接DE ，CE ．（1）求证：BD ＝CE ；（2）延长ED 交BC 于点F ，求证：F 为BC 的中点；（3）在（2）的条件下，若△ABC 的边长为1，直接写出EF 的最大值．17．如图，在平面直角坐标系中，Rt △ABC 的顶点分别是A （﹣3，1）B （0，4）C （0，2）．（1）将△ABC 以点C 为旋转中心旋转180°，画出旋转后对应的△A 1B 1C 1；（2）分别连接AB 1，BA 1后，求四边形AB 1A 1B 的面积．18．已知AOB 90∠=︒，COD 60∠=︒，按如图1所示摆放，将OA 、OC 边重合在直线MN 上，OB 、OD 边在直线MN 的两侧；(1)保持AOB ∠不动，将COD ∠绕点O 旋转至如图2所示的位置，则①AOC BOD ∠∠+= ；②BOC AOD ∠∠-= ；(2)若COD ∠按每分钟5︒的速度绕点O 逆时针方向旋转，AOB ∠按每分钟2︒的速度也绕点O 逆时针方向旋转，OC 旋转到射线ON 上时都停止运动，设旋转t 分钟，计算MOC AOD ∠∠-(用t 的代数式表示)。

2020年中考数学压轴题专题10 图形变换综合题探究专题学案(原版+解析)

专题十图形变换综合题探究专题【考题研究】本专题主要包括图形的变换和相似形．其中轴对称图形、平移、中心对称图形的识别，相似三角形性质以填空和选择题为主，主要是考查对图形的识别和性质；图形的折叠、平移、旋转与几何图形面积相关的计算问题以填空题和解答题为主，主要是考查对几何问题的综合运用能力；而相似三角形的性质及判断定的应用往往还会结合圆或者解直角三角形等问题一并考查，主要是以解答题为主。

【解题攻略】图形的轴对称、平移、旋转是近年中考的新题型、热点题型，它主要考查学生的观察与实验能力，探索与实践能力，因此在解题时应注意以下方面：1.熟练掌握图形的轴对称、图形的平移、图形的旋转的基本性质和基本方法。

2.结合具体问题大胆尝试，动手操作平移、旋转，探究发现其内在规律是解答操作题的基本方法。

3．注重图形与变换的创新题，弄清其本质，掌握其基本的解题方法，尤其是折叠与旋转等。

【解题类型及其思路】1.变换中求角度注意平移性质：平移前后图形全等，对应点连线平行且相等．2．变换中求线段长时把握折叠的性质：折线是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上．3．变换中求坐标时注意旋转性质：对应线段、对应角的大小不变，对应线段的夹角等于旋转角.4．变换中求面积，注意前后图形的变换性质及其位置等情况。

【典例指引】类型一【图形的平移】【典例指引1】1．两个三角板ABC，DEF按如图所示的位置摆放，点B与点D重合，边AB 与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内)，其中，∠C＝∠DEF＝90°，∠ABC＝∠F＝30°，AC＝DE＝4 cm.现固定三角板DEF，将三角板ABC沿射线DE方向平移，当点C落在边EF上时停止运动．设三角板平移的距离为x(cm)，两个三角板重叠部分的面积为y(cm2)．(1)当点C落在边EF上时，x＝________cm；(2)求y关于x的函数表达式，并写出自变量x的取值范围；(3)设边BC的中点为点M，边DF的中点为点N，直接写出在三角板平移过程中，点M与点N之间距离的最小值．【举一反三】如图①，将两块全等的三角板拼在一起，其中△ABC的边BC在直线l上，AC⊥BC 且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，EF⊥FP且EF=FP．（1）在图①中，通过观察、测量，猜想直接写出AB与AP满足的数量关系和位置关系，不要说明理由；（2）将三角板△EFP沿直线l向左平移到图②的位置时，EP交AC于点Q，连接AP、BQ．猜想写出BQ与AP满足的数量关系和位置关系，并说明理由．类型二【图形的轴对称--折叠】【典例指引2】将一个直角三角形纸片放置在平面直角坐标系中，点，点，点.是边上的一点(点不与点，重合)，沿着折叠该纸片，得点的对应点. (Ⅰ)如图①，当时，求点的坐标；(Ⅱ)如图②，当点落在轴上时，求点的坐标；(Ⅲ)当与坐标轴平行时，求点的坐标(直接写出结果即可).【举一反三】如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG．（1）求证：四边形DEFG为菱形；（2）若CD=8，CF=4，求CEDE的值．类型三【图形的旋转】【典例指引3】如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．（1）求证：DE⊥AG；（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．①在旋转过程中，当∠OAG′是直角时，求α的度数；②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．【举一反三】（1）（问题发现）如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为（2）（拓展研究）在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；（3）（问题发现）当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．类型四【图形的位似】【典例指引4】如图，二次函数y=x2﹣3x的图象经过O（0，0），A（4，4），B（3，0）三点，以点O为位似中心，在y轴的右侧将△OAB按相似比2：1放大，得到△OA′B′，二次函数y=ax2+bx+c（a≠0）的图象经过O，A′，B′三点．（1）画出△OA′B′，试求二次函数y=ax2+bx+c（a≠0）的表达式；（2）点P（m，n）在二次函数y=x2﹣3x的图象上，m≠0，直线OP与二次函数y=ax2+bx+c （a≠0）的图象交于点Q（异于点O）．①连接AP，若2AP＞OQ，求m的取值范围；②当点Q在第一象限内，过点Q作QQ′平行于x轴，与二次函数y=ax2+bx+c（a≠0）的图象交于另一点Q′，与二次函数y=x2﹣3x的图象交于点M，N（M在N的左侧），直线OQ′与二次函数y=x2﹣3x的图象交于点P′．△Q′P′M∽△QB′N，则线段NQ的长度等于．【举一反三】如图所示，网格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC是格点三角形．在建立平面直角坐标系后，点B的坐标为(－1，－1)．(1)把△ABC向下平移5格后得到△A1B1C1，写出点A1，B1，C1的坐标，并画出△A1B1C1；(2)把△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2，写出点A2，B2，C2的坐标，并画出△A2B2C2；(3)把△ABC以点O为位似中心放大得到△A3B3C3，使放大前后对应线段的比为1∶2，写出点A3，B3，C3的坐标，并画出△A3B3C3.【新题训练】1．在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．（1）请在如图所示的网格平面内作出平面直角坐标系；（2）写出点B的坐标；（3）将△ABC向右平移5个单位长度，向下平移2个单位长度，画出平移后的图形△A′B′C′；（4）计算△A′B′C′的面积﹒（5）在x轴上存在一点P，使PA+PC最小，直接写出点P的坐标.2．如图（1），在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），将线段AB 先向上平移2个单位长度，再向右平移1个单位长度，得到线段CD，连接AC，BD，构成平行四边形ABDC ．（1）请写出点C 的坐标为，点D 的坐标为，S 四边形ABDC ；（2）点Q 在y 轴上，且S △QAB ＝S 四边形ABDC ，求出点Q 的坐标；（3）如图（2），点P 是线段BD 上任意一个点（不与B 、D 重合），连接PC 、PO ，试探索∠DCP 、∠CPO 、∠BOP 之间的关系，并证明你的结论．3．（问题情境）在综合实践课上，同学们以“图形的平移”为主题开展数学活动，如图①，先将一张长为4，宽为3的矩形纸片沿对角线剪开，拼成如图所示的四边形ABCD ，3AD =，4BD =，则拼得的四边形ABCD 的周长是_____.（操作发现）将图①中的ABE △沿着射线DB 方向平移，连结AD 、BC 、AF 、CE ，如图②.当ABE △的平移距离是12BE 的长度时，求四边形AECF 的周长. （操作探究）将图②中的ABE △继续沿着射线DB 方向平移，其它条件不变，当四边形ABCD 是菱形时，将四边形ABCD 沿对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出所有可能拼成的矩形周长.4．如图，在66⨯的正方形方格中，每个小正方形的边长都为1，顶点都在网格线交点处的三角形，ABC V 是一个格点三角形．()1在图①中，请判断ABC V 与DEF V 是否相似，并说明理由；()2在图②中，以O 为位似中心，再画一个格点三角形，使它与ABC V 的位似比为2：1 ()3在图③中，请画出所有满足条件的格点三角形，它与ABC V 相似，且有一条公共边和一个公共角．5．已知：AD 是ABC ∆的高，且BD CD =.（1）如图1，求证：BAD CAD ∠=∠；（2）如图2，点E 在AD 上，连接BE ，将ABE ∆沿BE 折叠得到'A BE ∆，'A B 与AC 相交于点F ，若BE =BC ，求BFC ∠的大小；（3）如图3，在（2）的条件下，连接EF ，过点C 作CG EF ⊥，交EF 的延长线于点G ，若10BF =，6EG =，求线段CF 的长.图1. 图2. 图3.6．如图，长方形OABC 在平面直角坐标系xOy 的第一象限内，点A 在x 轴正半轴上，点C 在y 轴的正半轴上，点D 、E 分别是OC 、BC 的中点，30∠=︒CDE ，点E 的坐标为()2,a .（1）求a 的值及直线DE 的表达式；（2）现将长方形OABC 沿DE 折叠，使顶点C 落在平面内的点'C 处，过点'C 作y 轴的平行线分别交x 轴和BC 于点F ，G .①求'C 的坐标；②若点P 为直线DE 上一动点，连接'PC ，当'PC D 为等腰三角形，求点P 的坐标.（说明：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半）7．如图1，四边形ABCD 的对角线AC ，BD 相交于点O ，OB =OD ，OC =OA +AB ，AD =m ，BC =n ，∠ABD +∠ADB =∠ACB ．（1）填空：∠BAD 与∠ACB 的数量关系为________；（2）求m n的值；（3）将△ACD 沿CD 翻折，得到△A ′CD （如图2），连接BA ′，与CD 相交于点P ．若CD =5+12，求PC 的长．8．如图，直线：y 3x +4与x 轴、y 轴分别別交于点M 、点N ，等边△ABC 的高为3，边BC 在x 轴上，将△ABC 沿着x 轴的正方向平移，在平移过程中，得到△A 1B 1C 1，当点B 1与原点O 重合时，解答下列问题：（1）点A1的坐标为．（2）求△A1B1C1的边A1C1所在直线的解析式；（3）若以P、A1、C1、M为顶点的四边形是平行四边形，请直接写出P点坐标．9．已知：△ABC和△ADE均为等边三角形，连接BE，CD，点F，G，H分别为DE，BE，CD 中点．（1）当△ADE绕点A旋转时，如图1，则△FGH的形状为，说明理由；（2）在△ADE旋转的过程中，当B，D，E三点共线时，如图2，若AB=3，AD=2，求线段FH的长；（3）在△ADE旋转的过程中，若AB=a，AD=b（a＞b＞0），则△FGH的周长是否存在最大值和最小值，若存在，直接写出最大值和最小值；若不存在，说明理由．10．综合与实践问题背景折纸是一种许多人熟悉的活动，将折纸的一边二等分、四等分都是比较容易做到的，但将一边三等分就不是那么容易了，近些年，经过人们的不懈努力，已经找到了多种将正方形折纸一边三等分的精确折法，最著名的是由日本学者芳贺和夫发现的三种折法，现在被数学界称之为芳贺折纸三定理．其中，芳贺折纸第一定理的操作过程及内容如下（如图1）：操作1：將正方形ABCD对折，使点A与点D重合，点B与点C重合．再将正方形ABCD展开，得到折痕EF；操作2：再将正方形纸片的右下角向上翻折，使点C与点E重合，边BC翻折至B'E的位置，得到折痕MN ，B 'E 与AB 交于点P ．则P 即为AB 的三等分点，即AP ：PB =2：1．解决问题（1）在图1中，若EF 与MN 交于点Q ，连接CQ ．求证：四边形EQCM 是菱形；（2）请在图1中证明AP ：PB =2：l ．发现感悟若E 为正方形纸片ABCD 的边AD 上的任意一点，重复“问题背景”中操作2的折纸过程，请你思考并解决如下问题：（3）如图2．若DE AE =2．则AP BP= ；（4）如图3，若DE AE =3，则AP BP = ；（5）根据问题（2），（3），（4）给你的启示，你能发现一个更加一般化的结论吗？请把你的结论写出来，不要求证明．11．在平面直角坐标系中，四边形AOBC 是矩形，点(0,0)O ，点(5,0)A ，点(0,3)B .以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ，B ，C 的对应点分别为D ，E ，F .（Ⅰ）如图①，当点D 落在BC 边上时，求点D 的坐标；（Ⅱ）如图②，当点D 落在线段BE 上时，AD 与BC 交于点H .①求证ADB AOB △△≌；②求点H 的坐标.（Ⅲ）记K 为矩形AOBC 对角线的交点，S 为KDE △的面积，求S 的取值范围（直接写出结果即可）.12．已知O 为直线MN 上一点，OP ⊥MN ，在等腰Rt △ABO 中，90BAO ∠=︒，AC ∥OP 交OM 于C ，D 为OB 的中点，DE ⊥DC 交MN 于E ．(1) 如图1，若点B 在OP 上，则①AC OE (填“＜”，“＝”或“＞”)；②线段CA 、CO 、CD 满足的等量关系式是；(2) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α(045α︒<<︒)，如图2，那么(1)中的结论②是否成立？请说明理由；(3) 将图1中的等腰Rt △ABO 绕O 点顺时针旋转α()，请你在图3中画出图形，并直接写出线段CA 、CO 、CD 满足的等量关系式；13．如图1，在中，，，点，分别在边，上，，连接，点，，分别为，，的中点.（1）观察猜想图1中，线段与的数量关系是，位置关系是；（2）探究证明把绕点逆时针方向旋转到图2的位置，连接，，，判断的形状，并说明理由；（3）拓展延伸把绕点在平面内自由旋转，若，，请直接写出面积的最大值.14．已知∠MAN=135°，正方形ABCD绕点A旋转．（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD 的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是；②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．15．已知：如图，是由一个等边△ABE和一个矩形BCDE拼成的一个图形，其点B，C，D的坐标分别为(1，2)，(1，1)，(3，1)．(1)直接写出E点和A点的坐标；(2)试以点B为位似中心，作出位似图形A1B1C1D1E1，使所作的图形与原图形的位似比为3∶1；(3)直接写出图形A1B1C1D1E1的面积．16．如图1，将长为10的线段OA绕点O旋转90°得到OB，点A的运动轨迹为»AB，P是半径OB上一动点，Q是»AB上的一动点，连接PQ.发现：∠POQ＝________时，PQ有最大值，最大值为________；思考：（1）如图2，若P是OB中点，且QP⊥OB于点P，求»BQ的长；（2）如图3，将扇形AOB沿折痕AP折叠，使点B的对应点B′恰好落在OA的延长线上，求阴影部分面积；探究：如图4，将扇形OAB沿PQ折叠，使折叠后的弧QB′恰好与半径OA相切，切点为C，若OP＝6，求点O到折痕PQ的距离．17．（本小题10分）将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（3，0），点B（0，1），点O（0，0）．过边OA上的动点M（点M不与点O，A重合）作MN⊥AB 于点N，沿着MN折叠该纸片，得顶点A的对应点A′．设OM =m，折叠后的△A′MN与四边形OMNB重叠部分的面积为S．图①（Ⅰ）如图①，当点A′与顶点B重合时，求点M的坐标；（Ⅱ）如图②，当点A′落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S；（Ⅲ）当S 3M的坐标（直接写出结果即可）．18．如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°操作：将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E 旋转，并使边DE与边AB交于点P，边EF与边BC于点Q．探究一：在旋转过程中，（1）如图2，当1CEEA =时，EP 与EQ 满足怎样的数量关系？并给出证明；（2）如图3，当2CEEA=时，EP 与EQ 满足怎样的数量关系？并说明理由；（3）根据你对（1）、（2）的探究结果，试写出当CEm EA=时，EP 与EQ 满足的数量关系式为，其中m 的取值范围是．（直接写出结论，不必证明）探究二：若2CEEA=且AC =30cm ，连接PQ ，设△EPQ 的面积为S （cm 2），在旋转过程中：（1）S 是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，说明理由．（2）随着S 取不同的值，对应△EPQ 的个数有哪些变化，求出相应S 的值或取值范围．专题十图形变换综合题探究专题【考题研究】本专题主要包括图形的变换和相似形．其中轴对称图形、平移、中心对称图形的识别，相似三角形性质以填空和选择题为主，主要是考查对图形的识别和性质；图形的折叠、平移、旋转与几何图形面积相关的计算问题以填空题和解答题为主，主要是考查对几何问题的综合运用能力；而相似三角形的性质及判断定的应用往往还会结合圆或者解直角三角形等问题一并考查，主要是以解答题为主。

2020年中考数学复习解答题专题练图形的变换

2020年中考数学复习解答题专题练图形的变换1如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A′B′C,此时点A′恰好在AB边上,求点B′与点B之间的距离.2. 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,求△A′B′C的面积.3. 如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.(1)画出△ABC关于直线BM对称的△A1B1C1.(2)写出AA1的长度.4.如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE =4,S△CDE=16,求△ACD的面积.5. 如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(1)在图中画出一个面积最小的PAQB.(2)在图中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.6. 如图,在边长为a的正方形ABCD中,把边BC绕点B逆时针旋转60°,得到线段BM,连接AM并延长交CD于点N,连接MC,求△MNC的面积.7. 如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF经过点D.(1)求∠BDF的大小.(2)求CG的长.8. 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6√2,求FG的长.9. 如图，在△ABC中，∠A=90°，D为BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，试探索线段BE，EF，FC之间的数量关系.10阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数.小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决.(1)请你回答：图1中∠APB的度数等于__150°__.(直接写答案)参考小伟同学思考问题的方法，解决下列问题：如图3，在正方形ABCD内有一点P，且PA=2√2，PB=1，PD=√17.(2)求∠APB的度数.(3)求正方形的边长.11.已知:△ABC中,∠C=90°,AC=BC,点M,N分别在AC,BC上,将△ABC沿MN折叠,顶点C恰好落在斜边上的P点.(1)如图1,当MN∥AB时,①求证:AM=MC;②PAPB =CM CN;(2)如图2,当MN与AB不平行时,PAPB =CMCN还成立吗?请说明理由.12.(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①∠AEB的度数为______;②线段AD,BE之间的数量关系为______. (2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.【解析】(1)∵∠ACB=∠DCE,∠DCB=∠DCB,∴∠ACD=∠BCE,在△ACD和△BCE中,{AC=BC,∠ACD=∠BCE, CD=CE,∴△ACD≌△BCE,∴AD=BE,∠CEB=∠ADC=180°-∠CDE=120°, ∴∠AEB=∠CEB-∠CED=60°.答案:①60°②AD=BE(2)∠AEB=90°,AE=BE+2CM.理由:∵△ACB和△DCE均为等腰直角三角形, ∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACD=∠BCE.在△ACD和△BCE中,{CA=CB,∠ACD=∠BCE, CD=CE,∴△ACD≌△BCE,∴AD=BE,∠ADC=∠BEC. ∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°,∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°,∴∠AEB=∠BEC-∠CED=90°.∵CD=CE,CM⊥DE,∴DM=ME.∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.2020年中考数学复习解答题专题练图形的变换（解析版）1如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A′B′C,此时点A′恰好在AB边上,求点B′与点B之间的距离.【解析】连接B′B.在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,所以BC=ACtan ∠A=6×tan60°=6√3,由旋转的性质得:A′C=AC=6,B′C=BC,∠ACA′=∠BCB′.又因为∠A=60°,所以∠ACA′=∠BCB′=∠A=60°,即△BCB′是等边三角形,所以BB′=BC=6√3.2.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,求△A′B′C的面积.【解析】∵△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,∴A ′B ′=AB=4,∠A ′B ′C ′=∠B=60°,B ′C=6-2=4,过点A ′作A ′D ⊥B ′C 于点D,则A ′D=√32A ′B ′=√32×4=2√3,∴S △A ′B ′C =12B ′C ·A ′D=12×4×2√3=4√3.3. 如图,方格图中每个小正方形的边长为1,点A,B,C 都是格点.(1)画出△ABC 关于直线BM 对称的△A 1B 1C 1.(2)写出AA 1的长度.【解析】(1)作图如下:(2)由图直接读出AA 1=10.4.如图,在△ABC 中,D,E 分别是边AB,BC 上的点,且DE ∥AC,若S △BDE =4,S △CDE =16,求△ACD 的面积.【解析】∵S △BDE =4,S △CDE =16,∴S△BDE ∶S△CDE=1∶4,∵△BDE和△CDE的点D到BC的距离相等,∴BECE =14,∴BEBC=15,∵DE∥AC,∴△DBE∽△ABC,∴S△DBE ∶S△ABC=1∶25,5. 如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.(1)在图中画出一个面积最小的PAQB.(2)在图中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.【解析】(1)答案不唯一.(2)答案不唯一.6. 如图,在边长为a的正方形ABCD中,把边BC绕点B逆时针旋转60°,得到线段BM,连接AM并延长交CD于点N,连接MC,求△MNC的面积.【解析】作MG ⊥BC 于点G,MH ⊥CD 于点H,则BG=GC,AB ∥MG ∥CD,∴AM=MN,∵MH ⊥CD,∠D=90°,∴MH ∥AD,∴NH=HD,由旋转变换的性质可知,△MBC 是等边三角形,∴MC=BC=a,由题意得,∠MCD=30°,∴MH=12MC=12a,CH=√32a,∴DH=a-√32a,∴CN=CH-NH=√32a-(a-√32a)=(√3-1)a,∴△MNC 的面积=12×a 2×(√3-1)a=√3-14a 2. 7. 如图,在Rt △ABC 中,∠C=90°,AB=10,AC=8.线段AD 由AB 绕点A 按逆时针方向旋转90°得到,△EFG 由△ABC 沿CB 方向平移得到,且直线EF 经过点D.(1)求∠BDF的大小.(2)求CG的长.【解析】(1)由旋转知,AB=AD,∠DAB=90°, ∴∠ABD=∠ADB=12(180°-90°)=45°,由平移知:DF∥AB,∴∠BDF=∠ABD,∴∠BDF=45°,(2)由平移知EG∥AC,EG=AC,∴四边形ACGE是平行四边形,又∠C=90°, ∴四边形ACGE是矩形,∴AE∥CF,∠EAC=90°,AE=CG,又∵∠DAB=90°,∴∠EAB+∠EAD=∠CAB+∠EAB,∴∠DAE=∠CAB,由(1)知DF∥AB,∴∠EDA+∠DAB=180°,∴∠EDA=90°,∠EDA=∠C,∴△AED∽△ABC,∴AEAB =AD AC,∴AE10=108,∴AE=252,∴CG=252.8. 如图,在菱形ABCD中,∠BAD=120°,点E,F分别在边AB,BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6√2,求FG的长.【解析】∵四边形ABCD是菱形,∠BAD=120°,∴AB=BC=CD=AD,∠CAB=∠CAD=60°,∴△ABC,△ACD是等边三角形.∵EG⊥AC,∴∠AEG=∠AGE=30°,∵∠B=∠EGF=60°,∴∠AGF=90°,∴FG⊥BC,=BC·FG,∴2·S△ABC×(6√2)2=6√2·FG,∴2×√34∴FG=3√6.9. 如图，在△ABC中，∠A=90°，D为BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，试探索线段BE，EF，FC之间的数量关系.解：FC2+BE2=EF2，理由如下：∵D为BC的中点，∴BD=CD，作△BDE关于点D成中心对称的△CDG，由中心对称的性质可得△BDE≌△CDG，∴CG=BE，∠DCG=∠B，又∵∠B+∠ACB=90°，∴∠DCG+∠ACB=90°，即∠FCG=90°，∴FC2+GC2=FG2，又由题意知FD为EG的中垂线，∴FG=EF，∴FC2+BE2=EF2.10阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数.小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决.(1)请你回答：图1中∠APB的度数等于__150°__.(直接写答案)参考小伟同学思考问题的方法，解决下列问题：如图3，在正方形ABCD内有一点P，且PA=2√2，PB=1，PD=√17.(2)求∠APB的度数.(3)求正方形的边长.解：(1)150°(2)如图，把△APB绕点A逆时针旋转90°得到△ADP′，由旋转的性质，P′A=PA=2√2，P′D=PB=1，∠PAP′=90°，∴△APP ′是等腰直角三角形，∴PP ′=√2PA=√2×2√2=4，∠AP ′P=45°，∵PP ′2+P ′D 2=42+12=17，PD 2=(√17)2=17，∴PP ′2+P ′D 2=PD 2，∴∠PP ′D=90°，∴∠AP ′D=∠AP ′P+∠PP ′D=45°+90°=135°，故∠APB=∠AP ′D=135°.(3)∵∠APB+∠APP ′=135°+45°=180°，∴点P ′，P ，B 三点共线，过点A 作AE ⊥PP ′于E ，则AE=PE=12PP ′=12×4=2， ∴BE=PE+PB=2+1=3，在Rt △ABE 中，AB=√AE 2+BE 2=√22+32=√13.11.已知:△ABC 中,∠C=90°,AC=BC,点M,N 分别在AC,BC 上,将△ABC 沿MN 折叠,顶点C 恰好落在斜边上的P 点.(1)如图1,当MN ∥AB 时,①求证:AM=MC;②PA PB =CM CN ;(2)如图2,当MN 与AB 不平行时,PA PB =CM CN 还成立吗?请说明理由.【解析】(1)①由折叠可知∠CMN=∠NMP,CM=PM,∵MN ∥AB,∴∠CMN=∠A,∠NMP=∠MPA,∴∠A=∠MPA,∴MA=MP,∴AM=CM,②由①可知∠CMN=∠A=45°,∠CNM=∠B=45°,∠A=∠B=45°,∴MC=NC=AM=BN,∴∠PMA=∠PNB=90°,∴△APM ∽△BPN∴APPB =AMBN,∴APPB=CMCN;(2)成立,理由如下:过M,N分别作AB的垂线,垂足分别为E,F, 由题意可知,CM=PM,CN=PN,∠MPN=90°,∴∠MPE+∠NPF=90°,∵∠MPE+∠EMP=90°,∴∠EMP=∠NPF,∴△MEP∽△PFN,∴PMPN =MEPF=PENF,∵∠A=∠B=45°,ME⊥AP,NF⊥AB,∴△MAE和△NFB均为等腰直角三角形, ∴ME=AE,NF=BF,由△MEP∽△PFN,∴MEPE =PFNF,∴AEPE=PFBF,∴AE+PEPE =PF+BFBF,∴APPE=PBBF,∴APPB =PEBF=PENF,∴APPB=MPPN=CMCN.12.(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:①∠AEB的度数为______;②线段AD,BE之间的数量关系为______. (2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.【解析】(1)∵∠ACB=∠DCE,∠DCB=∠DCB,∴∠ACD=∠BCE,在△ACD和△BCE中,{AC=BC,∠ACD=∠BCE, CD=CE,∴△ACD≌△BCE,∴AD=BE,∠CEB=∠ADC=180°-∠CDE=120°, ∴∠AEB=∠CEB-∠CED=60°.答案:①60°②AD=BE(2)∠AEB=90°,AE=BE+2CM.理由:∵△ACB和△DCE均为等腰直角三角形, ∴CA=CB,CD=CE,∠ACB=∠DCE=90°,∴∠ACD=∠BCE.在△ACD和△BCE中,{CA=CB,∠ACD=∠BCE, CD=CE,∴△ACD≌△BCE,∴AD=BE,∠ADC=∠BEC. ∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°,∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°,∴∠AEB=∠BEC-∠CED=90°.∵CD=CE,CM⊥DE,∴DM=ME.∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.。

2020初中数学中考专题复习——图形变换旋转综合题填空题专项训练2(附答案详解)

2020初中数学中考专题复习——图形变换旋转综合题填空题专项训练2（附答案详解）1．如图，把△ABC纸片沿DE折叠，点A落在四边形BCDE的外部，用∠1和∠2表示出∠A，则关系式是______．2．如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC＝4，∠BAC＝30°，则线段PM的最大值是___．3．如图，△ABC是边长为6的等边三角形，点D在边AB上，AD＝2，点E是BC上一点连结DE，将DE绕点D逆时针旋转60°得DF，连结CF，则CF的最小值是_____．4．如图，已知在平面直角坐标系中，点A（0，3），点B为x轴上一动点，连接AB，线段AB绕着点B按顺时针方向旋转90°至线段CB，过点C作直线l∥y轴，在直线l上有一点D位于点C下方，满足CD＝BO，则当点B从（﹣3，0）平移到（3，0）的过程中，点D的运动路径长为_____．5．如图，点P为∠MON平分线OC上一点，以点P为顶点的∠APB两边分别与射线OM、ON相交于点A、B，如果∠APB在绕点P旋转时始终满足OA•OB＝OP2，我们就把∠APB叫做∠MON的关联角．如果∠MON＝50°，∠APB是∠MON的关联角，那么∠APB的度数为_____．6．如图，已知在△ABC中，AB＝3，AC＝2，∠A＝45o，将这个三角形绕点B旋转，使点A落在射线AC上的点A1处，点C落在点C1处，那么AC1＝_____．7．如图，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点，作正方形DEFG，连接AE，若BC＝DE＝4，将正方形DEFG绕点D逆时针方向旋转，在旋转过程中，当AE为最大值时，则AF的值_____．8．如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB＝5，AC＝4，BC＝2，则BE的长为_____．9．如图，在等腰直角三角形ABC中，∠B=90°，将△ABC绕顶点A逆时针方向旋转60°后得到△AB＇C＇，则∠BAC＇等于_______.10．若把一次函数y kx b =+的图像先绕着原点旋转180︒，再向左平移2个单位长度后，恰好经过点40A -（，）和点02B （，），则原一次函数的表达式是____. 11．如图，将边长为3cm 的正方形ABCD 绕顶点B 逆时针旋转30°得到正方形EBCF ，则两个图形重叠部分（阴影部分）的面积为______cm 2．12．如图，正方形OABC 的边长为6，以O 为圆心，EF 为直径的半圆经过点A ，连接AE ，CF 相交于点P ，将正方形OABC 从OA 与OF 重合的位置开始，绕着点O 逆时针旋转90°，交点P 运动的路径长是______．13．如图，已知Rt △ABC 中，∠ACB=90°，AC=8，BC=6．将△ABC 绕点B 旋转得到△DBE ，点A 的对应点D 落在射线BC 上．直线AC 交DE 于点F ，那么CF 的长为______．14．如图，在等腰ABC ∆中，AB AC =，030B ∠=．以点B 为旋转中心，旋转030，点,A C 分别落在点','A C 处，直线,'AC AC 交于点D ，那么AD AC的值为_______．15．如图，在Rt△ABC中，∠ACB=90°，AB=2，点D为线段AB的中点，将线段BC绕点B顺时针旋转90°，得到线段BE，连接DE，则DE最大值是______．\16．如图，点A的坐标为（﹣1，0），AB⊥x轴，∠AOB＝60°，点B在双曲线l上，将△AOB绕点B顺时针旋转90°得到△CDB，则点D_____双曲线l上（填“在”或“不在”）．17．如图，在△ABC中，AB=AC=23，∠BAC=120°，点D、E都在边BC上，∠DAE=60°．若BD=2CE，则DE的长为________.18．如图，△AOB的边OB在x轴上，AC⊥x轴于C，D为AC上一点，将△CBD沿BD翻折，使点C落在AB边上的E点．已知∠AOB＝60°，AO＝43，点B的坐标为（8+23，0），则点D的坐标为_____．19．如图，已知正方形ABCD的边长为2，以点A为圆心，1为半径作圆，E是⊙A上的任意一点，将点E绕点D按逆时针方向旋转90°得到点F，则线段AF的长的最小值_____．20．四边形ABCD 是边长为4的正方形，点P 是平面内一点．且满足BP ⊥PC ，现将点P 绕点D 顺时针旋转90度，则CQ 的最大值＝___________．21．如图，直线l 1，l 2，l 3相交于点A 、B 、C ，得到△ABC ，其中∠ACB=90°，AC=6，BC=8，点O 在线段AC 上，且OA=2OC ，将△ABC 绕点O 旋转得到△A 1B 1C 1，当点A 1落在这三条直线上时，线段AA 1长是_______.22．小明将一副三角板中的两块直角三角尺的直角顶点C 按如图所示的方式叠放在一起，当∠ACE ＜180°且点E 在直线AC 的上方时，他发现若∠ACE ＝_____，则三角板BCE 有一条边与斜边AD 平行．（写出所有可能情况）23．如图，两块相同的三角板完全重合在一起，A 30∠=o ，AC 10=，把上面一块绕直角顶点B 逆时针旋转到A'BC'V 的位置，点C'在AC 上，A'C'与AB 相交于点D ，则BC'=______．24．已知ABC V 中，AC 2=，C 30∠=o ，点M 为边AC 中点，把BCM V 沿中线BM 125．如图，点O 是等边△ABC 内一点，∠AOB ＝110°．将△BOC 绕点C 按顺时针方向旋转60°得△ADC ，连接OD ．当α为______度时，△AOD 是等腰三角形？26．定义：在平面直角坐标系中，一个图形先向右平移a 个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的()Y a,θ变换.如图，等边ABC V 的边长为1，点A 在第一象限，点B 与原点0重合，点C 在x 轴的正半轴上111.A B C V 就是ABC V 经()Y 1,180o 变换后所得的图形，则点1A 的坐标是______．27．如图，AOB V 中，AOB 90∠=o ，AO 3=，BO 6=，AOB V 绕顶点O 逆时针旋转到A'OB'V 处，此时线段A'B'与BO 的交点E 为BO 的中点，则线段B'E 的长度为______．28．如图，在正方形ABCD 中，点M 在CD 的边上，且DM=2，ΔAEM 与ΔADM 关于AM 所在的直线对称，将ΔADM 按顺时针方向绕点A 旋转90°得到ΔABF ，连接EF ，已知线段EF 34ABCD 的边长为_____29．Rt ABC ∆中，8AB =，6BC =，将它绕着斜边AC 中点O 逆时针旋转一定角度后得到'''A B C ∆，恰好使''//A B AC ，同时''A B 与,AB BC 分别交于点,E F ，则EF 的长为__________．30．如图，在△ABC 中，AC=BC=8，∠C=90°，点D 为BC 中点，将△ABC 绕点D 逆时针旋转45°，得到△A′B′C′，B′C′与AB 交于点E ，则S 四边形ACDE = ．参考答案1．∠A=12(∠1-∠2)【解析】∵△A′ED是△AED翻折变换而成，∴∠A=∠A′，∵∠AFE是△A′DF的外角，∴∠AFE=∠A′+∠2，∵∠1是△AEF的外角，∴∠1=∠A+∠AFE，即∠1=∠A+∠A′+∠2=2∠A′+∠2，即∠A=12(∠1-∠2)；故答案是∠A=12(∠1-∠2)。

2020中考数学图形的变化综合复习基础训练题(附答案)

2020中考数学图形的变化综合复习基础训练题（附答案）1．在平面直角坐标系中，以原点O 为位似中心，把△ABC 放大得到△A 1B 1C 1，使它们的相似比为1：2，若点A 的坐标为（2，2），则它的对应点A 1的坐标一定是（） A ．（﹣2，﹣2） B ．（1，1）C ．（4，4）D ．（4，4）或（﹣4，﹣4）2．如果35b a =，则a ba-＝（） A ．23 B ．85C ．25D ．833．在平面直角坐标系中，点A （1，3）绕原点顺时针旋转90°，得到点A'，则点A'的坐标为（） A ．（﹣3，1）B ．（3，﹣1）C ．（﹣1，3）D ．（1，3）4．将点(4,2)A 向左平移2个单位长度得到点'A ，则点'A 的坐标是（） A ．(6,2)B ．(4,0)C ．(2,2)D ．(4,4)5．如图，已知点D 、E 分别在ABC ∆的边AB 、AC 上，//DE BC ，点F 在CD 延长线上，//BC AF ，则下列结论错误的是（）A ．DE AFAF BC= B ．FD DCAE EC= C ．AD AEAB AC= D ．BD DEAB AF= 6．如图，点D 是△ABC 的边AB 上的一点，过点D 作BC 的平行线交AC 于点E ，连接BE ，过点D 作BE 的平行线交AC 于点F ，则下列结论错误的是（）A ．AD AEBD EC=B ．AF DFAE BE= C ．AE AFEC FE= D ．DE AFBC FE= 7．在下列图形中，不是中心对称图形的是（）A ．B ．C ．D ．8．在直角坐标中，将△ABC的三个顶点的纵坐标分别乘以-1，横坐标不变，则所得图形与原图的关系是（）A．关于x轴对称B．关于y轴对称C．关于原点对称D．将原图向下平移1个单位9．如图，A（3，1），B（1，3），将∆AOB绕点O旋转1500后，得到∆A’OB’，则此时点A的对应点A’的坐标为（）A．（-3，1）B．（-2，0）C．（-1，-3）或（-2,0）D．（-3，-1）或（-2,0）10．如图，在矩形ABCD中，AB=3，BC=4，O 为矩形ABCD对角线的交点，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）A．4 B．215C．358D．17411．如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是______．12．在比例尺是1:38000的交通游览图上，某隧道长约4cm，那么它的实际长度约为__m ．13．圆内接正六边形的边长为6，则该正六边形的边心距为_____．14．在ABC ∆中，90ACB ∠=o ，点D 、E 分别在边BC 、AC 上，3AC AE =，45CDE ∠=o（如图），DCE ∆沿直线DE 翻折，翻折后的点C 落在ABC ∆内部的点F ，直线AF 与边BC 相交于点G ，如果BG AE =，那么tan B =__________．15．下列4种图案中，是中心对称图形的有_____个．16．用计算器计算：sin35°=_______________.(结果保留两个有效数字) 17．已知在ABC △中，∠C=90°，AC=3，AB=4，那么tanA=____________18．在直角坐标系中，点(1,1)A -，点(3,2)B ，P 是x 轴上的一点，则PA PB +的最小值是__________．19．小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数为，则电子表的实际时刻是_____．20．如图，已知四边形ABCD ，画四边形A 1B 1C 1D 1，使它与四边形ABCD 关于C 点中心对称．21．抛物线l1：y＝x2+bx+c与它的对称轴x＝﹣2交于点A，且经过点B（0，﹣2）．（1）求抛物线l1的解析式；（2）如图1，直线y＝kx+2k﹣8（k＜0）与抛物线l1交于点E，F，若△AEF的面积为22，求k的值；（3）如图2，将抛物线l1向下平移n（n＞0）个单位长度得到抛物线l2，抛物线l2与y 轴交于点C，过点C作x轴的平行线交抛物线l2于另一点D；抛物线l2的对称轴与x轴的交于点M，P为线段OC上一点，若△POM与△PCD相似，并且符合该条件的点P 有且只有2个，求n的值及相应点P的坐标．22．如图，在△ABC中，点D，E分别在边AB，AC上，∠ACD=∠B，DE∥BC．（1）求证：△ADE∽△ACD；（2）若DE=6，BC=10，求线段CD的长．23．（2015秋•抚州校级期中）如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB 于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．（1）求线段CD的长；（2）当t为何值时，△CPQ与△ABC相似？（3）当t为何值时，△CPQ为等腰三角形？24．在直角坐标系中△ABC三个顶点坐标分别为A(7，1)、B(8，2)、C(9，0)．(1)请在图中画出△ABC的一个以点P (12，0)为位似中心，相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧)；(2)请直接写出点B′及点C′的坐标；(3)求线段BC的对应线段B′C′所在直线的解析式．25．如图，将绕着点B顺时针旋转至，使得C点落在AB的延长线上的D 点处，的边BC恰好是的角平分线.(1)试求旋转角的度数；(2)设BE与AC的交点为点P，求证：．26．（数学概念）若四边形ABCD的四条边满足AB⋅CD=AD⋅BC，则称四边形ABCD是和谐四边形．（特例辨别）（1）下列四边形：①平行四边形，②矩形，③菱形，④正方形．其中一定是和谐四边形的是________．（概念判定）（2）如图①，过⊙O外一点P引圆的两条切线PS、PT，切点分别为A、C，过点P作一条射线PM，分别交⊙O于点B、D，连接AB、BC、CD、DA．求证：四边形ABCD 是和谐四边形．（知识应用）（3）如图②，CD是⊙O的直径，和谐四边形ABCD内接于⊙O，且BC AD．请直接写出AB与CD的关系．27．在Rt△ABC中，BC=2，AC=4，点D为AB的中点，P为AC边上一动点．△BDP 沿着PD所在的直线翻折，点B的对应点为E．（1）若PD⊥AB，求AP．（2）当AD=PE时，求证：四边形BDEP为菱形．（3）若△PDE与△ABC重合部分的面积等于△PAB面积的14，求AP．参考答案1．D【解析】【分析】根据如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k进行解答．【详解】∵以原点O为位似中心，相似比为：1：2，把△ABC放大得到△A1B1C1，点A的坐标为（2，2），则它的对应点A1的坐标一定为：（4，4）或（-4，-4），故选D．【点睛】本题考查了位似变换：位似图形与坐标，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．2．C【解析】【分析】根据两內项之积等于两外项之积用b表示出a，然后代入比例式进行计算即可得解．【详解】解：∵35ba=，∴a=53 b，∴a ba-=5b-b35b3=25．故选：C．【点睛】本题考查了比例的性质，熟记“两內项之积等于两外项之积”，并用b表示出a是解题的关键．3．B【解析】【分析】如图，作AE⊥x轴于E，A′F⊥x轴于F．利用全等三角形的性质解决问题即可．【详解】如图，作AE⊥x轴于E，A′F⊥x轴于F．∵∠AEO＝∠OFA′＝∠AOA′＝90︒，∴∠AOE+∠A′OF＝90︒，∠A′OF+∠A′＝90︒，∴∠AOE＝∠A′，∵OA＝OA′，∴△AOE≌△OA′F（AAS），∴OF＝AE3，A′F＝OE＝1，∴A′3，﹣1）．故选：B．【点睛】本题考查旋转变换，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．4．C【解析】【分析】让点A的横坐标减2，纵坐标不变，可得A′的坐标．【详解】解：将点A（4，2）向左平移2个单位长度得到点A′，则点A′的坐标是（4−2，2），即（2，2），故选：C．【点睛】本题考查坐标的平移变化，用到的知识点为：左右平移只改变点的横坐标，左减右加．5．A【解析】【分析】由AF∥BC，DE∥BC，得到AF∥DE，根据平行线分线段成比例定理即可得到结论．【详解】∵AF∥BC,DE∥BC，∴AF∥DE,∴DE CDAF CF=,,AF DFBC CD=∴DE AFAF BC≠故A错误，∵AF∥DE，∴FD DCAE EC=,故B正确，∵DE∥BC，∴AD AEAB AC=，故C正确，∵AF∥DE，∴DE CD AF CF=，∵AF∥BC，∴BD CD AB CF=，∴BD DEAB AF=，故D正确，故选:A.【点睛】考查平行线分线段成比例定理，三条平行线被两条直线所截，所得的对应线段成比例.6．D【解析】【分析】由平行线分线段成比例和相似三角形的性质进行判断. 【详解】∵DE//BC，∴AD AEBD EC=，故A正确；∵DF//BE，∴△ADF∽△ABF, ∴AF DFAE BE=，故B正确；∵DF//BE，∴AD AFBD FE=，∵AD AEBD EC=，∴AE AFEC FE=，故C正确；∵DE//BC，∴△ADE∽△ABC,∴DE ADBC AB=，∵DF//BE，∴AF ADAE AB=，∴DE AFBC AE=，故D错误.故选D.【点睛】本题考查平行线分线段成比例性质，相似三角形的性质，由平行线得出比例关系是关键. 7．C【解析】【分析】根据中心对称图形的概念，对各选项分析判断即可得解．【详解】解：A、是中心对称图形，故本选项不符合题意；B、是中心对称图形，故本选项不符合题意；C、不是中心对称图形，故本选项符合题意；D、是中心对称图形，故本选项不符合题意．故选：C.【点睛】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后两部分重合．8．A【解析】纵坐标都乘以−1，即纵坐标变为相反数，横坐标不变，符合关于x轴对称，故选：A. 9．C. 【解析】试题分析：∵A （3，1），B （1，3），∴tanα=1333=， ∴OA 与x 轴正半轴夹角为30°，OB 与y 轴正半轴夹角为30°，∴∠AOB=90°-30°-30°=30°，根据勾股定理，22(3)12OA =+=，221(3)2OB =+=，①如图1，顺时针旋转时，∵150°+30°=180°，∴点A′、B 关于原点O 成中心对称，∴点A′（-1，-3）；②如图2，逆时针旋转时，∵150°+30°=180°，∴点A′在x 轴负半轴上，∴点A′的坐标是（-2，0）．综上所述，点A′的坐标为（-1，-3）或（-2，0）．故选C．考点: 坐标与图形变化-旋转．10．D【解析】【详解】解：当P点移动到平行于OA且与⊙D相切时，△AOP面积的最大，如图，∵P是⊙D的切线，∴DP垂直与切线，延长PD交AC于M，则DM⊥AC，∵在矩形ABCD中，AB=3，BC=4，∴AC= 22AB BC+=5，∴OA= 52，∵∠AMD=∠ADC=90°，∠DAM=∠CAD，∴△ADM∽△ACD，∴DM AD CD AC=，∵AD=4，CD=3，AC=5，∴DM= 125，∴PM=PD+DM=1+ 125=175，∴△AOP的最大面积= 12OA•PM=1517225⨯⨯=174，故选D．【点睛】本题考查了圆的切线的性质，矩形的性质，平行线的性质，勾股定理的应用以及三角形相似的判定和性质，本题的关键是判断出P 处于什么位置时面积最大．11．【解析】试题分析：∵∠AED 与∠ABC 都对， ∴∠AED=∠ABC ，在Rt △ABC 中，AB=2，AC=1，根据勾股定理得：BC=，则cos ∠AED=cos ∠ABC==．考点：1.圆周角定理；2.勾股定理；3.锐角三角函数的定义．12．1520【解析】【分析】根据游览图上的距离与实际距离的比就是比例尺，列出比例式求解即可．【详解】设隧道的实际长度是xcm ，根据题意得：4:1:38000x =．解得：1520001520x cm ==米．故答案为：1520【点睛】本题主要考查了比例尺的含义，实际就是比例的问题．13．3【解析】【分析】根据题意画出图形，利用等边三角形的性质及锐角三角函数的定义直接计算即可．【详解】如图所示，连接OB 、OC ，过O 作OG ⊥BC 于G ．∵此多边形是正六边形，∴△OBC 是等边三角形，∴∠OBG =60°，∴边心距OG =OB •sin ∠OBG =63⨯=33(cm )．故答案为：33．【点睛】本题考查了正多边形与圆、锐角三角函数的定义及特殊角的三角函数值，熟知正六边形的性质是解答本题的关键．14．37【解析】【分析】设k AE BG == ，()3k k 0AG =≠ ，可得2k EC = ，由折叠的性质可得2k EF EC == ，45FED DEC ==︒∠∠ ，根据相似三角形的性质可得13AE EF AC GC == ,即36k GC EF == ，即可求tan B 的值．【详解】根据题意，标记下图∵90ACB ∠=︒ ，45CDE ∠=︒∴45DEC ∠=︒∵3AC AE =∴设k AE BG == ，()3k k 0AG =≠∴2k EC =∵DEF V 由CDE △ 折叠得到∴2k EF EC == ，45FED DEC ==︒∠∠∴90FEC ∠=︒ ，且90ACB ∠=︒∴EF BC ∥∴AEF ACG ∽△△∴13AE EF AC GC == ∴36k GC EF ==∴7k BC BG GC =+=∴3tan =7AC B BC = 故答案为37 ．【点睛】本题考查了三角形的折叠问题，理解折叠后的等量关系，利用代数式求出tan B 的值即可．15．2【解析】【分析】根据中心对称图形的概念即可求解.【详解】第1个图形，是中心对称图形，符合题意；第2个图形，不是中心对称图形，不符合题意；第3个图形，是中心对称图形，符合题意；第4个图形，不是中心对称图形，不符合题意.故答案为：2.【点睛】本题考查了中心对称图形，掌握好中心对称图形，中心对称图形是要寻找对称中心，旋转180度后两部分重合.16．0.57【解析】试题解析：先按键“sin”，再输入“35”，最后按键“=”；sin350.57360.57.≈≈o故答案为0.57.点睛：有效数字：从左边第一个不是0的数字算起，到末尾数字为止都是有效数字. 17．7 【解析】【分析】先利用勾股定理计算BC 的长度，然后根据三角函数的定义可求得tanA 的值.【详解】如图，在Rt △ABC 中，∵∠C=90°，AC=3，AB=4∴根据勾股定理2222437BC AB AC =-=-=. ∴7tan 3BC A AC == . 故填7.【点睛】本题考查锐角三角函数的定义，解决本题需注意①熟记正切的计算方法是解决本题的关键；②可先根据题意画出相应的图象，这样方便正确找出对应的线段.18．5【解析】【分析】作点A 关于x 轴的对称点A’，连接A’B ，则A’B 的长就是PA PB +的最小值，然后结合图象利用勾股定理求解即可.【详解】解：如图，作点A关于x轴的对称点A’，连接A’B交x轴于点P’，则P’的位置就是符合题+的最小值，意的P点位置，A’B的长就是PA PB由图象可得：A’（－1，－1），B（3，2），+的最小值是5，∴A’B＝22345+=，即PA PB故答案为：5.【点睛】本题考查了轴对称－最短路径问题以及勾股定理的应用，熟练掌握求最短路径问题的方法是解题的关键.19．10：50【解析】【分析】镜子中看到的数字与实际数字是关于镜面成垂直的线对称．注意镜子的2实际应为5．【详解】解：电子表的实际时刻是10：50，可以把给定的读数写在纸上，然后把纸翻过来看到的读数就是实际读数．故答案为10：50【点睛】此题考查镜面对称，解题关键在于掌握对于这类题型常用的解题方法为把给定的读数写在纸上，然后把纸翻过来看到的读数就是实际读数．20．见解析【解析】试题分析：分别画出A、B、C、D各点关于点C的对称点，然后顺次连接即可．解：四边形A1B1C1D1如图所示.21．（1）y ＝x 2+4x ﹣2；（2）k ＝﹣4；（3）当n ＝2﹣2时，点P 的坐标为（0，﹣2）和（0，﹣23）；当n ＝4时，点P 坐标为（0，﹣2）和（0，﹣4）．【解析】【分析】（1）待定系数法求解可得；（2）设直线y=kx+2k-8与抛物线l 1的对称轴交点为G ，则G （-2，-8），由顶点A 坐标知AG=2，由S △AEF =S △AGE -S △AGF =12AG•（-2-x E ）-12AG•（-2-x F ）=12AG•（x F -x E ）2知x F -x E =22，再联立得24228y x x y kx k ⎧=+-⎨=+-⎩，消去y 整理得x 2+（4-k ）x-2k+6=0，据此知248k k x -±-=，继而得出x F -x E 28k -k 的方程，解之可得答案；（3）分△PCD ∽△MOP 和△PCD ∽△POM 得出t 关于n 的关系式，再根据符合该条件的点P 有且只有两个，进一步求解可得．【详解】解：（1）∵y ＝x 2+bx +c 与它的对称轴x ＝﹣2交于点A ，且经过点B （0，﹣2） ∴可得222b c ⎧-=-⎪⎨⎪=-⎩，解得42b c =⎧⎨=-⎩， ∴抛物线l 1的解析式为y ＝x 2+4x ﹣2．（2）如图1，设直线y ＝kx +2k ﹣8与抛物线l 1的对称轴交点为G ，则G （﹣2，﹣8），又可得抛物线l 1的顶点A （﹣2，﹣6）， ∴AG =2，S △AEF =S △AGE ﹣S △AGF11(2)(2)22E F AG x AG x =----- 1()2F E AG x x =- 又∵S △AEF ＝2，AG ＝2，∴x F ﹣x E ＝2，将抛物线l 1与直线y ＝kx +2k ﹣8联立得24228y x x y kx k ⎧=+-⎨=+-⎩，消去y 得x 2+4x ﹣2＝kx +2k ﹣8，整理得x 2+（4﹣k ）x ﹣2k +6＝0，得2482k k x -±-=， ∴x F ﹣x E 28k - 2822k -=解得k ＝±4，又k ＜0，∴k ＝﹣4．（3）设抛物线l 2的解析式为y ＝x 2+4x ﹣2﹣m ， ∴C （0，﹣2﹣n ），D （﹣4，﹣2﹣n ），M （﹣2，0）设P （0，t ）．①当△PCD∽△MOP时，PC MO CD OP=，∴224t nt ++=-，∴t2+（n+2）t+8＝0；②当△PCD∽△POM时，PC PO CD OM=，∴242t n t ++-=，∴t=23n+ -；（Ⅰ）当方程①有两个相等实数根时，△＝（n+2）2﹣4×1×8＝0，解得n＝±2﹣2，又n＞0，∴n＝2﹣2，此时方程①有两个相等实根t1＝t2＝﹣2，方程②有一个实数根t=423 -；∴n＝2﹣2，此时点P的坐标为（0，﹣2）和（0，423 -）；（Ⅱ）当方程①有两个不相等的实数根时，把②代入①，得：22(2)(2)8093n n++-+=，即（n+2）2＝36，解得n1＝4，n2＝﹣8，又n＞0，∴n＝4，此时方程①有两个不相等的实数根，t1＝﹣2，t2＝﹣4，方程①有一个实数根t＝﹣2；∴n＝4，此时点P坐标为（0，﹣2）和（0，﹣4），综上，当n＝﹣2时，点P的坐标为（0，﹣）和（0，3-）；当n＝4时，点P坐标为（0，﹣2）和（0，﹣4）．【点睛】本题是二次函数的综合问题，解题的关键是掌握待定系数法求函数解析式、割补法求三角形的面积、相似三角形的判定与性质及一元二次方程根的判别式等知识点．22．(1)证明见解析；（2）【解析】【分析】（1）由DE∥BC可得∠ADE=∠B，∠ACD=∠B，则∠ADE=∠ACD，结论得证；（2）可证△CDE∽△BCD，由比例线段可求出线段CD的长．【详解】（1）证明：∵DE∥BC∴∠ADE=∠B，∵∠ACD=∠B，∴∠ADE=∠ACD，∵∠DAE=∠CAD，∴△ADE∽△ACD；（2）解：∵DE∥BC，∴∠BCD=∠EDC，∵∠B=∠DCE，∴△CDE∽△BCD，∴DECD＝CDBC，∴610CD CD，∴CD=215．【点睛】本题主要考查了相似三角形的判定和性质，找准对应边是解题的关键．23．（1）4.8．（2）t为3或；（3）当t为2.4秒或秒或秒时，△CPQ为等腰三角形．【解析】试题分析：（1）先根据勾股定理求出AB的长，再由三角形的面积公式即可得出结论；（2）先用t表示出DP，CQ，CP的长，再分PQ⊥CD与PQ⊥AC两种情况进行讨论；（3）根据题意画出图形，分CQ=CP，PQ=PC，QC=QP三种情况进行讨论．解：（1）∵∠ACB=90°，AC=8，BC=6，∴AB=10．∵CD⊥AB，∴S△ABC=BC•AC=AB•CD．∴CD===4.8．∴线段CD的长为4.8．（2）由题可知有两种情形，设DP=t，CQ=t．则CP=4.8﹣t．①当PQ⊥CD时，如图a∵△QCP∽△△ABC∴=，即=，∴t=3；②当PQ⊥AC，如图b．∵△PCQ∽△ABC∴=，即=，解得t=，∴当t为3或时，△CPQ与△△ABC相似；（3）①若CQ=CP，如图1，则t=4.8﹣t．解得：t=2.4．②若PQ=PC，如图2所示．∵PQ=PC，PH⊥QC，∴QH=CH=QC=．∵△CHP∽△BCA．∴=．∴=，解得t=．③若QC=QP，过点Q作QE⊥CP，垂足为E，如图3所示．同理可得：t=．综上所述：当t为2.4秒或秒或秒时，△CPQ为等腰三角形．考点：相似形综合题．24．(1)见解析；(2)B′(0，6)，C′(3，0)；(3)y＝﹣2x+6．【解析】【分析】（1）根据画位似图形的一般步骤和相似比找出图形；（2）根据相似比和相似三角形的性质求出点B′及点C′的坐标；（3）运用待定系数法求出一次函数解析式．【详解】解：(1)如图△A′B′C′即为所求；(2)∵△ABC与△A′B′C′的相似比为1：3，∴B′(0，6)，C′(3，0)；(3)设B′C′所在直线的解析式为y＝kx+b，，解得，∴B′C′所在直线的解析式y＝﹣2x+6．【点睛】本题考查的知识点是作图-图形变换，解题关键是注意画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．25．(1)；(2)证明见解析.【解析】【分析】（1）根据旋转的性质，得到∠ABC=EBD，由BC平分∠EBD，得到∠ABE=∠EBC=∠CBD，根据平角定义，即可得到答案；（2）由（1）知，∠EBC=∠CBD=60°，由三角形外角定理可得，则即可得到结论成立.【详解】（1）解：由旋转的性质，得：∠ABC=∠EBD，即，∴∠ABE=∠CBD，∵BC平分∠EBD，∴∠EBC=∠CBD，∴∠ABE=∠EBC=∠CBD，∵∠ABE+∠EBC+∠CBD=180°，∴∠CBD=60°.（2）证明：如图，BE 与AC 相交与点P ，DE 与AC 相交与点F ，由（1）知，∠EBC=∠CBD=60°，由三角形外角定理，得：∠APB=∠EBC+∠C=60°+∠C ，∠CBD=∠A+∠C=60°, ∴∠APB=∠A+2∠C∴∠APB>∠A ，结论成立.【点睛】本题考查了旋转的性质，角平分线定理，三角形外角定理，解题的关键是正确找出角之间的关系.26．③④【解析】分析：（1）由于菱形和正方形的四条边相等，因此对边的乘积相等，所以菱形和正方形是和谐四边形；（2）连接CO 并延长，交⊙O 于点E ，连接BE ．通过证明△PBC ∽△PCD ，得CB PC CD PD =．同理，AB PA AD PD =．由P A 、PC 为⊙O 的切线，得P A =PC ，故CB AB CD AD=，所以AB ⋅CD =AD ⋅BC ，所以四边形ABCD 是和谐四边形．（3）AB ∥CD ，CD =3AB ．详解：（1）③④．（2）证明：连接CO 并延长，交⊙O 于点E ，连接BE ．∵PT是⊙O的切线，切点为C，∴∠PCE=90°．∴∠PCB+∠ECB=90°．∵CE是⊙O的直径，∴∠CBE=90°，∴∠BEC+∠ECB=90°，∴∠BEC=∠PCB．又∵∠BEC=∠BDC，∴∠PCB=∠BDC．又∵∠BPC=∠CPD，∴△PBC∽△PCD，∴CB PC CD PD=．同理，AB PA AD PD=．∵P A、PC为⊙O的切线，∴P A=PC，∴CB AB CD AD=．∴AB⋅CD=AD⋅BC．∴四边形ABCD是和谐四边形．（3）AB∥CD，CD=3AB．点睛：解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题.27．(1)52;(2)见解析：(3) AP=35【解析】【分析】（1）如图1，根据勾股定理可求出AB，从而得到AD、BD的值，易证△ADP∽△ACB，只需运用相似三角形的性质就可求出AP的值；（2）由折叠可得：PE=PB，DE=DB，又有AD=PE，AD=DB，从而PE=PB=DB=DE，然后根据四条边相等的四边形形是菱形即可证明四边形BDEP为菱形；（3）根据条件可得S△PDF=14S△P AB=12S△ADP=12S△EDP，从而可得AF=PF，EF=DF．而符合条件的位置有两个（图3、图4），需分两种情况讨论：①如图3，根据三角形中位线定理可得DF∥BP，则有∠EDP=∠BPD．由折叠可得∠BDP=∠EDP，从而可得∠BDP=∠BPD，即可得到BP=BD=25，在Rt△BCP中运用勾股定理可求出PC，就可得到AP的值；②如图4，连接AE，由AF=PF，EF=DF可得四边形AEDP是平行四边形，则有AP=ED，由折叠可得DE=DB，即可得到AP=DB=25．【详解】解：（1）如图1，∵∠C=90°，BC=2，AC=4，∴AB==2．∵点D为AB的中点，∴AD=BD=．∵PD⊥AB，∴∠ADP=90°．∵∠A=∠A，∠ADP=∠C，∴△ADP∽△ACB，∴=，∴=，∴AP=；（2）证明：如图2，由折叠可得：PE=PB，DE=DB．∵AD=PE，AD=DB，∴PE=PB=DB=DE，∴四边形BDEP为菱形；（3）∵点D是线段AB的中点，∴S△ADP=S△BDP=S△PAB．由折叠可得：S△EDP=S△BDP，∴S△PDF=S△PAB=S△ADP=S△EDP，∴AF=PF，EF=DF．①如图3，根据三角形中位线定理可得：DF∥BP，∴∠EDP=∠BPD．由折叠可得∠BDP=∠EDP，∴∠BDP=∠BPD，∴BP=BD=，∴PC===1，∴AP=4﹣1=3；②如图4，连接AE，∵AF=DF，EF=PF，∴四边形AEDP是平行四边形，∴AP=ED，由折叠可得：DE=DB，∴AP=DB=．综上所述：AP=3或．【点睛】本题考查了勾股定理，相似三角形的判定与性质，折叠的性质，菱形的判定，三角形的中位线，平行四边形的判定与性质及分类讨论的数学思想.证明△ADP∽△ACB是解答（1）的关键，熟练掌握菱形的判定方法是解（2）的关键，分两种情况讨论是解答（3）的关键.。

2020年中考数学图形的变换专题(附答案)

2020年中考数学图形的变换专题（附答案）一、单选题（共12题；共24分）1.若△ABC与△DEF的相似比是3：2，△DEF的最长边是6cm，那么△ABC的最长边是（）A. 4cmB. 9cmC. 4cm或9cmD. 以上答案都不对2.如果五边形ABCDE∽五边形POGMN且对应高之比为3：2，那么五边形ABCDE和五边形POGMN的面积之比是（）A. 2：3B. 3：2C. 6：4D. 9：43.如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在A1处，已知OA=，AB=1，则点A1的坐标是( ）A. (,)B. (,3)C. (,)D. (,)4.如图，小王在长江边某瞭望台D处，测得江面上的渔船A的俯角为40°，若DE=3米，CE=2米，CE平行于江面AB，迎水坡BC的坡度i=1：0.75，坡长BC=10米，则此时AB的长约为（）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）．A. 5.1米B. 6.3米C. 7.1米D. 9.2米5.设a、b、c分别为△ABC中∠A，∠B和∠C的对边，则△ABC的面积为（）A. B. C. D.6.如图，在ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF=4，则下列结论：① ：②S△BCE=36:③S△ABE=12：④△AEF∽△ACD；其中一定正确的是（）A. ①②③④B. ①④C. ②③④D. ①②③7.如图，E是平行四边形ABCD的边AB延长线上一点，DE交BC于F，连接AF，CE.则图中与△ABF面积一定相等的三角形是（）A. △BEFB. △DCFC. △ECFD. △EBC8.如图，一把梯子靠在垂直水平地面的墙上，梯子AB的长是3米。

若梯子与地面的夹角为α，则梯子顶端到地面的距离BC为（）A. 3sina米B. 3cosa米。

2020初中数学中考专题复习——图形变换旋转综合题专项训练(附答案详解)

A．1 个
B．2 个
C．3 个
D．4 个
15．在 Rt△ ABC 中，AC＝BC，点 D 为 AB 中点．∠GDH＝90°，∠GDH 绕点 D 旋转，
DG，DH 分别与边 AC，BC 交于 E，F 两点．下列结论：①AE+BF＝AC，②AE2+BF2
＝EF2，③S ＝四边形 CEDF 1 S△ ABC，④△DEF 始终为等腰直角三角形．其中正确的是(
A．45°
B．60°
C．70°
D．90°
14．如图，把 Rt△ ABC 绕顶点 C 顺时针旋转 90°得到 Rt△ DFC，若直线 DF 垂直平分
AB，垂足为点 E，连接 BF，CE，且 BC=2，下面四个结论：①BF= 2 2 ；②∠CBF=45°；
③△BEC 的面积=△ FBC 的面积；④△ECD 的面积为 2 2 3 ，其中正确的结论有（）
经过的路径为 BD ，则图中阴影部分的面积是（）
A． 2 3
B． 4 3
C．4π
D．条件不足，无法计算
21．如图，平面直角坐标系中，矩形 OABC 的顶点 A（﹣6，0），C（0，2 3 ）．将矩
形 OABC 绕点 O 顺时针方向旋转，使点 A 恰好落在 OB 上的点 A1 处，则点 B 的对应点 B1 的坐标为_____．
2020 初中数学中考专题复习——图形变换旋转综合题专项训练（附答案详解） 1．已知正方形 MNKO 和正六边形 ABCDEF 边长均为 1，把正方形放在正六边形外边，使 OK 边与 AB 边重合，如图所示．按下列步骤操作：将正方形在正六边形外绕点 B 顺时针旋转，使 KN 边与 BC 边重合，完成第一次旋转；再绕点 C 顺时针旋转，使 NM 边与 CD 边重合，完成第二次旋转；……在这样连续 6 次旋转的过程中，点 M 在图中直角坐标系中的纵坐标可能是（）

2020年中考复习专题练习图形的变换 (含答案)

2020年中考复习专题练习图形的变换（含答案）第一部分知识梳理图形的变换包括平移、对称和旋转一、平移：、把一个图形整体沿某一个方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，平移前后对应点的连线平行或在同一直线上且相等。

在平面直角坐标系下,平移前后图形个点的对应点的横坐标都加上（或减去）同一个常数a，同时纵坐标都加上（或减去）同一个常数b二、、对称包括轴对称和中心对称（一）轴对称：1、把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线轴对称，这条直线叫做对称轴，2、轴对称的性质①如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

②轴对称的两个图像是全等形③轴对称的两个图形中对应线段或对应线段所在直线的交点在对称轴上3.对称点的坐标：（1）点P（a，b）关于x轴对称的点的坐标为P1（ a，-b ）。

（2）点P（a，b）关于y轴对称的点的坐标为P2（-a ，b）。

（3）点P（a，b）关于原点对称的点的坐标为P3（-a，-b）。

(二)中心对称1、把一个图形绕着某点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于该点成中心对称，这点叫做对称中心，2、中心对称的性质①如果两个图形城中心对称，那么对称点的连线必经对称中心，并且被对称中心平分。

②成中心对称的两个图像是全等形三、旋转1、在平面内。

把一个平面图形绕着平面某一点O转动一定的角度，叫做图形旋转，点O叫旋转中心，转动的角叫旋转角2、旋转的性质（1）对应点到旋转中心的距离相等（2）对应点与旋转中心所连线段的夹角等于旋转角（3）旋转前后的两个图像全等第二部分中考链接1．（2018•海南）如图，在平面直角坐标系中，△ABC位于第一象限，点A的坐标是（4，3），把△ABC向左平移6个单位长度，得到△A1B1C1，则点B1的坐标是（）A．（﹣2，3） B．（3，﹣1） C．（﹣3，1） D．（﹣5，2）2．（2018•黄石）如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是（）A．（﹣1，6）B．（﹣9，6） C．（﹣1，2） D．（﹣9，2）1题图2题图3题图4题图3．（2018•宜宾）如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（）A．2 B．3 C．D．4．（2018•温州）如图，已知一个直角三角板的直角顶点与原点重合，另两个顶点A，B的坐标分别为（﹣1，0），（0，）．现将该三角板向右平移使点A与点O重合，得到△OCB′，则点B 的对应点B′的坐标是（）A．（1，0）B．（，）C．（1，）D．（﹣1，）5．（2019枣庄）在平面直角坐标系中，将点(1,2)A-向上平移3个单位长度，再向左平移2个单位长度，得到点A'，则点A'的坐标是()A．(1,1)-B．(1,2)--C．(1,2)-D．(1,2)6．（2019）在平面直角坐标系中，一个智能机器人接到的指令是：从原点O出发，按“向上→向右→向下→向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点A1，第二次移动到点A2……第n次移动到点A n，则点A2019的坐标是（）A．（1010，0）B．（1010，1）C．（1009，0）D．（1009，1）7．（2019枣庄）如图，将ABC沿BC边上的中线AD平移到A B C'''的位置．已知ABC的面积为16，阴影部分三角形的面积9．若1AA'=，则A D'等于()A．2 B．3 C．4 D．327题图9题图12题图13题图8. （2019乐山）下列四个图形中，可以由图1通过平移得到的是( )()A()B()C()D图1B9、（2019江苏苏州）如图，菱形ABCD的对角线AC，BD交于点O，416AC BD==，，将ABOV沿点A到点C的方向平移，得到A B C'''V，当点A'与点C重合时，点A与点B'之间的距离为（）A．6 B．8 C．10 D．1210．（2018•长沙）在平面直角坐标系中，将点A′（﹣2，3）向右平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A′的坐标是．11．（2018•宿迁）在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是．12．（2018•曲靖）如图：图象①②③均是以P为圆心，1个单位长度为半径的扇形，将图形①②③分别沿东北，正南，西北方向同时平移，每次移动一个单位长度，第一次移动后图形①②③的圆心依次为P1P2P3，第二次移动后图形①②③的圆心依次为P4P5P6…，依次规律，PP2018= 个单位长度．13．（2018•株洲）如图，O为坐标原点，△OAB是等腰直角三角形，∠OAB=90°，点B的坐标为（0，2），将该三角形沿x轴向右平移得到Rt△O′A′B′，此时点B′的坐标为（2，2），则线段OA在平移过程中扫过部分的图形面积为．二、对称（一）轴对称1．（2018•淄博）下列图形中，不是轴对称图形的是（）A．B．C．D．2 （2019年山东省德州市）下列图形中，是中心对称图形但不是轴对称图形的是（）A. B. C. D.3. （2019年山东省菏泽市）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．4. （2019年山东省济宁市）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．5. （2019年山东省青岛市）下列四个图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．6．（2018•枣庄）在平面直角坐标系中，将点A（﹣1，﹣2）向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为（）A．（﹣3，﹣2）B．（2，2）C．（﹣2，2） D．（2，﹣2）7．（2018•滨州）如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（）A． B． C．6 D．38．（2018•贵港）如图，在菱形ABCD中，AC=6，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（）A．6B．3C．2D．4.59．（2019聊城）如图，在Rt△ABO中，∠OBA＝90°，A（4，4），点C在边AB上，且＝，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P 的坐标为（）A．（2，2）B．（，）C．（，）D．（3，3）7题图10、（2019的值为（11.（2019A.m=3,n=2B.m=-3,n=2C.m=2,n=3D.m=-2,n=312. （2019年西藏）如图，在矩形ABCD中，AB＝6，AD＝3，动点P满足S△PAB＝S矩形ABCD，则点P 到A、B两点距离之和PA+PB的最小值为（）A．2B．2C．3D．13．（2018•东营）在平面直角坐标系内有两点A、B，其坐标为A（﹣1，﹣1），B（2，7），点M为x轴上的一个动点，若要使MB﹣MA的值最大，则点M的坐标为．（二）折叠1．（2018•青岛）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕相交于点F．已知EF=，则BC的长是（）A． B． C．3 D．1题图2题图3题图4题图2．（2018•烟台）对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O 折叠菱形，使B，B′两点重合，MN是折痕．若B'M=1，则CN的长为（）A ．7B ．6C ．5D ．43. （2019辽宁大连）如图，将矩形纸片ABCD 折叠，使点C 与点A 重合，折痕为EF ，若AB ＝4，BC ＝8．则D ′F 的长为（）A ．2 B ．4 C ．3 D ．24、（2018•泰安）如图，在矩形ABCD 中，AB=6，BC=10，将矩形ABCD 沿BE 折叠，点A 落在A'处，若EA'的延长线恰好过点C ，则sin ∠ABE 的值为．5．（2018威海）如图，将矩形ABCD （纸片）折叠，使点B 与AD 边上的点K 重合，EG 为折痕；点C 与AD 边上的点K 重合，FH 为折痕．已知∠1=67.5°，∠2=75°，EF=+1，求BC 的长．5题图 6题图6、（2019潍坊）如图，在矩形ABCD 中，AD =2．将∠A 向内翻折，点A 落在BC 上，记为A’，折痕为DE ．若将∠B 沿EA’向内翻折，点B 恰好落在DE 上，记为B’，则AB =__________．7．（2019青岛）如图，在正方形纸片ABCD 中，E 是CD 的中点，将正方形纸片折叠，点B 落在线段AE 上的点G 处，折痕为AF ．若AD ＝4cm ，则CF 的长为 cm ．7题图 8题图 9题图 10题图8、（2019随州）如图，已知正方形ABCD 的边长为a ，E 为CD 边上的一点（不与端点重合），将△ADE 沿AE 对折至△AFE，延长EF 交边BC 于点G ，连接AG ，CF.给出下列判断： ①∠EAG=45°；②若DE=a 31，则AG∥CF；③若E 为CD 的中点，则△GFC 的面积为2101a ； ④若CF=FG ，则DE=a )12( ；⑤BG·DE+AF·GE=a².其中正确的是 .（写出所有正确判断的序号）.9. （2019西藏）如图，把一张长为4，宽为2的矩形纸片，沿对角线折叠，则重叠部分的面积为．10、（2019四川资阳）如图，在△ABC 中，已知AC ＝3，BC ＝4，点D 为边AB 的中点，连结CD ，过点A 作AE ⊥CD 于点E ，将△ACE 沿直线AC 翻折到△ACE ′的位置．若CE ′∥AB ，则CE ′＝．11.(2019天津)如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE ，折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，若DE=5，则GE 的长为 .D 1A 1G P F E C DBA11题图 12题图 13题图12. （2019浙江杭州）如图，把某矩形纸片ABCD 沿EF 、GH 折叠（点E 、H 在AD 边上，点F 、G 在BC 边上），使得点B 、点C 落在AD 边上同一点P 处，A 点的对称点为A'点，D 点的对称点为D'点，若∠FPG=90°，△A'EP 的面积为4，△D'PH 的面积为1，则矩形ABCD 的面积等于________.13. （2019甘肃天水）如图，在矩形ABCD 中，AB ＝3，AD ＝5，点E 在DC 上，将矩形ABCD 沿AE 折叠，点D 恰好落在BC 边上的点F 处，那么sin∠EFC 的值为．中心对称1. （2019贵港）若点P （m -1，5）与点Q （3，2-n ）关于原点成中心对称，则m +n 的值是（）A. 1B. 3C. 5D. 72. （2019山东枣庄）下列图形，可以看作中心对称图形的是（）A ．B ．C ．D ．三、旋转1、（2018济宁）如图，在平面直角坐标系中，点 A ，C 在 x 轴上，点 C 的坐标为（﹣1，0），AC=2．将 Rt △ABC 先绕点 C 顺时针旋转 90°，再向右平移 3 个单位长度，则变换后点 A 的对应点坐标是（）A ．（2，2） B ．（1，2） C ．（﹣1，2） D ．（2，﹣1）1题图 2题图 3题图2．（2018•淄博）如图，P 为等边三角形ABC 内的一点，且P 到三个顶点A ，B ，C 的距离分别为3，4，5，则△ABC 的面积为（）A． B． C． D．3．（2018•德州）如图，等边三角形ABC 的边长为4，点O 是△ABC 的中心，∠FOG=120°，绕点O 旋转∠FOG ，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD=OE ；②S △ODE =S △BDE ；③四边形ODBE的面积始终等于；④△BDE 周长的最小值为6．上述结论中正确的个数是（）A ．1 B ．2 C ．3 D ．44．（2018•聊城）如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且OA=5，OC=3．若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的A 1处，则点C的对应点C的坐标为（）1A．（﹣，） B．（﹣，） C．（﹣，） D．（﹣，）4题图5题图6题图5．（2018青岛）如图，将线段AB绕点P按顺时针方向旋转90°，得到线段A'B'，其中点A、B 的对应点分别是点A'、B'，则点A'的坐标是（）A．（﹣1，3）B．（4，0）C．（3，﹣3）D．（5，﹣1）6．（2019聊城）如图，在等腰直角三角形ABC中，∠BAC＝90°，一个三角尺的直角顶点与BC 边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中错误的是（）A．AE+AF＝AC B．∠BEO+∠OFC＝180° C．OE+OF＝BC D．S四边形AEOF＝S△ABC7. （2019青岛）如图，将线段AB先向右平移5个单位，再将所得线段绕原点按顺时针方向旋转90°，得到线段A′B′，则点B的对应点B′的坐标是（）A．（﹣4，1）B．（﹣1，2）C．（4，﹣1）D．（1，﹣2）7题图8题图9题图8. （2019枣庄）如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置．若四边形AECF的面积为20，DE＝2，则AE的长为（）A．4 B．2C．6 D．29. (2019天津)如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB 上，点B的对应点为E，连接BE，下列结论一定正确的是（）A.AC=ADB.AB⊥EBC. BC=DED.∠A=∠EBC10. （2019湖北荆州）在平面直角坐标系中，点A的坐标为（1，），以原点为中心，将点A 顺时针旋转30°得到点A'，则点A'的坐标为（）A．（，1）B．（，﹣1）C．（2，1）D．（0，2）11. （2019湖北宜昌）如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是（）A．（﹣1，2+）B．（﹣，3）C．（﹣，2+）D．（﹣3，）12．（2018•枣庄）如图，在正方形ABCD中，AD=2，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为．11题图12题图13题图14题图13．（2018•潍坊）如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，则点M的坐标为．14. （2019广西贺州）如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC 于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为．15. （2019湖北随州）如图，在平面直角坐标系中，Rt△ABC的直角顶点C的坐标为（1，0），点A在x轴正半轴上，且AC=2．将△ABC先绕点C逆时针旋转90°，再向左平移3个单位，则变换后点A的对应点的坐标为______．16. （2019内蒙古包头）如图，在△ABC中，∠CAB＝55°，∠ABC＝25°，在同一平面内，将△ABC绕A点逆时针旋转70°得到△ADE，连接EC，则tan∠DEC的值是．16题图17题图18题图19题图17 （2019新疆）如图，在△ABC中，AB＝AC＝4，将△ABC绕点A顺时针旋转30°，得到△ACD，延长AD交BC的延长线于点E，则DE的长为．18、（2019海南）如图，将Rt△ABC的斜边AB绕点A顺时针旋转α（0°＜α＜90°）得到AE，直角边AC绕点A逆时针旋转β（0°＜β＜90°）得到AF，连结EF．若AB＝3，AC＝2，且α+β＝∠B，则EF＝．19. （2019湖北十堰）如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝．20．（2018•临沂）将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．（1）如图，当点E 在BD 上时．求证：FD=CD ；（2）当α为何值时，GC=GB ？画出图形，并说明理由．21、（2018菏泽）问题情境：在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1，将矩形纸片ABCD 沿对角线AC 剪开，得到ABC ∆和ACD ∆.并且量得2AB cm =，4AC cm =. 操作发现：（1）将图1中的ACD ∆以点A 为旋转中心，按逆时针方向旋转α∠，使BAC α∠=∠，得到如图2所示的'AC D ∆，过点C 作'AC 的平行线，与'DC 的延长线交于点E ，则四边形'ACEC 的形状是________.（2）创新小组将图1中的ACD ∆以点A 为旋转中心，按逆时针方向旋转，使B 、A 、D 三点在同一条直线上，得到如图3所示的'AC D ∆，连接'CC ，取'CC 的中点F ，连接AF 并延长至点G ，使FG AF =，连接CG 、'C G ，得到四边形'ACGC ，发现它是正方形，请你证明这个结论. 实践探究：（3）缜密小组在创新小组发现结论的基础上，进行如下操作：将ABC ∆沿着BD 方向平移，使点B 与点A 重合，此时A 点平移至'A 点，'A C 与'BC 相交于点H ，如图4所示，连接'CC ，试求tan 'C CH ∠的值.22．（2018•宁波）如图，在△ABC 中，∠ACB=90°，AC=BC ，D 是AB 边上一点（点D 与A ，B 不重合），连结CD ，将线段CD 绕点C 按逆时针方向旋转90°得到线段CE ，连结DE 交BC 于点F ，连接BE ．（1）求证：△ACD ≌△BCE ；（2）当AD=BF 时，求∠BEF 的度数．23．（2018•自贡）如图，已知∠AOB=60°，在∠AOB 的平分线OM 上有一点C ，将一个120°角的顶点与点C 重合，它的两条边分别与直线OA 、OB 相交于点D 、E ．（1）当∠DCE 绕点C 旋转到CD 与OA 垂直时（如图1），请猜想OE +OD 与OC 的数量关系，并说明理由；（2）当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；（3）当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．24．（2018•岳阳）已知在Rt△ABC中，∠BAC=90°，CD为∠ACB的平分线，将∠ACB沿CD所在的直线对折，使点B落在点B′处，连结AB'，BB'，延长CD交BB'于点E，设∠ABC=2α（0°＜α＜45°）．（1）如图1，若AB=AC，求证：CD=2BE；（2）如图2，若AB≠AC，试求CD与BE的数量关系（用含α的式子表示）；（3）如图3，将（2）中的线段BC绕点C逆时针旋转角（α+45°），得到线段FC，连结EF交BC于点O，设△COE的面积为S1，△COF的面积为S2，求（用含α的式子表示）．25．（2019日照）如图，在矩形ABCD中，对角线AC的中点为O，点G，H在对角线AC上，AG ＝CH，直线GH绕点O逆时针旋转α角，与边AB、CD分别相交于点E、F（点E不与点A、B重合）．（1）求证：四边形EHFG是平行四边形；（2）若∠α＝90°，AB＝9，AD＝3，求AE的长．26．（2019菏泽）如图，△ABC 和△ADE 是有公共顶点的等腰直角三角形，∠BAC ＝∠DAE ＝90°．（1）如图1，连接BE ，CD ，BE 的廷长线交AC 于点F ，交CD 于点P ，求证：BP ⊥CD ；（2）如图2，把△ADE 绕点A 顺时针旋转，当点D 落在AB 上时，连接BE ，CD ，CD 的延长线交BE 于点P ，若BC ＝6，AD ＝3，求△PDE 的面积．27.（2019济南）小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.（一）猜测探究在ABC ∆中，AB AC =，M 是平面内任意一点，将线段AM 绕点A 按顺时针方向旋转与BAC ∠相等的角度，得到线段AN ，连接NB ．（1）如图1，若M 是线段BC 上的任意一点，请直接写出NAB ∠与MAC ∠的数量关系是，NB 与MC 的数量关系是；（2）如图2，点E 是AB 延长线上点，若M 是CBE ∠内部射线BD 上任意一点，连接MC ，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．（二）拓展应用如图3，在111ABC ∆中，118A B =，11160A B C ∠=，11175B A C ∠=，P 是11B C 上的任意点，连接1AP ，将1A P 绕点1A 按顺时针方向旋转75，得到线段1A Q ，连接1B Q ．求线段1B Q 长度的最小值．28. （2019年北京市）已知∠AOB=30°，H 为射线OA 上一定点，，P 为射线OB 上一点，M为线段OH 上一动点，连接PM ，满足∠OMP 为钝角，以点P 为中心，将线段PM 顺时针旋转150°，得到线段PN ，连接ON ．（1）依题意补全图1；（2）求证：∠ OMP=∠OPN ；（3）点M 关于点H 的对称点为Q ，连接QP ．写出一个OP 的值，使得对于任意的点M 总有ON=QP ，并证明．备用图图1BAOB29、（2019年江苏省苏州市）如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G（1）求证：EF BC =；（2）若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数.30 （2019年湖北省荆州市）如图①C ，D 分别在OE 和OF 上，现将△OEF 绕点O 逆时针旋转α角（0°＜α＜90°），连接AF ，DE （如图②）．（1）在图②中，∠AOF ＝；（用含α的式子表示）（2）在图②中猜想AF 与DE 的数量关系，并证明你的结论．位似1. （2019甘肃武威市）如图，将图形用放大镜放大，应该属于（）A．平移变换B．相似变换C．旋转变换D．对称变换2.（2018菏泽）如图，OAB∆与OCD∆是以点O为位似中心的位似图形，相似比为3:4，90OCD∠=，60AOB∠=，若点B的坐标是(6,0)，则点C的坐标是．[来源:学&科& Z&X3. （2019滨州）在平面直角坐标系中，△ABO三个顶点的坐标分别为A（﹣2，4），B（﹣4，0），O（0，0）．以原点O为位似中心，把这个三角形缩小为原来的，得到△CDO，则点A的对应点C的坐标是．3. （2019辽宁本溪）在平面直角坐标系中，点A，B的坐标分别是A（4，2），B（5，0），以点O为位似中心，相们比为，把△ABO缩小，得到△A1B1O，则点A的对应点A1的坐标为．其它1．（2018•枣庄）如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中，画出一个与△ABC成中心对称的格点三角形；（2）在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；（3）在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．2．（2018•徐州）如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）①画出△ABC关于x轴对称的△A1B1C1；②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2；③△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标．3．（2018•黑龙江）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；（3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．4．（2018•广西）如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B （4，1），C（3，3）．（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）5．（2018•眉山）在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC 的顶点都在格点上，请解答下列问题：（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；（2）作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；（3）已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（﹣4，﹣2），请直接写出直线l的函数解析式．6．（2018•吉林）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是对称图形；（3）求所画图形的周长（结果保留π）．7. （2019年四川省广安市）在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）8. （2019年黑龙江省伊春市）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．（1）画出△OAB关于y轴对称的△OA1B1，并写出点A1的坐标；（2）画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2，并写出点A2的坐标；（3）在（2）的条件下，求线段OA在旋转过程中扫过的面积（结果保留π）．9．（2018•德州）再读教材：宽与长的比是（约为0.618）的矩形叫做黄金矩形，黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，下面，我们用宽为2的矩形纸片折叠黄金矩形．（提示：MN=2）第一步，在矩形纸片一端，利用图①的方法折出一个正方形，然后把纸片展平．第二步，如图②，把这个正方形折成两个相等的矩形，再把纸片展平．第三步，折出内侧矩形的对角线AB ，并把AB 折到图①中所示的AD 处．第四步，展平纸片，按照所得的点D 折出DE ，使DE ⊥ND ，则图④中就会出现黄金矩形．问题解决：（1）图③中AB=（保留根号）；（2）如图③，判断四边形BADQ 的形状，并说明理由；（3）请写出图④中所有的黄金矩形，并选择其中一个说明理由．实际操作（4）结合图④，请在矩形BCDE 中添加一条线段，设计一个新的黄金矩形，用字母表示出来，并写出它的长和宽．答案与提示平移1、C2、C3、A4、C5、A6、C7、B8、D9、C 10、（1，1） 11、（5，1） 12、673 13、41、解：∵点B 的坐标为（3，1），∴向左平移6个单位后，点B 1的坐标（﹣3，1），故选：C ．2、解：由题意P （﹣5，4），向右平移4个单位，再向下平移2个单位，点P 的对应点P'的坐标是（﹣1，2），故选：C ．3、解：如图，∵S △ABC =9、S △A′EF =4，且AD 为BC 边的中线，∴S △A′DE =S △A′EF =2，S △ABD =S △ABC =， ∵将△ABC 沿BC 边上的中线AD 平移得到△A'B'C'，∴A′E∥AB ，∴△DA′E∽△DAB ，则（）2=，即（）2=，解得A′D=2或A′D=﹣（舍），故选：A ．4、解：∵点A 与点O 对应，点A （﹣1，0），点O （0，0）， ∴图形向右平移1个单位长度，∴点B 的对应点B'的坐标为（0+1，），即（1，），故选：C ．5.平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，∴点(1,2)A -向上平移3个单位长度，再向左平移2个单位长度后，得到点A '横坐标为121-=-，纵坐标为231-+=，A ∴'的坐标为(1,1)-．故选A ．6．解：A 1（0，1），A 2（1，1），A 3（1，0），A 4（2，0），A 5（2，1），A 6（3，1），…， 2019÷4＝504…3，所以A 2019的坐标为（504×2+1，0），则A 2019的坐标是（1009，0）． C 7.解:16ABCS=、9A EFS'=，且AD 为BC 边的中线，1922A DEA EFSS ''∴==，182ABDABCS S ==，将ABC沿BC 边上的中线AD 平移得到A B C '''，//A E AB ∴'，∴DA E DAB '∽，则2()A DE ABDSA D AD S''=，即2992()1816A D A D '=='+，解得，3A D '=或37-(舍)，故选B ． 8、平移前后的图像的大小、形状、方向是不变的，故选D.9、由菱形的性质得28AO OC CO BO OD B O '''======，90AOB AO B ''∠=∠=oAO B ''∴V为直角三角形10AB '∴==故选C10、解：∵将点A′（﹣2，3）向右平移3个单位长度，∴得到（1，3），∵再向下平移2个单位长度，∴平移后对应的点A′的坐标是：（1，1）．故答案为：（1，1）． 11、解：∵将点（3，﹣2）先向右平移2个单位长度，∴得到（5，﹣2），∵再向上平移3个单位长度，∴所得点的坐标是：（5，1）．故答案为：（5，1）12、解：由图可得，P 0P 1=1，P 0P 2=1，P 0P 3=1；P 0P 4=2，P 0P 5=2，P 0P 6=2；P 0P 7=3，P 0P 8=3，P 0P 9=3； ∵2018=3×672+2，∴点P 2018在正南方向上，∴P 0P 2018=672+1=673，故答案为：673．13、解：∵点B 的坐标为（0，2），将该三角形沿x 轴向右平移得到Rt △O′A′B′，此时点B′的坐标为（2，2），∴AA′=BB′=2，∵△OAB 是等腰直角三角形，∴A（，），∴AA′对应的高，∴线段OA 在平移过程中扫过部分的图形面积为2×=4．故答案为：4．二、对称（一）轴对称 1、C2、解：A 、是轴对称图形，不是中心对称图形，故本选项错误， B 、是中心对称图形但不是轴对称图形，故本选项正确， C 、不是轴对称图形，也不是中心对称图形，故本选项错误， D 、是轴对称图形，也是中心对称图形，故本选项错误．故选：B ．3、解：A 、不是轴对称图形，是中心对称图形，故此选项错误； B 、是轴对称图形，不是中心对称图形，故此选项错误； C 、是轴对称图形，也是中心对称图形，故此选项正确；D 、不是轴对称图形，是中心对称图形，故此选项错误；故选：C ．4、解：A、既是中心对称图形也是轴对称图形，故此选项正确；B、不是轴对称图形，也不是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、不是轴对称图形，是中心对称图形，故此选项错误．故选：A．5、解：A、是轴对称图形，不是中心对称图形，故此选项错误；B、不是轴对称图形，是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、既是轴对称图形，又是中心对称图形，故此选项正确．故选：D．6、B7、解：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=OC=，CH=OH=，∴CD=2CH=3．故选：D．8、解：如图，作点E关于AC的对称点E′，过点E′作E′M⊥AB于点M，交AC于点P，则点P、M即为使PE+PM取得最小值，其PE+PM=PE′+PM=E′M，∵四边形ABCD是菱形，∴点E′在CD上，∵AC=6，BD=6，∴AB==3，由S=AC•BD=AB•E′M得×6×6=3•E′M，解得：E′M=2，菱形ABCD即PE+PM的最小值是2，故选：C．9．解：∵在Rt△ABO中，∠OBA＝90°，A（4，4），∴AB＝OB＝4，∠AOB＝45°，∵＝，点D为OB的中点，∴BC＝3，OD＝BD＝2，∴D（0，2），C（4，3），作D关于直线OA的对称点E，连接EC交OA于P，则此时，四边形PDBC周长最小，E（0，2），∵直线OA的解析式为y＝x，设直线EC的解析式为y＝kx+b，∴，解得：，∴直线EC的解析式为y＝x+2，解得，，∴P（，），10、∵点A（1，-3x轴的对称点A'的坐标为（1，3）∴把（1，3 A11、A，B关于y故选B12、解：设△ABP中AB边上的高是h．∵S△PAB＝S矩形ABCD，∴AB•h＝AB•AD，∴h＝AD＝2，∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，BE，则BE的长就是所求的最短距离．在Rt△ABE中，∵AB＝6，AE＝2+2＝4，∴BE＝＝＝2，即PA+PB的最小值为2．故选：A．13、解：取点B关于x轴的对称点B′，则直线AB′交x轴于点M．点M即为所求．设直线AB′解析式为：y=kx+b 把点A（﹣1，﹣1）B′（2，﹣7）代入解得∴直线AB′为：y=﹣2x﹣3，当y=0时，x=﹣∴M坐标为（﹣，0）故答案为：（﹣，0）（二）折叠1、解：∵沿过点E的直线折叠，使点B与点A重合，∴∠B=∠EAF=45°，∴∠AFB=90°，∵点E为AB中点，∴EF=AB，EF=，∴AB=AC=3，∵∠BAC=90°，∴BC==3，故选：B．2、、解：连接AC、BD，如图，∵点O为菱形ABCD的对角线的交点，∴OC=AC=3，OD=BD=4，∠COD=90°，在Rt△COD中，CD==5，∵AB∥CD，∴∠MBO=∠NDO，在△OBM和△ODN中，∴△OBM≌△ODN，∴DN=BM，∵过点O折叠菱形，使B，B′两点重合，MN是折痕，∴BM=B'M=1，∴DN=1，∴CN=CD﹣DN=5﹣1=4．故选：D．3、解：连接AC交EF于点O，如图所示：∵四边形ABCD是矩形，∴AD＝BC＝8，∠B＝∠D＝90°，AC＝＝＝4，∵折叠矩形使C与A重合时，EF⊥AC，AO＝CO＝AC＝2，∴∠AOF＝∠D＝90°，∠OAF＝∠DAC，∴则Rt△FOA∽Rt△ADC，∴＝，即：＝，解得：AF＝5，∴D′F＝DF＝AD﹣AF＝8﹣5＝3，故选：C．4、解：由折叠知，A'E=AE，A'B=AB=6，∠BA'E=90°，∴∠BA'C=90°，在Rt△A'CB中，A'C==8，设AE=x，则A'E=x，∴DE=10﹣x，CE=A'C+A'E=8+x，在Rt△CDE中，根据勾股定理得，（10﹣x）2+36=（8+x）2，∴x=2，∴AE=2，在Rt△ABE中，根据勾股定理得，BE==2，∴sin∠ABE==，故答案为：．5、解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K作KM⊥BC于点M，设KM=x，则EM=x、MF=x，∴x+x=+1，解得：x=1，∴EK=、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3++，∴BC的长为3++．6、7．解：设BF＝x，则FG＝x，CF＝4﹣x．。

2020年中考数学中考真题分类专题解析汇编：专题4：图形的变换

专题4：图形的变换一、选择题1. （2019广东省3分）如图所示几何体的主视图是【】A．B．C．D．【答案】B。

【考点】简单组合体的三视图。

【分析】从正面看，此图形的主视图有3列组成，从左到右小正方形的个数是：1，3，1。

故选B。

2.（2019广东佛山3分）一个几何体的展开图如图所示，这个几何体是【】A．三棱柱B．三棱锥C．四棱柱D．四棱锥【答案】A。

【考点】几何体的展开图。

【分析】通过图片可以想象出该物体由三条棱组成，底面是三角形，符合这个条件的几何体是三棱柱。

故选A 。

3. （2019广东佛山3分）如图，把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ，则在旋转过程中这个三角板扫过的图形的面积是【】A ．πB ．3C ．33+42πD ．113+124π【答案】D 。

【考点】旋转的性质，勾股定理，等边三角形的性质，扇形面积。

【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD 计算即可：在△ABC 中，∠ACB=90°，∠BAC=30°，AB=2，∴BC=12AB=1，∠B=90°－∠BAC=60°。

∴22AC AB BC 3=-=。

∴ABC 13S BC AC 22∆=⨯⨯=。

设点B 扫过的路线与AB 的交点为D ，连接CD ，∵BC=DC ，∴△BCD 是等边三角形。

∴BD=CD=1。

∴点D 是AB 的中点。

∴ACD ABC 1133S S 2224∆∆==⨯=S 。

∴1ACD ACA BCD ABC S S S ∆∆=++扇形扇形的面扫过积22903 601333113 3603604464124πππππ⨯⨯⨯⨯=++=++=+（）故选D 。

4. （2019广东广州3分）一个几何体的三视图如图所示，则这个几何体是【】A ．四棱锥B ．四棱柱C ．三棱锥D ．三棱柱【答案】D 。

2020初中数学中考专题复习——图形变换旋转综合题专项训练1(附答案详解)

2020初中数学中考专题复习——图形变换旋转综合题专项训练1（附答案详解） 1．如图，边长为1的正方形ABCD 绕点A 逆时针旋转45°后得到正方形AB 1C 1D 1，边B 1C 1与CD 交于点O ，则四边形AB 1OD 的面积是（）A ．B ．C ．D ． 2．如图，在△ABC 中，∠CAB ＝75°，在同一平面内，将△ABC 绕点A 逆时针旋转到△AB′C′的位置，使得CC′∥AB ，则∠CAC′为（）A ．30°B ．35°C ．40°D ．50°3．如图，△ABC 是等边三角形，D 为BC 边上的点，∠BAD ＝15°，△ABD 经旋转后到达△ACE 的位置，那么旋转了( )A ．75°B ．45°C ．60°D ．15°4．O 为线段AB 上一动点，且AB=2，绕O 点将AB 旋转半周，则线段AB 所扫过的面积的最小值为（）A ．4πB ．3πC ．2πD ．π5．如图，在OAB ∆中，顶点(0,0)O ，(3,4)A -，(3,4)B ，将OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转，每次旋转90︒，则第70次旋转结束时，点D 的坐标为（）A ．(10,3)B ．(3,10)-C ．(10,3)-）D ．(3,10)- 6．如图，在等边ABC ∆中，D 是边AC 上一点，连接BD ，将BCD ∆绕点B 逆时针旋转60︒得到BAE ∆，连接ED ，若6BC =，4BD =，则有以下四个结论：①BDE ∆是等边三角形；②//AE BC ；③ADE ∆的周长是10；④ADE BDC ∠=∠．其中正确结论的序号是（）A ．②③④B ．①③④C ．①②④D ．①②③ 7．如图，矩形 ABCD 中，AB=8，BC=6，将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG ，AE ，FG 分别交射线CD 于点 PH ，连结 AH ，若 P 是 CH 的中点，则△APH的周长为（）A ．15B ．18C ．20D ．248．如图，等边三角形ABC 的边长是2，M 是高CH 所在直线上的一个动点，连接MB ，将线段BM 绕点B 逆时针旋转60°得到BN ，连接MN ，则在点M 运动过程中，线段MN 长度的最小值是（）A ．12B ．1C ．3D ．3 9．如图，将△ABC 绕点A 旋转至△ADE 的位置，使点E 落在BC 边上，则对于结论：①DE ＝BC ；②∠EAC ＝∠DAB ；③EA 平分∠DEC ；④若DE ∥AC ，则∠DEB ＝60°；其中正确结论的个数是（）A ．4B ．3C ．2D ．110．如图，将边为3的正方形ABCD 绕点A 逆时针方向旋转30°后得到正方形AEFH ，则图中阴影部分的面积为（）A ．332-B ．33-C ．23-D ．33- 11．如图，点A 是抛物线24y x x =-对称轴上的一点，连接OA ，以A 为旋转中心将AO 逆时针旋转90°得到AO ′，当O ′恰好落在抛物线上时，点A 的坐标为______________．12．如图，将矩形ABCD 绕点A 旋转至矩形AB ′C ′D ′位置，此时AC ′的中点恰好与D 点重合，AB ′交CD 于点E ．若AB ＝3，则△AEC 的面积为_____．13．如图，点 A 的坐标是（﹣2，0），点 B 的坐标是（0，6），C 为 OB 的中点，将△ABC 绕点 B 逆时针旋转 90°后得到△A′B′C′．若反比例函数 y =k x的图象恰好经过 A′B 的中点 D ，则k _________．14．如图，正方形 ABCD 中，点 E ，F 分别在 BC 和 AB 上，BE ＝3，AF ＝2，BF＝4，将△ BEF 绕点 E 顺时针旋转，得到△GEH ，当点 H 落在 CD 边上时，F ，H 两点之间的距离为_____．15．把一副三角板如图1放置其中∠ACB =∠DEC =90°，∠A =45°，∠D =30°，斜边AB =6，CD =8，把三角板DCE 绕点C 顺时针旋转15︒得到三角形1D CE (如图2)，此时AB 与1CD 交于点O ，则线段1AD 的长度为_______．16．如图，等腰Rt ABC ∆与等腰Rt CDE ∆，AC BC =，CD DE =，212AC CD ==，DH AE ⊥，垂足为H ，直线HD 交BE 于点O .将CDE ∆绕点C 顺时针旋转，则OA 的长的最大值是______.17．如图，△ABC ，△ADE 均为等腰直角三角形，∠BAC=∠DAE=90°，将△ADE 绕点A 在平面内自由旋转，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点，若AD=3，AB=7，则线段MN 的取值范围是______．18．如图：已知Rt ABC ∆，对应的坐标如下，请利用学过的变换（平移、旋转、轴对称）知识经过若干次图形变化，使得点A 与点E 重合、点B 与点D 重合，写出一种变化的过程_____．19．如图，在菱形ABCD 中，2,60AB BAD =∠=︒，将菱形ABCD 绕点A 逆时针方向旋转，对应得到菱形AEFG ，点E 在AC 上，EF 与CD 交于点P ，则DP 的长是_____．20．如图，在ABC V 中，90ACB ∠=︒，10AC BC ==，在DCE V 中，90DCE ∠=︒，6DC EC ==，点D 在线段AC 上，点E 在线段BC 的延长线上．将DCE V 绕点C 顺时针方向旋转60°得到D CE ''△（点D 的对应点为D ¢，点E 的对应点为点E '），连接AD '、BE '，过点C 作CN BE '⊥，垂足为N ，直线CN 交线段AD '于M ，则MN 的长为__________．21．如图乙，ABC V 和ADE V 是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒，点P 为射线BD ，CE 的交点．（1）如图甲，将ADE V 绕点A 旋转，当C 、D 、E 在同一条直线上时，连接BD 、BE ，则下列给出的四个结论中，其中正确的是哪几个；（回答直接写序号） ①BD CE =；②BD CE ⊥；③45∠+∠=︒ACE DBC ；④()2222=+BE AD AB（2）若6AB =，3AD =，把ADE V 绕点A 旋转．①当90CAE ∠=︒时，求PB 的长；②直接写出旋转过程中线段PB 的最大值和最小值．22．如图，点E 是正方形ABCD 内的一点，将△BEC 绕点C 顺时针旋转至△DFC ．（1）请问最小旋转度数为多少？（2）指出图中的全等图形以及它们的对应角？（3）若∠EBC=30°，∠BCE=80°，求∠F 的度数．23．如图，四边形ABCD 中，AC ，BD 是对角线，△ABC 是等边三角形．线段CD 绕点C 顺时针旋转60°得到线段CE ，连接AE ．（1）求证：AE ＝BD ；（2）若∠ADC ＝30°，AD ＝3，BD ＝42．求CD 的长．24．如图，△ABC 中，AB ＝AC ，∠BAC ＝50°，P 是BC 边上一点，将△ABP 绕点A逆时针旋转50°，点P旋转后的对应点为点P′.(1)画出旋转后的三角形；(2)连接PP′，若∠BAP＝20°，求∠PP′C的度数．25．综合与实践﹣四边形旋转中的数学“智慧”数学小组在课外数学活动中研究了一个问题，请帮他们解答．任务一：如图1，在矩形ABCD中，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为矩形，连接CG．（1）请直接写出CG的长是______．（2）如图2，当矩形AEGF绕点A旋转（比如顺时针旋转）至点G落在边AB上时，请计算DF与CG的长，通过计算，试猜想DF与CG之间的数量关系．（3）当矩形AEGF绕点A旋转至如图3的位置时，（2）中DF与CG之间的数量关系是否还成立？请说明理由．任务二：“智慧”数学小组对图形的旋转进行了拓展研究，如图4，在▱ABCD中，∠B=60°，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为平行四边形，连接CG．“智慧”数学小组发现DF与CG仍然存在着特定的数量关系．（4）如图5，当▱AEGF绕点A旋转（比如顺时针旋转），其他条件不变时，“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系．请你直接写出这个特定的数量关系．26．综合与探究问题情境在综合实践课上，老师让同学们探究“平面直角坐标系中的旋转问题”．如图，在平面直角坐标系中，四边形AOBC 是矩形，点()0,0O ，点()5,0A ，点()0,3B ．操作发现以点A 为中心，顺时针旋转矩形AOBC ，得到矩形ADEF ，点O ，B ，C 的对应点分别为D ，E ，F ．（1）如图①，当点D 落在BC 边上时，求点D 的坐标；继续探究（2）如图②，当点D 落在线段BE 上时，AD 与BC 交于点H ．①求证ADB AOB ∆≅∆；②求点H 的坐标．拓展探究（3）如图①，点M 是x 轴上任意一点，点N 是平面内任意一点，是否存在点N 使以A 、D 、M 、N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．27．（1）如图1，点A 为线段BC 外一动点，且BC a =，AB b =，填空：当点A 位于__________时，线段AC 的长取到最大值__________，且最大值为；（用含a 、b 的式子表示）．（2）如图2，若点A 为线段BC 外一动点，且6BC =，3AB =，分别以AB ，AC 为边，作等边ABD △和等边ACE △，连接CD ，BE ．①图中与线段BE 相等的线段是线段__________，并说明理由；②直接写出线段BE 长的最大值为__________．（3）如图3，在平面直角坐标系中，点A 的坐标为(40)，，点B 的坐标为(100)，，点P 为线段AB 外一动点，且4PA =，PM PB =，90BPM ∠=︒，请直接写出线段AM 长的最大值为__________，及此时点P 的坐标为__________．（提示：等腰直角三角形的三边长a 、b 、c 满足::1:1:2a b c =）28．如图，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＋∠EAD ＝180°，△ABC 不动，△ADE 绕点A 旋转，连接BE ，CD ，F 为BE 的中点，连接AF.(1)如图①，当∠BAE ＝90°时，求证：CD ＝2AF ；(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．29．如图1，矩形ABCD 中，E 是AD 的中点，以点E 直角顶点的直角三角形EFG 的两边EF ，EG 分别过点B ，C ，∠F ＝30°. （1）求证：BE ＝CE（2）将△EFG 绕点E 按顺时针方向旋转，当旋转到EF 与AD 重合时停止转动.若EF ，EG 分别与AB ，BC 相交于点M ，N.（如图2）①求证：△BEM ≌△CEN ；②若AB ＝2，求△BMN 面积的最大值；③当旋转停止时，点B恰好在FG上（如图3），求sin∠EBG的值.30．如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°．若固定△ABC，将△DEC绕点C旋转．（1）当△DEC统点C旋转到点D恰好落在AB边上时，如图2．①当∠B=∠E=30°时，此时旋转角的大小为；②当∠B=∠E=α时，此时旋转角的大小为(用含a的式子表示)．（2）当△DEC绕点C旋转到如图3所示的位置时，小杨同学猜想：△BDC的面积与△AEC的面积相等，试判断小杨同学的猜想是否正确，若正确，请你证明小杨同学的猜想．若不正确，请说明理由．参考答案1．C【解析】【分析】连接AC1，AO，根据四边形AB1C1D1是正方形，得出∠C1AB1=∠AC1B1=45°，求出∠DAB1=45°，推出A、D、C1三点共线，在Rt△C1D1A中，由勾股定理求出AC1，进而求出DC1=OD，根据三角形的面积计算即可．【详解】连接AC1，∵四边形AB1C1D1是正方形，∴∠C1AB1=×90°=45°=∠AC1B1，∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，∴∠B1AB=45°，∴∠DAB1=90°-45°=45°，∴AC1过D点，即A、D、C1三点共线，∵正方形ABCD的边长是1，∴四边形AB1C1D1的边长是1，在Rt△C1D1A中，由勾股定理得：AC1=，则DC1=-1，∵∠AC1B1=45°，∠C1DO=90°，∴∠C1OD=45°=∠DC1O，∴DC1=OD=-1，∴S△ADO=×OD•AD=，∴四边形AB1OD的面积是=2×=-1，故选C．2．A【解析】【分析】根据旋转的性质可得AC=AC,∠BAC=∠BAC',再根据两直线平行,内错角相等求出∠ACC=∠CAB,然后利用等腰三角形两底角相等求出∠CAC,再求出∠BAB=∠CAC,从而得解【详解】∵CC′∥AB，∠CAB＝75°，∴∠C′CA＝∠CAB＝75°，又∵C、C′为对应点，点A为旋转中心，∴AC＝AC′，即△ACC′为等腰三角形，∴∠CAC′＝180°﹣2∠C′CA＝30°．故选A．【点睛】此题考查等腰三角形的性质，旋转的性质和平行线的性质，运用好旋转的性质是解题关键3．C【解析】【分析】首先根据题意寻找旋转后的重合点，根据重合点来找到旋转角.【详解】根据题意△ABC是等边三角形∴=AB AC∴可得B点旋转后的点为C∴旋转角为60∠=BAC︒故选C.【点睛】本题主要考查旋转角的计算，关键在于根据重合点来确定旋转角.4．D【解析】【分析】当O 是AB 中点时，线段AB 所扫过的面积的最小；【详解】解：当O 是AB 中点时，线段AB 所扫过的面积的最小，最小面积=π•12=π，故选D ．【点睛】本题考查扇形面积的计算、旋转变换的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．5．D【解析】【分析】先求出6AB =，再利用正方形的性质确定(3,10)D -，由于704172=⨯+，所以第70次旋转结束时，相当于OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转2次，每次旋转90︒，此时旋转前后的点D 关于原点对称，于是利用关于原点对称的点的坐标特征可出旋转后的点D 的坐标．【详解】解：(3,4)A -Q ，(3,4)B ，336AB ∴=+=，Q 四边形ABCD 为正方形，6AD AB ∴==，(3,10)D ∴-，704172=⨯+Q ，∴每4次一个循环，第70次旋转结束时，相当于OAB ∆与正方形ABCD 组成的图形绕点O 顺时针旋转2次，每次旋转90︒，∴点D 的坐标为(3,10)-．【点睛】本题考查了坐标与图形变化﹣旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30︒，45︒，60︒，90︒，180︒．6．D【解析】【分析】先由△BCD绕点B逆时针旋转60°，得到△BAE，可知：BD=BE，∠DBE=60°，则可判断△BDE是等边三角形；根据等边三角形的性质得BA=BC，∠ABC=∠C=∠BAC=60°，再根据旋转的性质得到∠BAE=∠BCD=60°，从而得∠BAE=∠ABC=60°，根据平行线的判定方法即可得到AE∥BC；根据等边三角形的性质得∠BDE=60°，而∠BDC>60°，则可判断∠ADE≠∠BDC；由△BDE是等边三角形得到DE=BD=4，再利用△BCD绕点B逆时针旋转60°，得到△BAE，则AE=CD，△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD=10．【详解】∵△BCD绕点B逆时针旋转60°，得到△BAE，∴BD=BE，∠DBE=60°，∴△BDE是等边三角形，∴①正确；∵△ABC为等边三角形，∴BA=BC，∠ABC=∠C=∠BAC=60°，∵△BCD绕点B逆时针旋转60°，得到△BAE，∴∠BAE=∠BCD=60°，∴∠BAE=∠ABC，∴AE∥BC，∴②正确；∵△BDE是等边三角形，∴DE=BD=4，∵△BCD绕点B逆时针旋转60°，得到△BAE，∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD=6+4=10，∴③正确；∵△BDE是等边三角形，∴∠BDE=60°，∵∠BDC=∠BAC+∠ABD＞60°，∴∠ADE=180°-∠BDE-∠BDC＜60°，∴∠ADE≠∠BDC，∴④错误．故选D．【点睛】本题主要考查旋转得性质，等边三角形的判定和性质定理，掌握旋转的性质以及等边三角形的性质定理，是解题的关键．7．C【解析】【分析】连结AC，先由△AGH≌△ADH得到∠GHA＝∠AHD，进而得到∠AHD＝∠HAP，所以△AHP是等腰三角形，所以PH＝PA＝PC，所以∠HAC是直角，再在Rt△ABC中由勾股定理求出AC的长，然后由△HAC∽△ADC，根据＝求出AH的长，再根据△HAC∽△HDA求出DH的长，进而求得HP和AP的长，最后得到△APH的周长.【详解】∵P是CH的中点，PH＝PC，∵AH＝AH，AG＝AD，且AGH与ADH都是直角，∴△AGH≌△ADH，∴∠GHA＝∠AHD，又∵GHA＝HAP，∴∠AHD＝∠HAP，∴△AHP 是等腰三角形，∴PH＝PA＝PC，∴∠HAC是直角，在Rt△ABC中，AC＝＝10，∵△HAC∽△ADC，∴＝，∴AH＝＝＝7.5，又∵△HAC∽△HAD，＝，∴DH＝4.5，∴HP＝＝6.25，AP＝HP＝6.25，∴△APH的周长＝AP＋PH＋AH＝6.25＋6.25＋7.5＝20.【点睛】本题主要考查直角三角形的性质以及相似三角形的性质，解题的关键是清楚直角三角形斜边上的中线是斜边的一半以及会运用相似三角形线段成比例求出各边长的长.8．B【解析】【分析】由旋转的特性以及∠MBN=60°，可知△BMN是等边三角形，从而得出MN=BN，再由点到直线的所有线段中，垂线段最短可得出结论．【详解】由旋转的特性可知，BM=BN．又∵∠MBN=60°，∴△BMN为等边三角形，∴MN=BM．∵点M是高CH所在直线上的一个动点，∴当BM⊥CH时，MN最短（到直线的所有线段中，垂线段最短）．又∵△ABC为等边三角形，且AB=BC=CA=2，∴当点M和点H重合时，MN最短，且有MN=BM=BH=12AB=1．故选B．【点睛】本题考查了旋转的特性、垂线段最短以及等边三角形的判定与性质．解题的关键是：得到当BM⊥CH时，MN最短．9．A【解析】【分析】由旋转的性质可知，△ABC≌△ADE，DE＝BC，可得①正确；∠CAE＝∠CAB﹣∠BAE，∠DAB＝∠DAE﹣∠BAE，可得∠EAC＝∠DAB，可判定②正确；AE＝AC，则∠AEC＝∠C，再由∠C＝∠AED，可得∠AEC＝∠AED；可判定③正确；根据平行线的性质可得可得∠C ＝∠BED，∠AEC＝∠AED=∠C，根据平角的定义可得∠DEB＝60°；综上即可得答案．【详解】∵将△ABC绕点A旋转至△ADE的位置，使点E落在BC边上，∴△ABC≌△ADE，∴DE＝BC，AE=AC，∠BAC＝∠DAE，∠C＝∠AED，故①正确；∴∠CAE＝∠CAB﹣∠BAE，∠DAB＝∠DAE﹣∠BAE，∴∠EAC＝∠DAB；故②正确；∵AE＝AC，∴∠AEC＝∠C，∴∠AEC＝∠AED，∴EA平分∠DEC；故③正确；∵DE∥AC，∴∠C＝∠BED，∵∠AEC＝∠AED=∠C，∴∠DEB＝∠AEC＝∠AED =60°，故④正确；综上所述：正确的结论是①②③④，共4个，故选：A．【点睛】本题考查旋转的性质，旋转前、后的两个图形全等，对应边、对应角相等，对应点与旋转中心所连线段的夹角等于旋转角．10．B【解析】【分析】根据正边形的性质求出DM的长，再求得四边形ADMB′的面积，然后由旋转的性质求得阴影部分面积．【详解】解：设CD、B′C′相交于点M，连接AM，DM＝x，∵ABCD绕点A逆时针方向旋转30°后得到正方形AEFH，∴∠MAD＝30°，AM＝2x，在△ADM中，x2+3＝4x2，解得：x＝1，∴S ADMB′＝3，∴图中阴影部分面积为：3﹣3．故选：B．【点睛】本题要把旋转的性质和正方形的性质结合求解．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，注意方程思想的运用．11．（2，2）或（2，-1）【解析】∵抛物线y=x2-4x对称轴为直线x=-42 2-=∴设点A坐标为（2，m），如图所示，作AP⊥y轴于点P，作O′Q⊥直线x=2，∴∠APO=∠AQO′=90°，∴∠QAO′+∠AO′Q=90°，∵∠QAO′+∠OAQ=90°，∴∠AO′Q=∠OAQ，又∠OAQ=∠AOP，∴∠AO′Q=∠AOP，在△AOP和△AO′Q中，APO AQO AOP AO QAO AO ∠∠'⎧⎪∠∠'⎨⎪'⎩＝＝＝∴△AOP ≌△AO′Q （AAS ），∴AP=AQ=2，PO=QO′=m ，则点O′坐标为（2+m ，m-2），代入y=x 2-4x 得：m-2=（2+m ）2-4（2+m ），解得：m=-1或m=2，∴点A 坐标为（2，-1）或（2，2），故答案是：（2，-1）或（2，2）．【点睛】本题考查了坐标与图形的变换-旋转，全等三角形的判定与性质，函数图形上点的特征，根据全等三角形的判定与性质得出点O′的坐标是解题的关键．12．3【解析】【分析】先求出∠ACD =30°，进而可算出CE 、AD ，再算出△AEC 的面积．【详解】如图，由旋转的性质可知：AC =AC '，∵D 为AC '的中点，∴AD =1122AC AC ='， ∵ABCD 是矩形，∴AD ⊥CD ，∴∠ACD=30°，∵AB∥CD，∴∠CAB=30°，∴∠C'AB'=∠CAB=30°，∴∠EAC=30°，∴AE=EC，∴DE=1122AE EC=，∴CE=222 33CD AB==，DE=11 3AB=，AD=3，∴132AECS EC AD==nn．故答案为：3．【点睛】本题考查了旋转的性质、矩形的性质、直角三角形中30度角的性质，三角形面积计算等知识点，难度不大．清楚旋转的“不变”特性是解答的关键．13．15【解析】【分析】作A′H⊥y轴于H．证明△AOB≌△BHA′（AAS），推出OA＝BH，OB＝A′H，求出点A′坐标，再利用中点坐标公式求出点D坐标即可解决问题．【详解】作A′H⊥y轴于H．∵∠AOB＝∠A′HB＝∠ABA′＝90°，∴∠ABO＋∠A′BH＝90°，∠ABO＋∠BAO＝90°，∴∠BAO＝∠A′BH，∵BA＝BA′，∴△AOB≌△BHA′（AAS），∴OA＝BH，OB＝A′H，∵点A的坐标是（−2，0），点B的坐标是（0，6），∴OA＝2，OB＝6，∴BH＝OA＝2，A′H＝OB＝6，∴OH＝4，∴A′（6，4），∵BD＝A′D，∴D（3，5），∵反比例函数y＝kx的图象经过点D，∴k＝15．故答案为：15．【点睛】本题考查反比例函数图形上的点的坐标特征，坐标与图形的变化−旋转等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．14．6【解析】【分析】先确定正方形ABCD的边长AB＝6，则CE＝3，再利用勾股定理计算出EF＝5，根据旋转的性质得EF＝EH＝5，接着计算出CH＝4，从而可得到CH＝BF，于是可判定四边形BCHF 为矩形，然后利用矩形的性质确定FH的长．【详解】正方形ABCD的边长AB＝6,而BE＝3，则CE＝3,在Rt△BEF中，EF5==,∵△BEF绕点E顺时针旋转，得到△GEH,∴EF＝EH＝5,在Rt△EHC中，CH＝22-=,534∴CH＝BF＝4，∴四边形BCHF为矩形，∴FH＝BC＝6．故答案为6．【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．15．34【解析】【分析】首先由旋转的角度为15°，可知∠ACD1=45°..已知∠CAO=45°，即可得AO⊥CD1，然后可在Rt△AOC和Rt△AOD1中，通过解直角三角形求得AD1的长．【详解】解：如图，∵∠A=45°，∠D=30°，若旋转角度为15°，则∠ACO=30°+15°=45°，∴∠AOC=180°−∠ACO−∠CAO=90°，在等腰Rt△ABC中，AB=6，则AC=BC=32同理可得：AO=OC=3，在Rt△AOD1中，OA=3，OD1=CD1−OC=5，由勾股定理得：AD122+3435故答案为34．【点睛】此题主要考查了旋转的性质以及解直角三角形的综合应用，能够发现AO⊥OC是解决此题的关键．16．6532+【解析】【分析】延长ED到N，使得DN=DE，连接CN，BN，延长BN交AE于M．取BC的中点F，连接AF，OF．利用矩形的性质证明OD∥BN，推导出OB=OE，求出OF，AF即可解决问题．【详解】如图，延长ED到N，使得DN=DE，连接CN，BN，延长BN交AE于M．取BC的中点F，连接AF，OF．∵CD⊥EN，DN=DE，∴CN=CE，∵DC=DE，∠CDE=90°，∴∠DCE=∠DCN=45°，∴∠ACB=∠NCE=90°，∴∠BCN=∠ACE，在△BCN和△ACE中，CB CABCN ACECN CE=⎧⎪∠=∠⎨⎪=⎩，∴△BCN≌△ACE（SAS），∴∠BNC=∠AEC，∵∠BNC+∠CNM=180°，∴∠CNM+∠AEC=180°，∴∠ECN+∠NME=180°，∵∠ECN=90°，∴∠NME=90°，∵DH⊥AE，∴∠NME=∠DHE=90°，∴OD∥BN，∵DN=DE，∴OB=OE，∵BF=CF，∴OF=12 EC，∵CD=DE=6，∠CDE=90°，∴，∴，在Rt△ACF中，∵AC=12，CF=6，∴AF==∵OA≤AF+OF，∴，∴OA的最大值为．故答案为【点睛】本题考查旋转变换，等腰直角三角形的性质，三角形的中位线定理，全等三角形的判定和性质等知识，题目综合性较强，难度较大，属于中考填空题中的压轴题．解题的关键是学会添加常用辅助线，构造全等三角形解决问题，17．【解析】【分析】根据中位线定理和等腰直角三角形的判定证明△PMN是等腰直角三角形，求出MN=2BD，然后根据点D在AB上时，BD最小和点D在BA延长线上时，BD最大进行分析解答即可．【详解】∵点P，M分别是CD，DE的中点，∴PM=12CE，PM∥CE，∵点P，N分别是DC，BC的中点，∴PN=12BD，PN∥BD，∵△ABC，△ADE均为等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°，∴∠BAD=∠CAE，∴△ABD≌△ACE（SAS），∴BD=CE，∴PM=PN，∴△PMN是等腰三角形，∵PM∥CE，∴∠DPM=∠DCE，∵PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DB C=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形，∴PM=PN=12 BD，∴MN=2BD，∴点D在AB上时，BD最小，∴BD=AB-AD=4，MN的最小值；点D在BA延长线上时，BD最大，∴BD=AB+AD=10，MN的最大值为，∴线段MN的取值范围是故答案为：．【点睛】此题考查了旋转的性质，三角形中位线定理，全等三角形的判定和性质，等腰直角三角形的判定和性质等，关键是根据全等三角形的判定和等腰直角三角形的判定证明△PMN是等腰三角形．18．答案不唯一（例：先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位向下平移2个单位即可）．【解析】【分析】根据“平移”、“轴对称”和“旋转”的性质进行分析解答即可．【详解】解：根据题意，可按下列方式变换使点A与点E重合，点B与点D重合：（1）先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位，并向下平移2个单位即可；（2）先将△ABC向右平移2个单位，再向下平移2个单位，然后将所得△ABC绕点B顺时针旋转90°即可；……故答案为：本题答案不唯一，如：先将△ABC以点B为旋转中心顺时针旋转90，再将得到的图形向右平移2个单位向下平移2个单位即可．【点睛】本题考查熟悉“平移”、“轴对称”和“旋转”这三种图形变换的性质，并认真观察所给图形的位置特征，是正确解答这类题的关键．191【解析】【分析】连接BD 交AC 于O ，由菱形的性质得出2,60CD AB BCD BAD ==∠=∠=︒，1302ACD BAC BAD ∠=∠=∠=︒，,OA OC AC BD =⊥，由直角三角形的性质求出112OB AB ==，OA ==，得出AC =2,60AE AB EAG BAD ==∠=∠=︒，得出2CE AC AE =-=，证出90CPE ∠=︒，由直角三角形的性质得出112PE CE ==，3PC ==，即可得出结果．【详解】解：连接BD 交AC 于O ，如图所示：∵四边形ABCD 是菱形，∴2,60CD AB BCD BAD ==∠=∠=︒， 1302ACD BAC BAD ∠=∠=∠=︒，,OA OC AC BD =⊥， ∴112OB AB ==，∴OA ==，∴AC =由旋转的性质得：2,60AE AB EAG BAD ==∠=∠=︒，∴2CE AC AE =-=，∵四边形AEFG 是菱形，∴EF AG ∕∕，∴60CEP EAG ∠=∠=︒，∴90CEP ACD ∠+∠=︒∴90CPE ∠=︒， ∴1312PE CE ==-，333PC PE ==-， ∴2(33)31DP CD PC =-=--=-；故答案为：31-．【点睛】考核知识点：菱形性质，旋转性质.解直角三角形是关键.20．7+ 1537. 【解析】【分析】先画出图形，过点B 作E′C 的垂线交其延长线于F 点，过点D′作CM 的垂线交CM 于H 点，过A 点作CM 的垂线交其延长线于G 点．在Rt △BFC 求出BF ，再在△BE′F 用“面积法”求CN ，证明△ACG ≌△BCN ，△CD′H ≌△CE′N ，将有关线段转化，可求CM ，从而可求MN ．【详解】解：如图，若将△DCE 绕点C 顺时针旋转60°得到△D′CE′，过点B 作E′C 的垂线交其延长线于F 点，过点D′作CM 的垂线交CM 于H 点，过A 点作CM 的垂线交其延长线于G 点．∵∠ACD′=60°，∠ACB=∠D′CE′=90°，∴∠BCE′=360°-∠ACD′-∠ACB-∠D′CE′=120°．∴∠BCF=180°-∠BCE′=60°，∴∠FBC=30°，∴FC=5，∴BF= =，∴S △BCE′=12BF•CE′= 162⨯⨯= ∵∠ACG+∠BCN=90°，∠BCN+∠CBN=90°，∴∠ACG=∠CBN ，又∵AC=BC ，∴Rt △ACG ≌Rt △CBN ，∴AG=CN ，CG=BN ．同理△CD′H ≌△E′CN ，D′H=CN ，CH=NE′．∴AG=D′H ，在△AMG 和△D′MH 中，90AGM D HM AMG D MHAG D H ︒⎧∠=∠=⎪∠=∠''⎨='⎪⎩， ∴△AMG ≌△D′MH ，∴HM=MG ，∴M 为GH 中点，CM= ()111()222CG CH NB NE BE ''+=+=，又∵BF= ，∠BCF=60°，∴CF=5，FE′=CF+CE′=11，∴14==，∴CM=12BE′=7．又∵S △BCE′=12CN•BE′， ∴CN=2S △BCE′÷BE′= 7∴MN=CM+CN=7+ .故答案是：7+ 153.【点睛】本题考查了旋转的性质、三角形全等的判定和性质、勾股定理的运用，通过作辅助线构造全等三角形是解题的关键．21．（1）①②③；（2）①655=PB或1855；②PB长的最小值是333-，最大值是333+．【解析】【分析】(1)①由条件证明△ABD≌△ACE，就可以得到结论②由△ABD≌△ACE就可以得出∠ABD=∠ACE，就可以得出∠BDC=90°，进而得出结论；③由条件知∠ABC=∠ABD+∠DBC=45°，由∠ABD=∠ACE就可以得出结论；④△BDE为直角三角形就可以得出BE2=BD2+DE2，由△DAE和△BAC是等腰直角三角形就有DE2=2AD2，BC2=2AB2，就有BC2=BD2+CD2≠B D2就可以得出结论．(2)①分两种情形a、如图2中，当点E在AB上时，BE=AB-AE=3，由△PEB∽△AEC，得PB BEAC EC=，由此即可解决问题．b、如图3中，当点E在BA延长线上时，BE=9，解法类似；②a、如图4中，以A为圆心AD为半径画圆，当CE在⊙A上方与⊙A相切时，PB的值最大．b、如图5中，以A为圆心AD为半径画圆，当CE在⊙A下方与⊙A相切时，PB的值最小，分别求出PB即可．【详解】(1)解：如图甲：①∵∠BAC=∠DAE=90°，∴∠BAC+∠DAC=∠DAE+∠DAC ，即∠BAD=∠CAE ．在△ABD 和△ACE 中，AD AE BAD CAE AB AC ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABD ≌△ACE(SAS)，∴BD=CE ，∴①正确；②∵△ABD ≌△ACE ，∴∠ABD=∠ACE ．∵∠CAB=90°，∴∠ABD+∠AFB=90°，∴∠ACE+∠AFB=90°．∵∠DFC=∠AFB ，∴∠ACE+∠DFC=90°，∴∠FDC=90°．∴BD ⊥CE ，∴②正确；③∵∠BAC=90°，AB=AC ，∴∠ABC=45°，∴∠ABD+∠DBC=45°．∴∠ACE+∠DBC=45°，∴③正确；④∵BD ⊥CE ，∴BE 2=BD 2+DE 2，∵∠BAC=∠DAE=90°，AB=AC ，AD=AE ，∴DE 2=2AD 2，BC 2=2AB 2，∵BC 2=BD 2+CD 2≠BD 2，∴2AB 2=BD 2+CD 2≠BD 2，∴BE 2≠2(AD 2+AB 2)，∴④错误．故答案为①②③．(2)①解：a ．如图2中，当点E 在AB 上时，3=-=BE AB AE ．∵90∠︒=EAC ， ∴2222335CE AE AC 6=+=+=，同(1)可证△≌△ADB AEC ，∴∠=∠DBA ECA ，∵∠=∠PEB AEC ，∴△∽△PEB AEC ，∴=PB BE AC EC， ∴635=PB ， ∴65PB =； b ．如图3中，当点E 在BA 延长线上时，639BE AB AE =+=+=,∵90∠︒=EAC ，∴22226353CE AE AC =+=+=，同(1)可证△≌△ADB AEC ，∴∠=∠DBA ECA ，∵∠=∠BEP CEA ，∴△∽△PEB AEC ，∴=BP BE AC EC， ∴635=BP ， ∴185=PB ，综上，65=PB 或185； ②解：a ．如图4中，以A 为圆心AD 为半径画圆，当CE 在A e 下方与A e 相切时，PB 的值最小．理由：此时BCE ∠最小，由(1)可知PBC V 是直角三角形，斜边BC 为定值，BCE ∠最小，因此PB 最小，∵⊥AE EC ， ∴22226333EC AC AE =-=-=，由(1)可知，ABD ACE △≌△，∴90∠=∠=︒ADB AEC ，33==BD CE∴90∠=∠=∠=︒ADP DAE AEP ，且AD=AE=3，∴四边形AEPD 是正方形，∴3==PD AE ，∴333=-=PB BD PD ；b ．如图5中，以A 为圆心AD 为半径画圆，当CE 在A e 上方与A e 相切时，PB 的值最大．理由：此时BCE ∠最大，因此PB 最大，(同理，PBC V 是直角三角形，斜边BC 为定值，BCE ∠最大，因此PB 最大)∵⊥AE EC ， ∴2233-=EC AC AE ，由(1)可知，ABD ACE △≌△，∴90∠=∠=︒ADB AEC ，33==BD CE∴90∠=∠=∠=︒ADP DAE AEP ，且AD=AE=3，∴四边形AEPD 是正方形，∴3==PD AE ， ∴333=+=PB BD PD ．综上所述，PB 长的最小值是333，最大值是333．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质、旋转变换、全等三角形的判定和性质、相似三角形的判定和性质、圆的有关知识，解题的关键是灵活运用这些知识解决问题，学会分类讨论的思想思考问题，学会利用图形的特殊位置解决最值问题，属于中考压轴题．22．（1）90°；（2）△BCE ≌△DCF ，对应角为：∠CBE 与∠CDF ，∠BCE 与∠DCF ，∠BEC 与∠DFC ；（3）70°．【解析】试题分析：（1）根据正方形的性质得CB=CA ，∠BCA=90°，然后根据旋转的定义得到△BEC绕点C 顺时针旋转得到△DFC 的最小旋转度数为90°；（2）根据旋转的性质得△BCE ≌△DCF ，再根据全等的性质写出对应角；（3）先根据三角形内角和定理计算出∠BEC=70°，然后根据（2）中的结论求解．试题解析：（1）∵四边形ABCD 为正方形，∴CB=CA，∠BCA=90°，∴△BEC绕点C顺时针旋转90°可得到△DFC，∴最小旋转度数为90°；（2）△BCE≌△DCF，对应角为：∠CBE与∠CDF，∠BCE与∠DCF，∠BEC与∠DFC；（3）∵∠EBC=30°，∠BCE=80°，∴∠BEC=180°-30°-80°=70°，∴∠F=∠BEC=70°．23．（1）见解析；（2【解析】【分析】(1)根据AC=BC、∠DCE+∠ACD=∠ACB+∠ACD、CE=CD证△ACE≌△BCD即可；(2)连接DE，可得△DCE是等边三角形，即∠CDE=60°、DC=DE，继而在Rt△ADE中，由勾股定理可得DE的长，即可求得CD．【详解】(1)∵△ABC是等边三角形，∴AC=BC，∠ACB=60°，由旋转的性质可得：CE=CD，∠DCE=60°，∴∠DCE+∠ACD=∠ACB+∠ACD，即∠ACE=∠BCD．在△ACE和△BCD中，∵AC BCACE BCDCE CD=⎧⎪∠=∠⎨⎪=⎩，∴△ACE≌△BCD(SAS)，∴AE=BD；(2)连接DE．∵CD=CE ，∠DCE=60°，∴△DCE 是等边三角形．∴∠CDE=60°，DC=DE ．∵∠ADC=30°，∴∠ADC+∠CDE=90°．∵AD=3，2，∴2．在Rt △ADE 中，由勾股定理，可得()222242323DE AE AD =-=-= ∴23【点睛】本题主要考查旋转的性质、全等三角形的判定与性质及勾股定理的应用，连接DE 发现等边三角形与直角三角形是解题的关键．24．（1）画图见解析；（2）∠PP′C ＝30°. 【解析】【分析】（1）如图，作∠PAP ′=50°，且AP=AP′，连接PP′，△ACP′即为所求；（2），连接PP′，由旋转的性质可得，∠PAP′＝∠BAC ＝50°，AP ＝AP′，△ABP ≌△ACP′，根据等腰三角形的性质及三角形的内角和定理可得∠APP′＝∠AP′P ＝65°，根据全等三角形的性质可得∠AP′C ＝∠APB ，在△ABC 中，∠BAC ＝50°，AB ＝AC ，可求得∠B ＝65°，再由∠BAP ＝20°，根据三角形的内角和定理求得∠APB ＝95°＝∠AP′C ，所以∠PP′C ＝∠AP′C －∠AP′P ＝30°. 【详解】(1)旋转后的△ACP′如图所示．(2)如图，连接PP′.由旋转可得，∠PAP′＝∠BAC＝50°，AP＝AP′，△ABP≌△ACP′，∴∠APP′＝∠AP′P＝65°，∠AP′C＝∠APB，∵∠BAC＝50°，AB＝AC，∴∠B＝65°，又∵∠BAP＝20°，∴∠APB＝95°＝∠AP′C，∴∠PP′C＝∠AP′C－∠AP′P＝95°－65°＝30°.【点睛】本题主要考查了旋转的性质，熟练运用旋转的性质、等腰三角形的性质及三角形的内角和定理是解决本题的关键.25．5【解析】【分析】（1）如图1中，由此EG交CD于H，则四边形FGHD是矩形．在Rt△CGH中，利用勾股定理即可解决问题；（2）如图2中，作FP⊥AD于P．利用勾股定理相似三角形的性质，分别求出CG、DF即可解决问题；（3）成立．连接AG、AC．只要证明△ADF∽△ACG，可得45DF ADCG AC==即可解决问题；（4）在图4中，通过计算即可解决问题；【详解】（1）如图1中，由此EG交CD于H，则四边形FGHD是矩形．在Rt△CGH中，GH=DF=4，CH=DH=AE=3，∴CG=22CH GH+=5．故答案为：5．（2）如图2中，作FP⊥AD于P．在矩形AEGF中，∵AE=3，EG=4，∴AG=5，BG=AB-AG=1，在Rt△CBG中，CG=228165+=，由△APF∽△AEG，可得AP PE AF AE EG AG==，∴4 345 AP PF==，∴AP=125，PF=165，DP=AD﹣AP=8﹣122855=，在Rt△PDF中，DF=22PD PF+=22465 5PD PF+=，∴DF=45 CG．（3）成立．理由如下：连接AG、AC．由旋转可知：∠DAF=∠CAG，由勾股定理可知：2210AD CD+=，AG=5，∵84105ADAC==，45AFAG=，。

专题11 图形的变换-2020年中考数学真题分专题训练(浙江专版)(教师版含解析)

专题11图形的变换1.【2020年浙江省杭州市中考数学试卷】如图是一张矩形纸片，点E在AB边上，把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，连接DF．若点E，F，D在同一条直线上，AE＝2，则DF＝2，BE＝﹣1．【分析】根据矩形的性质得到AD＝BC，∠ADC＝∠B＝∠DAE＝90°，根据折叠的性质得到CF＝BC，∠CFE＝∠B＝90°，EF＝BE，根据全等三角形的性质得到DF＝AE＝2；根据相似三角形的性质即可得到结论．【解答】解：∵四边形ABCD是矩形，∴AD＝BC，∠ADC＝∠B＝∠DAE＝90°，∵把△BCE沿直线CE对折，使点B落在对角线AC上的点F处，∴CF＝BC，∠CFE＝∠B＝90°，EF＝BE，∴CF＝AD，∠CFD＝90°，∴∠ADE+∠CDF＝∠CDF+∠DCF＝90°，∴∠ADF＝∠DCF，∴△ADE≌△FCD(ASA)，∴DF＝AE＝2；∵∠AFE＝∠CFD＝90°，∴∠AFE＝∠DAE＝90°，∵∠AEF＝∠DEA，∴△AEF∽△DEA，∴，∴＝，∴EF＝﹣1(负值舍去)，∴BE＝EF＝﹣1，故答案为：2，﹣1．2.【2020年浙江省湖州市中考数学试卷】七巧板是我国祖先的一项卓越创造，流行于世界各地．由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板，如图1所示．分别用这两副七巧板试拼如图2中的平行四边形或矩形，则这两个图形中，中国七巧板和日本七巧板能拼成的个数分别是()A．1和1B．1和2C．2和1D．2和2【分析】根据要求拼平行四边形矩形即可．【解答】解：中国七巧板和日本七巧板能拼成的个数都是2，如图所示：故选：D．3.【2020年浙江省湖州市中考数学试卷】已知在△ABC中，AC＝BC＝m，D是AB边上的一点，将∠B沿着过点D的直线折叠，使点B落在AC 边的点P处(不与点A，C重合)，折痕交BC边于点E．(1)特例感知如图1，若∠C＝60°，D是AB的中点，求证：AP＝AC；(2)变式求异如图2，若∠C＝90°，m＝6，AD＝7，过点D作DH⊥AC于点H，求DH和AP的长；(3)化归探究如图3，若m＝10，AB＝12，且当AD＝a时，存在两次不同的折叠，使点B落在AC边上两个不同的位置，请直接写出a的取值范围．【分析】(1)证明△ADP是等边三角形即可解决问题．(2)分两种情形：情形一：当点B落在线段CH上的点P1处时，如图2﹣1中．情形二：当点B落在线段AH上的点P2处时，如图2﹣2中，分别求解即可．(3)如图3中，过点C作CH⊥AB于H，过点D作DP⊥AC于P．求出DP＝DB时AD的值，结合图形即可判断．【解答】(1)证明：∵AC＝BC，∠C＝60°，∴△ABC是等边三角形，∴AC＝AB，∠A＝60°，由题意，得DB＝DP，DA＝DB，∴DA＝DP，∴△ADP使得等边三角形，∴AP＝AD＝AB＝AC．(2)解：∵AC＝BC＝6，∠C＝90°，∴AB＝＝＝12，∵DH⊥AC，∴DH∥BC，∴△ADH∽△ABC，∴＝，∵AD＝7，∴＝，∴DH＝，将∠B沿过点D的直线折叠，情形一：当点B落在线段CH上的点P1处时，如图2﹣1中，∵AB＝12，∴DP1＝DB＝AB﹣AD＝5，∴HP1＝＝＝，∴A1＝AH+HP1＝4，情形二：当点B落在线段AH上的点P2处时，如图2﹣2中，同法可证HP2＝，∴AP2＝AH﹣HP2＝3，综上所述，满足条件的AP的值为4或3．(3)如图3中，过点C作CH⊥AB于H，过点D作DP⊥AC于P．∵CA＝CB，CH⊥AB，∴AH＝HB＝6，∴CH＝＝＝8，当DB＝DP时，设BD＝PD＝x，则AD＝12﹣x，∵tan A＝＝，∴＝，∴x＝，∴AD＝AB﹣BD＝，观察图形可知当6≤a＜时，存在两次不同的折叠，使点B落在AC边上两个不同的位置．4.【2020年浙江省嘉兴、舟山市中考数学试卷】如图，正三角形ABC的边长为3，将△ABC绕它的外心O逆时针旋转60°得到△A'B'C'，则它们重叠部分的面积是()A．2B．C．D．【分析】根据重合部分是正六边形，连接O和正六边形的各个顶点，所得的三角形都是全等的等边三角形，据此即可求解．解：作AM⊥BC于M，如图：重合部分是正六边形，连接O和正六边形的各个顶点，所得的三角形都是全等的等边三角形．∵△ABC是等边三角形，AM⊥BC，∴AB＝BC＝3，BM＝CM＝BC＝，∠BAM＝30°，∴AM＝BM＝，∴△ABC的面积＝BC×AM＝×3×＝，∴重叠部分的面积＝△ABC的面积＝×＝；故选：C．5.【2020年浙江省嘉兴、舟山市中考数学试卷】如图，有一张矩形纸条ABCD，AB＝5cm，BC＝2cm，点M，N分别在边AB，CD上，CN＝1cm．现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上．当点B'恰好落在边CD上时，线段BM 的长为cm；在点M从点A运动到点B的过程中，若边MB'与边CD交于点E，则点E相应运动的路径长为(﹣)cm．【分析】第一个问题证明BM＝MB′＝NB′，求出NB即可解决问题．第二个问题，探究点E的运动轨迹，寻找特殊位置解决问题即可．解：如图1中，∵四边形ABCD是矩形，∴AB∥CD，∴∠1＝∠3，由翻折的性质可知：∠1＝∠2，BM＝MB′，∴∠2＝∠3，∴MB′＝NB′，∵NB′＝＝＝(cm)，∴BM＝NB′＝(cm)．如图2中，当点M与A重合时，AE＝EN，设AE＝EN＝xcm，在Rt△ADE中，则有x2＝22+(4﹣x)2，解得x＝，∴DE＝4﹣＝(cm)，如图3中，当点M运动到MB′⊥AB时，DE′的值最大，DE′＝5﹣1﹣2＝2(cm)，如图4中，当点M运动到点B′落在CD时，DB′(即DE″)＝5﹣1﹣＝(4﹣)(cm)，∴点E的运动轨迹E→E′→E″，运动路径＝EE′+E′B′＝2﹣+2﹣(4﹣)＝(﹣)(cm)．故答案为，(﹣)．6.【2020年浙江省嘉兴、舟山市中考数学试卷】在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合(如图1)，其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并进行如下研究活动．活动一：将图1中的纸片DEF沿AC方向平移，连结AE，BD(如图2)，当点F与点C重合时停止平移．【思考】图2中的四边形ABDE是平行四边形吗？请说明理由．【发现】当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形(如图3)．求AF的长．活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90)，连结OB，OE(如图4)．【探究】当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．【分析】【思考】由全等三角形的性质得出AB＝DE，∠BAC＝∠EDF，则AB∥DE，可得出结论；【发现】连接BE交AD于点O，设AF＝x(cm)，则OA＝OE＝(x+4)，得出OF＝OA﹣AF＝2﹣x，由勾股定理可得，解方程求出x，则AF可求出；【探究】如图2，延长OF交AE于点H，证明△EFO≌△EFH(ASA)，得出EO＝EH，FO＝FH，则∠EHO＝∠EOH ＝∠OBD＝∠ODB，可证得△EOH≌△OBD(AAS)，得出BD＝OH，则结论得证．解：【思考】四边形ABDE是平行四边形．证明：如图，∵△ABC≌△DEF，∴AB＝DE，∠BAC＝∠EDF，∴AB∥DE，∴四边形ABDE是平行四边形；【发现】如图1，连接BE交AD于点O，∵四边形ABDE为矩形，∴OA＝OD＝OB＝OE，设AF＝x(cm)，则OA＝OE＝(x+4)，∴OF＝OA﹣AF＝2﹣x，在Rt△OFE中，∵OF2+EF2＝OE2，∴，解得：x＝，∴AF＝cm．【探究】BD＝2OF，证明：如图2，延长OF交AE于点H，∵四边形ABDE为矩形，∴∠OAB＝∠OBA＝∠ODE＝∠OED，OA＝OB＝OE＝OD，∴∠OBD＝∠ODB，∠OAE＝∠OEA，∴∠ABD+∠BDE+∠DEA+∠EAB＝360°，∴∠ABD+∠BAE＝180°，∴AE∥BD，∴∠OHE＝∠ODB，∵EF平分∠OEH，∴∠OEF＝∠HEF，∵∠EFO＝∠EFH＝90°，EF＝EF，∴△EFO≌△EFH(ASA)，∴EO＝EH，FO＝FH，∴∠EHO＝∠EOH＝∠OBD＝∠ODB，∴△EOH≌△OBD(AAS)，∴BD＝OH＝2OF．7.【2020年浙江省丽水市中考数学试卷】下列四个图形中，是中心对称图形的是()A．B．C．D．【分析】根据中心对称图形的概念对各图形分析判断即可得解．【解答】解：A、该图形不是中心对称图形，故本选项不合题意；B、该图形不是中心对称图形，故本选项不合题意；C、该图形是中心对称图形，故本选项符合题意；D、该图形不是中心对称图形，故本选项不合题意；故选：C．8.【2020年浙江省丽水市中考数学试卷】如图，工人师傅用角尺画出工件边缘AB的垂线a和b，得到a∥b．理由是()A．连结直线外一点与直线上各点的所有线段中，垂线段最短B．在同一平面内，垂直于同一条直线的两条直线互相平行C．在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线D．经过直线外一点，有且只有一条直线与这条直线平行【分析】根据垂直于同一条直线的两条直线平行判断即可．【解答】解：由题意a⊥AB，b⊥AB，∴a∥b(垂直于同一条直线的两条直线平行)，故选：B．9.【2020年浙江省丽水市中考数学试卷】如图，平移图形M，与图形N可以拼成一个平行四边形，则图中α的度数是30°．【分析】根据平行四边形的性质解答即可．【解答】解：∵四边形ABCD是平行四边形，∴∠D＝180°﹣∠C＝60°，∴∠α＝180°﹣(540°﹣70°﹣140°﹣180°)＝30°，故答案为：30．10.【2020年浙江省丽水市中考数学试卷】图1是一个闭合时的夹子，图2是该夹子的主视示意图，夹子两边为AC，BD(点A与点B重合)，点O 是夹子转轴位置，OE⊥AC于点E，OF⊥BD于点F，OE＝OF＝1cm，AC＝BD＝6cm，CE＝DF，CE：AE＝2：3．按图示方式用手指按夹子，夹子两边绕点O转动．(1)当E，F两点的距离最大时，以点A，B，C，D为顶点的四边形的周长是16cm．(2)当夹子的开口最大(即点C与点D重合)时，A，B两点的距离为cm．【分析】(1)当E，F两点的距离最大时，E，O，F共线，此时四边形ABCD是矩形，求出矩形的长和宽即可解决问题．(2)如图3中，连接EF交OC于H．想办法求出EF，利用平行线分线段成比例定理即可解决问题．【解答】解：(1)当E，F两点的距离最大时，E，O，F共线，此时四边形ABCD是矩形，∵OE＝OF＝1cm，∴EF＝2cm，∴AB＝CD＝2cm，∴此时四边形ABCD的周长为2+2+6+6＝16(cm)，故答案为16．(2)如图3中，连接EF交OC于H．由题意CE＝CF＝×6＝(cm)，∵OE＝OF＝1cm，∴CO垂直平分线段EF，∵OC＝＝＝(cm)，∵•OE•EC＝•CO•EH，∴EH＝＝(cm)，∴EF＝2EH＝(cm)∵EF∥AB，∴＝＝，∴AB＝×＝(cm)．故答案为．11.【2020年浙江省丽水市中考数学试卷】如图，在△ABC中，AB＝4，∠B＝45°，∠C＝60°．(1)求BC边上的高线长．(2)点E为线段AB的中点，点F在边AC上，连结EF，沿EF将△AEF折叠得到△PEF．①如图2，当点P落在BC上时，求∠AEP的度数．②如图3，连结AP，当PF⊥AC时，求AP的长【分析】(1)如图1中，过点A作AD⊥BC于D．解直角三角形求出AD即可．(2)①证明BE＝EP，可得∠EPB＝∠B＝45°解决问题．②如图3中，由(1)可知：AC＝＝，证明△AEF∽△ACB，推出＝，由此求出AF 即可解决问题．【解答】解：(1)如图1中，过点A作AD⊥BC于D．在Rt△ABD中，AD＝AB•sin45°＝4×＝4．(2)①如图2中，∵△AEF≌△PEF，∴AE＝EP，∵AE＝EB，∴BE＝EP，∴∠EPB＝∠B＝45°，∴∠PEB＝90°，∴∠AEP＝180°﹣90°＝90°．②如图3中，由(1)可知：AC＝＝，∵PF⊥AC，∴∠PF A＝90°，∵△AEF≌△PEF，∴∠AFE＝∠PFE＝45°，∴∠AFE＝∠B，∵∠EAF＝∠CAB，∴△AEF∽△ACB，∴＝，即＝，∴AF＝2，在Rt△AFP，AF＝FP，∴AP＝AF＝2．12.【2020年浙江省绍兴市中考数学试卷】将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是()A．B．C．D．【分析】根据中心对称的定义，结合所给图形即可作出判断．【解答】解：A、不是中心对称图形，故本选项不符合题意；B、不是中心对称图形，故本选项不符合题意；C、不是中心对称图形，故本选项不符合题意；D、是中心对称图形，故本选项符合题意．故选：D．13.【2020年浙江省绍兴市中考数学试卷】如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B运动，移动到点B停止，延长EO 交CD于点F，则四边形AECF形状的变化依次为()A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形【分析】根据对称中心的定义，根据矩形的性质，可得四边形AECF形状的变化情况．【解答】解：观察图形可知，四边形AECF形状的变化依次为平行四边形→菱形→平行四边形→矩形．故选：B．14.【2020年浙江省绍兴市中考数学试卷】如图，等腰直角三角形ABC中，∠ABC＝90°，BA＝BC，将BC绕点B顺时针旋转θ(0°＜θ＜90°)，得到BP，连结CP，过点A作AH⊥CP交CP的延长线于点H，连结AP，则∠P AH的度数()A．随着θ的增大而增大B．随着θ的增大而减小C．不变D．随着θ的增大，先增大后减小【分析】由旋转的性质可得BC＝BP＝BA，由等腰三角形的性质和三角形内接和定理可求∠BPC+∠BP A＝135°＝∠CP A，由外角的性质可求∠P AH＝135°﹣90°＝45°，即可求解．【解答】解：∵将BC绕点B顺时针旋转θ(0°＜θ＜90°)，得到BP，∴BC＝BP＝BA，∴∠BCP＝∠BPC，∠BP A＝∠BAP，∵∠CBP+∠BCP+∠BPC＝180°，∠ABP+∠BAP+∠BP A＝180°，∠ABP+∠CBP＝90°，∴∠BPC+∠BP A＝135°＝∠CP A，∵∠CP A＝∠AHC+∠P AH＝135°，∴∠P AH＝135°﹣90°＝45°，∴∠P AH的度数是定值，故选：C．15.【2020年浙江省绍兴市中考数学试卷】如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙)，则图2中阴影部分面积为4．【分析】根据题意和图形，可以得到直角三角形的一条直角边的长和斜边的长，从而可以得到直角三角形的另一条直角边长，再根据图形，可知阴影部分的面积是四个直角三角形的面积，然后代入数据计算即可．【解答】解：由题意可得，直角三角形的斜边长为3，一条直角边长为2，故直角三角形的另一条直角边长为：＝，故阴影部分的面积是：＝4，故答案为：4．16.【2020年浙江省绍兴市中考数学试卷】将两条邻边长分别为，1的矩形纸片剪成四个等腰三角形纸片(无余纸片)，各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是下列数中的①②③④(填序号)．①，②1，③﹣1，④，⑤．【分析】首先作出图形，再根据矩形的性质和等腰三角形的判定即可求解．【解答】解：如图所示：则其中一个等腰三角形的腰长可以是①，②1，③﹣1，④，不可以是．故答案为：①②③④．17.【2020年浙江省绍兴市中考数学试卷】如图1，矩形DEFG中，DG＝2，DE＝3，Rt△ABC中，∠ACB＝90°，CA＝CB＝2，FG，BC的延长线相交于点O，且FG⊥BC，OG＝2，OC＝4．将△ABC绕点O逆时针旋转α(0°≤α＜180°)得到△A′B′C′．(1)当α＝30°时，求点C′到直线OF的距离．(2)在图1中，取A′B′的中点P，连结C′P，如图2．①当C′P与矩形DEFG的一条边平行时，求点C′到直线DE的距离．②当线段A′P与矩形DEFG的边有且只有一个交点时，求该交点到直线DG的距离的取值范围．【分析】(1)如图1中，过点C′作C′H⊥OF于H．解直角三角形求出CH即可．(2)①分两种情形：如图2中，当C′P∥OF时，过点C′作C′M⊥OF于M．如图3中，当C′P∥DG 时，过点C′作C′N⊥FG于N．分别求出C′M，C′N即可．②设d为所求的距离．第一种情形：如图4中，当点A′落在DE上时，连接OA′，延长ED交OC于M．如图5中，当点P落在DE上时，连接OP，过点P作PQ⊥C′B′于Q．结合图象可得结论．第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝2﹣2，即d＝2﹣2，如图6中，当点P落在EF上时，设OF交A′B′于Q，过点P作PT⊥B′C′于T，过点P作PR∥OQ交OB′于R，连接OP．求出QG可得结论．第三种情形：当A′P经过点F时，如图7中，显然d＝3．综上所述可得结论．【解答】解：(1)如图1中，过点C′作C′H⊥OF于H．∵∠HC′O＝α＝30°，∴C′H＝C′O•cos30°＝2，∴点C′到直线OF的距离为2．(2)①如图2中，当C′P∥OF时，过点C′作C′M⊥OF于M．∵C′P∥OF，∴∠O＝180°﹣∠OC′P＝45°，∴△OC′M是等腰直角三角形，∵OC′＝4，∴C′M＝2，∴点C′到直线DE的距离为2．如图3中，当C′P∥DG时，过点C′作C′N⊥FG于N．同法可证△OC′N是等腰直角三角形，∴′N＝2，∴点C′到直线DE的距离为2+2．②设d为所求的距离．第一种情形：如图4中，当点A′落在DE上时，连接OA′，延长ED交OC于M．∵OA′＝2，OM＝2，∠OMA′＝90°，∴A′M＝＝＝4，∴A′D＝2，即d＝2，如图5中，当点P落在DE上时，连接OP，过点P作PQ⊥C′B′于Q．∵PQ＝1，OQ＝5，∴OP＝＝，∴PM＝＝，∴PD＝﹣2，∴d＝﹣2，∴2≤d≤﹣2．第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝2﹣2，即d＝2﹣2，如图6中，当点P落在EF上时，设OF交A′B′于Q，过点P作PT⊥B′C′于T，过点P作PR∥OQ 交OB′于R，连接OP．∵OP＝，OF＝5，∴FP＝＝＝1，∵OF＝OT，PF＝PT，∠F＝∠PTO＝90°，∴Rt△OPF≌Rt△OPT(HL)，∴∠FOP＝∠TOP，∵PQ∥OQ，∴∠OPR＝∠POF，∴∠OPR＝∠POR，∴OR＝PR，∵PT2+TR2＝PR2，∴12+(5﹣PR)2＝PR2，∴PR＝2.6，RT＝2.4，∵△B′PR∽△B′QO，∴＝，∴＝，∴OQ＝，∴QG＝OQ﹣OG＝，即d＝∴2﹣2≤d＜，第三种情形：当A′P经过点F时，如图7中，显然d＝3．综上所述，2≤d≤﹣2或d＝3．18.【2020年浙江省宁波市中考数学试卷】图1，图2都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影．请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影：(1)使得4个阴影小等边三角形组成一个轴对称图形．(2)使得4个阴影小等边三角形组成一个中心对称图形．(请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形)【答案】(1)见解析；(2)见解析【解析】【分析】(1)根据轴对称图形的定义画出图形构成一个大的等边三角形即可(答案不唯一)．(2)根据中心对称图形的定义画出图形构成一个平行四边形即可(答案不唯一)．【详解】解：(1)轴对称图形如图1所示．(2)中心对称图形如图2所示．【点睛】本题考查利用中心对称设计图案，利用轴对称设计图案，解题的关键是理解题意，灵活运用所学知识解决问题．19.【2020年浙江省台州市中考数学试卷】如图，把△ABC先向右平移3个单位，再向上平移2个单位得到△DEF，则顶点C(0，-1)对应点的坐标为()A. (0，0)B. (1，2)C. (1，3)D. (3，1)【答案】D【解析】【分析】先找到顶点C的对应点为F，再根据直角坐标系的特点即可得到坐标．【详解】∵顶点C的对应点为F，由图可得F的坐标为(3，1)，故选D．【点睛】此题主要考查坐标与图形，解题的关键是熟知直角坐标系的特点．20.【2020年浙江省台州市中考数学试卷】把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为2cm的等腰直角三角形，则纸片的长AD(单位：cm)为()A. 7+B. 7+C. 8+D. 8+【答案】D【解析】【分析】如图，过点M作MH⊥A'R于H，过点N作NJ⊥A'W于J．想办法求出AR，RM，MN，NW，WD即可解决问题．【详解】解：如图，过点M作MH⊥A'R于H，过点N作NJ⊥A'W于J．由题意△EMN 是等腰直角三角形，EM=EN=2，MN=∵四边形EMHK 是矩形，∴EK= A'K=MH=1，KH=EM=2，∵△RMH 是等腰直角三角形，∴RH=MH=1，，同法可证，题意AR=R A'= A'W=WD=4，∴++4=8+故答案为：D.【点睛】本题考查翻折变换，等腰直角三角形的判定和性质，矩形的性质等知识，解题的关键是学会添加常用辅助线，构造特殊三角形或特殊四边形解决问题．21.【2020年浙江省台州市中考数学试卷】用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案，每块大正方形地砖面积为a ，小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD ．则正方形ABCD 的面积为____________(用含a ，b 的代数式表示)．【答案】+a b【解析】【分析】如图，连接AE 、AF ，先证明△GAE ≌△HAF ，由此可证得AEF GAHE S S =△四边形，进而同理可得，根据正方形ABCD 的面积等于四个相同四边形的面积之和及小正方形的面积即可求得答案．【详解】解：如图，连接AE 、AF ，∵点A 为大正方形的中心，△AE =AF ，△EAF =90°，△△AEF =△AFE =45°，△△GEF =90°，△△AEG =△GEF -△AEF =45°，△△AEG =△AFE ，∵四边形ABCD 为正方形，∴△DAB =△EAF =90°，∴∠GAE =△HAF ，在△GAE 与△HAF 中，GAE HAF AE AF AEG AFH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△GAE ≌△HAF (ASA )，∴GAE HAF S S =△△，∴GAE AEH HAF AEH S S S S +=+△△△△，即AEF GAHE S S =△四边形， △11=44AEF S S a =△大正方形， ∴11=44GAHE S S a =四边形大正方形， ∴同理可得：1=44ABCD S a b ⨯+正方形，即=ABCD S a b +正方形，故答案为：+a b ．【点睛】本题考查了正方形的性质及全等三角形的判定及性质，熟练掌握正方形的性质并能作出正确的辅助线是解决本题的关键．22.【2020年浙江省台州市中考数学试卷】如图，在△ABC 中，∠ACB=90°，将△ABC 沿直线AB 翻折得到△ABD ，连接CD 交AB 于点M ．E 是线段CM 上的点，连接BE ．F 是△BDE 的外接圆与AD 的另一个交点，连接EF ，BF ，(1)求证：△BEF 是直角三角形；(2)求证：△BEF ∽△BCA ；(3)当AB=6，BC=m 时，在线段CM 正存在点E ，使得EF 和AB 互相平分，求m 的值．【答案】(1)见解析；(2)见解析；(3)【解析】【分析】(1)想办法证明∠BEF=90°即可解决问题(也可以利用圆内接四边形的性质直接证明)．(2)根据两角对应相等两三角形相似证明．(3)证明四边形AFBE 是平行四边形，推出FJ=12BD=12m ，EF=m ，由△ABC ∽△CBM ，可得BM=26m ，由△BEF ∽△BCA ，推出 AC BC EF BE，由此构建方程求解即可. 【详解】(1)证明：由折叠可知，∠ADB=∠ACB=90°∵∠EFB=∠EDB ，∠EBF=∠EDF ，∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°，∴∠BEF=90°，∴△BEF 是直角三角形．(2) 证明：∵BC=BD ，∴∠BDC=∠BCD，∵∠EFB=∠EDB，∴∠EFB=∠BCD，∵AC=AD，BC=BD，∴AB⊥CD，∴∠AMC=90°，∵∠BCD+∠ACD=∠ACD+∠CAB=90°，∴∠BCD=∠CAB，∴∠BFE=∠CAB，∵∠ACB=∠FEB=90°，∴△BEF∽△BCA．(3) 设EF交AB于J．连接AE，如下图所示：∵EF与AB互相平分，∴四边形AFBE是平行四边形，∴∠EFA=∠FEB=90°，即EF⊥AD，∵BD⊥AD，∴EF∥BD，∵AJ=JB，∴AF=DF，△ FJ=1= 22m BD△ EF=m△ △ABC△△CBM ，△ BC:MB=AB:BC ， △ BM=26m ， △ △BEJ△△BME ，△ BE:BM=BJ:BE ，， △ △BEF△△BCA ，△=AC BC EF BE即=m m m，解得m =负根舍去).故答案为：【点睛】本题属于圆综合题，考查了圆周角定理，相似三角形的判定和性质平行四边形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考压轴题．23.【2020年浙江省温州市中考数学试卷】如图，在河对岸有一矩形场地ABCD ，为了估测场地大小，在笔直的河岸l 上依次取点E ，F ，N ，使AE ⊥l ，BF ⊥l ，点N ，A ，B 在同一直线上．在F 点观测A 点后，沿FN 方向走到M 点，观测C 点发现∠1＝∠2．测得EF ＝15米，FM ＝2米，MN ＝8米，∠ANE ＝45°，则场地的边AB 为_______米，BC 为_______米．【答案】(1). (2).【解析】【分析】过点C作CP⊥EF于点P，过点B作直线GH∥EF交AE于点G，交CP于点H，如图，则△ABG、△BCH 都是等腰直角三角形，四边形BGEF、BHPF是矩形，于是可根据等腰直角三角形的性质和勾股定理依次求出AG、BG、AB的长，设FP=BH=CH=x，则MP=x－2，CP=x+10，易证△AEF∽△CPM，然后根据相似三角形的性质即可得到关于x的方程，解方程即可求出x，再根据勾股定理即可求出BC的长．【详解】解：过点C作CP⊥EF于点P，过点B作直线GH∥EF交AE于点G，交CP于点H，如图，则GH⊥AE，GH⊥CP，∴四边形BGEF、BHPF是矩形，∵∠ANE＝45°，∴∠NAE＝45°，∴AE=EN=EF+FM+MN=15+2+8=25，∵∠ABG＝45°，∴∠GAB＝45°，∴AG=BG=EF=15，∴AB=，GE=BF=PH=10，∵∠ABG＝45°，∠ABC＝90°，∴∠CBH＝45°，∴∠BCH=45°，∴BH=CH，设FP=BH=CH=x，则MP=x－2，CP=x+10，∵∠1=∠2，∠A EF =∠CPM =90°，∴△AEF ∽△CPM ， ∴AE CP EF PM =，即2510152x x +=-，解得：x =20，即BH=CH =20，∴BC ==∴AB =BC =故答案为：【点睛】本题考查了等腰直角三角形的判定和性质、矩形的判定和性质、勾股定理以及相似三角形的判定和性质等知识，属于常考题型，正确作出辅助线、熟练掌握相关知识是解题的关键．24.【2020年浙江省温州市中考数学试卷】如图，在四边形ABCD 中，∠A ＝∠C ＝90°，DE ，BF 分别平分∠ADC ，∠ABC ，并交线段AB ，CD 于点E ，F (点E ，B 不重合)．在线段BF 上取点M ，N (点M 在BN 之间)，使BM ＝2FN ．当点P 从点D 匀速运动到点E 时，点Q 恰好从点M 匀速运动到点N ．记QN ＝x ，PD ＝y ，已知6125y x =-+，当Q 为BF 中点时，245y =． (1)判断DE 与BF 的位置关系，并说明理由；(2)求DE ，BF 的长；(3)若AD ＝6．①当DP ＝DF 时，通过计算比较BE 与BQ 的大小关系；②连结PQ ，当PQ 所在直线经过四边形ABCD 的一个顶点时，求所有满足条件的x 的值．【答案】(1)//DE BF ，理由见解析；(2)12,16DE BF == ；(3)①BQ BE >；②101410,,33【解析】【分析】(1)推出∠AED=∠ABF ，即可得出DE ∥BF ；(2)求出DE=12，MN=10，把254y =代入6125y x =-+，解得：x=6，得到NQ=6，得出QM=4，由FQ=QB ，BM=2FN ，得出FN=2，BM=4，即可得出结果；(3)①连接EM 并延长交BC 于点H ，易证四边形DFME 是平行四边形，得出DF=EM ，求出∠DEA=∠FBE=∠FBC=30°，∠ADE=∠CDE=∠FME=60°，∠MEB=∠FBE=30°，得出∠EHB=90°，DF=EM=BM=4，MH=2，EH=6，由勾股定理得BH =，BE =当DP=DF 时，求出223BQ = ，得到BQ ＞BE ；②(Ⅰ)当PQ 经过点D 时，y=0，则x=10；(Ⅱ)当PQ 经过点C 时，由FQ ∥DP ，得出△CFQ ∽△CDP ，则FQ CF DP CD =，即可求得103x = ；(Ⅲ)当PQ 经过点A 时，由PE ∥BQ ，得出△APE ∽△AQB ，则PE AE BQ AB = ，根据勾股定理得=AE则AB = ，143x = ；由图可知，PQ 不可能过点B ．【详解】解：(1)DE 与BF 的位置关系为：DE ∥BF ，理由如下：如图1所示：∵∠A=∠C=90°，∴∠ADC+∠ABC=360°-(∠A+∠C )=180°，∵DE 、BF 分别平分∠ADC 、∠ABC ，1122ADE ADC ABF ABC ∴∠=∠∠=∠，， 1180902ADE ABF ∴∠+∠=⨯︒=︒， ∵∠ADE+∠AED=90°，∴∠AED=∠ABF ，∴DE∥BF；(2)令x=0，得y=12，∴DE=12，令y=0，得x=10，∴MN=10，把254y=代入6125y x=-+，解得：x=6，即NQ=6，∴QM=10-6=4，∵Q是BF中点，∴FQ=QB，∵BM=2FN，∴FN+6=4+2FN，解得：FN=2，∴BM=4，∴BF=FN+MN+MB=16；(3)①连接EM并延长交BC于点H，如图2所示：∵FM=2+10=12=DE，DE∥BF，∴四边形DFME是平行四边形，∴DF=EM，∵AD=6，DE=12，∠A=90°，∴∠DEA=30°，∴∠DEA=∠FBE=∠FBC=30°，∴∠ADE=60°，∴∠ADE=∠CDE=∠FME=60°，∴∠DFM=∠DEM=120°，∴∠MEB=180°-120°-30°=30°，∴∠MEB=∠FBE=30°，∴∠EHB=180°-30°-30°-30°=90°，DF=EM=BM=4，122MH BM ∴==， ∴EH=4+2=6，由勾股定理得：BH === ，∴BE ===，当DP=DF 时，61245x -+= ，解得：302x = ， 2022141433BQ x ∴=-=-= ， 22433＞， BQ ＞BE ；②(Ⅰ)当PQ 经过点D 时，如图3所示：y=0，则x=10；(Ⅱ)当PQ 经过点C 时，如图4所示：∵BF=16，∠FCB=90°，∠CBF=30°，182CF BF == ， CD=8+4=12，∵FQ ∥DP ，∴△CFQ ∽△CDP ， ∴FQ CF DP CD= ， ∴28612125x +=-+ ，解得：103x = ； (Ⅲ)当PQ 经过点A 时，如图5所示：∵PE ∥BQ ，∴△APE ∽△AQB ， ∴PE AE BQ AB= ，根据勾股定理得：AE === ,∴AB ==，61212514x ⎛⎫--+ ⎪⎝⎭∴=- ，解得：143x = ；由图可知，PQ 不可能过点B ；综上所述，当x=10或103x =或143x =时，PQ 所在的直线经过四边形ABCD 的一个顶点．【点睛】本题是四边形综合题，主要考查了平行四边形的的判定与性质、勾股定理、角平分线的性质、平行线的判定与性质、相似三角形的判定与性质、含30°角的直角三角形的性质等知识；本题综合性强，难度较大，熟练掌握平行四边形的判定与性质是解题的关键．25.【2020年浙江省衢州市中考数学试卷】二次函数2y x =的图象平移后经过点(2，0)，则下列平移方法正确的是A ．向左平移2个单位，向下平移2个单位B ．向左平移1个单位，向上平移2个单位C ．向右平移1个单位，向下平移1个单位D ．向右平移2个单位，向上平移1个单位答案：C26.【2020年浙江省衢州市中考数学试卷】如图，把一张矩形纸片ABCD 按所示方法进行两次折叠，得到等腰直角三角形BEF ，若BC ＝1，则AB 的长度为AB．12 C．12 D ．43答案：A27.【2020年浙江省衢州市中考数学试卷】小慧用图1中的一副七巧板拼出如图2所示的“行礼图”．已知正方形ABCD 的边长为4dm ，则图2中h的值为dm．答案：28.【2020年浙江省衢州市中考数学试卷】图1是由七根连杆链接而成的机械装置，图2是其示意图．已知O，P两点固定，连杆PA＝PC＝140cm，AB＝BC＝CQ＝QA＝60cm，OQ＝50cm，O，P两点间距与OQ长度相等．当OQ绕点O转动时，点A，B，C的位置随之改变，点B恰好在线段MN上来回运动．当点B运动至点M或N时，点A，C重合，点P，Q，A，B在同一直线上(如图3)．(1)点P到MN的距离为cm；(2)当点P，O，A在同一直线上时，点Q到MN的距离为cm．答案：。

中考重难点之图形的变换综合知识(含经典例题)

中考重难点之图形的变换综合一、考情分析：“图形的旋转”是课改后的新增内容，也是近几年中考的必考内容，是中考的热点与重点.运用旋转的全等变换，证明线段与角相等或和、差、倍、分关系，以及在旋转中探索图形的变化，进行图案设计是近几年中考的常见题型，预计研究图形旋转变换的变化规律的开放探究题与二次函数的综合题，是中考的重点题型。

二、知识点睛1、旋转（1）定义：在平面内，一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转，定点叫作旋转中心，旋转的角度叫作旋转角，如果一个图形上的点A经过旋转变为A’，那么这两个点叫作旋转的对应点.如图所示，△A’OB’是△AOB绕定点O逆时针旋转30°得到的，其中点A与点A’叫作对应点，线段OB与线段OB’叫作对应线段，∠A与∠A’叫作对应角，点O叫作旋转中心，∠AOA’的度数叫作旋转的角度。

（2）性质①图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动；②对应点到旋转中心的距离相等；③旋转前后图形的大小和形状没有改变；④两组对应点分别与旋转中心的连线所成的角相等，都等于旋转角；⑤旋转中心是唯一不动的点2、旋转对称图形定义：在平面内，一个图形绕着一个定点旋转一定的角度后，能够与原图形重合，这样的图形叫作旋转对称图形。

3、旋转三要素①定点——旋转中心②旋转方向③旋转角度4、中心对称图形（1）中心对称图形在平面内，一个图形绕某一定点旋转180°，能够与原来的图形完全重合，那么这个图形叫作中心对称图形，这个定点叫作对称中心。

（倍长中线性实际上就是在作中心对称）（2）中心对称：把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点成中心对称三、技巧提炼：1、旋转是中考压轴题中的常见题型，在解这类题时，什么时候需要构造旋转，怎么构造旋转，下面，就不同类型的旋转问题给出构造旋转图形的解题方法：遇中点，旋180°，构造中心对称遇90°，旋90°，造垂直遇60°，旋60°，造等边遇等腰，旋顶角综上四点得出旋转的本质特征：等线段，共顶点，就可以有旋转2、图形旋转后我们需要证明旋转角全等，而旋转全等三角中的难点实际上就是倒角，下面给出旋转常用的倒角，只要是旋转，必然存在这两个倒角之一。

备战2020年中考数学解答题专题10 图形变换综合题探究专题(解析版)

备战2020年中考数学解答题专题十图形变换综合题探究专题【考题研究】本专题主要包括图形的变换和相似形．其中轴对称图形、平移、中心对称图形的识别，相似三角形性质以填空和选择题为主，主要是考查对图形的识别和性质；图形的折叠、平移、旋转与几何图形面积相关的计算问题以填空题和解答题为主，主要是考查对几何问题的综合运用能力；而相似三角形的性质及判断定的应用往往还会结合圆或者解直角三角形等问题一并考查，主要是以解答题为主。

2.结合具体问题大胆尝试，动手操作平移、旋转，探究发现其内在规律是解答操作题的基本方法。

3．注重图形与变换的创新题，弄清其本质，掌握其基本的解题方法，尤其是折叠与旋转等。

专题11 图形的变换-2020年中考数学真题分专题训练(四川专版)(教师版含解析)

专题11 图形的变换1．(3分)(2020•成都)在平面直角坐标系中，将点P(3，2)向下平移2个单位长度得到的点的坐标是() A．(3，0)B．(1，2)C．(5，2)D．(3，4)【答案】A【解析】将点P(3，2)向下平移2个单位长度所得到的点坐标为(3，2﹣2)，即(3，0)，故选：A．2．(3分)(2020•甘孜州)在平面直角坐标系中，点(2，﹣1)关于x轴对称的点是()A．(2，1)B．(1，﹣2)C．(﹣1，2)D．(﹣2，﹣1)【答案】A【解析】点(2，﹣1)关于x轴对称的点是：(2，1)．故选：A．3．(4分)(2020•凉山州)点P (2，3)关于x轴对称的点P'的坐标是()A．(2，﹣3)B．(﹣2，3)C．(﹣2，﹣3)D．(3，2)【答案】A【解析】点P(2，3)关于x轴对称的点P'的坐标是(2，﹣3)．故选：A．4．(3分)(2020•泸州)在平面直角坐标系中，将点A(﹣2，3)向右平移4个单位长度，得到的对应点A'的坐标为()A．(2，7)B．(﹣6，3)C．(2，3)D．(﹣2，﹣1)【答案】C【解析】∵将点A(﹣2，3)先向右平移4个单位，∴点A的对应点A′的坐标是(﹣2+4，3)，即(2，3)．故选：C．5．(4分)(2020•自贡)在平面直角坐标系中，将点(2，1)向下平移3个单位长度，所得点的坐标是() A．(﹣1，1)B．(5，1)C．(2，4)D．(2，﹣2)【答案】D【解析】将点(2，1)向下平移3个单位长度所得点的坐标为(2，1﹣3)即(2，﹣2)；故选：D．6．(4分)(2020•自贡)下列图形中，是轴对称图形，但不是中心对称图形的是()A．B．C．D．【答案】A【解析】A、是轴对称图形，不是中心对称图形，故本选项符合题意；B、不是轴对称图形，是中心对称图形，故本选项不合题意；C、既是轴对称图形，又是中心对称图形，故本选项不合题意；D、既不是轴对称图形，又不是中心对称图形，故本选项不合题意．故选：A．7．(3分)(2020•泸州)下列正多边形中，不是中心对称图形的是()A．B．C．D．【答案】B【解析】A．正方形是中心对称图形，故本选项不合题意；B．正五边形不是中心对称图形，故本选项符合题意；C．正六边形是中心对称图形，故本选项不合题意；D．正八边形是中心对称图形，故本选项不合题意；故选：B．8．(3分)(2020•乐山)观察下列各方格图中阴影部分所示的图形(每一小方格的边长为1)，如果将它们沿方格边线或对角线剪开重新拼接，不能拼成正方形的是()A．B．C．D．【答案】D【解析】由题意，选项D阴影部分面积为6，A，B，C的阴影部分的面积为5，如果能拼成正方形，选项D的正方形的边长为√6，选项A，B，C的正方形的边长为√5，观察图象可知，选项A，B，C阴影部分沿方格边线或对角线剪开均可得图1的5个图形，可以拼成图2的边长为√5的正方形，故选：D．9．(3分)(2020•达州)如图，点P(﹣2，1)与点Q(a，b)关于直线1(y＝﹣1)对称，则a+b＝﹣5．【答案】-5【解析】∵点P(﹣2，1)与点Q(a，b)关于直线1(y＝﹣1)对称，∴a＝﹣2，b＝﹣3，∴a+b＝﹣2﹣3＝﹣5，故答案为﹣5．。

2020年部编人教版绍兴市中考数学试题分类精析汇编(4)图形的变换

绍兴市2020年中考数学试题分类解析专题04 图形的变换一、选择题1. （2020年浙江绍兴3分）如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为【】（A ）30π （B ）76π （C ）20π （D ）74π2. （2020年浙江绍兴4分）圆锥的母线长为13cm ，底面半径为5cm ，则此圆锥的高线长为【】A ．6 cmB ．8 cmC ．10 cmD ．12 cm()22135cm -。

故选D 。

3. （2020年浙江绍兴4分）如图，有一矩形纸片ABCD ，AB=10，AD=6，将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，则△CEF 的面积为【】A．4 B．6 C．8 D．104. （2020年浙江绍兴4分）一个圆锥的底面半径为52，母线长为6，则此圆锥侧面展开图的圆心角是【】A．180° B．150° C．120°D．90°5. （2020年浙江绍兴4分）如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）.则∠OCD等于【】A．108°B．144°C．126°D．129°【答案】C。

【考点】矩形的性质，折叠对称的性质。

【分析】展开如图：五角星的每个角的度数是：0 180365=。

∵∠COD=3600÷10=360，∠ODC=360÷2=180，∴∠OCD=1800－360－180=1260。

故选C。

6. （2020年浙江绍兴4分）已知圆柱的侧面积为10π，则它的轴截面面积为【】（A） 5 （B）10 （C）12 （D）207. （2020年浙江绍兴4分）将一张正方形纸片，沿图的虚线对折，得图，然后剪去一个角，展开铺平后的图形如下图所示，则图中沿虚线的剪法是【】（A）（B）（C）（D）8. （2020年浙江绍兴4分）下图中几何体的正视图是【】A. B． C．D.9. （2020年浙江绍兴4分）如图，设M，N分别是直角梯形ABCD两腰AD，CB的中点，DE上AB于点E，将△ADE沿DE翻折，M与N恰好重合，则AE：BE等于【】A．2:1 B．1:2 C．3:2 D．2:3【答案】A。

2020年中考数学专题训练九图形变换问题

2020年中考数学专题训练九图形变换问题[考点导航]在近几年的中考试题中，出现了许多变化无穷、精彩纷呈、形式新颖的优秀试题，这已成为中考压轴题的一个新的发展趋势。

因此，我们在中考复习中要引起足够重视。

一、图形变换问题试题的特点图形与变换问题主要是指图形的轴对称、平移和旋转。

其本质特点是：变换后的图形与原来的图形比较，位置发生了变化，但是形状、大小不变，即与原图形是全等形。

这几类图形变换知识在中考中占有十分重要的地位。

二、中考图形变换复习应掌握的基本方法（一）平移变换的基本应用方法1.平移变换时通过作平行线的手段，把图形中的某条线段或某个角移动到一个新的位置上，使图形中分散的条件与结论有机地联系起来。

2.平移法在应用时有三种情况：首先把条件中的某条线段或角平移；其次把结论中的线段或角平移；最后把图形中条件或结论中的线段或角同时平移。

（二）旋转变换的基本应用方法一般情况下，当题目中出现“共端点、等线段”时，即可以尝试旋转变换；再通过把某个三角形旋转到一个新的位置上，使图形中分散（或过于密集）的条件与结论有机地联系起来，从而达到使已知条件可以应用，或使得求证可以转化的目的；最后旋转前、后图形的对应点到旋转中心的距离相等，即旋转中心在对应点所连线段的垂直平分线上，旋转前、后的图形对应点，与旋转中心所连线段的夹角等于旋转角。

（三）轴对称变换的基本应用方法轴对称变换是通过直线的对称图形的手段，把图形中的某一图形对称地移动到一个新的位置上，使图形中的分散条件和结论有机地联系起来。

[猜押题专练]1．如图，在正方形ABCD中，AB=3，点M在CD的边上，且DM=1，ΔAEM与ΔADM关于AM所在的直线对称，将ΔADM按顺时针方向绕点A旋转90°得到ΔABF，连接EF，则线段EF的长为（）A．3B．C D2．如图，在▱ABCD中，AB AD，将▱ABCD沿直线EF(点E、F分别在边AD和边BC上)折叠，使V的周长为()点D与点B重合，若▱ABCD的周长为12，则ABEA．5B．8C．6D．103．已知：如图，AC，BC分别是半圆O和半圆O'的直径，半圆O的弦MC交半圆O'于N．若2MN=，则AB等于（）A．2cosαB．2sinαC．2cosα⋅D．2sinα⋅4．如图所示，小杨在广场上的A处正面观测一座楼房墙上的广告屏幕，测得屏幕下端D处的仰角为30o，然后他正对大楼方向前进5m到达B处，又测得该屏幕上端C处的仰角为45o．若该楼高为26.65m，小杨的眼睛离地面1.65m，广告屏幕的上端与楼房的顶端平齐．求广告屏幕上端与下端之间的距离CD是________m 1.732≈，结果精确到0.1m）．5．如图1，已知线段BC=2，点B关于直线AC的对称点是点D，点E为射线CA上一点，且ED=BD，连接DE，BE.（1）依据题意补全图1，并证明：△BDE为等边三角形；（2）若∠ACB=45°,点C关于直线BD的对称点为点F，连接FD、FB，将△CDE绕点D顺时针旋转α度（0°<α<360°）得C DEV', 点E的对应点为E’,点C的对应点为点C’.(i)如图2，当30α=︒时，连接BC’.证明：EF=BC’；（ii）如图3，点M为DC中点，点P为线段C’E’上任意一点，试探究：在此旋转过程中，线段PM长度的取值范围？（直接写出答案）.6．AD是△ABC的中线，G是AD上任意一点时（点G不与A重合），过点G的直线交边AB于E，交射线AC于点F，设AE＝xAB，AF＝yAC（x、y≠0）．（1）如图1，若点G与D重合，△ABC为等边三角形，且∠BDE＝30°，证明：△AEF∽△DEA；（2）如图2，若点G 与D 重合，证明：11x y+＝2；（3）如图3，若AG ＝nAD ，x ＝12，y ＝32，直接写出n 的值．7．△ABC 中，点H 是BC 上一点，D 、E 分别是AB 、AC 中点，M 、N 分别为BH 、CH 中点(1)如图1，求证：四边形DENM 是平行四边形．(2)如图2，当AH 与BC 满足什么关系时，□DENM 是正方形，请直接写出结论．(3)当AH 与BC 满足（2）中的关系，且S △ABC =2时，若点P 为AB 边上的动点，过点P 作PQ ⊥BC 于Q ，PG ∥BC 交AC 于G ，GK ⊥BC 于K ，四边形PGKQ 的周长是否会随着P 点位置的变化而变化？若不变，请求出周长，若变化，请说明理由．图1 图2 备用图8．如图，已知Rt ABC ∆中，90,6,8C AC BC ∠=︒==，点P 以每秒1个单位的速度从A 向C 运动，同时点Q 以每秒2个单位的速度从B 向A 方向运动，Q 到达A 点后，P 点也停止运动，设点,P Q 运动的时间为t 秒.(1)求P 点停止运动时，BP 的长;(2) ,P Q 两点在运动过程中，点E 是Q 点关于直线AC 的对称点，是否存在时间t ，使四边形PQCE 为菱形?若存在，求出此时t 的值;若不存在，请说明理由.(3) ,P Q 两点在运动过程中，求使APQ ∆与ABC ∆相似的时间t 的值.9．如图，A B ∠=∠，AE BE =，点D 在AC 边上，12∠=∠．（1）求证：AEC BED ∆∆≌；（2）若70C ∠=︒，求AEB ∠的度数；（3）若90AEC ∠=︒，当AEC ∆的外心在直线DE 上时，2CE =，求AE 的长．10．如图1，△ABC 是等腰直角三角形，四边形ADEF 是正方形，D 、F 分别在AB 、AC 边上，此时BD=CF ，BD ⊥CF 成立．（1）当正方形ADEF 绕点A 逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF 成立吗？若成立，请证明；若不成立，请说明理由．（2）当正方形ADEF 绕点A 逆时针旋转45°时，如图3，延长BD 交CF 于点G ．①求证：BD ⊥CF ； ②当AB=4，AD=2时，求线段BG 的长．11．综合与探究如图（1），线段AB 的两个端点的坐标分别为（-12，4）（0，10），点P 从点B 出发，沿BA 方向匀速向点A 运动；同时，点Q 从坐标原点O 出发，沿x 轴的反方向以相同的速度运动，当点P 到达点A 时，P,Q 两点同时停止运动，设运动的时间为t 秒，ΔOPQ 的面积S （平方单位）与时间t （秒）之间的函数图象如图（2）所示。

2020河北中考数学精准大二轮复习(讲义+精练)专题突破专题3 图形变换的相关计算

专题三图形变换的相关计算类型一图形平移的相关计算如图，△ABC和△DBC是两个具有公共边的全等的等腰三角形，AB＝AC＝3 cm，BC＝2 cm，将△DBC沿射线BC平移一定的距离得到△D1B1C1，连接AC1，BD1，如果四边形ABD1C1是矩形，则平移的距离为( )A．2 cm B．5 cm C．7 cm D．9 cm【分析】要求平移的距离，可结合平移性质得到CC1即为平移的距离，结合四边形ABD1C1是矩形从而得到∠BAC1＝90°，而AB＝AC＝3 cm，BC＝2 cm，可过点A 作AE⊥BC于E，从而得到BE，再证明△ABE∽△C1BA即可利用对应边成比例求平移距离．【自主解答】对于图形的平移问题，掌握平移的性质：1.平移前后，对应线段相等、对应角相等；2.对应点所连接的线段平行(或在同一条直线上)且相等；3.对应点连线相等，都等于平移距离．因为将图形平移后出现平行线，从而易得到相似(A 字型)，故在平移有关的计算问题中，常会运用相似计算有关线段的长；而计算四边形面积时，常需要借助分割法，将图形分割成容易计算的几个部分来解．1．(2018·株洲改编)如图，已知△OAB是等腰直角三角形，∠OAB＝90°，OB＝22，将该三角形向右平移22个单位得到Rt△O′A′B′，则线段OA在平移过程中扫过部分的图形面积为( )A．4 B．4 2 C．2 D．2 22．(2019·保定竞秀区一模)如图，两张完全相同的正六边形纸片(边长为2a)重合在一起，下面一张保持不动，将上面一张纸片沿水平方向向左平移a个单位长度，则空白部分与阴影部分面积之比是( ) A．5∶2 B．3∶1 C．3∶2 D．2∶13．(2019·孝感改编)如图，正方形ABCD中，点E，F分别在边CD，AD上，BE与CF交于点G.BC＝4，DE＝AF＝1.将△BCG沿射线BE方向平移，使得点G与点E重合，得到△EB′C′，连接FB′，则此时FB′的长为( )A.2185B.2285C.109 D．21094．如图①，两个等边△ABD和△CBD的边长均为1，将△ABD沿AC方向向下平移到△A′B′D′的位置，得到图②，则阴影部分的周长为．类型二图形旋转的相关计算(2019·河北)对于题目：“如图①，平面上，正方形内有一长为12、宽为6的矩形，它可以在正方形的内部及边界通过移转(即平移或旋转)的方式，自由地从横放移转到竖放，求正方形边长的最小整数n.”甲、乙、丙作了自认为边长最小的正方形，先求出该边长x，再取最小整数n.甲：如图②，思路是当x为矩形对角线长时就可移转过去；结果取n＝13. 乙：如图③，思路是当x为矩形外接圆直径长时就可移转过去；结果取n＝14.丙：如图④，思路是当x为矩形的长与宽之和的22倍时就可移转过去；结果取n＝13.下列正确的是( )A．甲的思路错，他的n值对B．乙的思路和他的n值都对C．甲和丙的n值都对D．甲、乙的思路都错，而丙的思路对【分析】要将平放的矩形通过平移或旋转的方式变成竖放，关键是看矩形边上任意两点之间的最大距离能否恰好小于等于正方形的边长，由此来判断甲、乙、丙三人的作法是否正确即可．【自主解答】对于图形的旋转问题，掌握旋转的性质：1.对应点到旋转中心的距离相等；2.对应点与旋转中心连线所成角等于旋转角；3.旋转前后对应角、对应线段相等．对于旋转求角度问题，常需要利用旋转对应点到旋转中心距离相等得到等腰三角形，结合等腰三角形内角关系求解；求旋转角的问题常应用对应点与旋转中心所成的角等于旋转角来求；对于旋转求点经过的路线长实质是求弧长、旋转求线段扫过的面积实质是求扇形的面积．同时，旋转是有方向的，当题设中没有明确说明旋转方向(顺时针或者逆时针)，则一定要分情况讨论．1．(2019·河北中考说明)如图，在等边△ABC中，AC＝9，点O在AC上，且AO ＝3，点P是AB上一动点，连接OP，将线段OP绕点O逆时针旋转60°得到线段OD，要使点D恰好落在BC上，则AP的长是( )A．4 B．5 C．6 D．82．(2020·原创)如图，在矩形ABCD 中，点E 是边AD 上一点，过点E 作EF⊥BC，垂足为点F ，将△BEF 绕着点E 逆时针旋转，使点B 落在边BC 上的点N 处，点F落在边DC 上的点M 处．若点M 恰好是边CD 的中点，那么AD AB的值是( ) A.233 B.433 C.534 D.5363．(2019·廊坊安次区二模)如图，在等边△ABC 内有一点D ，AD ＝5，BD ＝6，CD ＝4，将△ABD 绕A 点逆时针旋转，使AB 与AC 重合，点D 旋转至点E.(1)DE ＝；(2)∠CDE 的正切值为．4．(2019·金华改编)如图，在等腰Rt△ABC 中，∠ACB＝90°，AB ＝142，D 是AB 的中点，E 是BC 上一点，将线段ED 绕点E 按逆时针方向旋转90°得到线段EF.(1)如图①，当点E 与点C 重合时，设AF 交CD 于点O ，则OD 的长为；(2)如图②，当CE ＝2时，设点G 为AF 的中点，连接DG ，则DG 的长为．5．(2019·石家庄裕华区二模)如图，扇形AOB 中，半径OA 在直线l 上，∠AOB＝120°，OA ＝1，矩形EFGH 的边EF 也在直线l 上，且EH ＝2，OE ＝10π3＋20＋22，将扇形AOB 在直线l 上向右滚动．(1)滚动一周时得到扇形A′O′B′，这时OO′＝；(2)当扇形与矩形EFGH 有公共点时停止滚动，设公共点为D ，则DE ＝．类型三图形折叠的相关计算(2019·河北结课卷)如图①，点E 是矩形ABCD 中AD 边上任意一点，连接BE ，把△ABE 沿BE 折叠，如图②所示，然后再过点A 作AF⊥CD 于点F ，如图③所示，当AB ＝8，BC ＝10，且∠BEA＝60°，则图③中AF 的长为( )A ．23＋2B ．8－4 3C ．23＋1D ．10－4 3【分析】先求∠ABC＝30°，再过A 作AG⊥BC 于G ，得四边形AGCF 是矩形，从而只需求CG 即可．【自主解答】忽略折叠前后的对应关系在利用折叠的性质解决问题时，易出错的是忽略折叠(翻折)前后两图形的关系，从而不能利用对应角相等，对应线段相等的性质解题．1．(2019·河北模拟)如图，在正方形ABCD 纸片中，EF 是BC 的垂直平分线，按以下四种方法折叠纸片，图中不能折出30°角的是( )2．如图，在Rt△ABC 中，AB ＝9，BC ＝6，∠B＝90°，将△ABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，则线段BN 的长为( )A.53B.52C ．4D ．5 3．(2019·辽阳)如图，直线EF 是矩形ABCD 的对称轴，点P 在CD 边上，将△BCP 沿BP 折叠，点C 恰好落在线段AP 与EF 的交点Q 处，BC ＝43，则线段AB 的长是( )A ．8B ．8 2C ．8 3D ．104．(2019·唐山路北区二模)将一个直角三角形纸片ABO 放置在平面直角坐标系中，点A(3，0)，点B(0，1)，点O(0，0)，过边OA 上的动点M(点M 不与点O ，A 重合)作MN⊥AB 于N ，沿着MN 折叠该纸片，得到△A′MN，顶点A 的对应点为A′，设OM ＝m ，折叠后的△A′MN 与四边形OMNB 重叠部分的面积为S.(1)当点A′与顶点B 重合时，点M 的坐标为；(2)当S ＝324时，点M 的坐标为．参考答案【例1】设平移的距离为x cm ，由平移性质得BC 1＝BC ＋CC 1＝(2＋x) cm ，过点A 作AE⊥BC 于E ，∵AB＝AC ，∴BE＝CE ＝1，∵四边形ABD 1C 1是矩形，∴∠BAC 1＝90°，∴∠BAE＋∠EAC 1＝90°，∵∠ABE＋∠BAE＝90°，∴∠BAE＝∠AC 1E ，∵∠AEB＝∠C 1AB ＝90°，∴△ABE∽△C 1BA ，∴AB BE ＝C 1B AB ，即31＝2＋x 3，解得x ＝7 cm.故选C.跟踪训练1．A 【解析】如解图，设AA′交OB 于E ，∵在△ABO 中，AB ＝AO ，∠OAB＝90°，△A′O′B′是由△AOB 向右平移22个单位得到的，∴OO′＝22，AA′⊥OB.∵O B ＝22，∴OE＝2，∴四边形AOO′A′的面积为OO ′·OE ＝22·2＝4.2．B3．A 【解析】∵四边形ABCD 是正方形，∴AD＝CD ＝BC ，∠D＝∠BCD＝90°.∵DE ＝AF ，∴DF＝CE ，∴△CDF≌△BCE，∴∠DCF＝∠CBE，∴∠DCF＋∠CEB＝∠CBE ＋∠BEC＝90°，∴∠FGB′＝90°.∵CE＝3，BC ＝4，∴BE＝5.∵CG⊥BE，∴GE ＝95，CG ＝125，∴BG＝BE －GE ＝165.∵将△BGC 沿BE 方向平移得到△EB′C′，∴BB′＝EG ＝95，∴B′G＝75.∵GF＝CF －CG ＝135，∴B′F＝FG 2＋B′G 2＝2185. 4．2【例2】 ∵要将正方形内平放的矩形通过移转的方式变成竖放，则正方形的边长应大于等于矩形对角线的长，∴矩形外接圆的直径是矩形的对角线的长，由此可知，甲、乙的思路正确，丙的思路错误；∴x ≥62＋122＝65>13 ，∵n 为整数，∴n＝14，故甲的结果错误，乙的思路和结果都正确．故选B. 跟踪训练1．C 【解析】如解图，连接DP ，∵线段OD 是由线段OP 绕点O 逆时针旋转60°得到的，∴△ODP 是等边三角形，∴DP＝OP ，∠OPD＝60°.∵△ABC 是等边三角形，∴∠A＝∠B＝60°.∵∠OPD＝60°，∴∠OPA＋∠DPB＝120°.∵∠A＝60°，∴∠AOP＋∠OPA＝120°，∴∠AOP＋∠OPA＝∠OPA＋∠BPD，∴∠AOP＝∠BPD，∴△AOP≌△BPD(AAS)，∴BP＝AO ＝3.∵AB＝9，∴AP＝6.2．D 【解析】 ∵将△BEF 绕着点E 逆时针旋转得到△EMN, ∴BE＝EN ，EM ＝EF ，MN ＝BF. ∵EF⊥BC, ∴BF＝FN, ∴BF＝FN ＝NM.∵EF⊥BC, ∴四边形EFCD 是矩形， ∴EF＝CD, ∵点M 恰好是边DC 的中点，∴DM＝12CD ＝12EM ，∴∠DEM＝30°，∴∠DME＝60°，∵∠NME＝90°，∴∠CMN＝30°，设CN ＝x ，∴MN＝2x ，CM ＝3x ，∴BC＝5x ，∴AD AB ＝BC CD ＝5x 23x ＝536. 3．5；37 【解析】 (1)∵△ACE 是由△ABD 绕点A 逆时针旋转得到的，∴∠DAB ＝∠EAC，DA ＝EA ，∴∠BAD＋∠DAC＝∠EAC＋∠CAD＝∠BAC.∵△ABC 是等边三角形，∴∠BAC＝60°，∴∠DAE＝60°，∴△DAE 是等边三角形，∴DE＝AD ＝5.(2)如解图，过点C 作CF⊥DE 于F ，设DF ＝x ，则EF ＝5－x ，在Rt△CDF 和Rt△CEF中，由勾股定理得42－x 2＝62－(5－x)2，解得x ＝12，则CF ＝CD 2－DF 2＝42－（12）2＝372，∴tan∠CDE＝CF FD＝37. 4.722；522 5.2π3＋2；22【例3】如解图，过点A 作AG⊥BC 于点G.∵∠AEB＝60°，△ABE 是由△A′BE 折叠得到的，∴∠A′EB＝∠AEB＝60°，AB ＝A′B＝8.∵四边形A′BCD 是矩形，∴∠A′＝∠A′BC＝∠C＝90°，∴∠A′BE＝∠ABE ＝30°，∴∠ABC＝∠A′BC －∠A′BE－∠ABE＝30°，∴BG＝43，∵AF⊥CD，∴四边形AGCF 是矩形，∴AF ＝CG ＝BC －BG ＝10－4 3.故选D.跟踪训练1．B 2.C 3.A 4.(33，0)；(233，0)。