温补晶振的热敏网络分析及参数计算
颇费一番精力整理的温补晶振

二、主要参数范围
温补晶振的常见频率:10MHz、12.288MHz、16.32MHz、16.368MHz、16.369MHz、16.8MHz、20MHz、24MHz、28.80MHz、30.72MHz、50MHz、52MHz等封装尺寸2520、3225、5032,精度有±0.25ppm、±0.6ppm、±1.0ppm、±2.0ppm等。
温度补偿晶体振荡器,简称为温补晶振。温补晶振属于有源晶振,它是在普通晶振的基础上,加了一个温度补偿网络,松季电子介绍从信号特征上它主要分为模拟温补晶振和数字温补晶振两种,也可从补偿方式分为:直接温度补偿晶体振荡器和间接温度补偿晶体振荡器。
一、应用领域
晶振在很多电子产品和通信设备商用到,要用到温补晶振的话一般稳定度会比较高了,是用于对稳定度要求比较高的设备,比如通信设备、要用到压控说明改设备使用的时间会比较就,不是消费类电子产品。
热敏晶振温度补偿算法

热敏晶振温度补偿算法你知道吗,热敏晶振其实就像是我们人类的“体温计”,不过它测的可不是人的体温,而是温度对晶体振荡频率的影响。
哎,说到这,你可能会好奇,温度和频率到底有啥关系呢?晶振就像是我们大脑的“钟表”,它工作的时候,是通过一个非常精确的频率来保持系统的稳定运转。
但是一旦温度变化,晶振的频率就像放风筝一样,控制不住,飞得偏了。
这时候,我们就需要温度补偿算法来帮忙,确保晶振在各种温度下都能稳稳地“报时”。
所以啊,咱们今天就来聊聊这个神奇的热敏晶振温度补偿算法,嗯,大家不用担心,咱们不讲什么艰深的公式,保证让你轻松懂。
其实热敏晶振温度补偿就是为了应对温度变化对晶振频率的影响。
有些晶振就很“娇气”,温度一高一低,它的“心情”就跟着变化。
你想想,温度一变,频率也随之“跳舞”,根本没办法维持在一个稳定的水平。
补偿算法就像是给晶振开了一张温度调整的“处方”,让它在不同温度下都能保持稳定,像是给它穿上了“防寒服”和“防晒衣”,不管外面温度怎么变,它都能安安稳稳地工作。
怎么补偿呢?很简单,补偿的原则就是通过一个特定的算法,精确地计算出温度变化对频率的影响,然后反向调整,使得频率始终保持在一个我们希望的数值范围内。
听起来是不是很神奇?但实际上,做到这一点并不容易,尤其是当温度变化幅度很大时,补偿的精度要求就会非常高。
这时,不少小伙伴就会想了:“哎呀,这种算法难不难啊?我是不是要去学好多数学?”放心,没那么复杂。
其实就像我们日常生活中调味料一样,掌握了比例,就能做出好吃的菜肴。
补偿算法就是通过对晶振在不同温度下的频率特性进行数据分析,得出一个数学模型。
然后,系统就能根据实时的温度变化,调整晶振的工作状态,做到“温度不改频率”的目标。
简单来说,就是温度和频率之间的关系早就被“摸透了”,然后再根据这个规律,做出一些微调。
就像你调整音响的音量,虽然听不见细微的变化,但声音就好听多了。
再说了,为什么这个补偿算法这么重要呢?你想啊,现在咱们用的电子设备无论是手机、电脑还是智能家居,都会依赖于高精度的晶振来保持系统的同步。
晶振电路的理论与应用计算完整版

晶振电路的理论与应用计算标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]晶振电路的理论与应用计算图1:典型的Pierce皮尔斯石英晶体振荡电路图2:振荡电路图3:石英晶体等效电路图4:泛音石英晶体振荡电路图5:DIP封装的晶振(石英晶体谐振器)图6:SMD封装的晶振(石英晶体谐振器)图7:SMD封装的晶振图8:SMD封装的钟振(多了下方的振荡电路、IC)常用的“贴片晶振-40MHz-15pF-15ppm-3225-亚陶”,可以从规格书上看到如下参数:1、说明:A、大部分的中低频、要求不是特别高的振荡电路都采用了图1的形式,也许增加了多级反相器(可视为AB类放大器)作为Buffer,也就是说,我们用的大部分的芯片内部就集成了图2振荡电路的”A”部分,如BCM5357、RT5350、IP175D、RT8169等;实际上,我们使用的大部分LVTTL/LVCOMS输出的钟振内部就是这种电路;在已停产的W54R产品上,CPU没有集成振荡电路,为Costdown,我们就直接使用这种电路替代钟振;在BCM6332 方案的ADSL产品上,选用了64Mhz 3次泛音石英晶体振荡电路,与图4有些类似;RF为反馈电阻,RS为串联的隔离电阻,C1、C2为外部的负载电容;B、如图2所示,振荡电路可视为由两大部分组成:放大器A,有电压增益a、相移α;反馈网络F,有传递函数f、相移β;振荡电路工作条件:|f|∗|a|∗exp[j(α+β)]≥1增益:|f|∗|a|≥1相位:(α+β)=2∗n∗π即闭环增益≥1,相移n∗360°;在振荡电路中,石英晶体谐振器与外部匹配元件组成反馈网络,其压电效应起到电子<->机械的耦合作用,对振荡电路起到很好的稳频作用;C、如图3所示,晶振的等效电路中:C0称为”分路/静态”电容(Shunt Capacitance),由晶体片上的电极、封装产生的寄生电容,通常约5pF;L称为动态电感,是由晶体机械振动产生的”动态臂”;通常为mH级,如100mH;C称为动态电容,是由晶体机械振动产生的”动态臂”;通常为fF级,如;R称为动态/ ESR电阻,是由晶体机械振动产生的”动态臂”;通常为级,如10;R为消耗性的,且R越小越易起振,但制造因难;2、Frequency Tolerance频率误差:频率误差:f=ff−ffff∗1000000 (fff)(E1)也称为调整频差,10ppm表示百万分之十的误差;在室温条件下晶振实测工作频率fm与标称频率fs的相对误差;稳定性:ft=ff−ffff∗1000000 (fff)(E2)也称为温率频差,指在一定温度范围内晶振的工作频率与其在室温25℃下标称频率的相对误差;3、串联谐振与并联谐振:图9:晶振的电抗频谱线因为R较小可以忽略,所以:晶振阻抗:Z=ff ∗f2∗f∗f−1(f0+f)−(f2∗f∗f∗f0)(E3)当晶振工作在串联谐振模式时,表现为纯阻性,Z ->0,XL=XC:串联谐振频率:fs=2f∗f∗f(E4)当晶振工作在并联谐振模式时,表现为感性,Z ->∞,晶振制造商会为其指定负载电容CL:并联谐振频率:fa=2f∗√f∗ff+f0≈ff∗√1+f0+ff(E5)因为CL>C0?C,所以:fa≈fs;常见的的振荡电路中,大多工作在并联谐振模式下,在图9电抗线中fs到fa的斜线区域内,通过调整晶振的负载,都可以很好地工作,输出频率在fs到fa两者之间;(E6)4、品质因素:Q=12∗f∗ff∗f∗fQ值越高,晶振频率的稳定度就越高5、负载电容CL:制造商设计时预设的与晶振最佳匹配的负载电容值,通常在15~30pF:+ff+fff (E6)负载电容:CL=f1∗f2f1+f2(E7)PCB漂移电容:Cs=f∗f∗ffa:PCB走线宽度,b:PCB走线长度,ε:单位PCB面积的电容值,d:走线与GND的间距;最可计算出PCB走线、PAD所产生的分布电容难以忽视,因而PCB LAYOUT时需密切关注;+Cfb (E8)IC内部及封装电容:Cic=Cin∗Coutfff+ffffCin:IC输入电容,Cout:IC输出电容,Cfb:IC晶圆电容;) (E9) 牵引灵敏度:S=负载输出频率:fL=fs∗(1+C2∗(f0+ff)−f(E10)2∗(f0+ff)表示负载电容对频率的调节能力;图10:负载对频率的牵引;反馈因子:Cf=f1(E11)f2工作在线性区的反相器(放大器)导入180°或更高一些的相移,而C1、C2构成的电容分压器,在C1=C2的情况下,引入另外的180°相移,从而满足振荡条件;Cf值偏大时,环路增益大,易于起振,但过大时,振荡电路稳定性会变差;6、反馈电阻Rf设置反相器(CMOS放大器)的输入阻抗Ri,为满足振荡条件,放大器的开环增益必须>1;晶振的并联谐振电阻Rp则由负载电容CL设置;而Rp必须与Ri相匹配,因而有:(E12)输入阻抗:Ri=ffa并联谐振电阻:Rp=1(E13)f∗f2∗(f0∗ff)2(E14)反馈电阻:Rf=Rp∗a=af∗f∗(f0∗ff)实际应用中,为获得高输入阻抗Ri、晶振电路良好地驱动,反馈电阻Rf通常≥1M,且大多集成在IC中;7、Rs串联的隔离电阻反相器(放大器)额外的相移:α1=fs∗Delay∗360°(E15)Delay是反相器的传输延时,频率越高、延时越大,180°以外的相移越大,需要调节C1、C2、Rs来补偿,以维护振荡电路的稳定性;Rs是放大输出与晶振之间串联的隔离电阻,除串联隔离,其作用大致有:放大输出的源终端匹配电阻、与Rs与C2组成低通滤波,抑制反射、高频谐波阻尼,防EMI;Rs与C2形成分压器,拉低输出电平、降低放大器增益,提高稳定性;但也除低振荡频率、提升相移;限制放大器输出电流,设定晶振DL值,防止晶振过驱动,保证可靠性与寿命; Rs还会影响输出时钟的占空比;(E16)Rs≈XC2≈12∗f∗ff∗f2通常稍小于计算式,大约在1K以内,或者在一些场合不需要,注意!Rs≈XC2将导置50%的压降,因而放大器必须能提供2或以上的增益;8、驱动电平DL,指晶振工作时消耗的功率,通常供应商会在晶振规格书中提供这一个参数,实际应用中需确保在这一限值之内:图11:使用电流探头测量晶振驱动电流I(RMS值)驱动电平(uW):P=f2∗f(E17)受仪器设备限制,可以另一种方法计算:驱动电平(uW ):P =f 2f ∗(1+f0ff )2 (E18)R 为晶振动态电阻,I 为实测的驱动电流,U 为晶振上实测的压降;9、起振条件的测算与分析:图12:振荡电路等效参考模型振荡电路环路增益等于放大器跨导Gm 、谐振电路等效并联电阻RL 、反馈系数Cf 之积,通常Cf 被设置为1;增益: |Gain |=|ff fff |=|ff ffff |∗|ffff fff|=|G1|∗|G2|=|gm ∗RL |≥1 (E19)RL =116∗f 2∗1ff 2∗(f0+ff )2∗f (E20)因此如果推算出的增益大于1并有一定余量,则表示能正常起振; 另一种方法为开环测量反相器(集成在IC 中放大器)增益G2,看是否能足够的余量来保证|G1|∗|G2|≥1;大致的测量方式为:移除晶振及外部元件,使用信号源输出合适幅值的fs 时钟到IC 的XTAL_in ,使用双通道示波器同时实际测量IC 的XTAL_out 、XTAL_in 信号幅值电压,两者比值即为开环增益G2,因为晶振及其匹配电路的G1为负增益,G2足够高即能正常起振;10、振荡电路的稳定性测算与分析——负性阻抗测量:负性阻抗简单来讲,是指从晶振的两个Pin脚向振荡电路看,所得到振荡电路在谐振频率时的阻抗特性值(注意:不是晶振、而是振而是振荡电路-更多是放大器的参数!);振荡电路必需提供足够的放大增益来补偿晶振在谐振时的机械能损推出;从共振子的角度而言,就是在振荡电路上的“负性阻抗”。
恒温晶体振荡器的参数

恒温晶体振荡器的参数恒温晶体振荡器(Temperature Compensated Crystal Oscillator,TCXO)是一种高精度、稳定性好的电子元件,被广泛应用于通信、航空等领域中精细的定时和频率控制。
TCXO的参数直接影响到其性能表现,本文将对TCXO的参数进行详细介绍。
频率稳定度频率稳定度是指晶体振荡器在恒温和适当负载条件下,其输出频率与标准频率的偏差。
频率稳定度是TCXO的主要性能指标,通常用ppm(百万分之一)作为评价单位。
TCXO的频率稳定度可分为短期稳定度和长期稳定度。
短期稳定度短期稳定度是指在秒钟至分钟级别的时序范畴内,晶体振荡器输出频率的稳定性。
其受到振荡器自身产生的相噪声和振荡器所处环境噪声的影响。
短期稳定度一般可以通过闪烁度(Allan Deviation,ADEV)来评估,单位为ppb(十亿分之一)。
长期稳定度长期稳定度是指在小时至年级别的时序范畴内,晶体振荡器输出频率的稳定性。
其主要受到器件产生的温度变化和老化的影响。
长期稳定度一般用ppm/年来衡量。
工作温度范围TCXO的工作温度范围通常由低温极限、高温极限和电气性能(如频率变化量、相位噪声等)限制。
在实际应用中,根据TCXO的工作环境,选择合适的工作温度范围可以提升性能稳定性。
电源电压和功耗电源电压和功耗是TCXO另一个重要的参数。
它们直接影响到TCXO的应用范围和功耗控制。
TCXO的功耗主要由振荡器电路和整体电路决定。
因此,根据具体应用的要求,选择合适的电源电压和功耗对于延长TCXO的使用寿命和提升性能十分关键。
阻尼比和载波抑制比阻尼比和载波抑制比是TCXO的两个次要参数,其影响不同场景下的使用效果。
阻尼比阻尼比是指TCXO在振荡过程中,由于容耦电路的存在,从振荡过程中移走的比例。
其目的是消除晶体振荡过程中容耦电路的特性带来的不良影响,提高振荡器的稳定性。
载波抑制比载波抑制比是指TCXO输出频率(基频)与第一谐波高频组成信号大小的比值。
温度补偿晶振

温度补偿晶振温度补偿晶振,又称为温度补偿型晶振或温度补偿晶体管(Temperature Compensated Crystal Oscillator, TCXO),是一种能够自动调整晶振频率以应对环境温度变化的电子元件。
它通常被用于无线通信、卫星导航、计时设备、军事应用等领域中,因为这些应用需要高精度的频率稳定性和可靠性。
一般来说,晶振频率会随着温度的变化而发生变化,这是因为晶振石英晶体的性质随温度变化而变化所致。
当温度变化时,晶体的物理特性随之改变,导致晶体的共振频率发生变化。
由于晶振是许多电子设备中基本的时钟信号源,所以这种频率的变化会导致设备无法正常工作,甚至损坏设备。
为了解决这个问题,工程师们研发了温度补偿晶振。
温度补偿晶振的基本原理是利用温度感测器来感测环境温度的变化,并通过外部电路将温度补偿信号导入到晶振电路中,使晶振在不同温度下保持相同的频率。
温度补偿晶振一般采用两种不同的温度感测器:热敏电阻(Thermistor)和温度传感器(Thermocouple)。
热敏电阻是一种可以测量温度变化的电阻,它的电阻值随温度变化而变化。
温度传感器可以测量温度变化并将其转化为电压信号输出。
当环境温度发生变化时,温度感测器会感受到这种变化并相应地改变电阻或电压输出。
将这个变化的信号送到温度补偿晶振的终端,温度补偿晶振就可以根据这个信号对自身的频率进行调整。
因此,晶振的频率就可以保持在设定的值附近,而不受环境温度的影响。
需要注意的是,温度补偿晶振虽然可以抵消环境温度变化带来的频率变化,但仍然可能受到其他因素的干扰,如机械冲击、电磁干扰和电力波动等。
因此,在实际应用中,需要采取相应的措施来最大程度地减少这些干扰的影响。
总的来说,温度补偿晶振是一种高精度、可靠的电子元件,它可以在广泛的应用中确保设备的高精度工作。
随着科技的不断进步,温度补偿晶振的性能和应用场景也在不断扩展和升级,这将为电子技术的发展带来更多的可能性。
晶振工作原理及参数详解
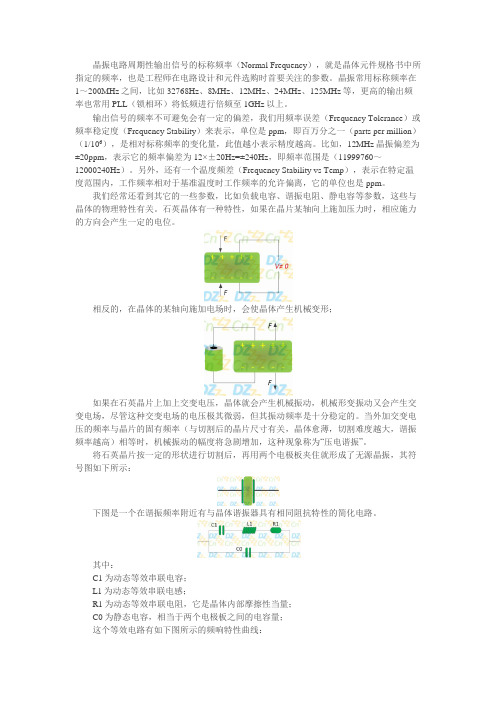
晶振电路周期性输出信号的标称频率(Normal Frequency),就是晶体元件规格书中所指定的频率,也是工程师在电路设计和元件选购时首要关注的参数。
晶振常用标称频率在1~200MHz之间,比如32768Hz、8MHz、12MHz、24MHz、125MHz等,更高的输出频率也常用PLL(锁相环)将低频进行倍频至1GHz以上。
输出信号的频率不可避免会有一定的偏差,我们用频率误差(Frequency Tolerance)或频率稳定度(Frequency Stability)来表示,单位是ppm,即百万分之一(parts per million)(1/106),是相对标称频率的变化量,此值越小表示精度越高。
比如,12MHz晶振偏差为±20ppm,表示它的频率偏差为12×±20Hz=±240Hz,即频率范围是(11999760~12000240Hz)。
另外,还有一个温度频差(Frequency Stability vs Temp),表示在特定温度范围内,工作频率相对于基准温度时工作频率的允许偏离,它的单位也是ppm。
我们经常还看到其它的一些参数,比如负载电容、谐振电阻、静电容等参数,这些与晶体的物理特性有关。
石英晶体有一种特性,如果在晶片某轴向上施加压力时,相应施力的方向会产生一定的电位。
相反的,在晶体的某轴向施加电场时,会使晶体产生机械变形;如果在石英晶片上加上交变电压,晶体就会产生机械振动,机械形变振动又会产生交变电场,尽管这种交变电场的电压极其微弱,但其振动频率是十分稳定的。
当外加交变电压的频率与晶片的固有频率(与切割后的晶片尺寸有关,晶体愈薄,切割难度越大,谐振频率越高)相等时,机械振动的幅度将急剧增加,这种现象称为“压电谐振”。
将石英晶片按一定的形状进行切割后,再用两个电极板夹住就形成了无源晶振,其符号图如下所示:下图是一个在谐振频率附近有与晶体谐振器具有相同阻抗特性的简化电路。
温补晶振的几个主要参数

温补晶振的几个主要参数
温补晶振是一种用于提高电子元件精度的技术,其主要参数包括
频率稳定度、温度系数、工作温度范围、工作电压等。
首先,频率稳定度是温补晶振的一个重要参数。
它表示晶振在不
同温度、电压和负载等条件下输出频率的稳定程度。
一个高质量的温
补晶振应具有高的频率稳定度,可以使电子设备在复杂环境下保持稳
定工作。
其次,温度系数也是一个关键参数。
它表示晶振的输出频率随着
温度的变化而产生的变化。
一个低温度系数的晶振可以保持在一个较
小的温度范围内保持稳定输出,从而提高电子设备的运行效率和精度。
此外,工作温度范围也是一个重要的参数。
它表示晶振可以在哪
些温度范围内稳定工作。
一般来说,工作温度范围越宽,晶振的使用
范围也就越广泛。
最后,工作电压是一个需要注意的参数。
它表示晶振在哪些电压
下可以正常工作。
如果工作电压不匹配,晶振就很难正常工作,可能
会产生不稳定的输出。
因此,在选择温补晶振时,需要根据实际需求选择具备合适参数
的晶振。
同时,在使用过程中还要注意对晶振进行正确的安装,避免
操作不当等因素对晶振的影响。
rtc温度补偿补偿晶振的精度

rtc温度补偿补偿晶振的精度1. 引言RTC(Real-Time Clock)是一种能够提供准确时间和日期信息的电子设备。
而晶振是RTC中的重要组成部分,负责提供稳定的时钟信号。
然而,晶振的频率会受到温度的影响而发生变化,从而影响RTC的准确性。
因此,为了提高RTC的精度,需要进行温度补偿。
2. 温度对晶振的影响温度会导致晶振的频率发生变化,主要原因是晶体的物理性质会随温度变化而改变。
一般来说,温度升高会导致晶体的振荡频率增加,温度降低则会使振荡频率减小。
这种频率变化对于RTC来说是不可忽视的,因为即使温度仅变化几度,晶振频率的变化也可能导致RTC的时间计算错误。
3. RTC温度补偿原理RTC温度补偿是通过测量环境温度并根据温度变化来调整晶振频率,从而实现对晶振精度的补偿。
一般来说,RTC温度补偿分为两个步骤:温度测量和频率补偿。
(1) 温度测量:通过传感器等设备测量环境温度,获取当前温度值。
(2) 频率补偿:根据温度的变化,计算需要补偿的频率值,并通过控制电路对晶振频率进行调整。
4. RTC温度补偿的应用RTC温度补偿广泛应用于需要高精度时间计算的领域,例如航空航天、通信设备、工业自动化等。
在这些领域中,时间的准确性对于系统的正常运行至关重要。
通过RTC温度补偿,可以提高系统的时间精度,减少时间误差,提高系统的可靠性和稳定性。
5. RTC温度补偿的实现RTC温度补偿的实现需要依赖精确的温度传感器、控制电路和补偿算法。
常见的温度传感器包括热敏电阻、温度传感器芯片等,用于测量环境温度。
控制电路则根据测量到的温度值计算需要补偿的频率值,并通过控制晶振的振荡电路对晶振频率进行调整。
补偿算法可以根据具体的应用需求进行设计,常见的有线性补偿、多项式补偿等。
6. RTC温度补偿的挑战与改进RTC温度补偿在实际应用中还面临一些挑战。
首先,温度传感器的精度和稳定性对补偿效果有重要影响,需要选择合适的传感器以确保温度测量的准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单, 加工方便. 目前所能达到的补偿精度一般为 10 ~10 .1998 年 12 月沈 阳 工 业 学 院 学 报V ol. 17 N o. 4第17卷 第4期JOURNAL OF SHENYANG INST IT U T E OF T ECH NOL OGYDec. 1 9 9 8温补晶振的热敏网络分析及参数计算崔旭晶( 沈阳工业学院自动控制系, 沈阳 110015)摘 要 论述了温度补偿石英晶体振荡器的工作原理, 对几种常见温 度补偿网络( 热敏网络) 进行试验分析, 利用 New t on 等方法计算热敏网络 参数并给出微机辅助设计.关键词 热敏网络, 曲线拟合, 残差.分类号 T M 1350 引言晶体振荡器的频率是随温度变化的. 为达到频率稳定的目的, 过去常加设一个恒温槽, 使 振荡器的体积大、造价高, 耗电功率增加, 还需预热时间. 而使用“温度补偿”的晶体振荡器可以 克服上述缺点, 并且对 AT 切晶体谐振器的各种频率温度系数曲线都能进行补偿, 有利于成批 生产. 温度补偿的方法是设计一个“热敏网络”, 该热敏网络由固定电阻和热敏电阻组成, 结构- 6 - 71 温补晶振的补偿原理及补偿过程如图 1 所示. 使用一个热敏网络和一个变容二极管, 变容二极管的结电容与其偏压成反 比. 晶体振荡器的负载电容基本上等于变容二极管的结电容. 当环境温度改变时, 使石英谐振 器的频率发生变化( 见图 2) , 热敏网络同时输出一个随温度变化的电压 V 0 , V 0 改变变容二极 管的结电容, 使石英晶体振荡器的频率变化. 当热敏网络随温度变化输出的 V 0 改变变容二极 管的结电容, 使晶体振荡器的频率变化( 曲线 b ) 和由于环境温度变化引起晶体振荡器的频率 变化( 曲线 a) 相反且相等时, 两种变化互相抵消得到稳定的频率曲线 c, 则达到补偿的目的.从上述补偿原理可得到补偿过程如下: 测试出补偿电压—温度曲线 ( V -T 曲线)用电位器代替热敏网络, 改变环境温度( 温度变化根据需要选取) , 使晶体振荡器的频率变 化, 记下对应温度的频率值. 调节电位器, 改变加在变容二极管上的偏压, 使晶体频率变化到等 于标称值, 记下对应温度变容二极管上的偏压值, 即得到第四象限中所需要的补偿电压 — 温R ( T ) = R 0eT28图 1 方框图沈 阳 工 业 学 院 学 报 1998 年图 2 温补晶振特性曲线间的关系度( V -T ) 曲线, 这样 V -T 曲线上的数据就测试出来了.根据 V -T 曲线上的数据, 计算出热敏网络中各电阻的阻值.总装后测试晶体振荡器的输出频率随环境温度变化的曲线( 即曲线 c) , 就得到补偿精度的结果.2 几种常见热敏网络分析热敏网络输出电压 V 0 的精度主要决定于热敏电阻的精度. 热敏电阻使用负温度系数, 其 阻值随温度变化的关系一般表示为B11 T - 1 0( 1)式中 T —— 绝对温度, T 0 = 293 K ;R 0——T 0 时的热敏电阻值; B 1—— 材料常数.从式( 1) 可以看出, 热敏电阻的阻值与温度成指数关系, B 1 是表征指数特性的一个常数, 可以用某些方法确定式( 1) 中的参数 R 0 和 B 1 值.用热敏电阻和固定电阻可组成各种形式的“温度补偿网络”, 即热敏网络. 补偿精度之高低 取决于热敏网络输出电压 — 温度( V 0 -T ) 曲线和所要求的补偿电压 — 温度( V -T ) 曲线的吻合 程度. 因此, 热敏网络的设计是整个补偿过程最关键的一步. 根据温补晶振频率稳定度的不同 要求, 热敏网络也各异, 一般频率稳定度愈高, 热敏网络愈复杂.常用的热敏网络有简单 型网络、单 型网络、双型网络、桥式网络和双臂网络五种型式. 图 3 给出其中三种型式.图 3a 是用得最多的一种网络. 这种网络只能输出二次曲线形状的电压, 因此只能补偿二 次曲线形状的晶体频率温度特性. 实验表明, 该网络从- 20~+ 60℃环温之间, 补偿精度可达 到±5×10- 7 , 少数可达到±2×10- 7, 但对晶体谐振器的切角要求比较严格.少数优于±1×10 .+ [ R 5 + R 4 ( T ) ]第 4 期 崔旭晶: 温补晶振的热敏网络分析及参数计算29( a) 简单 型网络 ( b) 单 型网络( c) 桥式网络图 3 热敏网络型式型网络有明显提高. 由实验得知, 在- 20~+ 60℃温度范围内, 补偿精度可以达到±2×10 - 7, 少数可以达到±1×10- 7 , 并且对二次形状和三次形状的晶体频率温度特性曲线都能补偿, 有 效地提高了晶体利用率.双臂网络实际上也是由两个网络同时补偿, 其作用和桥式网络相同, 但作用的温度范围比 桥式网络宽, 因而常用在- 55~+ 70℃环温范围内进行补偿. 补偿精度大部分优于±2×10 - 6, - 6实际设计时, 可根据温补晶振的技术要求, 采用上述各种不同的热敏网络. 现以简单型 网络为例, 说明热敏网络电阻分压与温度和各电阻 R i 的关系. 记 R 1、R 2( T ) 、R 3 组成的电阻为 f 1 ( T ) ; R 4 ( T ) 、R 5 组成的电阻为 f 2 ( T ) , 则根据电阻分压关系得R 3R 2( T )f 1( T ) = R 1 + R 3 + R 2( T ) f 2( T ) = R 5 + R 4( T )( 2) ( 3)V 0 ( T ) =E f 2( T ) f 1 ( T ) + f 2( T )= R 1 +E [ R 5 + R 4( T ) ] R 3R 2( T )R 3 + R 2( T )( 4)上式表明, 当电源电压 E 一定时, 热敏网络输出电压 V 0( T ) 是温度和各电阻 R i 的函数. 只要热 敏 电阻 B 值在一定取值范围, 各 R i 选择适当, V 0 ( T ) 就能按需要输出, 获得 V 0 随温度变化的 ( V 0-T ) 曲线和补偿电压 — 温度( V -T ) 曲线吻合一致.对于其它各种形式的热敏网络, 可以类似地推导出 V 0 依赖于 这些函数形式可用最一般的函数模型抽象地记为V 0 = f ( T , R 1, R 2, …, R m )和各参数 R i 的函数形式,这里 m 是任意整数, 简单 型网络中 m = 5. V 0 是各 R i 的非线性函数.= f ( T k , R 1 , R 2 , …, R m ) , ( T k , V k ) 为( T , V 0) 的 n 对观测值.- V ok ) =∑ j i, j = 1, 2, …, m a ij = g i = ∑( V k - f k 0), i = 1, 2, …, m 30沈 阳 工 业 学 院 学 报 1998 年3 热敏网络的参数计算3. 1 曲线拟合根据测试, 已知某振荡器所需要的补偿电压—温度 ( V -T ) 曲线; 若补偿网络的形式已定, 问各参数 R i 的值如何确定, 才能使热敏网络输出电压( V 0 -T ) 曲线和 V -T 曲线吻合.对于给定的热敏网络形式, 为求其参数 R i , 首先令 R i ( 0) 是 R i 的一个给定近似值( 初值) , 记 真值 R i 与近似值 R i ( 0) 之差为 i , 即R i = R i+ii = 1, 2, …, m( 5)这时确定 R i 的问题化为确定i的问题. 为了确定 i, 在 Ri附近对该网络的已知函数 V 0 = f ( T , R 1, R 2, …, R m ) 作台劳级数展开, 并略去二次以上高阶小量得f ( T k , R 1 , R 2 , …, R m ) ≈ f k 0 +n∑k = 1f R ii( 6)式中 fk 0( 0) ( 0) ( 0)R 1 = R 1( 0)f k 0 R i = f ( T k , R 1, R 2, …, R m ) R 2 = R 2( 0)i( 0)R m = R m在 R i给定时, 它们都可以直接求出.将式( 6) 代入残差平方和公式nnnQ =∑k = 12k=∑( Vk = 1k2∑[ Vk = 1k- f ( T k , R 1, R 2, …, R m ) ] 2并对各 Ri 求偏导数得Q R i = R in∑[ Vk = 1 k- f ( T k , R 1, R 2, …, R m ) ] 2n = - 2∑[ V k - f ( T k , R 1, R 2, …, R m ) ]k = 1 f kR in≈- 2∑ V k - f k 0 -k = 1 m∑j = 1f k 0 R jjf k 0R in= - 2∑( V k - f k 0)k = 1f k0R m+ 2∑ j = 1n∑k = 1f k 0 f k 0R i R jj记nnf k 0 f k 0k = 1R if k 0k = 1 R im在第一次迭代中, 先令 C = - 1, 则 d = p d = d , 若相应的 Q第 4 期 崔旭晶: 温补晶振的热敏网络分析及参数计算所以由上式便可得到 n 阶线性方程组:31a 11 1 + a 12 2 + … + a 1mm = g 1 a 21 1 …… + a 22 2+ … + a 2m m= g 2( 8)a m1 1 + a m 22 + … + a mmm= g m当给定测试值( T k , V k ) 及初值 R i后, 可按式( 7) 算出 a ij 和 g i , 然后用消去法解方程组( 8) 便可得到 i , 再按式( 5) 得 R i 的进一步估值.计算到此并没有结束, 因为线性化求解的关键 —— 台劳展开式( 6) 是近似的, 其前提是i较小, 以至可以忽略i二次以上的项. 当i值较大时, 式( 6) 的近似性可能很差, 此时可令当前 R i 值代替原来的 R i ( 0) 值, 重复式( 7) 求 a ij 和 g i , 并解式( 8) 得到新的 i , 及新的 R i . 这样反复迭代直到i 值可忽略不计, 就得到所需要的 R i 值. 上述计算方法称为高斯 -牛顿法. 此种算法的特点是对初值 R i ( 0) 的依赖非常强烈, 只有当 所给的 R i初值很接近真值 R i 时, 台劳展开式中方可略去二次以上的项. 若初值给得不好, 即i较大时, 台劳展开式( 6) 可能完全失真, 使上面的迭代过程“发散”, 得不到真解. 为了放宽 对初值的限制, 麦夸脱提出一种修改方案, 部分地克服了这个缺点.麦夸脱方法与牛顿法的差异仅在于确定i 的方程组不同, 这时方程组( 8) 改为: ( 1 + d ) a 11 1+ a 12 2 + … + a 1m m = g 1 a 21 1 …… + ( 1 + d ) a 222+ … + a 2mm= g 2( 9)a m11 + a m22 + … + ( 1 + d ) a m mm= g m即系数矩阵主对角线上加了一个常数因子 d ( d ≥ 0) , 当 d = 0 时为牛顿法.d 的选取方法如下:对于给定的初值 R i ( 0) , 先算出 Q ( 0) ;指定一个大于 1 的常数 p ( 如 p = 10) , 并给出 d 的初值 d ( 0)( 如 d= 0. 01) ;令 d = p Cd ( 0) , 式中 C = - 1, 0, 1, 2, …- 1= d( 0)/ p , 将 d 代入式( 9) 解出 i, 从而得到新 R i , 再算出 Q ( 1) . 若Q ( 1) ≤ Q ( 0) ( 10)则 C = - 1; 否则令 C = 0, 有 d = p( 0)d( 0)( 0)满足式( 10) , 则 C = 0; 否则令 C = 1, 有d = p 1 d ( 0) = p d ( 0) , 若相应Q ( 1) 满足式( 10) , 则 C = 1, 否则令C = 2, 有 d = p 2 d ( 0) …… 如此下去, 总能找到足够大的 C, 使式( 10) 满足.! 在下一次迭代时, 以 d 的当前值 p C d ( 0) 替代原来的 d ( 0) , 重复 的步骤, 直到迭代结束( 即 Q < 0. 02) .麦夸脱的改进方法比牛顿法对初值的选取可以放宽大约一个数量级, 但也不是任意的, 因 此仍存在选取较好初值的问题.3. 2 微机辅助设计感谢您试用AnyBizSoft PDF to Word。
