案例一:用回归模型预测木材剩余物_计量经济学
利用一元线性回归方程计算盗伐林木材积试验

利用一元线性回归方程计算盗伐林木材积试验粟军【摘要】盗伐林木案件中,如现地伐桩保存完好,但无采伐木,周围有林相、结构相同或相近林分的情况下,利用样木的根径和胸径测量数据,建立线性回归方程计算出盗伐林木的回归胸径,再利用其树高的测量数据建立树高曲线对数回归方程,计算出盗伐林木的回归树高,并利用统计学原理,对回归胸径进行相关系数检验,对回归树高进行F检验.试验结果认为,利用该方法能使盗伐林木的蓄积量计算值更加接近实际值.%For the illegal logging cases,in which stump was preserved without cutting wood and surroun -ded by stand with the same or similar forest form and structure,the linear regression equation was set up to calculate the regression DBH of the illegal logging based on the data of sample trees' ground diameter and DBH,and the logarithmic curve regression equation was set up to calculate the regression height of the illegal logging based on the data of sample trees' height.With the principle of Statistics,the related-coefficient test of regression DBH and F-test of regression tree height showed that stock volume of the ille-gal logging calculated by this method was precision.【期刊名称】《林业调查规划》【年(卷),期】2017(042)005【总页数】6页(P14-19)【关键词】盗伐林木;胸径回归;树高回归;一元线性回归;二元材积;相关系数检验;F 检验;材积计算【作者】粟军【作者单位】西双版纳布龙州级自然保护区管护所,云南景洪666100【正文语种】中文【中图分类】S711;S758在《云南省林地鉴定规范(暂行)》第十七条规定中,关于现地伐桩保存完好,但无采伐木,周围有林相、结构相同相近林分的,直接每木检尺伐桩、鉴定树种、查数年轮,统计株数。
《计量经济学》案例:用回归模型预测木材剩余物(一元线性回归)

案例:用回归模型预测木材剩余物(一元线性回归)伊春林区位于黑龙江省东北部。
全区有森林面积2189732公顷,木材蓄积量为23246.02万m 3。
森林覆盖率为62.5%,是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m 3。
按此速度44年之后,1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式,保护森林生态环境。
为缓解森林资源危机,并解决部分职工就业问题,除了做好木材的深加工外,还要充分利用木材剩余物生产林业产品,如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面,利用简单线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表2.1。
散点图见图2.14。
观测点近似服从线性关系。
建立一元线性回归模型如下:y t = β0 + β1 x t + u t表2.1 年剩余物y t 和年木材采伐量x t 数据林业局名 年木材剩余物y t (万m 3) 年木材采伐量x t(万m 3) 乌伊岭 26.1361.4 东风 23.49 48.3 新青 21.97 51.8 红星 11.53 35.9 五营 7.18 17.8 上甘岭 6.80 17.0 友好 18.43 55.0 翠峦 11.69 32.7 乌马河 6.80 17.0 美溪 9.69 27.3 大丰 7.99 21.5 南岔 12.15 35.5 带岭 6.80 17.0 朗乡 17.20 50.0 桃山 9.50 30.0 双丰 5.52 13.8 合计202.87532.005101520253010203040506070yx图2.14 年剩余物y t 和年木材采伐量x t 散点图图2.15 Eviews 输出结果Eviews 估计结果见图2.15。
建立Eviews 数据文件的方法见附录1。
Eviews应用举例

Eviews应用举例例1 估计线性回归模型下面结合关于木材剩余物案例介绍怎样(1)建立数据文件;(2)画图;(3)进行OLS 回归。
1. 建立数据文件建立新工作文件的方法是打开EViews。
从EViews主菜单中单击File键,选择New, Workfile。
则打开一个Workfile Range选择框(数据范围)。
三项选择是①Workfile frequenc y(数据频率);②Start date(启始期);③End date(终止期)。
因为样本是16个农场的截面观测值,所以在第①项选择中选Undated or irregular(非时序数据)(点击相应小方块)。
第②项选择中的1自动生成,第③项选择的位置键入16。
点击“OK”键。
这时会建立起一个尚未命名的工作文件(Workfile)。
输入数据的方法是从EViews主菜单中点击Quick键,选择Empty Group功能。
从而打开一个空白表格数据窗口(Group)。
每一个空格代表一个观测值位置。
按列依次输入每一个变量(或序列)的观测值。
键入每一个观测值后,可通过按回车键(Enter键)或方向指示键(↓)进行确认。
按方向指示键(↓)的好处是在确认了当前输入的观测值的同时,还把光标移到了下一个待输入位置。
从与1相对应的空格开始按列依次输入观测值。
每一列数据上方的灰色空格是用于输入变量名的。
给变量命名时,字符不得超过16个。
分别给变量定名为Y和X。
这时在工作文件中出现了Y和X两个序列名。
(在此之前用SER01, SER02表示)注意:下列名字具有特殊意义,给变量命名时,应避免使用。
它们是:ABS,ACOS ,AR,ASIN,C,CON,CNORM,COEF,COS,D,DLOG,DNORM,ELSE,ENDIF,EXP,LOG,LOGIT,LPT1,LPT2,MA,NA,NRND,PDL,RESID,RND,SAR,SIN,SMA,SQR,THEN。
基于多重多元回归的木材干燥质量预测模型

1t e h mii .a d d n i h n e e d n a a ls n rig srs d mosu o tn ste d p n e t ai u dt n 州 g t v y me a te id p n e tv rb e ,a d dyn tesa itr cne ta h e d n s i n e e
第4 0卷 第 6期
21 0 2年 6月 ቤተ መጻሕፍቲ ባይዱ
东
北
林
业
大
学
学
报
Vo. 0 No 6 14 .
J OURNAL OF NO UHEA T F ES RY I S OR T UNI RS T VE I Y
Jn 0 2 u .2 1
基 于 多 重 多 元 回 归 的木 材 干 燥 质 量 预 测 模 型
y
内部因子主要是树种 , 木料厚度 和含水率等。木材 干 燥过 程 中 , 内部 因子 是不 能控 制 的 , 只能通 过外 部
因子 的控制 来达 到提 高干燥 质 量 的最终 目的 。压 力
则 多 重多 兀线 性 回归模 型 可以缩 写成
y:( ) J
L J
() 2
和气流速度 , 在干燥设备 安装完毕后 , 一般 都 已固
v ra l s t t t a infc c s h w h t h d l t h a u e a awel i i h p e iin a ib e .S ai i lsg i a e t t o s t a e mo e st e me r d d t l,w t a h g rc s . sc in e s t i f s h o Ke wo d D i g q ai ;Mut a it e rs i n r d ci n mo e s y rs y r n u lt y l v rae r g e so :P e it d l i o
计量经济学回归分析模型

计量经济学回归分析模型计量经济学是经济学中的一个分支,通过运用数理统计和经济理论的工具,研究经济现象。
其中回归分析模型是计量经济学中最为常见的分析方法之一、回归分析模型主要用于确定自变量与因变量之间的关系,并通过统计推断来解释这种关系。
回归分析模型中的关系可以是线性的,也可以是非线性的。
线性回归模型是回归分析中最为常见和基础的模型。
它可以表示为:Y=β0+β1X1+β2X2+...+βkXk+ε其中,Y代表因变量,X1,X2,...,Xk代表自变量,β0,β1,β2,...,βk代表回归系数,ε代表随机误差项。
回归模型的核心是确定回归系数。
通过最小二乘法估计回归系数,使得预测值与实际观测值之间的差异最小化。
最小二乘法通过使得误差的平方和最小化来估计回归系数。
通过对数据进行拟合,我们可以得到回归系数的估计值。
回归分析模型的应用范围非常广泛。
它可以用于解释和预测经济现象,比如价格与需求的关系、生产力与劳动力的关系等。
此外,回归分析模型还可以用于政策评估和决策制定。
通过分析回归系数的显著性,可以判断自变量对因变量的影响程度,并进行政策建议和决策制定。
在实施回归分析模型时,有几个重要的假设需要满足。
首先,线性回归模型要求因变量和自变量之间存在线性关系。
其次,回归模型要求自变量之间不存在多重共线性,即自变量之间没有高度相关性。
此外,回归模型要求误差项具有同方差性和独立性。
在解释回归分析模型的结果时,可以通过回归系数的显著性来判断自变量对因变量的影响程度。
显著性水平一般为0.05或0.01,如果回归系数的p值小于显著性水平,则说明该自变量对因变量具有显著影响。
此外,还可以通过确定系数R^2来评估模型的拟合程度。
R^2可以解释因变量变异的百分比,值越接近1,说明模型的拟合程度越好。
总之,回归分析模型是计量经济学中非常重要的工具之一、它通过分析自变量和因变量之间的关系,能够解释经济现象和预测未来走势。
在应用回归分析模型时,需要满足一定的假设条件,并通过回归系数和拟合优度来解释结果。
一元回归案例数据
10.案例:用回归模型预测木材剩余物(1c)伊春林区位于黑龙江省东北部。
全区有森林面积218.9732万公顷,木材蓄积量为2.324602亿m3。
森林覆盖率为62.5%,是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m3。
按此速度44年之后,1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式,保护森林生态环境。
为缓解森林资源危机,并解决部分职工就业问题,除了做好木材的深加工外,还要充分利用木材剩余物生产林业产品,如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面,利用一元线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表2.1。
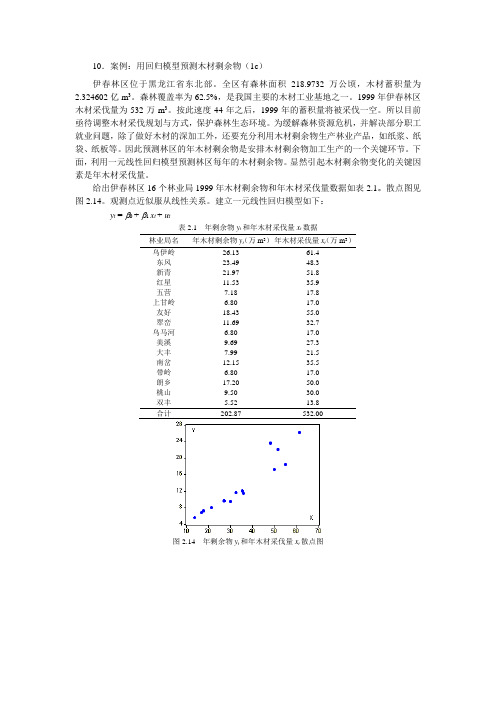
散点图见图2.14。
观测点近似服从线性关系。
建立一元线性回归模型如下:y t = β0 + β1 x t + u t表2.1 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t(万m3)年木材采伐量x t(万m3)乌伊岭26.13 61.4东风23.49 48.3新青21.97 51.8红星11.53 35.9五营7.18 17.8上甘岭 6.80 17.0友好18.43 55.0翠峦11.69 32.7乌马河 6.80 17.0美溪9.69 27.3大丰7.99 21.5南岔12.15 35.5带岭 6.80 17.0朗乡17.20 50.0桃山9.50 30.0双丰 5.52 13.8合计202.87 532.00图2.14 年剩余物y t和年木材采伐量x t散点图图2.15 EViews 输出结果EViews 估计结果见图2.15。
建立EViews 数据文件的方法见附录1。
在已建立Eviews 数据文件的基础上,进行OLS 估计的操作步骤如下:打开工作文件,从主菜单上点击Quick 键,选Estimate Equation 功能。
计量经济学模型应用例题和知识点总结

计量经济学模型应用例题和知识点总结计量经济学作为一门将经济理论、统计学和数学相结合的学科,旨在通过建立经济模型来分析和预测经济现象。
在实际应用中,计量经济学模型发挥着重要作用,为政策制定、企业决策等提供了有力的支持。
接下来,我们将通过一些具体的例题来展示计量经济学模型的应用,并对相关知识点进行总结。
一、简单线性回归模型简单线性回归模型是计量经济学中最基本的模型之一,其表达式为:$Y =\beta_0 +\beta_1 X +\epsilon$,其中$Y$是被解释变量,$X$是解释变量,$\beta_0$是截距项,$\beta_1$是斜率系数,$\epsilon$是随机误差项。
例如,我们想要研究家庭收入($X$)对家庭消费支出($Y$)的影响。
通过收集一定数量的家庭样本数据,运用最小二乘法估计出模型的参数$\beta_0$和$\beta_1$。
在这个例题中,需要掌握的知识点包括:1、最小二乘法的原理和计算方法,其目标是使残差平方和最小。
2、模型的假设条件,如随机误差项的均值为零、同方差、无自相关等。
3、参数的经济意义和统计显著性检验。
二、多元线性回归模型当影响被解释变量的因素不止一个时,就需要使用多元线性回归模型,其表达式为:$Y =\beta_0 +\beta_1 X_1 +\beta_2 X_2 +\cdots +\beta_k X_k +\epsilon$。
假设我们要研究一个地区的房价($Y$)与房屋面积($X_1$)、地理位置($X_2$)、房龄($X_3$)等因素的关系。
相关知识点:1、多重共线性的概念和检验方法,避免解释变量之间存在高度线性相关。
2、逐步回归法用于筛选重要的解释变量。
3、调整的可决系数用于比较不同模型的拟合优度。
三、异方差性在回归模型中,如果随机误差项的方差不是常数,就存在异方差性。
例如,研究不同规模企业的利润($Y$)与销售额($X$)的关系,可能会出现大企业的利润波动较大,小企业的利润波动较小的情况,即存在异方差。
最小二乘估计量的性质

第三节 最小二乘估计量的性质三大性质:线性特性、无偏性和最小偏差性 一、 线性特性的含义线性特性是指参数估计值1ˆβ和2ˆβ分别是观测值t Y 或者是扰动项t μ的线性组合,或者叫线性函数,也可以称之为可以用t Y 或者是t μ来表示。
1、2ˆβ的线性特征证明 (1)由2ˆβ的计算公式可得: 222222()ˆt tttt ttttttt tt tt x y x Y x Y xxx xx x x x β--===⎛⎫== ⎪ ⎪⎝⎭∑∑∑∑∑∑∑∑∑∑∑Y Y Y Y需要指出的是,这里用到了因为t x 不全为零,可设2tt tx b x =∑,从而,t b 不全为零,故2ˆt t b β=∑Y 。
这说明2ˆβ是t Y 的线性组合。
(2)因为12t t t Y X ββμ=++,所以有()212122ˆt t t t t t t t t t t tb b X b b X b b βββμββμβμ==++=++=+∑∑∑∑∑∑Y这说明2ˆβ是t μ的线性组合。
需要指出的是,这里用到了220t t t t t x x b x x ===∑∑∑∑∑以及 ()2222222201t t tt t t tt ttttttttx x X x b X X x x x x X x X x x x x x⎛⎫+⎪== ⎪⎝⎭++==+=∑∑∑∑∑∑∑∑∑∑∑∑∑2、1ˆβ的线性特征证明 (1)因为12ˆˆY X ββ=-,所以有 ()121ˆˆ1t t t t tY X Y X b nXb n ββ=-=-⎛⎫=- ⎪⎝⎭∑∑∑Y Y这里,令1a Xb n=-,则有1ˆt a β=∑Y 这说明1ˆβ是t Y 的线性组合。
(2)因为回归模型为12t t t Y X ββμ=++,所以()11212ˆt t t t t t t t t ta a X a a X a βββμββμ==++=++∑∑∑∑∑Y因为111t t t a Xb X b nn⎛⎫=-=-=⎪⎝⎭∑∑∑∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例一:用回归模型预测木材剩余物(file:b1c3)
伊春林区位于黑龙江省东北部。
全区有森林面积218.9732万公顷,木材蓄积量为2.324602亿m3。
森林覆盖率为62.5%,是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m3。
按此速度44年之后,1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式,保护森林生态环境。
为缓解森林资源危机,并解决部分职工就业问题,除了做好木材的深加工外,还要充分利用木材剩余物生产林业产品,如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面,利用一元线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
给出伊春林区16个林业局1999年木材剩余物和年木材采伐量数据如表1.1。
散点图见图1.1。
观测点近似服从线性关系。
建立一元线性回归模型如下:
y t = β0 + β1 x t + u t
表1.1 年剩余物y t和年木材采伐量x t数据
林业局名年木材剩余物y t(万m3)年木材采伐量x t(万m3)
乌伊岭26.13 61.4
东风23.49 48.3
新青21.97 51.8
红星11.53 35.9
五营7.18 17.8
上甘岭 6.80 17.0
友好18.43 55.0
翠峦11.69 32.7
乌马河 6.80 17.0
美溪9.69 27.3
大丰7.99 21.5
南岔12.15 35.5
带岭 6.80 17.0
朗乡17.20 50.0
桃山9.50 30.0
双丰 5.52 13.8
合计202.87 532.00
图1.1 年剩余物y t和年木材采伐量x t散点图
图1.2 EViews 输出结果
EViews 估计结果见图1.2。
在已建立Eviews 数据文件的基础上,进行OLS 估计的操作步骤如下:打开工作文件,从主菜单上点击Quick 键,选Estimate Equation 功能。
在出现的对话框中输入y c x 。
点击Ok 键。
立即会得到如图1.2所示的结果。
下面分析EViews 输出结果。
先看图1.2的最上部分。
被解释变量是y t 。
估计方法是最小二乘法。
本次估计用了16对样本观测值。
输出格式的中间部分给出5列。
第1列给出截
距项(C )和解释变量x t 。
第2列给出第1列相应项的回归参数估计值(0ˆβ和1ˆ
β)。
第3列
给出相应回归参数估计值的样本标准差(s(0ˆβ), s(1ˆ
β))。
第4列给出相应t 值。
第5列给出t 统计量取值大于用样本计算的t 值(绝对值)的概率值。
以t = 12.11266为例,相应概率0.0000表示统计量t 取值(绝对值)大于12.1的概率是一个比万分之一还小的数。
换句话说,若给定检验水平为0.05,则临界值为t 0.05 (14) = 2.15。
t = 12.1>2.15落在了H 0的拒绝域,所以结论是β1不为零。
输出格式的最下部分给出了评价估计的回归函数的若干个统计量的值。
依纵向顺序,这些统计量依次是可决系数R 2、调整的可决系数2
R (第3章介绍)、回归函
数的标准差(s.e.,即均方误差的算术根σˆ)、残差平方和、对数极大似然函数值(第2章介
绍)、DW 统计量的值、被解释变量的平均数(y )、被解释变量的标准差()(t y s )、赤池(Akaike )信息准则(是一个选择变量最优滞后期的统计量)、施瓦茨(Schwatz )准则(是一个选择变量最优滞后期的统计量)、F 统计量(第3章介绍)的值以及F 统计量取值大于该值的概率。
注意:S.D.和s.e.的区别。
s.e.和SSE 的关系。
根据EViews 输出结果(图1.2),写出OLS 估计式如下:
t y
ˆ=
-0.7629 + 0.4043
x t
(1.1)
(-0.6) (12.1) R 2
= 0.91, s. e . = 2.04
其中括号内数字是相应t 统计量的值。
s.e .是回归函数的标准误差,即σˆ=)216(ˆ2-∑t u 。
R 2是可决系数。
R 2 = 0.91说明上式的拟合情况较好。
y t 变差的91%由变量x t 解释。
检验回归系数显著性的原假设和备择假设是(给定α = 0.05)
H 0:β1 = 0; H 1:β1 ≠ 0
图1.3 残差图
因为t = 12.1 > t 0.05 (14) = 2.15,所以检验结果是拒绝β1 = 0,即认为年木材剩余物和年木材采伐量之间存在回归关系。
上述模型的经济解释是,对于伊春林区每采伐1 m 3木材,将平均产生0.4 m 3的剩余物。
图1.3给出相应的残差图。
Actual 表示y t 的实际观测值,Fitted 表示y t 的拟合值t y ˆ,Residual 表示残差t u ˆ。
残差图中的两条虚线与中心线的距离表示残差的一个标准差,即s.e .。
通过残差图可以看到,大部分残差值都落在了正、负一个标准差之内。
估计β1的置信区间。
由
t = P {
)
ˆ
(1
11
ˆβββs -≤ t 0.05 (14) } = 0.95
得
1
1ˆββ-≤ t 0.05 (14) )ˆ
(1βs β1的置信区间是
[1ˆβ- t 0.05 (14) )ˆ(1βs , 1ˆ
β+ t 0.05 (14) )ˆ(1βs ]
[0.4043 - 2.15 ⨯ 0.0334, 0.4043 + 2.15 ⨯ 0.0334]
[0.3325, 0.4761]
以95%的置信度认为,β1的真值范围应在[0.3325, 0.4761 ]范围中。
下面求y t 的点预测和平均木材剩余物产出量的置信区间预测。
假设乌伊岭林业局2000年计划采伐木材20万m 3,求木材剩余物的点预测值。
y
ˆ2000 = - 0.7629 + 0.4043 x 2000
= -0.7629 + 0.4043 ⨯ 20 = 7.3231万m 3
s 2(E (y ˆ2000
)) = 2ˆσ(T 1
+ ∑--22
)()(x x x x F ) = 4.1453 (161+2606.3722)25.3320(2
-) = 0.4546
s (E (y ˆ2000)) =
4546.0= 0.6742 因为
E (y ˆ2000) = E(0ˆβ+1ˆβx 2000 ) = β0 + β1 x 2000 = E(y 2000)
t = )ˆ()(ˆ200020002000y s y E y
-~ t (T -2)
则置信度为0.95的2000年平均木材剩余物E(y 2000)的置信区间是
y
ˆ2000 ± t 0.05 (14) s (E (
y
ˆ2000)) = 7.3231 ± 2.15 ⨯ 0.6742
= 5.8736, 8.7726
从而得出预测结果,2000年若采伐木材20万m 3,产生木材剩余物的点估计值是7.3231万m 3。
平均木材剩余物产出量的置信区间估计是在 [5.8736, 8.7726] 万m 3之间。
从而为恰当安排2000年木材剩余物的加工生产提供依据。
木材剩余物产出量单点的置信区间的计算。
s 2(y ˆ2000) = 2ˆσ(1+T 1+ ∑--22
)()(x x x x F )
= 4.1453 (1+161+2606.3722)25.3320(2
-) = 4.5999
s (y ˆ2000)
EViews 通过预测程序计算的结果是
,
木材剩余物产出量单点的置信区间的估计结果是
y
ˆ2000 ± t 0.05 (14) s (
y
ˆ2000) = 7.3231 ± 2.15 ⨯ 2.145 = [2.71,11.93]
问题:估计结果中0ˆ
β没有显著性,去掉截距项 β0可以吗?
答:依据实际意义可知,没有木材采伐量就没有木材剩余物,所以理论上β0是可以取零的。
而有些问题就不可以。
例如家庭消费和收入的关系。
即使家庭收入为零,消费仍然非零。
一般来说,截距项的估计量没有显著性时,也不做剔出处理。
本案例剔出截距项后的估计结果是
t y
ˆ= 0.3853 x t
(28.3) R 2
= 0.91, s. e . = 2.0
点预测值是
y
ˆ2000 = 0.3853 x 2000 = 0.3853 ⨯ 20 = 7.7060
万m 3。
