数学真题2018广东3+证书高职高考数学试题和参考答案解析
广东高职数学试题及答案
广东高职数学试题及答案一、选择题（每题3分，共30分）1. 以下哪个选项是函数\( f(x) = x^2 \)的导数？A. \( 2x \)B. \( x^2 \)C. \( x \)D. \( 2 \)答案：A2. 计算极限\( \lim_{x \to 0} \frac{\sin x}{x} \)的值是多少？A. 0B. 1C. \( \pi \)D. \( \infty \)答案：B3. 以下哪个选项是\( \ln e \)的值？A. 0B. 1C. \( e \)D. \( \infty \)答案：B4. 函数\( y = \frac{1}{x} \)在哪个区间上是增函数？A. \( (-\infty, 0) \)B. \( (0, +\infty) \)C. \( (-\infty, 0) \cup (0, +\infty) \)D. \( (-\infty, 0) \cap (0, +\infty) \)答案：C5. 以下哪个选项是方程\( x^2 - 4x + 4 = 0 \)的解？A. \( x = 2 \)B. \( x = -2 \)C. \( x = 1 \)D. \( x = 3 \)答案：A6. 以下哪个选项是双曲线\( \frac{x^2}{a^2} - \frac{y^2}{b^2} =1 \)的渐近线？A. \( y = \pm \frac{b}{a}x \)B. \( y = \pm \frac{a}{b}x \)C. \( y = \pm x \)D. \( y = \pm \sqrt{a^2 + b^2}x \)答案：B7. 以下哪个选项是函数\( y = \sin x \)的周期？A. \( 2\pi \)B. \( \pi \)C. \( \frac{\pi}{2} \)D. \( \frac{2\pi}{3} \)答案：A8. 以下哪个选项是函数\( y = \ln(x+1) \)的定义域？A. \( (-\infty, -1] \)B. \( (-1, +\infty) \)C. \( [0, +\infty) \)D. \( (-\infty, 0) \)答案：B9. 以下哪个选项是函数\( y = x^3 - 3x \)的极值点？A. \( x = 0 \)B. \( x = 1 \)C. \( x = -1 \)D. \( x = 2 \)答案：C10. 以下哪个选项是函数\( y = \frac{1}{x} \)的值域？A. \( (-\infty, 0) \cup (0, +\infty) \)B. \( (-\infty, 0) \)C. \( (0, +\infty) \)D. \( [0, +\infty) \)答案：A二、填空题（每题4分，共20分）1. 函数\( f(x) = x^3 \)的导数是\( \_\_\_\_\_\_ \)。
2018广东高职高考A卷数学试卷 教师版(学霸教育独家放送)
） D. 2(1－2n－1)
∴1+
1 2
+
1 22
+
1 23
+
1 24
+
1 2n1
＝
a1(qn 1) q 1
1 ＝
1 n 2
1 1
1
＝2(1－2－n)
2
9．（2018 广东高职高考 T9）若向量 AB (1，2) ， AC (3，4)，则 BC ＝
A. 3x－y－3＝0
B. 3x＋y－9＝0
C. 3x－y－10＝0
D. 3x＋y－8＝0
答案：A
解析：AB
中点（2，3）kAB＝
2-4 5-(-1)
＝
-
1 3
AB 垂直平分线 k＝3
∴AB 垂直平分线是 y＝3（x－2）＋3 即 3x－y－3＝0
14．（2018 广东高职高考 T14）数列an 为等比数列，前 n 项和 Sn＝3n＋1＋a，a＝（ ）
（2）由（1）得：A＝－（x－52）2＋245（0＜x＜5）
当 A＝52时，A 最大＝245
（3）由题得 C＝2πr＝10 解得：r＝5π
∴S＝πr2＝2π5
由（2）得 A 最大＝245 ∵π＜4 ∴S＞A
22．（2018 广东高职高考 T22）数列an 为等差数列 a1＋a2＋a3＝6，a5＋a6＝25，
∴f（π8）＝3sin（2×π8＋������）＝3sin（π4＋������） ＝3（sin������cosπ4＋ sinπ4cos������）
＝3（
2 3
×
22＋
2 2×
7） 3
＝ 14 +1 2
2018广东春季高考数学详解
2018广东春季高考数学详解2018年广东春季高考数学试卷是广东省实施的高考改革试点年度，在数学考试中，注重培养学生的综合能力、创新思维和实践能力等方面的综合素养。
下面将对2018年广东春季高考数学试卷进行详解。
首先，我们来看看试卷的整体框架。
2018年广东春季高考数学试卷共分为两卷，卷一为选择题，卷二为非选择题。
卷一中，共有25个选择题，分为A、B两卷，每卷有12个选择题和1个解答题。
卷二为非选择题，共有9个题目。
在选择题考查的知识点上，2018年广东春季高考数学试卷涵盖了高中数学的各个方面，如函数、二次函数、指数函数、对数函数、三角函数、数列等。
这些知识点在高中数学课程中是非常重要的，也是学生需要掌握的基本知识。
在解答题的部分，2018年广东春季高考数学试卷更加注重考查学生的综合能力和思维能力。
对于许多题目，要求学生综合运用不同的知识和方法进行解答。
例如第26题要求学生根据给定的方程，判断方程在坐标平面上的图象与所给图象的关系，并给出理由。
这个题目考查了学生对方程图象性质的理解和判断的能力。
再比如第35题，要求学生通过观察已知函数的图象，找到适当的函数表达式，并解答相关问题。
这个题目考查了学生利用已知条件得出结论的能力。
除了基本的知识和思维能力的考查外，2018年广东春季高考数学试卷还注重考查学生的实践能力。
例如第28题要求学生利用尺规作图的方法来解决问题。
这个题目考查了学生的实践操作能力和几何问题的解决能力。
总的来说，2018年广东春季高考数学试卷在考查的内容上比较全面，不仅注重基本知识的考察，还注重综合能力和实践能力的考察。
这要求学生对数学知识有较为全面和深入的理解，能够运用多种知识和方法来解决问题。
对于考生来说，要做好备考准备，掌握好基础知识，提高思维能力和实践能力，才能在考试中取得好的成绩。
最后，希望广东的考生们能够充分发挥自己的水平和能力，取得优异的成绩！。
最新-2018年普通高等学校招生全国统一考试数学理试题广东卷含答案 精品003
2018年普通高等学校招生全国统一考试数学理试题（广东卷，含答案）参考公式：柱体的体积公式V =Sh ，其中S 为柱体的底面积，h 为柱体的高； 线性回归方程y bx a =+中系数计算公式为1122211()()()nnii i ii i nniii i xx y y x yx y b xx xnxη====---==--∑∑∑∑，a y bx =-，其中,x y 表示样本均值；若n 是正整数，则()n n a b a b -=-12(n n a a b --++ (2)1n n ab b --+）.一、 选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．设复数z 满足()12i z +=，其中i 为虚数单位，则z = A ．1i + B. 1i -C. 22i +Ｄ．22i -２．已知集合(){,A x y =∣,x y 为实数，且}221xy +=，(){,B x y =∣,x y 为实数，且}y x =，则A B 的元素个数为Ａ．０ Ｂ．１ Ｃ．２ Ｄ．３ ３．若向量a, b, c 满足a ∥b 且a ⊥c ，则(2)⋅+=c a bＡ．４ Ｂ．３Ｃ．２Ｄ．０４．设函数()f x 和()g x 分别是Ｒ上的偶函数和奇函数，则下列结论恒成立的是 Ａ．()()f x g x +是偶函数 Ｂ．()()f x g x -是奇函数 Ｃ．()()f x g x +是偶函数 Ｄ．()()f x g x -是奇函数5．在平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定。
若(,)M x y 为D 上的动点，点A的坐标为，则=⋅z OM OA 的最大值为 A． B． C ．４D ．３６．甲、乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军，若两队胜每局的概率相同，则甲队获得冠军的概率为 A ．12 B ．35 C ．23 D ．34７．如下图，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则几何体的体积为正视图侧视图Ａ．Ｂ．Ｃ．Ｄ．8．设S 是整数集Z 的非空子集，如果,,a b S ∀∈有ab S ∈，则称S 关于数的乘法是封闭的，若T ,V 是Z 的两个不相交的非空子集，TV Z =且,,,a b c T ∀∈有;,,,abc T x y z V ∈∀∈有xyz V ∈，则下列结论恒成立的是A.,T V 中至少有一个关于乘法是封闭的B. ,T V 中至多有一个关于乘法是封闭的C.,T V 中有且只有一个关于乘法是封闭的D. ,T V 中每一个关于乘法都是封闭的二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分。
广东省高职高中高考数学试卷试题有包括答案.docx
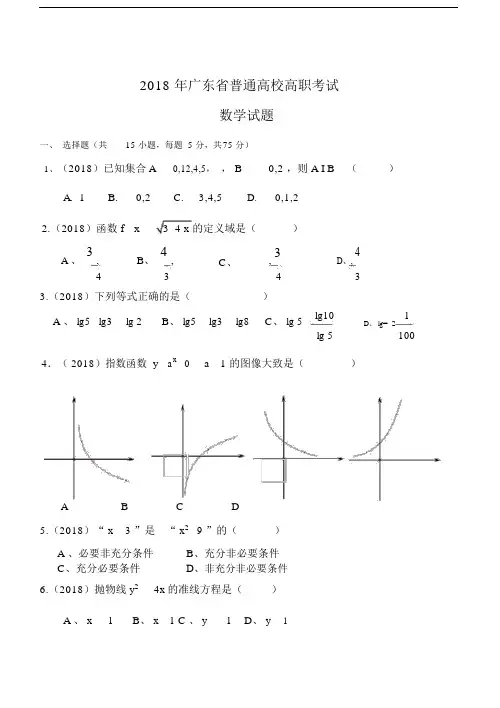
2018 年广东省普通高校高职考试数学试题一、 选择题（共15 小题，每题 5 分，共 75 分）1、（2018）已知集合 A 0,12,4,5， ， B 0,2 ，则 A I B （）A. 1B. 0,2C.3,4,5D.0,1,22.（2018）函数 f x3 4 x 的定义域是（）A 、 3,B 、 4,C 、,3D 、,4434 33.（2018）下列等式正确的是（）A 、 lg5 lg3lg 2B 、 lg5lg3lg8C 、 lg 5lg101 lg 5D 、 lg = 21004．（ 2018）指数函数 y a x 0a 1 的图像大致是（ ）AB C D5.（2018）“ x3 ”是 “ x 2 9 ”的（）A 、必要非充分条件B 、充分非必要条件C 、充分必要条件D 、非充分非必要条件6.（2018）抛物线 y 24x 的准线方程是（）A 、 x1B 、 x 1C 、 y 1D 、 y17. （ 2018）已知 ABC ， BC3, AC6, C90 ，则（ ）A 、 sin A2 B 、coA=62D 、 cos( A B)12C 、 tan A311 1 1L1（）8.（2018） 12223 24 2n 12A 、 2 ( 12 n ) B 、 2 ( 121 n )C 、 2 ( 12n 1 )D 、 2 ( 12n )uuuruuur 3,4uuur9.（2018）若向量 AB 1,2 , AC，则 BC （）A 、 4,6B 、 2, 2C 、 1,3D 、 2,210.（2018）现有 3000 棵树，其中 400 棵松树，现在提取 150 做样本，其中抽取松树 做样本的有（ ）棵A 、15B 、 20C 、25D 、 30 11.（2018） f xx3 , x 0，则 ff 2（）x 21, x 0A 、1B 、0C 、 1D 、 212. （2018）一个硬币抛两次，至少一次是正面的概率是（）A 、1B 、1C 、2D 、3323 413.（2018）已知点 A 1,4 , B 5,2 ，则 AB 的垂直平分线是（）A 、 3x y 3B 、 3xy 9 0C 、 3x y 100 D 、 3x y 8 0 14.（2018）已知数列 a n 为等比数列，前 n 项和 S n3n 1a ，则 a（）A 、 6B 、 3C 、0D 、315.（2018）设 f x 是定义在 R 上的奇函数，且对于任意实数 x ，有 fx 4f x ，若 f 1 3 ，则 f 4f 5（ ）A 、 3B 、3C 、 4D 、6二、二、填空题（共 5 小题，每题 5 分，共25 分）16、（2018）双曲线x2y21的离心率 e；432r r r r r17、（2018）已知向量 a，，，若 a b ，则 b；4 3 , b x 418、（2018）已知数据10, x,11, y,12, z的平均数为8，则 x, y, z 的平均数为；19、（2018）以两直线x y0 和 2x y 3 0 的交点为圆心，且与直线 2x y 2 0相切的圆的标准方程是；20 已知ABC对应边分别为的内角A B，C的对边分别为a, b, c ，已知 3b 4a, B 2 A，，则 cosA；三、解答题（ 50 分）21、（ 2018）矩形周长为10，面积为 A ，一边长为x。
(完整word版)高职高考数学试卷
2018年广东省高职高考数学模拟试卷一、选择题：本大题共15小题，没小题5分，满分75分. 1．若集合{}2,3,A a =，{}1,4B =，且{}4AB =，则a = A ．4 B ．3C ．2D ．12．函数 y =A ．(),-∞+∞B ．3,2⎛⎤-∞- ⎥⎝⎦C ．3,2⎡⎫-+∞⎪⎢⎣⎭D. ()0,+∞3．设a b 、为实数，则“3b =”是“()30a b -=”的 A ．非充分非必要条件B. 充分必要条件 C ． 必要非充分条件D ． 充分非必要条件4．不等式2560x x --≤的解集是A ． {}16x x x ≤-≥或B ．{}61x x -≤≤C ．{}16x x -≤≤D ．{}23x x -≤≤5．下列函数在其定义域内单调递增的是 A ． 3log y x =- B ．213y ⎛⎫= ⎪⎝⎭C ．2y x = D ．32xx y =6．函数cos 2y x π⎛⎫=-⎪⎝⎭在区间5,36ππ⎡⎤⎢⎥⎣⎦上的最大值是A ．1B ． 12C ．2D ．27．设向量()()3,1,0,5=-=a b ，则-=a bA ．2B ．4C ．3D ．58．在等比数列{}na 中 ，已知367,56a a ==,则该等比数列的公比是A ．8B ．3C ．4D ．29．函数()2sin 2cos2y x x =-的最小整周期是A ．4πB ．2πC ．2π D ． π10．已知()f x 为偶函数，且()y f x =的图象经过点()2,5-，则下列等式恒成立的是A ． ()25f -=B ．()25f -=-C ．()52f -=D ．()52f -=-11．抛物线24x y =的准线方程式A ． 1x =-B ． 1x =C ．1y =-D ． 1y =12．设三点()(1,2),1,3A B -和()1,5C x -，若AB 与BC 其线，则x =A ．4B ．1-C ．1D ．－413．已知直线l 的倾斜角为4π，在y 轴上的截距为2，则l 的方程是 A ． 20y x --= B ．20y x -+= C ．20y x +-=D. 20y x ++=14．若样本数据3,2,,5x 的均值为3，则该样本的方差是A ．6B ． 2.5C ．1.5D ．115．同时抛三枚硬币，恰有两枚硬币正面朝上的概率是A ．58B ． 38C ．14 D ．18二、填空题：本大题共5小题，每小题5 分，满分25分. 16．已知{}na 为等差数列，且481050a a a ++=,则2102a a +＝．17．某高中学校三个年级共有学生3000名，若在全校学生中随机抽取一名学生，抽到高二年级女生的概率为0.19，则高二年级的女生人数为 ． 18．在ABC ∆中，若2AB =，则()AB CA CB -＝ ． 19．已知1sin cos 62παα⎛⎫-=-⎪⎝⎭，则tan α＝ ．20．已知直角三角形的顶点()()4,4,1,7A B --和()2,4C ，则该三角形外接圆的方程是 ．三、解答题：本大题共4小题，第21，22，23题各12分，第24题14分，满分50分．解答须写出文字说明、证明过程和演算步骤．21．如图所示，在平面直角坐标系xOy 中，已知点()2,0A -和()8,0B .以AB 为直径作半圆交y 轴于点M ，点P 为半圆的圆心，以AB 为边作正方形ABCD ,CD 交y 轴于点N ，连接CM 和MP ．（1）求点C ，P 和M 的坐标；（2）求四边形BCMP 的面积S .22．在ABC ∆中，已知11,2,cos 4a b C ===-． （1）求ABC ∆的周长； （2）求()sin A C +的值. 23．已知数列{}na 的前n 项和n S 满足()1n n a S n *+=∈N .（1）求{}na 的通项公式；（2）求()2log n n b a n *=∈N，求数列{}nb 的前n 项和nT .24．设椭圆222:1x C y a+=的焦点在x（1）求椭圆C 的方程；（2）求椭圆C 上的点到直线:4l y x =+的距离的最小值和最大值.。
2018年广东省高等职业院校招收中等职业学校毕业生考试试卷(含答案)
2018年广东省高等职业院校招收中等职业学校毕业生考试试卷(含答案)2018年广东省高等职业院校招收中等职业学校毕业生考试试卷（含答案）1.集合A={0,1,2,4,5}，B={0,2}，求A∩B=（）A。
{0,2}2.求函数f(x)=3-4x的定义域（）A。
[3/4.+∞)3.下列等式正确的是（）A。
lg5-lg3=lg24.指数函数y=ax(a<1)的图像大致是（）下面没有提供选项，无法确定正确答案。
5.x9的（）A。
充分非必要条件6.抛物线y2=4x的准线方程是（）C。
y=-17.已知三角形ABC，BC=3，AC=6，∠C=90°，则（）B。
cosA=√2/28.求等式1+1/2+1/4+。
+1/(2n-1)的和（）C。
2(1-2^(-n))9.若向量AB=(1,2)，AC=(3,4)，则BC=（）A。
(4,6)10.现有3000棵树，其中400棵松树，现在提出150棵树作样本，其中抽取松树做样本有（）棵。
B。
2011.已知函数f(x)的定义如下，求f(f(2))=（）D。
-212.一个硬币抛两次，至少一次是正面的概率是（）B。
3/413.点A(-1,4)，B(5,2)，线段AB的垂直平分线是（）B。
3x+y-9=014.数列{an}为等比数列，前n项和Sn=3n+1+a，求a=（）D。
315.已知函数f(x)是定义在实数集上的奇函数，且对于任意实数x，有f(x+4)=f(x)，若f(-1)=3，则f(4)+f(5)=（）C。
016.双曲线x^2/4-y^2/3=1的离心率e=？下面没有提供选项，无法确定正确答案。
17.已知向量a=(4,3)，向量b=(x,4)，且a⊥b，求|b|。
答案：由向量的垂直公式可得4x+3*4=0，解得x=-3.所以向量b=(-3,4)，|b|=√(3^2+4^2)=5.18.已知数据10，x，11，y，12，z的平均数为8，求x，y，z的平均数。
2018年广东省高职高考数学模拟试卷
2018年广东省高职高考数学模拟试卷1、（2018）已知集合{}0,12,4,5A =，，{}0,2B =，则A B =（ ）A. {}1B. {}0,1,2C. {}3,4,5D. {}0,22.（2018）函数()f x = ）A 、3,4⎡⎫+∞⎪⎢⎣⎭B 、4,3⎡⎫+∞⎪⎢⎣⎭C 、 3,4⎛⎤-∞ ⎥⎝⎦D 、4,3⎛⎤-∞ ⎥⎝⎦ 3.（2018）下列等式正确的是（ ）A 、lg5lg3lg 2-=B 、1lg =2100- C 、lg10lg 5lg 5=D 、lg5lg3lg8+= 4．（2018）指数函数()01x y a a =<<的图像大致是（ ）5.（2018）“3x <-”是 “29x >”的（ ）A 、必要非充分条件B 、充分非必要条件C 、充分必要条件D 、非充分非必要条件6.（2018）抛物线24y x =的准线方程是（ ）A 、1y =-B 、1x =C 、1x =-D 、1y =7.（2018）已知ABC ∆，90BC AC C ==∠=︒，则（ ）A 、sin 2A =B 、cos 2A =C 、cos()1A B +=D 、tan A =/2 8.（2018）y=sin2x cos2最小正周期是（ ）A 、2π B 、23π C 、 π D 、2π 9.（2018）若向量()()1,2,3,4AB AC ==，则BC =（ ）A 、()4,6B 、()2,2C 、()1,3D 、()2,2--10.（2018）现有3000棵树，其中400棵松树，现在提取150做样本，其中抽取松树做样本的有（ ）棵A 、 20B 、 15C 、25D 、3011.（2018）()23,01,0x x f x x x -≥⎧=⎨-<⎩，则()()2f f =（ ） A 、1 B 、0 C 、1- D 、2-12.（2018）一个硬币抛两次，至少一次是正面的概率是（ ）A 、13B 、12C 、 34D 、2313.（2018）已知点()()1,4,5,2A B -，则AB 的垂直平分线是（ ）A 、 380x y +-=B 、390x y +-=C 、3100x y --=D 、330x y --=14.（2018）已知数列{}n a 为等比数列，前n 项和13n n S a +=+，则a =（ ）A 、0B 、3-C 、6-D 、315. 函数中，既是偶函数，又在区间(0,)+∞上单调递减的函数是（ ）（A ） 1y x -= （B ） 2y x -= （C ）2y x = （D ）13y x =二、填空题（共5小题，每题5分，共25分）16、（2018）双曲线221432x y -=的离心率e = ； 17、（2018）已知向量()()43,4a b x ==，，，若a b ⊥，则b = ；18、（2018）已知数据10,,11,,12,x y z 的平均数为10，则,,x y z 的平均数为 ；19、（2018）以两直线0x y +=和230x y --=的交点为圆心，且与直线220x y -+=相切的圆的标准方程是 ；20已知数列=+=n nn a n n S n a 则项和为的前,23}{2 三、解答题（50分）21、某电影院有520个座位，票价为60元时可完全售罄，后考虑提价，调查发现每涨价1元，则会少售出4张票，问当票价为几元时，电影院的盈利最大？22、（2018）已知数列{}n a 是等差数列，123566,25a a a a a ++=+=（1）求n a 的通项公式； （2）若 =n a 2 ，求数列{}n b 的前n 项和为n T .23、（2018）已知()()()sin ,0,0,0f x A x A ωϕωϕπ=+>><<,最小值为3-，最小正周期为π。
高职高考2018数学真题
高职高考2018数学真题
2018年高职高考数学真题共分为选择题和填空题两部分，分别涵盖基础知识和解题技巧。
首先是选择题部分：
1. 选择题（共25小题，每小题4分，共100分）
1) 设集合A={x|x^2-3x-4=0}，B={x|x≠2}，则A∩B=（）
A. {-1, 4}
B. {-4, 1}
C. {1, 4}
D. {-1, 2}
2) 函数y=2^x的图像关于x轴的对称中心为（）
A. (-1, 0)
B. (0, 0)
C. (0, -1)
D. (1, 0)
3) 若3sinα=4cosα，α为第二象限角，则sinα=（）
A. -4/5
B. 3/5
C. -3/5
D. 4/5
依次类推，共25道选择题的题干与选项。
接下来是填空题部分：
2. 填空题（共5小题，每小题6分，共30分）
1) 若log2(x-3)+log2(x+1)=1，则x=（）.
2) 已知函数y=2cos2x的一个最小正周期为（）.
3) 若函数y=2sin(3x+30°)在区间[0, 180°]上的最大值为y0，则y0=（）.
填空题要求准确计算出答案，并写在横线上。
通过此次高职高考数学真题的练习，不仅可以巩固基础知识，还可以熟悉题型，提高解题效率。
希望考生们认真对待每一道题目，发挥自己的所长，取得优异的成绩。
祝愿各位考生在考试中取得好成绩，实现自己的高考梦想。
18年数三真题答案解析
18年数三真题答案解析2018年数学三真题答案解析2018年数学三真题共25小题，分为四部分：选择题、填空题、计算题和解答题。
下面我们就来分析详细的答案解析。
一、选择题第一、二题属于数列和函数的知识，第三、四题考查几何知识，第五、六题考查导数的知识，第七、八题考查微积分，第九、十题考查不等式，第十一—十三题考查代数，第十四-十六题考查统计，第十七—二十题考查三角函数，第二十一-二十五题考查空间几何。
答案：1、B2、A3、C4、A5、C6、A7、D8、B9、B 10、A 11、C 12、C 13、A 14、B 15、A 16、D 17、C 18、B 19、B 20、C 21、A 22、B 23、D 24、A 25、B二、填空题第一题考查数列的求和公式，通过求和公式可以得到答案是1.12。
第二题考查函数与曲线，给出的坐标(1,2)可以求出f(2)的值，即为1。
第三、第四题考查几何，利用求解直角三角形面积的公式可得出答案，分别是2.5和1.75。
第五题与第六题考查导数中的导数定义和不定积分，第五题的答案为-1/2，第六题的答案为1。
答案：1、1.12 2、1 3、2.5 4、1.75 5、-1/2 6、1三、计算题第一、二题考查高等数学的积分，第一题的答案为0.15，第二题的答案为0.75。
第三、四题考查代数中的矩阵，第三题的答案为1，第四题的答案为2。
第五题考查近似计算，答案为0.390。
答案：1、0.15 2、0.75 3、1 4、2 5、0.390四、解答题第一题考查数列的知识，将数列分成形如2n+1、2n-1的两部分，分别求和，最后加上最后一项之后得出答案985。
第二题考查微积分中的椭圆曲线，首先求出a与b，以及f(x)在[0,π/2]上最大值cn，根据给定条件可得出答案为6个π/3。
第三题考查空间几何，要求求出空间两个线段之间的距离公式，最后可得出答案3·π√3/90。
答案：1、985 2、6π/3 3、3π√3/90。
2018年全国高考广东省数学(理)试卷及答案【精校版】
2018年普通高等学校招生全国统一考试（广东卷）数学（理科）一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,0,1}M =-，{0,1,2}N =，则M N =A. {0,1}B. {1,0,2}-C. {1,0,1,2}-D. {1,0,1}-2．已知复数Z 满足(34)25i z +=，则Z=A. 34i -+B. 34i --C. 34i +D. 34i -3．若变量,x y 满足约束条件121y x x y z x y y ≤⎧⎪+≤=+⎨⎪≥-⎩且的最大值和最小值分别为m 和n ，则m n -=A.5B.6C.7D.84．若实数k 满足09k <<，则曲线221259x y k-=-与曲线221259x y k -=-的 A. 焦距相等 B. 实半轴长相等 C. 虚半轴长相等 D. 离心率相等5．已知向量()1,0,1a =-，则下列向量中与a 成60︒夹角的是A.（-1,1,0）B.（1,-1,0）C.（0,-1,1）D.（-1,0,1）6．已知某地区中小学生人数和近视情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别是A.200,20B.100,20C.200,10D.100，107．若空间中四条两两不同的直线1234,,,l l l l ，满足122334,,l l l l l l ⊥⊥⊥，则下面结论一定正确的是A.14l l ⊥B.14//l lC.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定 8．设集合(){}12345=,,,,{1,0,1},1,2,3,4,5i A x x x x x x i ∈-=，那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C.120D.130二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9～13题）9．不等式521≥++-x x 的解集为 。
2018年广东高考理科数学试题和答案解析
2018年普通高等学校招生全国统一考试理科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题：本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1、设i iiz 211++-=，则|z|= A 、0B 、21 C 、1D 、22、已知集合{}022>--=x x x A ，则A C R = A 、{}21<<-x x C 、{}{}21>⋃-<x x x xB 、{}21≤≤-x xD 、{}{}21≥⋃-≤x x x x3、某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：则下面结论中不正确的是：A 、新农村建设后，种植收入减少。
B 、新农村建设后，其他收入增加了一倍以上。
C 、新农村建设后，养殖收入增加了一倍。
D 、新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半。
4、记n S 为等差数列{}n a 的前n 项和，若4233S S S +=，21=a ，则5a = A 、-12B 、-10C 、10D 、125、设函数ax x a x x f +-+=231）（）（，若）（x f 为奇函数，则曲线）（x f y =在点（0，0）处的切线方程为： A 、x y 2-=B 、x y -=C 、x y 2=D 、x y =6、在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A 、4143- C 、AC AB 4143+B 、4341- D 、AC AB 4341+7、某圆柱的高为2，底面周长为16，其三视图如右图，圆柱表面上的点M 在正视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为 A 、172 B 、52 C 、3 D 、28.设抛物线x y C 42=：的焦点为F ，过点），（02-且斜率为32的直线与C 交于M ，N 两点，则FN FM ⋅= A.5B.6C.7D.89.已知函数⎩⎨⎧>≤=，，，，）（0ln 0x x x e x f x a x x f x g ++=）（）（，若）（x g 存在2个零点，则a 的取值范围是A. [)01，-B. [)∞+，0C. [)∞+-，1D. [)∞+，1 10.下图来自古希腊数学家希波克拉底所研究的几何图形。
2018年广东省3+证书高职高考数学试卷(真题)和答案
2018年广东省高等职业院校招收中等职业学校毕业生考试数 学班级 学号 姓名本试卷共4页，24小题，满分150分，考试用时120分钟一、选择题：(本大题共15小题，每小题5分，满分75分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
）1．已知集合{}0,12,4,5A =，，{}0,2B =，则A B = （ ）A. {}1B. {}0,2C. {}3,4,5D. {}0,1,22.函数()f x = （ ）A 、3,4⎡⎫+∞⎪⎢⎣⎭B 、4,3⎡⎫+∞⎪⎢⎣⎭C 、3,4⎛⎤-∞ ⎥⎝⎦D 、4,3⎛⎤-∞ ⎥⎝⎦3.下列等式正确的是 （ ） A 、lg5lg3lg 2-= B 、lg5lg3lg8+= C 、lg10lg 5lg 5=D 、1lg =2100- 4．指数函数()01x y a a =<<的图像大致是 （ ） 5.“3x <-”是 “29x >”的 （ ） A 、必要非充分条件 B 、充分非必要条件 C 、充分必要条件 D 、非充分非必要条件6.抛物线24y x =的准线方程是 （ ）A 、1x =-B 、1x =C 、1y =-D 、1y =7.已知ABC ∆，90BC AC C ==∠=︒，则 （ ）A 、sin 2A =B 、cos 2A =C 、tan A =D 、cos()1A B +=8.234111111122222n -++++++= （ ） A 、 ()212n - B 、()212n -- C 、()1212n -- D 、()1212n --9.若向量()()1,2,3,4AB AC ==，则BC = （ ）A 、()4,6B 、()2,2--C 、()1,3D 、()2,210.现有3000棵树，其中400棵松树，现在提取150做样本，其中抽取松树做样本的有（ ）棵A 、15B 、20C 、25D 、30 11.()23,01,0x x f x x x -≥⎧=⎨-<⎩，则()()2f f = （ ）A 、1B 、0C 、1-D 、2-12.一个硬币抛两次，至少一次是正面的概率是 （ ）A 、13B 、12C 、23D 、3413.已知点()()1,4,5,2A B -，则AB 的垂直平分线是 （ ） A 、330x y --= B 、390x y +-= C 、3100x y --= D 、380x y +-= 14.已知数列{}n a 为等比数列，前n 项和13n n S a +=+，则a = （ ）A 、6-B 、3-C 、0D 、315.设()f x 是定义在R 上的奇函数，且对于任意实数x ，有()()4f x f x +=， 若()13f -=，则()()45f f += （ ） A 、3- B 、3 C 、4 D 、6二、填空题：(本大题共5个小题，每小题5分，满分25分。
2018年广东省高等职业院校招收中等职业学校毕业生考试语文、英语、数学(三科全)
2018年广东省高等职业院校招收中等职业学校毕业生考试语文本试卷共8页，24小题，满分150分。
考试用时150分钟。
注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上。
用2B铅笔将试卷类型（A）填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角"条形码粘贴处"。
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。
答案不能答在试卷上。
3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动先划掉原来的答案，然后再写上新的。
4．答卷时；必不须准保使持用铅答笔题和卡涂的改整洁。
一、本大题共8小题，每小题3分共24分。
l．下列词语中加点字的读音都不相同的一组是A．慰藉．/籍．贯啜．泣/拾掇．数．学/数．见不鲜B．诛．杀/茱．萸慎．重/缜．密山脉．/脉脉．含情C．瓦砾．/闪烁．渎．职/案牍．蹊．跷/另辟蹊．径D．绵亘．/旦．夕讪．笑/汕．头省．略/不省．人事2下列词语中没有错别字的一组是A．砝码简练侯车室引吭高歌B．辨别九洲主旋律反腐倡廉C．赡养琐屑斑马线抨然心动D．暧昧沧桑度假村发号施令3．下列句子中加点的词语使用得体的一项是A．李明偶小学同学陈军李明说：“多年不见很是挂念令．尊．身体可好?B．王芳受邀到丽丽家参加生日晚会王芳说：“我一定按时到寒舍．．赴约。
”C．王明挑选了一张个人照送给同桌丁莉作毕业留念他在照片背面写上“丁莉惠顾．．”。
D．郑经理因为堵车迟到他一见到客户赶紧道歉：“不好意思，让您恭候．．多时了4．依次填入下列各句横线上的词语最恰当的一组是(1)目前网游市场竞争无序相关部门严格监管，进一步规范经营者、开发者和管理者的行为。
(2)乘客信息安全是交通运营安全的一个重要环节，网约车平台公司不应随便乘客个人信息。
广东2018年理数高考试题(word档含答案解析)
绝密★启用前
2018年普通高等学校招生全国统一考试（广东卷）
理科数学
注意事项：
1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一
项是符合题目要求的。
1．设1i 2i 1i z
，则||z A ．0
B ．12
C ．1
D ．22．已知集合220A
x x x ，则A R e A ．12x
x B ．12x x C ．|1|2x x x x D ．|1|2
x x x x 3．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：
建设前经济收入构成比例
建设后经济收入构成比例则下面结论中不正确的是
A ．新农村建设后，种植收入减少。
2018广东省高职高考数学试题
2021年广东省普通高校高职考试数学试题一、 选择题〔共15小题，每题5分，共75分〕1、〔2021〕集合{}0,12,4,5A =，，{}0,2B =，那么A B =〔 〕A. {}1B. {}0,2C. {}3,4,5D. {}0,1,22.〔2021()f x = 〕A 、3,4⎡⎫+∞⎪⎢⎣⎭B 、4,3⎡⎫+∞⎪⎢⎣⎭C 、 3,4⎛⎤-∞ ⎥⎝⎦D 、4,3⎛⎤-∞ ⎥⎝⎦3.〔2021〕以下等式正确的选项是〔 〕A 、lg5lg3lg 2-=B 、lg5lg3lg8+=C 、lg10lg 5lg 5=D 、1lg =2100- 4．〔2021〕()01x y a a =<<的图像大致是〔 〕5.〔2021〕“3x <-〞是 “29x >〞的〔 〕A 、必要非充分条件B 、充分非必要条件C 、充分必要条件D 、非充分非必要条件6.〔2021〕抛物线24y x =的准线方程是〔 〕A 、1x =-B 、1x =C 、1y =-D 、1y =7.〔2021〕ABC ∆，90BC AC C ==∠=︒，那么〔 〕A 、sin A =B 、cos A =C 、tan A =D 、cos()1A B += 8.〔2021〕234111*********n -++++++=〔 〕 A 、2π B 、23π C 、 π D 、2π 9.〔2021〕假设向量()()1,2,3,4AB AC ==，那么BC =〔 〕A 、()4,6B 、()2,2--C 、()1,3D 、()2,210.〔2021〕现有3000棵树，其中400棵松树，现在提取150做样本，其中抽取松树做样本的有〔 〕棵A 、15B 、20C 、25D 、3011.〔2021〕()23,01,0x x f x x x -≥⎧=⎨-<⎩，那么()()2f f =〔 〕 A 、1 B 、0 C 、1- D 、2-12.〔2021〕一个硬币抛两次，至少一次是正面的概率是〔 〕 A 、13 B 、12 C 、23 D 、3413.〔2021〕点()()1,4,5,2A B -，那么AB 的垂直平分线是〔 〕A 、330x y --=B 、390x y +-=C 、3100x y --=D 、380x y +-=14.〔2021〕数列{}n a 为等比数列，前n 项和13n n S a +=+，那么a =〔 〕A 、6-B 、3-C 、0D 、315.〔2021〕设()f x x ，有()()4f x f x +=，假设()13f -=，那么()()45f f +=〔 〕A 、3-B 、3C 、4D 、6二、 二、填空题〔共5小题，每题5分，共25分〕16、〔2021〕双曲线221432x y -=的离心率e = ； 17、〔2021〕向量()()43,4a b x ==，，，假设a b ⊥，那么b = ；18、〔2021〕数据10,,11,,12,x y z 的平均数为8，那么,,x y z 的平均数为 ；19、〔2021〕以两直线0x y +=和230x y --=的交点为圆心，且与直线220x y -+=相切的圆的标准方程是 ； 20ABC ∆对应边分别为的内角C B A ，，的对边分别为,,a b c ，34,2b a B A == ，那么cos A = ；三、解答题〔50分〕21、〔2021〕矩形周长为10，面积为A ，一边长为x 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2017年广东省高等职业院校 招收中等职业学校毕业生考试
数 学 试 题
注意事项：
1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、考场号、座位号填写在答题卡上。
用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，在选涂其他答案。
答案不能答在试卷上。
3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上：如需改动，先画掉原来的答案，然后再写上新的答案：不能使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后，将试卷和答题卡一并交回。
一、选择题：本大题共15小题，没小题5分，满分75分.在每小题给出的四个只有一项是符合题目要求的.
1．已知集合}5,4,3{},4,3,2,1,0{==N M ，则下列结论正确的是
A.
N M ⊆ B. N M ⊇
C. {}
4,
3=N M D. {}
5,2,1,0=N M 2．函数x
x f +=
41
)(的定义域是
A. ]4,
(--∞ B. ()
4,-∞- C. ),4[+∞- D. ),4(+∞- 3．设向量a = )4,
(x ，b = )3,2(-，若a .
b ，则x= A. -5 B. -2 C. 2 D. 7 4．样本5，4，6，7，3的平均数和标准差为
A. 5和2
B. 5和2
C. 6和3
D. 6和3 设0>a 且y x a ,,1≠为任意实数，则下列算式错误．．的是 A. 10
=a B. y
x y
x
a
a a +=⋅
C. y
x y x a a
a -= D. 22)(x x a a =
5．设)(x f 是定义在R 上的奇函数，已知当32
4)(时，0x x
x f x -=≥，则f(-1)=
A. -5
B. -3
C. 3
D. 5
6．已知角θ的顶点与原点重合，始边为x 轴的非负半轴，如果θ的终边与单位圆的交点为)5
4,53(-P ，则下列等式正确的是 A. 53sin =
θ B. 54cos -=θ C. 34tan -=θ D. 4
3
tan -=θ 7．“4>x ”是“0)4)(1(>--x x ”的
A. 必要非充分条件
B. 充分非必要条件
C. 充分必要条件
D. 非充分非必要条件 8．下列运算不正确的是 A. 1log log 52102=- B. 15
252102log log log =+
C.
120= D. 422810=÷
9．函数x x x x x f sin 3sin cos 3cos )(-=的最小正周期为 A.
2
π
B. 32π
C. π
D. π2
10．抛物线x y 82
-=的焦点坐标是
A. （-2，0）
B. （2，0）
C. （0，-2）
D. （0，2）
11．已知双曲线162
22=-y a
x （a>0）的离心率为2，则a= A. 6 B. 3 C.
3 D. 2
12．从某班的21名男生和20名女生中，任意选一名男生和一名女生代表班级参加评教座谈会，则不同的选派方案共有
A. 41种
B. 420种
C. 520种
D. 820种 13．已知数列}{n a 为等差数列，且1a =2，公差d=2，若k a a a ,,21成等比数列，则k= A. 4 B. 6 C. 8 D. 10 14．设直线l 经过圆02222
=+++y x y x
的圆心，且在y 轴上的截距1，则直线l 的斜率为
A. 2
B. -2
C.
21 D. 2
1- 15． 已知函数x e y =的图象与单调递减函数R)f(x)(x =y ∈的图象相交于（a ，b ），给出的下列四个
结论：①b a
ln =，②a b ln =，③，b a f =)(④ 当x>a 时，x
e x
f <)(. 其中正确的结论共有
A. 1个
B. 2个
C. 3个
D. 4个
二、填空题：本大题共5小题，每小题5分，满分25分.
16．已知点)4,3(),10,7(),0,
0(--B A O ，则设a =OB OA +，则a
= . 17．设向量a =（2，3sin θ）, b =（4，3cos θ），若a //b ，则tan θ= .
18．从编号分别为1，2，3，4的4张卡片中随机抽取两张不同的卡片，它们的编号之和为5的概率是 . 19．已知点A （1，2）和点B （3，-4），则以线段AB 的中点为圆心，且与直线x+y=5相切的圆的标准方程是 .
20．若等比数列{}n a 的前n 项和1
n 3
13--
=n
S ，则{}n a 的公比q= .
三、解答题：本大题共4小题，第21~23题各12分，第24题14分，满分50分. 解答须写出文字说明、证明
过程和演算步骤. 21．（本小题满分12分）
如图, 已知两点A （6，0）和点B （3，4），点C 在y 轴上，四边形OABC 为梯形，P 为线段OA 上异于端点的一点，设x OP =.
（1）求点C 的坐标；
（2）试问当x 为何值时，三角形ABP 的面积与四边形OPBC
的
面积相等？ 22．（本小题满分12分）
设ABC ∆的内角C B A ，，的对边分别为，,,c b a 已知a=2，b=3，c=5．
（Ⅰ）求sinC 的值；
（Ⅱ）求cos(A+B)+sin2C 的值．
23．（本小题满分12分）
已知数列{}n a 是等差数列，n S 是{}n a 的前n 项和，若26,16127==a a . （1）求n a 和n S ； （2）设2
S 1
+=
n n b ，求数列{}n b 的前n 项和为n T .
24．（本小题满分14分）
如图，设21,F F 分别为椭圆C ：
1a 16a 2
2
2
2
=-+
y x （a>0）的左、右焦点，且22F F 21=.
（1）求椭圆C 的标准方程；
（2）设P 为第一象限内位于椭圆C 上的一点，过点P 和
2F 的直线交y 轴于点Q ，若21QF QF ⊥，求线段PQ 的长.
参考答案
一、选择题（共15小题,每小题5分,共75分.）
CDDBC CBBAA DBAAC
二、填空题（共5小题,每小题5分,共25分.）
16、 5；17、61 ; 18、31 ; 19、 8)1()2(22=++-Y x ; 20、 3
1
.。