浙教版九年级数学下册课件:3.4简单几何体的表面展开图(2)——圆柱的表面展开图(共24张PPT)
合集下载
浙教版九年级数学下册课件:3.4 简单几何体的表面展开图(第2课时)

分别是圆柱两底面圆周上的点,且 A,B 在同一母线上, 用一棉线从 A 顺着圆柱侧面绕 3 圈到 B,求棉线最短为
________cm.
答案:圆柱体的展开图如图所示:用一棉线从 A 顺着圆柱侧面 绕 3 圈到 B 的运动最短路线是:AC→CD→DB;即在圆柱体的展 开图长方形中,将长方形平均分成 3 个小长方形,A 沿着 3 个
长方形的对角线运动到 B 的路线最短;∵圆柱底面半径为 2cm, ∴长方形的宽即是圆柱体的底面周长:2π×2=4πcm; 又∵圆柱高为 9πcm,∴小长方形的一条边长是 3πcm; 根据勾股定理求得 AC=CD=DB=5πcm; ∴AC+CD+DB=15πcm.
例 一矩形纸板,两边长分别为 2cm 和 4cm,绕一边所
变式:如果圆柱的两底面积之和等于侧面积,那 么母线与底面直径之比等于________.
答案:1∶2
例 2 有一圆柱形油罐底面圆的周长为 24m,高为 6m,
一只老鼠从距底面 1m Hale Waihona Puke A 处爬行到对角 B 处吃食物,
它爬行的最短路线长为多少? 解 答案析::∵由A于C=老6鼠-是1=沿5着,圆∴柱BC的=表24面×爬12=行12的,,故需把圆 柱 由勾展股开定成理平得面图AB形2=.AC根2+据BC两2=点1之69间,线∴段AB=最1短3(,m)可.以发
例 1 如图,要用钢板制作一个无盖的圆柱形水
箱,它的高为 2.5m,容积为 10m3.需用钢板多少(不
计加工余量,精确到 0.1m2)? 解析:设水箱底面半径为 r(m),由水箱的容积为 10m3, 得 2.5×πr2=10.∴r= 2.5×103.14≈1.13(m).
反圆思柱:侧求面积圆柱S 侧的≈侧2×面3积.1、4×全1.面13积×,2.需5≈要17知.7道4(圆m2柱).的底 面圆半柱径底和面积母线S 底两≈个3.量14,×可1.1以32根≈据4.体01(积m2求),出底面半径. S 全≈17.74+4.01≈21.8(m2).所以,共需钢板约 21.8m2.
________cm.
答案:圆柱体的展开图如图所示:用一棉线从 A 顺着圆柱侧面 绕 3 圈到 B 的运动最短路线是:AC→CD→DB;即在圆柱体的展 开图长方形中,将长方形平均分成 3 个小长方形,A 沿着 3 个
长方形的对角线运动到 B 的路线最短;∵圆柱底面半径为 2cm, ∴长方形的宽即是圆柱体的底面周长:2π×2=4πcm; 又∵圆柱高为 9πcm,∴小长方形的一条边长是 3πcm; 根据勾股定理求得 AC=CD=DB=5πcm; ∴AC+CD+DB=15πcm.
例 一矩形纸板,两边长分别为 2cm 和 4cm,绕一边所
变式:如果圆柱的两底面积之和等于侧面积,那 么母线与底面直径之比等于________.
答案:1∶2
例 2 有一圆柱形油罐底面圆的周长为 24m,高为 6m,
一只老鼠从距底面 1m Hale Waihona Puke A 处爬行到对角 B 处吃食物,
它爬行的最短路线长为多少? 解 答案析::∵由A于C=老6鼠-是1=沿5着,圆∴柱BC的=表24面×爬12=行12的,,故需把圆 柱 由勾展股开定成理平得面图AB形2=.AC根2+据BC两2=点1之69间,线∴段AB=最1短3(,m)可.以发
例 1 如图,要用钢板制作一个无盖的圆柱形水
箱,它的高为 2.5m,容积为 10m3.需用钢板多少(不
计加工余量,精确到 0.1m2)? 解析:设水箱底面半径为 r(m),由水箱的容积为 10m3, 得 2.5×πr2=10.∴r= 2.5×103.14≈1.13(m).
反圆思柱:侧求面积圆柱S 侧的≈侧2×面3积.1、4×全1.面13积×,2.需5≈要17知.7道4(圆m2柱).的底 面圆半柱径底和面积母线S 底两≈个3.量14,×可1.1以32根≈据4.体01(积m2求),出底面半径. S 全≈17.74+4.01≈21.8(m2).所以,共需钢板约 21.8m2.
浙教版数学九年级下册3.4简单几何体的表面展开图(2)课件(共35张PPT)

S全
=2πr²+2πrl=2π×0.9²+2π×0.9×2.4
=5.94π (cm²). 答:这个圆柱的侧面积为4.32πcm²,全
面积为5.94πcm².
圆锥的定义:以直角三角形的直角边所在 直线为旋转轴,其余两边旋转而成的曲面 所围成的几何体叫做圆锥。(记作圆锥SO)
S O
轴 侧 面母 线 底 面
圆锥的表面展开图
将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展 开图为扇形,其半径等于母线长,弧长是底面圆的周长.
如图,若圆锥的底面半径为r,母线长为l,则
l2=h2+r2 S侧=πrl; S表=S侧+S底=πrl+πr2=πr(l+r).
若设圆锥的侧面展开图扇形的圆心角为θ ,则 r θ = l ·360°.
2
∴ 2π=
A
4
4 4 2
2
B
.
4 2 答:蚂蚁爬行的最短路线为
1
C
已知圆锥底面半径为10cm,母线长为40cm. 求它的侧面展开图的圆心角和全面积
B
S
A
解:
(1) r 10cm
l 2r 20cm
B
na l , a 40cm 180 180 l 180 20 0 n 90 a 40 A 1 2 S全=S侧+S底 20 40 10 500 2
S
例2 圆锥形烟囱帽的母线长为80cm,高 38.7cm (1)求这个烟囱帽的面积。 (2)以1:40的比例画出这个烟囱帽的展 开图
解: ( 1 ) l 80cm.h 38.7cm
r l h 80 38.7 70(cm)
2 2 2 2
浙教版数学九下课件3-4简单几何体的表面展开图

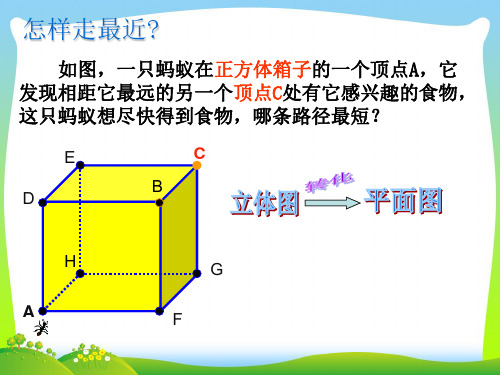
A
CF
图3-7
做一做
一个直六棱柱的上、下底面分别是边长为1cm 的正六边形,侧棱长为10cm.请计算它的表 面积.
初中数学课件
灿若寒星*****整理制作
浙教版九年级下
3.4简单几何体的表面展开图
几何体的展开图在生产时间中有着广泛的应用.通过 几何体的展开图可以确定和制作立体模型,也可以计算 相关集合体的侧面积和表面积.
观察与思考
某外包装盒的形状是棱柱(图3-1),它的两底面都是水平的 ,侧棱都是竖直的(这样的棱柱叫做直棱柱).沿它的棱剪 开、铺平,就得到了它的平面展开图(图3-2).
(1) (3)
(2) (4)
练习
下列各图是几何体的平面展开图,猜想下列展开图可折成什 么立体图形,并指出围成的几何体的形状.
一起探究
图3-4和图3-5分别是某几何体的三视图.(单位: mm)
(1)请分别说出他们所对应的几何体的名称. (2)分别计算这两个几何体的表面积. (3)小明认为,图3-5所示三视图所对应的几何体
关系?
做一做
1.制作圆锥并计算其相关的量. (1)在纸上画一个半径为6cm,圆心角为216°的扇形. (2)将这个扇形剪下来,按图37-36所示围成一个圆锥. (3)指出这个圆锥的母线长,并求圆锥的高和底面的半径(
粘合部分忽略不计).
S
216°
A
OB
做一做
2.图3-3是四个几何体的平面展开图,请用纸分别复制下来,猜想下列展 开图可折成什么立体图形,实际动手折一下,并指出围成的几何体的 形状.
观察与思考
底面
侧棱 侧面
底面
图3-1
图侧面是什么形状的? 2.这个棱柱的上、下底面的形状一样吗?他们各有几条边? 3.侧面的个数与底面图形的边数有什么关系? 4.这个棱柱有几条侧棱?它们的长度之间有什么关系? 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么
3.42 简单几何体的表面展开图(2)——圆柱的侧面积和全面积

• S侧=2πr • =2× π ×1 ×2.5 • =5 π (cm²) • S全=2πr²+ 2πrL • = 2πr×1²+ 2πr×1 ×2.5 • = 7 π (cm²) • 答:这个圆柱的侧面积为5 π cm²,全面积 为 7π cm².
①铝皮: S侧=ch =π×6×2.6 =π×15.6 =15.6π(dm²)
②羊皮: 2S底=πr²×2 =π×3²×2 =π×18 =18π(cm²)
• 3.如图,把一个圆柱形木块沿它的轴剖开 ,得矩形ABCD。已知AD=18cm,AB= 30cm,求这个圆柱形木块的表面积(精 确到1cm2)
2cm
.
2cm
.
小组合作计算出圆柱的表面积:
①S侧=ch =π×2×2 =4π(cm²) ③S表= S侧+ 2S底 ②S底=πr² =4π+2×π =π×1² =4π+2π =π(cm²) =6π(cm²)
判断:(对的画“√”,错的画“×”) 1、圆柱的侧面展开可以得到一个矩形,这个矩形的长等于 圆柱的底面直径,ห้องสมุดไป่ตู้等于圆柱的高。 ( )
×
2、给大厅的圆柱刷油漆,刷油漆的部分面积是圆柱的侧 面积。
(√
)
3、圆柱形通风管的表面积等于它的侧面积。(
√
)
4、一个圆柱的侧面展开是正方形,它的底面周长和高 相等。 ( )
√
• 例3.如图为一个圆柱的三视图.以相同的比 例画出它的表面展开图,并计算它的侧面 积和全面积. (结果保留π)
2.5
1
分析:由图知,圆柱底面 的半径r为1cm,母线长L为 2.5cm 。因此圆柱的表面 展开图中两个底面应画成 半径为1cm 的圆,侧面展 开图应画成2πr=2π×1=2π (cm),宽为2.5cm的长方 形。
浙教版九年级数学下册第三章《 3.4简单几何体的表面展开图》公开课课件(共21张PPT)
12 3456
一三二型
12 345
6
12 345
6
12 345 6
二个三型
126 345
例1
请分别用1,2,3,4,5,6中的同一个数字 表示立方体和它的展开图中各对对应的面.
2 5 1 34
6
56 45 61
32 13 24
让思维更活跃一点!
如图是一个正方体纸盒的展开图,图中的6个 正方形中分别已填入了-1、7、2 、a、b、c,使展 开图折叠成正方体后相对面上的两个数互为相反
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
3.4 简单几何体的表面展开图(课件)九年级数学下册(浙教版)

【解题关键】将实际问题转换为数学模型.
根据题意,下部圆柱的底面积12m2,高h2为1.8m;
上部圆锥的高hl=3.2-1.8=1.4m;
l
圆柱底面圆半径r=
12
≈1.954
h1
(m)
S圆柱的侧面积=2πrh2=2π×1.954×1.8 ≈22.10(m2)
圆锥的母线l= ℎ12 + 2 ≈2.404 (m)
锥的全面积是________cm
400π 2.
【分析】S全=S底+S侧
=πr2+πrl=π×102+π×10×30=400π.
讲授新课
2、(1)圆锥的母线长为5,圆锥高为3,则该圆锥的侧面积为
________;
20π
(2)已知圆锥的底面半径为7cm,高为24cm,则该圆锥的侧面积为
175π 2.
________cm
个这样的锚标浮筒,需要用多少锌?
【详解】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,则圆锥的母线长为: 0. 32 + 0. 42 =0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
扇形,则这个圆锥的底面圆半径是________cm.
1
【分析】
圆锥底面圆的周长2πr=扇形的弧长l弧,
×
2πr= =
,解得:r=1.
或直接公式法:n=
·360,即120= ·360.
当堂检测
5、如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,
根据题意,下部圆柱的底面积12m2,高h2为1.8m;
上部圆锥的高hl=3.2-1.8=1.4m;
l
圆柱底面圆半径r=
12
≈1.954
h1
(m)
S圆柱的侧面积=2πrh2=2π×1.954×1.8 ≈22.10(m2)
圆锥的母线l= ℎ12 + 2 ≈2.404 (m)
锥的全面积是________cm
400π 2.
【分析】S全=S底+S侧
=πr2+πrl=π×102+π×10×30=400π.
讲授新课
2、(1)圆锥的母线长为5,圆锥高为3,则该圆锥的侧面积为
________;
20π
(2)已知圆锥的底面半径为7cm,高为24cm,则该圆锥的侧面积为
175π 2.
________cm
个这样的锚标浮筒,需要用多少锌?
【详解】解:由图形可知圆锥的底面圆的半径为400mm=0.4m,
圆锥的高为300mm=0.3m,则圆锥的母线长为: 0. 32 + 0. 42 =0.5m.
∴圆锥的侧面积=π×0.4×0.5=0.2π(m2),
∵圆柱的高为800mm=0.8m.圆柱的侧面积=2π×0.4×0.8=0.64π(m2),
扇形,则这个圆锥的底面圆半径是________cm.
1
【分析】
圆锥底面圆的周长2πr=扇形的弧长l弧,
×
2πr= =
,解得:r=1.
或直接公式法:n=
·360,即120= ·360.
当堂检测
5、如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,
2022年浙教初中数学九下《简单几何体的表面展开图》PPT课件8

的表面积,就是图3-5中的两个主视图、两个左视 图和一个府视图的面积的和.你认为小明的想法正 确吗?为什么?
一起探究
—— 40 —— —— 40 —— —— 40 —— —20—
—20—
—20—
主 视 图
俯 视 图
—20—
—20—
左 视 图
主 视 图
—20—
俯 视 图
—20—
左 视 图
—— 40 ——
经过点(-1,2)和(1,0),且与y轴相交于负半轴. (1)给出四个结论:①a>0;②b>0;③c>0; ④a+b+c=0.其中正确结论的序号是__①___④___.
(2)给出四个结论:①abc<0;②2a+b>0;③a+c=1; ④a>1.其中正确结论的序号是___②___③____.
课堂小结
1.一般地,我们可以用配方法将 yax2bxc配方成 yaxb24acb2. 2a 4a
(1)二次函数 yax2bxc ( a≠0)的图像是一条 __抛__物__线___;
(2)直线 x b 2a
是二次函数
yax2bxc的对称轴;顶点坐
标是(
b
4acb2 ,
).
2a 4a
2.二次函数y=ax2+bx+c(a≠0)的图像和性质
观察与思考
底面
侧棱 侧面
底面
图3-1
图3-2
观察与思考
1.这个棱柱有几个侧面?每个侧面是什么形状的? 2.这个棱柱的上、下底面的形状一样吗?他们各有几条边? 3.侧面的个数与底面图形的边数有什么关系? 4.这个棱柱有几条侧棱?它们的长度之间有什么关系? 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么
一起探究
—— 40 —— —— 40 —— —— 40 —— —20—
—20—
—20—
主 视 图
俯 视 图
—20—
—20—
左 视 图
主 视 图
—20—
俯 视 图
—20—
左 视 图
—— 40 ——
经过点(-1,2)和(1,0),且与y轴相交于负半轴. (1)给出四个结论:①a>0;②b>0;③c>0; ④a+b+c=0.其中正确结论的序号是__①___④___.
(2)给出四个结论:①abc<0;②2a+b>0;③a+c=1; ④a>1.其中正确结论的序号是___②___③____.
课堂小结
1.一般地,我们可以用配方法将 yax2bxc配方成 yaxb24acb2. 2a 4a
(1)二次函数 yax2bxc ( a≠0)的图像是一条 __抛__物__线___;
(2)直线 x b 2a
是二次函数
yax2bxc的对称轴;顶点坐
标是(
b
4acb2 ,
).
2a 4a
2.二次函数y=ax2+bx+c(a≠0)的图像和性质
观察与思考
底面
侧棱 侧面
底面
图3-1
图3-2
观察与思考
1.这个棱柱有几个侧面?每个侧面是什么形状的? 2.这个棱柱的上、下底面的形状一样吗?他们各有几条边? 3.侧面的个数与底面图形的边数有什么关系? 4.这个棱柱有几条侧棱?它们的长度之间有什么关系? 5.侧面展开图的长和宽分别与棱柱底面的周长和侧棱长有什么
浙教版数学九年级下册同步课件:第1课时直棱柱的表面展开图

(2) 直棱柱的侧面积与底面周长及侧棱长有怎样的关系?
直棱柱的侧面积=底面周长× 侧棱长
随堂演练 1.下列各图中,经过折叠能围成一个立方体的是 ( A )
2.如图是一个长方体的包装盒,它的平面展开图是 ( A )
3.把如图中的三棱柱展开,所得到的展开图是 ( B )
4.如图是正方体的一种展开图,其中每个面上都标有 一个数字.那么在原正方体中,与数字“2”相对的面上 的数字是 ( B )
例题讲授 例1 图1 是一个立方体的表面展开图吗?如果是,分别用1,2,3, 4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面 (只要求给出一种表示法). 分析 可以先用折叠的方法试一试,看
它能否折成一个立方体.
解: 图1是一个立方体的表面展开图,各对应面上的数字表示如图2和图3.
2 4
A.1 B.4 C.5 D.6
5.右图是一个正方体纸盒的表面展开图,去掉其中一 个正方形,可以折成一个无盖的正方体盒子,去掉的 这个正方形的编号是__答__案__不__唯__一___,__如__1.(只填1个)
7.某工厂要加工一批正六棱柱形状的食品盒,其三视图如图, (单位:cm)问制作一个食品盒至少需要的硬纸板的面积为多少?
36 10
36 10
解:上下底面面积 3 102 6 2
4 300 3(cm2 )
答:所需面积为
六个侧面面积
36 10 6
2160(cm2 )
所需硬纸板面积为
300 3 2160(cm2 )
直棱柱的表面展开图
直棱柱的表 面展开图
立方体的各种表面展开图
用直棱柱表面展开图 进行相关计算
a b
h
h
b
甲
直棱柱的侧面积=底面周长× 侧棱长
随堂演练 1.下列各图中,经过折叠能围成一个立方体的是 ( A )
2.如图是一个长方体的包装盒,它的平面展开图是 ( A )
3.把如图中的三棱柱展开,所得到的展开图是 ( B )
4.如图是正方体的一种展开图,其中每个面上都标有 一个数字.那么在原正方体中,与数字“2”相对的面上 的数字是 ( B )
例题讲授 例1 图1 是一个立方体的表面展开图吗?如果是,分别用1,2,3, 4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面 (只要求给出一种表示法). 分析 可以先用折叠的方法试一试,看
它能否折成一个立方体.
解: 图1是一个立方体的表面展开图,各对应面上的数字表示如图2和图3.
2 4
A.1 B.4 C.5 D.6
5.右图是一个正方体纸盒的表面展开图,去掉其中一 个正方形,可以折成一个无盖的正方体盒子,去掉的 这个正方形的编号是__答__案__不__唯__一___,__如__1.(只填1个)
7.某工厂要加工一批正六棱柱形状的食品盒,其三视图如图, (单位:cm)问制作一个食品盒至少需要的硬纸板的面积为多少?
36 10
36 10
解:上下底面面积 3 102 6 2
4 300 3(cm2 )
答:所需面积为
六个侧面面积
36 10 6
2160(cm2 )
所需硬纸板面积为
300 3 2160(cm2 )
直棱柱的表面展开图
直棱柱的表 面展开图
立方体的各种表面展开图
用直棱柱表面展开图 进行相关计算
a b
h
h
b
甲
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱的侧面积和全面积
S 侧 = 长 宽 = 2 rl
S全 =S侧 +S底 =2 rl 2 r
2
S侧 =2 rl 2 12 10 3 720
S糖皮 =2 rl r 720+312 =720+432=1152
2 2
变式一:如图,如果制 作双层翻糖蛋糕,已知底层 蛋糕胚半径仍12cm,母线 长为10cm,二层蛋糕胚半 径为8cm,母线长为10cm, 请求出需要多少面积的糖 皮?(π取3)
例 如右图制作一款中 国风的翻糖蛋糕,已有现 成的蛋糕胚,根据三视图, 请以1:10的比例画出它的 表面展开图,并计算它的 糖皮面积.(π 取3)
主视图
左视图
例 如图是根据蛋糕 胚的尺寸所得到的的三 视图,以1:10的比例画出 它的表面展开图,并计算 它的糖皮面积.(π 取3)
10cm
12cm
俯视图
变式二:为了让蛋糕 更加美观,可以在表面制 作裱花,如图在A,B两朵 花之间裱上枝干,怎么设 计使枝干距离最短(所用 材料最少),并算出这条 最短枝干的长度.(结果 保留根号)
变式二:为了让蛋糕 更加美观,可以在表面制 作裱花,如图在A,B两朵花 之间裱上枝干,怎么设计 使枝干最短(所用材料最 少),并算出最短枝干的长 度.(结果保留根号)
义务教育教科书浙教版九年级下
3.4简单几何体的表面展开图(2)
————圆柱的表面展开图
把矩形绕直线旋转一周得到的图形是一个圆柱.
上底面
A D
侧面
母线
B C 下底面
落归根
底面
﹖
﹖
侧 面
底面
底面
侧 面
底面
ห้องสมุดไป่ตู้ 侧 面
底面
侧 面
底面
侧 面
底面
侧 面
底面
侧 面
底面
侧 面
底面
矩形的长 =圆柱的底面周长= 矩形的宽=圆柱的母线长=
2 r
l
如图,已知矩形ABCD,AB=25cm,AD=13cm,若以AD边为 轴,将矩形旋转一周,则所成的圆柱的底面直径是__ 13cm ,侧面展开图是一组邻边长分 50cm __,母线长是____ 50π和13cm 的一个矩形. 别为____
翻糖蛋糕源自于英国的艺术蛋糕, 延展性极强的翻糖可以塑造出各式各样 的造型,并将精细完美的展现出来,因此 成为当今蛋糕装饰的主流.右图是制作 翻糖蛋糕的教程,请你根据已有的蛋糕 胚制作一款尺寸相符的翻糖皮.
·
A
B
·
矩形ABCD绕着AB边 旋转所得到的的圆柱与矩 形ABCD绕着BC边旋转所 得到的的圆柱,侧面积与全 面积是否相同?
A
D A B C
D
B
C
1.基本知识
圆柱是一个旋转体 圆柱的表面展开图
圆柱的侧面积和全面积
2.基本思想
转化的思想:曲面转化为平面
