01背包问题动态规划详解

合集下载

01背包问题动态规划详解

动态规划是用空间换时间的一种方法的抽象。

其关键是发现子问题和记录其结果。

然后利用这些结果减轻运算量。

比如01背包问题。

因为背包最大容量M未知。

所以，我们的程序要从1到M一个一个的试。

比如，开始任选N件物品的一个。

看对应M的背包，能不能放进去，如果能放进去，并且还有多的空间，则，多出来的空间里能放N-1物品中的最大价值。

怎么能保证总选择是最大价值呢？看下表。

测试数据：10,33,44,55,6c[i][j]数组保存了1,2,3号物品依次选择后的最大价值.这个最大价值是怎么得来的呢?从背包容量为0开始,1号物品先试,0,1,2,的容量都不能放.所以置0,背包容量为3则里面放4.这样,这一排背包容量为4,5,6,....10的时候，最佳方案都是放4.假如1号物品放入背包.则再看2号物品.当背包容量为3的时候，最佳方案还是上一排的最价方案c为4.而背包容量为5的时候，则最佳方案为自己的重量5.背包容量为7的时候，很显然是5加上一个值了。

加谁??很显然是7-4=3的时候.上一排c3的最佳方案是4.所以。

总的最佳方案是5+4为9.这样.一排一排推下去。

最右下放的数据就是最大的价值了。

(注意第3排的背包容量为7的时候,最佳方案不是本身的6.而是上一排的9.说明这时候3号物品没有被选.选的是1,2号物品.所以得9.)从以上最大价值的构造过程中可以看出。

f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.这回清楚了吗?下面是实际程序:#include<stdio.h>int c[10][100];int knapsack(int m,int n){int i,j,w[10],p[10];for(i=1;i<n+1;i++)scanf("\n%d,%d",&w[i],&p[i]);for(i=0;i<10;i++)for(j=0;j<100;j++)c[i][j]=0;for(i=1;i<n+1;i++)for(j=1;j<m+1;j++){if(w[i]<=j){if(p[i]+c[i-1][j-w[i]]>c[i-1][j])c[i][j]=p[i]+c[i-1][j-w[i]];elsec[i][j]=c[i-1][j];}else c[i][j]=c[i-1][j];}return(c[n][m]);}int main(){int m,n;int i,j;scanf("%d,%d",&m,&n);printf("Input each one:\n");printf("%d",knapsack(m,n));printf("\n");for(i=0;i<10;i++)for(j=0;j<15;j++){printf("%d ",c[i][j]);if(j==14)printf("\n");}system("pause");}-----------------------------------------------------------------------------------------------------------------------------------题目有N件物品和一个容量为V的背包。

动态规划之01背包问题(最易理解的讲解)

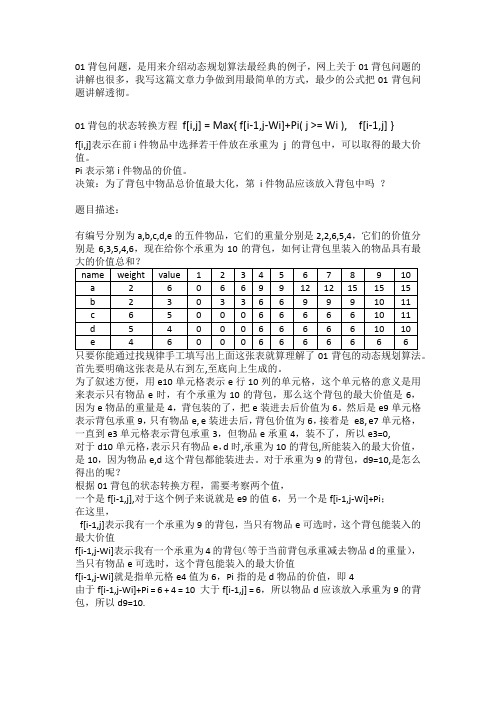
01背包问题，是用来介绍动态规划算法最经典的例子，网上关于01背包问题的讲解也很多，我写这篇文章力争做到用最简单的方式，最少的公式把01背包问题讲解透彻。

01背包的状态转换方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }f[i,j]表示在前i件物品中选择若干件放在承重为j 的背包中，可以取得的最大价值。

Pi表示第i件物品的价值。

决策：为了背包中物品总价值最大化，第i件物品应该放入背包中吗？题目描述：有编号分别为a,b,c,d,e的五件物品，它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，现在给你个承重为10的背包，如何让背包里装入的物品具有最首先要明确这张表是从右到左,至底向上生成的。

为了叙述方便，用e10单元格表示e行10列的单元格，这个单元格的意义是用来表示只有物品e时，有个承重为10的背包，那么这个背包的最大价值是6，因为e物品的重量是4，背包装的了，把e装进去后价值为6。

然后是e9单元格表示背包承重9，只有物品e, e装进去后，背包价值为6，接着是e8, e7单元格，一直到e3单元格表示背包承重3，但物品e承重4，装不了，所以e3=0,对于d10单元格，表示只有物品e，d时,承重为10的背包,所能装入的最大价值，是10，因为物品e,d这个背包都能装进去。

对于承重为9的背包，d9=10,是怎么得出的呢？根据01背包的状态转换方程，需要考察两个值，一个是f[i-1,j],对于这个例子来说就是e9的值6，另一个是f[i-1,j-Wi]+Pi；在这里，f[i-1,j]表示我有一个承重为9的背包，当只有物品e可选时，这个背包能装入的最大价值f[i-1,j-Wi]表示我有一个承重为4的背包（等于当前背包承重减去物品d的重量），当只有物品e可选时，这个背包能装入的最大价值f[i-1,j-Wi]就是指单元格e4值为6，Pi指的是d物品的价值，即4由于f[i-1,j-Wi]+Pi = 6 + 4 = 10 大于f[i-1,j] = 6，所以物品d应该放入承重为9的背包，所以d9=10.。

动态规划——01背包问题

动态规划——01背包问题⼀、最基础的动态规划之⼀01背包问题是动态规划中最基础的问题之⼀，它的解法完美地体现了动态规划的思想和性质。

01背包问题最常见的问题形式是：给定n件物品的体积和价值，将他们尽可能地放⼊⼀个体积固定的背包，最⼤的价值可以是多少。

我们可以⽤费⽤c和价值v来描述⼀件物品，再设允许的最⼤花费为w。

只要n稍⼤，我们就不可能通过搜索来遍查所有组合的可能。

运⽤动态规划的思想，我们把原来的问题拆分为⼦问题，⼦问题再进⼀步拆分直⾄不可再分（初始值），随后从初始值开始，尽可能地求取每⼀个⼦问题的最优解，最终就能求得原问题的解。

由于不同的问题可能有相同的⼦问题，⼦问题存在⼤量重叠，我们需要额外的空间来存储已经求得的⼦问题的最优解。

这样，可以⼤幅度地降低时间复杂度。

有了这样的思想，我们来看01背包问题可以怎样拆分成⼦问题：要求解的问题是：在n件物品中最⼤花费为w能得到的最⼤价值。

显然，对于0 <= i <= n,0 <= j <= w，在前i件物品中最⼤花费为j能得到的最⼤价值。

可以使⽤数组dp[n + 1][w + 1]来存储所有的⼦问题，dp[i][j]就代表从前i件物品中选出总花费不超过j时的最⼤价值。

可知dp[0][j]值⼀定为零。

那么，该怎么递推求取所有⼦问题的解呢。

显⽽易见，要考虑在前i件物品中拿取，⾸先要考虑前i - 1件物品中拿取的最优情况。

当我们从第i - 1件物品递推到第i件时，我们就要考虑这件物品是拿，还是不拿，怎样收益最⼤。

①：⾸先，如果j < c[i]，那第i件物品是⽆论如何拿不了的，dp[i][j] = dp[i - 1][j];②：如果可以拿，那就要考虑拿了之后收益是否更⼤。

拿这件物品需要花费c[i]，除去这c[i]的⼦问题应该是dp[i - 1][j - c[i]]，这时，就要⽐较dp[i - 1][j]和dp[i - 1][j - c[i]] + v[i]，得出最优⽅案。

01背包问题理解动态规划算法

01背包问题理解动态规划算法⼀.动态规划算法简单理解：在⼀些分治算法解决的问题中，需要将较⼤规模的问题转化为较⼩规模的问题，往往会⽤到递归。

但是在⼀些问题中，递归的⼩问题被多次重复运算，浪费了性能，因此可以使⽤数组或者其他合适的⽅式将运算过的⼩规模问题的结果记录下来，再运算⼩规模的问题时先看是不是已经运算过了，没有运算过再去运算并将结果保存，所以⼀般分治算法都是从⼤规模问题开始递归运算，不断将问题规模变⼩，⽽动态规划算法则⼀般从⼩规模问题开始运算，每次运算分解出的⼩规模问题都是已经运算过的。

如此便使⽤了存储空间换取了运算时间，减⼩了时间复杂度。

⼆.01背包问题1.穷举法可以先不考虑背包，考虑被拿⾛的物品的所有组合情况，n个物品有2n种拿法（每个物品都可以选择拿或者不拿），然后再判断每⼀种拿法是否能放⼊背包，能放⼊背包的情况下计算总价值并⽐较出最⼤价值。

static void Main(string[] args){//记录重量的数组，物品有3种重量，分别是3、4、5int[] w = { 0, 3, 4, 5 };//记录物品价值的数组，和重量数组对应，物品价值分别是4、5、6int[] p = { 0, 4, 5, 6 };//调⽤Exhaustivity函数得到7kg的背包放置物品的最⼤价值Console.WriteLine(Exhaustivity(9 , w, p));Console.ReadKey();}///<summary>///计算给定的mkg背包放置物品的最⼤价值///</summary>///<param name="m">给定的物品重量</param>///<param name="w">记录所有物品重量的数组</param>///<param name="p">记录所有物品对应价格的数组</param>///<returns>背包中放置物品的最⼤价值</returns>public static int Exhaustivity(int m,int[] w,int[] p){//记录放⼊物品的最⼤的价格int maxPrice = 0;//有3个物品，外层就循环2的3次⽅，即i值从0取到7，i的⼆进制数字最多3位，每⼀个i的取值的⼆进制数字都对应3个物品是否放⼊背包//如i为6，⼆进制为110，代表取前两个物品，不取第3个物品//⼜如i为0，⼆进制为000，代表3个物品均不取；i为1，⼆进制001，代表只取第3个物品//通过这种⽅式穷举所有物品放⼊背包的情况，然后判断每⼀种情况重量是否满⾜要求，再⽐较价格for(int i = 0;i < Math.Pow(2,w.Length - 1); i++){//记录所有被放⼊背包物品的总重量int weightTotal = 0;//记录所有被放⼊背包物品的总价格int priceTotal = 0;//内层循环负责计算并⽐较所有物品的总重量和总价格//内层循环的次数就是物品个数，然后分别判断当前情况下每个物品是否放⼊背包，j代表第⼏个物品for(int j = 1;j <= w.Length - 1; j++){//计算当前物品是否放⼊背包int result = Get2(i, j);//在放⼊背包的情况下，将重量和价格累加到总重量和总价格上if(result == 1){weightTotal += w[j];priceTotal += p[j];}}//判断是否超重，不超重的情况下判断价格是不是⼤于最⼤价格，如果是更新最⼤价格if (weightTotal <= m && priceTotal > maxPrice)maxPrice = priceTotal;}//返回最⼤价格return maxPrice;}///<summary>///通过按位与运算得到给定物品number在给定放⼊情况i中是否放⼊背包///</summary>///<param name="i">给定的物品放⼊情况</param>///<param name="number">给定的物品编号</param>///<returns></returns>public static int Get2(int i,int number){int A = i;int B = (int)Math.Pow(2,number - 1);int result = A & B;if (result == 0)return0;return1;}2.分治算法（⾃上⽽下分解问题）这个问题的分治算法的核⼼是将物品逐个放⼊背包，有以下⼏种情况：1）背包没有剩余重量了2）当前物品的编号为0，即所有的物品都试过了3）当前物品太重，⽆法放⼊背包4）当前物品可以放⼊背包在第4）种情况下，有两种情况，⼀种放⼊物品得到的价格最⼤，⼀种不放⼊物品得到的价格最⼤（因为放⼊物品后背包的剩余可放⼊重量也变⼩了，所以放⼊当前物品对后续物品能否放⼊的情况有影响，因此不⼀定是将当前物品放⼊得到的总价格最⾼，需要实际求解并判断），因此需要进⾏⽐较得到最⼤价格static void Main(string[] args){//记录重量的数组，物品有3种重量，分别是3、4、5int[] w = { 0, 3, 4, 5 };//记录物品价值的数组，和重量数组对应，物品价值分别是4、5、6int[] p = { 0, 4, 5, 6 };Console.WriteLine(UpDown(9, w.Length - 1, w, p));Console.ReadKey();}///<summary>///根据背包剩余重量和物品编号计算放⼊物品能获得最⼤价值还是不放⼊物品能获得最⼤价值///</summary>///<param name="m">背包剩余能装的重量</param>///<param name="i">当前放⼊背包的物品编号</param>///<param name="w">记录所有物品重量的数组</param>///<param name="p">记录所有物品价格的数组</param>///<returns>放⼊背包的物品的最⼤价格</returns>public static int UpDown(int m,int i,int[] w,int[] p){//如果背包还能装的重量为0或者放⼊的物品编号为0，价格⾃然都是0if (i == 0 || m == 0) return0;//将第i个物品放⼊背包，但是物品放⼊后超重，这种情况下就不放⼊这个物品，看下⼀个物品是否能放⼊背包（物品编号-1）if(w[i] > m)return UpDown(m,i - 1, w, p);//在第i个物品能放⼊背包的情况下需要计算⽐较价格else{//计算并记录将物品放⼊背包的情况下的最⼤价格（递归物品编号-1，从背包剩余重量中扣除当前物品重量，由于当前物品放⼊背包，背包中物品价格加上当前物品价格）int maxValue1 = UpDown(m - w[i], i - 1, w, p) + p[i];//计算并记录不将物品放⼊背包的情况下的最⼤价格（递归物品编号-1，但是由于没有放⼊物品，背包剩余重量不变）int maxValue2 = UpDown(m, i - 1, w, p);//⽐较并取其中价格最⼤的那个if (maxValue1 > maxValue2)return maxValue1;return maxValue2;}}3.改进分治算法，使⽤数组记录已经运算过的问题结果//定义⼀个规则⼆维数组记录结果，⾏数对应背包重量，列数对应放⼊的物品个数，值对应这种情况背包中的最⼤重量public static int[,] result = new int[11, 4];static void Main(string[] args){int[] w = { 0, 3, 4, 5 };int[] p = { 0, 4, 5, 6 };Console.WriteLine(UpDown(9, w.Length - 1, w, p));Console.ReadKey();}public static int UpDown(int m,int i,int[] w,int[] p){if (i == 0 || m == 0) return0;//判断这种情况是不是已经计算过了，计算过了就直接返回if (result[m, i] != 0)return result[m, i];//在计算完成后需要将计算结果存储起来if(w[i] > m)return result[m,i] = UpDown(m,i - 1, w, p);else{int maxValue1 = UpDown(m - w[i], i - 1, w, p) + p[i];int maxValue2 = UpDown(m, i - 1, w, p);if (maxValue1 > maxValue2)return result[m, i] = maxValue1;return result[m, i] = maxValue2;}}4.动态规划算法（⾃下⽽上计算问题）static void Main(string[] args){int[] w = { 0, 3, 4, 5 };int[] p = { 0, 4, 5, 6 };Console.WriteLine(BottomUp(9, w.Length - 1, w, p));Console.ReadKey();}//记录运算结果的数组，⾏数代表背包重量，列数代表物品编号public static int[,] result = new int[11, 4];///<summary>///计算指定重量m的背包种放置前i个物品放置的最⼤价值///</summary>///<param name="m">背包重量</param>///<param name="i">物品编号</param>///<param name="w">记录所有物品重量的数组</param>///<param name="p">记录所有物品价格的数组</param>///<returns></returns>public static int BottomUp(int m,int i,int[] w,int[] p){//外层循环从1到m，背包重量从⼩到⼤for(int tempM = 1;tempM <= m; tempM++){//内层循环从1到i，物品个数从1到ifor(int tempI = 1;tempI <= i;tempI++){//如果已经计算过，不⽤再计算了if (result[tempM, tempI] != 0) continue;//如果当前物品重量超过背包剩余可装重量，不放⼊物品，将物品编号减⼀if (w[tempI] > tempM)result[tempM, tempI] = result[tempM, tempI - 1];//当前放置的物品重量不超过背包剩余可装重量，说明物品能放⼊背包//物品不⼀定放⼊背包最后的总价值最⼤，所以需要⽐较放⼊和不放⼊的情况得到的价格哪种更⼤else{int maxValue1 = result[tempM - w[tempI], tempI - 1] + p[tempI];int maxValue2 = result[tempM, tempI - 1];result[tempM, tempI] = maxValue1 > maxValue2 ? maxValue1 : maxValue2;}}}//⾃下⽽上计算完成后，返回重量为m的背包放⼊i个物品的最⼤价格即可return result[m, i];}。

动态规划法求01背包问题

动态规划法求01背包问题思路状态表⽰:f[i][j]表⽰前i个物品在容量为j的背包下的最⼤价值v[i]表⽰第i个物品的价值,w[i]表⽰第i个物品的重量状态转换:对于第i个物品如果当前背包不可以装下这个物品,那么当前的f[i][j] = f[i - 1][j],也就是上⼀个状态的最⼤价值如果当前背包可以装下这个物品,那么当前的f[i][j] = f[i - 1][j - v[i]] + w[i]和f[i - 1][j]取较⼤的那⼀个,第⼀个是考虑把第i个物品装⼊背包,那么背包物品的价值就是前i-1个物品装⼊容量为j-w[i]再加上第i个物品v[i]的价值,第⼆个是不把当前物品装⼊背包的价值,两个取⼤的那⼀个作为最优解代码详解：1. 0/1背包问题#include<iostream>using namespace std;const int N = 1e3 + 10;int f[N], w[N], v[N];int main(){int n, c;cin >> n >> c;for(int i = 1; i <= n; i ++ )cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++)for(int j = c; j >= 0 && j >= v[i]; j --)f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[c] << endl;return 0;}}完全背包问题（每个物品可以使⽤⽆数次f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i])完全背包问题本来应该是在背包问题上再加⼀个循环的，但是可以推导出下⾯这个样⼦f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i])为什么呢，只是把0/1背包问题的f[i - 1][j - v[i] + w[i])的i-1换成了i就可以了？从头来说：完全背包问题，对于第i个物品，假设剩下的背包容量还可以装n个这个物品，那么⼀共就有n+1中决策⽅案，还有⼀种⽅案就是⼀个都不选那么对于第i个物品:它的最⼤价值就是f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]), f[i - 1][j - 2 * v[i]] + 2 * w[i]....)⼀直到n为⽌（①式）令 j = j - v[i] 那么f[i][j - v[i]] = max(f[i - 1][j - v[i]], f[i - 1][j - 2 * v[i]] + w[i].....)（②式）然后发现⼆式中的右边⽐较像⼀式中的第⼆项到最后⼀项，就是每⼀项都少了⼀个w[i]把⼆式带⼊⼀式，那么⼀式就是 f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]), 就是下⾯这个状态⽅程啦 ;#include<iostream>using namespace std;const int N = 1e3 + 10;int f[N][N], w[N], v[N];int main(){int n, c;cin >> n >> c;for(int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++ ){for(int j = 1; j <= c; j ++ ){f[i][j] = f[i - 1][j];if(j >= v[i])f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);}}cout << f[n][c] << endl;return 0;}完全背包优化：#include<iostream>using namespace std;const int N = 1e3 + 10;int f[N], w[N], v[N];int main(){int n, c;cin >> n >> c;for(int i = 1; i <= n; i ++)cin >> v[i] >> w[i]; for(int i = 1; i <= n; i ++ )for(int j = v[i]; j <= c; j ++ )//从前往后更新 f[j] = max(f[j], f[j - v[i]] + w[i]);cout << f[c] << endl;return 0;}。

利用动态规划解决01背包问题01背包问题动态规划

利用动态规划解决01背包问题01背包问题动态规划背包问题是一个经典的动态规划模型,很多关于算法的教材都把它作为一道例题,该问题既简单又容易理解,而且在某种程度上还能够揭示动态规划的本质。

将具有不同重量和价值的物体装入一个有固定载重量的背包,以获取最大价值,这类问题被称为背包问题。

背包问题可以扩展出很多种问题,而01背包问题是最常见、最有代表性的背包问题。

一、问题描述给定一个载重量为M的背包及n个物体,物体i的重量为wi、价值为pi,1≤i≤n,要求把这些物体装入背包,使背包内的物体价值总量最大。

此处我们讨论的物体是不可分割的,通常称这种物体不可分割的背包问题为01背包问题。

二、基本思路01背包问题的特点是:每种物体只有一件,可以选择放或者不放。

假设:xi表示物体i被装入背包的情况,xi=0,1。

当xi=0时,表示物体没有被装入背包;当xi=1时,表示物体被装入背包。

根据问题的要求,有如下的约束方程(1)和目标函数(2):三、利用动态规划法求解01背包问题(一)动态规划算法的基本思想动态规划算法通常用于求解具有某种最优性质的问题。

在这类问题中,可能会有许多可行解。

每一个解都对应于一个值,我们希望找到具有最优值的解。

动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。

与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。

若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算很多次。

如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。

我们可以用一个表来记录所有已解的子问题的答案。

不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中,这就是动态规划法的基本思路。

具体的动态规划算法多种多样,但它们具有相同的填表格式。

(二)算法设计假定背包的载重量范围为0～m。

01背包问题(动态规划法)

0/1背包问题1. 问题描述给定一个载重量为m，n个物品，其重量为w i，价值为v i，1<=i<=n，要求:把物品装入背包，并使包内物品价值最大2. 问题分析在0/1背包问题中，物体或者被装入背包，或者不被装入背包，只有两种选择。

循环变量i，j意义：前i个物品能够装入载重量为j的背包中(n+1)*(m+1)数组value意义：value[i][j]表示前i个物品能装入载重量为j的背包中物品的最大价值若w[i]>j，第i个物品不装入背包否则，若w[i]<=j且第i个物品装入背包后的价值>value[i-1][j]，则记录当前最大价值（替换为第i个物品装入背包后的价值）计算最大价值的动态规划算法如下：//计算for(i=1;i<row;i++){for(j=1;j<col;j++){//w[i]>j,第i个物品不装入背包value[i][j]=value[i-1][j];//w[i]<=j,且第i个物品装入背包后的价值>value[i-1][j],则记录当前最大价值int temp=value[i-1][j-w[i]]+v[i];if(w[i]<=j && temp>value[i][j])value[i][j]=temp;}}即该段程序完成以下n个阶段：1：只装入1个物品，确定在各种不同载重量的背包下，能够得到的最大价值2：装入2个物品，确定在各种不同载重量的背包下，能够得到的最大价值。

n：以此类推，装入n个物品，确定在各种不同载重量的背包下，能够得到的最大价值3. 问题求解确定装入背包的具体物品，从value[n][m]向前逆推：若value[n][m]>value[n-1][m]，则第n个物品被装入背包，且前n-1个物品被装入载重量为m-w[n]的背包中否则，第n个物品没有装入背包，且前n-1个物品被装入载重量为m的背包中以此类推，直到确定第一个物品是否被装入背包为止。

蛮力法、动态规划法、回溯法和分支限界法求解01背包问题【精选】

一、实验内容：分别用蛮力法、动态规划法、回溯法和分支限界法求解0/1背包问题。

注：0/1背包问题：给定种物品和一个容量为的背包，物品的重n C i 量是，其价值为，背包问题是如何使选择装入背包内的物品，使得装i w i v 入背包中的物品的总价值最大。

其中，每种物品只有全部装入背包或不装入背包两种选择。

二、所用算法的基本思想及复杂度分析：1.蛮力法求解0/1背包问题：1）基本思想：对于有n 种可选物品的0/1背包问题，其解空间由长度为n 的0-1向量组成,可用子集数表示。

在搜索解空间树时，深度优先遍历，搜索每一个结点，无论是否可能产生最优解，都遍历至叶子结点，记录每次得到的装入总价值，然后记录遍历过的最大价值。

2）代码:#include<iostream>#include<algorithm>using namespace std;#define N 100//最多可能物体数struct goods //物品结构体{int sign;//物品序号int w;//物品重量int p;//物品价值}a[N];bool m(goods a,goods b){return (a.p/a.w)>(b.p/b.w);}int max(int a,int b){return a<b?b:a;}int n,C,bestP=0,cp=0,cw=0;int X[N],cx[N];/*蛮力法求解0/1背包问题*/int Force(int i){if(i>n-1){if(bestP<cp&&cw+a[i].w<=C){for (int k=0;k<n;k++)X[k]=cx[k];//存储最优路径bestP=cp;}return bestP;}cw=cw+a[i].w;cp=cp+a[i].p;cx[i]=1;//装入背包Force(i+1);cw=cw-a[i].w;cp=cp-a[i].p;cx[i]=0;//不装入背包Force(i+1);return bestP;}int KnapSack1(int n,goods a[],int C,int x[]){Force(0);return bestP;}int main(){goods b[N];printf("物品种数n: ");scanf("%d",&n);//输入物品种数printf("背包容量C: ");scanf("%d",&C);//输入背包容量for (int i=0;i<n;i++)//输入物品i 的重量w 及其价值v {printf("物品%d 的重量w[%d]及其价值v[%d]:",i+1,i+1,i+1);scanf("%d%d",&a[i].w,&a[i].p);b[i]=a[i];}int sum1=KnapSack1(n,a,C,X);//调用蛮力法求0/1背包问题printf("蛮力法求解0/1背包问题:\nX=[ ");for(i=0;i<n;i++)cout<<X[i]<<" ";//输出所求X[n]矩阵printf("]装入总价值%d\n",sum1);bestP=0,cp=0,cw=0;//恢复初始化}3）复杂度分析：蛮力法求解0/1背包问题的时间复杂度为：。

第3章-动态规划3-0-1背包问题

(1) vn j wn m(n, j ) (3.4.4) 0 0 j wn (2)
注:(3-4-3)式此时背包容量为j，可选择物品为i。此时在对xi 作出决策之后,问题处于两种状态之一: 背包剩余容量是j,没产生任何效益; 剩余容量j-wi,效益值增长了vi . 从n推至i+1, i算出最优值m(i, j) （ i=n,…,1）。 m(1,C)为最优值。然后用算法traceback找出最优解xi ，其中i，C为整值。
5
2.递归关系
由0-1背包问题的最优子结构性质，可以建立计算 m(i，j)的递归式如下：第i个物品装入背包
第i个物品不装入背包
(3.4.3)
j wi m(i 1, j ), m(i 1, j wi ) vi } max{ m(i, j ) 0 j wi m(i 1, j )
}
3.算法描述
3.算法描述
m[1][c]=m[2][c]; //令m[1][c]=m[2][c]// if(c>=w[1]) //如果背包装得下w[1]// m[1][c]=max(m[1][c], m[2][c-w[1]]+v[1]); } void traceback(int [][]m, int []w, int c, int []x) //求最优解xi // { int n = w.length-1; for(int i=1; i<n; i++) knapsack算法的 if(m[i][c]==m[i+1][c]) x[i]=0; 一个缺点是要求 else { x[i]=1; 所给物品的重量 c= c- w[i]; } wi （1 i n） x[n]=(m[n][c]>0)?1:0; 是整数 } 说明:当wi为正整数时，用二维数组m[][]来存储m(i,j)相应的最优值。

动态规划求解01背包问题

动态规划求解01背包问题问题给定n种物品和⼀个背包，物品(1<=i<=n)重量是w I ，其价值v i,背包容量为C,对每种物品只有两种选择：装⼊背包和不装⼊背包，即物品是不可能部分装⼊，部分不装⼊。

如何选择装⼊背包的物品，使其价值最⼤？想法该问题是最优化问题，求解此问题⼀般采⽤动态规划（dynamic plan），很容易证明该问题满⾜最优性原理。

动态规划的求解过程分三部分：⼀：划分⼦问题：将原问题划分为若⼲个⼦问题，每个⼦问题对应⼀个决策阶段，并且⼦问题之间具有重叠关系⼆：确定动态规划函数：根据⼦问题之间的重叠关系找到⼦问题满⾜递推关系式（即动态规划函数），这是动态规划的关键三：填写表格：设计表格，以⾃底向上的⽅式计算各个⼦问题的解并填表，实现动态规划过程。

思路：如何定义⼦问题？0/1背包可以看做是决策⼀个序列（x1,x2,x3,…,xn）,对任何⼀个变量xi的决策时xi=1还是xi=0. 设V(n,C)是将n个物品装⼊容量为C的背包时背包所获得的的最⼤价值，显然初始⼦问题是将前i个物品装如容量为0的背包中和把0个物品装⼊容量为j的背包中，这些情况背包价值为0即V(i,0)=V(0,j)=0 0<=i<=n, 0<=j<=C接下来考虑原问题的⼀部分，设V(I,j)表⽰将前i个物品装⼊容量为j的背包获得的最⼤价值，在决策xi时，已经确定了(x1,x2,…,xi-1)，则问题处于下列两种情况之⼀：1. 背包容量不⾜以装⼊物品i，则装⼊前i-1个物品的最⼤价值和装⼊前i个物品最⼤价值相同，即xi=0，背包价值没有增加2. 背包容量⾜以装⼊物品i，如果把物品i装⼊背包，则背包物品价值等于把前i-1个物品装⼊容量为j-wi的背包中的价值加上第i个物品的价值vi；如果第i个物品没有装⼊背包，则背包价值等于把前i-1个物品装⼊容量为j的背包中所取得的价值，显然，取⼆者最⼤价值作为把物品i装⼊容量为j的背包中的最优解，得到如下递推公式为了确定装⼊背包中的具体物品，从V(n,C)的值向前推，如果V（n，C）>V(n-1,C),则表明第n个物品被装⼊背包中，前n-1个物品被装⼊容量为C-wn的背包中；否则，第n个物品没有被装⼊背包中，前n-1个物品被装⼊容量为C的背包中，依次类推，直到确认第⼀个物品是否被装⼊背包中代码C++实现1. // dp_01Knapsack.cpp : 定义控制台应⽤程序的⼊⼝点。

求解0—1背包问题算法综述

0-1背包问题是一种常见的动态规划问题，其目标是在给定背包容量和物品集合的情况下，选择某些物品放入背包，使得背包内物品的总价值最大。

以下是求解0-1背包问题的算法综述：
1. 定义变量和参数：
* 物品集合：包括每个物品的重量和价值。

* 背包容量：表示背包能够容纳的最大重量。

* dp数组：用于存储每个状态下的最大价值，dp[i][j]表示前i个物品、背包承重为j时的最大价值。

2. 初始化dp数组：
* 对于每个物品i和背包容量j，如果物品i能够装入背包，则令dp[i][j]为0；否则，令dp[i][j]为负无穷。

3. 递推计算dp数组：
* 对于每个物品i和背包容量j，如果物品i能够装入背包，则令dp[i][j]为当前物品的价值加上前i-1个物品、背包容量为j-w[i]时的最大价值，即dp[i][j] = dp[i-1][j-w[i]] + p[i]；否则，
令dp[i][j]为前i-1个物品、背包容量为j时的最大价值，即dp[i][j] = dp[i-1][j]。

4. 返回dp数组的最后一个元素，即为所求的最大价值。

以上是求解0-1背包问题的算法综述，实际实现时可以根据具体情况进行优化，以提高算法的效率和性能。

5.5动态规划求解01背包问题

xn-1: 若xn=0，则判断(Pl,Wl)∈ Sn－2？，以确定Xn-1的值若xn=1，则依据(Pl－pn,Wl-wn)∈ Sn－2？，以判断Xn-1的值
xn-2,…,x1将依次推导得出
例2的解向量推导
S0={(0,0)}
S1={(0,0),(1,2)}
S2={(0,0),(1,2), (2,3),(3,5)}
● Si的构造
记S1i 是fi-1(X-wi)+pi的所有序偶的集合，则
S1i {( P,W ) | (P pi ,W wi ) S i1}
其中，Si-1是fi-1的所有序偶的集合
Si的构造：由Si-1和 S1i 按照支配规则合并而成。
支配规则：如果Si-1和S1i 之一有序偶(Pj,Wj),另一有(Pk,Wk)，
5.5动态规划求解 0/1背包问题
1.问题描述背包容量M，n个物品，分别具有效益值P1…Pn,物
品重量w1…wn,从n个物品中，选择若干物品放入背包，物品要么整件放入背包，要么不放入。怎样决策可以使装入背包的物品总效益值最大？
形式化描述：
目标函数：
约束条件：
max pixi
1i j
wixi M
1in
xi
0或1,
pi
0, wi
0,1
i
n
0/1背包问题：KNAP(1,n,M)
❖ 0/1背包问题：M=6,N=3,W=(3,3,4),P=(3,3,5) ❖ 贪心法：p3/w3 > p1/w1 > p2/w2 ❖ 贪心解 ∑P=5（0,0,1） ❖ 最优解是：∑P=6（1,1,0）
❖ 贪心法求解0/1背包问题不一定得到最优解！ ❖ 动态规划求解的问题必须满足最优化原理

用动态规划解0-1背包问题

实验一用动态规划解0-1背包问题一、实验目的与要求1、掌握动态规划算法求解问题的一般特征和步骤2、使用动态规划法编程求解0/1背包问题。

二、实验内容0-1背包问题(knapsack problem)：某商店有n个物品，第i个物品价值为vi，重量(或称权值)为wi，其中vi和wi为非负数, 背包的容量为C，C为一非负数。

目标是如何选择装入背包的物品使装入背包的物品总价值最大，所选商品的一个可行解即所选商品的序列如何。

背包问题与0-1 背包问题的不同点在于：在选择物品装入背包时，可以只选择物品的一部分，而不一定要选择物品的全部。

三、问题描述给定n和物品和一人背包，物品i的重量是wi，其价值为vi，问：如何选择装入背包的物品，使得装入背包的物品的总价值最大。

举例: 若商店一共有5类商品，重量分别为：34789，价值分别为：45101113，则所选商品的最大价值为24，所选商品的一个序列为0 0 0 1 1。

四、问题分析与算法设计动态规划原理：动态规划是一种将问题实例分解为更小的、相似的子问题并存储子问题的解而避免计算重复的子问题以解决最优化问题的算法策略。

动态规划法所针对的问题有一个显著的特征，即它所对应的子问题树中的子问题呈现大量的重复。

动态规划法的关键就在于：对于重复出现的子问题，只在第一次遇到时加以求解，并把答案保存起来，让以后再遇到时直接引用而不必重新求解。

五、实验结果源程序：#include<iostream>using namespace std;void knapsack(int m[30][30],int w[30],int v[30],int n,int C){ for(int i = 0; i <= C; i ++) m[0][i] = 0;for(int i = 1; i <= n; i ++){ m[i][0] = 0;for(int j = 1; j <= C; j ++){ if(w[i] <= j){ if(v[i] + m[i - 1][j - w[i]] > m[i - 1][j])m[i][j] = v[i] + m[i - 1][j - w[i]];else m[i][j] = m[i - 1][j];}else m[i][j] = m[i - 1][j];}}}void traceback(int m[30][30],int x[30],int w[30],int n,int C){for(int k = n; k >= 2; k --){ if(m[k][C] == m[k-1][C])x[k] = 0;else { x[k] = 1; C = C - w[k]; }}x[1] = m[1][C] ? 1 : 0;}int main(){int m[30][30] , w[30] , v[30] , x[30] , C , n;cout<<"请输入物品的总个数："; cin>>n;cout<<"请输入背包的总容量："; cin>>C; cout<<endl;for(int i = 1; i <= n; i ++){ cout<<"请输入第"<<i<<"个物品的重量：";cin >> w[i];}cout<<endl;for(int i = 1; i <= n; i ++){ cout<<"请输入第"<<i<<"个物品的价值：";cin >> v[i];}knapsack(m, w, v, n, C);traceback(m, x, w, n, C);cout<<"最优解为："<<endl;for(int i = 1; i <= n; i ++) cout<<x[i]<<" ";cout<<endl<<"背包中物品的最大价值是："<<endl;cout<<m[n][C]<<endl;system("pause");return 0;}。

0-1背包问题动态规划详解及代码

0/1 背包问题动态规划详解及C代码动态规划是用空间换时间的一种方法的抽象。

其关键是发现子问题和记录其结果。

然后利用这些结果减轻运算量。

比如01背包问题。

/* 一个旅行者有一个最多能用M公斤的背包，现在有N件物品，它们的重量分别是W1，W2，...,Wn,它们的价值分别为P1,P2,...,Pn.若每种物品只有一件求旅行者能获得最大总价值。

输入格式：M,NW1,P1W2,P2......输出格式：X*/因为背包最大容量M未知。

所以，我们的程序要从1到M一个一个的试。

比如，开始任选N 件物品的一个。

看对应M的背包，能不能放进去，如果能放进去，并且还有多的空间，则，多出来的空间里能放N-1物品中的最大价值。

怎么能保证总选择是最大价值呢？看下表。

加谁??很显然是7-4=3的时候.上一排 c3的最佳方案是4.所以。

总的最佳方案是5+4为9.这样.一排一排推下去。

最右下放的数据就是最大的价值了。

f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.这回清楚了吗?下面是实际程序（在VC 6.0环境下通过）:#include<stdio.h>int c[10][100];/*对应每种情况的最大价值*/int knapsack(int m,int n){int i,j,w[10],p[10];printf("请输入每个物品的重量,价值：\n");for(i=1;i<=n;i++)scanf("%d,%d",&w[i],&p[i]);for(i=0;i<10;i++)for(j=0;j<100;j++)c[i][j]=0;/*初始化数组*/for(i=1;i<=n;i++)for(j=1;j<=m;j++){if(w[i]<=j) /*如果当前物品的容量小于背包容量*/{if(p[i]+c[i-1][j-w[i]]>c[i-1][j])/*如果本物品的价值加上背包剩下的空间能放的物品的价值*//*大于上一次选择的最佳方案则更新c[i][j]*/c[i][j]=p[i]+c[i-1][j-w[i]];elsec[i][j]=c[i-1][j];}else c[i][j]=c[i-1][j];}return(c[n][m]);}int main(){int m,n;int i,j;printf("请输入背包的承重量,物品的总个数：\n");scanf("%d,%d",&m,&n);printf("旅行者背包能装的最大总价值为%d",knapsack(m,n)); printf("\n");return 0;}。

#动态规划0-1背包问题思路概述

#动态规划0-1背包问题思路概述01背包问题是动态规划中的经典问题。

本篇⽂章主题：分析与优化最基本的01背包问题，对此类问题解题有⼀个基本的解题模板。

问题概述：有⼀个背包，他的容量为C（Capacity）。

现在有n种不同的物品编号分别为0、1....n-1。

其中每⼀件物品的重量为w(i)，价值为v(i)。

问可以向这个背包中放⼊哪些物品，使得在不超过背包容量的基础上，背包内物品价值最⼤。

思路：1.暴⼒法。

每⼀件物品都可以放进背包，也可以不放进背包。

找出所有可能组合⼀共2^n种组合时间复杂度：O((2^n)*n)2.动态规划法。

我们⾸先使⽤递归函数⾃上⽽下进⾏思考。

明确两点：第⼀、递归函数的定义第⼆、数据结构函数定义：F（n,C）递归函数定义：将n个物品放⼊容量为C的背包，使得价值最⼤。

这⾥要注意⼀下，第⼆个参数⼀定是剩余容量。

我们通过使⽤剩余容量来控制价值。

F（i，c） = F（i-1,c） = v(i) + F(i-1 , c-w(i))状态转移⽅程：F（i，c） = max( F(i-1 , c) , v(i) + F(i-1 , c-w(i) ) )即，当前价值的最⼤值为，不放⼊第i个物品(对应剩余容量为c)和放⼊第i个物品（对应剩余容量为C-w(i)）两种情况的最⼤值。

数据结构：借某盗版视频中的⼀个例⼦：我们这⾥选择⼀个⼆维数组，来迭代记录处理的结果。

这个⼆维数组dp[n][C] 其中n为物品数量，C为最⼤容量。

储存的值dp[i][j]含义为：考虑放⼊0~i 这些物品，背包容量为j我们考虑放⼊第⼀个物品。

由于第⼀个物品，编号为0，重量为1，价值为2。

对于容量为0的背包，放不下该物品，所以该背包价值为0.其余容量1~5，均可放下该物品。

所以只考虑物品0，不同背包⼤⼩对应的最⼤可能价值如图。

第⼀⾏处理为初始化，从第⼆⾏开始进⾏迭代。

第⼆⾏开始，就需要单独处理。

考虑dp[1][0]，背包容量为0，理所应当为0考虑dp[1][1]，此处我们依旧⽆法放⼊物品1，所以我们使⽤上⼀层的结果，即0~0物品在容量为1背包情况的最⼤价值。

0-1背包问题的递归方法

0-1背包问题的递归方法0-1背包问题是一个经典的动态规划问题，可以使用递归方法求解。

定义一个函数`knapsack(weights, values, capacity, n)`，其中`weights`和`values`分别代表物品的重量和价值，`capacity`代表背包的容量，`n`代表当前考虑的物品个数。

递归的思路是对于每个物品，有两种选择：放入背包中或者不放入背包中。

1. 如果第`n`个物品的重量大于背包的容量`capacity`，则不放入背包中，返回`0`；2. 否则，有两种选择：- 选择放入第`n`个物品，则总价值为第`n`个物品的价值加上考虑前`n-1`个物品，背包容量减去第`n`个物品重量的最优解； - 不放入第`n`个物品，则总价值为考虑前`n-1`个物品，背包容量不变的最优解。

代码如下所示：```pythondef knapsack(weights, values, capacity, n):if n == 0 or capacity == 0:return 0if weights[n-1] > capacity:return knapsack(weights, values, capacity, n-1)else:return max(values[n-1] + knapsack(weights, values, capacity-weights[n-1], n-1),knapsack(weights, values, capacity, n-1))```可以通过调用`knapsack`函数来求解0-1背包问题，如下所示：```pythonweights = [2, 3, 4, 5]values = [3, 4, 5, 6]capacity = 5n = len(weights)result = knapsack(weights, values, capacity, n)print(result)```以上代码会输出最优解的总价值。

动态规划之01背包问题

动态规划之01背包问题01背包问题问题描述：给定 n 件物品，物品的重量为 w[i]，物品的价值为 c[i]。

现挑选物品放⼊背包中，假定背包能承受的最⼤重量为 V，问应该如何选择装⼊背包中的物品，使得装⼊背包中物品的总价值最⼤？针对这个问题，本⼈理解了多次，也了看各种题解，尝试各种办法总还觉得抽象；或者说，看了多次以后，只是把题解的状态转移⽅程记住了⽽已，并没有真正的“掌握”其背后的逻辑。

直到我看了，在此感谢作者并记录于此。

01背包问题之另⼀种风格的描述：假设你是⼀个⼩偷，背着⼀个可装下4磅东西的背包，你可以偷窃的物品如下：为了让偷窃的商品价值最⾼，你该选择哪些商品？暴⼒解法最简单的算法是：尝试各种可能的商品组合，并找出价值最⾼的组合。

这样显然是可⾏的，但是速度⾮常慢。

在只有3件商品的情况下，你需要计算8个不同的集合；当有4件商品的时候，你需要计算16个不同的集合。

每增加⼀件商品，需要计算的集合数都将翻倍！对于每⼀件商品，都有选或不选两种可能，即这种算法的运⾏时间是O(2ⁿ)。

动态规划解决这样问题的答案就是使⽤动态规划！下⾯来看看动态规划的⼯作原理。

动态规划先解决⼦问题，再逐步解决⼤问题。

对于背包问题，你先解决⼩背包（⼦背包）问题，再逐步解决原来的问题。

⽐较有趣的⼀句话是：每个动态规划都从⼀个⽹格开始。

（所以学会⽹格的推导⾄关重要，⽽有些题解之所以写的不好，就是因为没有给出⽹格的推导过程，或者说，没有说清楚为什么要”这样“设计⽹格。

本⽂恰是解决了我这⽅⾯长久以来的困惑！）背包问题的⽹格如下：⽹格的各⾏表⽰商品，各列代表不同容量（1~4磅）的背包。

所有这些列你都需要，因为它们将帮助你计算⼦背包的价值。

⽹格最初是空的。

你将填充其中的每个单元格，⽹格填满后，就找到了问题的答案！1. 吉他⾏后⾯会列出计算这个⽹格中单元格值得公式，但现在我们先来⼀步⼀步做。

⾸先来看第⼀⾏。

这是吉他⾏，意味着你将尝试将吉他装⼊背包。

动态规划专题01背包问题详解【转】

动态规划专题01背包问题详解【转】对于动态规划，每个刚接触的⼈都需要⼀段时间来理解，特别是第⼀次接触的时候总是想不通为什么这种⽅法可⾏，这篇⽂章就是为了帮助⼤家理解动态规划，并通过讲解基本的01背包问题来引导读者如何去思考动态规划。

本⽂⼒求通俗易懂，⽆异性，不让读者感到迷惑，引导读者去思考，所以如果你在阅读中发现有不通顺的地⽅，让你产⽣错误理解的地⽅，让你难得读懂的地⽅，请跟贴指出，谢谢！初识动态规划经典的01背包问题是这样的：有⼀个包和n个物品，包的容量为m，每个物品都有各⾃的体积和价值，问当从这n个物品中选择多个物品放在包⾥⽽物品体积总数不超过包的容量m时，能够得到的最⼤价值是多少？[对于每个物品不可以取多次，最多只能取⼀次，之所以叫做01背包，0表⽰不取，1表⽰取]为了⽤⼀种⽣动⼜更形象的⽅式来讲解此题，我把此题⽤另⼀种⽅式来描述，如下：有⼀个国家，所有的国民都⾮常⽼实憨厚，某天他们在⾃⼰的国家发现了⼗座⾦矿，并且这⼗座⾦矿在地图上排成⼀条直线，国王知道这个消息后⾮常⾼兴，他希望能够把这些⾦⼦都挖出来造福国民，⾸先他把这些⾦矿按照在地图上的位置从西⾄东进⾏编号，依次为0、1、2、3、4、5、6、7、8、9，然后他命令他的⼿下去对每⼀座⾦矿进⾏勘测，以便知道挖取每⼀座⾦矿需要多少⼈⼒以及每座⾦矿能够挖出多少⾦⼦，然后动员国民都来挖⾦⼦。

题⽬补充1：挖每⼀座⾦矿需要的⼈数是固定的，多⼀个⼈少⼀个⼈都不⾏。

国王知道每个⾦矿各需要多少⼈⼿，⾦矿i需要的⼈数为peopleNeeded[i]。

题⽬补充2：每⼀座⾦矿所挖出来的⾦⼦数是固定的，当第i座⾦矿有peopleNeeded[i]⼈去挖的话，就⼀定能恰好挖出gold[i]个⾦⼦。

否则⼀个⾦⼦都挖不出来。

题⽬补充3：开采⼀座⾦矿的⼈完成开采⼯作后，他们不会再次去开采其它⾦矿，因此⼀个⼈最多只能使⽤⼀次。

题⽬补充4：国王在全国范围内仅招募到了10000名愿意为了国家去挖⾦⼦的⼈，因此这些⼈可能不够把所有的⾦⼦都挖出来，但是国王希望挖到的⾦⼦越多越好。