中心对称的作图
合集下载
《中心对称的作图》课件

04 中心对称的实例分析
几何图形中的中心对称实例
总结词
几何图形中的中心对称实例展示了对称美学的简洁和平衡。
详细描述
在几何图形中,中心对称是指图形关于某一点旋转180度后 与自身重合。常见的中心对称图形有圆形、正方形、正十二 面体等。这些图形具有高度的对称性和美感,常用于数学研 究和艺术创作。
建筑设计中的中心对称实例
寻找对称中心
观察图形是否有一个明显的对称中心 ,通过该点的任意直线都可以将图形 分成两个对称的部分。
02 中心对称的作图方法
确定对称中心
确定对称中心
在作图之前,需要先确定对称中 心的位置。对称中心是图形关于 其对称的点所组成的直线与平面 的交点。
确定对称轴
对称中心所在的直线被称为对称 轴,所有关于对称轴对称的点都 与对称中心等距。
在图案设计中的应用
01
02
03
图案设计原则
中心对称是图案设计的基 本原则之一,可以使图案 看起来更加协调、平衡和 有美感。
装饰图案
在装饰图案设计中,中心 对称被广泛应用,如花卉 、动物等图案的构图和造 型。
平面设计
在平面设计中,中心对称 可以用于标志、海报等设 计,使作品更加醒目、突 出和有吸引力。
确定对称点
找到已知点关于对称中心的对称点
在确定了对称中心后,需要找到图形中已知点关于该对称中心的对称点。
确定对称点的坐标
根据已知点和对称中心的坐标,可以计算出对称点的坐标。
连接对称点
连接对称点以形成图形
最后一步是将找到的对称点连接起来 ,形成完整的中心对称图形。
验证图形是否正确
完成作图后,需要验证所绘制的图形 是否真正关于对称中心对称,确保作 图的准确性。
中心对称作图方法

中心对称作图方法
【教学目标】:
知识与技能:了解中心对称、对称中心、关于中心的对称点等概念及掌握这些概念解决一些问题.
过程与方法:掌握关于中心对称的作图方法。
情感态度价值观:培养学生的观察分析、归纳能力,感受中心对称美,开展学生的作图能力。
【教学重点】利用中心对称、对称中心作图
【教学难点】根据要求作出不同图形的中心对称图形.
【教学方法】探究、归纳
【教具准备】多媒体
【课型】新授课
【教学过程】:
一、预习导航
1中心对称的定义。
二、中心对称的作图方法
例1、如图,选择点O为对称中心,画出点A关于点O的中心对称点A′。
解:连接AO,在AO的延长线上截取OA′=OA,点A′既为点A关于点O的对称点。
例2、如图,选择点O为对称中心,画出线段AB关于点O的中心对称线段A′B′。
解:第一步、分别作点A,点B关于点O的中心对称点A′,B′;
第二步、连接A′B′,线段A′B′既为线段AB关于点O的中心对称图形。
例3、如图,选择点O为对称中心,画出四边形ABCD关于点O的中心对称四边形A′B′C′D′。
解:第一步、:分别作点A、点B、点C、点D关于点O的中心对称点A′、B′、C′、D′,
第二步、依次连接A′B′、B′C′、C′D′、D′A′,四边形A′B′C′D′既为四边形ABCD关于点O的中心对称图形。
变式:当对称中心的位置比拟特殊的时候:1、在图形内;2、在图形某个顶点上。
以三角行为例讲解。
三、小结:中心对称的作图方法。
九年级数学中心对称图形课件

正方形中心对称图形的面积计算
总结词
正方形中心对称图形的面积计算与矩形类似,也是通过 计算一个正方形面积再除以2得到。
详细描述
正方形作为特殊的矩形,其中心对称图形的面积计算方 法与矩形相同。将正方形分成两个完全相同的部分,然 后计算一个正方形的面积,最后将结果除以2即可得到整 个中心对称图形的面积。假设正方形边长为a,则其面积 为a^2。所以,中心对称图形的面积为(a^2)/2。
THANKS
感谢观看
03
中心对称图形的判定
通过旋转判定中心对称图形
总结词
旋转法是判定中心对称图形的一种常 用方法。
详细描述
将图形绕着某点旋转180度,如果旋 转后的图形与原图形重合,则该图形 是中心对称图形。例如,正方形、圆 、正六边形等都是中心对称图形。
通过反射判定中心对称图形
总结词
反射法是通过图形的对称性来判定中心对称图形的方法。
05
中心对称图形的面积计算
矩形中心对称图形的面积计算
要点一
总结词
要点二
详细描述
矩形中心对称图形的面积计算相对简单,可以通过计算一 个矩形面积再除以2得到。
对于矩形中心对称图形,我们可以将其分成两个完全相同 的矩形,然后计算一个矩形的面积,最后将结果除以2即可 得到整个中心对称图形的面积。假设矩形长为a,宽为b, 则其面积为ab。所以,中心对称图形的面积为(ab)/2。
九年级数学中心对称图形ppt课件
目 录
• 中心对称图形的定义 • 中心对称图形的性质 • 中心对称图形的判定 • 中心对称图形的作图 • 中心对称图形的面积计算
01
中心对称图形的定义
中心对称图形的文字定义
总结词:简明扼要
23.2.1 中心对称(共43张PPT)
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
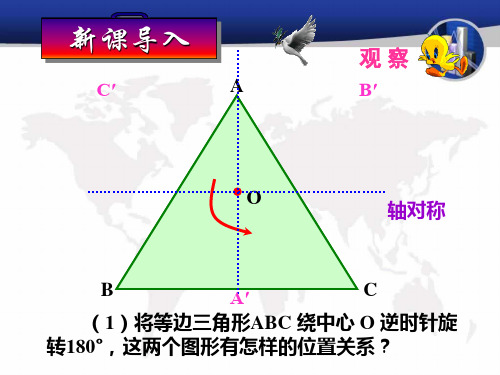
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
中心对称-精品文档

自然界中的中心对称
花朵
许多花朵的形状是对称的,如向 日葵、百合和菊花等。这种对称 不仅美观,还有助于吸引传粉昆 虫。
动物
自然界中许多动物的形状也是中 心对称的,如蝴蝶、蜜蜂和章鱼 等。这种对称有助于动物的运动 和生存。
03
中心对称的判定
平行四边形判定法
总结词
通过判断图形是否为平行四边形来判 定中心对称。
利用轴对称性质作图
总结词
利用轴对称的性质,将图形进行翻转或 旋转,以完成对称作图。
VS
详细描述
首先确定对称轴,然后将图形上的点或线 段按照对称轴进行翻转或旋转,以得到对 称的图形。这种方法适用于绘制轴对称的 图形,如长方形、三角形等。
05
中心对称的练习题与解析
基础练习题
总结词:理解中心对称的基本概念
绘画
艺术家可以利用中心对称的原理来构图,使画面更加平衡和 稳定。例如,在绘制圆形物体或对称图案时,可以找到一个 中心点,然后画出与该点相对称的形状或线条。
雕塑
在雕塑创作中,中心对称也被广泛应用。许多雕塑作品采用 了对称的设计,以突出稳定感和平衡感,如希腊的古典雕塑 和中国的石狮子。
建筑设计
建筑设计中的对称
在几何学中,这个特 性是判断一个图形是 否具有中心对称性的 标准。
几何图形中的中心对称
圆形、正方形、长方形等都是 常见的中心对称图形。
这些图形都有一个对称中心, 通过该中心可以将图形分成两 个对称的部分。
在这些图形中,任意一点关于 对称中心都有对称点,且这两 点与对称中心的距离相等。
中心对称的性质
01
中心对称图形一定是轴 对称图形,但轴对称图 称中心具有对称性,即 其对称中心是其几何中 心。
中心对称(课件)
中心对称是图形关于某一点旋转180°后能与另一图形重合的特性。这一点称为对称中心,重合的对应点称为关于中心的对称点。文档通过实例演示了如何识别和应用中心对称,如线段AC,BD相交于点O且OA=OC,OB=OD,把△OAB绕点O旋转180°后与△OCD重合,展示了中心对称的概念。此外,还探索了中心对称的性质,如对称点所连线段经过对称中心且被平分,中心对称的两个图形是全等形。文档还提供了利用这些性质作图的详细步骤,包图形的对称中心。通过练习和判断题,进一步巩固了对中心对称的理解和应用。最后,利用中心对称的性质求解了相关问题,如已知中心对称图形中的某些角度和长度,求其他未知量。
中心对称应用(3)

A''
b
A
O
C
B
A'
拓展
例1.如图,矩形ABCD中,AB=3,BC=4,若 将矩形折叠,使C点和A点重合,• 求折痕EF的 长. D E A
O
B F
www .czsx .com .cn
C
拓展
例2.将矩形ABCD沿 AE折叠,得到如图的 所示的图形,已知 ∠CED′=60°,则 ∠AED的大小是( ) A.60° B.50° C.75° D.55°
3.中 心 对 称 图 形 的 作 图: 4.中心对称与中心对称图形
几何中常见基本图形的对称性
对 图 形 性 称
轴对称图形
图形 对称轴条数
中心对称图形
图形 对称中心
线段 角 等腰三角形 等边三角形 平行四边形 矩形 菱形 正方形
2条 1条 1条 3条
中点
对角线交点
2条
对角线交点 对角线交点 对角线交点
想一想:
左
右
解: (1)轴对称 (2)左边的图形向右轴对称(翻转)得到右 边的图形。 平移不可以 旋转不可以
做一做:
乙
(1)弄清顺序, 怎样将甲图案变成乙图案? 注: 即原图是什么,变换后
甲
的图形是什么?
(2)图形的变换有3种,平 移,旋转,轴对称(翻 转),说变化时一定说 出要素。
可以先将甲图案绕图 还可以用
乙 B A
上的 A点旋转,使得 什么方法把
甲 图案被“扶直”,然 甲图案变成
乙图案? 后,再沿 AB方向将所
得图案平移到B点位
置,即可得到乙图案
B A
做一做:
方法不唯一
注: (1)弄清顺序, 即原图是什么,变换后 的图形是什么?
b
A
O
C
B
A'
拓展
例1.如图,矩形ABCD中,AB=3,BC=4,若 将矩形折叠,使C点和A点重合,• 求折痕EF的 长. D E A
O
B F
www .czsx .com .cn
C
拓展
例2.将矩形ABCD沿 AE折叠,得到如图的 所示的图形,已知 ∠CED′=60°,则 ∠AED的大小是( ) A.60° B.50° C.75° D.55°
3.中 心 对 称 图 形 的 作 图: 4.中心对称与中心对称图形
几何中常见基本图形的对称性
对 图 形 性 称
轴对称图形
图形 对称轴条数
中心对称图形
图形 对称中心
线段 角 等腰三角形 等边三角形 平行四边形 矩形 菱形 正方形
2条 1条 1条 3条
中点
对角线交点
2条
对角线交点 对角线交点 对角线交点
想一想:
左
右
解: (1)轴对称 (2)左边的图形向右轴对称(翻转)得到右 边的图形。 平移不可以 旋转不可以
做一做:
乙
(1)弄清顺序, 怎样将甲图案变成乙图案? 注: 即原图是什么,变换后
甲
的图形是什么?
(2)图形的变换有3种,平 移,旋转,轴对称(翻 转),说变化时一定说 出要素。
可以先将甲图案绕图 还可以用
乙 B A
上的 A点旋转,使得 什么方法把
甲 图案被“扶直”,然 甲图案变成
乙图案? 后,再沿 AB方向将所
得图案平移到B点位
置,即可得到乙图案
B A
做一做:
方法不唯一
注: (1)弄清顺序, 即原图是什么,变换后 的图形是什么?
23.中心对称图形课件

23.2.2中心对称图形
【导引】
中心对称的作图
先分别作出①②③④四种情况的图形,再运用中心对称图形的定义
加以辨认.根据题意,可作出四种情况的图形如图1,其中旋转
180°后能与自身重合的只有第2个图形,∴将②涂黑能构成中心对
称图形.如图2,故答案填②.
图1 图2
23.2.2中心对称图形
想一想 中心对称与中心对称图形之间有什么与区分?
23.2.2中心对称图形 例3 如图,有一张纸片,纸片被分为一个矩形和一个菱形,请你 画一条直线把这张纸片分成面积相等的两部分.
方法归纳:对于这种由两个中心对称图形组成的复合图
形,平分面积时,常用方法是找到它们的对称中心,再过
对称中心作直线.
23.2.2中心对称图形
【练一练】
1.如图,直线EF经过平行四边形ABCD的对角线的交点O,若 AE=2 cm,四边形AEFB的面积为12 cm2,则CF=__2_c_m____, 平行四边形ABCD的面积为_2_4_c_m__2__.
23.2.2中心对称图形
当堂练习
1. 下列图案都是由字母“ m ”经过变形、组合而成
的,其中不是中心对称图形的是 ( B )
A
B
C
D
2.下列图形中既是轴对称图形又是中心对称图形的是( C)
A. 锐角 B. 等边三角形 C. 线段 D. 平行四边形
23.2.2中心对称图形
3. 世界因为有了圆的图案,万物才显得富有生机,以下来自现实
A
O
B
O
(1)线段
(2)平行四边形
共同点:(1)都绕一点旋转了180°;
(2)都与原图形完全重合.
23.2.2中心对称图形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组对应点,连结BB’、CC’,BB’、CC’相交 于点O,则点O即为所求(如图)。
C A’
O B’
B
A
C’
2、如图所示的两个图形成中心对 称,你能找到对称中心吗?
A B’
B
O
A’
深入理解
你用什么方法识别两个图 形是否关于某点中心对称?
B A C'
C B' A'
判断两图形是否成轴对称的办法:
方法1:将其中一个图形绕某一点 旋转180度,如果能够与另一个完全重 合,那么它们关于这一点中心对称。 方法2:如果两个图形的对应点连 成的线段都经过某一点,并且都被该点平 分,那么这两个图形一定关于这一点成中 心对称.
中心对称图形的作图
把一个图形绕着某一点旋转180O,如果它能够 和另一个图形重合,那么,我们就说这两个图形成 中心对称,这个点叫做对称中心,这两个图形中的 对应点,叫做关于中心的对称点.
C E A O D
B
在成中心对称的两个图形中,连接对称 点的线段都___________ ,并且被 ____________.
(1)画一个点关于某点(对称中心)的对称点的画 法是先连接这个点与对称中心并延长一倍即可。 (2)画一个图形关于某点的对称图形的画法是 先画出图形中的几个特殊点(如多边形的顶点、 线段的端点,圆的圆心等)关于某点的对称点, 然后再顺次连结有关对称点即可。
反过来,如果两个图形的对应点连成的线段 都经过 ,并且都被该点 ,那么这两 个图形一定关于这一点成中心对称.这一点就是对称 中心.
F
例1、已知A点和O点,画出点A关于点O的对称点A' A 连结OA, O 并延长到A',使OA'=OA, A'
则A'是所求的点 例2.已知线段AB和O点,画出线段AB关于点O的对称线段A' B'
B´
C´
O
A D
.
B
C
D´
A´
画法:
1.连结AO 并延长到A´,使OA=OA´,得到点A的对称点A´ .
2.同样画B、C、D的对称点B´、C´、D´
3、顺次连结A´、B´、C´、D´各点 所以,四边形A´B´C´D´就是所求的四边形
提高练习
你知道 怎么办 画一个与已知四边形ABCD中心对称图形。 吗? (1) 连接AO并延长到A′,使
B’ 2. 同样画B、C的对称点 B′、C′. A’ C’ 3. 顺次连接A′、B′、C′各点. OA ′=OA,得到点A的对称点A′.
△A′B′C′即为所求的三角形.
你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所平分” 的?
例4.已知四边形ABCD和O点,画出四边形ABCD 关于O点的对称图形。
F B B
A
G C A
.
O C D
M
E
D
如图,已知△ABC与△A’B’C’中心对称, 求出它们的对称中心O。
C A’ B’ B A
C’
解法一:根据观察,B、B’应是对应点,连 结BB’,用刻度尺找出BB’的中点O,则点
O即为所求(如图)
C O B A C’ B’
A’
解法二:根据观察,B、B’及C、C’应是两
B'
连结AO并延长到A',使OA'=OA,A 则得A的对称点A' 连结BO并延长到B' ,使O B' =OB, 则得B的对称点B' 连结 A' B' ,则线段A' B'是所画线段
B O A'
例3.如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
分析:确定一个三角形需要几个点?作一 个三角形关于某点成中心对称的三角形,需 要作几个点的对称点呢?
C A’
O B’
B
A
C’
2、如图所示的两个图形成中心对 称,你能找到对称中心吗?
A B’
B
O
A’
深入理解
你用什么方法识别两个图 形是否关于某点中心对称?
B A C'
C B' A'
判断两图形是否成轴对称的办法:
方法1:将其中一个图形绕某一点 旋转180度,如果能够与另一个完全重 合,那么它们关于这一点中心对称。 方法2:如果两个图形的对应点连 成的线段都经过某一点,并且都被该点平 分,那么这两个图形一定关于这一点成中 心对称.
中心对称图形的作图
把一个图形绕着某一点旋转180O,如果它能够 和另一个图形重合,那么,我们就说这两个图形成 中心对称,这个点叫做对称中心,这两个图形中的 对应点,叫做关于中心的对称点.
C E A O D
B
在成中心对称的两个图形中,连接对称 点的线段都___________ ,并且被 ____________.
(1)画一个点关于某点(对称中心)的对称点的画 法是先连接这个点与对称中心并延长一倍即可。 (2)画一个图形关于某点的对称图形的画法是 先画出图形中的几个特殊点(如多边形的顶点、 线段的端点,圆的圆心等)关于某点的对称点, 然后再顺次连结有关对称点即可。
反过来,如果两个图形的对应点连成的线段 都经过 ,并且都被该点 ,那么这两 个图形一定关于这一点成中心对称.这一点就是对称 中心.
F
例1、已知A点和O点,画出点A关于点O的对称点A' A 连结OA, O 并延长到A',使OA'=OA, A'
则A'是所求的点 例2.已知线段AB和O点,画出线段AB关于点O的对称线段A' B'
B´
C´
O
A D
.
B
C
D´
A´
画法:
1.连结AO 并延长到A´,使OA=OA´,得到点A的对称点A´ .
2.同样画B、C、D的对称点B´、C´、D´
3、顺次连结A´、B´、C´、D´各点 所以,四边形A´B´C´D´就是所求的四边形
提高练习
你知道 怎么办 画一个与已知四边形ABCD中心对称图形。 吗? (1) 连接AO并延长到A′,使
B’ 2. 同样画B、C的对称点 B′、C′. A’ C’ 3. 顺次连接A′、B′、C′各点. OA ′=OA,得到点A的对称点A′.
△A′B′C′即为所求的三角形.
你是如何理解“对称点所连线段都经过对称中心,而且被对称中心所平分” 的?
例4.已知四边形ABCD和O点,画出四边形ABCD 关于O点的对称图形。
F B B
A
G C A
.
O C D
M
E
D
如图,已知△ABC与△A’B’C’中心对称, 求出它们的对称中心O。
C A’ B’ B A
C’
解法一:根据观察,B、B’应是对应点,连 结BB’,用刻度尺找出BB’的中点O,则点
O即为所求(如图)
C O B A C’ B’
A’
解法二:根据观察,B、B’及C、C’应是两
B'
连结AO并延长到A',使OA'=OA,A 则得A的对称点A' 连结BO并延长到B' ,使O B' =OB, 则得B的对称点B' 连结 A' B' ,则线段A' B'是所画线段
B O A'
例3.如图,选择点O为对称中心,画出与 △ABC关于点O对称的△A′B′C′.
分析:确定一个三角形需要几个点?作一 个三角形关于某点成中心对称的三角形,需 要作几个点的对称点呢?
