矩形波导中波模截止频率
矩形变形脊波导主模截止波长研究
第 ４期
兰
州
交
通
大
学
学
报
Ｖｏ ． ９ Ｎｏ ４ １２ ． Ａｕ ． ０ ０ ｇ ２ １
２ １ 年 ８月 ００
ＪＵ Ｉ ｆ ａ ｚｏ ｉ ｔｎ ｉｅｓ ｙ Ｏ Ｈａ ｏ ｎｈ ｕＪａ ｏ ｇＵｎｖ ｒｉ ｌ Ｌ ｏ ｔ
文 章 编 号 ：０ １４ ７ （ ０ ０ ０ —０ ８０ １０ —３ ３ ２ １） ４０ ２－４
并 绘 出它们 的相应 变化 趋势 图．
ｓ／ ｌａ一０ ３ 固定 脊的宽度 ， ．， 改变脊 的高度 ， 脊从 使 左侧逐渐向中间移动 ， １ 表 的计算结果显示 了脊的
位 置对 其传 输特性 的影 响． １显 示 了 当脊 从 左 侧 图
１ ４处 向 中间位 置 移动 时 ， ｃａ增 加 时 ， 一 化 截 ／ 即 ／ 归
式 中 ： 为横 向拉普 拉斯算 子．
脊下陷波导的截面图如图 １ 所示． 图中 ｎ 和ｂ 是
单 脊波 导 的外 部尺 寸 ，２ ｓ 是大脊 的宽 度 ，１ 下 陷部 ｓ是 分 的宽 度 ，２是下 陷 部分 距离 顶 端 的高 度 ， ｄ １是 大 脊 距离 顶端 的高度 ， 是大脊 距离 边界 的宽 度． Ｃ
止 波长 ／ 口的变 化趋 势 ， 算结果 显 示 最 大值 出现 计 在 中间位置 ． 同时 ， 论 脊 的 位置 如何 ， 止 波 长 都 无 截 会 随着脊 的高度 的减 小而减 小．
表 １ ｓ／ ｌ ａ＝ Ｏ、 ． ３改变脊位置时波导主模 归一化截止 波长 ／ ｎ
Ｔ ｂ １ Ｄ ａ． Ｅ ｃ ｆ ｈ ｕｏ ａｅｅｇｈ０ ｅｒ ｇ ｏｉｏ ｒ ｌ ａ； ０ ３ｗ ｔ ｉｅｅｔ ／ ｎ ｌ ｂ ｅｏ ｅｃｔｆ ｗ ｖｌｎｔ １ｔ ｄｅｐｓｔ ｎｆ ／ ｔ １ｈ ｉ ｉ ｏｓ ． ｉ ｄｆ ｒｎ ａａｄｄ ／ ｈ ｆ ｃ
矩形波导的模式(3篇)
第1篇一、矩形波导的模式分类矩形波导中的电磁波模式主要分为TE（横电磁波）模式和TM（纵电磁波）模式。
1. TE模式TE模式是指电场只在波导的横向（垂直于传播方向）分量存在，而磁场则在纵向（沿传播方向）分量存在。
根据电场和磁场在波导横截面上的分布，TE模式又可以分为TE10、TE20、TE01等模式。
（1）TE10模式：TE10模式是矩形波导中最基本、最常用的模式。
其电场分布呈矩形，磁场分布呈椭圆。
TE10模式的截止频率最高，适用于高频传输。
（2）TE20模式：TE20模式的电场分布呈矩形，磁场分布呈圆形。
其截止频率低于TE10模式，适用于中频传输。
（3）TE01模式：TE01模式的电场分布呈矩形，磁场分布呈椭圆。
其截止频率最低，适用于低频传输。
2. TM模式TM模式是指磁场只在波导的横向分量存在，而电场则在纵向分量存在。
根据电场和磁场在波导横截面上的分布，TM模式又可以分为TM01、TM11、TM21等模式。
（1）TM01模式：TM01模式的电场分布呈矩形，磁场分布呈圆形。
其截止频率最高，适用于高频传输。
（2）TM11模式：TM11模式的电场分布呈矩形，磁场分布呈椭圆。
其截止频率低于TM01模式，适用于中频传输。
（3）TM21模式：TM21模式的电场分布呈矩形，磁场分布呈圆形。
其截止频率最低，适用于低频传输。
二、矩形波导的模式特性1. 截止频率截止频率是矩形波导中一个重要的参数，它决定了电磁波在波导中能否有效传输。
不同模式的截止频率不同，其中TE10模式的截止频率最高，适用于高频传输。
2. 相速度相速度是指电磁波在波导中传播的速度。
不同模式的相速度不同，TE模式的相速度比TM模式快。
3. 模式损耗模式损耗是指电磁波在波导中传播时，由于波导壁的吸收和辐射等原因，能量逐渐衰减的现象。
不同模式的损耗不同，TE模式的损耗比TM模式小。
4. 传输特性矩形波导中不同模式的传输特性不同，如TE模式的传输特性较好，适用于高频传输；TM模式的传输特性较差，适用于低频传输。
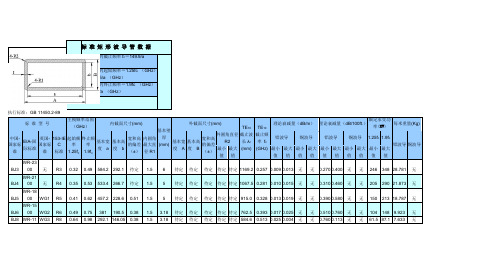
标 准 矩 形 波 导 管 数 据
0.8636
0.4318
0.0051
0.038
0.76
2.388
1.956
0.025
0.5
0.8
1.73
173.576
无
无
无
无
无
无
无
无
0.00054
0.00076
无
无
0.02
0.2
1.015
5.79
3.91
0.05
0.5
1
7.52
39.499
无
无
2.048
3.023
无
无
62.425
92.152
0.01
0.0144
无
0.138
BJ740
WR-12
WG26
R740
60.5
91.9
3.0988
1.5494
0.0127
0.15
1.015
5.13
3.58
0.05
0.5
1
6.2
0.038
0.8
1.27
21.59
12.06
0.05
0.65
1.15
38.1
7.869
0.151
0.222
0.180
0.265
4.590
6.775
5.472
8.078
0.26
0.34
0.213
0.702
BJ140
WR-62
WG18
R140
11.9
18
15.799
7.899
0.031
0.4
1.015
17.83
波导截止波数 -回复
波导截止波数-回复什么是波导截止波数？波导截止波数是电子学中的概念，涉及到电磁波在波导中的传播。
波导是一种特殊的导电结构，由封闭金属深槽或圆管构成。
电磁波在波导中传播是通过电磁场在波导内壁表面反射和传导的方式进行的。
当电磁波在波导中传播时，必须满足某些条件。
其中一个条件就是波导截止波数。
波导截止波数是波导中电磁波传播的一个界限，超过该界限的波数将无法在波导中传播。
波导截止波数通常表示为模式数，即波导内部所能存在的不同的电磁波模式数。
电磁波模式数越多，波导的通信能力就越强。
如何计算波导截止波数？波导截止波数的计算需要考虑波导的几何形状和材质，以及传播的电磁波的频率。
波导的几何形状和材质会影响电磁场的分布和传播特性，从而影响截止波数。
下面是基于矩形波导的截止波数计算方法：1. 确定波导的几何尺寸，包括波导的宽度和高度。
2. 根据波导的材质，确定波导内部的介电常数和磁导率。
3. 计算波导内部的截面阻抗，这是由波导的宽度、高度和材质决定的。
4. 根据波导内部的截面阻抗和波的频率，计算波导的截止波数。
这可以通过一个公式来计算：c = m·π·b/λ其中，c是波导的截止波数，m是波导内部的模式数，b是波导的宽度，λ是波的波长。
该公式适用于矩形波导，并且假设波导内部的介质为真空。
对于圆形波导或其他形状的波导，可以使用不同的公式来计算截止波数。
但通常都需要知道波导的几何尺寸、介质特性和频率等信息。
为什么需要考虑波导截止波数？波导截止波数是波导中电磁波传播的一个重要参数。
对于设计和使用波导的工程师和科学家来说，了解和掌握波导的截止波数是至关重要的。
首先，波导截止波数的大小会影响波导的通信能力。
当波导截止波数较大时，波导内能够传播的电磁波模式数也较多，这意味着更多的信息可以通过波导传输。
因此，工程师可以通过调整波导的几何尺寸和材质等参数来控制波导的截止波数，以满足特定的通信需求。
其次，波导截止波数也会影响波导内部的电磁场分布和传播特性。
波导类型及尺寸
R620
49.8
75.8
3.795
R740
60.5
91.9
3.0988
R900
ห้องสมุดไป่ตู้
73.8
112
2.54
R1200
92.2
140
2.032
R1400
113
173
1.651
内截面尺寸(mm)
基本高度 宽和高的偏
b
差（±）
292.1 266.7
待定 待定
228.6
0.51
190.5
0.38
146.05 123.82 97.79
0.5
1
6.35
0.05
0.5
1
5.59
0.05
0.5
1
4.88
0.05
0.5
1
4.42
0.05
0.5
1
3.91
0.05
0.5
1
3.58
0.05
0.5
1
3.3
0.05
0.5
1
2.54
0.025
0.5
0.8
2.35
0.025
0.5
0.8
TE10 截止 波长λc (mm)
1169.2 1067.5 915.0 762.5 584.6 495.6 391.4 330.4 259.1 218.4 172.7 144.3 116.3
0.259 0.382 0.309 0.456 12.09 17.1
0.334 0.494 0.399 0.588 8.6
12.2
0.475 0.702 0.567 0.837 5.4
矩形波导
微波技术基础考察小论文请讨论矩形波导TE 10模的截止波长、相速、波导波长、波阻抗；其外形结构尺寸的确定遵循什么原则？ 一、理论依据1） 通常将由金属材料制成的、矩形截面的、内充空气介质的规则金属波导称为矩形波导, 它是微波技术中最常用的传输系统之一 矩形波导TE 波的截止波数:22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=b n a m K c ππ它与波导尺寸、传输波型有关。
m 和n 分别代表TE 波沿x 方向和y 方向分布的半波个数, 一组m 、n, 对应一种TE 波, 称作TE mn 模; 但m 和n 不能同时为零, 否则场分量全部为零。
因此，矩形波导能够存在TE m0模和TE 0n 模及TE mn (m,n ≠0)模; 其中TE 10模是最低次模（主模）, 其余称为高次模。
2）单模传输在传输过程中，如若我们需要传输TE 10模，我们需要抑制高次模的传输。
因此工作波长应该满足：1020TE TE λλλ<<1001TE TE λλλ<<二、问题解答对于TE 10模即m = 1, n = 01）TE 10模的截止波数c K 为：a K c π=2） 截止波长c λ：a aK cc 222===πππλ 3）相速p v 表示波的等相位面沿波导的轴向（z ）传播的速度， 其值：22211⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==a v v wv c p λλλβ4）波导波长g λ表示波导内沿其轴向传播的电磁波，它的相邻的两个同相位点之间的距离， 其值：21⎪⎪⎭⎫ ⎝⎛-==c p g fv λλλλ将截止波长代入，则： 波导波长：22211⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-==a fv c p g λλλλλλ 5）在不计损耗的情况下，在行波状态下，电场的横向分量Et 和磁场的横向分量Ht 不仅构成了沿波导轴正Z 方向传播的波，而且对于同一波形而言，t E 和t H 的比值在波导横截面内处处相等，它与坐标Z 无关，并具有阻抗的量纲。
矩形波导中波模截止频率
vv D2 D1
nv1
vv B2 B1
0
理想导体边界条件（内部电磁场为零）
理想导体１
rr E1 H1 0
E２rr2真nr空Err或, 介质nvnvHEvv
0
v
H2 H
电场垂直于（理想）导体表面 磁场平行于（理想）导体表面
导体边界的电磁波方程
金属空腔平形镜面介质微腔二理想导体边界条件?边界条件beibtdhjidjt??????????????????????????????????定态情况下散度方程是冗余的0db??????????????电荷守恒????1211210neenhh????????????????????边界条件????1211210nddnbb??????????????????0nenh???????????????电场垂直于理想导体表面磁场平行于理想导体表面?理想导体边界条件内部电磁场为零12n?理想导体110eh????真空或介质22eehh??????导体边界的电磁波方程?对真空均匀介质电磁波方程helmholtz?导体边界条件0e???
Ex E0x sin kz
Ey E0 y sin kz
r E 0
Ez z
0
Ez
0
rr
E E0 sin kz
r E0
r E0xex
r E0 yey
在z=L导体面上：
nr
r E
0,
rr n ez ,
Ex Ey 0
kL n , n 1, 2,...
i
kx2
k
2 y
x波段矩形波导的工作模式
X波段矩形波导是一种常见的微波传输线结构，常用于高频电路和无线通信系统中。
它的工作模式取决于其尺寸和频率。
在X波段（8-12 GHz）中，矩形波导主要有两个常见的工作模式：
1. TE10模式：TE10模式是矩形波导中最基本的模式，也被称为基模。
在TE10模式下，电场沿着波导宽度方向（x方向）没有变化，磁场沿着波导长度方向（y方向）没有变化。
这种模式对应着矩形波导中的最低截止频率，通常是一种常用的工作模式。
2. TM11模式：TM11模式是矩形波导中的第一个副模式。
在TM11模式下，电场和磁场都存在于波导内部，并且在y和z方向上都有变化。
TM11模式对应着比TE10模式更高的截止频率，通常在设计中也是一个重要的工作模式。
这些工作模式的特性包括传输特性、模式分布和参数等，可以通过数值模拟软件或者实验来进一步研究和分析。
需要注意的是，具体的工作模式和特性还会受到矩形波导的尺寸、材料特性以及边界条件等因素的影响。
因此，在实际应用中，需要根据具体的设计要求和工作频率来选择合适的波导尺寸和工作模式。
9-3矩形波导中的TE10波
a x b
y
y
Hz
a
Ey
Hx
x
电场线
磁场线
y
g
Hx
z
TE10 波电场强度振幅和磁 场强度振幅的空间分布(电 场和磁场合在一起）
传播方向垂直于电场方向
y Hz
Ey
电场方向垂直于磁场方向
2019/6/15
电磁场理论
8
第九章 导行电磁波
几种高次模的场分布
TE10
TE11
TE20
TE21
第九章 导行电磁波
电磁场理论
第9章 导行电磁波 9-3 矩形波导中的TE10波
2019/6/15
电磁场与电磁波
1
第九章 导行电磁波 复习9-2矩形波导的传播特性(1)
矩形波导截止频率：能够传输的最低频率 y
fc
=
2
kc
2
1
(m)2 (n)2 ab
b ,
x
a
z
频率大于截止频率的电磁波才能在矩形波导中传输。
ez
jkz (
a )H0
sin( a
x)
exH0
cos(
a
x)
2019/6/15
z x
电磁场理论
x
a
内壁电流
11
第九章 导行电磁波
TE10波的主要传播特性参数
截止频率
fc
=
c 2
(1)2 (0)2 c a b 2a
截止波长 c 2
(1)2 (0)2 =2a ab
纵向波矢 kz k 1 ( fc f )2 k 1 ( c )2 波导波波长 g 1 ( fc f )2 1 ( c )2
微波技术与天线课后习题答案(西电版)
★了解同轴线的特性阻抗及分类。
1.4习题及参考解答[I. 1]设一特性阻抗为50 Q的均匀传输线终端接负4k/<=100 Q.求负我反对系数巧・在离负裁0.2入・0.25入及0.5入处的输入阳抗及反对系数分别为多少？解终端反射系数为=& - Z。
= 100 — 50 =丄11 _ K _ 100 + 50 _ T根拥传输线上任怠一恵的反肘糸数和输入阳抗的公贰r（z）= r lC ^和= z。
；兰：：二在离负载0.2入.0. 25A> 0.5入反射系数和输入阻抗分别为r（0.2A）= Y“初忌• r（0.25A）MZ.（0.2入）=29.43Z -23.79° Q・ Z in（0.25A） = 25 Q> Z lft（0.5A） = 100 Q[1.2]求内外导体直径分别为0.25 cm和0.75 cm的空气同轴线的持性阻抗。
若在两导体何塡充介电常数匕= 2.25的介质.求其特性阻抗及300 MHz时的波长。
解空气同轴线的持性阻抗为乙=60 In — = 65. 9 Qa塡充相对介电常数为€,=2.25的介质后.英持件阳抗为/=300 MHz时的波长为[1.3]设特性阻抗为乙的无耗传输线的址波比为"滾一个电爪波"•点离负我的距离为人讪.试证明此时终端负我应为r（0.5A） = Y证明根据输入阳抗公式Z： + jZ, tan" 乂Z o + jZ| tan/3 z在距负栈第一个波节点处的阻抗Z /（/“）=—P y Zl— j 乙I "1,3】Z.P将匕式整理即得17I318[I. 4] 何 持性阻抗为Z =50 Q 的无耗均匀传输线•导体间的媒质参敌为 £.=2.25 ・“, = 】，终瑞接仃&=】Q 的负我"/- 100 MHz 时•兀线长度为A/40试求： ①传输线实际长度'②负载终瑞反射系敌；③ 输入端反射系数'④ 输入瑞阻抗.解传输线上的波长= 2 m因而.传输线的实际长度/ = * = 0. 5 m4终瑞反射系数为…R]—Z 。
矩形波导中电磁波截止波长的计算(1)(1)
矩形波导中电磁波截止波长的计算(1)(1)矩形波导中电磁波截止波长的计算周和伟物理与电子信息工程学院 07物理学 07234030[摘要]:本文从麦克斯韦方程组出发，从理论上推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程；根据边值关系从理论上求出了时谐电磁波在矩形波导中的解，并对矩形波导管中传播的电磁波波解进行了讨论；计算了不同尺寸的矩形波导管的截止波长，截止波长大多属于厘米量级，说明波导管只适用于传播微波。
[关键词]:矩形波导电磁波截止波长1 绪言波导是一种用来约束或引导电磁波传输的装置，矩形波导是指横截面是矩形的波导，一般是中空的金属管。
也有其他形式的波导装置，如介质棒或由导电材料和介质材料组成的混合构件[1]。
因此，在广义的定义下，波导不仅是指矩形中空金属管，同时也包括其他波导形式如矩形介质波导等，还包括双导线、同轴线、带状线、微带和镜像线、单根表面波传输线等。
根据波导横截面的形状不同还有其他形状波导，如圆波导等。
尽管已存在很多不同波导形式，且新的形式还不断出现，但直到目前，在实际应用中矩形波导是一种最主要的波导形式。
由于无线信号传输媒介，具有传输频带宽、传输损耗小、可靠性高、抗干扰能力强等特点，因此波导技术在电子技术领域运用非常广泛，主要用于铁氧体结环形器，窄壁缝隙天线阵[2]，速调管矩形波导窗，高精度矩形弯铜波导管加工研究【3】等器件设备的制造生产，以及在地铁信号系统中的应用都很广泛。
为了加深对波导传输特性的理解，本文从麦克斯韦方程组出发，推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程；根据边值关系从理论上求出了时谐电磁波在矩形波导中的解，并对矩形波导管中传播的电磁波波解进行了讨论；计算了不同尺寸的矩形波导管的截止波长，发现其截止波长都在厘米量级，说明波导管只适用于传播微波。
2 电磁波基本原理2.1建立麦克斯韦方程组的历史背景⎰=-=Edl dld E ml φ (2.1) 应当指出：法拉第建立的电磁感应定律，只适用于由导体构成的回路，而根据麦克斯韦关于感生电场的假设，电磁感应定律有更深刻的意义，即不管有无导体构成闭合回路，也不管回路是在真空中还是在介质中，式(2.1)都是适用的。
波导型 及参数
9.99
28.499
R100
8.2
12.5
22.86
R120
9.84
15
19.05
R140
11.9
18
15.799
R180
14.5
22
12.95
R220
17.6
26.7
10.668
R260
21.7
33
8.636
R320
26.3
40
7.12
R400
32.9
50.1
5.69
R500
39.2
59.6
4.775
R620
49.8
75.8
3.795
R740
60.5
91.9
3.0988
R900
73.8
112
2.54
R1200
92.2
140
2.032
R1400
113
173
1.651
内截面尺寸(mm)
基本高度 宽和高的偏
b
差（±）
292.1 266.7
待定 待定
228.6
0.51
190.5
0.38
146.05 123.82 97.79
外截面尺寸(mm)
基本高度 宽和高的偏 外圆角直径R2
B
差（±） 最小值 最大值
待定
待定
待定 待定
待定
待定
待定 待定
待定
待定
待定 待定
待定
待定
待定 待定
待定
待定
待定 待定
待定
待定
待定 待定
待定
待定
矩形波导中传播模式的研究
矩形波导中传播模式的研究矩形波导中传播模式的研究矩形介质光波导作为波导光学系统最基本的单元之⼀，是研究光电器件以及波导传播技术等课题的核⼼内容。
为研究矩形介质波导中的传播模式，本⽂将从平板介质波导⼊⼿，运⽤电磁场基本理论，结合边界条件求解麦克斯韦⽅程组，得到光场传播模式的表达式，模的传播常数以及截⽌条件等相关参数。
再以此为基础，分别以马卡蒂⾥理论、库玛尔理论以及有效折射率法在不同电磁波模式下分析⽐较矩形介质波导，并结合MMI耦合器分析单模和多模中的模场分布。
最后使⽤Matlab绘制传播曲线并且基于BPM算法对不同条件的矩形波导进⾏模拟，分析并⽐较其传播模式。
1.1 引⾔随着为微纳加⼯⼯艺技术的不断提⾼，晶体管的特征尺⼨越来越⼩，单⽚集成的晶体管数⽬越来越多，由此带来的⾦属互联问题、漏电流问题以及散热问题难以解决。
紧靠减⼩晶体管尺⼨、提⾼⼯作频率的⼿段提⾼处理器性能的⽅式已遇到瓶颈[1]。
光具有⾼传播速度、⾼宽带、并⾏性等本征的特质，使得光⾮常适⽤于海量数据传输处理等领域，研究并开发以此为核⼼的新型信息处理技术已成为普遍共识。
⽽随着光通讯正在朝着⾼速率⼤容量的⽅向发展，在SOI材料上制备光波导是技术发展的必然趋势。
在此背景下，研究矩形光波导中的传播模式是尤为重要的[2]。
本课题中的矩形波导是指由半导体材料制成的，具有矩形的波导芯层以及包围着芯层但折射率更低的包层结构，可以使光限制在芯层内传播的器件。
本课题主要分析矩形光波导中存在的传播模式以及各种模式的传播特性。
在第⼆章中，⾸先对平板波导理论进⾏推导，分析了平板波导中单模和多模条件。
第三章中运⽤第⼆章中的关于平板波导的相关知识，分别在马卡蒂⾥理论、库玛尔理论以及有效折射率法下对矩形波导进⾏计算。
前两者给出了不同区域内的两种光场分布重点讨论在有效折射率法矩形波导中可以存在的模式同波导横向长度和材料的折射率之间的关系以及不同模式下的场分布，并结合MMI（多模⼲涉）耦合器对单模和多模的模场分布进⾏具体分析。
说明矩形波导的单模传输条件
说明矩形波导的单模传输条件光波导(optical waveguide)是引导光波在其中传播的介质装置，又称介质光波导。
光波导有两大类：一类是集成光波导，包括平面(薄膜)介质光波导和条形介质光波导，它们通常都是光电集成器件(或系统)中的一部分，所以叫作集成光波导;另一类是圆柱形光波导，通常称为光纤 (见光学纤维)。
光波导由光透明介质(如石英玻璃)构成的传输光频电磁波的导行结构。
光波导的传输原理不同于金属封闭波导，在不同折射率的介质分界面上，电磁波的全反射现象使光波局限在波导及其周围有限区域内传播。
多模和单模光纤已成功地应用于通信。
光纤的传输特性对外界的温度和压力等因素敏感，因而可制成光纤传感器，用于测量温度、压力、声场等物理量。
平面介质光波导就是最简单的光波导，它就是用折射率为n2的硅(或砷化镓，或玻璃)并作基片，用微电子工艺在它上面镀一层折射率为n1的介质膜，再加之折射率为n3的覆盖层做成。
通常挑n1>n2>n3，以便将光波局限在介质膜内传播。
条形介质光波导就是在折射率为n2的基体中产生一个折射率为n1的长条，挑n1>n2，以便将光波局限在长条内传播。
这种光波导常用作光的分路器、耦合器、控制器等功能器件。
光波导的横向尺寸比光的波长大很多时，光的波动性所产生的衍射现象一般可略去不计，可用几何光学定律来处理光在其中的传播问题。
如集成光波导和阶跃折射率光纤中，都是利用入射角大于临界角使光在边界上发生全反射，结果光便沿折线路径在其中传播。
梯度折射率光纤中，则利用光逐渐往折射率大的方向弯曲的规律，使光线沿曲线路径在其中传播。
光波导的纵向尺寸与光的波长差距并不大时，光的波动性所产生的绕射现象便无法省略，需以光的电磁理论去处置光在其中的传播问题。
即为由麦克斯韦方程组启程，列举边界条件，解光波的电场和磁场在光波导内的原产和传播特性，从而化解有关问题。
排序说明，对于一种取值形状和折射率的光波导，能够在其中传播的光波，其电场和磁场的原产存有各种相同形式，把每一种形式叫做一种传输模，缩写为模。
hfss 波导 截止频率
hfss 波导截止频率HFSS（High-Frequency Structure Simulator）是一种高频电磁场仿真软件，常用于分析波导的性能。
波导是一种能够导波的结构，常用于高频电路和微波器件中，具有广泛的应用。
波导的截止频率是指波导能够传导电磁波的最低频率。
在低于截止频率时，波导无法传输电磁波，而只能反射或吸收电磁波。
波导的截止频率与波导的几何形状、尺寸以及材料特性有关。
波导的几何形状和尺寸对截止频率的影响非常大。
波导的尺寸越大，截止频率越低，因为较大的尺寸会导致波导中的电磁波传播速度减小，从而影响截止频率。
此外，波导的截止频率还受到管道的形状和布局的影响。
例如，矩形波导的截止频率比同等尺寸的圆形波导低。
波导材料的特性也会影响波导的截止频率。
波导设计中常用的材料有金属和介质。
金属材料常用于波导的外壳，能够有效地屏蔽外界的电磁干扰。
介质材料常用于波导的芯片，能够提供传导电磁波的介质。
不同的材料具有不同的介电常数和导电性能，从而影响波导的截止频率。
在HFSS中，可以通过建立波导的几何模型，并设置波导的尺寸和材料特性，来模拟波导的截止频率。
HFSS利用有限元分析方法，求解Maxwell方程，并计算出波导的电场和磁场分布，从而得到波导的截止频率。
在实际应用中，波导的截止频率是一个重要的设计参数。
设计人员需要根据系统的需求和具体的应用场景，合理选择波导的尺寸和材料特性，以满足系统对截止频率的要求。
对于一些特殊的应用，如高速通信和雷达系统，截止频率的选择尤为重要，需要进行详细而准确的分析和设计。
总之，波导的截止频率是波导能够传导电磁波的最低频率。
波导的几何形状、尺寸和材料特性对截止频率有着重要影响。
HFSS是一种用于分析波导性能的仿真软件，能够帮助设计人员准确地计算波导的截止频率，从而实现优化设计和性能分析。
矩形波导中电磁波截止波长的理论计算
矩形波导中电磁波截止波长的理论计算许德富【期刊名称】《内江科技》【年(卷),期】2014(035)012【总页数】2页(P48-49)【作者】许德富【作者单位】乐山师范学院物理与电子工程学院【正文语种】中文本文根据边值关系从理论上求出了时谐电磁波在矩形波导中的解，并对矩形波导管中传播的电磁波波解进行了讨论，计算了不同尺寸的矩形波导管的截止波长，说明波导管只适用于传播微波。
波导是一种用来约束或引导电磁波传输的装置，矩形波导是指横截面是矩形的波导，一般是中空的金属管。
也有其他形式的波导装置，如介质棒或由导电材料和介质材料组成的混合构件[1]。
因此，在广义的定义下，波导不仅是指矩形中空金属管，同时也包括其他波导形式如矩形介质波导等，还包括双导线、同轴线、带状线、微带和镜像线、单根表面波传输线等[2]。
根据波导横截面的形状不同还有其他形状波导，如圆波导等。
尽管已存在很多不同波导形式，且新的形式还不断出现，但直到目前，在实际应用中矩形波导是一种最主要的波导形式。
由于无线信号传输媒介，具有传输频带宽、传输损，耗小、可靠性高、抗干扰能力强等特点，因此波导技术在电子技术领域运用非常广泛，主要用于铁氧体结环形器，窄壁缝隙天线阵[2]，速调管矩形波导窗，高精度矩形弯铜波导管加工研究等器件设备的制造生产，以及在地铁信号系统中的应用都很广泛。
为了加深对波导传输特性的理解，本文从麦克斯韦方程组出发，推导了电磁场遵循的波动方程和时谐电磁波遵循的波动方程；根据边值关系从理论上求出了时谐电磁波在矩形波导中的解，并对矩形波导管中传播的电磁波波解进行了讨论；计算了不同尺寸的矩形波导管的截止波长，发现其截止波长都在厘米量级，说明波导管只适用于传播微波。
一般情况下，电磁波遵循的基本方程是麦克斯韦方程组[3]：在自由空间中，没有电荷和电流存在，电磁和磁场互相激发，电磁场的运动规律是齐次得到麦克斯韦方程组：在真空中，，则和的满足的微分方程可以写为：在很多实际情况下，电磁波的激发源往往以大致确定的频率作正弦振荡，因而辐射出的电磁波也以相同的频率作正弦振荡，这种以一定频率作正弦振荡的波称为时谐电磁波。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
~L
( 1 )2 ( 1 )2
k
( m )2 ( n )2 ( p )2 本征模式的频率
L1
L2
L3 是分立的
截止频率（最低频率）
z mnp
( m )2 ( n )2 ( p )2
L1 v L2
L3
如果 L1, L2 L3
E
min 110 =
( 1 )2 ( 1 )2
v E
v H
v B
vt D t
v
iB
v
v
J iD
v J
电荷守恒
v
D v
B 0
边界条件
nv1
vv E2 E1
0
nv1
vv H2 H1
v
nv1
分离变量，令u x, y, z X (x)Y(y)Z(z)
L3
d2X
dx2
k
2 x
X
0
d 2Y
dy
2
k y2Y
0
d 2Z
dz 2
k
2 z
Z
0
O
y
L1
L2
x kx2
k
2 y
kz2
k2
导体构成边界的正六面腔体
通解：u x, y, z C1 cos kxx D1 sin kxx
L1
L2
fmnp
mnp 2
f min
f110
2
1
x
1 L1 2 1 L2 2
L3
y
L1
L2
Ez
0
kE 0
mnp
2
k
2[( m )2 ( n )2 ( p )2 ]1/2
L1
L2
L3
k L1 ex L2 e y
max
C2 cos ky y D2 sin ky y
C3 cos kz z D3 sin kz z
诸C、D为常数
矩形谐振腔驻波解
Ex x x0 0 Ex y0 0 Ex z0 0 Ey x0 0 Ey y y0 0 Ey z0 0 Ez x0 0 Ez y0 0 Ez z z0 0
Ex A1 cos kx x sin ky y sin kz z Ey A2 sin kx x cos ky y sin kz z Ez A3 sin kx x sin ky y cos kz z
z
L3
O
y
L1
L2
x
Ex x xL1 0 Ex yL2 0 Ex zL3 0 Ey xL1 0 Ey y yL2 0 Ey zL3 0 Ez xL1 0 Ez yL2 0 Ez z zL3 0
kx
m L1
ky
n L2
kz
p L3
m、n、p 为整数
电场各分量的 m、n、p，每一组表示一种本征模式
矩形谐振腔波模性质
Ex A1 cos(m x / L1) sin(n y / L2 ) sin( p z / L3)
Ey A2 sin(m x / L1) cos(n y / L2 ) sin( p z / L3)
vv D2 D1
nv1
vv B2 B1
0
理想导体边界条件（内部电磁场为零）
理想导体１
rr E1 H1 0
E２rr2真nr空Err或, 介质nvnvHEvv
0
v
H2 H
电场垂直于（理想）导体表面 磁场平行于（理想）导体表面
导体边界的电磁波方程
对真空（均匀介质）电磁波方程（Helmholtz）
vv 2E k2E 0
v E 0
k2 @2
导体边界条件
EP
0
En n
0
其它物理量的获取
电场的平行分量为零
电场的垂直分量法向导数为零
v E 0
v B
i
v E
v
nv
§4.4 谐振腔和波导
cavity resonator and Wave Guide
-- 谐振腔 -一．有界空间中的电磁波
1．无界空间中横电磁波（TEM波） TEM波：电场和磁场在垂直传播方向上振动的电磁波。
平面电磁波在无界空间中传播时就是典型的TEM波。
2．有界空间中的电磁波――边值问题 金属一般为良导体，电磁波几乎全部被反射。因此，若空
Ez A3 s in(m x / L1) sin(n y / L2 ) cos( p z / L3)
r
rr
在整个腔内： E 0 k A 0
kx A1 ky A2 kz A3 0
mn
p
L1
A1
L2
rL3
A3
0
本征模：
(m, n, p, A)
腔模
mnp
v H
v H
1
v B
nv
v D
vv
D E
理想导体为边界的边值问题 谐振腔
nr
r E
0,
r n
r H
r
谐振腔基本问题： （理想导体为边界的边值问题 ）
rr 2E k2E 0
区域里
E 0
nr
r E
0
边界上
r B
i
r E
r r
H B/
r
nr
r H
区域里 边界上
三．谐振腔
低频电磁波
LC 回路振荡器
1 频率越高，辐射损耗越大，焦耳热损耗越大
LC
趋肤效应，电磁能量大量损耗;
L、C 越小，电容电感不能集中分布电场和磁场，
向外辐射。
高频振荡电磁波 谐振腔：由几个金属板或反射镜（光学）构成。
例: 金属空腔、平形镜面、介质微腔
谐振腔基本问题：
间中的良导体构成电磁波存在的边界，特别是若电磁波在中 空的金属管中传播，金属边界制约管内电磁波的存在形式。 在这种情况下，亥姆霍兹方程的解不再是平面波解。 以介质或金属为边界构成的有限区域中的电磁波运动模式 例:金属空腔、平形镜面、介质微腔 电磁波怎样分布？是否存在TEM波？
二、理想导体边界条件
定态情况下，散度方程是冗余的
rr 2E k2E 0
E 0
nr
r E
0
区域里 边界上
rr 2E k2E 0
2u k 2u 0
u(x, y, z) : Ex , Ey , Ez
四、矩形谐振腔电磁波模
直角坐标，电场（磁场）任一分量满足： z
2u k 2u 0 k2 @2