西南交大信号与系统本科卷及答案2
2020年西南交通大学期末真题及答案信号与系统

《信号与系统》2005 年期末试题A 卷班级姓名学号成绩一一 30 分二二 30 分三三 26 分分四四 14 分分1 2 3 4 5 1 2 3 1 2 3一、共 5 5 小题,总分为 0 30 分1 、试判断下列式子代表的系统是否为线性系统,并说明理由(其中 y t为系统响应, 0 y 为初始条件, f t为系统输入)(8 分)201 0 2ty t y f d2 0 cos5 0 y t y t y f t2 33 3 0 y t y t f t3 2 2245 2d y t d y t d f ty t f tdt dt dt2、、试确定信号 1 cos 1000 sin 2000 x t t t 的奈奎斯特频率。
(3 分)3 、已知描述系统的方程为4 4 2y t y t y t f t ,初始条件为 0 0 2 y y 。
求(1 )系统传递算子 H p;;(2 )系统零输入响应 xy t。
(7 分)4 、已知系统的单位冲击响应 2h t t ,当系统输入为142f t t t t 时,用时域分析法求系统零状态响应 fy t。
(6 分)5 、已知 f t的波形如下图,求 F j 。
(6 分)二、共 3 3 小题,总分为 0 30 分1 、系统的微分方程为 5 62 8y t y t y t f t f t ,,激励 tf t e t ,利用复频域分析法求系统的零状态响应。
(7 分)2 、系统传递函数为 N sH sD s ,试分析下列系统是否渐近稳定。
(9 分)21 1 2D s s s s 5 3 22 4 3 2 9 D s s s s s 5 4 3 23 2 3 4 11 8 D s s s s s s 3 、作出下列系统直接实现形式的模拟框图和信号流图。
(注假定系统为零状态)(14 分)113sH ss 2423 2sH ss s 三、共 3 3 小题,总分为 6 26 分1 、系统信号流图如下图所示,求系统的传递函数 H s。
2010-2011《信号与系统A》期末考试试卷及答案,推荐文档

1 0.25z 1 1 1.1z 1 0.3z 2
1
H (z)
1 0.25 z (1 0.5z 1 )(1 0.6 z 1)
( 2) H (z)
1 0.25z 1 1 1.1z 1 0.3z 2
Y ( z) X ( z)
Y ( z) 1.1z 1Y (z) 0.3z 2Y ( z) X ( z) 0.25z 1 X (z)
y( n) 1.1y(n 1) 0.3 y(n 2) x(n) 0.25x(n 1)
(t ) ,求复合系统的冲激响应 h( t ) 。
x(t )
y(t)
h1( t)
h2 (t )
h3 (t)
h1 (t ) h(t ) u(t) u(t)* (t 1)*[ (t)] 解:
u(t) u(t)* (t 1) u(t ) u(t 1)
四、(10 分)求周期矩形脉冲信号的傅立叶级数(指数形式) ,并大概画出其频谱图。
(1) f (2t) 的波形
(2) f (t 2)u(t 2) 的波形
f (t) 1
-1
0
1
t
解: (1)
f 2t
1
1
1
t
2
2
(2)
f t 2ut 2
1
t
0
1
2
3
三、(10 分)如图所示,该 LTI 系统由多个子系统组成,各子系统的冲激响应分别为:
h1(t ) u(t), h2 (t) (t 1), h3(t)
-2ωm
2ωm
(8 分)
Ys ( jw )
-4ωm
-2ωm
w
2ωm
4ωm
七、(10 分)考查如图所示的离散时间 LTI 稳定系统;
精编《信号与系统》期末考试试卷a答案
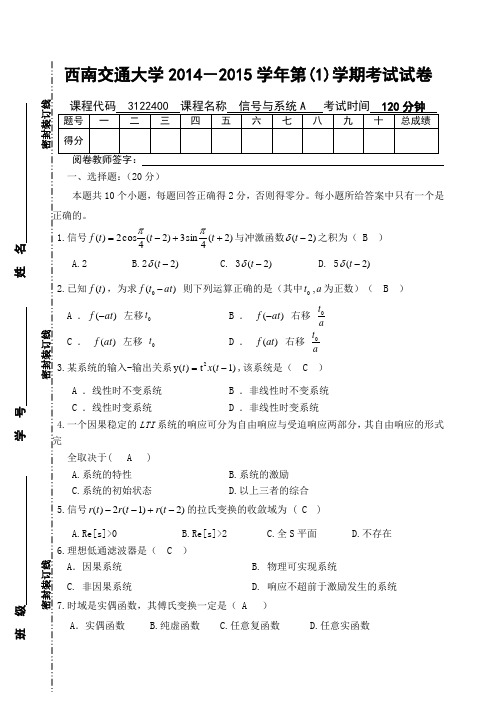
西南交通大学2014-2015学年第(1)学期考试试卷阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1.信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( B )A.2B.2)2(-t δC. 3)2(-t δD. 5)2(-t δ 2.已知)(t f ,为求)(0at t f - 则下列运算正确的是(其中a t ,0为正数)( B ) A .)(at f - 左移0t B . )(at f - 右移 at 0C . )(at f 左移 0tD . )(at f 右移at 03.某系统的输入-输出关系)1(t )(y 2-=t x t ,该系统是( C ) A .线性时不变系统 B .非线性时不变系统 C .线性时变系统 D .非线性时变系统4.一个因果稳定的LTI 系统的响应可分为自由响应与受迫响应两部分,其自由响应的形式完全取决于( A ) A.系统的特性 B.系统的激励 C.系统的初始状态D.以上三者的综合 5.信号)2()1(2)(-+--t r t r t r 的拉氏变换的收敛域为 ( C )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在 6.理想低通滤波器是( C )A .因果系统 B. 物理可实现系统C. 非因果系统D. 响应不超前于激励发生的系统 7.时域是实偶函数,其傅氏变换一定是( A )A .实偶函数 B.纯虚函数 C.任意复函数 D.任意实函数班 级 学 号 姓 名密封装订线 密封装订线 密封装订线8.信号)100()(t Sa t f =,其最低取样频率s f 为(A )A.π100B.π200C.100π D. 200π 9.已知信号)(t f 的傅氏变换为),(ωj F 则)3-2-(t f 的傅氏变换为( C ) A .ωω2)3(3j e j F - B.ωω2)3(3j e j F -- C .ωω6)3(3j e j F - D.ωω6)3(3j e j F -- 10.已知Z 变换Z 11[()]10.5x n z-=-,收敛域0.5z >,求逆变换得x (n )为( A ) A .0.5()n u n B. 0.5(1)n u n --- C. 0.5()n u n -- D. 0.5(1)n u n ---- 二、(14分)画图题1.已知)21(t f -波形如图所示,画出)(t f 的波形。
大学考试试卷《信号与系统》及参考答案

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。
西南交大信号与系统第二版课后答案

2.22 状态响应。
2.23 2.24
, 输入信号f(t)=e-''11(t)+e''u(-t), 求系统的零 巳知传输算子力H(p)= p+l 1-p 已知传输算子为H(p)= , 输入信号f(t)=e'u(-t), 求系统的零状态响应。 I+ p 已知系统的微分方程为
y'(t)+5y'(t)+6y(t) =f(t) 且初始条件为y(O_)=l, y'(O_)=O, 求在下列输入信号作用下的 系统完全响应y(t)' 并指出其零输入响应、 零状态响应、 自由 响应、 强迫响应、 暂态响应和秅态响应。
(c) /(1)=八(1)[11(1-l)-11(1-2)], 其中八(1)=IOcos(亢1
号)
(d) /(1) =111(1) -211(1- l)+(2-1)11(1-2)
(e) /(k)=3[11(k+l)-11(k-5)]
(t) /(k)=(-1)'[11(k+l)-11(k+5)]
1.7心岛-2) 1.10切线性系统 @非线性系统 1.11 心时变系统 �e-100"5(1-IO) @非线性系统 @非线性系统 @)非时变系统
@ L'sm2 to(t-3)dt
咽)
dt
已知信号f(t)的波形如题1.8图所示,绘出下列信号的波形。
第1章信号与系统概述
习题1参考答案
1.1 心非周期信号 @非周期信号 @周期信号,周期力2 @非周期信号 @周期信号,周期为二冗 3 @非周期信号 @眈不是功率信号也不是能曼信号 @功率信号P=l
2
@y x (t)飞e-2『 cos( 2.9 2.10
2013年西南交通大学考研真题和答案~~信号系统二

机密★启用前西南交通大学2013年全日制硕士研究生招生入学考试试卷试题代码:924试题名称:信号与系统二考试时间:2013年1月考生请注意:1.本试题共7题,共4页,满分150分,请认真检查;2.答题时直接将答题内容写在考场提供的答题纸上,答在试卷上的内容无效;3.请在答题纸上按要求填写试题代码和试题名称;4.试卷不得拆开,否则遗失后果自负。
一、(30分)选择题:本题共10个小题,每题回答正确得3分,否则得零分。
每小题所给答案中只有一个是正确的。
(请将答写在考场提供的答题纸上!)1. 连续周期信号f (t )的频谱F(jw)的特点是(D )。
A 、周期、连续频谱;B 、周期、离散频谱;C 、连续、非周期频谱;D 、离散、非周期频谱;解析:基本结论:周期信号离散,连续信号非周期,逆命题也成立。
2. 周期矩形脉冲的谱线间隔与(C )。
A 、脉冲幅度有关 B 、脉冲宽度有关 C 、脉冲周期有关D 、周期和脉冲宽度有关解析:由T π2=Ω可知。
3.已知Z 变换Z 1311)]([--=zn x ,收敛域3<z ,求逆变换的x (n )为(D )。
A 、)(3n u nB 、)(3n u n-- C 、)(3n u n-- D 、)1(3---n u n解析:z 变换与收敛域关系:ROC:)1(3)(3)]([,3||---=↔-=<n u n x z z n x Z Z z4. 若对f (t )进行理想取样,其奈奎斯特取样频率为s f ,则对进行取样)231(-t f ,其奈奎斯特取样频率为(B )。
A 、3s f B 、31s f C 、3(s f -2) D 、()231-s f 解析:(t)3322,22,3:2t 31,:2'121s s s f ww f w w f w w f w w ======-=ππππ)(则 5. 某系统的系统函数为)(s H ,若同时存在频响函数H (jw ),则该系统必须满足条件(C) A 、时不变系统 B 、因果系统 C 、稳定系统 D 、线性系统解析:一个信号的傅里叶变换是拉普拉斯变换沿jw 轴求值,因此系统函数的收敛域包含jw 轴,即系统稳定。
西南交大信号与系统第二版课后答案
1口 7 -, 刀、歹L
2.25
CD CD
f(t) = IOcosl 11(1) 证明: J(t)关8(1-1。) =f(t-1。)
@ f(t) = e-''u(t) (?) f(t)
状态响应可以表示力
2.26
已知线性时不变系统的输入力f(t)'系统的阶跃响应力g(t)'试证明系统的零 汕) = Lf'(,!)g(t-,!)d儿 2.27 2.28 2.29 用MATLAB求题2.7的全响 应。 用MATLAB求题2. 9的零输入响应。 (此式称为杜阿美尔积分)
=
心Yx (/)=7e-'-5e-2'(t汃0)
(2)yx (1)=6e-'-(4+5/)e-3'(t;>O) CZ) /,(1)= te-'11(1) 3 @i,(1) = -e-2'sin(21)11(1) 2
2.11 2.12
CD /,(1)�(-2e-'+2e-")的)+ 0(1)
心yx (t)�ze-" -2e-" (1;;, O) I 5 8 3 y(t) � - 3 e- '+ 2e-" + 6
第1章信号与系统概述
习题1
心f(t)=cost+2 sin(2 兀t) @ f(t)=e _,, srn(2 亢I) (J) f(k)=sm(2忒) 心f(t)=cos( 兀 I) @ 1.2 1.1 判断 下列信号是否是周期信号。若是周期信号,则确定信号周期。 @ f(t)= costu(t) CZ) f(t)= sin(3 兀t)+cos(2 兀t) @八I)= sin'[
西南交大信号与系统本科卷及答案2
西南交大信号与系统本科卷及答案2西南交通大学2006-2007学年第(2)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟 题号 一 二 三 四 五 六 七 八 九 十 总成绩 得分阅卷教师签字: 一、选择题(30分)下列各题所附的四个答案中,只有一个是正确的,试将正确答案的编号填入题中的括号内(每小题2分,共计30分)。
1.已知某系统的输入输出信号分别为x (n )和y (n ),则下面( )是因果、线性、时不变系统。
(a) )()1()(n nx n y n y =++ (b))2()()()1(+=-+n nx n y n x n y(c) )()1()(n x n y n y =-- (d))2()1()(+=+-n x n y n y 2.已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为( )。
(a) ω5)5(j e f - (b) ωω5)(j e j F - (c) )5(f (d) )(ωj F 3. 信号)2()()(--=t u t u t f ,则其傅立叶变换()F j ω=( )。
(a) ωωj e Sa )( (b) )1(2ωωj e j -- (c) ωωj e Sa -)(2 (d) 2)2sin(1ωωωj e -4.δ(-2t) 与δ(t)的关系是( )。
(a)δ(-2t)=21δ(t) (b)δ(-2t)=δ(t) (c)δ(-2t) =-2δ(t) (d) δ (-2t) =-δ (t)5.已知某线性时不变系统的系统函数为)21)(2.01(1)(111------=z z z z H ,若系统为因果的,则系统函数H(z)的收敛域ROC 应为( )。
(a)2.0<z (b)2>z(c)2<z (d)22.0<<z6.已知输入信号)(t x 的频带宽度为1ω,某信号处理系统的带宽为2ω,且12ωω>,则系统的输出信号1()()()y t x t h t =*的频带宽度为( )。
西南大学信号与系统作业答案
西南大学信号与系统作业答案西南大学网络与继续教育学院课程代码: 1073 学年学季:20172单项选择题1、连续系统的结构图如图所示,系统的系统函数为()。
1.H1(s) H2(s) - H3(s)2.h1(t) *h2(t)+h3(t)3.H1(s) H2(s) + H3(s)4.h1(t) *h2(t)-h3(t)2、1.h1(k)+h2(k)2.h1(k)*h2(k)3.h1(k)*h2(k)+14.h1(k)*h2(k)+δ(k)3、1. 32.3. 14. 24、LTI的含义是()1.线性因果2.线性稳定3.因果稳定4.线性时不变5、若数字滤波器在两点处的幅值为(1,1),则该滤波器为()1. A. lp2.bp3.bs4.hp6、利用Matlab求取系统的冲激响应,调用的函数是()1.step2.impulse3.initial4.lism7、关于序列的插值,下列叙述错误的是()1.插值过程可分为两步,先补零,再经过低通滤波器2.插值意味着抽样率的转换3.样点之间补零,意味着零阶插值4.零插值后的序列,频谱会被压缩并产生基带映像频谱8、已知,设抽样频率为100Hz,则所得序列的数字频率为( )1. E.2.3.4.9、已知周期序列,其周期为 ( )1.92. 63.124. 310、设,则 ( )1. 22. 13.04.-311、共轭对称的信号,其幅值与相位分别为()1. C. 偶、偶函数2.奇、偶函数3.偶、奇函数4.奇、奇函数12、()1. B. -12.03. 24. 113、( )1.f'(t)2.13.f(0)4.f(t)14、序列,其周期为()1.72. 23.不是周期序列4.1415、对信号进行采样,最大采样间隔为 ( )1.2.3.4.16、1.因果稳定2.因果不稳定3.非因果稳定4.非因果不稳定17、对离散系统系统频率响应仿真,调用的函数是()。
1.step2.impulse3.freqs4.freqz18、下列系统中,属于线性时不变系统的是()。
《信号与系统》A试卷答案
西南交通大学2011-2012学年第(1)学期考试试卷课程代码 3122400 课程名称 信号与系统A 考试时间 120分钟阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1. 已知f (t )的傅里叶变换为)(ωj F ,则f (1-t )的傅里叶变换为( C ) (A )ωωj e j F )(-- (B )ωωj ej F -)((C )ωωj e j F --)((D )ωωj ej F )(-2.连续周期信号的频谱具有( D )(A )连续性、周期性 (B )连续性、非周期性 (C )离散性、周期性 (D )离散性、非周期性3.某系统的系统函数为H (s ),若同时存在频响函数H (j ω),则该系统必须满足条件(C ) (A )时不变系统 (B )因果系统 (C )稳定系统 (D )线性系统4. 已知)(1n f 是1N 点的时限序列,)(2n f 是2N 点的时限序列,且12N N >,则)()()(21n f n f n y *= 是( A )点时限序列。
(A )121-+N N (B )2N (C )1N (D )21N N +5. 若对f (t )进行理想取样,其奈奎斯特取样频率为f s ,则对)231(-t f 进行取样,其奈奎斯特取样频率为( B )。
(A )3f s (B )s f 31 (C )3(f s -2) (D ))2(31-s f 班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6. 周期信号f(t)如题图所示,其直流分量等于( B )(A )0 (B )4 (C )2(D )67. 理想不失真传输系统的传输函数H (jω)是 ( B )。
(A )0j tKe ω- (B )0t j Ke ω-(C )0t j Ke ω-[]()()c c u u ωωωω+--(D )00j t Keω- (00,,,c t k ωω为常数)8.已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为( A )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西南交通大学2006-2007学年第(2)学期考试试卷
阅卷教师签字: 一、选择题(30分)
下列各题所附的四个答案中,只有一个是正确的,试将正确答案的编号填入题中的括号内(每小题2分,共计30分)。
1.已知某系统的输入输出信号分别为x (n )和y (n ),则下面( )是因果、线性、时不变系统。
(a) )()1()(n nx n y n y =++ (b))2()()()1(+=-+n nx n y n x n y
(c) )()1()(n x n y n y =-- (d))2()1()(+=+-n x n y n y 2.已知)()(ωj F t f ↔,则信号)5()()(-=t t f t y δ的频谱函数 )(ωj Y 为( )。
(a) ω
5)5(j e f - (b) ωω5)(j e j F - (c) )5(f (d) )(ωj F 3. 信号)2()()(--=t u t u t f ,则其傅立叶变换()F j ω=( )。
(a) ωωj e Sa )( (b) )1(2ωωj e j -- (c) ω
ωj e Sa -)(2 (d) 2)2sin(1ωωωj e -
4.δ(-2t) 与δ(t)的关系是( )。
(a)δ(-2t)=21
δ(t) (b)δ(-2t)=δ(t) (c)δ(-2t) =-2δ(t) (d) δ (-2t) =-δ (t)
5.已知某线性时不变系统的系统函数为
)21)(2.01(1)(1
11
------=z z z z H ,若系统为因果的,则系统函数H(z)的收敛域ROC 应为( )。
(a)
2.0<z (b)2>z
(c)
2<z (d)22.0<<z
6.已知输入信号)(t x 的频带宽度为1ω,某信号处理系统的带宽为2ω,且12ωω>,则系统的输出信号1()()()y t x t h t =*的频带宽度为( )。
(a) 21ωω+ (b) 12ωω- (c) 1ω (d) 2ω
7. 已知)()()(t h t x t y *=,则(2)(5)x t h t -*-=( )。
(a) (2)y t - (b) (5)y t - (c) )7(-t y (d) (3)y t -
8.信号)
51
31cos(4)21cos(4)32sin(2)(π-++=t t t t x 的周期T=( )。
(a) 7π (b) 10 π (c) 12π (d) ∞
9.已知f(t)的傅氏变换为()F j ω,则tf(-2t)的傅立叶变换为( ) (a)
()2dF j j
d ωω (b)()2
2j dF j
d ω
ω
-
(c)
()dF j j
d ωω
- (d)(
)2
2
j dF j
d ωω
10.以下表达式能正确反映)(n δ与)(n u 的是( )。
(a)
∑∞
=-=0
)
()(k k n n u δ (b)
∑∞
=-=1
)
()(k k n n u δ
(c) )1()()(+--=n u n u n δ (d)
∑∞
==0
)
()(k k n u δ
11.已知信号f(t)的频带宽度为Δω,所以信号y(t)=f(4t-9) 的频带宽度为( )。
(a) ω∆4 (b) 4ω∆ (c) 94-∆ω (d) 49
4-
∆ω 12.下列信号中只有( )是能量信号
(a) 0cos t ω (b) (2)4j t e π
+ (c) 2()t e u t - (d)
cos()4n π
13.20(5)t t dt
δ∞
-⎰= ( )
(a) 5 (b) 25 (c) 0 (d) ∞
14.
()
0sin()lim t t t ππ→=
(a) 10 (b) 1 (c) 0 (d) cos()t π 15.)*()(),()at at A at A δ
δδ==( (a) a (b) 1 /a (c) 1/a 2 (d) 1
二、画图题(25分)
1.(10分)如下图所示系统中,已知输入信号)(t x 的频谱)(ωj X 如图
所示,试确定并粗略画出()y t 的频谱)(ωj Y 。
2.(10分).有一LTI 系统,它对于图(1)的信号1()x t 的响应如图(2)所示,确定并画出该系统对于图(3
)的信号2()x t 的响应。
3.(5分)计算并画出下图信号的奇部和偶部。
2
t
2ω
2ω-
图(3)
三、(15分)设)(t f 为频带有限信号,频带宽度为5m ω=,其频谱()F j ω如所示。
(1) 求)(t f 的奈奎斯特抽样频率s ω和
s f 、奈奎斯特间隔s T ;
(2) 设用抽样序列
)
()(∑+∞
-∞
=-=
n s
T nT t t δδ对信号)(t f 进行抽样,得抽样信
号)(t f s ,
画出
)(t f s 的频谱()s F j ω的示意图。
(3)若用同一个)(t T δ对)2(t f 进行抽样试画出抽样信号)2(t f s 的频谱图。
四、(10分)有一离散线性时不变系统,差分方程为
)1()2(23
)1(27)(-=-+--
n x n y n y n y
(1) 求该系统的系统函数H(z),并画出零、极点图;
(2) 限定系统是因果的,写出H(z)的收敛域,并求出单位函数响应h(n),并说明系统是否稳定?
五、(20分)已知一线性时不变因果系统框图如下,试确定: (1)系统函数()H s ;
(2)画出零极点分布图,并判断系统的稳定性; (3)系统的单位冲激响应()h t ;
(4)写出描述系统输入输出关系的微分方程;
(5)当输入
)()(t u e t f t
-=,求系统的零状态响应)(t y 。
答案:
一、1、c ;2、a ;3、c ;4、a ;5、b ;
6、c ;
7、c ;
8、c ;
9、b ;10、a ;11、a ; 12、c ;13、b ;14、b ;15、b 二
、
1
、
()()()[]()()[]000000534341534341w w u w w u w w w w u w w u w w jw Y -----⎪⎪⎭⎫
⎝⎛--+---⎪⎪⎭⎫ ⎝⎛-=
2、()()()()[]()()[]()()()[]2142121222---+-+--+-++=t u t u t t u t u t u t u t t y
3w
0.5
w
()jw X
5w
3w -
5w -
+
+
+
2S
1S
-4
-2
()
x t ()
y t ()t y 2
3、
()()()2t x t x t x e -+=
()()()2t x t x t x o --=
三、(1)10=s w ;
π5
=
s f ;
5π
=
s T ;
(2)
(3)
1 0.5
t
2
-1
-2 ()
t X e
四、(1)
()
3
7
2
2
2+
-
=
z
z
z
z
H
(2)
()()()
[]()n u n
h n
n3
2.1
5.0
2.0+
-
=
不是稳定系统
五、(1)
()()
()()2
8
4
3
+
+
+
=
s
s
s
s
H
(2)
稳定系统
(3)
()()()t u
e
e
t
h t
t2
8
2-
-+
=
(4)
()()()()()t x
t
x
t
y
t
y
t
y12
'
3
16
'
10
"+
=
+
+
(5) ()()t u
e
e
e
t y t
t
t⎪
⎭
⎫
⎝
⎛
-
-
=-
-
-8
2
7
2
7
9
Re[]z Im[]z
0.5 3。
