矩阵位移法小结
结构力学10第十章.矩阵位移法
2
6 EI F 2 l
1e 1 e M e 2 EI y 2
l
x
19
F EA / l 1
e x1
EI l
Fxe2 EA / l 2
y
e
x u 1
e 2
12 EI M e 6 EI 1 Fye1 3 l2 l l EI 1
2
e 2
12 EI F 3 l
F
e
M 1e e M 2
e
1e e 2
连续梁单元的杆端无线位移。
6
2）平面刚架单元
F
e x1
Fye 1
F
e y1
Fxe 1 1e M 1e M 1
x
e
2
v1e 1
1
u1e
v
e 1
x
e 2
y
y
单元杆端力
同理有
{}e [T ]{}e
[T ]称为单元坐标转换矩阵。14对于平面桁架单元，其单元坐标转换矩阵为：
cos sin [T ] 0 0 sin cos 0 0 0 0 cos sin 0 0 sin cos
单元局部坐标系
结构整体坐标系
8
3）桁架单元
F
e
Fxe 1 e Fy1 e Fx 2 F e y2
e
u1e e v1 e u2 v e 2
F
e
Fxe1 e Fy1 e Fx 2 F e y2
e e e e Fxe , Fye1 , u1 , v2 , Fxe2 , Fye2 , u2 , v2 1
结构力学之矩阵位移法
第十二章 矩阵位移法【例12-1】 图 a 所示 连 续 梁 ，EI=常数，只 考 虑 杆 件 的 弯 曲 变 形 。
分别用位移法和矩阵位移法计算。
图12-1解：（1）位移法解•基本未知量和基本结构的确定用位移法解的基本结构如图c 所示。
这里我们将结点1处的转角也作为基本未知数，这样本题仅一种基本单元，即两端固定梁。
•位移法基本方程的建立⎪⎭⎪⎬⎫=+θ+θ+θ=+θ+θ+θ=+θ+θ+θ000333323213123232221211313212111P P P R K K K R K K K R K K K 将上式写成矩阵形式⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000321321333231232221131211P P P R R R K K K K K K K K K•系数项和自由项 计算（须绘出单位弯矩图和荷载弯矩图）由图d ，结点力矩平衡条件∑=0M ，得 EI K 411=，l EI K 221=，031=K由图e ，结点力矩平衡条件∑=0M ，得l EI K 212=，l EI l EI l EI K 84422=+=，l EI K 232=由图f ，结点力矩平衡条件∑=0M ，得 013=K ，l EI K 223=，l EI EI EI K 84433=+=由图g ，结点力矩平衡条件∑=0M ，得81Pl R p -=，2Pl R P -=，03=P R将系数项和自由项代入位移法基本方程，得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0000118820282024321Pl l EI •解方程，得⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧θθθ14114162321EI Pl •由叠加法绘弯矩图，如图h 所示。
（2）矩阵位移法解•对单元和结点编号（图a ） 本题只考虑弯曲变形的影响，故连续梁每个结点只有一个角位移未知数。
结构力学十三讲矩阵位移法
-6EI l2
4EI l
4
§13-3 单元刚度矩阵(整体座标系)
一、单元座标转换矩阵 Y1
X1
X1
Y1
MM21
e
x
M2 X2
正交矩阵 [T]-1 =[T]T
e e
e T T e
v1
y e
X 2
Y2
Fⓔ T T F ⓔ
ee
F T F ee
座标转换矩阵
5
二、整体座标系中旳单元刚度矩阵
[k] e = [T]T k e [T]
(4)
(6)
00
(5)
y
单元 局部码总码
单元 局部码总码
（1） 1 （2） 2 （3） 3 （4） 0 （5） 0 （6） 4
1
2
3 0
0
4
（1） 1
1
（2） 2
2
（3） 3 （4） 0
3 0
（5） 0
0
（6） 0
0
18
1 2
[k] 1 = 3
0 0 4
1 2
[k] 2= 3
0 0 0
123004 101 102 103 104 105 106 201 202 203 204 205 206 301 302 303 304 305 306 401 402 403 404 405 406 501 502 503 504 505 506 601 602 603 604 605 606 123000 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66
09矩阵位移法(学习版)(1)
1
2
3 6
4
y
5
θ x
O
练习：
3 ④ 2 ① 1
8 ⑨ ⑤ 6 ⑦ ② 4 5 ⑧ 7 ⑩ ⑥
13
12 10 11 ③ 9
（2）结点位移编码 矩阵位移法基本未知量的确定： 矩阵位移法基本未知量的确定不是唯一的，它与 单元如何划分，是否考虑轴向变形以及如何编写程序 有关。 结点位移的统一编码 —— 整体码 用矩阵位移法进行结构分析时，基本未知量是结点 位移，这就需要将结构中全部结点位移分量进行统一编 码。
第九章
矩阵位移法
9.1 概述
1. 概述
结构矩阵分析是采用矩阵方法分析结构力学问题的 一种方法。与传统的力法、位移法相对应，结构矩阵分 析中也有矩阵力法和矩阵位移法，或柔度法与刚度法。 矩阵位移法易于实现计算过程程序化而被广泛应用。 矩阵位移法是以结点位移为基本未知量，借助矩阵 进行分析，并用计算机解决各种杆系结构受力、变形等 计算的方法。
e
e
建立单元的杆端力和杆端 位移之间关系的过程称单元分 析，形成的方程称单元刚度方 程。
e
⎡δ 1 ⎤ ⎡ u i ⎤ ⎢ ⎥ ⎢ ⎥ δ 2 ⎥ ⎢ vi ⎥ ⎢ e ⎡ δ i ⎤ ⎢δ 3 ⎥ ⎢θ i ⎥ e δ =⎢ ⎥ =⎢ ⎥ =⎢ ⎥ ⎣δ j ⎦ ⎢δ 4 ⎥ ⎢u j ⎥ ⎢δ 5 ⎥ ⎢ v j ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎦ ⎦ ⎢ ⎣θ j ⎥ ⎣δ 6 ⎥
2. 单元分析
y y e i x
α
j x
局部坐标系（单元坐标系）：进行某一单元的单元分析时所 建立的坐标系。 局部坐标系相对于整体坐标系的方位角用α表示。α的方向 以 x 轴向 x 轴逆时针转动为正。即便在一个结构中，各单元的局 部坐标系也不完全相同。
矩阵位移法——精选推荐
第十二章矩阵位移法12-1 概述用经典的力法和位移法求解超静定结构，随着基本未知量数目的增多，相应需要建立和求解的多元代数方程的个数也增多，计算工作极为冗繁和困难。
由于计算技术的飞速发展，电子计算机广泛应用于结构分析，使力学学科在计算技术上实现了现代化，大大推动了工程设计技术上的改进和结构理论的发展。
基于上述情况，结构矩阵分析方法已从本世纪六十年代迅速发展起来。
在结构矩阵分析中，运用矩阵进行计算，不仅能使公式非常紧凑，而且在形式上规格统一，便于使计算过程程序化，因而适用于电子计算机进行自动化的数学计算。
结构矩阵分析的两种基本方法是矩阵位移法(刚度法)和矩阵力法(柔度法)，前者在计算中采用结点位移作为基本未知量，后者则采用多余力作为基本未知量。
对于杆件结构，矩阵位移法比矩阵力法便于编制通用的程序，因而在工程界应用较为广泛。
矩阵位移法与位移法在本质上并无区别，两者的差异仅在于矩阵位移法是从电算这一角度出发，它在解题步骤上以矩阵作为组织运算的数学工具。
在杆件结构的矩阵位移法中，把复杂的结构视为有限个单元(杆件)的集合，各单元彼此在结点处连接而组成整体。
因而先把结构分解成有限个单元和结点，即对结构进行离散化。
继而对单元进行分析，建立单元杆端力与杆端位移之间的关系。
再根据变形谐调条件、静力平衡条件使离散化的结构恢复为原结构，从而形成结构刚度方程，据此不难求解结构的结点位移和单元杆端力。
矩阵位移法的基本思路是“先分后合”，即先将结构离散然后集合，这样一分一合的过程，就把复杂结构的计算问题转化为简单杆件的分析与综合问题了。
因此，它的解题方法可分为两大步骤:(1)单元分析。
研究单元的力学特性。
(2)整体分析。
考虑单元的集合，研究整体方程的组成原理和求解方法。
12一2 单元刚度矩阵一、单元的划分在杆件结构中，一般是把每个杆件作为一个单元。
为了计算方便起见，只采用等截面直杆这种形式的单元，并且还规定荷载只作用于结点处。
矩阵位移法
第9章矩阵位移法9.1 概述前面介绍的力法、位移法和渐近法都是传统的解算超静定结构的方法，它们是建立在手算基础上的。
随着基本未知量数目的增加，其计算工作极为冗繁和困难。
而计算机的问世及其广泛应用，为结构计算提供了有效工具。
矩阵位移法就是以计算机为运算工具的一种新的结构分析方法，它完全可以代替人来完成大型复杂结构的计算问题。
矩阵位移法是以位移法为理论基础，结构分析的全部过程中运用了线性代数中的矩阵理论。
引入矩阵运算的目的就是使计算过程程序化，便于把结构分析的过程用算法语言编成计算程序，实现计算机自动化处理。
目前，应用矩阵位移法编制的结构分析软件，已在结构设计中得到了广泛的应用。
矩阵位移法又称为杆件有限元法。
它的主要解题思路是：首先将结构离散成为有限个独立的单元，进行单元分析，建立单元杆端力与单元杆端位移之间的关系式——单元刚度方程；然后利用结构的变形连续条件和平衡条件将各单元组合成整体，建立结点力与结点位移之间的关系式——结构刚度方程，这一过程称为整体分析；最后求得结构的位移和内力。
矩阵位移法就是在一分一合，先拆后搭的过程中，把复杂结构计算问题转化为简单的单元分析和集合问题。
本章主要讨论杆系结构的单元刚度矩阵及其在单元局部坐标系与结构整体坐标系间的变换、结构刚度矩阵的形成、荷载及边界条件处理等内容。
9.2 单元分析9.2.1 结构离散化结构离散化是指把结构分离成有限个独立杆件(单元)，由单元的组合体代替原结构(图9.1)。
一般单元为等截面直杆，杆系结构中每根杆件可以作为一个或几个单元。
单元的联接点称为结点。
对于等截面直杆所组成的杆系结构，只要确定了一个结构的所有结点，则它的各个单元也就随之确定了。
根据杆件联接的方式，可以将构造结点，如转折点、汇交点、支承点和截面的突变点取为结点。
在有些情况下，非构造点，如集中力作用点，也可作为结点处理。
离散化的结构用数字进行描述，即对各结点和单元进行编号。
通常用①,②,…表示单元编号，用1,2,…表示结点编号。
《结构力学》第十章矩阵位移法
《结构力学》第十章矩阵位移法矩阵位移法是结构力学中的一种重要分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。
本文将分为四个部分来介绍矩阵位移法的基本原理和应用。
第一部分将介绍矩阵位移法的基本原理。
矩阵位移法基于结构的受力平衡方程和变形条件，建立了适用于不同类型结构的一般形式的位移函数。
通过对这些位移函数进行适当组合，可以得到一个较为简化的位移矩阵方程。
这个方程可以通过矩阵运算求解，从而得到结构的位移和应力分布。
第二部分将介绍矩阵位移法的应用。
矩阵位移法可以用于求解各种类型的结构，包括梁、柱、框架等。
具体应用时，首先需要确定结构的边界条件和受力情况，然后根据结构的几何形状和材料性质，建立相应的位移函数。
之后，将位移函数按照一定的规则组合起来，建立一个位移矩阵方程。
通过解这个方程，可以得到结构的位移和应力分布。
第三部分将介绍矩阵位移法的优点。
相比于传统的力方法，矩阵位移法具有计算简单、准确性高、适用范围广等优点。
这是因为矩阵位移法可以通过矩阵运算将结构的受力分析转化为代数运算，减少了繁琐的计算过程，并且可以应用于各种不规则结构。
第四部分将介绍矩阵位移法的局限性。
矩阵位移法虽然具有很多优点，但也有一些限制。
首先，矩阵位移法对结构的刚度矩阵的求取较为复杂，需要通过精确和谐振数法等途径进行求解。
其次，矩阵位移法不能用于解决非线性和动力问题。
总结起来，矩阵位移法是一种重要的结构力学分析方法，通过将结构的受力分析转化为矩阵运算，可以有效地求解复杂结构的位移和应力分布。
它具有计算简单、准确性高、适用范围广等优点，但也有一些局限性。
因此，在实际应用中需要根据具体情况选择合适的方法。
同时，矩阵位移法的进一步研究和发展也是一个非常重要的方向。
矩阵位移法
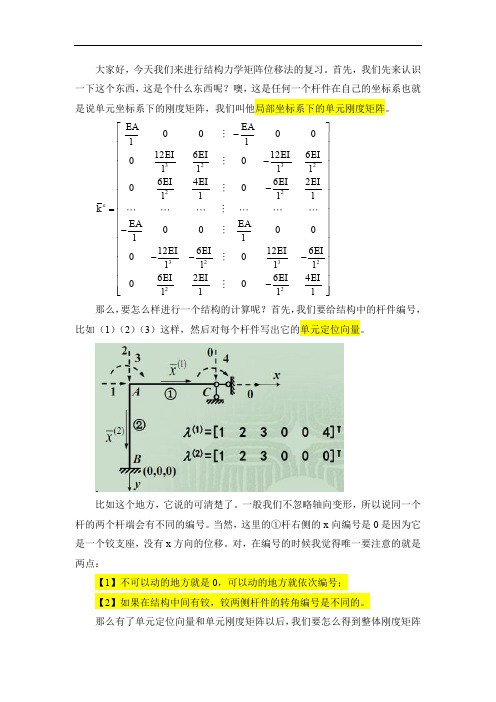
那么就是说，这个杆端力它首先呢，是在局部坐标系下的（我只想知道我的 杆的轴力，剪力啊，什么的，并不想知道某个大方向上的力） ，那么就要用到局 部坐标系的各种参数。 其次，力是刚度乘位移的。 所以就是说，应该有这样
e e e F e k e e F e P k T F P
不过这个位移的话， 其实之前求出来了的话反正就这样吧。注意如果原来有 节点荷载的话这里是不用加它的， 我们只要加杆内荷载计算得到的固端力就好了， 这个力之前是查表得到的，非常方便加上去哦。 然后这里就告一段落啦。
呢？ 在这之前， 必须要把局部坐标系下的单元刚度矩阵转化为整体坐标系下的单 元刚度矩阵。 那么必须要有这个杆件的方位角。假设这个杆件的正方形和水平向 右的夹角 （顺时针） 是 ， 那么， 就有一个坐标变换矩阵的问题， 这个玩意叫 T 。 还有一个玩意叫坐标变化子矩阵，这玩意叫 t 。 这两个家伙有这么个关系。
e
e
t T kii et
其实还是挺麻烦的。如果说刚好是 90°的话，倒是就把对角线上第一第二 排换一下，然后右上角左下角的和旁边的换一下位子就 OK 了。 然后就可以用整体坐标系下的单元刚度矩阵集成整体刚度矩阵了。 这个其实 非常简单， 只要在整体坐标系下的单元刚度矩阵的周围写好它的定位向量，然后 在空白的地方把 0 以外的数字从小到大写好， 在相应的空位里把上面的抄下来加 起来就好啦。 因为这个整体刚度矩阵具有对称性和带状稀疏性， 所以只要把左下角三角形 的都写出来就好了，右上角是一模一样的。至于带状稀疏性的话，就是说它中间 的是有的，周围的基本都是 0，这是编码造成的，很小的码和很大的码应该是没 有交集的。 那么现在我们得到了一个整体刚度矩阵。
12 EI l3 6 EI l2 ke k e 12 EI 3 l 6 EI l2 6 EI l2 4 EI l 6 EI l2 2 EI l 12 EI l3 6 EI 2 l 12 EI l3 6 EI 2 l 6 EI 2 l 4 EI l 6 EI l2 2 EI l
结构力学矩阵位移法学习
第8章 矩阵位移法 ♍♦♐ 制作同济大学教材笔记(本章答案陆续上传中)一、知识要点： 1.结构坐标系一般采用右手坐标系，记为xoy 。
此时，结点位移和结点力均取与结构坐标系方向一致为正，其中结点的角位移和结点力矩按右手法则均取逆时针方向为正。
2.局部坐标系主要注意α角的定义，看如下图示即明白。
yxoijexyα3.桁架单元刚度方程000000000000eeexi i yi i xj j yj j EAEA F u l lF v EA EAF u l l F v ⎛⎫-⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪-⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎪⎝⎭桁架结构变换矩阵Tcos sin 00sin cos 0000cos sin 00sin cos T αααααααα⎛⎫⎪-⎪= ⎪ ⎪-⎝⎭桁架在结构坐标系下的单元刚度矩阵22222222ee c sc c sc sc s sc s EA k l c sc c sc sc s sc s ⎛⎫-- ⎪-- ⎪=⎪-- ⎪⎪--⎝⎭4.刚架单元刚度方程32322232322212612664621261266264eeeyi i i i yj j j j EIEI EI EI l l l l F v EI EI EI EI M l l l l EI EI EI EI F v l l l l M EI EI EI EI l l l l θθ⎛⎫- ⎪⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎪-⎝⎭5.受轴向力作用的一般刚架单元刚度方程32322232322200001261260064620000001261260062640eexi i yi i i i xj j yj j EAEA ll EI EIEI EI F u l l l l F v EI EI EI EI M l l l l EA EA F u l l F v EIEI EI EI M l l l l EI EI EI EI l lllθ⎛⎫- ⎪⎪ ⎪⎛⎫- ⎪ ⎪⎪ ⎪ ⎪ ⎪- ⎪ ⎪=⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--- ⎪⎝⎭⎪ ⎪- ⎪⎝⎭ej j ⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭一般刚架单元刚度方程的坐标变换矩阵Tcos sin 0000sin cos 0000001000000cos sin 0000sin cos 0001T αααααααα⎛⎫⎪- ⎪ ⎪=⎪ ⎪ ⎪- ⎪ ⎪⎝⎭结构坐标系下的一般刚架单元刚度矩阵e k12412423523545645612412423523545645622ea a a a a a a a a a a a a a a a a a k a a a a a a a a a a a a a a a a a a --⎛-- --=---- ---- --⎝6.为什么已知杆端位移能求得单元的唯一杆端力，而已知杆端力却无法唯一确定杆端位移这是因为支座位移条件不已知，可能相差一个刚体位移，即位移的绝对值不同。
第八章矩阵位移法
第八章矩阵位移法主要内容有限单元法的基本概念，结构离散化。
平面杆系结构的单元分析：局部坐标系下的单元刚度矩阵和整体坐标系下的单元刚度矩阵。
平面杆系结构的整体分析：结构整体刚度矩阵和结构整体刚度方程。
支承条件的处理，单元内力计算。
利用对称性简化位移法计算。
矩阵位移法的计算步骤和应用举例。
学习目的和要求矩阵位移法是以计算机为计算工具的现代化结构分析方法。
基于该法的结构分析程序在结构设计中得到了广泛的应用。
因此，以计算机进行结构分析是本章的学习目的。
本章的基本要求：矩阵位移法包含两个基本环节：单元分析和整体分析。
在单元分析中，熟练掌握单元刚度矩阵和单元等效荷载的概念和形成。
熟练掌握已知结点位移后求单元杆端力的计算方法。
在整体分析中，熟练掌握结构整体刚度矩阵中元素的物理意义和集成过程，熟练掌握结构综合结点荷载的集成过程。
掌握单元定位向量的建立，支撑条件的处理。
自由式单元的单元刚度矩阵不要求背记，但要领会其物理意义，并会由它来推出特殊单元的单元刚度矩阵。
§ 8-1 概述杆系结构矩阵分析又叫杆系结构的有限元法, 分为矩阵力法和矩阵位移法, 亦称为柔度法和刚度法。
由于矩阵位移法比矩阵力法更容易实现计算过程程序化, 因而应用很广泛, 故本章只讨论矩阵位移法。
矩阵位移法的内容包括以下两部分：(1) 将整体结构分成为有限个较小的单元( 在杆系结构中常把一个等截面直杆作为一个单元), 即进行结构的离散化。
然后分析单元内力与位移之间的关系式, 建立单元刚度矩阵, 形成单元的刚度方程, 称该过程为单元分析。
(2) 把各单元按结点处的变形协调条件和结点的平衡条件集合成原整体结构, 建立结构刚度矩阵, 形成结构刚度方程, 解方程后求出原结构的结点位移和内力, 称该过程为整体分析。
上述一分一合,先拆后搭的过程中, 是将复杂结构的计算问题转化为简单单元的分析及集合问题。
而由单元刚度矩阵直接形成结构刚度矩阵是直接刚度法的核心内容。
矩阵位移法
矩阵位移法
矩阵位移法是一种用于解决多项式方程组的数学方法。
它利用行和列变化将原系数矩阵转换成一个三角矩阵。
然后，从底端开始一行行解对角线的方程，最终求出未知数的值，解决多项式方程组。
矩阵位移法的基本步骤如下：
1.将系数矩阵进行行变换和列变换，转换成三角矩阵。
2.从最下面的方程开始，先求解最后一个未知数。
3.从次下面的方程开始，根据前面的结果一行行解出剩余未知数。
矩阵位移法比较容易理解和应用，可以有效地解决多项式方程组，但也存在一些缺点，比如容易出现几何错误，计算精度较低。
▲矩阵位移法小结
▲矩阵位移法小结
计算步骤 1.编号及建立坐标； （注意正确判定结点位移） 2.形成整体刚度矩阵[K]
e （注意单刚的选取） （1）求出局部坐标系下的单元刚度矩阵 [k ] ；
e （2）求出整体坐标系下的单元刚度矩阵 [k ] ； （坐标变换） e （3）按照各单元的定位向量，依次将各 [k ] “对号入座” 集合进整体刚度矩阵[K] 。
3.形成结构的荷载列阵 {P }
（1）将各原始结点荷载集合进结构的荷载列阵 {P } ； （2）将各杆上荷载转化后，集合叠加进结构荷载列阵 {P }。
4.解方程 [ K ]{} P ，求出结点位移{Δ}（整体坐标系）； 5.求杆端内力
（1）由定位向量确定各单元 ，并转换为 （局部坐标系）；
kk??????????????????????103345652523152505883305837437427869400000123456124集合整体刚度矩阵结点位移码结点位移码103694k?37437437437437437405805883352523152513927827813927827869406940000003456xmnm1236455杆上荷载处理集合进结构荷载列阵aby612m1kn000000量未知量n6cd303t????????5杆上荷载处理集合进结构荷载列阵033??????????1单元固端力2等效单元结点力3集合进结构荷载列阵1单元固端力2等效单元结点力3集合进结构荷载列阵123303????????123局部坐标整体坐标局部坐标整体坐标p3ptf303t???????????????p3f033?????????????30003000?????????????p456此题无原始结点荷载因此没有原始结点荷载的集合
矩阵位移法
X 1 EA l Y1 0 M1 0 EA X l 2 0 Y2 0 M 2
e
0 12 EI l3 6EI l2 0 12EI l3 6EI l2
6
将上面六个方程合并，写成矩阵形式： M1 4 EI 1 2 EI 2 6EI v1 v2 l l l2 2 EI 4 EI 6EI M2 1 2 2 v1 v2 EA u1 u2 X1 l l l l 6EI 12 EI EA Y v v 1 1 2 1 2 2 3 u1 u2 X2 l l l 6EI 12 EI Y2 2 1 2 3 v1 v2 l l
凡是符号上面带了一横杠的就表示是基于局部座标系而言的。
4
§13-2
单元刚度矩阵(局部座标系)
进行单元分析，推导单元刚度方程和单元刚度矩阵。 单元刚度方程是指由单元杆端位移求单元杆端力时的一组方程，可以用 “ F ”表示，由位移求力称为正问题。
一、一般单元
在单元两端加上人为控制的附加约束，使基本杆单元的两端产生任意指
2
2
u2 0 v2 0
0 12EI l3 6EI 2 l 0 12 EI l3 6EI 2 l 0 6EI l2 2 EI l 0 6EI l2 4 EI l
e X 1 EA
l Y1 0 M1 0 EA X l 2 0 Y2 0 M 2
EA l 0 0
矩阵位移法小结
《矩阵位移法》计算
一、求总刚
1、先处理法 2、后处理法并引入边界条件
二求荷载向量
1、先处理法 2、后处理法并引入边界条件
三、已知单元杆端力向量，作M、Q、N图。 四、已知杆端位移向量，求杆端力向量。
矩阵位移法小结
矩阵位移法步骤
一、建立局部坐标系下的单元刚度矩阵
（1）结点编号 局部坐标系 （2）单元编号 （3）局部坐标系下的单元刚度矩阵 （两端固定、一端固定一端铰支、两端铰支）
二、 建立整体坐标系下的单元刚度矩阵
K T (e)T K (e)T (e) 三、 建立结构的整体刚度矩阵（先处理法和后处理法） 四、 建立菏载向量（先处理法和后处理法） 五、建立结构的刚度方程（后处理法要引入边界条件）
(e )
P=KΔ
六、求解方程，得结构的结点位移Δ 七、由结点位移求杆端内力
F K
(e)
(e) (e)
F
(e)
T
(e) (e)
(e)
《矩阵位移法》概念
一、单元刚度矩阵任一系数Kij表示第j号位移为1时所 引起的第i号杆端力。 二、单元刚度矩阵第i列的元素表示第i号位移为1时所 引起的六个杆端力。 三、总刚K的特性。 1、对称 2、稀疏（d =（C+1)*m） 3、奇异 四、结构刚度方程是反映结点力向量P与结点位移向量 Δ 之间的变换关系，即 ： P=KΔ
矩阵位移法心得
结构力学学习心得——矩阵位移法结构力学是力学的分支，它主要研究工程结构受力和传力的规律以及如何进行结构优化的学科。
所谓工程结构是指能够承受和传递外载荷的系统，包括杆、板、壳等以及它们的组合体，如飞机机身和机翼、桥梁、屋架和承力墙等。
结构力学的任务是：研究在工程结构在外载荷作用下的应力、应变和位移等的规律；分析不同形式和不同材料的工程结构，为工程设计提供分析方法和计算公式；确定工程结构承受和传递外力的能力；研究和开展新型工程结构。
结构力学中的求解方法有很多种，比方力法、位移法、力矩分配法、矩阵位移法，在结构动力学中还有刚度法、柔度法、极限荷载法等等。
在一个半学期的结构力学学习中，我对矩阵位移法犹为深刻，而且较为难理解，在结构力学书里短短的一章书，学校就安排了我们为期十周的学习，可见矩阵位移法的重要和学习的难度。
首先简单介绍一下矩阵位移法：矩阵位移法是以位移法为理论根底，以矩阵为表现形式，以计算机作为运算工具的综合分析方法。
基于该法的结构分析程序在结构设计中得到了广泛的应用。
因此，以计算机进行结构分析是本章的学习的重点。
引入矩阵运算的目的是使计算过程程序化，便于计算机自动化处理。
尽管矩阵位移法从手算的角度来看运算模式呆板，过程繁杂，但这些正是计算机所需要的和十分容易解决的。
矩阵位移法的特点是用“机算〞代替“手算〞。
因此，学习本章是既要了解它与位移法的共同点，更要了解它的一些新手法和新思想。
矩阵位移法包含两个根本环节：单元分析和整体分析，同时把整个结构看作是由假设干单个杆件〔称为单元〕所组成的集合体作为根本思路。
单元分析：首先把结构拆散成有限数目的杆件单元〔结构的离散化〕，写出各单元杆端的力与位移两者的关系式。
整体分析：将这些单元再集合一起，使其满足平衡条件和位移连续条件，也就是保证离散化了的杆件单元重新集合后仍恢复为原结构。
一般单元局部坐标下的单元刚度方程：323222323222000012612600646200000012612600626400e EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l k EA EA l l EI EI EI EI l l l l EI EI EI EI l l l l ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦一般单元坐标转换矩阵：整体坐标系下的单元刚度矩阵：利用公式，可将局部坐标系下的单元刚度矩阵转换成整体坐标系下的单元刚度矩阵。
关于矩阵位移法和位移法的异同的文章
关于矩阵位移法和位移法的异同的文章矩阵位移法和位移法是两种常用的结构分析方法，它们在工程领域中被广泛应用。
虽然它们都是用来计算结构的位移和应力，但在具体的计算过程和应用范围上存在一些异同。
首先，矩阵位移法是一种基于矩阵运算的结构分析方法。
它将结构划分为若干个单元，每个单元内部的位移通过节点间的约束关系来求解。
通过建立整个结构的刚度矩阵和载荷向量，可以得到结构的整体位移和应力分布。
矩阵位移法适用于各种类型的结构，包括梁、柱、板等。
它具有计算精度高、适用范围广等优点。
而位移法则是一种基于力平衡原理的结构分析方法。
它将结构看作一个整体，在给定边界条件下求解结构内部各点的位移和应力。
通过建立平衡方程和边界条件，可以得到结构内部各点的位移和应力分布。
与矩阵位移法相比，位移法更加直观且易于理解，适用于简单且对称的结构。
在计算过程上，矩阵位移法需要建立结构的刚度矩阵和载荷向量，并通过矩阵运算求解未知位移。
而位移法则需要建立平衡方程和边界条件，并通过代数运算求解未知位移。
相对而言，矩阵位移法的计算过程更加复杂，但可以处理更加复杂的结构。
此外，矩阵位移法和位移法在应用范围上也存在一些差异。
矩阵位移法适用于各种类型的结构，包括非线性和动力学问题。
它可以考虑材料非线性、几何非线性等因素，并能够进行动力学分析。
而位移法则适用于简单且对称的结构，对于复杂的非线性和动力学问题处理能力有限。
综上所述，矩阵位移法和位移法是两种常用的结构分析方法。
它们在计算过程、应用范围等方面存在一些异同。
选择何种方法取决于具体的工程需求和结构特点。
无论是哪种方法，在工程实践中都发挥着重要作用，为工程师提供了有效的工具来分析和设计各种类型的结构。
第十七章矩阵位移法
Xi
e e
EA l
ui 0 0 12 EI l
3
e
EA l
2
uj 0 0
e
e
Yi 0
vi vi
e
e
6 EI l
i 0
12 EI l
3
vj vj
e
e
6 EI l
2 i1 M
2
4 i1 3 i 2 4 i1 M 2 4 i1 3 i 2
M 2 3i 2 M 2 4 i1 3 i 2 4 i1 3 i 2 M 2 0 ( 4 i1 3 i 2 ) 2
K 11 K K 21 K 31
1 K 11 1 K 21 0
K 12 K 22 K 32 K 12
1
K 13 K 23 K 33 0 2 K 23 2 K 33 0 2i2 4i2
K 22 K 22
• 简式为：
F
e
K
e
e
返回 下一张 上一张 小结
• 17.2.4 单元刚度矩阵的特性
• 1）[K]e是对称方阵 • 单元刚度矩阵中的行数等于单元杆端力向量的分量数，列数 等于单元杆端位移向量的分量数。因为这两个向量的分量数相等， 所以[K]e是一个方阵。又因 Kij=Kji ，故单元刚度矩阵是对称矩 阵。 • 2）[K]e是奇异矩阵 • 矩阵[K]e相应行列式的值为零，故知单元刚度矩阵是奇异矩 阵。其逆矩阵不存在。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式中K为总刚度矩阵，为结构的结点位移列向量，P
为结点力列向量。
总刚度矩阵K反应了整个结构的刚度，是描述结点 力与结点位移之间关系的系数矩阵。其矩阵的性质与 特点：
总结
( 1 )元素kij的物理意义为：当△j=1而其他位移分量为零 时产生在△i方向的杆端力。
（2）主子块Kii是由结点i的相关单元中与结点i相应的主 子块叠加而得。
3. 弹性支座的处理 通常用主对角元素叠加法处理弹性支座。如果结构的 第j个自由度是弹性约束，那么，把弹性支座的刚度系数 叠加到原始刚度矩阵主对角线的第j个元素上即可得到经 约束处理后的总刚度方程。
总结
4. 总刚度方程和总刚度矩阵的性质与特点 总刚度方程为整体结构的结点荷载与结点位移之间的 关系式，是结构应满足的平衡条件。无论何种结构，其总 刚度方程都具有统一的形式:
总结
对于每个结点位移分量数相同的结构，原始刚度矩阵 的阶数为结构的总结点数乘以结点位移分量的数目，例 如，每个结点位移分量数为3的平面刚架，结构原始刚 度矩阵的阶数为3n×3n 。
总结
（2）边界条件处理
对于刚性支座，用划行划列法处理刚性支座，即直接 划去原始刚度方程中与零位移对应的行和列。这样做有 时要改变原方程的排列顺序,会给编程带来麻烦。为了不 改变原方程的排列顺序，同时又要引入边界条件,采用 “主一副零”法。
的单元刚度方程中求杆端内
力
总结
一、基本概念
结构矩阵分析是采用矩阵方法分析结构力学问题的一种 方法。与传统的力法、位移法相对应，在结构矩阵分析中 也有矩阵力法和矩阵位移法，或柔度法与刚度法。矩阵位 移法易于实现计算过程程序化而被广泛应用。
矩阵位移法是结构力学中的位移法加上矩阵方法。矩阵 位移法的基本未知量也是结点位移——独立的线位移和转 角。但由于有时考虑杆件的轴向变形，且把杆件铰结端的 转角也作为基本未知量，因此，基本未知量数目比传统位 移法的基本未知量多一些。
设结点位移向量中第r个位移等于零, 即r=0 ，则在结
构的原始刚度矩阵k中的第r行第r列中主对角元素krr改为1 其余元素改为零。同时将结点结点荷载列向量P中的第r个
分量也改为零。 即
krr 1 krs ksr 0 Pr 0
(s r)
总结
对于支座位移等于给定值时，采用“乘大数法”。设 结点位移向量，中第r个位移等于d0，在矩阵K与向量P中， 主对角元素krr 改为Gkrr，将Pr改为d0Gkrr，其中G为一大 数通常取108～1010 。
总结
矩阵位移法与位移法在理论上并无区别，只是在 表达方式上有所不同。
(1)矩阵位移法的理论基础与一般位移法完全相 同，只是表达方式不同。用矩阵形式表示具有更强 的概括性。
(2)总刚度矩阵是由各单元刚度矩阵装配成的，只 要找出了装配的规律，总刚度矩阵不必计算而可直 接由单元刚度矩阵装配而成。
(3)矩阵位移法与一般位移法解题步骤的对应关 系可以由下表表示：
总结
表 8-1
一般位移法
矩阵位移法1． 写出各Fra bibliotek的转角位移方程 1．列出各单元的单元刚度矩
阵和单元刚度方程
2．考虑结点和截面平衡建立 2．由各单元刚度矩阵装配总
位移法典型方程
刚度矩阵
3．解方程求结点位移
3．考虑约束条件建立结构刚 度方程并求解
4．将结点位移回代到转角位 4．将结点位移回代到各单元
移方程中求杆端弯矩
（3）当i、j为相关结点时，副子块Kij就等于连接ij的杆 单元中相应的子块；若i、j不相关，则Kij为零子块。
（4）总刚度矩阵为对称矩阵。
（5）总刚度矩阵为稀疏带状矩阵。愈是大型结构，带 状分布规律就愈明显。
（6）总刚度矩阵主对角元素都大于零。通常是主对角 元素占优势的矩阵，因此，线形方程组的解有较好的稳定 性。
总结
5. 总刚度矩阵的最大半带宽
总刚度矩阵的上三角部分，从某行的主对角元素到该行 最末一个非零元素所具有的元素的个数称为该行的半带宽。 各行半带宽的最大值称为总刚度矩阵的最大半带宽。
对应于后处理法，结构内部不存在组合结点时最大半带 宽的计算公式为:d=(b+1)c ，其中b为单元两端结点编码的 最大差; c为结构中一个结点的位移分量数，显然，最大半 带宽与结构的结点编码的顺序有关。通常应使相邻结点编 码的最大差值为最小，即d 值为最小。
单元定位向量：按单元连接结点编号顺序由结点未知 位移编号组成的向量。
总结
（2）边界条件处理。对于刚性支座，其位移总码均编 为零。对于支座位移等于给定值时，通常也将其位移总码 均编为零，将支座结点位移的影响转换成单元非结点荷载, 即，将支座结点位移转换成与该支座结点位移连接的各单 元在单元坐标系中的杆端位移，求出由此给定的杆端位移 产生的单元固端力，然后转换成等效结点荷载。
总结
2. 先处理法
(1) 集成。将单元刚度矩阵先按边界条件进行处理,然后 按照单元连接结点的总位移编号将单元刚度矩阵的元素在 结构的刚度矩阵中对号入座，形成总刚后即可进行求解。 上述过程可通过引入定位向量来实现。在单元定位向量中 考虑边界条件，凡给定的结点位移分量，其位移总码均编 为零，与总码编为零相应的行、列元素在集成总刚时被屏 弃在外。
总结
矩阵位移法的基本思路是:
(1) 先把结构离散成单元，进行单元分析,建立单元杆 端力与杆端位移之间的关系；
(2)在单元分析的基础上，考虑结构的几何条件和平衡条 件，将这些离散单元组合成原来的结构，进行整体分析， 建立结构的结点力与结点位移之间的关系，即结构的总刚 度方程，进而求解结构的结点位移和单元杆端力。
在从单元分析到整体分析的计算过程中，全部采用矩阵 运算。
总结
二、总刚度矩阵的集成及约束处理
集成总刚度矩阵最常用的方法是直接刚度法，即由单元 刚度矩阵直接集成结构刚度矩阵，又可分为后处理法和先 处理法。
1. 后处理法
(1) 集成。对所有单元不做边界条件处理，均采用自由 式的单元刚度矩阵，按单元的结点编号将单元刚度矩阵分 为四个子块（阶数相同），逐块地将结点所对应的子块在 结构的原始刚度矩阵中对号入座，形成结构的原始刚度矩 阵。由于结点位移分量中包括了非自由结点的已知位移， 原始刚度矩阵为奇异的，需进行边界条件处理，才能求解 自由结点位移。由于原始刚度矩阵的阶数较高，所以后处 理法的主要缺点是占用较多的计算机内存。