2021年材料力学(金忠谋)第六版答案第06章
材料力学(金忠谋)第六版课后习题及答案

解
(1) ∆l1
=
1 3
Ρxl1
Ε 1Α1
∆l1 = ∆l2 x = 0.6m
∆l 2
=
1 3
Ρ (3 − x)l2
Ε 2Α2
(2) Ρ ≤ 3Ε1Α1 = 3× 200 × 2 ×10−1 = 200ΚΝ
xl1
0.6× 2
2-11 铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[σ +]=400kg/cm2, 许用压应力[σ − ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
习题
2-1 一木柱受力如图示,柱的横截面为边长20cm的正方形,材料服从虎克定律,其
弹性模量 E = 0.10 ×105 MPa.如不计柱自重,试求:
(1) (2) (3) (4)
作轴力图; 各段柱横截面上的应力; 各段柱的纵向线应变; 柱的总变形.
解:
(1) 轴力图
(2) AC 段应力
σ
=
−100 ×103 0.2 2
= −2.5×106 Ρa = −2.5ΜΡa
CB 段应力
σ
=
− 260 ×103 0.2 2
= −6.5×106 Ρa = −6.5ΜΡa
(3) AC 段线应变
ε = σ = −2.5 = −2.5×10−4 Ε 0.1×105 CB 段线应变
ε
=σ Ε
=
−6.5 0.1×10 5
解:
AC、CB、BD、DA 杆受拉力,大小为 Τ1 =
Ρ 2
DC 杆受压力,大小为 Τ2 = Ρ
[σ
+
]≥
Τ1 Α
得 Ρ1 ≤ 2 × 400 × 25 = 14142kg
材料力学(金忠谋)第六版答案第06章.doc

弯曲应力6-1 求图示各梁在m-m截面上A点的正应力和危险截面上最大正应力。
题6-1图解:(a)mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ(压)MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ(b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
材力习题册(第六版)参考答案(1-3章)

解①②③④式,得 =xF 当 x=l 时, 当 x=0 时, 当 x=l/2 时, /l, =(1-x/l)F, =(l-x)Fx/l =F =F =Fl/4
达到最大值,即 达到最大值,即 达到最大值,即
-5-
第二章
一、选择题
轴 向 拉 压
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将 ( A.平动 应是( C ) B.转动 C.不动 D.平动加转动
2
D.
h 3d D 4
(图 9)
(图 10)
(图 11)
二、填空题
1.直径为 d 的圆柱放在直径为 D=3d,厚为 t 的圆基座上,如图 11 所示地基对基座的支 反力为均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力 Q = 8P/9 。 2. 判断剪切面和挤压面时应注意的是: 剪切面是构件的两部分有发生 相对错动 趋势的 平面;挤压面是构件 受挤压 的表面。 3.试判断图 12 所示各试件的材料是低碳钢还是铸铁? A 为 铸铁 ,B 为 低碳钢 ,C 为 铸铁(45 度螺旋面) ,D 为 低碳钢,E 为 铸铁 , F 为 低碳钢 。
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
2 3
A
)。
B σ 2>σ 3>σ D σ 2>σ 1>σ A
1 3
C σ 3>σ 1>σ
13. 图 8 所示钢梁AB由长度和横截面面积相等的钢杆1和铝杆2支承,在载荷P作用 下,欲使钢梁平行下移,则载荷P的作用点应 ( A 靠近 A 端 C 在 AB 梁的中点 A 分别是横截面、 45 斜截面 C 分别是 45 斜截面、横截面 A 分别为 σ /2 和 σ C 分别为 σ 和 σ /2 16. 材料的塑性指标有 ( A σ s和δ C )。 B σ s和ψ
材料力学习题第六章应力状态分析答案详解

第6章 应力状态分析一、选择题1、对于图示各点应力状态,属于单向应力状态的是(A )。
(A )a 点;(B )b 点;(C )c 点;(D )d 点 。
2、在平面应力状态下,对于任意两斜截面上的正应力αβσσ=成立的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ,现关于AC 面上应力有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==; (B)AC AC /2,/2ττσ=; (C)AC AC /2,/2ττσ==;(D)AC AC /2,/2ττσ=-。
4、矩形截面简支梁受力如图(a )所示,横截面上各点的应力状态如图(b )所示。
关于它们的正确性,现有四种答案,正确答案是( D )。
(A )点1、2的应力状态是正确的;(B )点2、3的应力状态是正确的; (C )点3、4的应力状态是正确的;(D )点1、5的应力状态是正确的。
5、对于图示三种应力状态(a )、(b )、(c )之间的关系,有下列四种答案,正确答案是( D )。
(A )三种应力状态均相同;(B )三种应力状态均不同; (C )(b )和(c )相同; (D )(a )和(c )相同;6、关于图示主应力单元体的最大切应力作用面有下列四种答案,正确答案是( B )。
解答:max τ发生在1σ成45的斜截面上7、广义胡克定律适用范围,有下列四种答案,正确答案是( C )。
(A )脆性材料;(B )塑性材料;(C )材料为各向同性,且处于线弹性范围内;(D )任何材料; 8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适用于( C )。
(A )任何材料在任何变形阶级; (B )各向同性材料在任何变形阶级; (C )各向同性材料应力在比例极限范围内;(D )任何材料在弹性变形范围内。
材料力学(金忠谋)第六版完整编辑版规范标准答案

解:(a):(I)截面:内力为零。
(II)截面:M = Pa(弯矩)
Q = -P(剪力)
(b):(I)截面:
(II)截面:
(c):(I)截面:
(II)截面:
1-3图示AB梁之左端固定在墙内,试求(1)支座反力,(2)1-1、2-2、3-3各横截面上的内力(1-1,2-2是无限接近集中力偶作用点.)
解:
(1)
(2)
即
解得
各杆的长度为
2-37图示三杆结构中,杆(1)是铸铁的,E1=120Gpa, =80MPa;杆(2)是铜的,EA=100GPa, =60Gpa;杆(3)是钢的,EA=200GPa, =120Mpa。载荷P=160kN,设A1:A2:A3=2:2:1,试确定各杆的截面积。
解:
各杆的应力关系为
解
(1)
(2)
2-11铰接的正方形结构如图所示,各杆材料皆为铸铁,许用拉应力[ +]=400kg/cm2,许用压应力[ ]=600kg/cm2,各杆的截面积均等于25cm2。试求结构的许用载荷P。
解:
AC、CB、BD、DA杆受拉力,大小为
DC杆受压力,大小为
得
得
故
2-12图示拉杆沿斜截面m-n由两部分胶合而成,设在胶合面上许用拉应力[ ]=100MPa,许用剪应力 =50MPa,胶合面的强度控制杆件的拉力,试求:为使杆件承受最大拉力P, 角的值应为多少?若横截面面积为4cm2,并规定 ,试确定许可载荷P。
解:
只计P时,有
只计2P时,有
且有
联立,解得
(方向水平向左) (方向水平向右)
(b)
家电公司研发部资料材料力学习题答案(六)
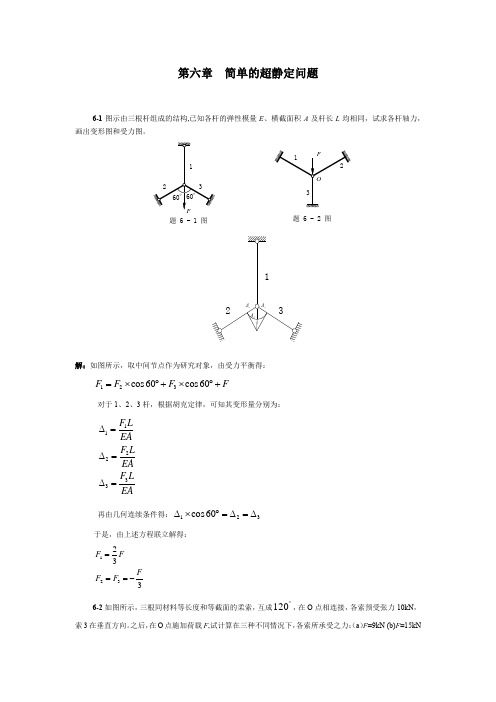
第六章 简单的超静定问题6-1图示由三根杆组成的结构,已知各杆的弹性模量E 、横截面积A 及杆长L 均相同,试求各杆轴力,画出变形图和受力图。
123Δ2Δ3Δ1解:如图所示,取中间节点作为研究对象,由受力平衡得:123cos60cos60F F F F =⨯︒+⨯︒+对于1、2、3杆,根据胡克定律,可知其变形量分别为:112233F L EA F L EA F L EA ∆=∆=∆=再由几何连续条件得:123cos60∆⨯︒=∆=∆于是,由上述方程联立解得:123233F F FF F ===-6-2如图所示,三根同材料等长度和等截面的柔索,互成︒120,在O 点相连接,各索预受张力10kN ,索3在垂直方向。
之后,在O 点施加荷载F ,试计算在三种不同情况下,各索所承受之力:(a )F =9kN (b)F =15kN题 6 - 1 图题 6 - 2 图(c)F =21kN 。
答:(a )F =9kN 时,12313,4N N kN N kN ===(b )F =15kN 时,12315,0N N kN N ===(c )F =21kN 时,12321,0N N kN N === 解:首先计算当绳索3刚好无拉力时荷载F 的值。
如图所示,取节点O 作为研究对象。
由于绳索上实现施加了10KN 的拉力,因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则F=10KN(1)由于F=9KN<10KN (不太明白怎么做)于是绳索3中仍然有拉力。
……(2)由于F=15KN>10KN 于是绳索3中没有拉力。
因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则123150F F KN F KN===(3)由于F=21KN>10KN 于是绳索3中没有拉力。
因此由节点的竖向平衡可知:12cos60cos60F F F =⨯︒+⨯︒则123210F F KN F KN===6-3图示对称结构中,杆BC 为刚性杆,其余四根杆的EA 均相同,试求荷载F 作用下四根杆的轴力。
材料力学金忠谋第六版答案第章

(a) (b)
(c )(d)
(e)
8-6已知矩形截面梁某截面上的弯矩和剪力分别为M=10kN·m,FS=120kN,试绘出截面上1、2、3、4各点单元体的应力状态,并求其主应力。
解:
8-7在棱柱形单元体的AB面上以及与ABC面平行的前后面上(与纸平面平行的面),均无应力作用。在AC面和BC面上的正应力均为-15MPa,试求AC和BC面上的剪应力与此单元体主应力的大小和方向。
解:(a)
(b)
(c)
(d)
8-12直径d=2cm的受扭圆轴,今测得与轴线成 方向的线应变 。已知E=200GPa, =,试求扭转力矩 。
解:
8-13一个No28a工字钢梁,受力如图所示,今测得在梁的中性层上K点、与轴线成 方向上的线应变 。已知E=200GPa, =。试求此时梁承受的载荷P。
解: :
解:
8-22图示半径为 ,厚度为t的圆板,在周边受径向均有载荷q作用,试求圆板厚度变化量 及体积应变 。
解:
(1)
(2)
解:
所以三个主应力:
8-10在一块厚钢块上挖了一条贯穿的槽,槽的宽度和深度都是1cm。在此槽内紧密无隙地嵌入了一铝质立方块,其尺寸是111cm,并受P=6kN压缩力如图示,试求铝立方块的三个主应力。假定厚钢块是不变形的,铝的E=71GPa, =。
解
8-11已知单元体的应力圆如图所示(应力单位:MPa)。试作出主单元体的受力图,并指出与应力圆上A点相对应的截面位置(在主单元体图上标出)。
解:(a)
(与 方向夹角)
(b)
(与 方向夹角)或 (与水平方向交角)
(c)
(与 方向夹角)
(d)
8-4单元体各面的应力如图示(应力单位为MPa),试用解析法和图解法计算主应力的大小及所在截面的方位,并在单元体内注明。
材料力学课后习题答案6章
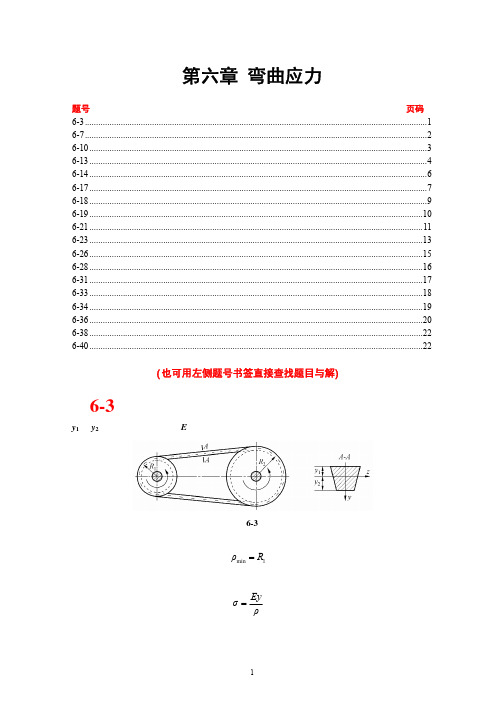
由切应力互等定理可知,纵截面上的切应力 τ x 与 τ 2max 一样大。 左、右端面上弯曲正应力构成的轴向合力分别为
Fx1 =
bh Fa 1 σ1max ( ) = 2 2 2h bh Fa 1 Fx 2 = σ 2max ( ) = h 2 2
左、右端面上弯曲切应力构成的竖向合力大小相等,其值为
(也可用左侧题号书签直接查找题目与解)
6-3
图示带传动装置,胶带的横截面为梯形,截面形心至上、下边缘的距离分别为
y1 与 y2,材料的弹性模量为 E。试求胶带内的最大弯曲拉应力与最大弯曲压应力。
题 6-3 图 解:由题图可见,胶带中性层的最小曲率半径为
ρmin = R1
依据
σ=
Ey ρ
可得胶带内的最大弯曲拉应力和最大弯曲压应力分别为
Fy 1 = F y 2 =
1ห้องสมุดไป่ตู้F 6
Fa 2h
顺便指出,纵截面上弯曲切应力构成的轴向合力为
FSx = τ x ( ab) =
3.检查单元体的平衡方程是否满足
∑F ∑F
x
= 0,Fx 2 − Fx1 − FSx = = 0,Fy1 − Fy 2
y
Fa Fa Fa − − =0 h 2 h 2h F F = − =0 6 6
题 6-10 图 解:1.查№18 工字钢的有关数据 工字钢截面大致形状及尺寸符号示如图 6-10。
图 6-10 由附录 F 表 4 查得
h = 180mm,b = 94mm t = 10.7mm,I z = 1660cm 4,Wz = 185cm 3
2.计算顶边 AB 的长度改变量 顶边处有
3
σ max =
计算中用到 h1 = h / 2 − t = 79.3mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯曲应力欧阳光明(2021.03.07)6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2m KN M ⋅=75.3maxMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压) (b )m KN M m m ⋅=-60m KN M ⋅=5.67maxMPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) (c )m KN M m m ⋅=-1m KN M ⋅=1maxMPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x6-3T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知Iz=10170cm4,h1=9.65cm ,h2=15.35cm 。
解:A 截面:Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ (拉) Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ(压) E 截面Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ (拉) Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ (压) 6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。
(1) 求钢丝由于弯曲而产生的最大弯曲正应力(设钢丝处于弹性状态)(2) 若d =lmm ,材料的屈服极限s σ=700MPa ,弹性模量E=210GPa ,求不使钢丝产生残余变形的轴径D 。
解:EJM =ρ16-5 矩形悬臂梁如图示.已知l= 4 m ,32=h b ,q=10kN/m ,许用应力[σ]=10Mpa 。
试确定此梁横截面尺寸。
解:m KN ql M ⋅=⨯⨯==80410212122max6-6 20a 工字钢梁的支承和受力情况如图所示。
若[σ]=160MPa ,试求许用载荷P 。
解:3237cm W =P 32 [][]P W M 32102371016066=⨯⨯⨯=⋅=-σ (M 图) P 326-7压板的尺寸和载荷情况如图所示。
材料为 45钢,s σ=380 MPa ,取安全系数5.1=n 。
试校核压板强度。
解:2331568)121230122030(101mm W =⨯-⨯⨯= 6-8由两个槽钢组成的梁受力如图示。
已知材料的许用应力[σ]=150 MPa ,试选择槽钢号码。
解:m KN M ⋅=60max查表:(22a , 332006.217cm cm W x >=)( M 图)6-9割刀在切割工件时,受到P =1kN 的切销力的作用。
割刀尺寸如图所示。
试求割刀内最大弯曲应力。
解:m N p M ⋅=⨯⨯=-I 810836-10 图示圆木,直径为D ,需要从中切取一矩形截面梁。
试问(1)如要使所切矩形截面的抗弯强度最高,h 、b 分别为何值?(2)如要使所切矩形截面的抗弯刚度最高,h 、b 又分别为何值?解:6)(6222b D b bh W -== ∴从强度讲:D b 57735.0=∴从刚度讲D b 50.0=6-11T 字形截面的铸铁梁受纯弯曲如图示,欲使其最大压应力为最大拉应力的3倍,巳知h= 12cm ,t=3cm ,试确定其翼板宽度b 之值。
解:3max max =下上拉压y y =σσ 6-12 图示简支梁,由No.18工字钢制成,在外载荷作用下,测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε,试计算梁的最大弯曲正应力σmax 。
已知钢的弹性模量E=200GPa, a=1m 。
解:MPa E A 60100.31020049=⨯⨯⨯==-εσ(M 图)6-13 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。
解:1-1截面6-14 计算在均布载荷q =10 kN /m 作用下,圆截面简支梁的最大正应力和最大剪应力,并指出它们发生在何处。
解:232max 110108181⨯⨯⨯==ql MMPa 86.101= 在跨中点上、下边缘MPa 46.25= 在梁端,中性轴上 6-15试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。
解: MPa Wqa 60832=qa 41 KN qa Q 2.2216.294343max =⨯⨯== (Q 图)6-16 矩形截面木梁所受载荷如图示,材料的许用应力[σ]=10Mpa 。
试选择该梁的截面尺寸,设1:2:=b h(Q 图) ( M 图)解:KN R A 19=KN R B 29=6-17 试为图示外伸梁选择一工字形截面,材料的许用应力[σ]= 160MPa ,[τ]=80Mpa 。
解:[]3612510160100020cm MW =⨯⨯==σ 取16I , 3141cm W =故 取No16工字钢(Q 图) (M 图)6-18 图示起重机安装在两根工字形钢梁上,试求起重机在移动时的最危险位置及所采用工字型钢的号码。
已知 l =10 m ,a =4 m ,d=2 m 。
起重机的重量W =50 kN ,起重机的吊重P=10 kN ,钢梁材料的许用应力[σ]=160 MPa ,[τ]= 100Mpa 。
解:轻压:KN 10 ,KN 50取 a 2833215.508W cm W z =>=6-19等腰梯形截面梁,其截面高度为h 。
用应变仪测得其上边的纵向线应变611042-⨯-=ε,下边的纵向线应变621014-⨯=ε。
试求此截面形心的位置。
解:11M εσ⋅=⋅E J y b=上 6-20 简支梁承受均布载荷q ,截面为矩形h b ⨯,材料弹性模量E ,试求梁最底层纤维的总伸长。
解:22)(2qx x ql x M -= 6-21矩形截面悬臂梁受力如图(a )所示,若假想沿中性层把梁分开为上下两部分:(1)试求中性层截面上剪应力沿x 轴向的变化规律,参见图(b );(2)试说明梁被截下的部分是怎样平衡的?解:(1)bhqx A Q x 2323==τ (2)由τ产生的合力为T由弯曲产生的轴间力为Nbdy h b y ql dy b J M dy b N h h h ⎰⎰⎰=⋅=⋅⋅=2/02/02/032max 122σ(自证) 6-22 正方形截面边长为a ,设水平对角线为中性轴。
试求(1)证明切去边长为9a 的上下两棱角后,截面的抗弯模量最大;(2)若截面上的弯矩不变,新截面的最大正应力是原截面的几倍?(提示:计算Iz 时可按图中虚线分三块来处理)。
解:原来正方形:削去x 后:6-23 悬臂梁AB 受均布载荷q 及集中力P 作用如图示。
横截面为正方形a a ⨯,中性轴即正方形的对角线。
试计算最大剪应力τmax 值及其所在位置。
解:)(Q ql P +=6-24试绘出图中所示各截面的剪应力流方向,并指出弯曲中心的大致位置。
解:6-25确定开口薄壁圆环截面弯曲中心的位置。
设环的平均半径R0,壁厚t ,设壁厚t 与半径0R 相比很小。
解:ϕϕsin 00⋅⋅⋅=R t d R dS6-26试导出图示不对称工字形截面的弯曲中心位置(当在垂直于对称轴的平面内弯曲时)。
假设厚度t 与其他尺寸相比很小。
解:z J t h b e 4)2(221= 6-27 在均布载荷作用下的等强度悬臂梁,其横截面为矩形,并宽度b=常量,试求截面高度沿梁轴线的变化规律解:2022023621bh ql bh ql W M l ===σ6-28 图示变截面梁,自由端受铅垂载荷P 作用,梁的尺寸l 、b 、h 均为已知。
试计算梁内的最大弯曲正应力。
解:x P x M ⋅=)(6-29当载荷P 直接作用在跨长为l =6m 的简支梁AB 的中点时,梁内最大正应力超过容许值30%。
为了消除此过载现象,配置如图所示的辅助梁CD ,试求此梁的最小跨长a 。
解:x P Pl 270.04=⨯ 6-30 图示外伸梁由25a 号工字钢制成,跨长l=6 rn ,在全梁上受集度为q 的均布载荷作用。
当支座截面A 、B 处及跨度中央截面C 的最大正应力σ均为140MPa 时,试问外伸部分的长度及载荷集度q 等于多少?解:lqa qa ql R A 2832++= 查表:(M 图)6-31 图示悬臂梁跨长L=40cm ,集中力P =250N ,作用在弯曲中心上,梁的截面为等肢角形,尺寸如图,试绘剪应力流分布图,并计算了m ax σ和m ax τ之值。
解:444999.3957112381240mm J z =-= 6-32 圆锥形变截面悬臂梁其两端直径之比db:da =3:1,在自由端承受集中力P 作用,试求梁内的最大弯曲正应力,并将此应力与支承处的最大应力比较。
解:Px x M =)(6-33工字形截面的简支钢梁,跨度l =4m ,跨度中央受集中载荷P 作用。
如材料屈服点s σ=240MPa ,安全系数n=1.6,试按极限载荷法计算此梁的许可载荷。
解:[]2550)300(5010025)50(5020011⨯--+⨯=⨯-+⨯y y6-34 矩形截面简支梁,在跨度中央承受集中力P 。
论确定塑性区域的长度和塑性区城边界方程式()x f a =。
解:261bh W z =故 5.1=sjxM M Pl M jx 41= 故 l e 61=将s σ及a M 代入上方程:。
