根据系统结构图绘制信号流图
合集下载
2011-2结构图与信号流图
39
(3)混合节点
既有输入支点又有输出支点的节点称为混 合节点。
(4)通路
从某一节点开始，沿支路箭头方向经过各 相连支路到另一节点（或同一节点）构成的路 径，称为通路。通路中各支路传输的乘积称为 通路传输（通路增益）。
40
(5)开通路 与任一节点相交不多于一次的通路称为开通路。 (6)闭通路 如果通路的终点就是通路的起点，并且与任何 其他 节点相交不多于一次的通路称为闭通路或称为回环。 (7)回环增益 回环中各支路传输的乘积称为回环增益（或传 输）。
45
1 1
2 1 La 1 be
T11 T2 2 1 2 T Tk k k 1 abcd fd (1 be) 1 be ( f abc bef ) dg
46
例2-15
xc xc x1 x1 求：Tr ，T y ，Tr1 ，T y1 xr y xr y
……
Lm
——m个互不接触回环的传输乘积之和； k ——称为第k条通路特征式的余因子，是在
中除去
第k 条前向通路相接触的各回环传输（即将其置 零）。
44
例 2-14
T1 abcd , T2 fd
1 L1 L2 1 ( La Lb Lc ) La Lc 1 be abcdg fdg befdg 1 be ( f abc bef )dg
对于单位反馈系统，有 X c ( s) WK ( s) WB ( s) X r ( s) 1 WK ( s)
34
5.系统对给定作用和扰动作用的传递函数
原则：对于线性系统来说，可以运用叠加原理， 即对每一个输入量分别求出输出量，然后再进行 叠加，就得到系统的输出量。
(3)混合节点
既有输入支点又有输出支点的节点称为混 合节点。
(4)通路
从某一节点开始，沿支路箭头方向经过各 相连支路到另一节点（或同一节点）构成的路 径，称为通路。通路中各支路传输的乘积称为 通路传输（通路增益）。
40
(5)开通路 与任一节点相交不多于一次的通路称为开通路。 (6)闭通路 如果通路的终点就是通路的起点，并且与任何 其他 节点相交不多于一次的通路称为闭通路或称为回环。 (7)回环增益 回环中各支路传输的乘积称为回环增益（或传 输）。
45
1 1
2 1 La 1 be
T11 T2 2 1 2 T Tk k k 1 abcd fd (1 be) 1 be ( f abc bef ) dg
46
例2-15
xc xc x1 x1 求：Tr ，T y ，Tr1 ，T y1 xr y xr y
……
Lm
——m个互不接触回环的传输乘积之和； k ——称为第k条通路特征式的余因子，是在
中除去
第k 条前向通路相接触的各回环传输（即将其置 零）。
44
例 2-14
T1 abcd , T2 fd
1 L1 L2 1 ( La Lb Lc ) La Lc 1 be abcdg fdg befdg 1 be ( f abc bef )dg
对于单位反馈系统，有 X c ( s) WK ( s) WB ( s) X r ( s) 1 WK ( s)
34
5.系统对给定作用和扰动作用的传递函数
原则：对于线性系统来说，可以运用叠加原理， 即对每一个输入量分别求出输出量，然后再进行 叠加，就得到系统的输出量。
自动控制理论结构图和信号流图
R1C2 s
ui ( s )
-
-
1
R1
1
C1sห้องสมุดไป่ตู้
u (s)
1 R2C2 s 1
uo ( s )
② 16
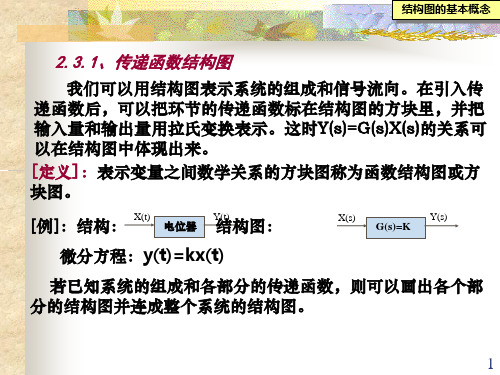
结构图等效变换例子||例2-11
R1C2 s
ui ( s ) -
1
R1
1
C1s
u (s)
1 R2C2 s 1
uo ( s )
③
R1C2 s
uo ( s )
④
ui ( s ) -
1 R1C1 s 1
[注意]： 相临的信号相加点位置可以互换；见下例
X 1 ( s) X 2 ( s)
Y ( s)
X 1 ( s)
X 3 (s)
Y ( s)
X 3 (s)
X 2 ( s)
13
比较点和分支点的移动和互换
同一信号的分支点位置可以互换：见下例
X 1 ( s)
X 2 ( s)
X ( s)
Y ( s ) G (s)
u (s) I ( s) 1 C1s
-
1
R1
I1 ( s )
I 2 ( s)
1 u ( s) C1s 1 [u ( s) uo ( s)] I 2 ( s) R2 I (s) 1 I 2 ( s) uo ( s ) C2 s
u (s)
1 R2
uo ( s )
1 C2 s
I 2 ( s)
[例2-11]利用结构图等效变换讨论两级RC串联电路的传递函数。 R1 R2
ui
i1
i, u
C1
i2
控制系统结构图与信号流图
第四节
控制系统结构图与信号流图
1
提纲：
❖ 一 、控制系统的结构图 ❖ 二、控制系统的信号流图 ❖ 三、控制系统的传递函数
2
引言：
求系统的传递函数时，需要对微分方程组 或经拉氏变换后的代数方程组进行消元。而 采用结构图或信号流图，更便于求取系统的 传递函数，还能直观地表明输入信号以及各 中间变量在系统中的传递过程。因此，结构 图和信号流图作为一种数学模型，在控制理 论中得到了广泛的应用。
J s2 Bs
(f)
Eb (s) Kesm (s) (g)
c
(s)
1
i
m
(s)
(h)
图2-27 式(2.80)(e)~(h)子方程框图
10
按系统中各元件的相互关系，分清各输入量和输出量， 将各结构图正确地连接起来（图2-28）。
图2-28 位置随动系统结构图
11
略去La，系统结构图如图2-29所示：
8
Ia
(s)
U
a (s) La s
Eb (s) Ra
(2.80)(a)
e(s) r(s)c(s)
(b)
Us(s) Kse(s)
(c)
Ua (s) KaU s (s)
(d)
图2-27 式(2.80)(a)~(d)子方程框图
9
M d (s) KmIa (s) (e)
m(s)
M d(s) M L(s)
3
一 、控制系统的结构图
（一 ）结构图的概念 图2-24 RC网络的微分方程式为:
1
ur Ri C idt
uc
1 C
idt
也可写为:
uc
1 C
ห้องสมุดไป่ตู้ idt
控制系统结构图与信号流图
1
提纲：
❖ 一 、控制系统的结构图 ❖ 二、控制系统的信号流图 ❖ 三、控制系统的传递函数
2
引言：
求系统的传递函数时，需要对微分方程组 或经拉氏变换后的代数方程组进行消元。而 采用结构图或信号流图，更便于求取系统的 传递函数，还能直观地表明输入信号以及各 中间变量在系统中的传递过程。因此，结构 图和信号流图作为一种数学模型，在控制理 论中得到了广泛的应用。
J s2 Bs
(f)
Eb (s) Kesm (s) (g)
c
(s)
1
i
m
(s)
(h)
图2-27 式(2.80)(e)~(h)子方程框图
10
按系统中各元件的相互关系，分清各输入量和输出量， 将各结构图正确地连接起来（图2-28）。
图2-28 位置随动系统结构图
11
略去La，系统结构图如图2-29所示：
8
Ia
(s)
U
a (s) La s
Eb (s) Ra
(2.80)(a)
e(s) r(s)c(s)
(b)
Us(s) Kse(s)
(c)
Ua (s) KaU s (s)
(d)
图2-27 式(2.80)(a)~(d)子方程框图
9
M d (s) KmIa (s) (e)
m(s)
M d(s) M L(s)
3
一 、控制系统的结构图
（一 ）结构图的概念 图2-24 RC网络的微分方程式为:
1
ur Ri C idt
uc
1 C
idt
也可写为:
uc
1 C
ห้องสมุดไป่ตู้ idt
结构图与信号流图
C(s) R(s) G(s) Q(s) G(s)
(5) 引出点的移动
(1) 引出点前移
R (s)
G (s )
C (s)
C (s)
C(s) = R(s)G(s)
R (s)
G (s ) G (s )
C (s) C (s)
C(s) = R(s)G(s)
（2) 引出点后移
R (s) G (s )
C (s) R (s)
R (s ) -
G 1(s )
C (s)
G 23 (s )
HH11((ss))
G23(s) =
1+
G 2(s )G 3(s )G 4 (s ) G3(s)G4(s)H 3(s) + G2(s)G3(s)H 2(s)
F(s) = C (s) =
G 1(s )G 23 (s )
R (s) 1 + G1(s)G23(s)H1(s)
2-3 结构图与信号流图
引言 一、结构图的基本单元和等效规则 二、信号流图的组成和性质 三、信号流图的绘制 四、Mason公式 五、闭环系统的传递函数
1
引言
何谓结构图
由单向运算框图和信号流向线组成的描写一般系统中 信号传递关系的定量分析图形。
何谓信号流图 由单向增益支路和节点运算框图和信号流向线组成的
V3 dV1 kV2
f
m
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
h
Ⅳ
C
V1 d Ⅴ e V2 1
g
以R为输入，V2为输出则可整理成下列方程
1 m 0 l V1 b
g
1 h
e V2
f
R
d k 1 V3 0
(5) 引出点的移动
(1) 引出点前移
R (s)
G (s )
C (s)
C (s)
C(s) = R(s)G(s)
R (s)
G (s ) G (s )
C (s) C (s)
C(s) = R(s)G(s)
（2) 引出点后移
R (s) G (s )
C (s) R (s)
R (s ) -
G 1(s )
C (s)
G 23 (s )
HH11((ss))
G23(s) =
1+
G 2(s )G 3(s )G 4 (s ) G3(s)G4(s)H 3(s) + G2(s)G3(s)H 2(s)
F(s) = C (s) =
G 1(s )G 23 (s )
R (s) 1 + G1(s)G23(s)H1(s)
2-3 结构图与信号流图
引言 一、结构图的基本单元和等效规则 二、信号流图的组成和性质 三、信号流图的绘制 四、Mason公式 五、闭环系统的传递函数
1
引言
何谓结构图
由单向运算框图和信号流向线组成的描写一般系统中 信号传递关系的定量分析图形。
何谓信号流图 由单向增益支路和节点运算框图和信号流向线组成的
V3 dV1 kV2
f
m
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
h
Ⅳ
C
V1 d Ⅴ e V2 1
g
以R为输入，V2为输出则可整理成下列方程
1 m 0 l V1 b
g
1 h
e V2
f
R
d k 1 V3 0
控制系统结构图与信号流图
如图2-39所示。n个传递函数依次串联的等效传递函数， 等于n个传递函数的乘积。
（2）并联连接的等效变换 G1(s)与G2(s)两个环节并联连接，其等效传递函数等于
该两个传递函数的代数和，即：
G(s)= G1(s)±G2(s)
(2.82)
等效变换结果见图2-40(b)。
18
图2-40
n个传递函数并联其等效传递函数为该n个传递函数的代 数和，如图2-41所示：
5
图2-25 RC网络的结构图
结构图：根据由微分方程组得到的拉氏变换方程组，对 每个子方程都用上述符号表示，并将各图形正确地连接 起来，即为结构图，又称为方框图。
结构图也是系统的一种数学模型，它实际上是数学模型 的图解化 。
6
（二）系统结构图的建立 建立系统的结构图，其步骤如下： （1）建立控制系统各元部件的微分方程。
图2-29 La=0的位置随动系统结构图
12
例2.2 试绘制图2-30所示无源网络的结构图。
图2-30 例2.3网络图
图2-31 例2.3网络的结构图
解：ur为网络输入，uc为网络输出。
一个系统的结构图不是唯一的，但经过变换求得的总 传递函数都应该是相同的。上例所示网络的结构图还可 用图2-32表示。
第四节
控制系统结构图与信号流图
1
提纲：
❖ 一 、控制系统的结构图 ❖ 二、控制系统的信号流图 ❖ 三、控制系统的传递函数
2
引言：
求系统的传递函数时，需要对微分方程组 或经拉氏变换后的代数方程组进行消元。而 采用结构图或信号流图，更便于求取系统的 传递函数，还能直观地表明输入信号以及各 中间变量在系统中的传递过程。因此，结构 图和信号流图作为一种数学模型，在控制理 论中得到了广泛的应用。
自动控制
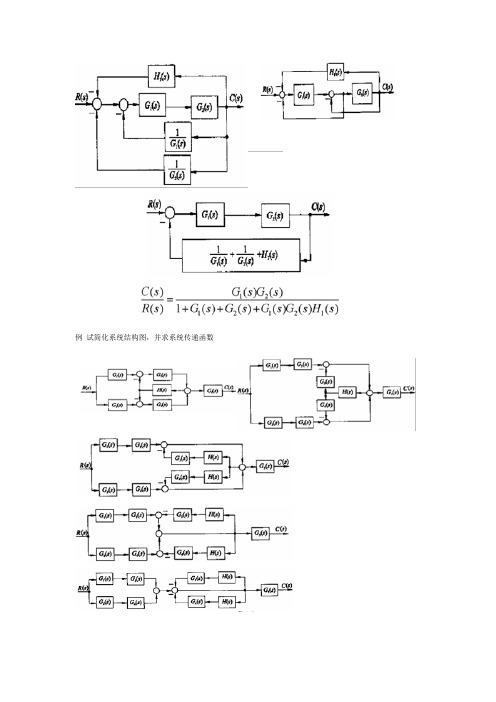
例试简化系统结构图，并求系统传递函数3、信号流图的组成及性质(1)、信号流图的组成：由节点和支路组成的一种信号传递网络。
A、节点：即变量，用小圆圈表示，为流向该节点的信号的代数和。
B、支路：定向线段，标支路增益，相当于乘法器，表因果关系。
(2)、信号流图的性质A、节点标志系统的变量；B、支路相当于乘法器；C、信号沿箭头单向传递；D、系统的信号流图不是惟一的。
下图为典型的信号流图(3)、常用术语源节点（或输入节点）：只有输出支路而没有输入支路的节点，如图中的节点X1 。
阱节点（或输出节点）：只有输出支路而没有输入支路的节点，如图中的节点X5 。
混合节点：既有输入支路又有输出支路的节点，如图中的节点X2X3X4X5。
前向通路：信号从输入节点到输出节点传递时，每个节点只通过一次的通路。
从源节点X1到阱节点X5，共有两条前向通路：一条是X1－＞X2－＞X3－＞X4－＞X5，其前向通路总增益P1＝abc；另一条是X1－＞X2－＞X5，其前向通路总增益P2=d。
回路：起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路。
X2－＞X3－＞X2，其回路增益L1=ae，X3－＞X4－＞X3其回路增益L2=bf；X5－＞X5 的自回路，其回路增益是g。
不接触回路：回路之间没有公共节点时，这种回路叫做不接触回路。
一对X5－＞X5 是和X2－＞X3－＞X2；另一对是X5－＞X5和X3－＞X4－＞X3。
4、信号流图的绘制(1)由系统微分方程绘制信号流图微分方程先拉氏变换，指定系统变量，按因果关系排列，连成信号流图。
下面结合示例说明：例试绘制RC无源网络的信号流图。
设电容初始电压为U1(0)。
解由基尔霍夫定律，列写微分方程式如下：各微分方程式进行拉氏变换，则有对变量Ui(s)，Ui(s)-U0(s)，I1(s)，I2(s)，I(s)，U0(s)及U1(0)分别设置七个节点；然后，用相应增益的支路将个节点连接起来，便得到RC无源网络的信号流图。
自动控制原理第2章(2)
(3) 按信号流向将各框图连起来
Ur(s) + _ I1(s) 1/R1
Uc(s)
华中科技大学文华学院机电学部 自动控制理论
控制系统的结构图与信号流图
方框图等效变换 基本连接方式：串联、并联、反馈 基本连接方式：串联、并联、
1.串联方框的等效变换 1.串联方框的等效变换
R(s) C(s) G1(s) G2(s) R(s) C(s) G1(s) G2(s)
华中科技大学文华学院机电学部 自动控制理论
控制系统的结构图与信号流图
例3 试化简如下系统结构图，并求传递函数C(s)/R(s) 试化简如下系统结构图，并求传递函数C(s)/R(s)
H2(s) R(s)
_ _
G1(s)
G2(s)
_
G3(s) H3(s)
G4(s)
C(s)
H1(s)
解：①将G3(s)输出端的分支点后移得： (s)输出端的分支点后移得： 输出端的分支点后移得
x1 = xr gxc x2 = ax1 fx4 x3 = bx2 exc x4 = cx3 xc = dx4
xr x1
a x2 b -f
x3 c
-g
x4 d
-e
xc
华中科技大学文华学院机电学部 自动控制理论
控制系统的结构图与信号流图
2、由系统结构图绘制信号流图 在结构图的信号线上用小圆圈标志出传递的信号， ①在结构图的信号线上用小圆圈标志出传递的信号，得到节点 用标有传递函数的线段代替结构图中的方框， ②用标有传递函数的线段代替结构图中的方框，得到支路
G(s) H(s)
R(s)
C(s) G(s) 1m G(s)H(s)
化简一般方法：移动分支点或相加点 化简一般方法： 交换相加点 合并
控制系统的结构图与信号流图
2-3 控制系统的结构图与信号流图
控制系统的结构图和信号流图：描述系统各元部件之间的信号传 递关系的一种图形化表示，特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成：（1）信号线； （2）引 出点（或测量点）；（3）比较点（或信号综合点）表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构： L( s ) r m ( s )
测量电位器：
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上，而且信号通过每个节点不多 于一次的闭合通路（单独回路）。 •不接触回路 回路之间没有公共节点时，该回路称为不接触回路。
信号流图的绘制
（1）由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积，记为 H(s)
开环传递函数：反馈引入点断开时，输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积，记为GK(s), GK(s)=G(s)H(s) E (s) C (s)
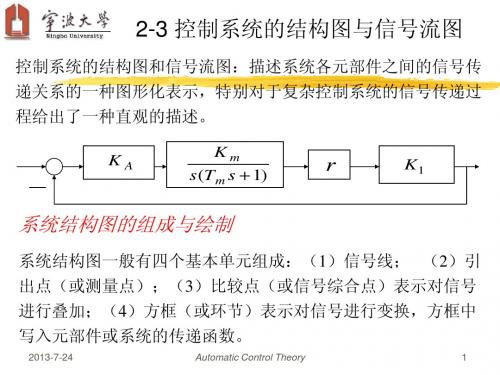
控制系统的结构图和信号流图：描述系统各元部件之间的信号传 递关系的一种图形化表示，特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成：（1）信号线； （2）引 出点（或测量点）；（3）比较点（或信号综合点）表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构： L( s ) r m ( s )
测量电位器：
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上，而且信号通过每个节点不多 于一次的闭合通路（单独回路）。 •不接触回路 回路之间没有公共节点时，该回路称为不接触回路。
信号流图的绘制
（1）由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积，记为 H(s)
开环传递函数：反馈引入点断开时，输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积，记为GK(s), GK(s)=G(s)H(s) E (s) C (s)