欧拉公式的证明(整理)Word版
欧拉公式的几何证明

欧拉公式的几何证明
嘿呀,咱来说说欧拉公式的几何证明哈!欧拉公式那可是超级厉害的,就是e^(iθ)=cosθ+isinθ。
比如说吧,就像我们在生活中遇到一个特别复杂的迷宫,你觉得很难走出去,但是突然有了一条神奇的线索,一下子就豁然开朗啦!这欧拉公式就有点像这样神奇的线索!
我们来想想看哈,cosθ和sinθ 多熟悉啊,它们就像是我们的老朋友,在三角函数的世界里经常碰面。
然后呢,e^(iθ)就像是突然冒出来的神秘嘉宾,但它其实和我们的老朋友有着紧密的联系呢!
比如说,当θ=π的时候,e^(iπ)=-1,哇塞,这不是很神奇吗?就好像你原本以为不相干的几样东西,突然之间发现它们有着如此紧密而奇妙的关联,是不是特别有意思呀!这就是欧拉公式的魅力所在呀!你难道不觉得很惊叹吗!。
欧拉函数证明过程

欧拉函数证明过程
欧拉函数是一个重要的数论函数,用来计算小于或等于某个正整数n 的所有与n互质的正整数的个数。
欧拉函数记作φ(n),其定义为:
φ(n) = |{k∈N|1≤k≤n且gcd(k,n)=1}|
其中,gcd(k,n)表示k和n的最大公约数。
欧拉函数的证明过程如下:
1. 先证明当n是质数时,φ(n)=n-1。
证明:对于任意一个质数n,小于或等于n的正整数中,只有1和n本身与n不互质。
其余的n-1个数(2,3,...,n-1)都与n互质。
因此,φ(n)=n-1。
2. 再证明当n=p^k(p为质数,k为正整数)时,φ(n)=p^k-p^(k-1)。
证明:根据算术基本定理,n=p^k可以唯一分解为p的k次幂的形式。
那么小于或等于n的正整数中,与n不互质的数就是p的所有非零次幂,共有p^(k-1)个。
其余的p^k-p^(k-1)个数都与n互质。
因此,φ(n)=p^k-p^(k-1)。
3. 对于一般的正整数n,利用算术基本定理,将n分解为不同质数的幂的乘积:n=p_1^(k_1)*p_2^(k_2)*...*p_r^(k_r)。
根据乘法函数的性质,有:
φ(n)=φ(p_1^(k_1))*φ(p_2^(k_2))*...*φ(p_r^(k_r))
=(p_1^(k_1)-p_1^(k_1-1))*(p_2^(k_2)-p_2^(k_2-1))*...*(p_r^(k_r)-p_r^(k_r-1))
这就是著名的欧拉函数计算公式。
通过上述三步,我们就完整地证明了欧拉函数的计算方法。
(完整word版)球面三角形的面积与欧拉公式

§6 球面三角形的面积与欧拉公式问题提出1.如何计算球面三角形的面积?球面三角形面积与平面三角形面积有什么区别?2.如何利用球面三角形面积公式证明球面多面体的欧拉公式?3.如何利用球面知识证明简单多面体的欧拉公式?6.1球面二角形与三角形的面积我们知道,若球面半径为R ,则球面面积为24S R π=,现在考虑球面上的一个小区域:球面上由两个大圆的半周所围成的较小部分叫做一个球面二角形。
如图所示,大圆半周PAP '和PBP '所围成的阴影部分就是一个球面二角形。
显然P 和P '是对径点,大圆半周'PAP 和'PBP 称为球面二角形的边。
球面角P P '∠=∠称为球面二角形的夹角。
如果大圆弧AB 以P 和P '为极点,AB 所对的球心角为α,则P P '∠=∠=α。
例1 计算地球上一个时区所占有的面积。
解 如图所示,设O 为地心,N 、S 为北极点和南极点,A 、B 为赤道上两点,且15AOB ∠=,地球半径为R=6400km ,根据地理知识,地球共分为24个时区,一个时区跨越地球表面15,所以由经线NAS 与经线NBS 围成的二角形就是一个时区,它所占面积为地球表面积的15136024=, 即 22241640021446605.85246R km ππ=⨯⨯≈ 如何计算一般球面二角形的面积?1. 二角形的夹角α,就是平面PA P '与PB P '所夹的二面角的平面角;2. 这个二角形可以看成半个大圆PAP '绕直径P P '旋转α角所生成;3. 球面二角形的面积与其夹角成比例。
设这个二角形得面积为U ,则42U αππ=即 2U α=抽象概括:球面上,夹角为α的二角形的面积为2U α=。
如何计算球面三角形的面积?设()S ABC 表示球面三角形ABC 的面积,1. 对球面三角形ABC ,分别画出三条边所在的大圆。
欧拉公式19种证明

欧拉公式19种证明欧拉公式是数学中的一个重要公式,它的表达式为e^(ix)=cos(x)+i*sin(x),其中e表示自然对数的底数2.71828…,i表示虚数单位。
欧拉公式有多种证明方法,下面我们将介绍其中19种常见的证明方法。
1. 泰勒级数证明法:利用泰勒级数展开式展开e^(ix)和cos(x)+i*sin(x),然后将它们相等的系数进行比较,即可得出欧拉公式。
2. 复合函数证明法:将e^(ix)看作复数函数f(x)=e^x,将cos(x)和sin(x)看作f(x)的实部和虚部,则有f(ix)=cos(x)+i*sin(x),即e^(ix)=cos(x)+i*sin(x)。
3. 微积分证明法:将欧拉公式两边分别对x求导,得到ie^(ix)=-sin(x)+i*cos(x),再将其两边同时乘以i,即可得到欧拉公式。
4. 积分证明法:将欧拉公式两边同时积分,得到e^(ix)/i=-sin(x)/i+cos(x),再将其两边同时乘以i,即可得到欧拉公式。
5. 欧拉级数证明法:将e^(ix)和cos(x)+i*sin(x)的泰勒级数展开式进行对比,即可得到欧拉公式。
6. 幂级数证明法:将e^(ix)和cos(x)+i*sin(x)的幂级数展开式进行对比,即可得到欧拉公式。
7. 矩阵证明法:构造一个2x2矩阵,使其特征值为e^(ix)和e^(-ix),然后求解该矩阵的本征向量,即可得到欧拉公式。
8. 矩阵幂证明法:将e^(ix)表示为矩阵的形式,然后对该矩阵进行幂运算,即可得到欧拉公式。
9. 极限证明法:将e^(ix)表示为极限的形式,然后通过极限的性质推导出欧拉公式。
10. 解微分方程证明法:将e^(ix)看作微分方程y'=iy的解,并利用欧拉公式将其转化为y=cos(x)+i*sin(x),即可得到欧拉公式。
11. 解偏微分方程证明法:将e^(ix)看作偏微分方程u_t+iu_x=0的解,并利用欧拉公式将其转化为u=cos(x-t)+i*sin(x-t),即可得到欧拉公式。
证明欧拉公式

证明欧拉公式欧拉公式简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2这个公式叫欧拉公式。
公式描述了简单多面体顶点数、面数、棱数特有的规律。
认识欧拉欧拉,瑞士数学家,13岁进巴塞尔大学读书,得到著名数学家贝努利的精心指导.欧拉是科学史上最多产的一位杰出的数学家,他从19岁开始发表论文,直到76岁,他那不倦的一生,共写下了886本书籍和论文,其中在世时发表了700多篇论文。
彼得堡科学院为了整理他的著作,整整用了47年。
欧拉著作惊人的高产并不是偶然的。
他那顽强的毅力和孜孜不倦的治学精神,可以使他在任何不良的环境中工作:他常常抱着孩子在膝盖上完成论文。
即使在他双目失明后的17年间,也没有停止对数学的研究,口述了好几本书和400余篇的论文。
当他写出了计算天王星轨道的计算要领后离开了人世。
欧拉永远是我们可敬的老师。
欧拉研究论著几乎涉及到所有数学分支,对物理力学、天文学、弹道学、航海学、建筑学、音乐都有研究!有许多公式、定理、解法、函数、方程、常数等是以欧拉名字命名的。
欧拉写的数学教材在当时一直被当作标准教程。
19世纪伟大的数学家高斯(Gauss,1777-1855)曾说过“研究欧拉的著作永远是了解数学的最好方法”。
欧拉还是数学符号发明者,他创设的许多数学符号,例如π,i,e,sin,cos,tg,∑,f (x)等等,至今沿用。
欧拉不仅解决了彗星轨迹的计算问题,还解决了使牛顿头痛的月离问题。
对著名的“哥尼斯堡七桥问题”的完美解答开创了“图论”的研究。
欧拉发现,不论什么形状的凸多面体,其顶点数V、棱数E、面数F之间总有关系V+F-E=2,此式称为欧拉公式。
V+F-E即欧拉示性数,已成为“拓扑学”的基础概念。
那么什么是“拓扑学”?欧拉是如何发现这个关系的?他是用什么方法研究的?今天让我们沿着欧拉的足迹,怀着崇敬的心情和欣赏的态度探索这个公式......欧拉定理的意义(1)数学规律:公式描述了简单多面体中顶点数、面数、棱数之间特有的规律(2)思想方法创新:定理发现证明过程中,观念上,假设它的表面是橡皮薄膜制成的,可随意拉伸;方法上将底面剪掉,化为平面图形(立体图→平面拉开图)。
(word完整版)用欧拉公式证明只有五种正多面体
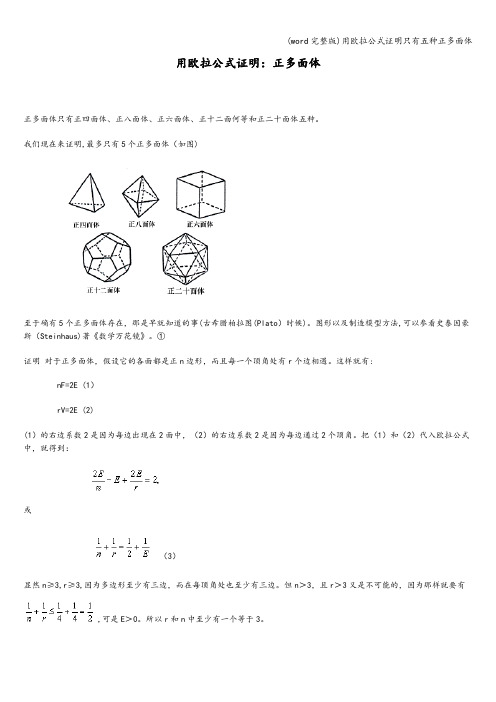
用欧拉公式证明:正多面体
正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。
我们现在来证明,最多只有5个正多面体(如图)
至于确有5个正多面体存在,那是早就知道的事(古希腊柏拉图(Plato)时候)。
图形以及制造模型方法,可以参看史泰因豪斯(Steinhaus)著《数学万花镜》。
①
证明对于正多面体,假设它的各面都是正n边形,而且每一个顶角处有r个边相遇。
这样就有:
nF=2E (1)
rV=2E (2)
(1)的右边系数2是因为每边出现在2面中,(2)的右边系数2是因为每边通过2个顶角。
把(1)和(2)代入欧拉公式中,就得到:
或
(3)
显然n≥3,r≥3,因为多边形至少有三边,而在每顶角处也至少有三边。
但n>3,且r>3又是不可能的,因为那样就要有 ,可是E>0。
所以r和n中至少有一个等于3。
设n=3,那末,因此r=3,4,5,由是E=6,12,30,而F=4,8,20,这就给出了正四面体,正八面体和正二十面体。
设r=3,那末,因此n=3,4,5,由是E=6,12,30,而F=4,6,12,这就给出了正四面体,正六面体(即立方体)和正十二面体.。
欧拉公式

方法一是不严格的。
再 请看这2个积分
∫sqrt(x^2-1)dx=x*sqrt(x^2-1)/2-ln(2*sqrt(x^2-1)+2x)/2
∫sqrt(1-x^2)dx=arcsin(x)/2+x*sqrt(1-x^2)/2;
上式左边相当于下式左边乘以i
于是上式右边相当于下式右边乘以i
u'(θ)=logae 4
4取积分有:
T=(logae)*θ+Ψ 5
θ→0时,t=limt=Ψ,带入3有:
a^(iΨ)=1 即:
Ψ=0 6
6代入5有:
T=(logae)*θ 7
7代入3有:
[a^(logae)]^(iθ)=cosθ+isinθ 化简得欧拉公式:
方法一:用幂级数展开形式证明,但这只是形式证明(严格的说,在实函数域带着i只是形式上的) (就是q239urju空间里的那个)
再抄一遍: 设z = x+iy 这样 e^z = e^(x+iy)=e^x*e^(iy),就是e^z/e^x = e^(iy)
用牛顿幂级数展开式
e^x = 1+x+x^2/2!+x^3/3!+.....+x^n/n!+......
把 e^(iy) 展开,就得到
e^z/e^x = e^(iy)
=1+iy-y^2/2!-iy^3/3!+y^4/4!+iy^5/5!-y^6/6!-.....
=(1-y^2/2!+y^4/4!-y^6/6!+.....)
+i(y-y^3/3!+y^5/5!-....)
欧拉公式证明

多面体欧拉定理:定理简单多面体的顶点数V、棱数E及面数F间有关系对于简单多面体,有著名的欧拉公式:V-E+F=2简单多面体即表面经过连续变形可以变为球面的多面体。
欧拉定理:定理简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2;公式描述了简单多面体中顶点数、面数、棱数之间特有的规律。
定理的证明:分析:以四面体ABCD为例。
将它的一个面BCD去掉,再使它变为平面图形,四面体的顶点数V、棱数E与剩下的面数F1变形后都没有变(这里F1=F-1)。
因此,要研究V、E 和F的关系,只要去掉一个面,将它变形为平面图形即可。
只需平面图形证明:V+F1-E=1;(1)去掉一条棱,就减少一个面,V+F1-E的值不变。
例如去掉BC,就减少一个面ABC。
同理,去掉棱CD、BD,也就各减少一个面ACD、ABD,由于V、F1-E的值都不变,因此V+F1-E的值不变;(2)再从剩下的树枝形中,去掉一条棱,就减少一个顶点,V+F1-E的值不变。
例如去掉CA,就减少一个顶点C。
同理去AD就减少一个顶点D,最后剩下AB。
在以上变化过程中,V+F1-E的值不变,V+F1-E=2-0-1=1,所以 V+F-E= V+F1-E+1=2。
对任意的简单多面体,运用这样的方法,都是只剩下一条线段。
公式对任意简单多面体都是正确的。
欧拉定理又一证法:多面体,设顶点数V,面数F,棱数E。
剪掉一个面,将其余的面拉平,使它变为平面图形,我们在两个图中求所有面的内角总和Σα。
一方面,利用面求内角总和。
设有F个面,各面的边数分别为n1,n2,…,nF,各面的内角总和为:Σα = [(n1-2)•180+(n2-2)•180+…+(nF-2)•180] = (n1+n2+…+nF -2F)•180 =(2E-2F)•180= (E-F)•360(1)另一方面,在拉开图中,利用顶点来求内角总和。
设剪去的一个面为n 边形,其内角和为(n-2)•180,则所有V个顶点中,有n个顶点在边上,V-n个顶点在中间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欧拉公式的证明
著名的欧拉公式e^(iθ)=cosθ+isinθ是人们公认的优美公式。
原因是指数函数和三角函数在实数域中几乎没有什么联系,而在复数域中却发现了他们可以相互转化,并被一个非常简单的关系式联系在一起。
特别是当θ=π时,欧拉公式便写成了e^(iπ)+1=0,就这个等式将数中最富有特色的五个数0,1,i , e , π ,绝妙地联系在一起
方法一:用幂级数展开形式证明,但这只是形式证明(严格的说,在实函数域带着i只是形式上的)
再抄一遍:设z = x+iy 这样 e^z = e^(x+iy)=e^x*e^(iy),就是e^z/e^x = e^(iy)
用牛顿幂级数展开式
e^x = 1+x+x^2/2!+x^3/3!+.....+x^n/n!+......
把 e^(iy) 展开,就得到
e^z/e^x = e^(iy)
=1+iy-y^2/2!-iy^3/3!+y^4/4!+iy^5/5!-y^6/6!-.....
=(1-y^2/2!+y^4/4!-y^6/6!+.....)
+i(y-y^3/3!+y^5/5!-....)
由于 cosy = 1-y^2/2!+y^4/4!-y^6/6!+.....,
siny = y-y^3/3!+y^5/5!-....
所以 e^(x+iy)=e^x*e^(iy)=e^x*(cosy+isiny)
即 e^(iy) = (cosy+isiny)
方法二:见复变函数第2章,在整个负数域内重新定义了sinz cosz而后根据关系推导出了欧拉公式。
着个才是根基。
由来缘于此。
方法一是不严格的。
再请看这2个积分
∫sqrt(x^2-1)dx=x*sqrt(x^2-1)/2-ln(2*sqrt(x^2-1)+2x)/2
∫sqrt(1-x^2)dx=arcsin(x)/2+x*sqrt(1-x^2)/2;
上式左边相当于下式左边乘以i
于是上式右边相当于下式右边乘以i
然后化简就得到欧拉公式
这个证明方法不太严密
但很有启发性
历史上先是有人用上述方法得到了对数函数和反三角函数的关系
然后被欧拉看到了,才得到了欧拉公式
设a t θ ЄR,ρЄR+,a^(it)Єz有:
a^(it)=ρ(cosθ+isinθ) 1
因共轭解适合方程,用-i替换i有:
a^(-it)=ρ(cosθ-isinθ) 2
由1,2得ρ=1,点P[a^(it)]在单位圆上,a^(it)可表达为:
a^(it)=cosθ+isinθ 3
设t=u(θ),对3微商有:
[a^(it)]*(lna)*u'(θ)*i=-sinθ+icosθ 整理有:
[a^(it)]*(lna)*u'(θ)*i=(cosθ+isinθ)(cosπ/2+isinπ/2)约去a^(it)有: u'(θ)=logae 4
4取积分有:
T=(logae)*θ+Ψ 5
θ→0时,t=limt=Ψ,带入3有:
a^(iΨ)=1 即:
Ψ=0 6
6代入5有:
T=(logae)*θ 7
7代入3有:
[a^(logae)]^(iθ)=cosθ+isinθ 化简得欧拉公式:
e^(iθ)=cosθ+isinθ
(后两者才是真正让我震惊的!!!!)。
