衍射光强分布测量实验报告
光强衍射实验报告

1. 观察并验证单缝衍射和多缝衍射的图样及其规律。
2. 理解衍射光强分布的原理,并掌握相关计算方法。
3. 掌握衍射实验装置的组装与调整。
二、实验原理光的衍射现象是光的波动性的一种表现。
当光波遇到障碍物或孔径时,会发生衍射现象,即光波绕过障碍物传播。
根据障碍物与波长的相对大小,衍射现象可分为单缝衍射和多缝衍射。
1. 单缝衍射:当光波通过单缝时,会发生衍射现象,形成一系列明暗相间的衍射条纹。
根据惠更斯-菲涅尔原理,衍射光强分布公式为:\[ I(\theta) = I_0 \left(\frac{\sin(\beta)}{\beta}\right)^2 \]其中,\( I(\theta) \)为衍射角为\(\theta\)处的光强,\( I_0 \)为入射光强,\(\beta\)为衍射角。
2. 多缝衍射:当光波通过多个狭缝时,会发生多缝衍射现象。
多缝衍射的光强分布与单缝衍射类似,但衍射条纹间距和强度分布有所不同。
多缝衍射的光强分布公式为:\[ I(\theta) = I_0 \left(\frac{\sin(\beta)}{\beta}\right)^2\frac{\cos^2(\alpha)}{\sin^2(\alpha)} \]其中,\(\alpha\)为相邻狭缝之间的夹角。
三、实验仪器与装置1. 激光器:用于产生单色光。
2. 单缝装置:用于产生单缝衍射。
3. 多缝装置:用于产生多缝衍射。
4. 光屏:用于观察衍射条纹。
5. 摄像头:用于记录衍射条纹图像。
6. 计算机软件:用于数据处理和分析。
1. 组装实验装置,确保激光器、单缝装置、多缝装置和光屏的位置正确。
2. 打开激光器,调整光束方向,使其垂直照射到单缝装置上。
3. 观察并记录单缝衍射条纹,使用摄像头记录图像。
4. 调整多缝装置,观察并记录多缝衍射条纹,使用摄像头记录图像。
5. 使用计算机软件对衍射条纹图像进行处理和分析,计算衍射条纹间距和光强分布。
大学光强分布实验报告

一、实验目的1. 理解光强分布的基本原理,掌握光强分布的测量方法。
2. 观察并分析单缝衍射和多缝衍射的光强分布规律。
3. 利用衍射光强分布公式计算单缝的缝宽。
二、实验原理光的衍射是指光波遇到障碍物或通过狭缝时,发生偏离直线传播的现象。
根据衍射光束与障碍物或狭缝的距离关系,衍射现象可分为夫琅禾费衍射和费涅耳衍射。
本实验主要研究夫琅禾费衍射。
1. 单缝衍射当单缝的宽度与光的波长大致相等时,光通过单缝后会发生衍射,形成明暗相间的衍射条纹。
单缝衍射的光强分布公式为:\[ I = I_0 \left( \frac{\sin \beta}{\beta} \right)^2 \]其中,\( I \) 为衍射条纹的光强,\( I_0 \) 为中央亮条纹的光强,\( \beta \) 为衍射角。
2. 多缝衍射当多缝的宽度与光的波长相比很小时,光通过多缝后会发生多缝衍射,形成明暗相间的衍射条纹。
多缝衍射的光强分布公式为:\[ I = I_0 \left( \frac{\sin \beta}{\beta} \right)^2 \left( \frac{\sin\beta_1}{\beta_1} \right)^2 \left( \frac{\sin \beta_2}{\beta_2}\right)^2 \ldots \]其中,\( I \) 为衍射条纹的光强,\( I_0 \) 为中央亮条纹的光强,\( \beta \) 为衍射角,\( \beta_1, \beta_2, \ldots \) 为各缝的衍射角。
三、实验仪器与设备1. 激光器:提供单色光源。
2. 单缝衍射装置:包括狭缝、透镜、光屏等。
3. 多缝衍射装置:包括狭缝、透镜、光屏等。
4. 自动光强记录仪:记录衍射光强分布。
5. 计算机及软件:处理实验数据。
四、实验步骤1. 将激光器、单缝衍射装置和光屏放置在光学导轨上,调整光路,使激光束垂直照射到单缝上。
2. 打开激光器,观察单缝衍射条纹的形状、亮暗程度及间距。
单缝衍射光强的分布测量实验报告

竭诚为您提供优质文档/双击可除单缝衍射光强的分布测量实验报告篇一:衍射光强分布测量衍射光强分布测量***,物理学系摘要:本实验利用激光为光源研究激光经过单缝与单丝时的衍射光强度分布情况。
激光的高准直性符合夫琅和费远场条件,且高单色性保证测量时没有不同波长光的叠加影响。
光感应器方面使用光栅尺与电脑连接做0.02毫米/点的高精度自动扫描。
通过巴比涅原理迂回得到了没有直射光时单丝的衍射光强分布,完整验证了运用衍射光强分布来测量小微物体的长度的方法和可行性,并实际运用此法测量了铜丝和头发丝的直径。
关键词:衍射分布巴比涅原理单缝直径测量ThemeasurementoftheDistributionofLightDiffraction YixiongKeYiLin,DepartmentofphysicsAbstarct:Thisexperimentmadeuseoflaserasthelightsourcetoverif yaseriesofdiffractionpatternsof633nmlaserviadiffere ntsingleslitsandmonofilaments.Thecollimationfeature ofthelasermeetstheconditionofFraunhoferdiffraction, themonochromicfeatureoflaserprovideabetterexperimen talenvironmentthatthediffractionpatternwon`tbeinter ferebythelightofotherwavelength.weuselinearencorder connectedtopcviauLI(universalLaboratoryInterface)as thesensortoautomaticallyscanthediffractionpatternwi ththeratioof0.02mmperdot.weusebabinet’sprincipletogetthediffractionpatternofamonofilament p letelyverifiedthemethodandfeasibilityofmeasuringati nyobjectwithitsdiffractionpattern.Inaddition,wetryt omeasurethediameterofacopperwireandpeople’shairinthiswayKeywords:Diffractiondistributionbabinet`sprinciplesingleslitsmeasureDiameterofthewire1一、引言衍射是波遇到障碍物时便利直线传播的现象。
光强分布的测量实验报告

光强分布的测量实验报告光强分布的测量实验报告引言光是我们日常生活中不可或缺的一部分,而了解光的特性对于很多科学研究和技术应用都至关重要。
光强分布是指光在空间中的强度变化情况,它对于光的传播和衍射现象有着重要影响。
本实验旨在通过测量光强分布,深入了解光的特性,并探索光在不同介质中的传播规律。
实验方法1. 实验器材准备为了测量光强分布,我们需要准备以下器材:激光器、光电二极管、光屏、光强测量仪等。
2. 实验设置将激光器置于实验室中央,调整其位置和角度,使得激光束尽可能垂直地照射到光屏上。
在激光束出射方向上放置光电二极管,并将其连接到光强测量仪上。
3. 实验步骤a. 打开激光器,并调整其功率,使得激光束的强度适中。
b. 将光屏放置在激光束的传播路径上,确保激光束能够均匀地照射到光屏上。
c. 将光电二极管放置在离光屏一定距离的位置上,并将其与光强测量仪连接好。
d. 打开光强测量仪,并进行校准。
e. 将光电二极管沿着光屏上的一条直线移动,同时记录下每个位置对应的光强数值。
f. 重复以上步骤,改变光屏和光电二极管的相对位置,测量不同条件下的光强分布。
实验结果与讨论通过实验测量,我们得到了不同位置处的光强数值,并绘制出了光强分布曲线。
在理想情况下,我们预期光强应该呈现出中心亮度高、向周围逐渐减弱的分布形态。
然而,在实际测量中,我们发现光强分布曲线并不完全符合这一预期。
首先,我们观察到在光束中心位置,光强确实较高,符合我们的预期。
然而,随着距离光束中心的远离,光强并没有像预期的那样逐渐减弱。
相反,我们观察到在一定距离后,光强开始出现周期性的变化。
这种现象可以解释为光的衍射现象,即光波在通过障碍物或边缘时发生弯曲和扩散。
此外,我们还发现光强分布曲线的形状与光屏和光电二极管的相对位置有关。
当光电二极管与光屏的距离较近时,我们观察到光强分布曲线更加集中,而距离较远时,曲线更加扩散。
这说明光在不同介质中的传播会受到介质的影响,光的传播路径会发生变化。
光强的分布实验报告

光强的分布实验报告实验报告:光强的分布实验引言:在光学研究中,了解光的强度分布对于了解光的行为、优化光学系统的设计具有重要意义。
本实验旨在通过测量光源强度随距离的变化,以探究光强在空间中的分布规律。
实验步骤:1.实验器材准备:双缝衍射装置、光源、刻度尺、测光仪、读数卡等。
2.在实验室安全规范下,设置实验装置并保证光源正常发光。
3.将测光仪与光源间距离设置为一定值,测光仪初始读数归零。
4.以一定的间隔将测光仪沿与光源间距离平行方向移动,并记录每个位置的光强读数值。
5.重复上述步骤多次,取平均值,以增加实验数据的准确性。
6.将实验数据整理成表格,并绘制出光强随距离变化的图像。
7.通过图像分析,得出实验结果,并进行数据处理和讨论。
实验结果与分析:根据实验数据,制作出光强随距离变化的图像,图像中横坐标表示距离,纵坐标表示光强的读数值。
图像显示出光强随距离增加而逐渐减小的趋势,但光强分布并不均匀。
在图像中,我们可以观察到光强的最大值和最小值,并且这些值随距离变化呈现出其中一种规律。
通过对图像的观察和分析,我们发现光强的分布呈现出衍射图案,即具有明显的干涉效应。
在实验中,衍射是由双缝装置引起的,而衍射效应导致了光强的分布不均匀。
根据衍射理论,当光通过一个尺寸较小的孔或缝时,光波会在孔或缝周围扩散,形成衍射图案。
在实验中,双缝装置提供了两个互相平行的缝,使得光通过这两个缝时发生衍射。
衍射的结果是在屏幕上形成一系列的亮暗条纹,显示了在空间中的光强的分布。
实验中观察到的光强图案与理论预测相符。
根据理论分析,光强的分布遵循夫琅禾费衍射公式。
根据夫琅禾费衍射公式可知,衍射的图案与光的波长、缝宽和观察位置有关。
实验中的结果也表明光的传播遵循光的干涉和衍射现象,这意味着光是一种波动现象,并且具有粒子性和波动性的二重性质。
实验结果的合理解释需要结合波动光学理论来理解。
结论:通过本实验,我们探究了光强在空间中的分布规律。
实验结果表明光强分布非均匀,呈现出明显的衍射图案。
实验二四 衍射光强测量实验 实验报告 精品
实验二四 衍射光强测量实验实验目的1、了解衍射的基本原理及光强分布;2、熟悉实验操作及软件的使用;3、理论知识与实验操作相结合,相互验证,掌握衍射光强的分布。
实验原理夫琅和费衍射是指光源和观察者离衍射物体均为无穷远时的衍射。
实际实验中只要满足光源S 与衍射体D 之间的距离u 与D 至观察屏P 之间的距离v 均远大于λ2a 就能观察到夫琅和费衍射现象,其中a 为衍射物的孔径,λ为光源的波长。
单缝夫琅和费衍射的光强公式为:()20sin αθI I = (1)λθπαsin a = (2)式中0I 是中心处的光强,与缝宽的平方成正比。
公式的推导过程可参照光学教科书。
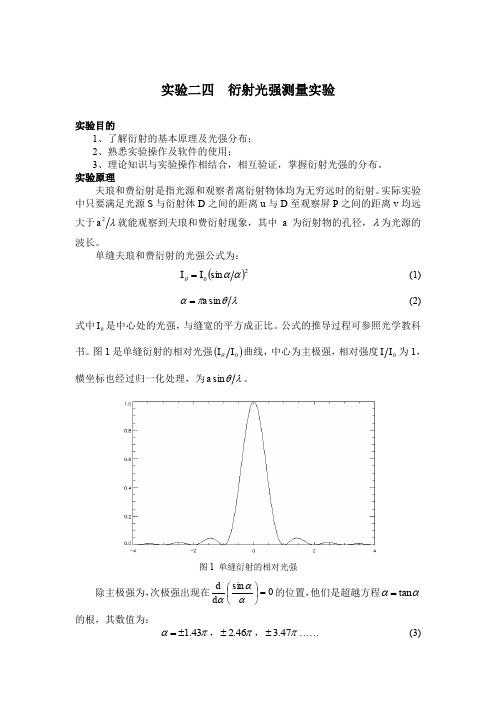
图1是单缝衍射的相对光强()0I I θ曲线,中心为主极强,相对强度0I I 为1,横坐标也经过归一化处理,为λθsin a 。
图1 单缝衍射的相对光强除主极强为,次极强出现在0sin =⎪⎭⎫ ⎝⎛αααd d 的位置,他们是超越方程ααtan =的根,其数值为: πα43.1±=,π46.2±,π47.3± (3)次极强的强度为:01%7.4I I =,02%7.1I I =,03%8.0I I = (4)由式(4)可知,次极强的强度较主极强弱得多,如考虑到倾斜因素,其实际强度较式(4)所得的数值还要小些。
实验装置实验系统由光源、衍射板组、接收单元、计算机、A/D 转换器、工作软件组成。
在本实验系统用光电转换器测量光强,用高精度的位移传感器——光栅尺测量位移,因而可定量的精确测出衍射光强的分布。
全部数据采集和处理由计算机控制,所得测量结果可与理论公式对比。
此系统还可用于测定其它光强分布的实验。
光源:氦氖激光器,波长632.8nm ,功率>1.5mW单缝:宽度连续可调0-2mm ,精度0.01mm ;高度14mm衍射板组:四个多缝2、3、4、5,缝宽0.03mm ,间隔0.06mm光学传感器:硅光电池测量范围:200mm测量精度:01.0±mm如图2所示单色光通过衍射元件(单缝、双缝、圆孔等)在X 轴方向产生图2 实验框图 衍射图形。
单缝衍射光强分布实验报告

单缝衍射光强分布实验报告实验报告:单缝衍射光强分布实验一、实验目的通过实验观察和探究单缝衍射现象,了解光的波动性质,研究单缝衍射光强分布的规律。
二、实验原理单缝衍射是指当光线通过一个狭缝时,由于光的波动性质,光波会发生衍射现象,即光线会向周围扩散。
根据夫琅禾费衍射公式,单缝衍射光强分布的规律可以通过以下两个公式推导得出:1.衍射公式:θ=mλ/b其中,θ为衍射角,m为条纹的级次(m=0,±1,±2,...),λ为波长,b为狭缝宽度。
2. 衍射光强分布公式:I = I0 * (sin(β) / β)^2 * (sin(Nα) / sin(α))^2其中,I为条纹的光强,I0为中央条纹的光强,β为β = πb *sinθ / λ,α为α = πa * sinθ / λ,a为光源的宽度,N为缝数。
三、实验步骤1.将光源与被研究的缝隙间隔一定距离,并确保光源垂直照射缝隙。
2.使用光屏接收衍射光,并根据需要调整光屏距离缝隙的距离,以便更好地观察衍射条纹。
3.用CCD相机拍摄光屏上的衍射条纹,通过图像处理软件量化光强,得到光强分布曲线。
4.调整狭缝的宽度,观察并记录不同宽度下的光强分布情况。
5.重复实验多次,取平均值以减小误差。
四、实验结果与分析通过实验观察到的结果,我们可以得到以下结论:1.光强分布呈现明暗相间的条纹状,其中最中央的一条条纹最亮,两侧的条纹逐渐减弱。
2.随着波长λ的增大,条纹间距减小,光强分布也发生变化。
3.随着缝宽b的增大,条纹变得更为集中,光强分布呈现更明显的周期性变化。
4.当缝数N增加时,条纹的光强分布曲线会发生明显的变化,呈现出更多的衍射条纹。
五、实验注意事项1.实验过程中需要保证光源的稳定性,尽量避免光强波动引起的误差。
2.调整光屏与缝隙距离时,需注意确保垂直照射,并尽可能保持一定的距离以获得更清晰的图像。
3.使用CCD相机拍摄图像时,应注意调整曝光时间和对比度以获得最佳的图像质量。
单缝衍射的光强分布实验报告

#### 一、实验目的1. 理解单缝衍射现象及其光强分布规律。
2. 通过实验验证单缝衍射的光强分布公式。
3. 掌握使用光学仪器进行单缝衍射实验的方法。
#### 二、实验原理单缝衍射是光波通过狭缝后,在屏幕上形成明暗相间的衍射条纹现象。
根据夫琅禾费衍射理论,单缝衍射的光强分布可以由以下公式描述:\[ I(\theta) = I_0 \left( \frac{\sin\left(\frac{\pi a\sin\theta}{\lambda}\right)}{\frac{\pi a \sin\theta}{\lambda}} \right)^2 \]其中,\( I(\theta) \) 是与光轴成 \( \theta \) 角度的光强,\( I_0 \) 是中心亮条纹的光强,\( a \) 是狭缝宽度,\( \lambda \) 是入射光的波长。
#### 三、实验仪器1. 激光器2. 单缝狭缝板3. 光学导轨4. 屏幕板5. 光电传感器6. 数据采集系统7. 计算机软件#### 四、实验步骤1. 将激光器、单缝狭缝板、光学导轨、屏幕板和光电传感器依次安装在光学导轨上。
2. 调节激光器,使其发出的激光束垂直照射到单缝狭缝板上。
3. 将光电传感器放置在屏幕板上,确保其与屏幕板平行。
4. 打开数据采集系统,记录光电传感器接收到的光强数据。
5. 调节单缝狭缝板的宽度,重复步骤4,记录不同缝宽下的光强数据。
6. 改变光电传感器与屏幕板之间的距离,重复步骤4和5,记录不同距离下的光强数据。
7. 根据记录的数据,绘制光强分布曲线,并与理论公式进行比较。
#### 五、实验结果与分析1. 实验结果表明,随着缝宽的减小,衍射条纹的宽度增加,主极大值的光强降低。
2. 实验结果与理论公式基本吻合,说明单缝衍射的光强分布符合夫琅禾费衍射理论。
3. 通过实验验证了单缝衍射光强分布公式,加深了对单缝衍射现象的理解。
#### 六、实验总结本次实验成功观察到了单缝衍射现象,并验证了单缝衍射的光强分布规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衍射光强分布测量査凡物理系摘要:为了观察并验证单缝衍射和多缝衍射的图样以及它们的规律,本实验设计了基于水平光路的测量方法。
运用自动光强记录仪来对衍射现象进行比较函数化的观察。
实验观察到衍射条纹随着缝宽变窄而模糊和间距扩大,并且通过仪器对光强图样的位置定位和夫琅禾费光强的公式来计算单缝的缝宽。
该实验装置结构简单、调节方便、条纹移动清晰。
关键词:衍射自动光强记录仪单缝多缝The Experiment Of Light Distribution Of DiffractionFan Zha Department of PhysicsAbstract: In order to observe and validate the rule of light distribution of single slit diffraction and multiple slits diffraction, the automatic grapher of light intensity is used in this experiment in a horizontal light path. We have verified that the diffraction stripes become dim and far away from each other since the slit(s) become narrow, and calculated the width of slit by using the formulas of light intensity. The experimental instrument is simple and convenient to adjust, and the moving interference fringes are clear.Key Words: diffraction automatic grapher of light intensity single slit multiple slits一、引言光的衍射现象是光的波动性的重要表现,并在实际生活中有较多应用,如运用单缝衍射测量物体之间的微小间隔和位移,或者用于测量细微物体的尺寸等。
本实验要求通过观察、测量夫琅禾费衍射光强分布,加深对光的衍射现象的理解和掌握。
二、实验原理1,衍射的定义: 波遇到障碍物或小孔后通过散射继续传播的现象。
衍射现象是波的特有现象,一切波都会发生衍射现象,而光也是波的一种, 光在传播路径中,遇到不透明或透明的障碍物或者小孔(窄缝),绕过障碍物,产生偏离直线传播的现象称为光的衍射。
衍射时产生的明暗条纹或光环,叫衍射图样2,光的衍射分为夫琅禾费衍射和菲涅尔衍射, 夫琅禾费衍射是指光源和观察点距障碍物为无限远,即平行光的衍射;而菲涅尔衍射是指光源和观察点距障碍物为有限远的衍射.本实验研究的只是夫琅禾费衍射.实际实验中只要满足光源与衍射体之间的距离u,衍射体至观察屏之间的距离v都远大于a2λ就满足了夫琅禾费衍射的条件,其中a为衍射物的孔径,λ为光源的波长.3,单缝、单丝衍射原理:如上图所示,a为单缝宽度,缝和屏之间的距离为v,θ为衍射角,其在观察屏上的位置为x,x离屏幕中心o的距离为OX=θ∗v,设光源波长为λ,则有单缝夫琅禾费衍射的光强公式为:Iθ=I0sinαα2α=πa∗sinθ/λ式中I0是中心处的光强,与缝宽的平方成正比。
若将所成衍射图样的光强画成函数图象在坐标系中,则所成函数图象大致如下除主极强外,次极强出现在ddαsinαα=0的位置,它们是超越方程α=tanα的根,其数值为:α=±1.43π±2.46π±3.47π……对应的θ值为sinθ=±1.43λa ±2.46λa ±3.47λa……当角度很小时,满足sinθ≈θ,则OX可以近似为OX=v∗θ=±1.43vλa ±2.46vλa ±3.47vλa……因而我们可以通过得出函数中次级强的峰值的横坐标只差来确定狭缝的宽度a 4,多缝衍射和干涉原理多缝衍射的示意图如上图,每条缝的宽度为a,两条缝的中心距离为d,其中的每个单缝的衍射光强强度都和之前的单缝衍射光强公式一致。
多缝衍射与单缝的最大区别在于缝之间存在着干涉,如上图所示,对相同的衍射角θ,相邻两缝之间的光程差为∆L=d∗sinθ,如果缝的数目为N,则干涉引起的强度分布因子为:(sinNβ)2其中β=πdsinθλ干涉因子的函数曲线为干涉因子曲线的特点是:1,主极强的位置与缝的数目N无关,只要β=kπ (k=0,±1,±2 …)即满足sinθ=kλ/d就能出现主极强。
此时sinNβ=0 sinβ=0,但sinNβsinβ=N2,次级强的数目为N-2,当sinNβ=0 sinβ≠0时,sinNβsinβ=0,即出现强度为0的点,也就满足:β=k+mn∗π sinθ=k+mn∗λ/d式中k=0,±1,±2 … ; m=1,2,3,…N−1在同一k之内共有N-1个零点,即有N-2个次级大。
同时上式也说明N越大,主极强的角宽度越小,峰越锐。
多缝衍射的强度受单缝衍射和多缝干涉共同影响,其强度公式为Iθ=I0sinαα2sinNββ2其中α=πa∗sinθ/λβ=πdsinθλ其函数图象就是单缝衍射函数图象和干涉因子的函数图象的合成,如下图三、实验仪器He-Ne激光器、衍射光强分布记录仪、衍射片(单缝,多缝,圆孔,圆屏),支柱若干主要实验仪器如下图摆放仪器的时候沿一条直线,要求激光的光点正好打在记录仪的横狭缝的正中心,再在中间放上和交换各种衍射片进行实验。
四、实验步骤1,将激光器打开预热2,打开电脑和衍射光强记录仪的电源,并且熟悉该电脑软件的操作3,将衍射片的位置调好,最好是离光源和记录仪均为50cm左右,这样才能较好的满足夫琅禾费衍射的条件4,调节激光器和衍射片的高度和位置,使得激光恰好经过衍射片上的单缝(或者多缝等等),并且衍射图样生成在记录仪的横向的狭缝中5,调节狭缝的宽度,观察衍射图样,并使用软件将光强分布的函数记录下来,在观察单缝之后还要以函数图样来估算出狭缝的宽度。
6,(单缝)将估算出的单缝宽度与实际测量的单缝宽度进行比较并且计算误差7,改变狭缝宽度(单缝),改变缝的数量(多缝)再重复进行测量五、实验数据及计算单缝我在实验时先粗略的用软件测了一遍光强的函数分布,这次粗略的测量采集间隔是1mm,采集的范围是整个狭缝,而强度增益我选择的是6倍,这次粗略的扫描我发现峰值出现的范围是55mm到85mm,为了以防万一,我在精确测量的时候,把范围扩大到了40mm到100mm,为保证精确度,采集间隔定在了最小的0.02mm 测出的第一组的函数图象还算不错,在oringin上显示如下图并且我用自动光强记录仪具体的记录下了几个肉眼能看见的峰的强度和它们的横坐标主极强峰无法测量其横坐标和光强,因为我选用的增益过大,导致主极强峰超出了测量的范围,所以只测出了次级强峰的峰值。
此时的实际测量的缝宽是40*0.01-0.01=0.39mm之所以要减去0.01mm是因为该千分尺归零的时候(即缝宽为0的时候)读数是0.01mm。
衍射片与记录仪之间的距离V=81.0cm+5cm+1.5cm=875mm加5cm是因为测量距离的尺只能延伸到衍射光强记录仪的外面,而真正的接收处和记录仪表面却还有一段距离,我估算这段距离大约在5cm左右。
而还有一个加1.5cm则是因为衍射片的单缝和读数的线并不是在一个垂面上,它们还有一个水平距离差,我也是估计这段水平距离大约为1.5cm。
然后保持这个条件,只改变缝宽,我又测了一组,此时的缝宽为60*0.01-0.01=0.59mm。
函数图象如下然后记录下几个靠近主极强的峰值其中,从本组的函数图象上可以看出,感觉上这次主极强峰旁边有两个倾斜的痕迹,虽然没有峰的痕迹,但是给人感觉像是有两个次级强峰并了一大半到这个主极强之中。
所以为了保险起见,我还是将这两个倾斜的当做峰来处理,表格中粗体标出来的数据就是这两个“疑似峰”,而判断它们到底是不是次级强峰等会会详细介绍办法后来又测了一组,不过测这一组的时候已经是第二次做实验,条件和之前的两次都不一样,所以我又重新测量v=83.1cm+5cm+1.5cm=89.6cm=896mm这次的缝宽为0.45+0.02=0.47mm并且重新粗略的扫描了一遍,发现峰值的范围是95mm到115mm,于是在精确测量的时候的范围是80mm到130mm,增益还是6倍,精度还是0.02mm,精确测量得到的函数图象如下:记录下次级强峰的数据:单缝的缝宽估算:由实验原理可以得到,缝宽a有:a=1.03vλr1=1.01vλr2=⋯其中r1、r2分别为一级次级强峰与二级次级强峰的距离、二级次级强峰与三级次级强峰之间的距离。
没有采用主极强峰和次级强峰之间的距离是因为无法确定主极强峰的位置。
不过首先先要确定函数图象上显示的一级次级强峰的确是一级次级强峰,确定的方法是:1,首先算出左右两个“一级”次级强峰之间的距离R,再根据表格算出r12,算出Rr1,倘若满足:R r1≈1.43∗22.46−1.43=2.78则说明这两个的确是一级次级强峰。
待确定了一级次级强峰之后,随后得出r1,r2,…再算出缝宽a,最后算出的很多a取平均值算得最终的缝宽。
第一组数据首先确定一级次级强峰r1left=69.98−68.28=1.7r1right=76.28−74.64=1.64R=74.64−69.98=4.66则有R r1left =4.661.7=2.74R 1right =4.66=2.84都和2.78相近,说明确实是一级次级强。
下面计算缝宽:V=875mm λ=632.8∗10−6mmr1left=1.7 r1right=1.64 r2left=1.62 r2right=1.56则a1=1.03vλr1left≈0.335mma2=1.03vλr1right≈0.348mma3=1.01vλr2left≈0.345mma4=1.01vλr2right≈0.358mm算得平均缝宽为:a=0.3465mm 真实测得a=0.39mm误差=(0.39-0.3465)/0.39=0.11第二组数据首先确定一级次级强峰r1left=1.2r1right=1.24R=2.68则有R r1left =2.681.2=2.23R r1right =2.681.24=2.16感觉这结果和2.78有些差距,则尝试一下r2当做r1:r2left=1.02r2right=1.06R`=5.12则有R` 2left =5.12=5.02R` 2right =5.12=4.83和2.78差距更大,则说明一级次级强峰就是主极强旁边那两道斜坡。
