世界数学史上的十个著名不等式
八个著名的不等式

第八讲 几个著名的不等式在数学领域里,不等式知识占有广阔的天地,而一个个的重要不等式又把这片天地装点得更加丰富多彩.这些著名不等式是数学家们长期致力于不等式理论研究的重要成果,它们将成为我们学习数学、研究数学、应用数学的得力工具。
下面择要介绍一些著名的不等式. 1.柯西(Cauchy )不等式 定理:设()n i R b a i i Λ2,1,=∈则()22211nn b a b a ba Λ++≤()()2222122221n n b b b a a aΛΛ++⋅++等号成立当且仅当()n i ka b i i ≤≤=1.。
[一般形式的证明] 作函数()()()()()())(222222122112222212222211≥+++++-+++=-++-+-=x b b b x b a b a b a x a a a b x a b x a b x a x f n n n n n n ΛΛΛΛ0≤∆∴ 此时044121221≤⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=∆∑∑∑===n i i n i i ni i i b a b a⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛≤⎪⎭⎫ ⎝⎛∴∑∑∑===n i i n i i ni i i b a b a 121221,得证。
[向量形式的证明]令(),2,1n a a a A Λρ= (),2,1n b b b B Λρ=()()()22221222212211cos nn n n b b b a a aB A B A b a b a b a B A ΛΛρρρρΛρρ++⋅+++=≤=++=⋅θ()1cos 1≤≤-θ两边同时平方得:()22211nn b a b a ba Λ++≤()()2222122221n n b b b a a aΛΛ++⋅++,得证。
[柯西不等式的应用]例1.1设()()22121111,1n a a a a a a n i R a n n i ≥⎪⎪⎭⎫ ⎝⎛++++++≤≤∈+ΛΛ求证 解:由柯西不等式可知,原不等式可化为()()()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡+++2222122221111n na a a a a a ΛΛ()22111n n =++≥43421Λ个 当且仅当,1,1,12211n na k a a k a a k a ===Λ时等号成立即n a a a Λ==21,故原不等式得证。
几个著名的不等式公式

⼏个著名的不等式公式在数学领域⾥,不等式知识占有⼴阔的天地,⽽⼀个个的重要不等式⼜把这⽚天地装点得更加丰富多彩.下⾯择要介绍⼀些著名的不等式。
三⾓形内⾓的嵌⼊不等式三⾓形内⾓的嵌⼊不等式,在不⾄于引起歧义的情况下简称嵌⼊不等式。
该不等式指出,若A、B、C是⼀个三⾓形的三个内⾓,则对任意实数 x、y、z,有:算术-⼏何平均值不等式在数学中,算术-⼏何平均值不等式是⼀个常见⽽基本的不等式,表现了两类平均数:算术平均数和⼏何平均数之间恒定的不等关系。
设为 n 个正实数,它们的算术平均数是,它们的⼏何平均数是。
算术-⼏何平均值不等式表明,对任意的正实数,总有:等号成⽴当且仅当。
算术-⼏何平均值不等式仅适⽤于正实数,是对数函数之凹性的体现,在数学、⾃然科学、⼯程科学以及经济学等其它学科都有应⽤。
算术-⼏何平均值不等式经常被简称为平均值不等式(或均值不等式),尽管后者是⼀组包括它的不等式的合称。
例⼦在 n = 4 的情况,设: ,那么可见。
历史上,算术-⼏何平均值不等式拥有众多证明。
n = 2的情况很早就为⼈所知,但对于⼀般的 n,不等式并不容易证明。
1729年,英国数学家麦克劳林最早给出了⼀般情况的证明,⽤的是调整法,然⽽这个证明并不严谨,是错误的。
柯西的证明1821年,法国数学家柯西在他的著作《分析教程》中给出了⼀个使⽤逆向归纳法的证明:命题P n:对任意的 n 个正实数,1. 当 n=2 时,P2显然成⽴。
2. 假设Pn成⽴,那么P2n成⽴。
证明:对于2n 个正实数,3. 假设P n成⽴,那么P n-1成⽴。
证明:对于n - 1 个正实数,设,,那么由于Pn成⽴,。
但是,,因此上式正好变成综合以上三点,就可以得到结论:对任意的⾃然数,命题P n都成⽴。
这是因为由前两条可以得到:对任意的⾃然数 k,命题都成⽴。
因此对任意的,可以先找 k 使得,再结合第三条就可以得到命题P n成⽴了。
归纳法的证明使⽤常规数学归纳法的证明则有乔治·克⾥斯托(George Chrystal)在其著作《代数论》(algebra)的第⼆卷中给出的:由对称性不妨设xn+1是中最⼤的,由于,设,则,并且有。
世界数学史上的十个著名不等式
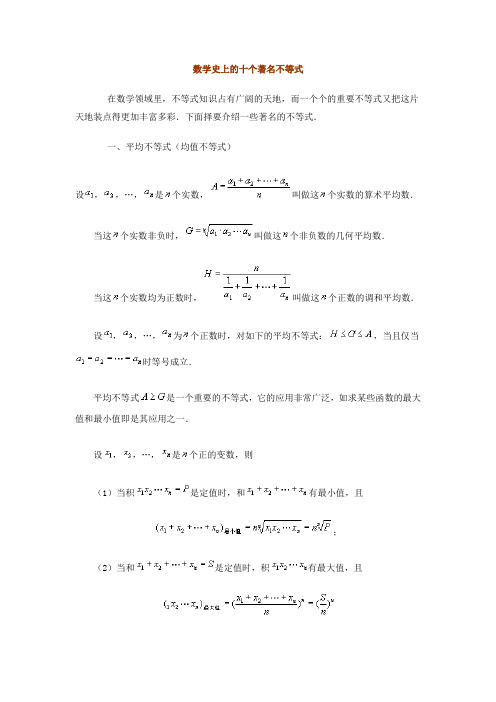
数学史上的十个著名不等式在数学领域里,不等式知识占有广阔的天地,而一个个的重要不等式又把这片天地装点得更加丰富多彩.下面择要介绍一些著名的不等式.一、平均不等式(均值不等式)设,,…,是个实数,叫做这个实数的算术平均数.当这个实数非负时,叫做这个非负数的几何平均数.当这个实数均为正数时,叫做这个正数的调和平均数.设,,…,为个正数时,对如下的平均不等式:,当且仅当时等号成立.平均不等式是一个重要的不等式,它的应用非常广泛,如求某些函数的最大值和最小值即是其应用之一.设,,…,是个正的变数,则(1)当积是定值时,和有最小值,且;(2)当和是定值时,积有最大值,且两者都是当且仅当个变数彼此相等时,即时,才能取得最大值或最小值.在中,当时,分别有,平均不等式经常用到的几个特例是(下面出现的时等号成立;(3),当且仅当时等号成立;(4),当且仅当时等号成立.二、柯西不等式(柯西—许瓦兹不等式或柯西—布尼雅可夫斯基不等式)对任意两组实数,,…,;,,…,,有,其中等号当且仅当时成立.柯西不等式经常用到的几个特例(下面出现的,…,;,…,都表示实数)是:(1),,则(2)(3)柯西不等式是又一个重要不等式,有许多应用和推广,与柯西不等式有关的竞赛题也频频出现,这充分显示了它的独特地位.三、闵可夫斯基不等式设,,…,;,,…,是两组正数,,则()()当且仅当时等号成立.闵可夫斯基不等式是用某种长度度量下的三角形不等式,当时得平面上的三角形不等式:右图给出了对上式的一个直观理解.若记,,则上式为四、贝努利不等式(1)设,且同号,则(2)设,则(ⅰ)当时,有;(ⅱ)当或时,有,上两式当且仅当时等号成立.不等式(1)的一个重要特例是().五、赫尔德不等式已知()是个正实数,,则上式中若令,,,则此赫尔德不等式即为柯西不等式.六、契比雪夫不等式(1)若,则;(2)若,则下面给出一个时的契比雪夫不等式的直观理解.如图,矩形OPAQ中,,,显然阴影部分的矩形的面积之和不小于空白部分的矩形的面积之和,(这可沿图中线段MN向上翻折比较即知).于是有,也即七、排序不等式设有两组数,,…,;,,…,满足,则有,式中的,,…,是1,2,…,的任意一个排列,式中的等号当且仅当或时成立.以上排序不等式也可简记为:反序和乱序和同序和这个不等式在不等式证明中占有重要地位,它使不少困难问题迎刃而解.八、含有绝对值的不等式为复数,则,左边的等号仅当的幅角差为时成立,右边的等号仅当的幅角相等时成立,这个不等式也称为三角形不等式,其一般形式是,也可记为绝对值不等式在实数的条件下用得较多。
53几个重要的不等式

5.3几个重要的不等式具备了不等式的基本知识和技能之后,就可以进一步欣赏一些优美而又魅力无限的重要结果。
正如音乐家能够将很少几组音符变化发展为动听美妙的旋律一样,数学家则往往能够通过不多几步逻辑推理揭示出简明优美的结果。
这里要介绍的一些有关不等式的结果就是数学家依靠并不复杂的逻辑推理得到的,然而在其来龙去脉被领悟以前,却常常象变戏法似的神秘莫测。
除了前面已经介绍的贝努利不等式之外,本节将讨论的一些重要不等式包括:柯西不等式,排序不等式,平均不等式等。
这些重要的不等式不仅形式优美、应用广泛,而且也是今后进一步学习高等数学的重要工具。
1. 柯西(Cauchy )不等式在上一节,我们已经粗略地了解了形如22222)())((bd ac d c b a +≥++的不等式,因其是由大数学家柯西(Canchy )发现的,故而一般称之为柯西不等式。
柯西不等式有着丰富的几何背景。
可以通过几何解释加深对其本质特征的认识与理解。
请同学们回忆一下我们曾经学过的余弦定理的内容?我们将利用它来解释柯西不等式。
如图,在三角形OPQ 中,θ=∠QOP d c Q b a P ),,(),,(,则 ,,2222d c OQ b a OP +=+=.)()(22d b c a PQ -+-=将以上三式代入余弦定理2222⋅-+=OP OQ OP PQ2222cos dc b a bdac +⋅++=θ或.))(()(cos 222222d c b a bd ac +++=θ 因为1cos 02≤≤θ,所以,1))(()(22222≤+++d c b a bd ac ,于是22222)())((bd ac d c b a +≥++.讨论:借助图形分析,柯西不等式中等号成立的条件是什么?柯西不等式应用相当广泛,我们先通过一些简单的例子加以体会。
例1.已知.1,12222=+=+y x b a 求证:.1≤+by ax (1) 证明:由柯西不等式,.1))(()(22222=++≤+y x b a by ax 所以(1)成立。
几个著名的不等式

(1)
(1
x)n
1
nx( x
0)
,推广为
(1
x)n
1
nx
n(n 1) 2
x2(x
0)
等等.
(2) (1
x )n n
1
x
x2
xn (x
0) .
6.
2n 2n
1
的放缩
n
n
1
(2n 1)2 (2n)2
1
2n 1 2n
(2n 1)2 (2n)2 1
2n 2n
1 1
.
7.
2n 2n
b
2
.
特别地,
(1)若 a12 a22 an2 1 , b12 b22 bn2 1,则 a1 b1 a2bn anbn 1 . (2) a1a2 a2a3 a3a1 a12 a22 a32 . (3) (a1 a2 an )2 n(a12 a22 an2 ) . (二)推论
1
aikbik ) k
;
当且仅当 a1 a2 an 或 b1 b2 bn 时取等号.
特别地,若
a1
a2
, b1
b2
,则
a1b1
a2b2 2
(a1
a2 )(b1 22
b2
)
;
若
a1
a2
, b1
b2
,则
a1b1
a2b2 2
(a1
a2 )(bБайду номын сангаас 22
b2 )
.
推论 2. 多组正数 a1, a2 ,, an ;b1, b2 ,, bn ;…; z1, z2 ,, zn ;满足 a1 a2 an , b1 b2 bn , … , z1 z2 zn , 每 组 取 一 个 数 相 乘 再 求 和 S , 则 有
高中赫尔德不等式

高中赫尔德不等式摘要:1.简介赫尔德不等式的背景和意义2.赫尔德不等式的数学表达式及条件3.赫尔德不等式的证明思路和方法4.赫尔德不等式在实际问题中的应用5.赫尔德不等式与其他不等式关系的对比6.结论与展望正文:赫尔德不等式(Holder"s Inequality)是数学领域中一个重要的不等式,广泛应用于不等式分析、概率论、数值分析等领域。
本文将对赫尔德不等式进行详细的阐述,包括其数学表达式、证明方法以及在实际问题中的应用。
赫尔德不等式是由德国数学家赫尔德(Holder)于19世纪末提出,其目的是为了研究函数的积分和不等式之间的关系。
赫尔德不等式的数学表达式如下:设函数f(x)在区间[a, b]上可积,函数g(x)在区间[a, b]上连续,则有:∫[a, b]f(x)g(x)dx ≥ μ∫[a, b]f(x)dx × ∫[a, b]g(x)dx其中,μ为常数,且μ> 0。
要证明赫尔德不等式,我们可以采用数学分析的方法。
首先,我们将赫尔德不等式的左右两边分别看作两个函数的乘积,然后通过积分区间分割、放缩法等手段,将问题转化为比较两个积分的大小。
具体证明过程较为复杂,这里不再详细展开。
赫尔德不等式在实际问题中具有广泛的应用,例如在概率论中,它可以用来估计随机变量的不确定性;在数值分析中,它可以用于求解偏微分方程的解。
此外,赫尔德不等式还与其他著名的不等式(如柯西不等式、闵可夫斯基不等式等)有密切关系,通过对比研究,我们可以更深入地理解这些不等式的本质。
总之,赫尔德不等式是数学领域中一道亮丽的风景线,它不仅丰富了不等式理论,还在诸多实际问题中发挥着重要作用。
对赫尔德不等式的深入研究,有助于我们更好地把握不等式的应用范围,提高解决问题的效率。
著名不等式公式

三角形内角的嵌入不等式三角形内角的嵌入不等式,在不至于引起歧义的情况下简称嵌入不等式。
该不等式指出,若A、B、C是一个三角形的三个内角,则对任意实数x、y、z,有:算术-几何平均值不等式在数学中,算术-几何平均值不等式是一个常见而基本的不等式,表现了两类平均数:算术平均数和几何平均数之间恒定的不等关系。
设为n个正实数,它们的算术平均数是,它们的几何平均数是。
算术-几何平均值不等式表明,对任意的正实数,总有:等号成立当且仅当。
算术-几何平均值不等式仅适用于正实数,是对数函数之凹性的体现,在数学、自然科学、工程科学以及经济学等其它学科都有应用。
算术-几何平均值不等式经常被简称为平均值不等式(或均值不等式),尽管后者是一组包括它的不等式的合称。
例子在n = 4 的情况,设: ,那么.可见。
历史上的证明历史上,算术-几何平均值不等式拥有众多证明。
n = 2的情况很早就为人所知,但对于一般的n,不等式并不容易证明。
1729年,英国数学家麦克劳林最早给出了一般情况的证明,用的是调整法,然而这个证明并不严谨,是错误的。
柯西的证明1821年,法国数学家柯西在他的著作《分析教程》中给出了一个使用逆向归纳法的证明[1]:命题P n:对任意的n个正实数,1. 当n=2 时,P2显然成立。
2. 假设P n成立,那么P2n成立。
证明:对于2n个正实数,3. 假设Pn成立,那么P n− 1成立。
证明:对于n- 1 个正实数,设,,那么由于P n成立,。
但是,,因此上式正好变成综合以上三点,就可以得到结论:对任意的自然数,命题P n都成立。
这是因为由前两条可以得到:对任意的自然数k,命题都成立。
因此对任意的,可以先找k使得,再结合第三条就可以得到命题P n成立了。
归纳法的证明使用常规数学归纳法的证明则有乔治·克里斯托(George Chrystal)在其著作《代数论》(algebra)的第二卷中给出的[2]:由对称性不妨设xn + 1是中最大的,由于,设,则,并且有。
切比雪夫不等式xi

切比雪夫不等式xi切比雪夫不等式xi是19月科学家乔治切比雪夫发现的一个重要的数学定理,也被称为“切比雪夫不等式”。
它与其他不等式有着根本的不同,它只能定义有限多个未知数,而不是无限多个未知数。
它是数学家和科学家们许多工作和研究中不可或缺的重要理论。
历史上,切比雪夫不等式是由俄罗斯数学家切比雪夫发现的。
切比雪夫发现这个不等式有助于描述多变量函数的最大值和最小值。
它被用来给出多变量的解析解,从而为多变量函数的计算打开了大门。
此外,它还被用来推导数学空间的完备性定理,证明某些数学定理的正确性。
切比雪夫不等式的原理非常简单:如果两个变量(a和b)满足不等式xi,则它们之间的差值不能超过常数xi,即:|a - b|此外,它还表明如果N个变量满足不等式xi,则它们之间差值的大小不能超过N-1倍的常数xi:|a1 - a2||a2 - a3||an-1 - an|这是切比雪夫不等式xi的核心原理,它表明不等式xi对多变量函数的行为具有极大的约束力。
迄今为止,切比雪夫不等式一直是数学界的一个重要问题,因为它的许多应用可以帮助解决难题。
例如,它可以用来优化多变量函数,求解最佳参数,以及构建函数图像。
此外,它还可以引入数值近似解,有效解决多变量函数的极值点查找问题。
可以看出,切比雪夫不等式xi是一个伟大的数学定理,它的发现为数学研究提供了极大的帮助。
它的基本原理既简单又有效,因此一直被许多学者所重视。
它的强大优势可以帮助研究人员解决复杂的数学问题,从而为科学的发展做出重大贡献。
总之,切比雪夫不等式是一个著名的数学定理,由于它极大地促进了数学研究的发展,因此得到了众多学者的赞誉和推崇。
它将为科学界做出更多贡献,持续推动数学研究的发展,并且将来还会帮助解决更多科学难题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学史上的十个著名不等式
在数学领域里,不等式知识占有广阔的天地,而一个个的重要不等式又把这片天地装点得更加丰富多彩.下面择要介绍一些著名的不等式.
一、平均不等式(均值不等式)
设,,…,是个实数,叫做这个实数的算术平均数.当这个实数非负时,叫做这个非负数的几何平均数.
当这个实数均为正数时,叫做这个正数的调和平均数.设,,…,为个正数时,对如下的平均不等式:,当且仅当时等号成立.
平均不等式是一个重要的不等式,它的应用非常广泛,如求某些函数的最大值和最小值即是其应用之一.
设,,…,是个正的变数,则
(1)当积是定值时,和有最小值,且
;
(2)当和是定值时,积有最大值,且
两者都是当且仅当个变数彼此相等时,即时,才能取得最大值或最小值.
在中,当时,分别有,
平均不等式经常用到的几个特例是(下面出现的时等号成立;
(3),当且仅当时等号成立;
(4),当且仅当时等号成立.
二、柯西不等式(柯西—许瓦兹不等式或柯西—布尼雅可夫斯基不等式)
对任意两组实数,,…,;,,…,,有
,其中等号当且仅当
时成立.
柯西不等式经常用到的几个特例(下面出现的,…,;,…,都表示实数)是:
(1),,则
(2)
(3)
柯西不等式是又一个重要不等式,有许多应用和推广,与柯西不等式有关的竞赛题也频频出现,这充分显示了它的独特地位.
三、闵可夫斯基不等式
设,,…,;,,…,是两组正数,,则
()
()
当且仅当时等号成立.
闵可夫斯基不等式是用某种长度度量下的三角形不等式,当时得平面上的三角形不等式:
右图给出了对上式的一个直观理解.
若记,,则上式为
四、贝努利不等式
(1)设,且同号,则
(2)设,则(ⅰ)当时,有;(ⅱ)当或
时,有,上两式当且仅当时等号成立.
不等式(1)的一个重要特例是().五、赫尔德不等式
已知()是个正实数,,则
上式中若令,,,则此赫尔德不等式即为柯西不等式.六、契比雪夫不等式
(1)若,则
;
(2)若,则
下面给出一个时的契比雪夫不等式的直观理解.
如图,矩形OPAQ中,,,显然
阴影部分的矩形的面积之和不小于空白部分的
矩形的面积之和,(这可沿图中线段MN向上翻
折比较即知).于是有
,也即
七、排序不等式
设有两组数,,…,;,,…,满足,
则有,式中的
,,…,是1,2,…,的任意一个排列,式中的等号当且仅当
或时成立.
以上排序不等式也可简记为:反序和乱序和同序和
这个不等式在不等式证明中占有重要地位,它使不少困难问题迎刃而解.
八、含有绝对值的不等式
为复数,则,左边的等号仅当的幅角差为时成立,右边的等号仅当的幅角相等时成立,这个不等式也称为三角形不等式,其一般形式是
,
也可记为
绝对值不等式在实数的条件下用得较多。
九、琴生不等式
设是()内的凸函数,则对于()内任意的几个实数有
,
等号当且仅当时取得.
琴生不等式是丹麦数学家琴生于1905年到1906年间建立的。
利用琴生不等式我们可以得到一系列不等式,比如“幂平均不等式”,“加权的琴生不等式”等等.
十、艾尔多斯—莫迪尔不等式
设P为内部或边界上一点,P到三边距离分别为PD,PE,PF,则
,
当且仅当为正三角形,且P为三角形中心时上式取等号.
这是用于几何问题的证明和求最大(小)值时的一个重要不等式.
以上这些著名不等式是数学家们长期致力于不等式理论研究的重要成果,如果它们已变成了我们学习数学、研究数学、应用数学的得力工具.。
