2021届中考数学热点题型专练：四边形【含答案】
四边形解答题(精选32道)-三年(2021-2023)中考数学真题分项汇编【山东】(原卷版)
三年（2021-2023）中考数学真题分项汇编【山东专用】专题14四边形解答题（精选32道）一．解答题（共32小题）1．（2023•日照）如图，平行四边形ABCD中，点E是对角线AC上一点，连接BE，DE，且BE＝DE．（1）求证：四边形ABCD是菱形；（2）若AB＝10，tan∠BAC＝2，求四边形ABCD的面积．2．（2023•菏泽）如图，在▱ABCD中，AE平分∠BAD，交BC于点E，CF平分∠BCD，交AD于点F．求证：AE＝CF．3．（2023•东营）（1）用数学的眼光观察如图①，在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是AB的中点，N是DC的中点．求证：∠PMN＝∠PNM．（2）用数学的思维思考如图②，延长图①中的线段AD交MN的延长线于点E，延长线段BC交MN的延长线于点F．求证：∠AEM＝∠F．（3）用数学的语言表达如图③，在△ABC中，AC＜AB，点D在AC上，AD＝BC，M是AB的中点，N是DC的中点，连接MN 并延长，与BC的延长线交于点G，连接GD．若∠ANM＝60°，试判断△CGD的形状，并进行证明．4．（2023•滨州）如图，在平面直角坐标系中，菱形OABC的一边OC在x轴正半轴上，顶点A的坐标为（2，2），点D是边OC上的动点，过点D作DE⊥OB交边OA于点E，作DF∥OB交边BC于点F，连接EF，设OD＝x，△DEF的面积为S．（1）求S关于x的函数解析式；（2）当x取何值时，S的值最大？请求出最大值．5．（2023•枣庄）问题情境：如图1，在△ABC中，AB＝AC＝17，BC＝30，AD是BC边上的中线．如图2，将△ABC的两个顶点B，C分别沿EF，GH折叠后均与点D重合，折痕分别交AB，AC，BC于点E，F，G，H．猜想证明：（1）如图2，试判断四边形AEDG的形状，并说明理由；问题解决：（2）如图3，将图2中左侧折叠的三角形展开后，重新沿MN折叠，使得顶点B与点H重合，折痕分别交AB，BC于点M，N，BM的对应线段交DG于点K，求四边形MKGA的面积．6．（2023•烟台）【问题背景】如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形ABCD进行如下操作：①分别以点B，C为圆心，以大于BC的长度为半径作弧，两弧相交于点E，F，作直线EF交BC于点O，连接AO；②将△ABO沿AO翻折，点B的对应点落在点P处，作射线AP交CD于点Q．【问题提出】在矩形ABCD中，AD＝5，AB＝3，求线段CQ的长；【问题解决】经过小组合作、探究、展示，其中的两个方案如下：方案一：连接OQ，如图2．经过推理、计算可求出线段CQ的长；方案二：将△ABO绕点O旋转180°至△RCO处，如图3．经过推理、计算可求出线段CQ的长．请你任选其中一种方案求线段CQ的长．7．（2022•滨州）如图，菱形ABCD的边长为10，∠ABC＝60°，对角线AC、BD相交于点O，点E在对角线BD上，连接AE，作∠AEF＝120°且边EF与直线DC相交于点F．（1）求菱形ABCD的面积；（2）求证：AE＝EF．8．（2022•聊城）如图，△ABC中，点D是AB上一点，点E是AC的中点，过点C作CF∥AB，交DE的延长线于点F．（1）求证：AD＝CF；（2）连接AF，CD．如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF是菱形，证明你的结论．9．（2022•临沂）已知△ABC是等边三角形，点B，D关于直线AC对称，连接AD，CD．（1）求证：四边形ABCD是菱形；（2）在线段AC上任取一点P（端点除外），连接PD．将线段PD绕点P逆时针旋转，使点D落在BA 延长线上的点Q处．请探究：当点P在线段AC上的位置发生变化时，∠DPQ的大小是否发生变化？说明理由．（3）在满足（2）的条件下，探究线段AQ与CP之间的数量关系，并加以证明．10．（2022•济南）已知：如图，在菱形ABCD中，E，F是对角线AC上两点，连接DE，DF，∠ADF＝∠CDE．求证：AE＝CF．11．（2022•东营）△ABC和△ADF均为等边三角形，点E、D分别从点A，B同时出发，以相同的速度沿AB、BC运动，运动到点B、C停止．（1）如图1，当点E、D分别与点A、B重合时，请判断：线段CD、EF的数量关系是，位置关系是；（2）如图2，当点E、D不与点A，B重合时，（1）中的结论是否依然成立？若成立，请给予证明；若不成立，请说明理由；（3）当点D运动到什么位置时，四边形CEFD的面积是△ABC面积的一半，请直接写出答案；此时，四边形BDEF是哪种特殊四边形？请在备用图中画出图形并给予证明．12．（2022•青岛）如图，在四边形ABCD中，AB∥CD，点E，F在对角线BD上，BE＝EF＝FD，∠BAF＝∠DCE＝90°．（1）求证：△ABF≌△CDE；（2）连接AE，CF，已知（从以下两个条件中选择一个作为已知，填写序号），请判断四边形AECF的形状，并证明你的结论．条件①：∠ABD＝30°；条件②：AB＝BC．（注：如果选择条件①条件②分别进行解答，按第一个解答计分）13．（2022•德州）教材呈现以下是人教版八年级上册数学教材第53页的部分内容．如图，四边形ABCD中，AD＝CD，AB＝CB．我们把这种两组邻边分别相等的四边形叫做“筝形”．概念理解（1）根据上面教材的内容，请写出“筝形”的一条性质：；（2）如图1，在△ABC中，AD⊥BC，垂足为D，△EAB与△DAB关于AB所在的直线对称，△F AC与△DAC关于AC所在的直线对称，延长EB，FC相交于点G．请写出图中的“筝形”：；（写出一个即可）应用拓展（3）如图2，在（2）的条件下，连接EF，分别交AB，AC于点M，H，连接BH．①求证：∠BAC＝∠FEG；②求证：∠AHB＝90°．14．（2022•烟台）如图，在▱ABCD中，DF平分∠ADC，交AB于点F，BE∥DF，交AD的延长线于点E．若∠A＝40°，求∠ABE的度数．15．（2022•日照）如图1，△ABC是等腰直角三角形，AC＝BC＝4，∠C＝90°，M，N分别是边AC，BC上的点，以CM，CN为邻边作矩形PMCN，交AB于E，F．设CM＝a，CN＝b，若ab＝8．（1）判断由线段AE，EF，BF组成的三角形的形状，并说明理由；（2）①当a＝b时，求∠ECF的度数；②当a≠b时，①中的结论是否成立？并说明理由．16．（2022•威海）（1）将两张长为8，宽为4的矩形纸片如图1叠放．①判断四边形AGCH的形状，并说明理由；②求四边形AGCH的面积．（2）如图2，在矩形ABCD和矩形AFCE中，AB＝2，BC＝7，CF＝，求四边形AGCH的面积．17．（2021•烟台）有公共顶点A的正方形ABCD与正方形AEGF按如图1所示放置，点E，F分别在边AB 和AD上，连接BF，DE，M是BF的中点，连接AM交DE于点N．【观察猜想】（1）线段DE与AM之间的数量关系是，位置关系是；【探究证明】（2）将图1中的正方形AEGF绕点A顺时针旋转45°，点G恰好落在边AB上，如图2，其他条件不变，线段DE与AM之间的关系是否仍然成立？并说明理由．18．（2021•日照）问题背景：如图1，在矩形ABCD中，AB＝2，∠ABD＝30°，点E是边AB的中点，过点E作EF⊥AB交BD于点F．实验探究：（1）在一次数学活动中，小王同学将图1中的△BEF绕点B按逆时针方向旋转90°，如图2所示，得到结论：①＝；②直线AE与DF所夹锐角的度数为．（2）小王同学继续将△BEF绕点B按逆时针方向旋转，旋转至如图3所示位置．请问探究（1）中的结论是否仍然成立？并说明理由．拓展延伸：在以上探究中，当△BEF旋转至D、E、F三点共线时，则△ADE的面积为．19．（2021•青岛）如图，在▱ABCD中，E为CD边的中点，连接BE并延长，交AD的延长线于点F，延长ED至点G，使DG＝DE，分别连接AE，AG，FG．（1）求证：△BCE≌△FDE；（2）当BF平分∠ABC时，四边形AEFG是什么特殊四边形？请说明理由．20．（2021•泰安）四边形ABCD为矩形，E是AB延长线上的一点．（1）若AC＝EC，如图1，求证：四边形BECD为平行四边形；（2）若AB＝AD，点F是AB上的点，AF＝BE，EG⊥AC于点G，如图2，求证：△DGF是等腰直角三角形．21．（2021•济南）已知：如图，在菱形ABCD中，E，F分别是边AD和CD上的点，且∠ABE＝∠CBF．求证：DE＝DF．22．（2021•济南）在△ABC中，∠BAC＝90°，AB＝AC，点D在边BC上，BD＝BC，将线段DB绕点D 顺时针旋转至DE，记旋转角为α，连接BE，CE，以CE为斜边在其一侧作等腰直角三角形CEF，连接AF．（1）如图1，当α＝180°时，请直接写出线段AF与线段BE的数量关系；（2）当0°＜α＜180°时，①如图2，（1）中线段AF与线段BE的数量关系是否仍然成立？请说明理由；②如图3，当B，E，F三点共线时，连接AE，判断四边形AECF的形状，并说明理由．23．（2021•枣庄）如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，垂美四边形ABCD的对角线AC，BD交于点O．猜想：AB2+CD2与AD2+BC2有什么关系？并证明你的猜想．（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结CE，BG，GE．已知AC＝4，AB＝5，求GE的长．24．（2021•德州）如图，点E，F分别在正方形ABCD的边AB，AD上，且AE＝DF，点G，H分别在边AB，BC上，且FG⊥EH，垂足为P．（1）求证：FG＝EH；（2）若正方形ABCD边长为5，AE＝2，tan∠AGF＝，求PF的长度．25．（2021•菏泽）如图，在菱形ABCD中，点M、N分别在AB、CB上，且∠ADM＝∠CDN，求证：BM＝BN．26．（2021•滨州）如图，矩形ABCD的对角线AC、BD相交于点O，BE∥AC，AE∥BD．（1）求证：四边形AOBE是菱形；（2）若∠AOB＝60°，AC＝4，求菱形AOBE的面积．27．（2021•聊城）如图，在四边形ABCD中，AC与BD相交于点O，且AO＝CO，点E在BD上，满足∠EAO＝∠DCO．（1）求证：四边形AECD是平行四边形；（2）若AB＝BC，CD＝5，AC＝8，求四边形AECD的面积．28．（2021•临沂）如图，已知正方形ABCD，点E是BC边上一点，将△ABE沿直线AE折叠，点B落在F 处，连接BF并延长，与∠DAF的平分线相交于点H，与AE，CD分别相交于点G，M，连接HC．（1）求证：AG＝GH；（2）若AB＝3，BE＝1，求点D到直线BH的距离；（3）当点E在BC边上（端点除外）运动时，∠BHC的大小是否变化？为什么？29．（2021•菏泽）在矩形ABCD中，BC＝CD，点E、F分别是边AD、BC上的动点，且AE＝CF，连接EF，将矩形ABCD沿EF折叠，点C落在点G处，点D落在点H处．（1）如图1，当EH与线段BC交于点P时，求证：PE＝PF；（2）如图2，当点P在线段CB的延长线上时，GH交AB于点M，求证：点M在线段EF的垂直平分线上；（3）当AB＝5时，在点E由点A移动到AD中点的过程中，计算出点G运动的路线长．30．（2021•青岛）已知：如图，在矩形ABCD和等腰Rt△ADE中，AB＝8cm，AD＝AE＝6cm，∠DAE＝90°．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DB方向匀速运动，速度为1cm/s．过点Q作QM∥BE，交AD于点H，交DE于点M，过点Q作QN∥BC，交CD于点N．分别连接PQ，PM，设运动时间为t（s）（0＜t＜8）．解答下列问题：（1）当PQ⊥BD时，求t的值；（2）设五边形PMDNQ的面积为S（cm2），求S与t之间的函数关系式；（3）当PQ＝PM时，求t的值；（4）若PM与AD相交于点W，分别连接QW和EW．在运动过程中，是否存在某一时刻t，使∠AWE ＝∠QWD？若存在，求出t的值；若不存在，请说明理由．31．（2021•淄博）已知：在正方形ABCD的边BC上任取一点F，连接AF，一条与AF垂直的直线l（垂足为点P）沿AF方向，从点A开始向下平移，交边AB于点E．（1）当直线l经过正方形ABCD的顶点D时，如图1所示．求证：AE＝BF；（2）当直线l经过AF的中点时，与对角线BD交于点Q，连接FQ，如图2所示．求∠AFQ的度数；（3）直线l继续向下平移，当点P恰好落在对角线BD上时，交边CD于点G，如图3所示．设AB＝2，BF＝x，DG＝y，求y与x之间的关系式．32．（2022•青岛）如图，在Rt△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD．点P从点B出发，沿BA方向匀速运动、速度为1cm/s；同时，点Q 从点A出发，沿AD方向匀速运动，速度为1cm/s．PQ交AC于点F，连接CP，EQ，设运动时间为t（s）（0＜t＜5）．解答下列问题：（1）当EQ⊥AD时，求t的值；（2）设四边形PCDQ的面积为S（cm2），求S与t之间的函数关系式；（3）是否存在某一时刻t，使PQ∥CD？若存在，求出t的值；若不存在，请说明理由．。
2021年中考数学专题复习：《四边形》 专项练习题精选(含答案)
2021年中考数学专题复习：《四边形》专项练习题精选一．选择题1．（2020•河池）如图，在▱ABCD中，CE平分∠BCD，交AB于点E，EA＝3，EB＝5，ED＝4．则CE的长是（）A．5B．6C．4D．5 2．（2020•玉林）已知：点D，E分别是△ABC的边AB，AC的中点，如图所示．求证：DE∥BC，且DE＝BC．证明：延长DE到点F，使EF＝DE，连接FC，DC，AF，又AE＝EC，则四边形ADCF是平行四边形，接着以下是排序错误的证明过程：①∴DF BC；②∴CF AD．即CF BD；③∴四边形DBCF是平行四边形；④∴DE∥BC，且DE＝BC．则正确的证明顺序应是：（）A．②→③→①→④B．②→①→③→④C．①→③→④→②D．①→③→②→④3．（2019•梧州）正九边形的一个内角的度数是（）A．108°B．120°C．135°D．140°4．（2019•柳州）如图，在▱ABCD中，全等三角形的对数共有（）A ．2对B ．3对C ．4对D ．5对5．（2019•河池）如图，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，BE ＝CF ，则图中与∠AEB 相等的角的个数是（ ）A ．1B ．2C ．3D ．46．（2019•贵港）如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为S 1，S 2，则下列结论错误的是（ ）A ．S 1+S 2＝CP 2B ．AF ＝2FDC ．CD ＝4PD D ．cos ∠HCD ＝7．（2019•河池）如图，在△ABC 中，D ，E 分别是AB ，BC 的中点，点F 在DE 延长线上，添加一个条件使四边形ADFC 为平行四边形，则这个条件是（ ）A ．∠B ＝∠F B ．∠B ＝∠BCFC ．AC ＝CFD ．AD ＝CF8．（2018•河池）如图，要判定▱ABCD 是菱形，需要添加的条件是（ ）A．AB＝AC B．BC＝BD C．AC＝BD D．AB＝BC 9．（2018•梧州）如图，在正方形ABCD中，A、B、C三点的坐标分别是（﹣1，2）、（﹣1，0）、（﹣3，0），将正方形ABCD向右平移3个单位，则平移后点D的坐标是（）A．（﹣6，2）B．（0，2）C．（2，0）D．（2，2）二．填空题10．（2020•河池）如图，菱形ABCD的周长为16，AC，BD交于点O，点E在BC上，OE∥AB，则OE的长是．11．（2020•玉林）如图，将两张对边平行且等宽的纸条交叉叠放在一起，则重合部分构成的四边形ABCD菱形（填“是”或“不是”）．12．（2019•百色）四边形具有不稳定性．如图，矩形ABCD按箭头方向变形成平行四边形A'B'C'D'，当变形后图形面积是原图形面积的一半时，则∠A'＝．13．（2019•玉林）如图，在矩形ABCD中，AB＝8，BC＝4，一发光电子开始置于AB边的点P处，并设定此时为发光电子第一次与矩形的边碰撞，将发光电子沿着PR方向发射，碰撞到矩形的边时均反射，每次反射的反射角和入射角都等于45°，若发光电子与矩形的边碰撞次数经过2019次后，则它与AB边的碰撞次数是．14．（2019•梧州）如图，▱ABCD中，∠ADC＝119°，BE⊥DC于点E，DF⊥BC于点F，BE与DF交于点H，则∠BHF＝度．15．（2019•广西）如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AH⊥BC于点H，已知BO＝4，S＝24，则AH＝．菱形ABCD16．（2018•河池）如图，四边形OABC为正方形，点D（3，1）在AB上，把△CBD绕点C 顺时针旋转90°，则点D旋转后的对应点D′的坐标是．三．解答题17．（2020•桂林）如图，在菱形ABCD中，点E，F分别是边AD，AB的中点．（1）求证：△ABE≌△ADF；（2）若BE＝，∠C＝60°，求菱形ABCD的面积．18．（2020•广西）如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF．（1）求证：△ABC≌△DEF；（2）连接AD，求证：四边形ABED是平行四边形．19．（2019•百色）如图，菱形ABCD中，作BE⊥AD、CF⊥AB，分别交AD、AB的延长线于点E、F．（1）求证：AE＝BF；（2）若点E恰好是AD的中点，AB＝2，求BD的值．20．（2019•玉林）如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．21．（2019•柳州）平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．已知：如图，在四边形ABCD中，AB＝CD，AD＝BC．求证：四边形ABCD是平行四边形．证明：22．（2019•贺州）如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF．（1）求证：△ABE≌△CDF；（2）当AC⊥EF时，四边形AECF是菱形吗？请说明理由．23．（2018•百色）平行四边形ABCD中，∠A＝60°，AB＝2AD，BD的中垂线分别交AB，CD 于点E，F，垂足为O．（1）求证：OE＝OF；（2）若AD＝6，求tan∠ABD的值．24．（2018•梧州）如图，在▱ABCD中，对角线AC，BD相交于点O，过点O的一条直线分别交AD，BC于点E，F．求证：AE＝CF．25．（2018•贺州）如图，在△ABC中，∠ACB＝90°，O、D分别是边AC、AB的中点，过点C作CE∥AB交DO的延长线于点E，连接AE．（1）求证：四边形AECD是菱形；（2）若四边形AECD的面积为24，tan∠BAC＝，求BC的长．26．（2018•柳州）如图，四边形ABCD是菱形，对角线AC，BD相交于点O，且AB＝2．（1）求菱形ABCD的周长；（2）若AC＝2，求BD的长．27．（2018•玉林）如图，在▱ABCD中，DC＞AD，四个角的平分线AE，DE，BF，CF的交点分别是E，F，过点E，F分别作DC与AB间的垂线MM'与NN'，在DC与AB上的垂足分别是M，N与M′，N′，连接EF．（1）求证：四边形EFNM是矩形；（2）已知：AE＝4，DE＝3，DC＝9，求EF的长．参考答案1．解：∵CE平分∠BCD，∴∠BCE＝∠DCE，∵四边形ABCD是平行四边形，∴AB＝CD，AD＝BC，AB∥CD，∴∠BEC＝∠DCE，∴∠BEC＝∠BCE，∴BC＝BE＝5，∴AD＝5，∵EA＝3，ED＝4，在△AED中，32+42＝52，即EA2+ED2＝AD2，∴∠AED＝90°，∴CD＝AB＝3+5＝8，∠EDC＝90°，在Rt△EDC中，CE＝＝＝4．故选：C．2．证明：延长DE到点F，使EF＝DE，连接FC，DC，AF，∵点D，E分别是△ABC的边AB，AC的中点，∴AD＝BD，AE＝EC，∴四边形ADCF是平行四边形，∴CF AD．即CF BD，∴四边形DBCF是平行四边形，∴DF BC，∴DE∥BC，且DE＝BC．∴正确的证明顺序是②→③→①→④，故选：A．3．解：该正九边形内角和＝180°×（9﹣2）＝1260°， 则每个内角的度数＝．故选：D ．4．解：∵四边形ABCD 是平行四边形，∴AB ＝CD ，AD ＝BC ；OD ＝OB ，OA ＝OC ；∵OD ＝OB ，OA ＝OC ，∠AOD ＝∠BOC ；∴△AOD ≌△COB （SAS ）；①同理可得出△AOB ≌△COD （SAS ）；②∵BC ＝AD ，CD ＝AB ，BD ＝BD ；∴△ABD ≌△CDB （SSS ）；③同理可得：△ACD ≌△CAB （SSS ）．④因此本题共有4对全等三角形．故选：C ．5．证明：∵四边形ABCD 是正方形，∴AB ∥CD ，AD ∥BC ，AB ＝BC ，∠ABE ＝∠BCF ＝90°， 在△ABE 和△BCF 中，，∴△ABE ≌△BCF （SAS ），∴∠BFC ＝∠AEB ，∵AD ∥BC ，AB ∥CD ，∴∠DAE ＝∠AEB ，∠BFC ＝∠ABF ，故图中与∠AEB 相等的角的个数是3．故选：C ．6．解：∵正方形ABCD ，DPMN 的面积分别为S 1，S 2， ∴S 1＝CD 2，S 2＝PD 2，在Rt △PCD 中，PC 2＝CD 2+PD 2，∴S 1+S 2＝CP 2，故A 结论正确；连接CF ，∵点H与B关于CE对称，∴CH＝CB，∠BCE＝∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE＝EH，∠EHC＝∠B＝90°，∠BEC＝∠HEC，∴CH＝CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH＝∠FCD，FH＝FD，∴∠ECH+∠FCH＝∠BCD＝45°，即∠ECF＝45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG＝CG，∵∠BEC＝∠HEC，∠B＝∠FGE＝90°，∴△FEG∽△CEB，∴＝＝，∴FG＝2EG，设EG＝x，则FG＝2x，∴CG＝2x，CF＝2x，∴EC＝3x，∵EB2+BC2＝EC2，∴BC2＝9x2，∴BC2＝x2，∴BC＝x，在Rt△FDC中，FD＝＝＝x，∴3FD＝AD，∴AF＝2FD，故B结论正确；∵AB∥CN，∴＝，∵PD＝ND，AE＝CD，∴CD＝4PD，故C结论正确；∵EG＝x，FG＝2x，∴EF＝x，∵FH＝FD＝x，∵BC＝x，∴AE＝x，作HQ⊥AD于Q，HS⊥CD于S，∴HQ∥AB，∴＝，即＝，∴HQ＝x，∴CS＝CD﹣HQ＝x﹣x＝x∴cos∠HCD＝＝＝，故结论D错误，故选：D．7．解：∵在△ABC中，D，E分别是AB，BC的中点，∴DE是△ABC的中位线，∴DE AC．A、根据∠B＝∠F不能判定AC∥DF，即不能判定四边形ADFC为平行四边形，故本选项错误．B、根据∠B＝∠BCF可以判定CF∥AB，即CF∥AD，由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形，故本选项正确．C、根据AC＝CF不能判定AC∥DF，即不能判定四边形ADFC为平行四边形，故本选项错误．D、根据AD＝CF，FD∥AC不能判定四边形ADFC为平行四边形，故本选项错误．故选：B．8．解：根据邻边相等的平行四边形是菱形，可知选项D正确，故选：D．9．解：∵在正方形ABCD中，A、B、C三点的坐标分别是（﹣1，2）、（﹣1，0）、（﹣3，0），∴D（﹣3，2），∴将正方形ABCD向右平移3个单位，则平移后点D的坐标是（0，2），故选：B．二．填空题（共7小题）10．解：∵菱形ABCD的周长为16，∴AB＝BC＝CD＝AD＝4，OA＝OC，∵OE∥AB，∴BE＝CE，∴OE是△ABC的中位线，∴OE＝AB＝2，故答案为：2．11．解：如图，∵AB∥CD，AD∥BC，∴四边形ABCD是平行四边形，作AE⊥BC于点E，AF⊥DC于点F，∵两张等宽的长方形纸条交叉叠放在一起，∴AE＝AF，＝BC•AE＝DC•AF，∴S平行四边形ABCD∴BC＝DC，∴▱ABCD是菱形．故答案为：是．12．解：∵，∴平行四边形A'B'C'D'的底边A′D′边上的高等于A′B′的一半，∴∠A'＝30°．故答案为：30°13．解：如图以AB为x轴，AD为y轴，建立平面直角坐标系，根据图形可以得到：每6次反弹为一个循环组依次循环，经过6次反弹后动点回到出发点（6，0），且每次循环它与AB边的碰撞有2次，∵2019÷6＝336…3，当点P第2019次碰到矩形的边时为第337个循环组的第3次反弹，点P的坐标为（6，4）∴它与AB边的碰撞次数是＝336×2+1＝673次故答案为67314．解：∵四边形ABCD是平行四边形，∴AD∥BC，DC∥AB，∵∠ADC＝119°，DF⊥BC，∴∠ADF＝90°，则∠EDH＝29°，∵BE⊥DC，∴∠DEH＝90°，∴∠DHE＝∠BHF＝90°﹣29°＝61°．故答案为：61．15．解：∵四边形ABCD是菱形，∴BO＝DO＝4，AO＝CO，AC⊥BD，∴BD＝8，∵S＝AC×BD＝24，菱形ABCD∴AC＝6，∴OC＝AC＝3，∴BC＝＝5，＝BC×AH＝24，∵S菱形ABCD∴AH＝；故答案为：．16．解：△CBD绕点C顺时针旋转90°得到的图形如上图所示．∵D的坐标为（3，1），∴OA＝3，AD＝1∵在正方形OABC中，OA＝AB，∴BD＝AB﹣AD＝2，∴OD'＝BD＝2，∴D'的坐标为（﹣2，0），故答案为（﹣2，0）．三．解答题（共11小题）17．（1）证明：∵四边形ABCD是菱形，∴AB＝AD，∵点E，F分别是边AD，AB的中点，∴AF＝AE，在△ABE和△ADF中，，∴△ABE≌△ADF（SAS）；（2）解：连接BD，如图：∵四边形ABCD是菱形，∴AB＝AD，∠A＝∠C＝60°，∴△ABD是等边三角形，∵点E是边AD的中点，∴BE⊥AD，∴∠ABE＝30°，∴AE＝tan30°BE＝BE＝1，AB＝2AE＝2，∴AD＝AB＝2，∴菱形ABCD的面积＝AD×BE＝2×＝2．18．（1）证明：∵BE＝CF，∴BE+EC＝CF+EC，在△ABC和△DEF中，，∴△ABC≌△DEF（SSS）；（2）证明：由（1）得：△ABC≌△DEF，∴∠B＝∠DEF，∴AB∥DE，又∵AB＝DE，∴四边形ABED是平行四边形．19．（1）证明：四边形ABCD是菱形∴AB＝BC，AD∥BC∴∠A＝∠CBF∵BE⊥AD、CF⊥AB∴∠AEB＝∠BFC＝90°∴△AEB≌△BFC（AAS）∴AE＝BF（2）∵E是AD中点，且BE⊥AD∴直线BE为AD的垂直平分线∴BD＝AB＝220．解：（1）∵四边形ABCD是正方形，∴AB＝CD，AB∥CD，∴∠DCA＝∠BAC，∵DF∥BE，∴∠CFD＝∠BEA，∵∠BAC＝∠BEA+∠ABE，∠DCA＝∠CFD+∠CDF，∴∠ABE＝∠CDF，在△ABE和△CDF中，∵，∴△ABE≌△CDF（AAS），∵BH＝DG，∴BE+BH＝DF+DG，即EH＝GF，∵EH∥GF，∴四边形EHFG是平行四边形；（2）如图，连接BD，交EF于O，∵四边形ABCD是正方形，∴BD⊥AC，∴∠AOB＝90°，∵AB＝2，∴OA＝OB＝2，Rt△BOE中，EB＝4，∴∠OEB＝30°，∴EO＝2，∵OD＝OB，∠EOB＝∠DOF，∵DF∥EB，∴∠DFC＝∠BEA，∴△DOF≌△BOE（AAS），∴OF＝OE＝2，∴EF＝4，∴FM＝2，EM＝6，过F作FM⊥EH于M，交EH的延长线于M，∵EG∥FH，∴∠FHM＝∠GEH，∵tan∠GEH＝tan∠FHM＝＝2，∴，∴HM＝1，∴EH＝EM﹣HM＝6﹣1＝5，FH＝＝＝，∴四边形EHFG的周长＝2EH+2FH＝2×5+2＝10+2．21．证明：连接AC，如图所示：在△ABC和△CDA中，，∴△ABC≌△CDA（SSS），∴∠BAC＝∠DCA，∠ACB＝∠CAD，∴AB∥CD，BC∥AD，∴四边形ABCD是平行四边形．22．（1）证明：∵四边形ABCD是矩形，∴∠B＝∠D＝90°，AB＝CD，AD＝BC，AD∥BC，在Rt△ABE和Rt△CDF中，，∴Rt△ABE≌Rt△CDF（HL）；（2）解：当AC⊥EF时，四边形AECF是菱形，理由如下：∵△ABE≌△CDF，∴BE＝DF，∵BC＝AD，∴CE＝AF，∵CE∥AF，∴四边形AECF是平行四边形，又∵AC⊥EF，∴四边形AECF是菱形．23．证明：（1）∵四边形ABCD是平行四边形，∴AB∥DC，∴∠1＝∠2，∵EF是BD的中垂线，∴OD＝OB，∠3＝∠4＝90°，∴△DOF≌△BOE，∴OE＝OF；（2）作DG⊥AB，垂足为G，∵∠A＝60°，AD＝6，∴∠ADG＝30°，∴AG＝AD＝3，∴DG＝，∵AB＝2AD，∴AB＝2×6＝12，BG＝AB﹣AG＝12﹣3＝9，∴tan∠ABD＝24．证明：∵▱ABCD的对角线AC，BD交于点O，∴AO＝CO，AD∥BC，∴∠EAC＝∠FCO，在△AOE和△COF中，∴△AOE≌△COF（ASA），∴AE＝CF．25．（1）证明：∵点O是AC中点，∴OA＝OC，∵CE∥AB，∴∠DAO＝∠ECO，在△AOD和△COE中，，∴△AOD≌△COE（ASA），∴AD＝CE，∵CE∥AB，∴四边形AECD是平行四边形，又∵CD是Rt△ABC斜边AB上的中线，∴CD＝AD，∴四边形AECD是菱形；（2）由（1）知，四边形AECD是菱形，∴AC⊥ED，在Rt△AOD中，tan∠DAO＝，设OD＝3x，OA＝4x，则ED＝2OD＝6x，AC＝2OA＝8x，由题意可得：，解得：x＝1，∴OD＝3，∵O，D分别是AC，AB的中点，∴OD是△ABC的中位线，∴BC＝2OD＝6．26．解：（1）∵四边形ABCD是菱形，AB＝2，∴菱形ABCD的周长为：8；（2）∵四边形ABCD是菱形，AC＝2，AB＝2∴AC⊥BD，AO＝1，∴BO＝，∴BD＝227．解：（1）证明：过点E、F分别作AD、BC的垂线，垂足分别是G、H．∵∠3＝∠4，∠1＝∠2，EG⊥AD，EM⊥CD，EM′⊥AB∴EG＝ME，EG＝EM′∴EG＝ME＝M′E＝MM′同理可证：FH＝NF＝N′F＝NN′∵CD∥AB，MM′⊥CD，NN′⊥CD，∴MM′＝NN′∴ME＝NF＝EG＝FH又∵MM′∥NN′，MM′⊥CD∴四边形EFNM是矩形．（2）∵DC∥AB，∴∠CDA+∠DAB＝180°，∵，∠2＝∠DAB∴∠3+∠2＝90°在Rt△DEA，∵AE＝4，DE＝3，∴AD＝＝5．∵四边形ABCD是平行四边形，∴∠DAB＝∠DCB，又∵∠2＝∠DAB，∠5＝∠DCB，∴∠2＝∠5由（1）知GE＝NF在Rt△GEA和Rt△CNF中∴△GEA≌△CNF∴AG＝CN在Rt△DME和Rt△DGE中∵DE＝DE，ME＝EG∴△DME≌△DGE∴DG＝DM∴DM+CN＝DG+AG＝AD＝5∴MN＝CD﹣DM﹣CN＝9﹣5＝4．∵四边形EFNM是矩形．∴EF＝MN＝4。
2021年全国中考数学真题分类汇编--四边形：矩形、菱形、正方形(答案版 )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
【分析】延长 ，交 于点 ，交 于点 ，连接 ，交 于点 ，先根据正方形的性质、三角形全等的判定定理与性质得出 ，再根据矩形的判定与性质可得 ，由此可判断①；先根据三角形全等的性质可得 ，再根据矩形的性质可得 ，然后根据等腰三角形的性质可得 ，由此可判断③；根据直角三角形的性质可得 ，从而可得 ，由此可判断②；先根据垂线段最短可得当 时， 取得最小值，再解直角三角形可得 的最小值，从而可得 的最小值，由此可判断④．
而 于 都不一定成立，故 都不符合题意，
故选：A
8.（2021•浙江省温州市）由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结CG，延长BE交CG于点H．若AE＝2BE，则 （ ）
A． B． C． D．
【分析】如图，过点G作GT⊥CF交CF的延长线于T,设BH交CF于M,AE交DF于N．设BE＝AN＝CH＝DF＝a,则AE＝BM＝CF＝DN＝2a,想办法求出BH,CG,可得结论．
∵ ，∴ ，
∴ ，故④正确．
故选B．
二．填空题
1.（2021•湖南省衡阳市）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P的运动路线为O﹣A﹣D﹣O，点Q的运动路线为O﹣C﹣B﹣O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为(2 +3)厘米．
【详解】解：由题意得，△AED和△BCG是等腰直角三角形，
2021届中考数学压轴题专项训练 四边形【含答案】
2021届中考数学压轴题专项训练四边形【含答案】1．如图①，在矩形ABCD中，已知BC＝8cm，点G为BC边上一点，满足BG＝AB＝6cm，动点E以1cm/s的速度沿线段BG从点B移动到点G，连接AE，作EF⊥AE，交线段CD于点F．设点E移动的时间为t（s），CF的长度为y（cm），y与t的函数关系如图②所示．（1）图①中，CG＝ 2 cm，图②中，m＝ 2 ；（2）点F能否为线段CD的中点？若可能，求出此时t的值，若不可能，请说明理由；（3）在图①中，连接AF，AG，设AG与EF交于点H，若AG平分△AEF的面积，求此时t的值．解：（1）∵BC＝8cm，BG＝AB＝6cm，∴CG＝2cm，∵EF⊥AE，∴∠AEB+∠FEC＝90°，且∠AEB+∠BAE＝90°，∴∠BAE＝∠FEC，且∠B＝∠C＝90°，∴△ABE∽△ECF，∴，∵t＝6，∴BE＝6cm，CE＝2cm，∴∴CF＝2cm，∴m＝2，故答案为：2，2；（2）若点F是CD中点，∴CF＝DF＝3cm，∵△ABE∽△ECF，∴，∴∴EC2﹣8EC+18＝0∵△＝64﹣72＝﹣8＜0，∴点F不可能是CD中点；（3）如图①，过点H作HM⊥BC于点M，∵∠C＝90°，HM⊥BC，∴HM∥CD，∴△EHM∽△EFC，∴∵AG平分△AEF的面积，∴EH＝FH，∴EM＝MC，∵BE＝t，EC＝8﹣t，∴EM＝CM＝4﹣t，∴MG＝CM﹣CG＝2﹣，∵，∴∴CF＝∵EM＝MC，EH＝FH，∴MH＝CF＝∵AB＝BG＝6，∴∠AGB＝45°，且HM⊥BC，∴∠HGM＝∠GHM＝45°，∴HM＝GM，∴＝2﹣，∴t＝2或t＝12，且t≤6，∴t＝2．2．问题提出：（1）如图1，△ABC的边BC在直线n上，过顶点A作直线m∥n，在直线m上任取一点D，连接BD、CD，则△ABC的面积＝△DBC的面积．问题探究：（2）如图2，在菱形ABCD和菱形BGFE中，BG＝6，∠A＝60°，求△DGE的面积；问题解决：（3）如图3，在矩形ABCD中，AB＝12，BC＝10，在矩形ABCD内（也可以在边上）存在一点P，使得△ABP的面积等于矩形ABCD的面积的，求△ABP周长的最小值．解：问题提出：（1）∵两条平行线间的距离一定，∴△ABC与△DBC同底等高，即△ABC的面积＝△DBC的面积，故答案为：＝；问题探究：（2）如图2，连接BD，∵四边形ABCD，四边形BGFE是菱形，∴AD∥BC，BC∥EF，AD＝AB，BG＝BE，∴∠A＝∠CBE＝60°，∴△ADB是等边三角形，△BGE是等边三角形，∴∠ABD＝∠GBE＝60°，∴BD∥GE，∴S△DGE＝S△BGE＝BG2＝9；（3）如图3，过点P作PE∥AB，交AD于点E，∵△ABP的面积等于矩形ABCD的面积的，∴×12×AE＝×12×10∴AE＝8，作点A关于PE的对称点A'，连接A'B交PE于点P，此时△ABP周长最小，∴A'E＝AE＝8，∴AA'＝16，∴A'B＝＝＝20，∴△ABP周长的最小值＝AP+AB+PB＝A'P+PB+AB＝20+12＝32．3．（1）方法感悟：如图①，在正方形ABCD中，点E、F分别为DC、BC边上的点，且满足∠EAF＝45°，连接EF．将△ADE绕点A顺时针旋转90°得到△ABG，易证△GAF≌△EAF，从而得到结论：DE+BF＝EF．根据这个结论，若CD＝6，DE＝2，求EF的长．（2）方法迁移：如图②，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，且∠EAF＝∠BAD，试猜想DE，BF，EF之间有何数量关系，证明你的结论．（3）问题拓展：如图③，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F 分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，试探究线段EF、BE、FD之间的数量关系，请直接写出你的猜想（不必说明理由）．解：（1）方法感悟：∵将△ADE绕点A顺时针旋转90°得到△ABG，∴GB＝DE＝2，∵△GAF≌△EAF∴GF＝EF，∵CD＝6，DE＝2∴CE＝4，∵EF2＝CF2+CE2，∴EF2＝（8﹣EF）2+16，∴EF＝5；（2）方法迁移：DE+BF＝EF，理由如下：如图②，将△ADE绕点A顺时针旋转90°得到△ABH，由旋转可得，AH＝AE，BH＝DE，∠1＝∠2，∠D＝∠ABH，∵∠EAF＝∠DAB，∴∠HAF＝∠1+∠3＝∠2+∠3＝∠BAD，∴∠HAF＝∠EAF，∵∠ABH+∠ABF＝∠D+∠ABF＝180°，∴点H、B、F三点共线，在△AEF和△AHF中，∴△AEF≌△AHF（SAS），∴EF＝HF，∵HF＝BH+BF，∴EF＝DE+BF．（3）问题拓展：EF＝BF﹣FD，理由如下：在BC上截取BH＝DF，∵∠B+∠ADC＝180°，∠ADC+∠ADF＝180°，∴∠B＝∠ADF，且AB＝AD，BH＝DF，∴△ABH≌△ADF（SAS）∴∠BAH＝∠DAF，AH＝AD，∵∠EAF＝∠BAD，∴∠DAE+∠BAH＝∠BAD，∴∠HAE＝∠BAD＝∠EAF，且AE＝AE，AH＝AD，∴△HAE≌△FAE（SAS）∴HE＝EF，∴EF＝HE＝BE﹣BH＝BE﹣DF．4．如图1，在▱ABCD中，AB＝3cm，BC＝5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图2，设移动时间为t（s）（0＜＜4），连结PQ，MQ，解答下列问题：（1）当t为何值时，PQ∥MN？（2）当t为何值时，∠CPQ＝45°？（3）当t为何值时，PQ⊥MQ？解：（1）∵AB＝3cm，BC＝5cm，AC⊥AB，∴AC＝＝4cm，∵MN∥AB，PQ∥MN，∴PQ∥AB，∴，∴，∴t＝s（2）如图2，过点Q作QE⊥AC，则QE∥AB，∴，∴，∴CE＝，QE＝t，∵∠CPQ＝45°，∴PE＝QE＝t，∴t+t+t＝4，∴t＝s（3）如图2，过点P作PF⊥BC于F点，过点M作MH⊥BC，交BC延长线于点H，∴四边形PMHF是矩形，∴PM＝FH＝5，∵∠A＝∠PFC＝90°，∠ACB＝∠PCF，∴△ABC∽△FPC，∴，∴＝∴PF＝，CF＝，∴QH＝5﹣FQ＝5﹣（CF﹣CQ）＝，∵PQ⊥MQ，∴∠PQF+∠MQH＝90°，且∠PQF+∠FPQ＝90°，∴∠FPQ＝∠MQH，且∠PFQ＝∠H＝90°，∴△PFQ∽△QHM，∴，∴∴t＝s．5．问题背景：如图1，在正方形ABCD的内部，作∠DAE＝∠ABF＝∠BCG＝∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得四边形EFGH是正方形．类比探究：如图2，在正△ABC的内部，作∠1＝∠2＝∠3，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）．（1）△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；（2）△DEF是否为正三角形？请说明理由；（3）如图3，进一步探究发现，△ABD的三边存在一定的等量关系，设BD＝a，AD＝b，AB＝c，请探索a，b，c满足的等量关系．（1）△ABD≌△BCE≌△CAF；理由如下：∵△ABC是正三角形，∴∠CAB＝∠ABC＝∠BCA＝60°，AB＝BC＝AC，又∵∠1＝∠2＝∠3，∴∠ABD＝∠BCE＝∠CAF，在△ABD、△BCE和△CAF中，，∴△ABD≌△BCE≌△CAF（ASA）；（2）△DEF是正三角形；理由如下：∵△ABD≌△BCE≌△CAF，∴∠ADB＝∠BEC＝∠CFA，∴∠FDE＝∠DEF＝∠EFD，∴△DEF是正三角形；（3）c2＝a2+ab+b2．作AG⊥BD于G，如图所示：∵△DEF是正三角形，∴∠ADG＝60°，在Rt△ADG中，DG＝b，AG＝b，在Rt△ABG中，c2＝（a+b）2+（b）2，∴c2＝a2+ab+b2．6．如图，在四边形ABCD中，AC是对角线，∠ABC＝∠CDA＝90°，BC＝CD，延长BC交AD的延长线于点E．（1）求证：AB＝AD；（2）若AE＝BE+DE，求∠BAC的值；（3）过点E作ME∥AB，交AC的延长线于点M，过点M作MP⊥DC，交DC的延长线于点P，连接PB．设PB＝a，点O是直线AE上的动点，当MO+PO的值最小时，点O与点E是否可能重合？若可能，请说明理由并求此时MO+PO的值（用含a的式子表示）；若不可能，请说明理由．（1）证明：∵∠ABC＝∠CDA＝90°，∵BC＝CD，AC＝AC，∴Rt△ABC≌Rt△ADC（HL）．∴AB＝AD．（2）解：∵AE＝BE+DE，又∵AE＝AD+DE，∴AD＝BE．∵AB＝AD，∴AB＝BE．∴∠BAD＝∠BEA．∵∠ABC＝90°，∴∠BAD═45°．∵由（1）得△ABC≌△ADC，∴∠BAC＝∠DAC．∴∠BAC═22.5°．（3）解：当MO+PO的值最小时，点O与点E可以重合，理由如下：∵ME∥AB，∴∠ABC＝∠MEC＝90°，∠MAB＝∠EMA．∵MP⊥DC，∴∠MPC＝90°．∴∠MPC＝∠ADC＝90°．∴PM∥AD．∴∠EAM＝∠PMA．由（1）得，Rt△ABC≌Rt△ADC，∴∠EAC＝∠MAB，∴∠EMA＝∠AMP．即MC平分∠PME．又∵MP⊥CP，ME⊥CE，∴PC＝EC．如图，连接PB，连接PE，延长ME交PD的延长线于点Q．设∠EAM＝α，则∠MAP＝α．在Rt△ABE中，∠BEA＝90°﹣2α．在Rt△CDE中，∠ECD＝90°﹣∠BEA＝2α．∵PC＝EC，∴∠PEB＝∠EPC＝∠ECD＝α．∴∠PED＝∠BEA+∠PEB＝90°﹣α．∵ME∥AB，∴∠QED＝∠BAD＝2α．当∠PED＝∠QED时，∵∠PDE＝∠QDE，DE＝DE，∴△PDE≌△QDE（ASA）．∴PD＝DQ．即点P与点Q关于直线AE成轴对称，也即点M、点E、点P关于直线AE的对称点Q，这三点共线，也即MO+PO的值最小时，点O与点E重合．因为当∠PED＝∠QED时，90°﹣α＝2α，也即α＝30°．所以，当∠ABD＝60°时，MO+PO取最小值时的点O与点E重合．此时MO+PO的最小值即为ME+PE．∵PC＝EC，∠PCB＝∠ECD，CB＝CD，∴△PCB≌△ECD（SAS）．∴∠CBP＝∠CDE＝90°．∴∠CBP+∠ABC＝180°．∴A，B，P三点共线．当∠ABD＝60°时，在△PEA中，∠PAE＝∠PEA＝60°．∴∠EPA＝60°．∴△PEA为等边三角形．∵EB⊥AP，∴AP＝2AB＝2a．∴EP＝AE＝2a．∵∠EMA＝∠EAM＝30°，∴EM＝AE＝2a．∴MO+PO的最小值为4a．7．已知：如图，在正方形ABCD中，点E在AD边上运动，从点A出发向点D运动，到达D点停止运动．作射线CE，并将射线CE绕着点C逆时针旋转45°，旋转后的射线与AB边交于点F，连接EF．（1）依题意补全图形；（2）猜想线段DE，EF，BF的数量关系并证明；（3）过点C作CG⊥EF，垂足为点G，若正方形ABCD的边长是4，请直接写出点G 运动的路线长．解：（1）补全图形如图1所示：（2）线段DE，EF，BF的数量关系为：EF＝DE+BF．理由如下：延长AD到点H，使DH＝BF，连接CH，如图2所示：∵四边形ABCD是正方形，∴∠BCD＝∠ADC＝∠B＝90°，BC＝DC，∴∠CDH＝90°＝∠B，在△CDH和△CBF中，，∴△CDH≌△CBF（SAS）．∴CH＝CF，∠DCH＝∠BCF．∵∠ECF＝45°，∴∠ECH＝∠ECD+∠DCH＝∠ECD+∠BCF＝45°．∴∠ECH＝∠ECF＝45°．在△ECH和△ECF中，，∴△EC H≌△ECF（SAS）．∴EH＝EF．∵EH＝DE+DH，∴EF＝DE+BF；（3）由（2）得：△ECH≌△ECF（SAS），∴∠CEH＝∠CEF，∵CD⊥AD，CG⊥EF，∴CD＝CG＝4，∴点G的运动轨迹是以C为圆心4为半径的弧DB，∴点G运动的路线长＝＝2π．8．如图，在正方形ABCD中，P是边BC上的一动点（不与点B，C重合），点B关于直线AP的对称点为E，连接AE．连接DE并延长交射线AP于点F，连接BF．（1）若∠BAP＝α，直接写出∠ADF的大小（用含α的式子表示）；（2）求证：BF⊥DF；（3）连接CF，用等式表示线段AF，BF，CF之间的数量关系，并证明．（1）解：由轴对称的性质得：∠EAP＝∠BAP＝α，AE＝AB，∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∴∠DAE＝90°﹣2α，AD＝AE，∴∠ADF＝∠AED＝（180°﹣∠DAE）＝（90°+2α）＝45°+α；（2）证明：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∵点E与点B关于直线AP对称，∴∠AEF＝∠ABF，AE＝AB．∴AE＝AD．∴∠ADE＝∠AED．∵∠AED+∠AEF＝180°，∴在四边形ABFD中，∠ADE+∠ABF＝180°，∴∠BFD+∠BAD＝180°，∴∠BFD＝90°∴BF⊥DF；（3）解：线段AF，BF，CF之间的数量关系为AF＝BF+CF，理由如下：过点B作BM⊥BF交AF于点M，如图所示：∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°，∴∠ABM＝∠CBF，∵点E与点B关于直线AP对称，∠BFD＝90°，∴∠MFB＝∠MFE＝45°，∴△BMF是等腰直角三角形，∴BM＝BF，FM＝BF，在△AMB和△CFB中，，∴△AMB≌△CFB（SAS），∴AM＝CF，∵AF＝FM+AM，∴AF＝BF+CF．9．如图1，已知等腰Rt△ABC中，E为边AC上一点，过E点作EF⊥AB于F点，以为边作正方形，且AC＝3，EF＝．（1）如图1，连接CF，求线段CF的长；（2）将等腰Rt△ABC绕点旋转至如图2的位置，连接BE，M点为BE的中点，连接MC，MF，求MC与MF关系．解：（1）如图1，∵△ABC是等腰直角三角形，AC＝3，∴AB＝3，过点C作CM⊥AB于M，连接CF，∴CM＝AM＝AB＝，∵四边形AGEF是正方形，∴AF＝EF＝，∴MF＝AM﹣AF＝﹣，在Rt△CMF中，CF＝＝＝；（2）CM＝FM，CM⊥FM，理由：如图2，过点B作BH∥EF交FM的延长线于H，连接CF，CH，∴∠BHM＝∠EFM，∵四边形AGEF是正方形，∴EF＝AF∵点M是BE的中点，∴BM＝EM，在△BMH和△EMF中，，∴△BMH≌△EMF（AAS），∴MH＝MF，BH＝EF＝AF∵四边形AGEF是正方形，∴∠FAG＝90°，EF∥AG，∵BH∥EF，∴BH∥AG，∴∠BAG+∠ABH＝180°，∴∠CBH+∠ABC+∠BAC+∠CAG＝180°．∵△ABC是等腰直角三角形，∴BC＝AC，∠ABC＝∠BAC＝45°，∴∠CBH+∠CAG＝90°，∵∠CAG+∠CAF＝90°，∴∠CBH＝∠CAF，在△BCH和△ACF中，，∴△BCH≌△ACF（SAS），∴CH＝CF，∠BCH＝∠ACF，∴∠HCF＝∠BCH+∠BCF＝∠ACF+∠BCF＝90°，∴△FCH是等腰直角三角形，∵MH＝MF，∴CM＝FM，CM⊥FM；10．如图将正方形ABCD绕点A顺时针旋转角度α（0°＜α＜90°）得到正方形AB′C′D′．（1）如图1，B′C′与AC交于点M，C′D′与AD所在直线交于点N，若MN∥B′D′，求α；（2）如图2，C′B′与CD交于点Q，延长C′B′与BC交于点P，当α＝30°时．①求∠DAQ的度数；②若AB＝6，求PQ的长度．解：（1）如图1中，∵MN∥B′D′，∴∠C′MN＝∠C′B′D′＝45°，∠C′NM＝∠C′D′B′＝45°，∴∠C′MN＝∠C′NM，∴C′M＝C′N，∵C′B′＝C′D′，'∴MB′＝ND′，∵AB′＝AD′，∠AB′M＝∠AD′N＝90°，∴△AB′M≌△AD′N（SAS），∴∠B′AM＝∠D′AN，∵∠B′AD′＝90°，∠MAN＝45°，∴∠B′AM＝∠D′AN＝22.5°，∵∠BAC＝45°，∴∠BAB′＝22.5°，∴α＝22.5°．（2）①如图2中，∵∠AB′Q＝∠ADQ＝90°，AQ＝AQ，AB′＝AD，∴Rt△AQB′≌Rt△AQD（HL），∴∠QAB′＝∠QAD，∵∠BAB′＝30°，∠BAD＝90°，∴∠B′AD＝30°，∴∠QAD＝∠B′AD＝30°．②如图2中，连接AP，在AB上取一点E，使得AE＝EP，连接EP．设PB＝a．∵∠ABP＝∠AB′P＝90°，AP＝AP，AB＝AB′，∴Rt△APB≌Rt△APB′（HL），∴∠BAP＝∠PAB′＝15°，∵EA＝EP，∴∠EAP＝∠EPA＝15°，∴∠BEP＝∠EAP+∠EPA＝30°，∴PE＝AE＝2a，BE＝a，∵AB＝6，∴2a+a＝6，∴a＝6（2﹣）．∴PB＝6（2﹣），∴PC＝BC﹣PB＝6﹣6（2﹣）＝6﹣6，∵∠CPQ+∠BPB′＝180°，∠BAB′+∠BPB′＝180°，∴∠CPQ＝∠BAB′＝30°，∴PQ＝＝＝12﹣4．11．已知，如图1，在边长为2的正方形ABCD中，E是边AB的中点，点F在边AD上，过点A作AG⊥EF，分别交线段CD、EF于点G、H（点G不与线段CD的端点重合）．（1）如图2，当G是边CD中点时，求AF的长；（2）设AF＝x，四边形FHGD的面积是y，求y关于x的函数关系式，并写出x的取值范围；（3）联结ED，当∠FED＝45°时，求AF的长．解：（1）∵E是AB的中点，AB＝2，∴AE＝AB＝1，同理可得DG＝1，∵AG⊥EF，∴∠AHF＝∠HAF+∠AFH＝90°，∵四边形ABCD是正方形，∴∠ADG＝90°＝∠DAG+∠AGD，∴∠AFH＝∠AGD，∵∠EAF＝∠ADG＝90°，∴△EAF∽△ADG，∴，即，∴AF＝；（2）如图1，由（1）知：△EAF∽△ADG，∴，即，∴DG＝2x，∵∠HAF＝∠DAG，∠AHF＝∠ADG＝90°，∴∠AHF∽△ADG，∴＝，∴＝，∴AH＝＝，FH＝＝，∴y＝S△ADG﹣S△AFH，＝，＝2x﹣，如图2，当G与C重合时，∵EF⊥AG，∴∠AHE＝90°，∵∠EAH＝45°，∴∠AEH＝45°，∴AF＝AE＝1，∴0＜x＜1；∴y关于x的函数关系式为：y＝2x﹣（0＜x＜1）；（3）如图3，过D作DM⊥AG，交BC于M，连接EM，延长EA至N，使AN＝CM，连接DN，设CM＝a，则AN＝a，∵AD＝CD，∠NAD＝∠DCM＝90°，∴△NAD≌△MCD（SAS），∴∠ADN＝∠CDM，DN＝DM，∵EF⊥AG，DM⊥AG，∴EF∥DM，∴∠EDM＝∠FED＝45°，∴∠ADE+∠CDM＝∠EDM＝45°，∴∠NDA+∠ADE＝∠NDE＝∠EDM，∵ED＝ED，∴△NDE≌△MDE（SAS），∴EN＝EM＝a+1，∵BM＝2﹣a，在Rt△EBM中，由勾股定理得：BE2+BM2＝EM2，∴12+（2﹣a）2＝（a+1）2，a＝，∵∠AEF+∠EAG＝∠EAG+∠DAG，∴∠AEF＝∠DAG＝∠CDM，∴tan∠AEF＝tan∠CDM，∴，∴，∴AF＝．12．如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD 是垂美四边形吗？请说明理由；（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD．试证明：AB2+CD2＝AD2+BC2；（3）解决问题：如图3，△ACB中，∠ACB＝90°，AC⊥AG且AC＝AG，AB⊥AE 且AE＝AB，连结CE、BG、GE．已知AC＝4，AB＝5，求GE的长．解：（1）四边形ABCD是垂美四边形，理由如下：连接AC，BD，∵AB＝AD，∴点A在线段BD的垂直平分线上，∵CB＝CD，∴点C在线段BD的垂直平分线上，∴AC是线段BD的垂直平分线，∴四边形ABCD是垂美四边形；（2）∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°，由勾股定理得，AD2+BC2＝AO2+DO2+BO2+CO2，AB2+CD2＝AO2+BO2+CO2+DO2，∴AD2+BC2＝AB2+CD2；故答案为：AB2+CD2＝AD2+BC2；（3）∵∠CAG＝∠BAE＝90°，∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，在△GAB和△CAE中，，∴△GAB≌△CAE（SAS），∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，∴∠ABG+∠AME＝90°，即CE⊥BG，∴四边形CGEB是垂美四边形，由（2）得，CG2+BE2＝CB2+GE2，∵AC＝4，AB＝5，∴BC＝3，CG＝4，BE＝5，∴GE2＝CG2+BE2﹣CB2＝73，∴GE＝．13．如图1，四边形ACEB，连接BC，∠ACB＝∠BEC＝90°，D在AB上，连接CD，∠ACD＝∠ABC，BE＝CD．（1）求证：四边形CDBE为矩形；（2）如图2，连接DE，DE交BC于点O，若tan∠A＝2，在不添加任何辅助线和字母的情况下，请直接写出图中所有长度与AD的长度相等的线段．（1）证明：∵∠ACB＝90°，∴∠A+∠ABC＝90°，∵∠ACD＝∠ABC，∴∠A+∠ACD＝90°，∴∠ADC＝90°，∴∠BDC＝180°﹣90°＝90°＝∠BEC，在Rt△BCD和Rt△CBE中，，∴Rt△BCD≌Rt△CBE（HL），∴BD＝CE，∵CD＝BE，∴四边形CDBE是平行四边形，又∵∠BEC＝90°，∴四边形CDBE为矩形；（2）解：图中所有长度与AD的长度相等的线段为AC＝OC＝OB＝OD＝OE＝AD．理由如下：由（1）得：四边形CDBE为矩形，∠ADC＝90°，∴BC＝DE，OD＝OE，OB＝OC，∴OC＝OB＝OD＝OE＝BC，∵∠ADC＝∠ACB＝90°，∴tan∠A＝2＝＝，∴CD＝2AD，BC＝2AC，∴AC＝＝＝AD，∴DE＝BC＝2AC，∴OC＝OB＝OD＝OE＝BC＝AC＝AD，∴AC＝OC＝OB＝OD＝OE＝AD．14．如图在直角坐标系中，四边形ABCO为正方形，A点的坐标为（a，0），D点的坐标为（0，b），且a，b满足（a﹣3）2+|b﹣|＝0．（1）求A点和D点的坐标；（2）若∠DAE＝∠OAB，请猜想DE，OD和EB的数量关系，说明理由．（3）若∠OAD＝30°，以AD为三角形的一边，坐标轴上是否存在点P，使得△PAD 为等腰三角形，若存在，直接写出有多少个点P，并写出P点的坐标，选择一种情况证明．解：（1）∵（a﹣3）2+|b﹣|＝0，∴a＝3，b＝，∴D（0，），A（3，0）；（2）DE＝OD+EB；理由如下：如图1，在CO的延长线上找一点F，使OF＝BE，连接AF，在△AOF和△ABE中，，∴△AOF≌△ABE（SAS），∴AF＝AE，∠OAF＝∠BAE，又∵∠OAB＝90°，∠DAE＝，∴∠BAE+∠DAO＝45°，∴∠DAF＝∠OAF+∠DAO＝45°，∴∠DAF＝∠EAD，在△AFD和△AED中，，∴△AFD≌△AED（SAS），∴DF＝DE＝OD+EB；（3）有3种情况共6个点：①当DA＝DP时，如图2，Rt△ADO中，OD＝，OA＝3，∴AD＝＝＝2，∴P 1（﹣3，0），P2（0，3），P3（0，﹣）；②当AP4＝DP4时，如图3，∴∠ADP4＝∠DAP4＝30°，∴∠OP4D＝60°，Rt△ODP 4中，∠ODP4＝30°，OD＝，∴OP4＝1，∴P4（1，0）；③当AD＝AP时，如图4，∴AD＝AP 5＝AP6＝2，∴P 5（3+2，0），P6（3﹣2，0），综上，点P的坐标为：∴P（﹣3，0）或（0，3）或（0，﹣）或（1，0）或（3+2，0）或（3﹣2，0）．证明：P 5（3+2，0），∵∠OAD＝30°且△ADO是直角三角形，又∵AO＝3，DO＝，∴DA＝2，而P 5A＝|3+2﹣3|＝2，∴P5A＝DA，∴△P5AD是等腰三角形．15．已知，在四边形ABCD中，点M、N、P、Q分别为边AB、AD、CD、BC的中点，连接MN、NP、PQ、MQ．（1）如图1，求证：四边形MNPQ为平行四边形；（2）如图2，连接AC，AC分别交MN、PQ于点E、F，连接BD，BD分别交MQ、NP于点G、H，AC与BD交于点O，且AC⊥BD，若tan∠ADB＝，在不添加任何辅助线的情况下，请直接写出图2中所有长度等于OD的线段．（1）证明：如图1，连接BD．∵Q，P分别是BC，CD的中点，所以PQ∥BD，PQ＝BD．∵M，N分别是AB，AD的中点．∴MN∥BD，MN＝BD．∴PQ∥MN，且PQ＝MN．∴四边形MNPQ是平行四边形．（2）解：∵四边形MNPQ是平行四边形，AC⊥BD，∴四边形MNPQ是矩形，∴四边形NHOE和四边形EOGM都是矩形，∴NH＝OE＝MG＝AE＝，∵tan∠ADB＝，∴，∴NH＝OE＝MG＝AE＝．即长度等于OD的线段有NH，OE，MG，AE．。
2021届中考数学热点题型专练12 四边形【含答案】
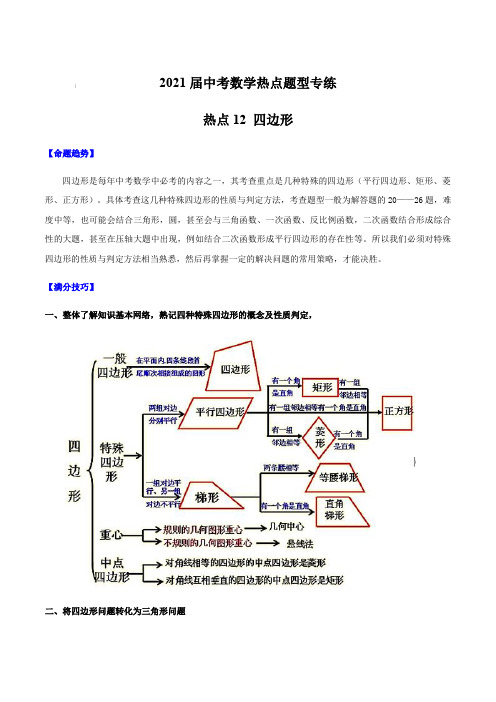
2021届中考数学热点题型专练热点12 四边形【命题趋势】四边形是每年中考数学中必考的内容之一，其考查重点是几种特殊的四边形（平行四边形、矩形、菱形、正方形）。
具体考查这几种特殊四边形的性质与判定方法，考查题型一般为解答题的20——26题，难度中等，也可能会结合三角形，圆，甚至会与三角函数、一次函数、反比例函数，二次函数结合形成综合性的大题，甚至在压轴大题中出现，例如结合二次函数形成平行四边形的存在性等。
所以我们必须对特殊四边形的性质与判定方法相当熟悉，然后再掌握一定的解决问题的常用策略，才能决胜。
【满分技巧】一、整体了解知识基本网络，熟记四种特殊四边形的概念及性质判定，二、将四边形问题转化为三角形问题其实四边形问题的解决最终都会转化到三角形的问题，所以思考问题时一定不能只想着四边形，只要考查四边形的综合题一定会利用到三角形的相关知识，一定要想着将四边形的问题转化成三角形的问题，然后利用三角形的相关知识解决。
三、做一定量的基础练习，培养分析问题和分析图形的能力【限时检测】（建议用时：30分钟）一、选择题1.如图，足球图片正中的黑色正五边形的内角和是（）A．180°B．360°C．540°D．720°【答案】C【解析】黑色正五边形的内角和为：（5﹣2）×180°＝540°，故选：C2.如图，在ABCD中，全等三角形的对数共有()A．2对B．3对C．4对D．5对【答案】C【解析】四边形ABCD是平行四边形，∴AB=CD,AD=BC,OD=OB,OA=OC∴OD=OB,OA=OC,∴AOD=∴BOC∴∴AOD∴∴COB同理可得∴AOB∴∴COD∴BC=AD,CD=AB,BD=BD∴∴ABD∴∴CDB同理可得∴ACD∴∴CAB因此本题共有4对全等三角形故选：C．3.已知一个多边形的内角和是1080°，则这个多边形是（）A．五边形B．六边形C．七边形D．八边形【答案】D【解析】设所求多边形边数为n，则（n﹣2）•180°＝1080°，解得n＝8．故选：D．4.如图，在正方形ABCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且∴EOF＝90°，OC、EF交于点G．给出下列结论：∴∴COE∴∴DOF；∴∴OGE∴∴FGC；∴四边形CEOF的面积为正方形ABCD面积的；∴DF2+BE2＝OG•OC．其中正确的是（）A ．∴∴∴∴B ．∴∴∴C ．∴∴∴D ．∴∴【答案】B【解析】∴∴四边形ABCD 是正方形， ∴OC ＝OD ，AC ∴BD ，∴ODF ＝∴OCE ＝45°， ∴∴MON ＝90°， ∴∴COM ＝∴DOF ， ∴∴COE ∴∴DOF （ASA ）， 故∴正确；∴∴∴EOF ＝∴ECF ＝90°， ∴点O 、E 、C 、F 四点共圆， ∴∴EOG ＝∴CFG ，∴OEG ＝∴FCG ， ∴OGE ∴∴FGC ， 故∴正确；∴∴∴COE ∴∴DOF ， ∴S ∴COE ＝S ∴DOF ，∴S 四边形CEOF =S∴OCD=14S 正方形ABCD ，故∴正确；∴）∴∴COE ∴∴DOF ， ∴OE ＝OF ，又∴∴EOF ＝90°， ∴∴EOF 是等腰直角三角形， ∴∴OEG ＝∴OCE ＝45°，∴∴OEG ∴∴OCE ， ∴OE ：OC ＝OG ：OE ， ∴OG •OC ＝OE 2， ∴OC =12 AC ，OE ＝EF ，∴OG •AC ＝EF 2， ∴CE ＝DF ，BC ＝CD ， ∴BE ＝CF ，又∴Rt∴CEF 中，CF 2+CE 2＝EF 2， ∴BE 2+DF 2＝EF 2， ∴OG •AC ＝BE 2+DF 2， 故∴错误， 故选：B ．5.如图，在平行四边形ABCD 中，M 、N 是BD 上两点，BM ＝DN ，连接AM 、MC 、CN 、NA ，添加一个条件，使四边形AMCN 是矩形，这个条件是（ ）A ．OM ＝ACB ．MB ＝MOC ．BD ∴ACD ．∴AMB ＝∴CND【答案】A【解析】∴四边形ABCD 是平行四边形，∴对角线BD上的两点M、N满足BM＝DN，∴OB﹣BM＝OD﹣DN，即OM＝ON，∴四边形AMCN是平行四边形，∴OM＝AC，∴MN＝AC，∴四边形AMCN是矩形．故选：A．6.如图，四边形ABCD为菱形，A，B两点的坐标分别是（2，0），（0，1），点C，D在坐标轴上，则菱形ABCD的周长等于（）A．B．4C．4D．20【答案】C【解析】∴A，B两点的坐标分别是（2，0），（0，1），∴AB＝，∴四边形ABCD是菱形，∴菱形的周长为4，故选：C．7. .一个十二边形的内角和等于（）A．2160°B．2080°C．1980°D．1800°【答案】D【解析】十二边形的内角和等于：（12﹣2）•180°＝1800°；故选：D．8. .下列命题正确的是（）A．有一个角是直角的平行四边形是矩形B．四条边相等的四边形是矩形C．有一组邻边相等的平行四边形是矩形D．对角线相等的四边形是矩形【答案】A【解析】A、有一个角是直角的平行四边形是矩形，是真命题；B、四条边相等的四边形是菱形，是假命题；C、有一组邻边相等的平行四边形是菱形，是假命题；D、对角线相等的平行四边形是矩形，是假命题；故选：A．9. .如图，E是∴ABCD边AD延长线上一点，连接BE，CE，BD，BE交CD于点F．添加以下条件，不能判定四边形BCED为平行四边形的是（）A．∴ABD＝∴DCE B．DF＝CF C．∴AEB＝∴BCD D．∴AEC＝∴CBD【答案】C【解析】∴四边形ABCD是平行四边形，∴AD∴BC，AB∴CD，∴DE∴BC，∴ABD＝∴CDB，∴∴ABD＝∴DCE，∴∴DCE＝∴CDB，∴BD∴CE，∴BCED为平行四边形，故A正确；∴DE∴BC，∴∴DEF＝∴CBF，在∴DEF与∴CBF中，，∴∴DEF∴∴CBF（AAS），∴EF＝BF，∴DF＝CF，∴四边形BCED为平行四边形，故B正确；∴AE∴BC，∴∴AEB＝∴CBF，∴∴AEB＝∴BCD，∴∴CBF＝∴BCD，∴CF＝BF，同理，EF＝DF，∴不能判定四边形BCED为平行四边形；故C错误；∴AE∴BC，∴∴DEC+∴BCE＝∴EDB+∴DBC＝180°，∴∴AEC＝∴CBD，∴∴BDE＝∴BCE，∴四边形BCED为平行四边形，故D正确，故选：C．10..菱形不具备的性质是()A．是轴对称图形B．是中心对称图形C．对角线互相垂直D．对角线一定相等【答案】D【解析】A、是轴对称图形，故正确；B、是中心对称图形，故正确；C、对角线互相垂直，故正确；D、对角线不一定相等，故不正确；故选：D．11..如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（）A ．2.5B ．3C ．4D ．5【答案】A【解析】∴四边形ABCD 为菱形， ∴CD ＝BC ＝＝5，且O 为BD 的中点，∴E 为CD 的中点， ∴OE 为∴BCD 的中位线， ∴OE ＝CB ＝2.5，故选：A ．12. .如图，在正方形ABCD 中，E 是BC 边上的一点，4BE =，8EC =，将正方形边AB 沿AE 折叠到AF ，延长EF 交DC 于G ，连接AC ，现在有如下4个结论： ∴45EAC ∠=︒；∴FG FC =；∴//FC AG ；∴14GFC S ∆=． 其中正确结论的个数是( )A ．1B ．2C ．3D ．4【答案】B【解析】如图，连接DF ．四边形ABC 都是正方形，AB AD BC CD ∴===，90ABE BAD ADG ECG ∠=∠=∠=∠=︒，由翻折可知：AB AF =，90ABE AFE AFG ∠=∠=∠=︒，2BE EF ==，BAE EAF ∠=∠， 90AFG ADG ∠=∠=︒，AG AG =，AD AF =， Rt AGD Rt ∴∆≅∴()AGF HL ∆，DG FG ∴=，GAF GAD ∠=∠，设GD GF x ==，1()452EAG EAF GAF BAF DAF ∴∠=∠+∠=∠+∠=︒，故∴正确，在Rt ECG ∆中，222EG EC CG =+，222(2)8(12)x x ∴+=+-， 6x ∴=，12CD BC BE EC ==+=， 6DG CG ∴==， FG GC ∴=，易知GFC ∆不是等边三角形，显然FG FC ≠，故∴错误， GF GD GC ==， 90DFC ∴∠=︒， CF DF ∴⊥，AD AF =，GD GF =，AG DF ∴⊥，//CF AG ∴，故∴正确，168242ECG S ∆=⨯⨯=，:6:43:2FG FE ==，:3:5FG EG ∴=，3722455GFC S ∆∴=⨯=，故∴错误，故选：B ． 二、填空题13.如图，矩形ABCD 中，AC 、BD 交于点O ，M 、N 分别为BC 、OC 的中点．若4MN =，则AC 的长为 ．【答案】16【解析】M 、N 分别为BC 、OC 的中点， 28BO MN ∴==．四边形ABCD 是矩形， 216AC BD BO ∴===．故答案为16．14. .如图，该硬币边缘镌刻的正九边形每个内角的度数是 ．【答案】140° 【解析】该正九边形内角和＝180°×（9﹣2）＝1260°， 则每个内角的度数＝＝140°．故答案为：140°．15.如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE 、折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，若DE ＝5，则GE 的长为 ．【答案】4913【解析】∴四边形ABCD 为正方形， ∴AB ＝AD ＝12，∴BAD ＝∴D ＝90°，由折叠及轴对称的性质可知，∴ABF ∴∴GBF ，BF 垂直平分AG ， ∴BF ∴AE ，AH ＝GH ， ∴∴F AH +∴AFH ＝90°， 又∴∴F AH +∴BAH ＝90°， ∴∴AFH ＝∴BAH ，∴∴ABF∴∴DAE（AAS），∴AF＝DE＝5，在Rt∴ADF中，BF＝＝＝13，S∴ABF＝AB•AF＝BF•AH，∴12×5＝13AH，∴AH＝，∴AG＝2AH＝，∴AE＝BF＝13，∴GE＝AE﹣AG＝13﹣＝，故答案为：．16.在平行四边形ABCD中，∴A＝30°，AD＝4，BD＝4，则平行四边形ABCD的面积等于．【答案】16 3【解析】过D作DE∴AB于E，在Rt∴ADE中，∴∴A＝30°，AD＝4，∴DE＝AD＝2，AE＝AD＝6，在Rt∴BDE中，∴BD＝4，∴BE＝＝＝2，∴AB＝8，∴平行四边形ABCD的面积＝AB•DE＝8×2＝16 3 ，故答案为：16 3 ．17.三个形状大小相同的菱形按如图所示方式摆放，已知∴AOB＝∴AOE＝90°，菱形的较短对角线长为2cm．若点C落在AH的延长线上，则∴ABE的周长为cm．【答案】12+8 2【解析】如图所示，连接IC，连接CH交OI于K，则A，H，C在同一直线上，CI＝2，∴三个菱形全等，∴CO＝HO，∴AOH＝∴BOC，又∴∴AOB＝∴AOH+∴BOH＝90°，∴∴COH＝∴BOC+∴BOH＝90°，即∴COH是等腰直角三角形，∴∴HCO＝∴CHO＝45°＝∴HOG＝∴COK，∴∴CKO＝90°，即CK∴IO，设CK＝OK＝x，则CO＝IO＝x，IK＝x﹣x，∴Rt∴CIK中，（x﹣x）2+x2＝22，解得x2＝2+，又∴S菱形BCOI＝IO×CK＝IC×BO，∴x2＝×2×BO，∴BO＝2+2，∴BE＝2BO＝4+4，AB＝AE＝BO＝4+2，∴∴ABE的周长＝4+4+2（4+2）＝12+8，故答案为：12+8．三、解答题18.如图1，在正方形ABCD中，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B 作BF CE⊥于点G，交AD于点F．（1）求证：ABF BCE∆≅∆；（2）如图2，当点E运动到AB中点时，连接DG，求证：DC DG=；（3）如图3，在（2）的条件下，过点C作CM DG⊥于点H，分别交AD，BF于点M，N，求MNNH的值．【解析】（1）证明：BF CE ⊥， 90CGB ∴∠=︒， 90GCB CBG ∴∠+∠=，四边形ABCD 是正方形， 90CBE A ∴∠=︒=∠，BC AB =， 90FBA CBG ∴∠+∠=， GCB FBA ∴∠=∠，()ABF BCE ASA ∴∆≅∆；（2）证明：如图2，过点D 作DH CE ⊥于H ， 设2AB CD BC a ===， 点E 是AB 的中点， 12EA EB AB a ∴===， 5CE a ∴，在Rt CEB ∆中，根据面积相等，得BG CE CB EB =，25BG ∴=， 2245CG CB BG ∴=-，90DCE BCE ∠+∠=︒，90CBF BCE ∠+∠=︒， DCE CBF ∴∠=∠，CD BC =，90CQD CGB ∠=∠=︒，()CQD BGC AAS ∴∆≅∆，25CQ BG ∴==， 25GQ CG CQ CQ ∴=-=， DQ DQ =，90CQD GQD ∠=∠=︒， ()DGQ CDQ SAS ∴∆≅∆， CD GD ∴=；（3）解：如图3，过点D 作DH CE ⊥于H ， 1122CDG S DQ CH DG ∆==， 85CG DQ CH a DG ∴==， 在Rt CHD ∆中，2CD a =， 2265DH CD CH a ∴=-=，90MDH HDC ∠+∠=︒，90HCD HDC ∠+∠=︒， MDH HCD ∴∠=∠， CHD DHM ∴∆∆∽， ∴34DH DH CH HM ==， 910HM a ∴=，在Rt CHG ∆中，45CG =，85CH a =， 2245GH CG CH a ∴-=，90MGH CGH ∠+∠=︒，90HCG CGH ∠+∠=︒，QGH HCG ∴∠=∠， QGH GCH ∴∆∆∽， ∴HN HGHG CH=， 225HG HN a CG ∴==，12MN HM HN a ∴=-=，∴152245aMN NH a ==19.如图，在四边形ABCD 中，AD ∴BC ，延长BC 到E ，使CE ＝BC ，连接AE 交CD 于点F ，点F 是CD 的中点．求证：（1）∴ADF∴∴ECF．（2）四边形ABCD是平行四边形．【解析】（1）∴AD∴BC，∴∴DAF＝∴E，∴点F是CD的中点，∴DF＝CF，在∴ADF与∴ECF中，，∴∴ADF∴∴ECF（AAS）；（2）∴∴ADF∴∴ECF，∴AD＝EC，∴CE＝BC，∴AD＝BC，∴AD∴BC，∴四边形ABCD是平行四边形．20.如图，在正方形ABCD中，分别过顶点B，D作//BE DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：22AB =4EB =，tan 23GEH ∠=EHFG 的周长．【解析】（1）四边形ABCD 是正方形， AB CD ∴=，//AB CD ，DCA BAC ∴∠=∠， //DF BE ，CFD BEA ∴∠=∠，BAC BEA ABE ∠=∠+∠，DCA CFD CDF ∠=∠+∠， ABE CDF ∴∠=∠，在ABE ∆和CDF ∆中，ABE CDF AEB CFD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE CDF AAS ∴∆≅∆，BE DF ∴=，BH DG =，BE BH DF DG ∴+=+，即EH GF =，//EH GF ，∴四边形EHFG 是平行四边形；（2）如图，连接BD ，交EF 于O ，四边形ABCD 是正方形，BD AC ∴⊥，90AOB ∴∠=︒， 22AB =2OA OB ∴==，Rt BOE ∆中，4EB =，30OEB ∴∠=︒，∴EO=2 3 ，OD OB =，EOB DOF ∠=∠， //DF EB ，DFC BEA ∴∠=∠，()DOF BOE AAS ∴∆≅∆，23OF OE ∴==43EF ∴= 23FM ∴=，6EM =，过F 作FM EH ⊥于M ，交EH 的延长线于M ， ∴EG//FH ，FHM GEH ∴∠=∠，tan tan 23FM GEH FHM HM∠=∠== ∴2323= ∴HM=1，∴EH=EM -HM=6-1=52222(23)113FH FM HM ++ ∴四边形EHFG 的周长222521310213EH FH =+=⨯+=+。
2021年湖北省各市中考数学分类解析专题10四边形
专题10：四边形一、选择题1. 〔2021年湖北恩施3分〕如下图，以下四个选项中，不是正方体外表展开图的是【】2. 〔2021年湖北恩施3分〕如下图，在平行四边形纸片上作随机扎针实验，针头扎在阴影区域内的概率为【】A．13B．14C．15D．163. 〔2021年湖北恩施3分〕如下图，在平行四边形ABCD中，AC与BD相交于点O，E 为OD的中点，连接AE并延长交DC于点F，那么DF：FC=【】A．1：4 B．1：3 C．2：3 D．1：24. 〔2021年湖北荆门3分〕四边形ABCD中，对角线AC、BD相交于点O，给出以下四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD从中任选两个条件，能使四边形ABCD为平行四边形的选法有【】A．3种B．4种C．5种D．6种5. 〔2021年湖北荆门3分〕如以下图所示，等腰梯形ABCD，AD∥BC，假设动直线l垂直于BC，且向右平移，设扫过的阴影局部的面积为S，BP为x，那么S关于x的函数图象大致是【】6. 〔2021年湖北荆州3分〕将一边长为2的正方形纸片折成四局部，再沿折痕折起来，恰好能不重叠地搭建成一个三棱锥，那么三棱锥四个面中最小的面积是【】A．1 B．32C．12D．237. 〔2021年湖北潜江、仙桃、天门、江汉油田3分〕假设平行四边形的一边长为2，面积为46】A．3与4之间B．4与5之间C．5与6之间D．6与7之间【答案】B。
8. 〔2021年湖北十堰3分〕如图，梯形ABCD中，AD∥BC，AB=DC=3，AD=5，∠C=60°，那么下底BC的长为【】A．8 B．9 C．10 D．119. 〔2021年湖北随州4分〕如图，在菱形ABCD中，∠BAD=120°．△ABC的周长是15，那么菱形ABCD的周长是【】A．25 B．20 C．15 D．1010. 〔2021年湖北随州4分〕如图，正方形ABCD 中，AB=3，点E 在边CD 上，且CD=3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连接AG ，CF ．以下结论：①点G 是BC 中点；②FG=FC ；③FGC 9S 10∆=．其中正确的选项是【 】A ．①②B ．①③C ．②③D ．①②③11. 〔2021年湖北咸宁3分〕如图，正方形ABCD是一块绿化带，其中阴影局部EOFB，GHMN都是正方形的花圃．自由飞翔的小鸟，将随机落在这块绿化带上，那么小鸟在花圃上的概率为【】A．1732B．12C．1736D．173812. 〔2021年湖北襄阳3分〕如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD 的周长为23，那么平行四边形ABCD的两条对角线的和是【】A．18 B．28 C．36 D．46∴平行四边形ABCD的两条对角线的和=BD+AC=2〔DO+OC〕=36。
【2021中考数学】四边形压轴题含答案
2021年中考九年级数学：四边形压轴题1、解答下列各题（1）已知：如图1，直线AB、CD被直线AC所截，点E在AC上，且A D CED∠=∠+∠，求证：//AB CD；（2）如图2，在正方形ABCD中，8DF=．AB=，6BE=，4①试判断AEF∆的形状，并说明理由；②求AEF∆的面积．2、如图，在梯形ABCD中，AD∥BC，AD＝3，DC＝5，BC＝10，梯形的高为4．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t（秒）．（1）当MN∥AB时，求t的值；（2）试探究：t为何值时，△MNC为等腰三角形．3、如图1，已知矩形ABCD，连接AC，将△ABC沿AC所在直线翻折，得到△AEC，AE交CD于点F．（1）求证：DF＝EF；（2）如图2，若∠BAC＝30°，点G是AC的中点，连接DE，EG，求证：四边形ADEG 是菱形．4、如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．5、如图1，在ABCD中，以BC为边作等边BCP=．∆，交AD于点E，F，且AE DF （1）求证：四边形ABCD是矩形；（2）如图2，连接AP，AC，若1EF=，3BC=．①求证：AP PC⊥；②求AC的长．6、已知：正方形ABCD，等腰直角三角板的直角顶点落在正方形的顶点D处，使三角板绕点D旋转．（1）当三角板旋转到图1的位置时，猜想CE与AF的数量关系，并加以证明；（2）在（1）的条件下，若DE＝1，AE＝，CE＝3，求∠AED的度数；（3）若BC＝4，点M是边AB的中点，连结DM，DM与AC交于点O，当三角板的一边DF与边DM重合时（如图2），若OF＝，求CN的长．7、如图1，在ABCD中，60ABC∠=︒，:7:8AB AD=，E为CD边上一点，8CE=，连接AE，BE，且AE AB=．（1）求证：EB平分AEC∠；（2）当:2:5CE ED=时，在AD上找一点P，使PB PE+的和最小，并求出最小值；（3）如图2，过点E作EF BE⊥交AD于点F，求DFDE的值．8、问题探究（1）如图①，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，则线段BE、EF、FD之间的数量关系为______；（2）如图②，在△ADC中，AD＝2，CD＝4，∠ADC是一个不固定的角，以AC为边向△ADC的另一侧作等边△ABC，连接BD，则BD的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由；问题解决（3）如图③，在四边形ABCD中，AB＝AD，∠BAD＝60°，BC＝4，若BD⊥CD，垂足为点D，则对角线AC的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由．9、如图，已知正方形ABCD，AB＝8，点E是射线DC上一个动点（点E与点D不重合），连接AE，BE，以BE为边在线段AD的右侧作正方形BEFG，连结CG．（1）当点E在线段DC上时，求证：△BAE≌△BCG；（2）在（1）的条件下，若CE＝2，求CG的长；（3）连接CF，当△CFG为等腰三角形时，求DE的长．10、在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上点F处．（1）如图1，若BC＝2BA，求∠CBE的度数；（2）如图2，当AB＝5，且AF•FD＝10时，求BC的长；（3）如图3，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝AN+FD时，求的值．11、已知在梯形ABCD中，AD∥BC，AC＝BC＝10，cos∠ACB＝，点E在对角线AC上（不与点A、C重合），∠EDC＝∠ACB，DE的延长线与射线CB交于点F，设AD的长为x．（1）如图1，当DF⊥BC时，求AD的长；（2）设EC＝y，求y关于x的函数解析式，并直接写出定义域；（3）当△DFC是等腰三角形时，求AD的长．12、如图，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8cm，矩形ABCD的长和宽分别为8cm和2cm，C点和M点重合，BC和MN在一条直线上．令Rt△PMN不动，矩形ABCD 沿MN所在直线向右以每秒1cm的速度移动（如图2），直到C点与N点重合为止．设移动x秒后，矩形ABCD与△PMN重叠部分的面积为ycm2．求y与x之间的函数关系式．13、如图①所示，已知正方形ABCD和正方形AEFG，连接DG，BE．（1）发现：当正方形AEFG绕点A旋转，如图②所示．①线段DG与BE之间的数量关系是；②直线DG与直线BE之间的位置关系是；（2）探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG ＝2AE时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG、DE，若AE＝1，AB＝2，求BG2+DE2的值（直接写出结果）．14、（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为BE＝AF （2）【拓展研究】在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF 的数量关系有无变化？请仅就图2的情形给出证明；（3）【问题发现】当正方形CDEF旋转到B，E，F三点共线的时候，直接写出线段AF的长．参考答案1、解答下列各题（1）已知：如图1，直线AB、CD被直线AC所截，点E在AC上，且A D CED∠=∠+∠，求证：//AB CD；（2）如图2，在正方形ABCD中，8DF=．BE=，4AB=，6①试判断AEF∆的形状，并说明理由；②求AEF∆的面积．【解答】解：（1）延长AC至F，如图1，∠=∠+∠，∠=∠+∠，A D CEDFCD CED D∴∠=∠，FCD A∴；//AB CD（2）①如图2，延长AF交BC的延长线于点G，正方形ABCD中，8CF=，AB=，4∴==，DF CF4∠=∠=︒，AFD CFG∠=∠，D FCG90∴∆≅∆，()ADF GCF ASA∴=，AF FG8BE=，AB=，6∴，AE102810EG CE CG =+=+=，AE EG ∴=，EF AG ∴⊥，AEF ∴∆是直角三角形；②AEF ABE ADF CEF ABCD S S S S S ∆∆∆∆=---正方形11164868442222=-⨯⨯-⨯⨯-⨯⨯， 20=．2、如图，在梯形ABCD 中，AD ∥BC ，AD ＝3，DC ＝5，BC ＝10，梯形的高为4．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t （秒）．（1）当MN ∥AB 时，求t 的值；（2）试探究：t 为何值时，△MNC 为等腰三角形．【解答】解：（1）如图1，过D 作DG ∥AB 交BC 于G 点．则四边形ADGB 是平行四边形．∵MN ∥AB ，∴MN ∥DG ，∴BG ＝AD ＝3．∴GC＝10﹣3＝7．由题意知，当M、N运动到t秒时，CN＝t，CM＝10﹣2t．∵DG∥MN，∴△MNC∽△GDC．∴＝，即＝．解得，t＝；（2）分三种情况讨论：①当NC＝MC时，如图2，即t＝10﹣2t，解得：t＝；②当MN＝NC时，如图3，过N作NE⊥MC于E．由等腰三角形三线合一性质得EC＝MC＝（10﹣2t）＝5﹣t．在Rt△CEN中，cos C＝＝，又在Rt△DHC中，cos C＝＝，∴＝．解得：t＝；③当MC＝MN时，如图4，过M作MF⊥CN于F点，FC＝NC＝t．∵∠C＝∠C，∠MFC＝∠DHC＝90°，∴△MFC∽△DHC，∴＝，即＝，解得：t＝．综上所述，当t＝、t＝或t＝时，△MNC为等腰三角形．3、如图1，已知矩形ABCD，连接AC，将△ABC沿AC所在直线翻折，得到△AEC，AE交CD于点F．（1）求证：DF＝EF；（2）如图2，若∠BAC＝30°，点G是AC的中点，连接DE，EG，求证：四边形ADEG 是菱形．【解答】解：（1）∵四边形ABCD是矩形，∴AD＝BC，∠D＝∠B＝90°，∵将△ABC沿AC所在直线翻折，得到△AEC，∴∠E＝∠B＝90°，CE＝BC．∴∠D＝∠E，AD＝CE，∵∠AFD＝∠CFE，∴△ADF≌△CEF（AAS），∴DF＝EF；（2）∵四边形ABCD是矩形，∴AD＝BC，∠ADC＝∠B＝90°，∵将△ABC沿AC所在直线翻折，得到△AEC，∴∠AEC＝∠B＝90°，CE＝BC，∵∠CAB＝30°，∴∠CAE＝30°，∴CE＝AC，∵点G是AC的中点，∴CE＝AG＝EG＝AD，∴∠AEG＝∠EAG＝30°，∴∠DAE＝30°，∴∠DAE＝∠AEG，∴AD∥GE，∴四边形ADEG是菱形．4、如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E．作DF⊥AE于点H，分别交AB，AC于点F，G．（1）判断△AFG的形状并说明理由．（2）求证：BF＝2OG．【迁移应用】（3）记△DGO的面积为S1，△DBF的面积为S2，当＝时，求的值．【拓展延伸】（4）若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF，当△BEF的面积为矩形ABCD面积的时，请直接写出tan∠BAE的值．【解答】（1）解：如图1中，△AFG是等腰三角形．理由：∵AE平分∠BAC，∴∠1＝∠2，∵DF⊥AE，∴∠AHF＝∠AHG＝90°，∵AH＝AH，∴△AHF≌△AHG（ASA），∴AF＝AG，∴△AFG是等腰三角形．（2）证明：如图2中，过点O作OL∥AB交DF于L，则∠AFG＝∠OLG．∵AF＝AG，∴∠AFG＝∠AGF，∵∠AGF＝∠OGL，∴∠OGL＝∠OLG，∴OG＝OL，∵OL∥AB，∴△DLO∽△DFB，∴＝，∵四边形ABCD是矩形，∴BD＝2OD，∴BF＝2OL，∴BF＝2OG．（3）解：如图3中，过点D作DK⊥AC于K，则∠DKA＝∠CDA＝90°，∵∠DAK＝∠CAD，∴△ADK∽△ACD，∴＝，∵S1＝•OG•DK，S2＝•BF•AD，又∵BF＝2OG，＝，∴＝＝，设CD＝2x，AC＝3x，则AD＝x，∴＝＝．（4）解：设OG＝a，AG＝k．①如图4中，连接EF，当点F在线段AB上时，点G在OA上．∵AF＝AG，BF＝2OG，∴AF＝AG＝k，BF＝2a，∴AB＝k+2a，AC＝2（k+a），∴AD2＝AC2﹣CD2＝[2（k+a）]2﹣（k+2a）2＝3k2+4ka，∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，∴△ABE∽△DAF，∴＝，即＝，∴＝，∴BE＝，由题意：10××2a×＝AD•（k+2a），∴AD2＝10ka，即10ka＝3k2+4ka，∴k＝2a，∴AD＝2a，∴BE＝＝a，AB＝4a，∴tan∠BAE＝＝．②如图5中，当点F在AB的延长线上时，点G在线段OC上，连接EF．∵AF＝AG，BF＝2OG，∴AF＝AG＝k，BF＝2a，∴AB＝k﹣2a，AC＝2（k﹣a），∴AD2＝AC2﹣CD2＝[2（k﹣a）]2﹣（k﹣2a）2＝3k2﹣4ka，∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF，∴△ABE∽△DAF，∴＝，即＝，∴＝，∴BE＝，由题意：10××2a×＝AD•（k﹣2a），∴AD2＝10ka，即10ka＝3k2﹣4ka，∴k＝a，∴AD＝a，∴BE＝＝a，AB＝a，∴tan∠BAE＝＝，综上所述，tan∠BAE的值为或．5、如图1，在ABCD中，以BC为边作等边BCP=．∆，交AD于点E，F，且AE DF （1）求证：四边形ABCD是矩形；（2）如图2，连接AP，AC，若1EF=，3BC=．①求证：AP PC⊥；②求AC的长．【解答】证明：（1）BCP ∆是等边三角形，60PBC PCB P ∴∠=∠=︒=∠，PB PC =，四边形ABCD 是平行四边形，AB CD ∴=，//AD BC ，180A D ∠+∠=︒，60PEF PBC ∴∠=∠=︒，60PFE PBC ∠=∠=︒，PEF ∴∆是等边三角形，PE PF ∴=，PB PE PC PF ∴-=-，BE CF ∴=，又AB CD =，AE DF =，()ABE DCF SSS ∴∆≅∆，A D ∴∠=∠，180A D ∠+∠=︒，90A D ∴∠=∠=︒，∴平行四边形ABCD 是矩形；（2）①PEF ∆是等边三角形，1PE PF EF ∴===，PBC ∆是等边三角形，3PB BC PC ∴===，2BE CF ∴==，3AD BC ==，1EF =，AE DF =，1AE DF ∴==，2AF CF ∴==，1PF DF ==，又AFP CFD ∠=∠，()AFP CFD SAS ∴∆≅∆，90APC D ∴∠=∠=︒，AP PC ∴⊥；②AFP CFD ∆≅∆，AP CD ∴=，AB AP ∴=，又BC CP =，AC AC =，()APC ABC SSS ∴∆≅∆，30ACB ACP ∴∠=∠=︒，2AC AB ∴=，3BC =，AB ∴AC =6、已知：正方形ABCD ，等腰直角三角板的直角顶点落在正方形的顶点D 处，使三角板绕点D 旋转．（1）当三角板旋转到图1的位置时，猜想CE 与AF 的数量关系，并加以证明；（2）在（1）的条件下，若DE ＝1，AE ＝，CE ＝3，求∠AED 的度数；（3）若BC ＝4，点M 是边AB 的中点，连结DM ，DM 与AC 交于点O ，当三角板的一边DF 与边DM 重合时（如图2），若OF ＝，求CN 的长．【分析】（1）由正方形与等腰直角三角形的性质判断出△ADF≌△CDE即可；（2）设DE＝k，表示出AE，CE，EF，判断出△AEF为直角三角形，即可求出∠AED；（3）由AB∥CD，得出＝＝＝，求出DM，DO，再判断出△DFN∽△DCO，得到＝，求出DN即可【解答】解：（1）CE＝AF；证明：在正方形ABCD，等腰直角三角形CEF中，FD＝DE，CD＝CA，∠ADC＝∠EDF ＝90°∴∠ADF＝∠CDE，∴△ADF≌△CDE，∴CE＝AF，（2）∵DE＝1，AE＝，CE＝3，∴EF＝，∴AE2+EF2＝AF2∴△AEF为直角三角形，∴∠AEF＝90°∴∠AED＝∠AEF+DEF＝90°+45°＝135°；（3）∵M是AB中点，∴MA＝AB＝AD，∵AB∥CD，∴＝＝＝，在Rt△DAM中，DM＝＝＝2，∴DO＝，∵OF＝，∴DF＝，∵∠DFN＝∠DCO＝45°，∠FDN＝∠CDO，∴△DFN∽△DCO，∴＝，∴＝，∴DN＝，∴CN＝CD﹣DN＝4﹣＝7、如图1，在ABCD中，60CE=，连AB AD=，E为CD边上一点，8ABC∠=︒，:7:8接AE，BE，且AE AB=．（1）求证：EB 平分AEC ∠；（2）当:2:5CE ED =时，在AD 上找一点P ，使PB PE +的和最小，并求出最小值；（3）如图2，过点E 作EF BE ⊥交AD 于点F ，求DF DE的值．【解答】（1）证明：如图1中，四边形ABCD 是平行四边形，//AB CD ∴，ABE BEC ∴∠=∠，AB AE =，ABE AEB ∴∠=∠，BEC AEB ∴∠=∠，BE ∴平分AEC ∠．（2）解：如图1中，作的E 关于AD 的对称点M ，直线EM 交AD 于H ，交BC 的延长线于T ，连接BM ，PM ．四边形ABCD 是平行四边形，:7:8AB AD =，∴可以假设7AB CD k ==，8AD BC k ==，60ABC D ∠=∠=︒8EC =，90T EHD ∠=∠=︒，60D ECT ∠=∠=︒，cos604CT EC ∴=︒=，sin 60ET EC =︒=，78DE k ∴=-，1(78)2DH k =-，8)EH k =-，198(78)422AH k k k =--=+， 在Rt AHE ∆中，222AE AH EH =+，222949(4)8)]2k k k ∴=++-， 解得2k =或4，:2:5CE DE =，2k ∴=时，不符合题意舍弃，4k ∴=，32BC AD ∴==，EH EM ==，32436BT ∴=+=，TM ==BM ∴=，PE PM =，PB PE PB PM BM ∴+=+， 1221PB PE ∴+，PB PE ∴+的最小值为．（3）解：如图2中，过点E 作EH AD ⊥于H 交BC 的延长线于T ．由（2）可知，当4k =时，20DE =，10DH =，EH =4ET ==，36BT =． 90T EHF BEF ∠=∠=∠=︒，90BET FEH ∴∠+∠=︒，90FEH EFH ∠+∠=︒，BET EFH ∴∠=∠，BTE EHF ∴∆∆∽， ∴BT ET EH FH=，∴=， 103FH ∴=， 403DF FH DH ∴=+=， ∴4023203DF DE ==．当2k =时，6DE =，3DH -，EH =4CT =，ET =20BT ∴=，BTE EHF ∆∆∽， ∴BT ET EH FH=，∴=， 95FH ∴=，924355DF =+=， ∴244565DF DE ==， 综上所述，DF DE 的值为23或45．8、问题探究（1）如图①，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，则线段BE、EF、FD之间的数量关系为BE+DF＝EF；（2）如图②，在△ADC中，AD＝2，CD＝4，∠ADC是一个不固定的角，以AC为边向△ADC的另一侧作等边△ABC，连接BD，则BD的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由；问题解决（3）如图③，在四边形ABCD中，AB＝AD，∠BAD＝60°，BC＝4，若BD⊥CD，垂足为点D，则对角线AC的长是否存在最大值？若存在，请求出其最大值；若不存在，请说明理由．【解答】解：（1）如图①，延长CD至G，使得DG＝BE，∵正方形ABCD中，AB＝AD，∠B＝∠AFG＝90°，∴△ABE≌△ADG，∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝45°，∠BAD＝90°，∴∠BAE+∠DAF＝45°，∴∠DAG+∠DAF＝45°，即∠GAF＝∠EAF，又∵AF＝AF，∴△AEF≌△AEG，∴EF＝GF＝DG+DF＝BE+DF，故答案为：BE+DF＝EF；（2）存在．在等边三角形ABC中，AB＝BC，∠ABC＝60°，如图②，将△ABD绕着点B顺时针旋转60°，得到△BCE，连接DE．由旋转可得，CE＝AD＝2，BD＝BE，∠DBE＝60°，∴△DBE是等边三角形，∴DE＝BD，∴在△DCE中，DE＜DC+CE＝4+2＝6，∴当D、C、E三点共线时，DE存在最大值，且最大值为6，∴BD的最大值为6；（3）存在．如图③，以BC为边作等边三角形BCE，过点E作EF⊥BC于点F，连接DE，∵AB＝BD，∠ABC＝∠DBE，BC＝BE，∴△ABC≌△DBE，∴DE＝AC，∵在等边三角形BCE中，EF⊥BC，∴BF＝BC＝2，∴EF＝BF＝×2＝2，以BC为直径作⊙F，则点D在⊙F上，连接DF，∴DF＝BC＝×4＝2，∴AC＝DE≤DF+EF＝2+2，即AC的最大值为2+2．9、如图，已知正方形ABCD，AB＝8，点E是射线DC上一个动点（点E与点D不重合），连接AE，BE，以BE为边在线段AD的右侧作正方形BEFG，连结CG．（1）当点E在线段DC上时，求证：△BAE≌△BCG；（2）在（1）的条件下，若CE＝2，求CG的长；（3）连接CF，当△CFG为等腰三角形时，求DE的长．【解答】（1）证明：∵四边形ABCD和四边形BEFG都是正方形，∴AB＝BC，BE＝BG，∴∠ABC﹣∠EBC＝∠EBG﹣∠EBC，即∠ABE＝∠CBG，在△BAE和△BCG中，，∴△BAE≌△BCG（SAS）；（2）解：∵△BAE≌△BCG，∴AE＝CG，∵四边形ABCD正方形，∴AB＝AD＝CD＝8，∠D＝90°，∴DE＝CD﹣CE＝8﹣5＝6，∴AE＝＝＝10，∴CG＝10；（3）解：①当CG＝FG时，如图1所示：∵△BAE≌△BCG，∴AE＝CG，∵四边形BEFG是正方形，∴FG＝BE，∴AE＝BE，在Rt△ADE和Rt△BCE中，，∴Rt△ADE≌Rt△BCE（HL），∴DE＝CE＝DC＝；②当CF＝FG时，如图2所示：点E与点C重合，即正方形ABCD和正方形BEFG的一条边重合；③当CF＝CG时，如图3所示：点E与点D重合，DE＝5；∵点E与点D不重合，∴不存在这种情况；④CF＝CG，当点E在DC延长线上时DE＝CD+CE＝16；综上所述，当△CFG为等腰三角形时．10、在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上点F处．（1）如图1，若BC＝2BA，求∠CBE的度数；（2）如图2，当AB＝5，且AF•FD＝10时，求BC的长；（3）如图3，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝AN+FD时，求的值．【解答】解：（1）∵四边形ABCD是矩形，∴∠C＝90°，∵将△BCE沿BE翻折，使点C恰好落在AD边上点F处，∴BC＝BF，∠FBE＝∠EBC，∠C＝∠BFE＝90°，∵BC＝2AB，∴BF＝2AB，∴∠AFB＝30°，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFB＝∠CBF＝30°，∴∠CBE＝∠FBC＝15°；（2）∵将△BCE沿BE翻折，使点C恰好落在AD边上点F处，∴∠BFE＝∠C＝90°，CE＝EF，又∵矩形ABCD中，∠A＝∠D＝90°，∴∠AFB+∠DFE＝90°，∠DEF+∠DFE＝90°，∴∠AFB＝∠DEF，∴△F AB∽△EDF，∴，∴AF•DF＝AB•DE，∵AF•DF＝10，AB＝5，∴DE＝2，∴CE＝DC﹣DE＝5﹣2＝3，∴EF＝3，∴DF＝＝＝，∴AF＝＝2，∴BC＝AD＝AF+DF＝2＝3．（3）过点N作NG⊥BF于点G，∵NF＝AN+FD，∴NF＝AD＝BC，∵BC＝BF，∴NF＝BF，∵∠NFG＝∠AFB，∠NGF＝∠BAF＝90°，∴△NFG∽△BF A，∴，设AN＝x，∵BN平分∠ABF，AN⊥AB，NG⊥BF，∴AN＝NG＝x，AB＝BG＝2x，设FG＝y，则AF＝2y，∵AB2+AF2＝BF2，∴（2x）2+（2y）2＝（2x+y）2，解得y＝x．∴BF＝BG+GF＝2x+x＝x．∴＝．11、已知在梯形ABCD中，AD∥BC，AC＝BC＝10，cos∠ACB＝，点E在对角线AC上（不与点A、C重合），∠EDC＝∠ACB，DE的延长线与射线CB交于点F，设AD的长为x．（1）如图1，当DF⊥BC时，求AD的长；（2）设EC＝y，求y关于x的函数解析式，并直接写出定义域；（3）当△DFC是等腰三角形时，求AD的长．【解答】解：（1）设：∠ACB＝∠EDC＝∠α＝∠CAD，∵cosα＝，∴sinα＝，过点A作AH⊥BC交于点H，AH＝AC•sinα＝6＝DF，BH＝2，如图1，设：FC＝4a，∴cos∠ACB＝，则EF＝3a，EC＝5a，∵∠EDC＝∠α＝∠CAD，∠ACD＝∠ACD，∴△ADC∽△DCE，∴AC•CE＝CD2＝DF2+FC2＝36+16a2＝10•5a，解得：a＝2或（舍去a＝2），AD＝HF＝10﹣2﹣4a＝；（2）过点C作CH⊥AD交AD的延长线于点H，CD2＝CH2+DH2＝（AC sinα）2+（AC cosα﹣x）2，即：CD2＝36+（8﹣x）2，由（1）得：AC•CE＝CD2，即：y＝x2﹣x+10（0＜x＜16且x≠10）…①，（3）①当DF＝DC时，∵∠ECF＝∠FDC＝α，∠DFC＝∠DFC，∴△DFC∽△CFE，∵DF＝DC，∴FC＝EC＝y，∴x+y＝10，即：10＝x2﹣x+10+x，解得：x＝6；②当FC＝DC，则∠DFC＝∠FDC＝α，则：EF＝EC＝y，DE＝AE＝10﹣y，在等腰△ADE中，cos∠DAE＝cosα＝＝＝，即：5x+8y＝80，将上式代入①式并解得：x＝；③当FC＝FD，则∠FCD＝∠FDC＝α，而∠ECF＝α≠∠FCD，不成立，故：该情况不存在；故：AD的长为6和．12、如图，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8cm，矩形ABCD的长和宽分别为8cm和2cm，C点和M点重合，BC和MN在一条直线上．令Rt△PMN不动，矩形ABCD 沿MN所在直线向右以每秒1cm的速度移动（如图2），直到C点与N点重合为止．设移动x秒后，矩形ABCD与△PMN重叠部分的面积为ycm2．求y与x之间的函数关系式．【解答】解：在Rt△PMN中，∵PM＝PN，∠P＝90°∴∠PMN＝∠PNM＝45°，延长AD分别交PM，PN于点G、H．过G作GF⊥MN于F，过H作HT⊥MN于T．∵DC＝2cm，∴MF＝GF＝2cm，TN＝HT＝2cm．∵MN＝8cm，∴MT＝6cm．因此，矩形ABCD以每秒1cm的速度由开始向右移动到停止，和Rt△PMN重叠部分的形状可分为下列三种情况：（1）当C点由M点运动到F点的过程中（0≤x≤2），如图①所示，设CD与PM交于点E，则重叠部分图形是Rt△MCE，且MC＝EC＝x．∴y＝MC•EC＝x2（0≤x≤2）．（2）当C点由F点运动到T点的过程中（2＜x≤6），如图②所示，重叠部分图形是直角梯形MCDG．∵MC＝x，MF＝2，∴FC＝DG＝x﹣2，且DC＝2，∴y＝（MC+GD）•DC＝2x﹣2（2＜x≤6）．（3）当C点由T点运动到N点的过程中（6＜x≤8），如图③所示，设CD与PN交于点Q，则重叠部分图形是五边形MCQHG．∵MC＝x，∴CN＝CQ＝8﹣x，且DC＝2，∴y＝（MN+GH）•DC﹣CN×CQ＝﹣（8﹣x）2+12（6＜x≤8）．13、如图①所示，已知正方形ABCD和正方形AEFG，连接DG，BE．（1）发现：当正方形AEFG绕点A旋转，如图②所示．①线段DG与BE之间的数量关系是DG＝BE；②直线DG与直线BE之间的位置关系是DG⊥BE；（2）探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG ＝2AE时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG、DE，若AE＝1，AB＝2，求BG2+DE2的值（直接写出结果）．【解答】解：（1）①如图②中，∵四边形ABCD和四边形AEFG是正方形，∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，∴∠BAE＝∠DAG，在△ABE和△DAG中，，∴△ABE≌△ADG（SAS），∴BE＝DG；②如图2，延长BE交AD于T，交DG于H．由①知，△ABE≌△DAG，∴∠ABE＝∠ADG，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG，故答案为：BE＝DG，BE⊥DG；（2）数量关系不成立，DG＝2BE，位置关系成立．如图③中，延长BE交AD于T，交DG于H．∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴＝＝，∴△ABE∽△ADG，∴∠ABE＝∠ADG，＝，∴DG＝2BE，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图④中，作ET⊥AD于T，GH⊥BA交BA的延长线于H．设ET＝x，AT＝y．∵△AHG∽△ATE，∴＝＝＝2，∴GH＝2x，AH＝2y，∴4x2+4y2＝4，∴x2+y2＝1，∴BG2+DE2＝（2x）2+（2y+2）2+x2+（4﹣y）2＝5x2+5y2+20＝25．14、（1）【问题发现】如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为BE＝AF （2）【拓展研究】在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF 的数量关系有无变化？请仅就图2的情形给出证明；（3）【问题发现】当正方形CDEF旋转到B，E，F三点共线的时候，直接写出线段AF的长．【解答】解：（1）在Rt△ABC中，AB＝AC＝2，根据勾股定理得，BC＝AB＝2，点D为BC的中点，∴AD＝BC＝，∵四边形CDEF是正方形，∴AF＝EF＝AD＝，∵BE＝AB＝2，∴BE＝AF，故答案为BE＝AF；（2）无变化；如图2，在Rt△ABC中，AB＝AC＝2，∴∠ABC＝∠ACB＝45°，∴sin∠ABC＝＝，在正方形CDEF中，∠FEC＝∠FED＝45°，在Rt△CEF中，sin∠FEC＝，∴，∵∠FCE＝∠ACB＝45°，∴∠FCE﹣∠ACE＝∠ACB﹣∠ACE，∴∠FCA＝∠ECB，∴△ACF∽△BCE，∴，∴BE＝AF，∴线段BE与AF的数量关系无变化；（3）当点E在线段AF上时，如图2，由（1）知，CF＝EF＝CD＝，在Rt△BCF中，CF＝，BC＝2，根据勾股定理得，BF＝，∴BE＝BF﹣EF＝﹣，由（2）知，BE＝AF，∴AF＝﹣1，当点E在线段BF的延长线上时，如图3，由（1）知，CF＝EF＝CD＝，在Rt△BCF中，CF＝，BC＝2，根据勾股定理得，BF＝，∴BE＝BF+EF＝+，由（2）知，BE＝AF，∴AF＝+1．即：当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为﹣1或+1．。
2021年九年级中考数学复习：四边形专练
11．如图，▱ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则BO的长为（ ）
A．5B．8C．10D．11
12．如图，在 中， ，点 是斜边 的中点，分别以点 ， 为圆心，以 的长为半径画弧，两弧交于点 ，连接 ， ， 得到四边形 ，依次连接四边形 四条边中点得到四边形 ，若 ，那么四边形 的周长为（）
A． B． C． D．
13．如图，菱形 的边长为 ，对角线 ， 交于点 ， ，则菱形 的面积为（）
A． B． C．2D．4
14．如图，在菱形 中， ，E、F分别是边 、 的中点， 于点P，则 的度数是（）．
A．50°B．45°C．40°D．30°
15．如图，在矩形 中， 平分 交 于点 ， 交 于点 ，若 ， ，则 等于（）
A．5B．6C．7D．8
16．如图，在正方形ABCD中，E、F分别是BC、CD上的点，若△AEF是边长为2的等边三角形，则正方形的边长是（ ）
A． B． +1C． D．
17．如图，边长为 的正方形 的对角线 与 交于点 ，将正方形 沿直线 折叠，点 落在对角线 上的点 处，折痕 交 于点 ，则 长是（）．
A．①②B．③④C．①③④D．①②③④
23．如图，在平面直角坐标系中，菱形 的顶点A，D在反比例函数 的图象上，对角线 平行x轴，点O在 上，且 ，连接 ， ，若 ，则k的值为（）
A．25B． C．45D．
24．如图，在平面直角坐标系中，平行四边形 的边 在y轴的正半轴上，反比例函数 的图像分别交 于中点D，交 于点E，且 ，连接 ，若 ，则k的值为（）
21．如图，在平面直角坐标系中，四边形OABC是菱形，∠AOC＝120°，点B的坐标为（6，0），点D是边BC的中点，现将菱形OABC绕点O顺时针旋转，每秒旋转60°，则第2021秒时，点D的坐标为（ ）
专练11 四边形中的最值问题-2021年中考数学压轴题专项高分突破训练(全国通用)(解析版)
专练11四边形中的最值问题1.综合与实践（1）任意一个四边形ABCD通过剪裁，都可以拼接成一个三角形，方法如下：如图1，E，F，G，H分别是边AB，BC，CD，DA的中点，连接EH，P是线段EH的中点，连接PF，PG，沿线段EH，PF，PG剪开，将四边形ABCD分成①，②，③，④四部分，按如图2所示的方式即可拼成一个无缝隙也不重叠的△P′MN．关于在拼接过程中用到的图形的变换，说法正确的是（）A.①→①是轴对称B.②→②是平移C.③→③是中心对称D.④→④是中心对称（2）如图3，连接EF′，F′C′，C′H，判断四边形EF′C′H的形状，并说明理由．（3）若△P′MN是一个边长为4的等边三角形，则四边形EF′C′H的对角线F′H+C′E的最小值为________．【答案】（1）C（2）四边形F′C′HE是平行四边形．理由：由题意可知，P′F′=F′M，P′C′=C′N，MN，F′C′∥EH，∴F′C′=12∵PH=HN，PE=EM，MN，∴EH=12∴F′C′=EH，∴四边形F′C′HE是平行四边形．（3）2√7【解析】（1）观察图象可知②→②，③→③是中心对称，①→①，④→④是平移．故答案为：C．（3）如图4，过点O作直线l∥MN，作F′T⊥MN于点T，连接TC′交直线l于点O′，连接F′O′，此时F′O′+O′C′的值最小，最小值=TC′的长．∵在Rt△MTF′中，MF′=C′F′=2，∠TMF′=60°，∴TF′=2⋅sin60°=√3．∵C′F′∥MN，∴∠C′F′T=∠F′TM=90°，∴C′T=√F′T2+C′F′2=√3+4=√7，∴F′H+C′E的最小值=2C′T=2√7．2.阅读下面材料，并解决问题：（1）如图1，等边三角形ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数；为了解决本题，我们可以将ΔABP绕顶点A逆时针旋转到ΔACP′处，此时ΔACP′≌ΔABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=________；（2）基本运用：请你利用第（1）题的思想方法，解答下面问题：如图2，在ΔABC中，∠CAB=90°，AB=AC，E，F为BC上的点，且∠EAF=45°．求证：EF2=BE2+FC2；（3）能力提升：在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB=4．①如图3，将ΔADE绕点D逆时针旋转90°得到ΔDCF，连结EF．a．把图形补充完整（无需写画法）；b．求EF2的取值范围；②如图4，求BE+AE+DE的最小值．【答案】（1）150°（2）证明：如图，把△ABE绕点A逆时针旋转90°得到ΔACE′．由旋转的性质得，AE′=AE，CE′=BE，∠CAE′=∠BAE，∠ACE′=∠B，∠EAE′=90°．∵∠EAF=45°，∴∠E′AF=∠CAE′+∠CAF=∠BAE+∠CAF=∠BAC－∠EAF=90°－45°=45°，∴∠EAF=∠E′AF．在ΔEAF和ΔE′AF中，{AE=AE′∠EAF=∠E′AFAF=AF，∴ΔEAF≌ΔE′AF(SAS)，∴E′F=EF．∵∠CAB=90°，AB=AC，∴∠B=∠ACB=45°，∴∠E′CF=45°+45°=90°，由勾股定理得，E′F2=CE′2+FC2 ，即EF2=BE2+FC2 ．（3）解：①a．如图，ΔDCF即为所求．b．方法一：∵2√2≤DE≤4，ΔFDE是等腰直角三角形，∴EF2=2DE2 ，∴16≤EF2≤32．方法二：∵四边形ABCD是正方形，∴BC=AB=4，∠B=90°，∠DAE=∠ACD=45°，∴AC=√AB2+BC2=4√2．∵ΔADE绕点D逆时针旋转90°得到ΔDCF，∴∠DCF=∠DAE=45°，AE=CF，∴∠ECF=∠ACD+∠DCF=90°．设AE=CF=x，EF2=y，则EC= 4√2−x，∴y=(4√2−x)2+x2=2x2−8√2x+32(0<x≤4√2)，即y=2(x−2√2)2+16．∵2>0，∴当x=2√2时，y有最小值，最小值为16，当x=42时，y有最大值，最大值为32，∴16≤EF2≤32．②如图，将ΔABE绕点A顺时针旋转60°得到△AFG，连结EG，DF．作FH⊥AD，交DA的延长线于点H．由旋转的性质可知：AF=AB=4，ΔAEG是等边三角形，∴AE=EG．∵DF≤FG+EG+DE，BE=FG，∴AE+BE+DE的最小值为线段DF的长．在Rt ΔAFH中，∠FAH=30°，AF=2，AH=√42−22=2√3，∴FH=12在Rt ΔDFH中，DF=√(2√3+4)2+22=2√6+2√2，∴BE+AE+ED的最小值为2√6+2√2．【解析】（1）解：150°【解法提示】∵ΔACP′≌ΔABP，∴AP′=AP=3，CP′=BP=4，∠AP′C=∠APB．由题意知旋转角∠PAP′=60°，∴ΔAPP′为等边三角形，∴PP′=AP=3，∠AP′P=60°．易证ΔPP′C为直角三角形，且∠PP′C=90°，∴∠APB=∠AP′C=∠AP′P+∠PP′C=60°+90°=150°．3.如图，在矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ADM．（1）如图1，当直线AN经过点C时，求DM的长．（2）如图2，连接BN，当DM=1时，求△ABN的面积．（3）如图3，当射线BN交线段CD于点E时，求DE的最大值．【答案】（1）解：当AN经过点C时，即A，N，C三点共线∵AB=4，AD=3∴CN=AC−AN=5−3=2∵将△ADM沿直线AM对折∴DM=MN设DM=MN=a，CM=4−a，在Rt△MNC中，CM2=MN2+CN2，(4−a)2=a2+4，∴a=32∴DM=32（2）解：过N作PQ//AD交CD于点P，交AB于Q结合题意，得：∠MNP+∠PMN=90∘∠MNP+∠ANQ=90∘∴∠PMN=∠ANQ∵∠ANM=∠AQN=90∘∴△MNP∽△NAQ∴NPAQ =MPNQ=MNAN=13设MP=m，则NQ=3m，NP=3−3m，AQ=9−9m 在Rt△ANQ中，AN2=NQ2+AQ29=9m2+(9−9m)2解得：m=1（舍）或m=45∴S△ABN=12×AB⋅NQ=12×4×125=245（3）解：∵AD=AN=3∴N在以A为圆心，半径为3的圆弧上运动如图，当BE与圆只有一个交点时，DE取最大值，此时∠ANB=90∘在△ANB和△BCE中{∠ABN=∠CEB∠ANB=∠C=90∘AN=BC∴△ANB≌△BCE∴CE=NB=√AB2−AN2=√7∴DE=4−√7．4.[阅读]如图1，四边形OABC中，OA=a，OC=4，BC=3，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a].[理解]若点D与点A重合，则这个操作过程为FZ[45°，4]；[尝试]（1）若点D与OA的中点重合，则这个操作过程为FZ[________，________]；（2）若点D恰为AB的中点（如图2），求θ=________；（3）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形OABC的边AB上，试解决下列问题：①求出a的值；②点P，Q分别为边OA上的两个动点，且点Q始终在点P右边，PQ=1，连接CP，QE，在P，Q两点的运动过程中，PC+PQ+QE是否存在最小值，若存在，请求出最小值，若不存在，请说明理由.【答案】（1）45°；8（2）30°（3）①如图3：过点B作BH⊥OA于点H，∠COA=90°，∠COF=45°∴∠FOA=45°∵点B与点E关于直线1对称∴∠OFA=∠OFB=90°∴∠OAB=45°∴∠HBA=90-45°=45°=∠HAB∴BH=AH∵OC⊥OA，BH⊥OA∴.OC//BH∵BC//OA.∴四边形BCOH是平行四边形∴BH=CO=4，OH=BC=3∴OA=OH+AH=OH+BH=3+4=7∴a的值为7；②如图4：过点B作BH⊥OA于点H，过点F作OA的对称点Q，连接AQ、EQ、OB∴∠QAO=∠FAO=45°，QA=FA ， ∴∠QAF=90°在Rt △BHA 中，AB= √BH 2+AH 2=√42+42=4√2 在Rt △OFA 中，∠AFO=90°，∠AOF=∠OAF=45° ∴AF=OF=√2=7√22∴AQ=AF= 7√22在R △OCB ，OB= √OC 2+BC 2=√42+32=5在Rt △OFB 中，BF=AB-AF=5- 7√22由折叠可得：BF=EF= 4√2 - 7√22= √22∴AE=AF-EF= 7√22- √22= 3√2在Rt △QAE 中: EQ 2=AE 2+AQ 2=(3√2)2+(7√22)2=852根据两点之间线段最短可得,当点E 、P 、Q 三点共线时，PE+PF=PE+PQ 最短，最小值为线段EQ 长 ∴PE+PF 的最小值的是 √852=√1702【解析】（1）点D 与OA 的中点重合，如图1:由折叠得：∠COP=∠DOP=45°，∠C=∠ODP=90°∴CP=FD∵OP=OP∴Rt△OCP≌Rt△ODP（HL）∴OD=OC=4∵D为OA的中点∴OA=a=8则这个操作过程为FZ[45°，8]；故答案为：45°，8；（ 2 ）如图2:延长MD、OA交于点N∵∠AOC=∠BCO=90°∴∠AOC+∠BCO= 180°∴BC//OA∴∠B=∠DAN在△BDM和△ADN中∠B=∠DAN ,BD=AD, ∠BDM=∠ADN∴△BDM≌△ADN（ASA）∴DM=DN∵∠ODM=∠OCM=90°∴OM=ON.∴∠MOD=∠NOD由折可得∠MOD=∠MOC=θ∴∠COA=3θ=90°∴θ=30°5.如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM 绕点B逆时针旋转60°得到BN，连接EN、AM、CM.（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；（3）当AM＋BM＋CM的最小值为√3+1时，求正方形的边长.【答案】（1）证明：∵△ABE是等边三角形，∴BA＝BE，∠ABE＝60°.∵∠MBN＝60°，∴∠MBN－∠ABN＝∠ABE－∠ABN.即∠BMA＝∠NBE.又∵MB＝NB，∴△AMB≌△ENB（SAS）（2）解：①当M点落在BD的中点时，AM＋CM的值最小②如图，连接CE，当M点位于BD与CE的交点处时，AM＋BM＋CM的值最小.理由如下：连接MN.由⑴知，△AMB≌△ENB，∴AM＝EN.∵∠MBN＝60°，MB＝NB，∴△BMN是等边三角形.∴BM＝MN.∴AM＋BM＋CM＝EN＋MN＋CM.根据“两点之间线段最短”，得EN＋MN＋CM＝EC最短∴当M点位于BD与CE的交点处时，AM＋BM＋CM的值最小，即等于EC的长（3）解：过E点作EF⊥BC交CB的延长线于F，∴∠EBF＝90°－60°＝30°.设正方形的边长为x，则BF＝√32x，EF＝x2.在Rt△EFC中，∵EF2＋FC2＝EC2 ，∴（x2）2＋（√32x＋x）2＝(√3+1)2解得，x＝√2（舍去负值）.∴正方形的边长为√2.6.定义：若四边形有一组对角互补，一组邻边相等，且相等邻边的夹角为直角，像这样的图形称为“直角等邻对补”四边形，简称“直等补”四边形，根据以上定义，解决下列问题：（1）如图1，正方形ABCD中，E是CD上的点，将ΔBCE绕B点旋转，使BC与BA重合，此时点E 的对应点F在DA的延长线上，则四边形BEDF为“直等补”四边形，为什么？（2）如图2，已知四边形ABCD是“直等补”四边形，AB=BC=5，CD=1，AD>AB，点B到直线AD的距离为BE．①求BE的长．②若M、N分别是AB、AD边上的动点，求ΔMNC周长的最小值．【答案】（1）解：如图1由旋转的性质得：∠F=∠BEC，∠ABF=∠CBE，BF=BE∵∠BEC+∠BED=180°，∠CBE+∠ABE=90°，∴∠F+∠BED=180°，∠ABF+∠ABE=90°即∠FBE=90°，故满足“直等补”四边形的定义，∴四边形BEDF为“直等补”四边形；（2）解：①∵四边形ABCD是“直等补”四边形，AB=BC，∴∠A+∠BCD=180°，∠ABC=∠D=90°，如图2，将△ABE绕点B顺时针旋转90°得到△CBF，则∠F=∠AEB=90°，∠BCF+∠BCD=180°，BF=BE∴D、C、F共线，∴四边形EBFD是正方形，∴BE=FD，设BE=x，则CF=x-1，在Rt△BFC中，BC=5，由勾股定理得：x2+(x−1)2=25，即x2−x−12=0，解得：x=4或x=﹣3(舍去)，∴BE=4②如图3，延长CD到P，使DP=CD=1，延长CB到T，使TB=BC=5,则NP=NC，MT=MC,∴△MNC的周长=MC+MN+NC=MT+MN+NP≥PT当T、M、N、P共线时，△MNC的周长取得最小值PT，过P作PH⊥BC，交BC延长线于H，∵∠F=∠PHC=90°,∠BCF=∠PCH,∴△BCF∽△PCH,∴BCPC =BFPH=CFCH,即52=4PH=3CH，解得：CH=65,PH=85,在Rt△PHT中，TH= 5+5+65=565,PT=√PH2+HT2=8√2,∴ΔMNC周长的最小值为8√2．7.如图，在菱形ABCD中，∠ABC＝120°，AB＝4 √3，E为对角线AC上的动点（点E不与A，C重合），连接BE，将射线EB绕点E逆时针旋转120°后交射线AD于点F．（1）如图1，当AE＝AF时，求∠AEB的度数；（2）如图2，分别过点B，F作EF，BE的平行线，且两直线相交于点G．①试探究四边形BGFE的形状，并求出四边形BGFE的周长的最小值；②连接AG，设CE＝x，AG＝y，请直接写出y与x之间满足的关系式，不必写出求解过程．【答案】（1）如图1中，∵四边形ABCD是菱形，∴BC∥AD，∠BAC＝∠DAC，∴∠ABC+∠BAD＝180°，∵∠ABC＝120°，∴∠BAD＝60°，∴∠EAF＝30°，∵AE＝AF，∴∠AEF＝∠AFE＝75°，∵∠BEF＝120°，∴∠AEB＝120°﹣75°＝45°．（2）①如图2中，连接DE．∵AB＝AD，∠BAE＝∠DAE，AE＝AE，∴△BAE≌△DAE（SAS），∴BE＝DE，∠ABE＝∠ADE，∵∠BAF+∠BEF＝60°+120°＝180°，∴∠ABE+∠AFE＝180°，∵∠AFE+∠EFD＝180°，∴∠EFD＝∠ABE，∴∠EFD＝∠ADE，∴EF＝ED，∴EF＝BE，∵BE∥FG，BG∥EF，∴四边形BEFG是平行四边形，∵EB＝EF，∴四边形BEFG是菱形，∴当BE⊥AC时，菱形BEFG的周长最小，此时BE＝AB•sin30°＝2 √3，∴四边形BGFE的周长的最小值为8 √3．②如图2﹣1中，连接BD，DE，过点E作EH⊥CD于H．∵AB＝AD，∠BAD＝60°，∴△ABD是等边三角形，∴BD＝BA，∠ABD＝60°，∵BG∥EF，∴∠EBG＝180°﹣120°＝60°，∴∠ABD＝∠GBE，∴∠ABG＝∠DBE，∵BG＝BE，∴△ABG≌△DBE（SAS），∴AG＝DE＝y，在Rt△CEH中，EH＝12EC＝12x．CH＝√32x，∴DH＝|4 √3﹣√32x|，在Rt△DEH中，∵DE2＝EH2+DH2 ，∴y2＝14x2+（4 √3﹣√32x）2 ，∴y2＝x2﹣12x+48，∴y＝√x2−12x+48（0＜x＜12）．8.如图1，菱形ABCD的对角线AC、BD相交于点O，且AC＝6cm，BD＝8cm，分别过点B、C作AC与BD的平行线相交于点E．（1）判断四边形BOCE的形状并证明；（2）点G从点A沿射线AC的方向以2cm/s的速度移动了t秒，连接BG，当S△ABG＝2S△OBG时，求t的值．（3）如图2，长度为3cm的线段GH在射线AC上运动，求BG＋BH的最小值．【答案】（1）结论：四边形BOCE是矩形．理由：∵BE∥OC，EC∥OB，∴四边形OBEC是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，∴∠BOC＝90°，∴四边形BOCE是矩形．（2）如图2中，∵四边形ABCD是菱形，∴OA＝OC＝3cm，OB＝OD＝4cm，∵S△ABG＝2S△OBG ，∴AG＝2OG，∴2t＝2（3﹣2t）或2t＝2（2t﹣3），解得t＝1或t＝3，∴满足条件的t的值为1或3．（3）如图2中，设OG＝x，则BG＋BH＝√x2+42＋√(x−3)2+42，欲求BG＋BH的最小值，相当于在x轴上找一点P(x，0)，使得点P(x，0)到A(0，4)和B(3，4)的距离最小，如图3中，作点B关于x轴的对称点B′，连接AB′交x轴于P，连接BP，此时PA＋PB的值最小，∵A(0，4)，B′(3，﹣4)，∴当B点在y轴右侧时，AP＋PB＝AP＋PB′＝AB′＝√82+32＝√73，当B点在y轴左侧时，由于线段整体移动，同理，得AP＋PB＝AP＋PB′＝AB′＝√73，∴BG＋BH的最小值为√73．9.如图，O为坐标原点，四边形OABC为矩形，顶点A，C分别在x轴，y轴的正半轴上，点B的坐标为(10，4)，点D是OA的中点，动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.（1）当t=________时，四边形PODB是平行四边形？（2）在直线CB上是否存在一点Q，使得四边形ODPQ是菱形？若存在，求t的值，并求出Q点的坐标，若不存在，请说明理由；（3）在点P运动的过程中，线段PB上有一点M，且PM=5，求四边形OAMP的周长最小值.【答案】（1）2.5s（2）解：①当点Q在线段BC上时，如图1，∵四边形ODPQ是菱形，∴OQ=OD=5，在Rt△OCQ中，CQ=√52−42=3，CP=3+5=8，∴t=4，点Q的坐标为(3，4)；②当点Q在射线BC上时，如图2，∵四边形ODPQ是菱形，∴OQ=OD=5，在Rt△OCQ中，CQ=√52−42=3，CP=5﹣3=2，∴t=1，点Q的坐标为(﹣3，4)；（3）解：如图3，连接DM，∵PM=OD=5，PM∥OD，∴四边形ODMP是平行四边形，∴OP=DM，∴四边形OAMP的周长=OA+AM+MP+PO=15+AM+PO=15+AM+DM作点A关于直线BC的对称点A'，连接A'M，A'D.∵AM=A'M，∴四边形OAMP的周长=15+A'M+DM，所以，当点A'，M，D三点在同一直线上时，四边形OAMP的周长最小，在Rt△A'DA中，A′D=√A′A2+AD2=√52+82=√89，所以四边形OAMP的周长最小值为15+√89.【解析】解：（1）∵四边形OABC为矩形，点B的坐标为(10，4)，∴BC=OA=10，AB=OC=4.∵点D是OA的中点，∴OD =1OA=5，2由题意知，PC=2t，∴BP=BC﹣PC=10﹣2t.∵四边形PODB是平行四边形，∴PB=OD=5，∴10﹣2t=5，∴t=2.5，即当t=2.5s时，四边形PODB是平行四边形.故答案为：2.5s；10.如图1，矩形ABCD中，AB=3，BC=4 ，将矩形ABCD绕着点A顺时针旋转，得到矩形BEFG.（1）当点E落在BD上时，则线段DE的长度等于________ ；（2）如图2，当点E落在AC上时，求△BCE的面积；（3）如图3，连接AE、CE、AG、CG，判断线段AE与CG的位置关系且说明理由，并求CE 2+AG 2的值；（4）在旋转过程中，请直接写出S△BCE+S△ABG的最大值.【答案】（1）2（2）解：当点E落在AC上时，过点B作BM⊥AC于点M，在RtΔABC中，由勾股定理得：AC=√AB2+BC2=√32+42=5,∵ ΔABC 是直角三角形，BM ⊥AC ， ∴ 12×3×4=12·BM ·AC ,∴ BM =125，在 RtΔBME 中，由勾股定理得：ME =√BE 2−BM 2=√32−(125)2=95，在 RtΔBMC 中，由勾股定理得： MC =√BC 2−BM 2=√42−(125)2=165，∴ CE =MC −ME =165−95=75 ，∴ S ΔBCE =12·CE ·BM =12×75×125=4225 ；（3）解：线段AE 与CG 的位置关系是垂直，理由如下：证明：连接AC 、EG ，设AE 与CG 相交于点N ，AE 与BC 相交于点P ，由旋转的性质知： ∠ABE =∠CBG ， AB =BE ，BC =BG ， ∴在等腰 ΔABE 和等腰 ΔCBG 中得到： ∠EAB =180°−∠ABE2， ∠BCG =180°−∠CBG2，∴ ∠EAB =∠BCG ， ∵ ∠1=∠2 ，∴ ∠CNP =∠ABP =90° ， 即 AE ⊥CG ； ∵ AE ⊥CG ，∴ CE 2+AG 2=CN 2+NE 2+AN 2+NG 2=(CN 2+AN 2)+(NE 2+NG 2)=AC 2+EG 2 ，由矩形的性质可以得到：EG=AC=5，∴CE2+AG2=AC2+EG2=52+52=50；（4）解：过点C作CH⊥直线BE于点H，过点G作EQ⊥直线AB于点Q，∴SΔBCE=12·CH·BE，SΔABG=12·GQ·AB，∵AB=BE=3∴S△BCE+S△ABG=12·CH·BE+12·GQ·AB=12×3×(CH+GQ)，∴当CH+GQ最大时，S△BCE+S△ABG最大，在旋转过程中，0≤CH≤4,0≤GQ≤4，∴0≤CH+GQ≤8，∴当点A、B、E三点共线时，CH+GQ=8，此时最大，∴S△BCE+S△ABG的最大值为：12×3×8=12.【解析】解：（1）解：当E落在BD上时，如图所示：∵四边形ABCD是矩形，∴每个内角都等于90°，∵AB=3，BC=4，由勾股定理得：BD =√AB 2+AD 2=√AB 2+BC 2=√32+42=5 ， 由旋转的性质可知： AB =BE =3 ， ∴ DE =BD −BE =5−3=2 ， 故答案为：2；11.如图1，在等边 △ ABC 中，AB ＝6cm ，动点P 从点A 出发以1cm/s 的速度沿AB 匀速运动，动点Q 同时从点C 出发以同样的速度沿BC 的延长线方向匀速运动，当点P 到达点B 时，点P 、Q 同时停止运动，设运动时间为t （s ）．过点P 作PE ⊥AC 于E ，以CQ 、CE 为边作平行四边形CQFE ．（1）AE ＝________，CE ＝________；（用含t 的代数式表示） （2）当平行四边形CQFE 为菱形时，请求出t 的值； （3）如图1，连接PQ ，交AC 边于点D ，求线段DE 的长；（4）如图2，取线段BC 的中点M ，连接PM ，将 △ BPM 沿直线PM 翻折，得 △B ′PM ，连接 AB ′ ，请求出 AB ′ 的最小值． 【答案】 （1）t2；6−t2（2）解：当平行四边形CQFE 为菱形时，则 CE =CQ ， ∴ 6−t2=t ，解得： t =4即当 t =4 时． CE =CQ ，当平行四边形CQFE 为菱形 （3）解：如图2中，作 PK//BC 交 AC 于 K ．∵ΔABC 是等边三角形，∴∠B=∠A=60°，∵PK//BC，∴∠APK=∠B=60°，∠PKD=∠DCQ，∴∠A=∠APK=60°，∴ΔAPK是等边三角形，∴PA=PK，∵PE⊥AK，∴AE=EK=12AK，在△PKD和△QCD中，{CQ=PK∠PKD=∠DCQ∠PDK=∠QDC，∴△PKD≅△QCD(AAS)，∴DK=DC=12CK，∴DE=EK+DK=12(AK+CK)=12AC=3(cm)．（4）解：如图3中，连接AM，AB′∵BM=CM=3，AB=AC，∴AM⊥BC，∴AM=√AB2−BM2=√62−32=3√3，∵AB′⩾AM−MB′，由折叠性质可知，BM=B′M=3∴AB′⩾3√3−3，∴AB′的最小值为3√3−3，此时A、M、B′三点共线．【解析】解：（1）依题意可知：AP=CQ=t，∵ΔABC是等边三角形，∴∠A=60°，AB=AC=BC=8，又∵PE⊥AC，∴∠APE=30°，∴AE=12AP=t2，∴CE=6−AE=6−t2，故答案为：t2，6−t212.如图(1)，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点.作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG.（1）试猜想线段BG和AE的关系(位置关系及数量关系)，请直接写出你得到的结论；（2）将正方形DEFG绕点D逆时针方向旋转一角度α后(0°＜α＜90°)，如图(2)，通过观察或测量等方法判断(1)中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由；（3）若BC＝DE＝2，正方形DEFG绕点D逆时针方向旋转角度α (0°＜α＜360°)过程中，当BG为最小值时，求AF的值.【答案】（1）解：如图（1）∵△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，∴BD=CD=AD，∵在△BDG和△ADE中{BD＝AD∠BDG＝∠ADEDG＝DE∴△BDG≌△ADE（SAS），∴BG=AE，∠DGB=∠DEA，延长EA到BG于一点M，∴∠GAM=∠DAE，∴∠GMA=∠EDA=90°，∴线段BG和AE相等且垂直；（2）解：成立，如图（2），延长EA分别交DG、BG于点M′、N′两点，∵△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，∴∠ADB=90°，且BD=AD，∵∠BDG=∠ADB-∠ADG=90°-∠ADG=∠ADE，∵在△BDG和△ADE中{BD＝AD∠BDG＝∠ADEDG＝DE∴△BDG≌△ADE（SAS），∴BG=AE，∠DEA=∠DGB，∵∠DEA+∠DNE=90°，∠DNE=∠MNG，∴∠MNG+∠DGM=90°，即BG⊥AE且BG=AE；（3）解：由（2）知，要使AE最大，只要将正方形绕点D逆时针旋旋转270°，即A，D，E在一条直线上时，AE最大；∵正方形DEFG在绕点D旋转的过程中，E点运动的图形是以点D为圆心，DE为半径的圆，∴当正方形DEFG旋转到G点位于BC的延长线上（即正方形DEFG绕点D逆时针方向旋转270°）时，BG 最大，如图（3），若BC=DE=m，则AD= m2，EF=m，在Rt△AEF中，AF2=AE2+EF2=（AD+DE）2+EF2= 134m2∴AF= √132m，即在正方形DEFG旋转过程中，当AE为最大值时，AF= √132m.。
2021年北京市各区中考数学模拟真题专练：四边形综合
2021年北京市各区中考数学模拟真题专练：四边形综合1．（2021•房山区二模）如图，已知AC是矩形ABCD的对角线，∠BAC＝30°，点M 是DC延长线上一点，∠BAC的平分线与∠BCM的平分线交于点E，将线段CA绕点C逆时针旋转，得到线段CF，使点F在射线CB上，连接EF．（1）依题意补全图形；（2）求∠AEC的度数；（3）用等式表示线段AE，CE，EF之间的数量关系，并证明．2．（2021•房山区二模）如图，已知△ACB中，∠ACB＝90°，E是AB的中点，连接CE，分别过点A，C作CE和AB的平行线相交于点D．（1）求证：四边形ADCE是菱形；（2）若AB＝4，∠DAE＝60°，求△ACB的面积．3．（2021•平谷区二模）如图，在Rt△ABC中，∠ACB＝90°，D，E分别是边AB，BC的中点，连接DE并延长到点F，使EF＝DE，连接CF，BF．（1）求证：四边形CFBD是菱形；（2）连接AE，若CF＝，DF＝2，求AE的长．4．（2021•门头沟区二模）已知，如图，在△ABC中，AB＝AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E，连接DE交AB于点O．（1）求证：四边形ADBE是矩形；（2）若BC＝8，AO＝，求四边形AEBC的面积．5．（2021•北京二模）如图，在平行四边形ABCD中，F是AD的中点，延长BC到点E，使CE＝BC，连接DE，CF．（1）求证：四边形CEDF是平行四边形；（2）若AB＝4，AD＝6，∠A＝120°，求△DCE的底边CE上的高及DE的长．6．（2021•朝阳区二模）如图，在菱形ABCD中，AC，BD相交于点O，过B，C两点分别作AC，BD的平行线，相交于点E．（1）求证：四边形BOCE是矩形；（2）连接EO交BC于点F，连接AF，若∠ABC＝60°，AB＝2，求AF的长．7．（2021•丰台区二模）如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，AE∥BC，CE∥AD．（1）求证：四边形ADCE是菱形；（2）连接BE，若∠ABC＝30°，AC＝2，求BE的长．8．（2021•顺义区二模）如图，平行四边形ABCD的对角线AC，BD交于点O，AE⊥BC于点E，点F在BC延长线上，且CF＝BE．（1）求证：四边形AEFD是矩形；（2）连接AF，若tan∠ABC＝2，BE＝1，AD＝3，求AF的长．9．（2021•朝阳区二模）在平面直角坐标系xOy中，对于图形Q和∠P，给出如下定义：若图形Q上的所有的点都在∠P的内部或∠P的边上，则∠P的最小值称为点P对图形Q的可视度．如图1，∠AOB的度数为点O对线段AB的可视度．（1）已知点N（2，0），在点M1（0，），M2（1，），M3（2，3）中，对线段ON的可视度为60°的点是．（2）如图2，已知点A（﹣2，2），B（﹣2，﹣2），C（2，﹣2），D（2，2），E （0，4）．①直接写出点E对四边形ABCD的可视度为°；②已知点F（a，4），若点F对四边形ABCD的可视度为45°，求a的值．10．（2021•西城区二模）如图，在△ABC中，AC＝BC，CD为△ABC的角平分线，AE ∥DC，AE＝DC，连接CE．（1）求证：四边形ADCE为矩形；（2）连接DE，若AB＝10，CD＝12，求DE的长．11．（2021•石景山区二模）如图，在平行四边形ABCD中，CE⊥AD于点E，延长DA 至点F，使得EF＝DA，连接BF，CF．（1）求证：四边形BCEF是矩形；（2）若AB＝3，CF＝4，DF＝5，求EF的长．12．（2021•东城区二模）对于平面直角坐标系xOy中的图形W，给出如下定义：点P是图形W上任意一点，若存在点Q，使得∠OQP是直角，则称点Q是图形W的“直角点”．（1）已知点A（6，8），在点Q1（0，8），Q2（﹣4，2），Q3（8，4）中，是点A的“直角点”；（2）已知点B（﹣3，4），C（4，4），若点Q是线段BC的“直角点”，求点Q的横坐标n的取值范围；（3）在（2）的条件下，已知点D（t，0），E（t+1，0），以线段DE为边在x轴上方作正方形DEFG．若正方形DEFG上的所有点均为线段BC的“直角点”，直接写出t的取值范围．13．（2021•西城区校级模拟）如图，在四边形ABCD中，AB∥CD，AB＝AD，AC平分∠BAD．（1）求证：四边形ABCD是菱形；（2）若菱形ABCD的边长为13，对角线AC＝24，点E、F分别是边CD、BC的中点，连接EF并延长，与AB的延长线相交于点G，求EG的长．14．（2021春•海淀区校级月考）对于平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“闭距离”，记作d（M，N）．如图，已知点A（﹣2，6），B（﹣2，﹣2），C（6，﹣2），D（6，6）．（1）d（点O，CD）＝，d（点B，AC）＝；（2）记线段BC，AD组成图形G已知点T（4，m），若d（点T，G）≤2，求m的取值范围；（3）若E（t，0），F（t+1，0），d（EF，四边形ABCD）＝2，直接写出t的取值范围．参考答案1．（1）补全图形如图所示：（2）∵AC是矩形ABCD的对角线，延长DC至M，∴∠ABC＝∠BCD＝∠BCM＝90°．∵将线段CA绕点C逆时针旋转，得到线段CF，使线段CF在射线CB上，∠BAC＝30°，∴∠ACF＝60°，∵∠BAC的平分线与∠BCM的平分线交于点E，∴∠BAE＝∠CAE＝15°，∠ECF＝45°，∴∠ACE＝∠ACF+∠ECF＝60°+45°＝105°，∴∠AEC＝180°﹣∠ACE﹣∠CAE＝180°﹣105°﹣15°＝60°；（3）答：AE＝CE+EF．证明：在EA上截取EH＝EC，连接CH，∵∠AEC＝60°，∴△ECH是等边三角形，∴∠EHC＝∠ECH＝60°，CE＝CH＝EH．∴∠ECF+∠FCH＝∠FCH+∠HCA＝60°，∴∠ECF＝∠HCA，∵将线段CA绕点C逆时针旋转，得到线段CF，∴CF＝CA．在△ECF与△HCA中，，∴△ECF≌△HCA（SAS）．∴EF＝HA．∵AE＝EH+HA，∴AE＝CE+EF．2．（1）证明：∵AD∥CE，CD∥AE，∴四边形ADCE是平行四边形，∵∠ACB＝90°，E是AB的中点，∴CE＝AE，∴四边形ADCE是菱形；（2）解：∵AB＝4，AE＝CE＝EB，∴CE＝AE＝2．∵四边形ADCE是菱形，∠DAE＝60°，∴∠CAE＝30°．在Rt△ABC中，∠ACB＝90°，∠CAE＝30°，AB＝4，∴，∴．∴S△ACB＝AC•BC＝2．3．证明：（1）∵点E为BC的中点，∴CE＝BE，又∵EF＝DE，∴四边形CFBD是平行四边形，∵D，E分别是边AB，BC的中点，∠ACB＝90°，∴DE∥AC，∴∠DEB＝∠ACB＝90°，即DF⊥CB，∴四边形CFBD是菱形；（2）∵D，E分别是边AB，BC的中点，∴AC＝2DE，∵DF＝2DE＝2EF，DF＝2，∴AC＝2，EF＝1，∵CF＝，四边形CFDB是菱形，∴∠CEF＝90°，∴CE＝＝＝3，∵∠ACE＝90°，∴AE＝＝＝，即AE的长是．4．解：（1）∵AE∥BC，BE∥AD，∴四边形ADBE是平行四边形，∵AB＝AC，AD是BC边的中线，∴AD⊥BC，即∠ADB＝90°．∴四边形ADBE为矩形．（2）∵在矩形ADBE中，AO＝，∴DE＝AB＝5，∵D是BC的中点，∴AE＝DB＝4，∴AB＝2AO＝5，∵∠ADB＝90°，根据勾股定理，∴S△ABC＝×BC×AD＝×8×3＝12，∴S△ABE＝×AE×BE＝×4×3＝6，∴S四边形AEBC＝S△ABC+S△ABE＝12+6＝18，即S四边形AEBC为18．5．证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵F是AD的中点，∴FD＝AD，∵CE＝BC，∴FD＝CE，∵FD∥CE，∴四边形CEDF是平行四边形；（2）过点D作DG⊥CE于点G，∵四边形ABCD是平行四边形，∴AB∥CD，CD＝AB＝4，∠A＝120°，BC＝AD＝6，∴∠DCE＝∠B＝60°，在Rt△DGC中，∠DGC＝90°，∴CG＝CD•cos∠DCE＝2，DG＝CD•sin∠DCE＝2，∵CE＝BC＝3，∴GE＝1，在Rt△DGE中，∠DGE＝90°，∴DE＝＝．6．（1）证明：∵BE∥AC，EC∥BD，∴四边形BOCE是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD，∴∠BOC＝90°，∴平行四边形BOCE是矩形；（2）解：如图，∵四边形ABCD是菱形，∴AB＝BC，∵∠ABC＝60°，∴△ABC是等边三角形，∴BC＝AB＝2，∠BAC＝60°，∵四边形BOCE是矩形，∴BF＝CF＝BC＝1，∴AF⊥BC，∠BAF＝∠BAC＝30°，∴∠AFB＝90°，∴AF＝BF＝．7．解：（1）证明：∵AE∥BC，CE∥AD．∴四边形ADCE是平行四边形．∵∠BAC＝90°，AD是斜边BC边上的中线．∴AD＝CD．∴四边形ADCE是菱形．（2）连接BE，过点E作EF垂直BA，垂足为F，如图：∵∠ABC＝30°，AC＝2．∴BC＝4，AB＝．∵∠BAC＝90°，AD是斜边BC边上的中线．∴AD＝BD＝CD．∴∠DAB＝∠DBA．∵∠ABC＝30°．∴∠CDA＝60°．∴△ADC的等边三角形．∵AC＝2．∴AD＝AE＝2∵四边形ADCE是菱形．∴∠ECA＝∠CAD＝60°．∴∠EAF＝30°．∴＝1．∴AF＝＝．∴BF＝3．∴BE＝．8．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵CF＝BE，∴CF+EC＝BE+EC，即BC＝EF，∴AD＝EF，且AD∥EF，∴四边形AEFD是平行四边形，∵AE⊥BC，∴∠AEF＝90°，∴四边形AEFD是矩形；（2）解：在Rt△ABE中，∠AEB＝90°，BE＝1，∵tan∠ABC＝，∴AE＝2BE＝2，∵四边形AEFD为矩形，∴FD＝AE＝2，∠ADF＝90°，∵AD＝3，∴AF＝＝＝．9．解：（1）如图1，连结M1N、M2O、M2N、M3O、M3N，作M2G⊥x轴于点G，则G （1，0），OG＝ON＝1，∴OM2＝NM2，∴∠OM2G＝∠NM2G．∵tan∠OM1N＝＝＝，∴∠OM1N＝60°，∴点M1对线段ON的可视度为60°；∵tan∠OM2G＝＝＝，∴∠OM2G＝∠NM2G＝30°，∴∠OM2N＝60°，∴点M2对线段ON的可视度为60°；∵tan∠OM3N＝＜1，∴∠OM3N＜45°，∴点M3对线段ON的可视度不是60°．故答案为：M1，M2．（2）①∵A（﹣2，2），B（﹣2，﹣2），C（2，﹣2），D（2，2），∴四边形ABCD是正方形，且各边与坐标轴垂直（或平行）．如图2，设AD交y轴于点I，则∠AIE＝∠DIE＝90°．∵E（0，4），∴AI＝EI＝DI＝2，∴∠IEA＝∠IED＝45°，∴∠AED＝90°，∴点E对四边形ABCD的可视度为90°．故答案为：90．②由题意可知，点F在直线y＝4上．延长CD交直线y＝4于点H，以点D为圆心、DA长为半径作⊙D，则点C在⊙D上；∵DH与直线y＝4垂直，且DH＜DA，∴直线y＝4与⊙D有两个交点．设⊙D与直线y＝4在直线CD右侧的交点为点F，连结AF、CF、DF．∵∠AFC＝∠ADC＝45°，∴点F对四边形ABCD的可视度为45°．∵∠DHF＝90°，DH＝2，DF＝DA＝4，∴sin∠DFH＝，∴∠DFH＝30°，∴FH＝DF•cos30°＝4×＝2，∴F（2+2，4），∴a＝2+2；同理，如图4，以点A为圆心、AD长为半径作⊙A，交直线y＝4于点F，点F在直线AB左侧，此时，F（，4），∴a＝．综上所述，a＝2+2或a＝．10．（1）证明：∵AE∥DC，AE＝DC，∴四边形ADCE是平行四边形，∵AC＝BC，CD为△ABC的角平分线，∴CD⊥AB，∴∠ADC＝90°，∴平行四边形ADCE为矩形；（2）解：∵AC＝BC，CD为△ABC的角平分线，∴BD＝AD＝AB＝5，CD⊥AB，∴∠BDC＝90°，∴AC＝＝＝13，由（1）得：四边形ADCE为矩形，∴DE＝AC＝13．11．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵EF＝DA，∴EF＝BC，EF∥BC，∴四边形BCEF是平行四边形，又∵CE⊥AD，∴∠CEF＝90°，∴平行四边形BCEF是矩形；（2）解：∵四边形ABCD是平行四边形，∴CD＝AB＝3，∵CF＝4，DF＝5，∴CD2+CF2＝DF2，∴△CDF是直角三角形，∠DCF＝90°，∴△CDF的面积＝DF×CE＝CF×CD，∴CE＝＝＝，由（1）得：EF＝BC，四边形BCEF是矩形，∴∠FBC＝90°，BF＝CE＝，∴BC＝＝＝，∴EF＝．12．解：（1）∵点Q1（0，8），Q2（﹣4，2），Q3（8，4），点A（6，8），∴OQ1＝＝8，OQ＝＝，2OQ＝＝＝，3OA＝＝10，AQ＝＝6，1AQ＝＝＝，2AQ＝＝＝，3∴OQ12+AQ12＝OA2，OQ32+AQ32＝OA2，OQ22+AQ22≠OA2，∴∠OQ1A＝90°，∠OQ3A＝90°，∴Q1和Q3是点A的直角点；故答案为：Q1和Q3；（2）如图所示，连接OB，OC，取BO的中点M，OC的中点N，分别以M，N为圆心，OB，OC为直径作圆，由图可知，Q1，Q2为两个临界点，则＝x M﹣Q2M＝﹣﹣＝﹣4，同理，＝2+2，∴﹣4≤n≤2+2；（3）如图2，⊙M、⊙N分别与x轴交于B′（﹣3，0），C′（4，0），∴，解得：﹣3≤t≤3，∵D（t，0），E（t+1，0），∴DE＝1，由（2）可知，Q为BC的“直角点”，Q的横坐标n的取值范围为﹣4≤n≤2+2，∴，解得：﹣3≤t≤3，综上所述，﹣3≤t≤3．13．解：（1）∵AC平分∠BAD，AB∥CD．∴∠DAC＝∠BAC，∠DCA＝∠BAC．∴∠DAC＝∠DCA．∴AD＝DC．又∵AB∥CD，AB＝AD．∴AB∥CD且AB＝CD∴四边形ABCD是平行四边形．∵AB＝AD．∴四边形ABCD是菱形．（2）连接BD，交AC于点O，如图：∵菱形ABCD的边长为13，对角线AC＝24．∴CD＝13，AO＝CO＝12．∵点E、F分别是边CD、BC的中点．∴EF∥BD（中位线）．∵AC、BD是菱形的对角线．∴AC⊥BD，OB＝OD．又∵AB∥CD，EF∥BD．∴DE∥BG，BD∥EG．∴四边形BDEG是平行四边形．∴BD＝EG．在△COD中．∵OC⊥OD，CD＝13，CO＝12．∴．∴EG＝BD＝10．14．解（1）设CD交x轴于M，连接AC，过B作BN⊥AC，如图：∵A（﹣2，6），B（﹣2，﹣2），C（6，﹣2），D（6，6）．∴O到CD的距离CM＝6，AB＝8，BC＝8，AC＝8，∴根据“闭距离”定义得：d（点O，CD）＝6，∵S△ABC＝AB•BC＝AC•BN，∴B到AC的距离BN＝＝4，∴d（点B，AC）＝4，故答案为：6，4；（2）作直线x＝4，取E（4，8）、F（4，4）、G（4，0）、H（4，﹣4），如图：在直线x＝4上，E（4，8）、F（4，4）到AD距离为2，线段EF上的点到AD距离都小于2，同理G（4，0）、H（4，﹣4）到BC的距离为2，线段GH上的点到BC的距离都小于2，∴记线段BC，AD组成图形G已知点T（4，m），若d（点T，G）≤2，则4≤m≤8或﹣4≤m≤0；（3）取G（﹣5，0）、H（﹣4，0）、M（4，0）、N（8，0），如图：∵E（t，0），F（t+1，0），∴线段EF在x轴上，F在E右侧1个单位，①EF在AB左侧时，∵H到AB距离为2，∴F与H重合，此时EF上的点F到AB的距离最小为2，故d（EF，四边形ABCD）＝2，∴t+1＝﹣4，可得t＝﹣5，②EF在正方形ABCD内时，当EF在线段OM上，则EF的点到BC的距离都为2，故d（EF，四边形ABCD）＝2，此时，∴0≤t≤3，③EF在AB右侧时，E与N重合，此时EF上的点E到AB的距离最小为2，故d（EF，四边形ABCD）＝2，∴t＝8，综上所述，d（EF，四边形ABCD）＝2，t＝﹣5或0≤t≤3或t＝8．。
2021学年初中数学三年全国经典中考题15四边形解答题(含答案解析)
专题15四边形解答题学校:___________姓名：__________班级：___________考号：___________一、解答题1．已知：如图，E是▱ABCD的边BC延长线上的一点，且CE＝BC．求证：△ABC≌△DCE．2．如图，已知平行四边形ABCD中，E是BC的中点，连接AE并延长，交DC的延长线于点F，且AF＝AD，连接BF，求证：四边形ABFC是矩形．3．如图，在ABC中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE BF=，连接AE，CF．（1）求证：ADE≌CBF；（2）连接AF，CE，当BD平分ABC∠时，四边形AFCE是什么特殊四边形？请说明理由．4．某兴趣小组为了测量大楼CD的高度，先沿着斜坡AB走了52米到达坡顶点B处，然后在点B处测得大楼顶点C的仰角为53︒，已知斜坡AB的坡度为1:2.4i=，点A到大楼的距离AD为72米，求大楼的高度CD．（参考数据：sin534 5︒≈，cos533 5︒≈，tan534 3︒≈）5．如图，在平行四边形ABCD 中，∠D ＝60°，对角线AC ⊥BC ，⊙O 经过点A ，B ，与AC 交于点M ，连接AO 并延长与⊙O 交于点F ，与CB 的延长线交于点E ，AB ＝EB ． （1）求证：EC 是⊙O 的切线；（2）若AD ＝，求AM 的长（结果保留π）．6．如图，过□ABCD 对角线AC 与BD 的交点E 作两条互相垂直的直线，分别交边AB 、BC ．CD 、DA 于点P 、M 、Q 、N ． （1）求证：PBE ≌QDE ；（2）顺次连接点P 、M 、Q 、N ，求证：四边形PMQN 是菱形．7．如图1，四边形ABCD 的对角线AC ，BD 相交于点O ，OA OC =，OB OD CD =+．图1 图2（1）过点A 作//AE DC 交BD 于点E ，求证：AE BE =； （2）如图2，将ABD △沿AB 翻折得到ABD '△． ①求证：//BD CD '；②若//AD BC '，求证：22CD OD BD =⋅．8．已知1O 的半径为1r ，2O 的半径为2r ，以1O 为圆心，以12r r +的长为半径画弧，再以线段12O O 的中点P 为圆心，以1212O O 的长为半径画弧，两弧交于点A ，连接1Q A ，2O A ，1O A 交1O 于点B ，过点B 作2O A 的平行线BC 交12O O 于点C ．（1）求证：BC 是2O 的切线；（2）若12r =，21r =，126O O =，求阴影部分的面积．9．如图，在ABC 中，AB ＝BC ，以△ABC 的边AB 为直径作⊙O ，交AC 于点D ，过点D 作DE ⊥BC ，垂足为点E ． （1）试证明DE 是⊙O 的切线；（2）若⊙O 的半径为5，AC ＝，求此时DE 的长．10．如图，菱形ABCD 的边长为1，=60ABC ∠︒，点E 是边AB 上任意一点（端点除外），线段CE 的垂直平分线交BD ，CE 分别于点F ，G ，AE ，EF 的中点分别为M ，N ．（1）求证：AF EF =； （2）求MN NG +的最小值；（3）当点E 在AB 上运动时，CEF ∠的大小是否变化？为什么？ 11．若ABC 和AED 均为等腰三角形，且90BAC EAD ∠=∠=︒．（1）如图（1），点B 是DE 的中点，判定四边形BEAC 的形状，并说明理由； （2）如图（2），若点G 是EC 的中点，连接GB 并延长至点F ，使CF CD =．求证：①EB DC =，②EBG BFC ∠=∠．12．小明将两个直角三角形纸片如图（1）那样拼放在同一平面上，抽象出如图（2）的平面图形，ACB ∠与ECD ∠恰好为对顶角，90ABC CDE ∠=∠=︒，连接BD ，AB BD =，点F 是线段CE 上一点．探究发现：（1）当点F 为线段CE 的中点时，连接DF （如图（2），小明经过探究，得到结论：BD DF ⊥．你认为此结论是否成立？_________．（填“是”或“否”） 拓展延伸：（2）将（1）中的条件与结论互换，即：若BD DF ⊥，则点F 为线段CE 的中点．请判断此结论是否成立．若成立，请写出证明过程；若不成立，请说明理由． 问题解决：（3）若6,9AB CE ==，求AD 的长． 13．问题探究：小红遇到这样一个问题：如图1，ABC 中，6AB =，4AC =，AD 是中线，求AD 的取值范围．她的做法是：延长AD 到E ，使DE AD =，连接BE ，证明BED CAD △≌△，经过推理和计算使问题得到解决．请回答：（1）小红证明BED CAD △≌△的判定定理是：__________________________________________； （2）AD 的取值范围是________________________； 方法运用：（3）如图2，AD 是ABC 的中线，在AD 上取一点F ，连结BF 并延长交AC 于点E ，使AE EF =，求证：BF AC =． （4）如图3，在矩形ABCD 中，12AB BC =，在BD 上取一点F ，以BF 为斜边作Rt BEF △，且12EF BE =，点G 是DF 的中点，连接EG ，CG ，求证：=EG CG ．14．已知：如图，在四边形ABCD 和Rt EBF △中，//AB CD ，CD AB >，点C 在EB 上，90ABC EBF ∠=∠=︒，8AB BE cm ==，6BC BF cm ==，延长DC 交EF 于点M ，点P 从点A 出发，沿AC 方向匀速运动，速度为2cm s ；同时，点Q 从点M 出发，沿MF 方向匀速运动，速度为1cm s ，过点P 作GH AB ⊥于点H ，交CD 于点G ．设运动时间为()()05t s t <<．解答下列问题：（1）当t为何值时，点M在线段CQ的垂直平分线上？（2）连接PQ，作QN AF⊥于点N，当四边形PQNH为矩形时，求t的值；（3）连接QC，QH，设四边形QCGH的面积为()2S cm，求S与t的函数关系式；（4）点P在运动过程中，是否存在某一时刻t，使点P在AFE∠的平分线上？若存在，求出t的值；若不存在，请说明理由．15．如图，在菱形ABCD中，AB=AC，点E、F、G分别在边BC、CD上，BE=CG，AF平分∠EAG，点H是线段AF上一动点(与点A不重合)．(1)求证:△AEH≌△AGH；(2)当AB=12，BE=4时：①求△DGH周长的最小值；②若点O是AC的中点，是否存在直线OH将△ACE分成三角形和四边形两部分，其中三角形的面积与四边形的面积比为1:3．若存在，请求出AHAF的值；若不存在，请说明理由．16．如图，在直角坐标系中，四边形OABC是平行四边形，经过A（﹣2，0），B，C三点的抛物线y＝ax2+bx+83（a＜0）与x轴的另一个交点为D，其顶点为M，对称轴与x轴交于点E．（1）求这条抛物线对应的函数表达式；（2）已知R是抛物线上的点，使得△ADR的面积是平行四边形OABC的面积的34，求点R的坐标；（3）已知P是抛物线对称轴上的点，满足在直线MD上存在唯一的点Q，使得∠PQE ＝45°，求点P的坐标．17．如图，二次函数y ＝ax 2＋bx ＋4的图象与x 轴交于点A(－1，0)，B(4，0)，与y 轴交于点C ，抛物线的顶点为D ，其对称轴与线段BC 交于点E ．垂直于x 轴的动直线l 分别交抛物线和线段BC 于点P 和点F ，动直线l 在抛物线的对称轴的右侧（不含对称轴）沿x 轴正方向移动到B 点．（1）求出二次函数y ＝ax 2＋bx ＋4和BC 所在直线的表达式；（2）在动直线l 移动的过程中，试求使四边形DEFP 为平行四边形的点P 的坐标； （3）连接CP ，CD ，在移动直线l 移动的过程中，抛物线上是否存在点P ，使得以点P ，C ，F 为顶点的三角形与DCE 相似，如果存在，求出点P 的坐标，如果不存在，请说明理由．18．如图，二次函数24y ax bx =++的图象与x 轴交于点(1,0)A -，(4,0)B ，与y 轴交于点C ，抛物线的顶点为D ，其对称轴与线段BC 交于点E ，垂直于x 轴的动直线l 分别交抛物线和线段BC 于点P 和点F ，动直线l 在抛物线的对称轴的右侧（不含对称轴）沿x 轴正方向移动到B 点．（1）求出二次函数24y ax bx =++和BC 所在直线的表达式；（2）在动直线l 移动的过程中，试求使四边形DEFP 为平行四边形的点P 的坐标； （3）连接CP ，CD ，在动直线l 移动的过程中，抛物线上是否存在点P ，使得以点P ，C ，F 为顶点的三角形与DCE 相似，如果存在，求出点P 的坐标，如果不存在，请说明理由．参考答案1．见解析 【详解】证明：∵四边形ABCD 是平行四边形， ∴AB ∥CD ，AB ＝CD ， ∴∠B ＝∠DCE ， 在△ABC 和△DCE 中，∴△ABC ≌△DCE （SAS ）．由平行四边形的性质得出AB ∥CD ，AB ＝CD ，由平行线的性质得出∠B ＝∠DCE ，由SAS 即可得出结论．本题考查了平行四边形的性质、全等三角形的判定与性质等知识； 【点评】熟练掌握平行四边形的性质和全等三角形的判定方法是解题的关键． 2．见解析 【分析】先根据平行四边形的性质、平行线的性质得到两角一边对应相等，再根据三角形全等的判定定理与性质可得AB CF =，然后根据平行四边形的判定可得四边形ABFC 是平行四边形，又根据等量代换可得BC AF =，最后根据矩形的判定（对角线相等的平行四边形是矩形）可得四边形ABFC 是矩形． 【详解】∵四边形ABCD 是平行四边形 ∴//,,AB CD AB CD AD BC == ∴,BAE CFE ABE FCE ∠=∠∠=∠ ∵E 为BC 的中点 ∴EB EC =∴()ABE FCE AAS ≅ ∴AB CF = ∵//AB CF∴四边形ABFC 是平行四边形AF AD =BC AF ∴=∴平行四边形ABFC 是矩形． 【点睛】本题考查了平行四边形的判定与性质、三角形全等的判定定理与性质、矩形的判定等知识点，熟练运用各判定与性质是解题关键． 3．（1）见解析（2）菱形，见解析 【分析】（1）利用SAS 证明ADE ≌CBF 即可求解；（2）先证明四边形AFCE 是平行四边形，再证明对角线互相垂直即可得到为菱形． 【详解】（1）∵四边形ABCD 是平行四边形， ∴AD=BC,∠ADB=∠CBD ，又∵∠ADB+∠ADE=180°，∠CBF+∠CBD=180°， ∴∠ADE=∠CBF 在△ADE 和△CBF 中AD BC ADE CBF DE BF =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CBF ； （2）四边形AFCE 是菱形 理由如下：如图，连接AF ，CE ， 由（1）得△ADE ≌△CBF ∴CF=AE, ∠E=∠F ∴AE ∥CF ∴AE CF∴四边形AFCE 是平行四边形当BD平分∠ABC时，∠ABD=∠CBD又∵AD∥CB，∴∠ADB=∠DBC∴∠ABD=∠ABD∴AD=AB=BC∴△ABC为等腰三角形由等腰三角形性质三线合一可得AC⊥EF∴平行四边形AFCE是菱形【点睛】此题主要考查特殊平行四边形的性质与判定，解题的关键是熟知菱形的判定定理．4．大楼的高度CD为52米【分析】i 及勾股过点B作BE⊥AD于点E，作BF⊥CD于点F，在Rt△ABE中，根据坡度1:2.4定理求出BE和AE的长，进而由三个角是直角的四边形是矩形判断四边形BEDF是矩形，得到BF和FD的长，再在Rt△BCF中，根据∠CBF的正切函数解直角三角形，得到CF的长，由CD=CF+FD得解．【详解】解：如下图，过点B作BE⊥AD于点E，作BF⊥CD于点F，在Rt△ABE中，AB=52，∵1:2.4 i=∴tan∠BAE=BEAE=12.4，∴AE=2.4BE，又∵BE2+AE2=AB2，∴BE2+(2.4BE)2=522，解得：BE=20，∴AE=2.4BE=48；∵∠BED=∠D=∠BFD=90°，∴四边形BEDF是矩形，∴FD=BE=20，BF=ED=AD-AE=72-48=24；在Rt△BCF中，tan∠CBF=CF BF，即：tan53°=CF BF=43∴CF=43BF=32，∴CD=CF+FD=32+20=52．答：大楼的高度CD为52米．【点睛】本题考查解直角三角形的实际应用，熟练掌握仰角的定义，准确确定合适的直角三角形并且根据勾股定理或三角函数列出方程是解题的关键．5．（1）见解析；（2）4 3π【分析】（1）证明：连接OB，根据平行四边形的性质得到∠ABC＝∠D＝60°，求得∠BAC＝30°，根据等腰三角形的性质和三角形的外角的性质得到∠ABO＝∠OAB＝30°，于是得到结论；（2）根据平行四边形的性质得到BC＝AD＝过O作OH⊥AM于H，则四边形OBCH 是矩形，解直角三角形即可得到结论．【详解】（1）证明：连接OB，∵四边形ABCD是平行四边形，∴∠ABC＝∠D＝60°，∵AC⊥BC，∴∠ACB＝90°，∴∠BAC＝30°，∵BE＝AB，∴∠E＝∠BAE，∵∠ABC＝∠E+∠BAE＝60°，∴∠E＝∠BAE＝30°，∵OA＝OB，∴∠ABO＝∠OAB＝30°，∴∠OBC＝30°+60°＝90°，∴OB⊥CE，∴EC是⊙O的切线；（2）∵四边形ABCD是平行四边形，∴BC＝AD＝过O作OH⊥AM于H，则四边形OBCH是矩形，∴OH ＝BC ＝∴OA ＝sin 60OH ︒＝4，∠AOM ＝2∠AOH ＝60°， ∴AM 的长度＝604180π⋅⨯＝43π． 【点睛】本题考查了切线的判定，锐角三角函数，平行四边形的性质，矩形的判定和性质，弧长的计算，正确的作出辅助线是解题的关键．6．（1）见解析；（2）见解析【分析】（1）由ASA 证△PBE ≌△QDE 即可；（2）由全等三角形的性质得出EP=EQ ，同理△BME ≌△DNE （ASA ），得出EM=EN ，证出四边形PMQN 是平行四边形，由对角线PQ ⊥MN ，即可得出结论．【详解】（1）证明：∵四边形ABCD 是平行四边形，∴EB=ED ，AB ∥CD ，∴∠EBP=∠EDQ ，在△PBE 和△QDE 中，EBP EDQ EB EDBEP DEQ ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△PBE ≌△QDE （ASA ）；（2）证明：如图所示：∵△PBE ≌△QDE ，∴EP=EQ ，同理：△BME ≌△DNE （ASA ），∴四边形PMQN 是平行四边形，∵PQ ⊥MN ，∴四边形PMQN 是菱形．【点睛】本题考查了平行四边形的判定与性质，菱形的判定，全等三角形的判定与性质；熟练掌握菱形的判定和平行四边形的判定与性质，证明三角形全等是解题的关键．7．（１）见解析；（２）①见解析；②见解析．【分析】（1）连接CE ，根据全等证得AE=CD ，进而AECD 为平行四边形，由=OB OD CD +进行等边代换，即可得到AE BE =；（2）①过A 作AE ∥CD 交BD 于E ，交BC 于F ，连接CE ，AE BE =，得ABE BAE ∠=∠，利用翻折的性质得到D BA BAE '∠=∠，即可证明；②证△BEF ≌△CDE ，从而得BFE CED ∠=∠，进而得∠CED=∠BCD ，且CDE BDC ∠=，得到△BCD ∽△CDE ，得CD DE BD CD=，即可证明． 【详解】解：（1）连接CE ，∵//AE DC ，∴OAE OCD ∠=∠，∵OAE OCD ∠=∠，OA OC =，AOE COD ∠=∠，∴△OAE ≌△OCD ，∴AE=CD ，∴四边形AECD 为平行四边形，∴AE=CD ，OE=OD ，∵==+B OB OD CD OE E +，∴AE BE =；（2）①过A 作AE ∥CD 交BD 于E ，交BC 于F ，连接CE ，由（1）得，AE BE =，∴ABE BAE ∠=∠，由翻折的性质得D BA ABE '∠=∠，∴D BA BAE '∠=∠，∴//BD AF '，∴//BD CD '；②∵//AD BC '，//BD AF '，∴四边形AFBD '为平行四边形，∴=D AFB '∠∠，'BD AF =，∴AF BD =，∵AE BE =，∴EF=DE ，∵四边形AECD 是平行四边形，∴CD=AE=BE ，∵AF ∥CD ，∴BEF CDE ∠=∠，∵EF=DE ，CD=BE ，BEF CDE ∠=∠，∴△BEF ≌△CDE （SAS ），∴BFE CED ∠=∠，∵BFE BCD ∠=∠，∴∠CED=∠BCD ，又∵∠BDC=∠CDE ，∴△BCD∽△CDE，∴CD DEBD CD=，即2CD BD DE=⨯，∵DE=2OD，∴22CD OD BD=⋅．【点睛】本题考查相似三角形的判定与性质以及平行四边形的判定和性质，考查等腰三角形的判定与性质综合，熟练掌握各图形的性质并灵活运用是解题的关键．8．（1）见解析；（2）2 3π【分析】（1）过点O2作O2D⊥BC，交BC于点D，根据作图过程可得AP=O1P=O2P，利用等腰三角形的性质和三角形内角和证明AO2⊥AO1，再根据BC∥AO2，证明四边形ABDO2为矩形，得到O2D=2r，点D在圆O2上，可得结论；（2）证明△AO1O2∽△BO1C，求出O1C，利用△BO1C的面积减去扇形BO1E的面积即可. 【详解】解：（1）由作图过程可得：AP=O1P=O2P=12O1O2，AO1=AB+BO1=12r r+，∴∠PAO1=PO1A，∠PAO2=∠PO2A，AB=2r，而∠PAO1+∠PO1A+∠PAO2+∠PO2A=180°，∴∠PAO1+∠PAO2=90°，即AO2⊥AO1，∵BC∥AO2，∴O1B⊥BC，即BC与圆O1相切，过点O2作O2D⊥BC，交BC于点D，可知四边形ABDO2为矩形，∴AB=O2D=2r，而圆O2的半径为2r，∴点D在圆O2上，即BC是2O的切线；（2）∵AO 2∥BC ，∴△AO 1O 2∽△BO 1C ， ∴11211AO O O BO O C=， ∵12r =，21r =，126O O =，即AO 1=12r r +=3，BO 1=2， ∴1362O C=， ∴O 1C=4，∵BO 1⊥BC ，∴cos ∠BO 1C=112142BO CO ==， ∴∠BO 1C=60°，∴=，∴S 阴影=1BO C S △-1BO E S 扇形=2160222360π⨯⨯⨯-=23π 【点睛】本题考查了尺规作图的原理，切线的判定和性质，矩形的判定和性质，扇形面积，相似三角形的判定和性质，等边对等角，知识点较多，解题的关键是根据作图过程得到相应的线段关系.9．（1）见解析；（2）3【分析】（1）连接OD、BD，求出BD⊥AD，AD=DC，根据三角形的中位线得出OD∥BC，推出OD⊥DE，根据切线的判定推出即可；（2）先利用勾股定理求出BD的长，证得Rt△CDE和Rt△ABD，利用对应边成比例即可求解．【详解】（1）证明：连接OD，BD，∵AB为⊙O的直径，∴BD⊥AD，又∵AB=BC，△ABC是等腰三角形，∴AD=DC，∴OD是△ABC的中位线，∴OD∥BC，又DE⊥BC，∴DE⊥OD，∴DE是⊙O的切线；（2）由（1）知，BD是AC边上的中线，AC=，得AD=CD=∵⊙O的半径为5，∴AB=10，在Rt△ABD中，BD==，∵AB=BC，∴∠A =∠C ，在Rt △CDE 和Rt △ABD 中，∵∠DEC =∠ADB =90°，∠C =∠A ，∴Rt △CDE ∽Rt △ABD ，∴CD DEAB BD =，即10=， 解得：DE =3．【点睛】本题综合考查了切线的判定、圆周角定理、相似三角形的判定与性质以及三角形中位线的判定与性质．解题的关键是熟练掌握和圆有关的各种性质定理，并且能够熟练运用． 10．（1）见解析；（2）12；（3）不变，理由见解析. 【分析】（1）连接CF ，根据垂直平分线的性质和菱形的对称性得到CF=EF 和CF=AF 即可得证； （2）连接AC ，根据菱形对称性得到AF+CF 最小值为AC ，再根据中位线的性质得到MN+NG 的最小值为AC 的一半，即可求解；（3）延长EF ，交DC 于H ，利用外角的性质证明∠AFC=∠FCE+∠FEC+∠FAE+∠FEA ，再由AF=CF=EF ，得到∠AEF=∠EAF ，∠FEC=∠FCE ，从而推断出∠AFD=∠FAE+∠ABF=∠FAE+∠CEF ，从而可求出∠ABF=∠CEF=30°，即可证明.【详解】解：（1）连接CF ，∵FG 垂直平分CE ，∴CF=EF ，∵四边形ABCD 为菱形，∴A 和C 关于对角线BD 对称，∴CF=AF ，∴AF=EF ；（2）连接AC，∵M和N分别是AE和EF的中点，点G为CE中点，∴MN=12AF，NG=12CF，即MN+NG=12（AF+CF），当点F与菱形ABCD对角线交点O重合时，AF+CF最小，即此时MN+NG最小，∵菱形ABCD边长为1，∠ABC=60°，∴△ABC为等边三角形，AC=AB=1，即MN+NG的最小值为12；（3）不变，理由是：延长EF，交DC于H，∵∠CFH=∠FCE+∠FEC，∠AFH=∠FAE+∠FEA，∴∠AFC=∠FCE+∠FEC+∠FAE+∠FEA，∵点F在菱形ABCD对角线BD上，根据菱形的对称性可得：∠AFD=∠CFD=12∠AFC，∵AF=CF=EF，∴∠AEF=∠EAF ，∠FEC=∠FCE ，∴∠AFD=∠FAE+∠ABF=∠FAE+∠CEF ，∴∠ABF=∠CEF ，∵∠ABC=60°，∴∠ABF=∠CEF=30°，为定值.【点睛】本题考查了菱形的性质，最短路径，等边三角形的判定和性质，中位线定理，难度一般，题中线段较多，需要理清线段之间的关系．11．（1）四边形BEAC 是平行四边形，证明见解析；（2）①见解析；②见解析【分析】（1）利用等腰直角三角形的性质证得45BAE ∠=︒，45CBA ∠=︒，推出//BC EA ，再根据平行于同一直线的两直线平行即可推出结论；（2）①利用“SAS ”证得AEB ADC △≌△，即可证明结论；②延长FG 至点H ，使GH FG =，证得EHG CFG ≌，推出BFC H CF EH ∠=∠=，，利用①的结论即可证明EBG BFC ∠=∠．【详解】（1）证明：四边形BEAC 是平行四边形．理由如下：∵EAD 为等腰三角形且90EAD ∠=︒，∴45E ∠=︒，∵B 是DE 的中点，∴AB DE ⊥，∴45BAE ∠=︒，∵ABC 是等腰三角形，90BAC ∠=︒，∴45CBA ∠=︒，∴BAE CBA =∠∠，∴//BC EA ，又∵AB DE ⊥，∴90EBA BAC ∠=∠=︒．∴//BE AC ．∴四边形BEAC 是平行四边形．（2）证明：①∵AED 和ABC 为等腰三角形，∴AE AD AB AC ==，，∵90EAD BAC ∠=∠=︒，∴EAD DAB BAC DAB ∠+∠=∠+∠，即EAB DAC ∠=∠，∴AEB ADC △≌△，∴EB DC =；②延长FG 至点H ，使GH FG =．∵G 是EC 中点，∴=EG CG ，又EGH FGC ∠=∠，∴EHG CFG ≌，∴BFC H CF EH ∠=∠=，，∵CF CD =，∴BE CF =，∴BE EH =，∴EBG H ∠=∠，∴EBG BFC ∠=∠．【点睛】本题考查了平行四边形的判定，等腰直角三角形的判定和性质，全等三角形的判定和性质，正确作出辅助线构建全等三角形是解答（2）②的关键．12．（1）是；（2）结论成立，理由见解析；（3）5 【分析】（1）利用等角的余角相等求出∠A=∠E ，再通过AB=BD 求出∠A=∠ADB ，紧接着根据直角三角形斜边的中线等于斜边的一半求出FD=FE=FC ，由此得出∠E=∠FDE ，据此进一步得出∠ADB=∠FDE ，最终通过证明∠ADB +∠EDC=90°证明结论成立即可；（2）根据垂直的性质可以得出BDC CDF ∠+∠=90°，EDF CDF ∠+∠=90°，从而可得BDC EDF ∠=∠，接着证明出A EDF ∠=∠，利用A E ∠=∠可知E EDF ∠=∠，从而推出=EF FD ，最后通过证明ECD CDF ∠=∠得出CF DF =，据此加以分析即可证明结论；（3）如图，设G 为EC 的中点，连接GD ，由（1）得DG BD ⊥，故而92GD GC ==，在Rt GDB △中，利用勾股定理求出152GB =，由此得出159322CB =-=，紧接着，继续通过勾股定理求出AC ==ABC EDC ，再根据相似三角形性质得出39CD =，从而求出5CD =，最后进一步分析求解即可.【详解】（1）∵∠ABC=∠CDE=90°，∴∠A +∠ACB=∠E +∠ECD ，∵∠ACB=∠ECD ，∴∠A=∠E ，∵AB=BD ，∴∠A=∠ADB ，在Rt ECD △中，∵F 是斜边CE 的中点，∴FD=FE=FC ，∴∠E=∠FDE ，∵∠A=∠E ，∴∠ADB=∠FDE ，∵∠FDE +∠FDC=90°，∴∠ADB +∠FDC=90°，即∠FDB=90°，∴BD ⊥DF ，结论成立，故答案为：是；（2）结论成立，理由如下：∵BD DF ⊥，ED AD ⊥∴BDC CDF ∠+∠=90°，EDF CDF ∠+∠=90°，∴BDC EDF ∠=∠，∵AB BD =，∴A BDC ∠=∠．∴A EDF ∠=∠．又∵A E ∠=∠，∴E EDF ∠=∠．∴=EF FD ．又E ECD ∠+∠=90°，EDF FDC ∠+∠=90°，E EDF ∠=∠，∴ECD CDF ∠=∠，∴CF DF =．∴CF EF =．∴F 为CE 的中点；（3）如图，设G 为EC 的中点，连接GD ，由（1）可知DG BD ⊥，∴1922GD EC EG GC ====， 又∵6BD AB ==，在Rt GDB △中，152GB ==， ∴159322CB =-=，在Rt ABC 中，AC ==在ABC 与EDC △中，∵∠ABC=∠EDC ，∠ACB=∠ECD ，∴ABC EDC ，3CD=，∴CD =，∴55AD AC CD =+=+= 【点睛】本题主要考查了直角三角形的性质和相似三角形的性质及判定的综合运用，熟练掌握相关方法是解题关键.13．（1）SAS ；（2）15AD <<；（3）见解析；（4）见解析【分析】（1）利用三角形的中线与辅助线条件，直接证明BED CAD △≌△，从而可得证明全等的依据；（2）利用全等三角形的性质得到,AC BE =求解AE 的范围，从而可得答案；（3）延长AD 至点A '，使A D AD '=，证明ADC A DB '≌，利用全等三角形的性质与AE EF =，证明BFD A '∠=∠，得到BF A B '=，从而可得答案；（4）延长CG 至点H 使HG CG =，连接HF 、CE 、HE ，证明HGF CGD ≌，得到,HF CD HFG CDG =∠=∠，利用锐角三角函数证明EBF ADB ∠=∠，再证明EFH EBC ∽，利用相似三角形的性质可得CEH △是直角三角形，从而可得答案．【详解】解：（1）如图，AD 是中线，,BD CD ∴=在ADC 与EDB △中，AD ED ADC EDB CD BD =⎧⎪∠=∠⎨⎪=⎩().ADC EDB SAS ∴≌故答案为：SAS（2）,ADC EDB ≌4,AC BE ∴==6,AB =210,AE ∴＜＜2,AE AD =15,AD ∴＜＜故答案为：15AD <<（3）证明：延长AD 至点A '，使A D AD '=，∵AD 是ABC 的中线∴BD CD =在ADC 和A DB '中AD A D ADC A DB CD BD ''=⎧⎪∠=∠⎨⎪=⎩∴ADC A DB '≌，∴,CAD A AC A B ''∠=∠=，又∵AE EF =，∵CAD AFE ∠=∠，∴A AFE '∠=∠，又∵AFE BFD ∠=∠，∴BFD A '∠=∠∴BF A B '=，又∵A B AC '=∴BF AC =（4）证明：延长CG 至点H 使HG CG =，连接HF 、CE 、HE∵G 为FD 的中点∴FG DG =在HGF △和CGD △中HG CG HGF CGD FG DG =⎧⎪∠=∠⎨⎪=⎩∴HGF CGD ≌∴,HF CD HFG CDG =∠=∠在Rt BEF △中，∵12EF BE =， ∴1tan 2EBF ∠= 又矩形ABCD 中，12AB BC = ∴12AB AD =， ∴1tan 2ADB =∠， ∴EBF ADB ∠=∠，又//AD BC ，∴ADB DBC ∠=∠，∴EBF ADB DBC ∠=∠=∠，又EFD ∠为BEF 的外角，∴EFD EBF BEF ∠=∠+∠，即90EFH HFD EBF ∠+∠=∠+︒，∵90ADB BDC ∠+∠=︒，∴EFH HFD EBF ADB BDC ∠+∠=∠+∠+∠，∴2EFH EBF ∠=∠，即EFH EBC ∠=∠，在EFH △和EBC 中，11,22EF HF BEBC == ∴EF HF BE BC=， 又EBC EFH ∠=∠，∴EFH EBC ∽，∴FEH BEC ∠=∠，∵HEC CEF BEF CEF ∠+∠=∠+∠，∴90HEC BEF ∠=∠=︒，∴CEH △是直角三角形，∵G 为CH 的中点， ∴12EG CH =， 即=EG CG ．【点睛】本题考查的是倍长中线法证明三角形全等，同时考查全等三角形的性质，等腰三角形的判定与性质，直角三角形的性质，矩形的性质，三角形相似的判定与性质，锐角三角函数的应用，掌握以上知识是解题的关键．14．（1） t=32；（2）t=3;（3）S 与t 的函数关系式为2161572552S t t =-++；（4）存在，t=72, 【分析】（1）要使点M 在线段CQ 的垂直平分线上，只需证CM=MQ 即可；（2）由矩形性质得PH=QN ，由已知和AP=2t ，MQ=t ，解直角三角形推导出PH 、QN ，进而得关于t 的方程，解之即可；（3）分别用t 表示出梯形GHFM 的面积、△QHF 的面积、△CMQ 的面积，即可得到S 与t 的函数关系式；（4）延长AC 交EF 与T ，证得AT ⊥EF ，要使点P 在∠AFE 的平分线上，只需PT=PH ，分别用t 表示PT 、PH ，代入得关于t 的方程，解之即可．【详解】（1）当t =32时，点M 在线段CQ 的垂直平分线上，理由为： 由题意，CE=2，CM ∥BF ， ∴CM CE BF BE =即：268CM =， 解得：CM=32， 要使点M 在线段CQ 的垂直平分线上，只需QM=CM=32， ∴t=32； （2）如图，∵90ABC EBF ∠=∠=︒，8AB BE ==，6BC BF ==， ∴AC=10，EF=10，sin ∠PAH=35BC AC =，cos ∠PAH=45AB AC =，sin ∠EFB=45BE EF =， 在Rt △APH 中，AP=2t ，∴PH=AP ·sin ∠PAH=65t ， 在Rt △ECM 中，CE=2,CM=32,由勾股定理得：EM=52， 在Rt △QNF 中，QF=10-t-52=152t -，∴QN=QF ·sin ∠EFB=(152t -)×45=465t -， 四边形PQNH 为矩形，∴PH=QN ， ∴65t =465t -， 解得：t=3；（3）如图，过Q 作QN ⊥AF 于N ，由（2）中知QN=465t -，AH=AP ·cos ∠PAH=85t ， ∴BH=GC=8-85t ，∴GM=GC+CM=8319885225t t -+=-，HF=HB+BF=8145t -， ∴QHF CMQ GHFM S S S S =--梯形 =111()6(6)222GM HF HF QN CM QN +⨯--- =11988184134(14)6(14)(6)(66)2255255225t t t t t -+-⨯-----+ =2161572552t t -++， ∴S 与t 的函数关系式为：2161572552S t t =-++；（4）存在，t=72．证明：如图，延长AC 交EF 于T ，∵AB=BF,BC=BF, 90ABC EBF ∠=∠=︒，∴△ABC ≌△EBF ，∴∠BAC=∠BEF ，∵∠EFB+∠BEF=90º，∴∠BAC+∠EFB=90º，∴∠A TE=90º即PT ⊥EF ，要使点P 在AFE ∠的平分线上，只需PH=PT ，在Rt △ECM 中，CE=2,sin ∠BEF=35CT BF CE EF ==， CT=CE ·sin ∠BEF =65， PT=10+65-2t=5625t -，又PH=65t ， 65t =5625t -， 解得：t=72．【点睛】本题属于四边形的综合题，考查了解直角三角形、锐角三角函数、垂直平分线、角平分线、矩形的性质、全等三角形的判定与性质、多边形的面积等知识、解答的关键是认真审题，分析相关知识，利用参数构建方程解决问题，是中考常考题型．15．（1）见解析；（2）①8；②存在，12或57【分析】（1）证明△ABE ≌△ACG 得到AE=AG ，再结合角平分线，即可利用SAS 证明△AEH ≌△AGH ；（2）①根据题意可得点E 和点G 关于AF 对称，从而连接ED ，与AF 交于点H ，连接HG ，得到△DGH周长最小时即为DE+DG，构造三角形DCM进行求解即可；②分当OH与AE相交时，当OH与CE相交时两种情况分别讨论，结合中位线，三角形面积进行求解即可.【详解】解：（1）∵四边形ABCD为菱形，∴AB=BC，∵AB=AC，∴△ABC是等边三角形，∴∠B=∠ACB=∠ACD=60°，∵BE=CG，AB=AC，∴△ABE≌△ACG，∴AE=AG，∵AF平分∠EAG，∴∠EAH=∠GAH，∵AH=AH，∴△AEH≌△AGH；（2）①如图，连接ED，与AF交于点H，连接HG，∵点H在AF上，AF平分∠EAG，且AE=AG，∴点E和点G关于AF对称，∴此时△DGH的周长最小，过点D作DM⊥BC，交BC的延长线于点M，由（1）得：∠BCD=∠ACB+∠ACD=120°，∴∠DCM=60°，∠CDM=30°，∴CM=12CD=6，∴=∵AB=12=BC，BE=4，∴EC=DG=8，EM=EC+CM=14，∴=，∴DH+HG+DG=8∴△DGH周长的最小值为8；②当OH与AE相交时，如图，AE与OH交于点N，可知S△AON：S四边形HNEF=1:3，即S△AON：S△AEC=1:4，∵O是AC中点，∴N为AE中点，此时ON∥EC，∴12 AN AO AHAE AC AF===，当OH与EC相交时，如图，EC与OH交于点N，同理S△NOC：S四边形ONEA=1:3，∴S△NOC：S△AEC=1:4，∵O为AC中点，∴N为EC中点，则ON∥AE，∴AH EN AF EF=，∵BE=4，AB=12，∴EC=8，EN=4，过点G作GP⊥BC，交BNC延长线于点P，∵∠BCD=120°，∴∠GCP=60°，∠CGP=30°，∴CG=2CP ，∵CG=BE=4，∴CP=2，GP=∵AE=AG ，AF=AF ，∠EAF=∠GAF ，∴△AEF ≌△AGF ，∴EF=FG ，设EF=FG=x ，则FC=8-x ，FP=10-x ，在△FGP 中，()(22210x x -+=， 解得：x=285， ∴EF=285， ∴452875AH EN AF EF ===，综上：存在直线OH ，AH AF 的值为12或57. 【点睛】 本题考查了菱形的性质，全等三角形的判定和性质，直角三角形的性质，中位线，最短路径问题，知识点较多，难度较大，解题时要注意分情况讨论.16．（1）y ＝﹣13x 2+23x+83；（2）（34）或（134）或（34-）或（134-）；（3）点P 的坐标为（1，32）或（1，3）或（1，-3）． 【分析】 （1）根据平行四边形的性质及点A 坐标可得抛物线的对称轴为直线x=1，可得﹣2b a ＝1，把点A坐标代入抛物线不等式可得0＝4a﹣2b+83，解方程组求出a、b的值即可得答案；（2）根据抛物线对称轴方程及点A坐标可得点D坐标，根据△ADR的面积是平行四边形OABC的面积的34可得出点R的纵坐标，代入抛物线解析式可求出点R横坐标，即可得答案；（3）作△PEQ的外接圆R，根据圆周角定理可得∠PRE=90°，可得△PRE为等腰直角三角形，由在直线MD上存在唯一的点Q，使得∠PQE＝45°可得⊙R与直线MD相切，可得RQ⊥MD，根据对称轴可得点M坐标，即可得出DE、DE的长，根据勾股定理可求出DM 的长，设点P（1，2m），根据等腰直角三角形的性质可得PH＝HE＝HR＝m，即可得出R （1+m，m），利用S△MED＝S△MRD+S△MRE+S△DRE可求出m的值，即可得点P坐标；根据DE=ME 可得∠MDE=45°，可得点M符合题意，过点D作DF⊥DM交对称轴于F，可得∠FDE=45°，可得点F符合题意，根据DE=EF可求出点F坐标，综上即可得答案．【详解】（1）∵A（-2，0），四边形OABC是平行四边形，∴BC//OA，BC=OA=2，∵抛物线与y轴交于点B，∴抛物线的对称轴为直线x＝022+=1，则x＝﹣2ba＝1①，将点A的坐标代入抛物线表达式得：0＝4a﹣2b+83②，联立①②得1284203baa b⎧-=⎪⎪⎨⎪-+=⎪⎩，解得1323ab⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线的表达式为：y＝﹣13x2+23x+83；（2）∵A（-2，0），抛物线对称轴为直线x＝1，∴点D（4，0）；∵△ADR 的面积是▱OABC 的面积的34， ∴12×AD×|y R |＝34×OA×OB ，则12×6×|y R |＝34×2×83， 解得：y R ＝±34，当y=34时，212843333x x -++=，解得：11x =21x =∴R 1（1，34）或R 2（134）， 当y=-34时，212843333x x -++=-，解得：x 3=1，x 2=1∴R 3（1+，34-）或R 4（1-34-）综上所述：点R 的坐标为（，34）或（1，34）或（34-）或（134-）． （3）作△PEQ 的外接圆R ，过点R 作RH ⊥ME 于点H ，∵∠PQE ＝45°，∴∠PRE ＝90°，∵RP=RE ，∴△PRE 为等腰直角三角形，∵直线MD 上存在唯一的点Q ，∴⊙R 与直线MD 相切，∴RQ ⊥MD ，∵抛物线对称轴为直线x=1，∴当x=1时y=128333-++=3，∴点M 坐标为（1，3），∵D （4，0），∴ME ＝3，ED ＝4﹣1＝3，∴MD设点P （1，2m ），则PH ＝HE ＝HR ＝m ，则圆R m ，则点R （1+m ，m ），∵S △MED ＝S △MRD +S △MRE +S △DRE ，即12×ME•ED ＝12×MD×RQ+12×ED•y R +12×ME•RH ，∴12×3×3＝12×m+12×4×m+12×3×m ， 解得m ＝34， ∴点P 坐标为（1，32），∵ME=MD=3，∴∠MDE=45°，∴点P 与点M 重合时，符合题意，即P （1，3），过点D 作DF ⊥MD ，交对称轴于F ，则∠FDE=45°，符合题意，∴EF=DE=3，∴点F 坐标为（1，-3），∴点P 坐标为（1，-3），综上所述：点P 的坐标为（1，32）或（1，3）或（1，-3）． 【点睛】 本题考查平行四边形的性质、待定系数法求二次函数解析式，熟练掌握二次函数的性质并灵活运用分类讨论的思想是解题关键．17．（1）y =-x 2＋3x ＋4，y =-x ＋4；（2）521,24⎛⎫ ⎪⎝⎭；（3）存在，1684,525⎛⎫ ⎪⎝⎭ 【分析】（1）运用待定系数法，利用A ，B 两点的坐标构建二元一次方程组求解二次函数的表达式，利用B ，C 两点的坐标确定直线BC 的表达式；（2）先求得DE 的长，根据平行四边形的性质得到PF=DE ，点P 与点F 的横坐标相同，故利用抛物线与直线的解析式表示它们的纵坐标，根据其差等于DE 长构建一元二次方程求解； （3）结合图形与已知条件，易于发现若两三角形相似，只可能存在△PCF ∽△CDE 一种情况．△CDE 的三边均可求，（2）中已表示PF 的长，再构建直角三角形或借助两点间距离公式，利用勾股定理表示出CF 的长，这样根据比例式列方程求解，从而可判断点P 是否存在，以及求解点P 的值．【详解】（1）由题意，将A(-1．0)，B(4．0)代入24y ax bx =++，得 4016440a b a b -+=⎧⎨++=⎩，解得13a b =-⎧⎨=⎩， ∴二次函数的表达式为234y x x =-++，当0x =时，y=4，∴点C 的坐标为(0，4)，又点B 的坐标为(4，0)，设线段BC 所在直线的表达式为y mx n =+，∴440n m n =⎧⎨+=⎩，解得14m n =-⎧⎨=⎩， ∴BC 所在直线的表达式为4y x =-+；（2）∵DE ⊥x 轴，PF ⊥x 轴，∴DE ∥PF ，只要DE=PF ，此时四边形DEFP 即为平行四边形．由二次函数y=-2x +3x +4=(x -32) 2+254，得D 的坐标为(32，254)， 将32x =代入4y x =-+，即y=-32+4=52，得点E 的坐标为(32，52)， ∴DE=254-52=154， 设点P 的横坐标为t ，则P(t ，-t 2+3t+4)，F(t ，-t+4)，PF=-t 2+3t+4-(-t+4)=-t 2+4t ，由DE=PF ，得-t 2+4t=154， 解之，得t 1=32 (不合题意，舍去)，t 2=52， 当t=52时，-t 2+3t+4=-(52)2+3×52+4=214， ∴P 的坐标为(52，214)； （3）由（2）知，PF ∥DE ，∴∠CED=∠CFP ，又∠PCF 与∠DCE 有共同的顶点C ，且∠PCF 在∠DCE 的内部，∴∠PCF≠∠DCE ，∴只有当∠PCF=∠CDE 时，△PCF ∽△CDE ，由D (32，254)，C(0，4)，E(32，52)，利用勾股定理，可得=DE=25515 424-=，由（2）以及勾股定理知，PF=-t2+4t，F(t，-t+4)，CF==，∵△PCF∽△CDE，∴PF CFCE DE=2154=，∵t≠0，∴154(4t-+)=3，∴t=165，当t=165时，-t2+3t+4=-(165)2+3×165+4=8425．∴点P的坐标是(165，8425)．【点睛】本题属于二次函数综合题，考查了一次函数的性质，二次函数的性质，相似三角形的判定和性质，平行四边形的判定和性质，勾股定理的应用等知识，解题的关键是，学会用数形结合的思想思考问题，学会利用参数构建方程解决问题，属于中考压轴题．18．（1）234y x x =-++，4y x =-+；（2）521,24P ⎛⎫ ⎪⎝⎭；（3）存在，点P 的坐标是1684,525⎛⎫ ⎪⎝⎭． 【分析】（1）将(1,0)A -，(4,0)B 代入24y ax bx =++，解出a ，b 得值即可；求出C 点坐标，将C ，B 代入线段BC 所在直线的表达式y mx n =+，求解即可；（2）根据题意只要DE PF =，四边形DEFP 即为平行四边形，先求出点D 坐标，然后求出DE ，设点P 的横坐标为t ，则()2,34P t t t -++，(,4)F t t -+，得出24PF t t =-+，根据DE PF =，得21544t t -+=，求解即可； （3）由（2）知，CED CFP ∠=∠，根据PCF ∠与DCE ∠有共同的顶点C ，且PCF ∠在DCE ∠的内部，只有当PCF CDE ∠=∠时，PCF CDE ∆∆∽，利用勾股定理，可得CE ==25515424DE =-=，根据PF CF CE DE =，即243154t t -+=，解出t 值，即可得出答案． 【详解】解：（1）由题意，将(1,0)A -，(4,0)B 代入24y ax bx =++， 得4016440a b a b -+=⎧⎨++-⎩， 解得13a b =-⎧⎨=⎩， ∴二次函数的表达式234y x x =-++，当0x =时，4y =，得点(0,4)C ，又点(4,0)B ，设线段BC 所在直线的表达式y mx n =+，∴440n m n -⎧⎨+-⎩，解得14m n =-⎧⎨=⎩， ∴BC 所在直线的表达式4y x =-+；（2）∵DE x ⊥轴，PF x ⊥轴，。
中考数学综合题专练：四边形(含答案)
中考综合题（三季-四边形）（共七季）1.如图，抛物线y =-x 2+bx +c 与直线221+=x y 交于C 、D 两点，其中点C 在y 轴上，点D 的坐标为)27 3(，. 点P 是y 轴右侧的抛物线上一动点，过点P 作PE ⊥x 轴于点E ，交CD 于点F . （1）求抛物线的解析式；（2）若点P 的横坐标为m ，当m 为何值时，以O 、C 、P 、F 为顶点的四边形是平行四边形？请说明理由. （3）若存在点P ，使∠PCF =45°，请直接写出．．．．相应的点P 的坐标.∵当x =0时，y =2 ∴C （0，2） 将C 、D 坐标代入抛物线解析式得：27932c b c =⎧⎪⎨-++=⎪⎩ 解得b =72，c =2∴抛物线的解析式为y =-x 2+72x +2 （2）∵PF ∥OC∴当四边形OCPF 是平行四边形时，PF=OC=2 由题意得，P （m ，-m 2+72m+2），F （m ，12m+2） ∵点P 在y 轴右侧 ∴m ＞0 ∴PF=|-m 2+72m+2-(12m+2)|=|-m 2+3m |=2 当P 在CD 上方时，-m 2+3m=2 则m 2-3m+2=0，解得m=1或2 当P 在CD 下方时，-m 2+3m=-2备用图则m 2-3m-2=0解得舍去)故，当m=1或2或32时，四边形OCPF 是平行四边形 （3）点P 坐标为（12，72）或（236，1318） ① 当P 在CD 上方时，PF=-m 2+3m ，如下左图。
由△PKF ∽△CHF ∽△GOC 可求得：(6m-2m 2)，(3m-m 2)，m ∵∠PCF =45° ∴PK=CK=CF+FK(6m-2m 2(3m-m 2m 整理得2m 2-m=0 解得m=0(舍去)或12∴P （12，72） ② 当P 在CD 下方时，PF=m 2-3m ，如下右图。
与①同理，可求得：(2m 2-6m)，(m 2-3m)，m 由PK=CK=CF-FK 得5(2m 2-6m)=2m-5(m 2-3m) 整理得6m 2-23m=0 解得m=0(舍去)或236∴P （236，1318）2．如图，已知抛物线42-+=bx ax y 经过A （-8，0），B （2，0）两点，直线4-=x 交x 轴于点C ，交抛物线于点D .（1）求该抛物线的解析式；（2）点P 在抛物线上，点E 在直线4-=x 上，若以A ，O ，E ，P 为顶点的四边形是平行四边形，求点P 的坐标；（3）若B ，D ，C 三点到同一条直线的距离分别是1d ，2d ，3d ，问是否存在直线l ，使2321d d d ==？若存在，请直接写出3d 的值；若不存在，请说明理由.解：（1）∵抛物线42-+=bx ax y 经过A （-8，0），B （2，0）两点，∴⎩⎨⎧=-+=--042404864b a b a ， 解得：⎪⎪⎩⎪⎪⎨⎧==.2341b a ²²²²²²²²²²² 2分∴423412-+=x x y ；²²²²²²²²²²²²²²²²²²² 3分 （2）∵点P 在抛物线上，点E 在直线4-=x 上，设点P 的坐标为m (，)423412-+m m ，点E 的坐标为4(-,)n . 如图1，∵点A （-8，0），∴8=AO . ①当AO 为一边时，EP ∥AO , 且8==AO EP ， ∴84=+m ，解得：121-=m ，42=m .∴P 1(12-，14)，P 2(4，6) ²²²²²²²²²²²²²²²²²² 5分 ②当AO 为对角线时，则点P 和点E 必关于点C 成中心对称，故CP CE =.∴⎪⎩⎪⎨⎧-=-+-=,4234142n m m m 解得：⎩⎨⎧=-=,64n m ∴P 3 (4-，6-).∴当P 1(12-，14)，P 2(4，6)，P 3 (4-，6-)时，A ，O ，E ，P 为顶点 的四边形是平行四边形. ²²²²²²²²²²²²²²²²²² 7分 （3）存在直线l ，使2321d d d ==. ²²²²²²²²²²²²²²²² 8分 3d 的值为：22，26，1056，1056. ²²²²²²²²² 12分（1221 由题意得C (-4，0) ，B (2，0) ，D (-4，-6）， ∴OC =4 ，OB =2，CD=6.∴△CDB 为等腰直角三角形.∴CH=CD 45sin ⋅，即:23226=⨯=CH . ∵BD=2CH ，∴BD=26.①∵CO ：OB=2：1，∴过点O 且平行于BD 的直线满足条件 作BE ⊥直线1l 于点E ，DF ⊥直线1l 于点F ，设CH 交直线1l 于点G . ∴DF BE =，即:21d d = . 则12==BO CO BE CG ，12=GH CH ，即1213=d d ，∴132d d =,∴2321d d d ==. ∴CH CG 32=，即2223323=⨯=d . ②如图2，在△CDB 外作直线l 2平行于DB ，延长CH 交l 2于点G ′, 使G H CH '=, ∴2623=='=CH G C d .③如图3，过H ，O 作直线3l ，作BE ⊥3l 于点E ，DF ⊥3l 于点F ，CG ⊥3l 于点G ，由①可知，BH DH = 则DF BE =，即:21d d = . ∵CO ：OB=2：1，∴2321d d d ==. 作HI ⊥x 轴于点I ，∴HI= CI=CB 21=3. ∴OI =4-3=1， ∴10132222=+=+=OI HI OH . ∵△OCH 的面积=310213421d ⋅=⨯⨯，∴51063=d . ④如图3，根据等腰直角三角形的对称性，可作出直线4l ，易证：2321d d d ==，51063=d .∴存在直线l ，使2321d d d ==.3d 的值为：22，26，1056，1056.3、如图1，已知正方形ABCD 的边长为1，点E 在边BC 上，若AEF ∠=90°，且EF 交正方形外角的平分线CF 于点F 。
专练10 四边形中比值问题-2021年中考数学压轴题专项高分突破训练(全国通用)(解析版)
专练10四边形中比值问题1.在矩形ABCD的CD边上取一点E，将ΔBCE沿BE翻折，使点C恰好落在AD边上点F处．（1）如图1，若BC=2BA，求∠CBE的度数；（2）如图2，当AB=5，且AF⋅FD=10时，求BC的长；（3）如图3，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF=AN+FD时，出的值．求ABBC【答案】（1）解：∵矩形ABCD，∴∠A=90°，AD//BC∠CBF，由折叠的性质可知BF=BC=2AB，∠CBE=12∴∠AFB=30°，∴∠FBC=∠AFB=30°，∴∠CBE=15°（2）解：由题意可得∠A=∠D=90°，∠AFB+∠DFE=90°，∠FED+∠DFE=90°∴∠AFB=∠DEF∴ΔFAB∽ΔEDF∴AFDE =ABDF，∴DE=AF·DFAB =105=2∴EF=CE=3，由勾股定理得DF=√32−22=√5，∴AF=√5=2√5，∴BC=AD=AF+FD=3√5；（3）解：过点N作NG⊥BF于点G．∴∠NGF=∠A=90°又∵∠BFA=∠NFG∴ΔNFG∽ΔBFA．∴NGAB =FGFA=NFBF．∵NF=AN+FD，即NF=12AD=12BC=12BF∴NGAB =FGFA=NFBF=12，又∵BM平分∠ABF，NG⊥BF，∠A=90°，∴NG=AN，∴NG=AN=12AB，∴FGFA=BF−BGAN+NF=BC−AB12AB+12BC=12整理得：ABBC =35．2.如图1，将直角三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角板的一边交边CD于点F，另一边交CB的延长线于点G。
（1）求证：EF=EG；（2）如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，(1)中的结论是否仍然成立？若成立，请给予证明：若不成立，请说明理由；（3）如图3，将(2)中的“正方形ABCD”改为“矩形ABCD"，且使三角板的一边经过点B，其他条件不变，若AB=3，BC=6，则EFEG=________。
2021年广东省中考数学总复习第17讲：四边形(含答案解析)
第 1 页 共 59 页
2021年广东省中考数学总复习第17讲：四边形
一．选择题（共39小题）
1．（2020•广州）如图，矩形ABCD 的对角线AC ，BD 交于点O ，AB ＝6，BC ＝8，过点O
作OE ⊥AC ，交AD 于点E ，过点E 作EF ⊥BD ，垂足为F ，则OE +EF 的值为（ ）
A ．485
B ．325
C ．245
D ．125
2．（2020•广东）若一个多边形的内角和是540°，则该多边形的边数为（ ）
A ．4
B ．5
C ．6
D ．7
3．（2019•深圳）已知菱形ABCD ，E 、F 是动点，边长为4，BE ＝AF ，∠BAD ＝120°，则
下列结论正确的有几个（ ）
①△BEC ≌△AFC ；②△ECF 为等边三角形；③∠AGE ＝∠AFC ；④若AF ＝1，则GF EG =13．
A ．1
B ．2
C ．3
D ．4
4．（2019•广州）如图，▱ABCD 中，AB ＝2，AD ＝4，对角线AC ，BD 相交于点O ，且E ，
F ，
G ，
H 分别是AO ，BO ，CO ，DO 的中点，则下列说法正确的是（ ）
A ．EH ＝HG
B ．四边形EFGH 是平行四边形
C ．AC ⊥BD
D ．△ABO 的面积是△EFO 的面积的2倍
5．（2019•广州）如图，矩形ABCD 中，对角线AC 的垂直平分线EF 分别交BC ，AD 于点E ，
F ，若BE ＝3，AF ＝5，则AC 的长为（ ）。
2021年中考数学真题分类专题选编：四边形(含答案)
交于点 O ，过点 C 作 CE CD ，垂足为 C ， AD 相交于点 E ，若 AD 8 ， BC 6 ，则 2OE AE 的值为 ( BD
)
A． 4 3
B． 3 4
二、填空题（共 20 小题）
C． 5 3
D． 5 4
21．（2021•淄博）两张宽为 3cm 的纸条交叉重叠成四边形 ABCD ，如图所示．若 30 ，则对角线 BD 上
A．用 3 个相同的菱形放置，最多能得到 6 个菱形 B．用 4 个相同的菱形放置，最多能得到 16 个菱形 C．用 5 个相同的菱形放置，最多能得到 27 个菱形 D．用 6 个相同的菱形放置，最多能得到 41 个菱形 11．（2021•宁波）如图是一个由 5 张纸片拼成的平行四边形 ABCD ，相邻纸片之间互不重叠也无缝隙，其 中两张等腰直角三角形纸片的面积都为 S1 ，另两张直角三角形纸片的面积都为 S2 ，中间一张矩形纸片 EFGH 的面积为 S3 ， FH 与 GE 相交于点 O ．当 AEO ， BFO ， CGO ， DHO 的面积相等时，下列结 论一定成立的是 ( )
A．10
B．12
C．14
D．15
3．（2021•株洲）如图所示，四边形 ABCD 是平行四边形，点 E 在线段 BC 的延长线上，若 DCE 132 ，
则 A ( )
A． 38
B． 48
C． 58
D． 66
4．（2021•扬州）如图，点 A 、B 、C 、D 、E 在同一平面内连接 AB 、BC 、CD 、DE 、EA ，若 BCD 100 ，
的动点 P 到 A ， B ， C 三点距离之和的最小值是 ．
第 6 页（共 96 页）
22．（2021•株洲）如图所示，线段 BC 为等腰 ABC 的底边，矩形 ADBE 的对角线 AB 与 DE 交于点 O ，若 OD 2 ，则 AC ．
2020-2021初中数学四边形专项训练解析含答案(1)
2020-2021初中数学四边形专项训练解析含答案(1)一、选择题1．如图，ABCD Y 的对角线AC 与BD 相交于点O ，AD BD ⊥，30ABD ∠=︒，若23AD =．则OC 的长为（ ）A ．3B ．3C 21D ．6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =，再根据平行四边形的性质求得3OD =，然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解：∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中，30ABD ∠=︒，23AD =∴243AB AD ==∴226BD AB AD =-=∵四边形ABCD 是平行四边形∴132OB OD BD ===，12OA OC AC == ∴在Rt AOD △中，23AD =3OD = ∴2221OA AD OD +=∴21OC OA ==故选：C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点，熟练掌握相关知识点是解决问题的关键．2．如图，在平行四边形ABCD 中，对角线AC 、BD 相交于点O ，BD ＝2AD ，E 、F 、G 分别是OC 、OD 、AB 的中点，下列结论：①BE ⊥AC ；②四边形BEFG 是平行四边形；③△EFG ≌△GBE ；④EG ＝EF ，其中正确的个数是（ ）A．1 B．2 C．3 D．4【答案】D【解析】【分析】由平行四边形的性质可得AB＝CD，AD＝BC，BO＝DO＝12BD，AO＝CO，AB∥CD，即可得BO＝DO＝AD＝BC，由等腰三角形的性质可判断①，由中位线定理和直角三角形的性质可判断②④，由平行四边形的性质可判断③，即可求解．【详解】解：∵四边形ABCD是平行四边形∴AB＝CD，AD＝BC，BO＝DO＝12BD，AO＝CO，AB∥CD∵BD＝2AD∴BO＝DO＝AD＝BC，且点E是OC中点∴BE⊥AC，∴①正确∵E、F、分别是OC、OD中点∴EF∥DC，CD＝2EF∵G是AB中点，BE⊥AC∴AB＝2BG＝2GE，且CD＝AB，CD∥AB∴BG＝EF＝GE，EF∥CD∥AB∴四边形BGFE是平行四边形，∴②④正确，∵四边形BGFE是平行四边形，∴BG＝EF，GF＝BE，且GE＝GE∴△BGE≌△FEG（SSS）∴③正确故选D．【点睛】本题考查了平行四边形的判定和性质，全等三角形的判定和性质，直角三角形的性质，三角形的中位线及等腰三角形的性质，熟练运用这些性质进行推理是本题的关键．3．如图，小莹用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，BC长为10cm．当小莹折叠时，顶点D落在BC边上的点F处(折痕为AE)．则此时EC=()cmA ．4B ．2C ．22D ．3【答案】D【解析】【分析】 根据矩形的性质得AB=CD=8，BC=AD=10，∠B=∠C=90°，再根据折叠的性质得AF=AD=10，DE=EF ，在Rt △ABF 中，利用勾股定理计算出BF=6，则CF=BC ﹣BF=4，设CE=x ，则DE=EF=8﹣x ，在Rt △CEF 中利用勾股定理得到:42+x 2=（8﹣x ）2，然后解方程即可．【详解】解：∵四边形ABCD 为矩形，∴AB=CD=8，BC=AD=10，∠B=∠C=90°．∵长方形纸片ABCD 折纸，顶点D 落在BC 边上的点F 处（折痕为AE ），∴AF=AD=10，DE=EF ，在Rt △ABF 中，AB=8，AF=10，∴BF=226AF AB -=∴CF=BC ﹣BF=4．设CE=x ，则DE=EF=8﹣x ，在Rt △CEF 中，∵CF 2+CE 2=EF 2，∴42+x 2=（8﹣x ）2，解得x=3∴EC 的长为3cm ．故选：D【点睛】本题考查了折叠的性质、矩形的性质、勾股定理的综合运用；熟练掌握折叠的性质和矩形的性质，根据勾股定理得出方程是解题关键．4．如图，四边形ABCD 是菱形，30ACD ∠=︒，2BD =，则AC 的长度为（ ）A ．3B ．2C ．4D ．2【答案】A【解析】【分析】 由菱形的性质，得到AC ⊥BD ，由直角三角形的性质，得到BO=1，BC=2，根据勾股定理求出CO ，即可求出AC 的长度.【详解】解，如图，∵四边形ABCD 是菱形，∴AC ⊥BD ，AO=CO ，BO=DO ，∵2BD =，∴BO=1，在Rt △OBC 中，30BCO ACD ∠=∠=︒，∴BC=2， ∴22213CO =-=；∴23AC =；故选：A.【点睛】本题考查了菱形的性质，勾股定理解直角三角形，解题的关键是熟练掌握菱形的性质，利用勾股定理求出OC 的长度.5．如图，足球图片正中的黑色正五边形的内角和是( )．A ．180°B ．360°C ．540°D ．720°【答案】C【解析】【分析】 根据多边形内角和公式2180()n -⨯︒即可求出结果．【详解】解：黑色正五边形的内角和为：5218540(0)-⨯︒=︒，故选：C ．【点睛】本题考查了多边形的内角和公式，解题关键是牢记多边形的内角和公式．6．如图，矩形ABCD 的对角线AC 、BD 相交于点O ，AB ：BC ＝2：1，且BE ∥AC ，CE ∥DB ，连接DE ，则tan ∠EDC ＝（ ）A．14B．16C．26D．310【答案】B【解析】【分析】过点E作EF⊥直线DC交线段DC延长线于点F，连接OE交BC于点G．根据邻边相等的平行四边形是菱形即可判断四边形OBEC是菱形，则OE与BC垂直平分，易得EF=12x，CF=x．再由锐角三角函数定义作答即可．【详解】解：∵矩形ABCD的对角线AC、BD相交于点O，AB：BC＝2：1，∴BC＝AD，设AB＝2x，则BC＝x．如图，过点E作EF⊥直线DC交线段DC延长线于点F，连接OE交BC于点G．∵BE∥AC，CE∥BD，∴四边形BOCE是平行四边形，∵四边形ABCD是矩形，∴OB＝OC，∴四边形BOCE是菱形．∴OE与BC垂直平分，∴EF＝12AD＝12x，OE∥AB，∴四边形AOEB是平行四边形，∴OE＝AB＝2x，∴CF＝12OE＝x．∴tan∠EDC＝EFDF＝122xx x＝16．故选：B．【点睛】本题考查矩形的性质、平行四边形的判定与性质、菱形的判定与性质以及解直角三角形，解题的关键是熟练掌握矩形的性质和菱形的判定与性质，属于中考常考题型．7．已知一个多边形的每一个外角都相等，一个内角与一个外角的度数之比是3：1，这个多边形的边数是()A．8 B．9 C．10 D．12【答案】A【解析】试题分析：设这个多边形的外角为x°，则内角为3x°，根据多边形的相邻的内角与外角互补可的方程x+3x=180，解可得外角的度数，再用外角和除以外角度数即可得到边数．解：设这个多边形的外角为x°，则内角为3x°，由题意得：x+3x=180，解得x=45，这个多边形的边数：360°÷45°=8，故选A．考点：多边形内角与外角．8．如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点，作BM⊥AE于点M，作KN⊥AE于点N，连结MO、NO，以下四个结论：①△OMN是等腰三角形；②tan∠OMN=33；③BP=4PK；④PM•PA=3PD2，其中正确的是（）A．①②③B．①②④C．①③④D．②③④【答案】B【解析】【分析】根据菱形的性质得到AD∥BC，根据平行线的性质得到对应角相等，根据全等三角形的判定定理△ADP≌△ECP，由相似三角形的性质得到AD=CE，作PI∥CE交DE于I，根据点P是CD的中点证明CE=2PI，BE=4PI，根据相似三角形的性质得到1=4KP PIKB BE，得到BP=3PK，故③错误；作OG⊥AE于G，根据平行线等分线段定理得到MG=NG，又OG⊥MN，证明△MON是等腰三角形，故①正确；根据直角三角形的性质和锐角三角函数求出∠OMN=33，故②正确；然后根据射影定理和三角函数即可得到PM•PA=3PD2，故④正确．【详解】解：作PI ∥CE 交DE 于I ，∵四边形ABCD 为菱形，∴AD ∥BC ，∴∠DAP=∠CEP ，∠ADP=∠ECP ，在△ADP 和△ECP 中，DAP CEP ADP ECP DP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADP ≌△ECP ，∴AD=CE ， 则PI PD CE DC =，又点P 是CD 的中点， ∴1=2PI CE ， ∵AD=CE ， ∴1=4KP PI KB BE =， ∴BP=3PK ，故③错误；作OG ⊥AE 于G ， ∵BM 丄AE 于M ，KN 丄AE 于N ，∴BM ∥OG ∥KN ，∵点O 是线段BK 的中点，∴MG=NG ，又OG ⊥MN ，∴OM=ON ，即△MON 是等腰三角形，故①正确；由题意得，△BPC ，△AMB ，△ABP 为直角三角形，设BC=2，则CP=1，由勾股定理得，则根据三角形面积公式，BM=7， ∵点O 是线段BK 的中点，∴PB=3PO ，∴OG=13BM=21， MG=23MP=27，tan ∠OMN=3=3OG MG ，故②正确； ∵∠ABP=90°，BM ⊥AP ，∴PB 2=PM•PA ，∵∠BCD=60°，∴∠ABC=120°，∴∠PBC=30°，∴∠BPC=90°，∴PB=3PC ，∵PD=PC ，∴PB 2=3PD ，∴PM•PA=3PD 2，故④正确．故选B ．【点睛】本题考查相似形综合题．9．已知，如图，在ABC V 中，90ACB ∠=︒，30A ∠=︒，求证：12BC AB =．在证明该结论时，需添加辅助线，则作法不正确的是（ ）A ．延长BC 至点D ，使CD BC =，连接ADB ．在ACB ∠中作BCE B ∠=∠，CE 交AB 于点EC ．取AB 的中点P ，连接CPD ．作ACB ∠的平分线CM ，交AB 于点M【答案】D【解析】【分析】分别根据各选项的要求进行证明，推出正确结论，则问题可解.【详解】解：选项A ： 如图，由辅助线可知，ABC ADC ≅V ;，则有AB=AD ，再由90ACB ∠=︒，由30BAC ∠=︒，则60B ∠=︒，∴ABD △是等边三角形 ∴1122BC DB AB == 故选项A 正确；选项B:如图，由辅助线可知，EBD △是等边三角形则60BEC EAC ECA ∠=∠+∠=︒,BE=EC∵30A ∠=︒∴30ECA A ∠=∠=︒∴AE=EC∴12BC AB =故选项B 正确选项C 如图，有辅助线可知，CP 为直角三角形斜边上的中线∴AP=CP=BP∵30A ∠=︒∴60B ∠=︒∴PBC V 是等边三角形 ∴12BC BP AB ==综上可知选项D 错误故应选D【点睛】 此题主要考查了全等三角形的判定，等边三角形的判定与性质的综合应用，根据条件选择正确的证明方法是解题的关键．10．一个多边形的每个内角均为108º，则这个多边形是（ ）A ．七边形B ．六边形C ．五边形D ．四边形【答案】C【解析】试题分析：因为这个多边形的每个内角都为108°，所以它的每一个外角都为72°，所以它的边数=360÷72=5（边）.考点：⒈多边形的内角和；⒉多边形的外角和.11．下列说法正确的是（ ）A ．对角线相等的四边形一定是矩形B ．任意掷一枚质地均匀的硬币10次，一定有5次正面向上C ．如果有一组数据为5，3，6，4，2，那么它的中位数是6D ．“用长分别为5cm 、12cm 、6cm 的三条线段可以围成三角形”这一事件是不可能事件【答案】D【解析】【分析】根据矩形的判定定理，数据出现的可能性的大小，中位数的计算方法，不可能事件的定义依次判断即可.【详解】A.对角线相等的平行四边形是矩形，故该项错误；B. 任意掷一枚质地均匀的硬币10次，不一定有5次正面向上，故该项错误；C. 一组数据为5，3，6，4，2，它的中位数是4，故该项错误；D. “用长分别为5cm 、12cm 、6cm 的三条线段可以围成三角形” 这一事件是不可能事件，正确，故选：D.【点睛】此题矩形的判定定理，数据出现的可能性的大小，中位数的计算方法，不可能事件的定义，综合掌握各知识点是解题的关键.12．用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正多边形的边数为x ，y ，z ，则111x y z ++的值为（ ） A ．1B ．23C ．12D ．13【答案】C【解析】分析：根据边数求出各个多边形的每个内角的度数，结合镶嵌的条件列出方程，进而即可求出答案．详解：由题意知，这3种多边形的3个内角之和为360度，已知正多边形的边数为x 、y 、z ，那么这三个多边形的内角和可表示为：2180x x -⨯（）+2180y y -⨯（）+2180z z （）-⨯=360，两边都除以180得：1﹣2x+1﹣2y +1﹣2z =2，两边都除以2得：1x +1y +1z =12． 故选C ．点睛：解决本题的关键是知道这3种多边形的3个内角之和为360度，据此进行整理分析得解．13．如图，在□ABCD 中，E 、F 分别是边BC 、CD 的中点，AE 、AF 分别交BD 于点G 、H ，则图中阴影部分图形的面积与□ABCD 的面积之比为（ ）A ．7 : 12B ．7 : 24C ．13 : 36D ．13 : 72【答案】B【解析】【分析】 根据已知条件想办法证明BG=GH=DH ，即可解决问题；【详解】解：∵四边形ABCD 是平行四边形，∴AB ∥CD ，AD ∥BC ，AB=CD ，AD=BC ，∵DF=CF ，BE=CE ，∴12DH DF HB AB ==，12BG BE DG AD ==，∴13DH BG BD BD ==， ∴BG=GH=DH， ∴S △ABG =S △AGH =S △ADH ，∴S 平行四边形ABCD =6 S △AGH ，∴S △AGH ：ABCD S 平行四边形=1：6，∵E 、F 分别是边BC 、CD 的中点,∴12EF BD =, ∴14EFC BCDD S S =V V , ∴18EFCABCD S S =V 四边形, ∴1176824AGH EFC ABCD S S S +=+=V V 四边形=7∶24, 故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质，题目的综合性很强，难度中等．14．如图，在矩形ABCD 中，AD=2AB ，∠BAD 的平分线交BC 于点E ，DH ⊥AE 于点H ，连接BH 并延长交CD 于点F ，连接DE 交BF 于点O ，下列结论：①∠AED=∠CED ；②OE=OD ；③BH=HF ；④BC ﹣CF=2HE ；⑤AB=HF ，其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个【答案】C【解析】【分析】【详解】 试题分析：∵在矩形ABCD 中，AE 平分∠BAD ，∴∠BAE=∠DAE=45°，∴△ABE 是等腰直角三角形，∴2AB ，∵AB ，∴AE=AD ，又∠ABE=∠AHD=90°∴△ABE ≌△AHD （AAS ），∴BE=DH ，∴AB=BE=AH=HD ，∴∠ADE=∠AED=12（180°﹣45°）=67.5°， ∴∠CED=180°﹣45°﹣67.5°=67.5°，∴∠AED=∠CED ，故①正确； ∵∠AHB=12（180°﹣45°）=67.5°，∠OHE=∠AHB （对顶角相等）， ∴∠OHE=∠AED ，∴OE=OH ，∵∠OHD=90°﹣67.5°=22.5°，∠ODH=67.5°﹣45°=22.5°，∴∠OHD=∠ODH ，∴OH=OD ，∴OE=OD=OH ，故②正确；∵∠EBH=90°﹣67.5°=22.5°，∴∠EBH=∠OHD ，又BE=DH ，∠AEB=∠HDF=45°∴△BEH ≌△HDF （ASA ），∴BH=HF ，HE=DF ，故③正确；由上述①、②、③可得CD=BE 、DF=EH=CE ，CF=CD-DF ，∴BC-CF=（CD+HE ）-（CD-HE ）=2HE ，所以④正确；∵AB=AH ，∠BAE=45°，∴△ABH 不是等边三角形，∴AB ≠BH ，∴即AB≠HF ，故⑤错误；综上所述，结论正确的是①②③④共4个．故选C ．【点睛】 考点：1、矩形的性质；2、全等三角形的判定与性质；3、角平分线的性质；4、等腰三角形的判定与性质15．如图，在ABCD Y 中，8AC =，6BD =，5AD =，则ABCD Y 的面积为( )A ．6B ．12C ．24D ．48【答案】C【解析】【分析】 由勾股定理的逆定理得出90AOD ∠=o ，即AC BD ⊥，得出ABCD Y 是菱形，由菱形面积公式即可得出结果．【详解】∵四边形ABCD 是平行四边形， ∴142OC OC AC ===，132OB OD BD ===， ∴22225OA OD AD +==，∴90AOD ∠=o ，即AC BD ⊥，∴ABCD Y 是菱形，∴ABCD Y 的面积11862422AC BD =⨯=⨯⨯=； 故选C ．【点睛】本题考查平行四边形的性质、勾股定理的逆定理、菱形的判定与性质，熟练掌握平行四边形的性质，证明四边形ABCD 是菱形是解题的关键．16．已知ABCD Y (AB BC >)，用尺规在ABCD 内作菱形，下列作法错误的是( )A ．如图1所示，作对角线AC 的垂直平分线EF ，则四边形AECF 为所求B ．如图2所示，在AB DC ，上截取AE AD DF DA ==，，则四边形AEFD 为所求 C ．如图3所示，作ADC ABC ∠∠、的平分线DE BF ，，则四边形DEBF 为所求 D ．如图4所示，作BDE BDC DBF DBA ∠=∠∠=∠，，则四边形DEBF 为所求【答案】C【解析】【分析】根据平行四边形的性质及判定、菱形的判定逐个判断即可．【详解】解：A、根据线段的垂直平分线的性质可知AB＝AD，一组邻边相等的平行四边形是菱形；符合题意；B、根据四条边相等的四边形是菱形，符合题意；C、根据两组对边分别平行四边形是平行四边形，不符合题意；D、根据一组邻边相等的平行四边形是菱形，符合题意．故选：C．【点睛】本题考查了复杂作图，解决本题的关键是利用平行四边形的性质及判定、菱形的判定．17．为了研究特殊四边形，李老师制作了这样一个教具（如图1）：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C、B与D两点之间分别用一根橡皮筋拉直固定，课上，李老师右手拿住木条BC，用左手向右推动框架至AB⊥BC（如图2）观察所得到的四边形，下列判断正确的是（）A．∠BCA＝45°B．AC＝BDC．BD的长度变小D．AC⊥BD【答案】B【解析】【分析】根据矩形的性质即可判断；【详解】解：∵四边形ABCD是平行四边形，又∵AB⊥BC，∴∠ABC＝90°，∴四边形ABCD是矩形，∴AC＝BD．故选B．【点睛】本题考查平行四边形的性质．矩形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．18．如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠ADC＝∠GCD；③CA平分∠BCG；④∠DFB＝12∠CGE．其中正确的结论是( )A．②③B．①②④C．①③④D．①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案．【详解】①∵EG∥BC，∴∠CEG=∠ACB，又∵CD是△ABC的角平分线，∴∠CEG=∠ACB=2∠DCB，故正确；②∵∠A=90°，∴∠ADC+∠ACD=90°，∵CD平分∠ACB，∴∠ACD=∠BCD，∴∠ADC+∠BCD=90°．∵EG∥BC，且CG⊥EG，∴∠GCB=90°，即∠GCD+∠BCD=90°，∴∠ADC=∠GCD，故正确；③条件不足，无法证明CA平分∠BCG，故错误；④∵∠EBC+∠ACB=∠AEB，∠DCB+∠ABC=∠ADC，∴∠AEB+∠ADC=90°+12（∠ABC+∠ACB）=135°，∴∠DFE=360°-135°-90°=135°，∴∠DFB=45°=12∠CGE，，正确．故选B．【点睛】本题主要考查了角平分线的定义，平行线的性质，三角形内角和定理及多边形内角和，三角形外角的性质，熟知直角三角形的两锐角互余是解答此题的关键．19．如图点P是矩形ABCD的对角线AC上一点，过点P作//EF BC，分别交AB、CD于点E、F，连接PB、PD，若1AE=，8PF=，则图中阴影部分的面积为（）A ．5B ．6C ．8D ．9【答案】C【解析】【分析】 由矩形的性质可证明S △PEB =S △PFD ，即可求解．【详解】作PM ⊥AD 于M ，交BC 于N ．则有四边形AEPM ，四边形DFPM ，四边形CFPN ，四边形BEPN 都是矩形，S △ADC =S △ABC ，S △AMP =S △AEP ，S △PBE =S △PBN ，S △PFD =S △PDM ，S △PFC =S △PCN ，∴S △DFP =S △PBE =12×1×8=4， ∴S 阴=4+4=8，故选：C ． 【点睛】 此题考查矩形的性质、三角形的面积，解题的关键是证明S △PEB =S △PFD ．20．如图，在边长为8的菱形ABCD 中，∠DAB =60°，以点D 为圆心，菱形的高DF 为半径画弧，交AD 于点E ，交CD 于点G ，则图中阴影部分的面积是 （ ）A ．183π-B ．183πC ．32316πD ．1839π-【答案】C【解析】【分析】 由菱形的性质得出AD=AB=8，∠ADC=120°，由三角函数求出菱形的高DF ，图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积，根据面积公式计算即可．【详解】解：∵四边形ABCD是菱形，∠DAB=60°，∴AD=AB=8，∠ADC=180°-60°=120°，∵DF是菱形的高，∴DF⊥AB，∴DF=AD•sin60°=8=∴图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积=816π⨯=．故选：C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算；由三角函数求出菱形的高是解决问题的关键．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021届中考数学热点题型专练四边形【命题趋势】四边形是每年中考数学中必考的内容之一，其考查重点是几种特殊的四边形（平行四边形、矩形、菱形、正方形）。
具体考查这几种特殊四边形的性质与判定方法，考查题型一般为解答题的20——26题，难度中等，也可能会结合三角形，圆，甚至会与三角函数、一次函数、反比例函数，二次函数结合形成综合性的大题，甚至在压轴大题中出现，例如结合二次函数形成平行四边形的存在性等。
所以我们必须对特殊四边形的性质与判定方法相当熟悉，然后再掌握一定的解决问题的常用策略，才能决胜。
【满分技巧】一、整体了解知识基本网络，熟记四种特殊四边形的概念及性质判定，二、将四边形问题转化为三角形问题其实四边形问题的解决最终都会转化到三角形的问题，所以思考问题时一定不能只想着四边形，只要考查四边形的综合题一定会利用到三角形的相关知识，一定要想着将四边形的问题转化成三角形的问题，然后利用三角形的相关知识解决。
三、做一定量的基础练习，培养分析问题和分析图形的能力【限时检测】（建议用时：30分钟）一、选择题1.如图，足球图片正中的黑色正五边形的内角和是（）A．180°B．360°C．540°D．720°【答案】C【解析】黑色正五边形的内角和为：（5﹣2）×180°＝540°，故选：C2.如图，在ABCD中，全等三角形的对数共有()A．2对B．3对C．4对D．5对【答案】C【解析】四边形ABCD是平行四边形，∴AB=CD,AD=BC,OD=OB,OA=OC∴OD=OB,OA=OC,∴AOD=∴BOC∴∴AOD∴∴COB同理可得∴AOB∴∴COD∴BC=AD,CD=AB,BD=BD∴∴ABD∴∴CDB同理可得∴ACD∴∴CAB因此本题共有4对全等三角形故选：C．3.已知一个多边形的内角和是1080°，则这个多边形是（）A．五边形B．六边形C．七边形D．八边形【答案】D【解析】设所求多边形边数为n，则（n﹣2）•180°＝1080°，解得n＝8．故选：D．4.如图，在正方形ABCD中，点O是对角线AC、BD的交点，过点O作射线OM、ON分别交BC、CD于点E、F，且∴EOF＝90°，OC、EF交于点G．给出下列结论：∴∴COE∴∴DOF；∴∴OGE∴∴FGC；∴四边形CEOF的面积为正方形ABCD面积的；∴DF2+BE2＝OG•OC．其中正确的是（）A．∴∴∴∴B．∴∴∴C．∴∴∴D．∴∴【答案】B【解析】∴∴四边形ABCD 是正方形， ∴OC ＝OD ，AC ∴BD ，∴ODF ＝∴OCE ＝45°， ∴∴MON ＝90°， ∴∴COM ＝∴DOF ， ∴∴COE ∴∴DOF （ASA ）， 故∴正确；∴∴∴EOF ＝∴ECF ＝90°， ∴点O 、E 、C 、F 四点共圆， ∴∴EOG ＝∴CFG ，∴OEG ＝∴FCG ， ∴OGE ∴∴FGC ， 故∴正确；∴∴∴COE ∴∴DOF ， ∴S ∴COE ＝S ∴DOF ，∴S 四边形CEOF =S∴OCD=14S 正方形ABCD ，故∴正确；∴）∴∴COE ∴∴DOF ， ∴OE ＝OF ，又∴∴EOF ＝90°， ∴∴EOF 是等腰直角三角形， ∴∴OEG ＝∴OCE ＝45°， ∴∴EOG ＝∴COE ，∴∴OEG ∴∴OCE ， ∴OE ：OC ＝OG ：OE ， ∴OG •OC ＝OE 2， ∴OC =12 AC ，OE ＝EF ，∴OG •AC ＝EF 2， ∴CE ＝DF ，BC ＝CD ， ∴BE ＝CF ，又∴Rt∴CEF 中，CF 2+CE 2＝EF 2， ∴BE 2+DF 2＝EF 2， ∴OG •AC ＝BE 2+DF 2， 故∴错误， 故选：B ．5.如图，在平行四边形ABCD 中，M 、N 是BD 上两点，BM ＝DN ，连接AM 、MC 、CN 、NA ，添加一个条件，使四边形AMCN 是矩形，这个条件是（ ）A ．OM ＝ACB ．MB ＝MOC ．BD ∴ACD ．∴AMB ＝∴CND【答案】A【解析】∴四边形ABCD 是平行四边形， ∴OA ＝OC ，OB ＝OD∴对角线BD上的两点M、N满足BM＝DN，∴OB﹣BM＝OD﹣DN，即OM＝ON，∴四边形AMCN是平行四边形，∴OM＝AC，∴MN＝AC，∴四边形AMCN是矩形．故选：A．6.如图，四边形ABCD为菱形，A，B两点的坐标分别是（2，0），（0，1），点C，D在坐标轴上，则菱形ABCD的周长等于（）A．B．4C．4D．20【答案】C【解析】∴A，B两点的坐标分别是（2，0），（0，1），∴AB＝，∴四边形ABCD是菱形，∴菱形的周长为4，故选：C．7. .一个十二边形的内角和等于（）A．2160°B．2080°C．1980°D．1800°【答案】D【解析】十二边形的内角和等于：（12﹣2）•180°＝1800°；故选：D．8. .下列命题正确的是（）A．有一个角是直角的平行四边形是矩形B．四条边相等的四边形是矩形C．有一组邻边相等的平行四边形是矩形D．对角线相等的四边形是矩形【答案】A【解析】A、有一个角是直角的平行四边形是矩形，是真命题；B、四条边相等的四边形是菱形，是假命题；C、有一组邻边相等的平行四边形是菱形，是假命题；D、对角线相等的平行四边形是矩形，是假命题；故选：A．9. .如图，E是∴ABCD边AD延长线上一点，连接BE，CE，BD，BE交CD于点F．添加以下条件，不能判定四边形BCED为平行四边形的是（）A．∴ABD＝∴DCE B．DF＝CF C．∴AEB＝∴BCD D．∴AEC＝∴CBD【答案】C【解析】∴四边形ABCD是平行四边形，∴AD∴BC，AB∴CD，∴DE∴BC，∴ABD＝∴CDB，∴∴ABD＝∴DCE，∴∴DCE＝∴CDB，∴BD∴CE，∴BCED为平行四边形，故A正确；∴DE∴BC，∴∴DEF＝∴CBF，在∴DEF与∴CBF中，，∴∴DEF∴∴CBF（AAS），∴EF＝BF，∴DF＝CF，∴四边形BCED为平行四边形，故B正确；∴AE∴BC，∴∴AEB＝∴CBF，∴∴AEB＝∴BCD，∴∴CBF＝∴BCD，∴CF＝BF，同理，EF＝DF，∴不能判定四边形BCED为平行四边形；故C错误；∴AE∴BC，∴∴DEC+∴BCE＝∴EDB+∴DBC＝180°，∴∴AEC＝∴CBD，∴∴BDE＝∴BCE，∴四边形BCED为平行四边形，故D正确，故选：C．10..菱形不具备的性质是()A．是轴对称图形B．是中心对称图形C．对角线互相垂直D．对角线一定相等【答案】D【解析】A、是轴对称图形，故正确；B、是中心对称图形，故正确；C、对角线互相垂直，故正确；D、对角线不一定相等，故不正确；故选：D．11..如图，菱形ABCD周长为20，对角线AC、BD相交于点O，E是CD的中点，则OE的长是（）A．2.5B．3C．4D．5【答案】A【解析】∴四边形ABCD 为菱形， ∴CD ＝BC ＝＝5，且O 为BD 的中点，∴E 为CD 的中点， ∴OE 为∴BCD 的中位线， ∴OE ＝CB ＝2.5，故选：A ．12. .如图，在正方形ABCD 中，E 是BC 边上的一点，4BE =，8EC =，将正方形边AB 沿AE 折叠到AF ，延长EF 交DC 于G ，连接AC ，现在有如下4个结论： ∴45EAC ∠=︒；∴FG FC =；∴//FC AG ；∴14GFC S ∆=． 其中正确结论的个数是( )A ．1B ．2C ．3D ．4【答案】B【解析】如图，连接DF ．四边形ABC 都是正方形，AB AD BC CD ∴===，90ABE BAD ADG ECG ∠=∠=∠=∠=︒，由翻折可知：AB AF =，90ABE AFE AFG ∠=∠=∠=︒，2BE EF ==，BAE EAF ∠=∠， 90AFG ADG ∠=∠=︒，AG AG =，AD AF =， Rt AGD Rt ∴∆≅∴()AGF HL ∆，DG FG ∴=，GAF GAD ∠=∠，设GD GF x ==，1()452EAG EAF GAF BAF DAF ∴∠=∠+∠=∠+∠=︒，故∴正确，在Rt ECG ∆中，222EG EC CG =+，222(2)8(12)x x ∴+=+-， 6x ∴=，12CD BC BE EC ==+=， 6DG CG ∴==， FG GC ∴=，易知GFC ∆不是等边三角形，显然FG FC ≠，故∴错误， GF GD GC ==， 90DFC ∴∠=︒， CF DF ∴⊥，AD AF =，GD GF =，AG DF ∴⊥，//CF AG ∴，故∴正确，168242ECG S ∆=⨯⨯=，:6:43:2FG FE ==，:3:5FG EG ∴=，3722455GFC S ∆∴=⨯=，故∴错误，故选：B ． 二、填空题13.如图，矩形ABCD 中，AC 、BD 交于点O ，M 、N 分别为BC 、OC 的中点．若4MN =，则AC 的长为 ．【答案】16【解析】M 、N 分别为BC 、OC 的中点， 28BO MN ∴==．四边形ABCD 是矩形， 216AC BD BO ∴===．故答案为16．14. .如图，该硬币边缘镌刻的正九边形每个内角的度数是 ．【答案】140°【解析】该正九边形内角和＝180°×（9﹣2）＝1260°， 则每个内角的度数＝＝140°．故答案为：140°．15.如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE 、折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，若DE ＝5，则GE 的长为 ．【答案】4913【解析】∴四边形ABCD 为正方形， ∴AB ＝AD ＝12，∴BAD ＝∴D ＝90°，由折叠及轴对称的性质可知，∴ABF ∴∴GBF ，BF 垂直平分AG ， ∴BF ∴AE ，AH ＝GH ， ∴∴F AH +∴AFH ＝90°， 又∴∴F AH +∴BAH ＝90°， ∴∴AFH ＝∴BAH ， ∴∴ABF ∴∴DAE （AAS ）， ∴AF ＝DE ＝5， 在Rt∴ADF 中，BF＝＝＝13，S∴ABF＝AB•AF＝BF•AH，∴12×5＝13AH，∴AH＝，∴AG＝2AH＝，∴AE＝BF＝13，∴GE＝AE﹣AG＝13﹣＝，故答案为：．16.在平行四边形ABCD中，∴A＝30°，AD＝4，BD＝4，则平行四边形ABCD的面积等于．【答案】16 3【解析】过D作DE∴AB于E，在Rt∴ADE中，∴∴A＝30°，AD＝4，∴DE＝AD＝2，AE＝AD＝6，在Rt∴BDE中，∴BD＝4，∴BE＝＝＝2，∴AB＝8，∴平行四边形ABCD的面积＝AB•DE＝8×2＝16 3 ，故答案为：16 3 ．17.三个形状大小相同的菱形按如图所示方式摆放，已知∴AOB＝∴AOE＝90°，菱形的较短对角线长为2cm．若点C落在AH的延长线上，则∴ABE的周长为cm．【答案】12+8 2【解析】如图所示，连接IC，连接CH交OI于K，则A，H，C在同一直线上，CI＝2，∴三个菱形全等，∴CO＝HO，∴AOH＝∴BOC，又∴∴AOB＝∴AOH+∴BOH＝90°，∴∴COH＝∴BOC+∴BOH＝90°，即∴COH是等腰直角三角形，∴∴HCO＝∴CHO＝45°＝∴HOG＝∴COK，∴∴CKO＝90°，即CK∴IO，设CK＝OK＝x，则CO＝IO＝x，IK＝x﹣x，∴Rt∴CIK中，（x﹣x）2+x2＝22，解得x2＝2+，又∴S菱形BCOI＝IO×CK＝IC×BO，∴x2＝×2×BO，∴BO＝2+2，∴BE＝2BO＝4+4，AB＝AE＝BO＝4+2，∴∴ABE的周长＝4+4+2（4+2）＝12+8，故答案为：12+8．三、解答题18.如图1，在正方形ABCD中，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B 作BF CE⊥于点G，交AD于点F．（1）求证：ABF BCE∆≅∆；（2）如图2，当点E运动到AB中点时，连接DG，求证：DC DG=；（3）如图3，在（2）的条件下，过点C作CM DG⊥于点H，分别交AD，BF于点M，N，求MNNH的值．【解析】（1）证明：BF CE ⊥， 90CGB ∴∠=︒， 90GCB CBG ∴∠+∠=，四边形ABCD 是正方形， 90CBE A ∴∠=︒=∠，BC AB =， 90FBA CBG ∴∠+∠=， GCB FBA ∴∠=∠，()ABF BCE ASA ∴∆≅∆；（2）证明：如图2，过点D 作DH CE ⊥于H ， 设2AB CD BC a ===， 点E 是AB 的中点， 12EA EB AB a ∴===， 5CE a ∴，在Rt CEB ∆中，根据面积相等，得BG CE CB EB =，25BG ∴=， 2245CG CB BG ∴=-， 90DCE BCE ∠+∠=︒，90CBF BCE ∠+∠=︒， DCE CBF ∴∠=∠，CD BC =，90CQD CGB ∠=∠=︒，()CQD BGC AAS ∴∆≅∆，25CQ BG ∴==， 25GQ CG CQ CQ ∴=-=， DQ DQ =，90CQD GQD ∠=∠=︒， ()DGQ CDQ SAS ∴∆≅∆， CD GD ∴=；（3）解：如图3，过点D 作DH CE ⊥于H ， 1122CDG S DQ CH DG ∆==， 85CG DQ CH a DG ∴==， 在Rt CHD ∆中，2CD a =， 2265DH CD CH a ∴=-=，90MDH HDC ∠+∠=︒，90HCD HDC ∠+∠=︒， MDH HCD ∴∠=∠， CHD DHM ∴∆∆∽， ∴34DH DH CH HM ==， 910HM a ∴=， 在Rt CHG ∆中，45CG =，85CH a =， 2245GH CG CH a ∴-=，90MGH CGH ∠+∠=︒，90HCG CGH ∠+∠=︒，QGH HCG ∴∠=∠，QGH GCH ∴∆∆∽， ∴HN HGHG CH=， 225HG HN a CG ∴==，12MN HM HN a ∴=-=，∴152245aMN NH a ==19.如图，在四边形ABCD 中，AD ∴BC ，延长BC 到E ，使CE ＝BC ，连接AE 交CD 于点F ，点F 是CD 的中点．求证： （1）∴ADF ∴∴ECF ．（2）四边形ABCD 是平行四边形．【解析】（1）∴AD ∴BC ， ∴∴DAF ＝∴E ， ∴点F 是CD 的中点， ∴DF ＝CF ，在∴ADF 与∴ECF 中，，∴∴ADF ∴∴ECF （AAS ）； （2）∴∴ADF ∴∴ECF ， ∴AD ＝EC ， ∴CE ＝BC ， ∴AD ＝BC ， ∴AD ∴BC ，∴四边形ABCD 是平行四边形．20.如图，在正方形ABCD 中，分别过顶点B ，D 作//BE DF 交对角线AC 所在直线于E ，F 点，并分别延长EB ，FD 到点H ，G ，使BH DG =，连接EG ，FH ． （1）求证：四边形EHFG 是平行四边形；（2）已知：22AB =4EB =，tan 23GEH ∠=EHFG 的周长．【解析】（1）四边形ABCD是正方形，AB CD∴=，//AB CD，DCA BAC∴∠=∠，//DF BE，CFD BEA∴∠=∠，BAC BEA ABE∠=∠+∠，DCA CFD CDF∠=∠+∠，ABE CDF∴∠=∠，在ABE∆和CDF∆中，ABE CDFAEB CFD AB CD∠=∠⎧⎪∠=∠⎨⎪=⎩，()ABE CDF AAS∴∆≅∆，BE DF∴=，BH DG=，BE BH DF DG∴+=+，即EH GF=，//EH GF，∴四边形EHFG是平行四边形；（2）如图，连接BD，交EF于O，四边形ABCD 是正方形，BD AC ∴⊥，90AOB ∴∠=︒， 22AB =2OA OB ∴==，Rt BOE ∆中，4EB =，30OEB ∴∠=︒，∴EO=2 3 ，OD OB =，EOB DOF ∠=∠， //DF EB ，DFC BEA ∴∠=∠，()DOF BOE AAS ∴∆≅∆，23OF OE ∴==43EF ∴= 23FM ∴=，6EM =，过F 作FM EH ⊥于M ，交EH 的延长线于M ， ∴EG//FH ，FHM GEH ∴∠=∠，tan tan 23FM GEH FHM HM∠=∠== ∴2323= ∴HM=1，∴EH=EM -HM=6-1=52222(23)113FH FM HM ++ ∴四边形EHFG 的周长222521310213EH FH =+=⨯+=+。