交通工程学电子课件第7章三参数的关系
合集下载
第七章交通流三参数之间的关系
参考文献
1、任福田,刘小明,荣建等.交通工程学. 北京：人民交通 出版社,2003.7
2、刘建军.交通工程学基础. 北京：人民交通出版社, 1995.7
第七章 交通流量、速度和密度之间来自关系授课内容：1、三参数之间的关系
2、速度—密度之间的关系
3、交通流量—密度之间的关系
4、交通流量—速度之间的关系
授课要求：
掌握交通流中交通流量、速度和密度各参数之间
的关系，会分析和应用三参数之间的关系。
第一节 三参数之间的关系
一、交通流的三个参数关系
描述交通流的三个参数是交通量、速度和交通密 度，它们之间的关系可以用下式表示：
Q VK
式中：Q——交通量（辆/h）；
V——速度（km／h）；
K——交通密度（辆／km）。
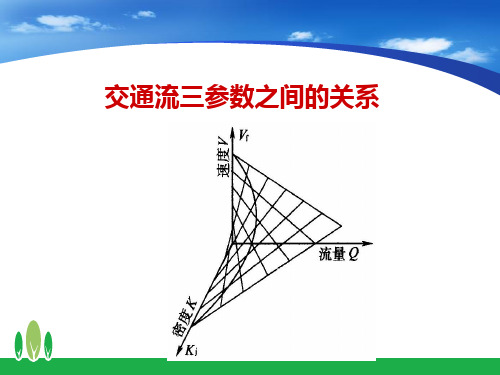
二、交通量、速度和交通密度的关系曲线 由交通量、速度和交通密度三者关系图（图 7-1 ） 可见：
图7—1交通量、速度和交通密度的关系
（1）Qm是速度-流量图上的峰值，表示最大流量。
（2）Vm是流量取最大值（Q＝Qm）时的速度，称为 临界速度。
例7-1已知某公路上畅行速度Vf=80 km/h，阻塞密度Kj =105veh／km，速度一密度符合直线关系式。 求：（1）在该路段上期望得到的最大流量？ （2）此时所对应的车速是多少？ 解：（1）该路段上期望得到的最大流量为： Qm=1/4 KjVf=1/4*80*105= 2100（veh／h）
阻塞密度值：kj=1000／hd＝1000／8.05=124辆 ／km，如假定ht＝1.5s，由于 ht＝3600／Q
因此，最大通行能力Qm＝3600／1.5＝2400辆／h。 此时的速度Vm＝Qm／Km＝2400／62＝38.7km／ h。
华东交通大学《交通工程学》复习题
华东交通大学《交通工程学原理》练习题第一章绪论1、什么是交通工程学?交通工程学主要研究哪几个方面？2、我国目前的交通工程进展情况如何?从现状和国外交通工程的发展进程来看，你认为我国交通的发展方向应如何？第二章人、车的交通特性分析1、为什么要研究交通特性？一般包括哪些特性？这些特性具体表现在哪些方面？2、感觉和知觉的差异。
3、驾驶员在交通系统中所处的地位及职责是什么？驾驶员的交通行为及心理特性如何？4、驾驶员的哪些个性特征可以影响到驾驶行为？其影响如何？5、交通设施（设计。
）中哪些情况考虑了驾驶员（行人或者乘客。
）的交通特性？举例说明。
6、疲劳驾驶、饮酒与驾驶的危害。
第三章交通量调查1、交通量的定义是什么？如何表达？有何用途？2、什么叫高峰小时系数？如何计算确定？有何用途？3、何谓车辆换算系数？路段和交叉口该系数是否相同？你认为应如何求算较合理？4、试述交通量的空间分布和时间分布特性。
5、何谓第三十位小时交通量？有什么意义及用途？6、某双向道路，两个方向的交通量分别为400辆/小时和600辆/小时，该道路的方向不均匀系数K d应为_______a、40%b、60%c、50%d、66.7%7、、某双向两车道乡间公路，2012年3月20日测得三月份星期一平均日交通量为15800辆/日，月变系数为0.96，星期一的日变系数为0.97，第30位小时系数为12.5%，方向不均匀系数为0.6，单车道通行能力取800辆/小时，则该公路需________a、不需扩建b、至少修建4车道c、至少修建3车道d、至少修建5车道8、表为城市观测站与研究周交通量变化系数和月变系数记录的交通量，试由这些数据计算周变系数、月变系数值表4表59、试述流动车法的基本原理、适用范围、测定方法10、交通量调查有哪些方法？各有何优、缺点？11、交通量调查观测站的类型如何选定？如何设置？12、在编制《南昌某小区的交通影响评价》报告时，对解放西路/上海南路交叉口进行了交通调查，调查的统计结果如下表，据表完成该交叉口的流量流向图。
交通工程学课件(完整版)-
§1－4 我国的交通工程 现状及发展趋势
一. 我国的交通现状
1. 综合运输 2. 公路交通 3. 城市交通
二. 我国交通工程学科的产生及面临的任务
1. 我国交通工程学科的产生 2. 我国交通工程学科面临的任务
(1) 城市交通规划理论与方法研究
①城市交通规划中规划化的交通调查内容、方法研究； ②城市交通需求预测理论与方法规范化的研究； ③城市交通网络计算机模拟技术的研究； ④城市交通网络规划理论与方法的研究； ⑤城市交通规划方案评价技术的研究； ⑥城市公共交通系统优化理论与技术的研究； ⑦城市交通规划快速反应系统的理论与方法的研究； ⑧现代先进科学方法在城市交通规划中应用的研究。
(3) 适应我国交通特点的交通控制理论与方法研 究
①区域交通控制软件系统开发与实施的研究； ②区域交通控制系统设备与配套技术的研究； ③高等级公路情报采集与信息传输、监控技术的研究； ④高等级公路与城市道路的交通管理体制、理论方法
与设施的研究； ⑤高等级公路立交规划设计与评价理论与方法的研究。
(4) 交通流理论方面基础研究
hs
V 3.6
ht
式中：V――汽车行驶速度（km/h）。
§2－2 交通量特性
一. 交通量的定义
交通量 是指在单位时间段内，通过道路某一地点、
某一段面或某一条车道的交通实体数。按交通类型分， 有机动车交通量、非机动车交通量和行人交通量，一 般不加说明则指机动车交通量，且指来往两个方向的 车辆数。
1. 年平均日交通量（AADT）
AADT
1 365
365
KN L
K Q Vs
式中：K――车流密度（辆/km）；
N――单车道路段内的车辆数（辆）；
交通工程-交通流三参数之间的关系06
❖
V=60-3/4*70=7.5（km／h）
❖
Q= KV=7.5*70=525（veh／h）
❖ Qm=1/4 KjVf=1/4*60*80=1200（veh ／h）
❖ 4、假定车辆平均长度为6.lm，在阻塞密度时，
单车道车辆间的平均距离5m，试说明流量与密度的关系。
❖试计算该道路的最大流量。 ❖解：对照车速-密度的对数模型，可得： ❖Vm=40km/h；则Vf=80km/h； ❖Kj=82辆/km； ❖则Qm=1/4Vf*Kj=1640辆/h。
3、交通量三参数之间关系的应用
拥挤收费——交通需求管理策略
流量-密度关系曲线
交通量三参数之间关系的应用
拥挤收费
通过对驶入城市中心区的车辆征收额外的 通行费达到调节中心区交通流的目的，从 而使城市中心区的交通流运行在最佳状态。
❖ 1998年8月，新加坡政府将ERP扩充到整个中心 商业区、高速公路和交通拥挤的区域。新加坡拥 挤收费的目的非常单一，就是为了控制交通拥挤 现象，同时辅以高达130%的小汽车牌照税进一 步限制小汽车的保有，削弱了拥挤收费政策的负 面影响，增强了拥挤收费实施的效果。
❖ 技术手段
❖ 早期的ALS和RPS均采取出入收费区域出示纸质凭证 的方式运行。
实施效果： 收费区域交 通量减少了 22%；
交通事故降 低5~10%；
公交利用率 大幅提高， 增减了16条 公交线路和 200多辆公交 车。
3、交通量三参数之间关系的应用
拥挤收费需解 决的关键问题
拥挤区域、拥挤收费时段、拥挤收费 费率、收费方式等。
新加 坡电 子拥 挤收 费区 域入 口图
❖ 新加坡交通拥挤收费典型成功案例
❖ 收费水平和收益分析 ❖ 新加坡的电子收费系统(ERP)是一种单次分级
道路交通流理论
i 1 n i i
n
n
f
i 1
i 1
i i
N
i
• 其中：n——观测数据分组数； • fi——计算间隔T内到达xi辆车(人)发生的次（频） • •
数； xi——计数间隔T内的到达数或各组的中值； N——观测的总计间隔数。
泊松分布
• 递推公式
P( X 0) e m P( X x) P( X x 1) x
算p、n： • p=(m-S2)/m • n=m/p=m2/(m-S2)(取整数)
二项分布
• 递推公式
P( X 0) （ 1 p) n n x 1 p P( X x) P( X x 1) x 1 p
• 应用条件：车流比较拥挤，自由行驶机会
不多的车流。
• 均值m显著大于方差S2。
n
2 χ 检验
• 确定统计量的临界值 • 当n相当大时，就可以应用χ2分布确定上式统计量 • • •
的临界值，作为取舍H0的依据。 当选定了置信度水平α后，根据自由度DF的值， 可由表8-1查出临界值。 判定统计检验结果 2 比较 的计算值与临界值，
2 2
• 若 ≥ ，则假设H0被接受，即认为随机变量
负指数分布
• 若车辆到达符合泊松分布，则车头时距就
是负指数分布。 • 在记数间隔t内没有车到达的概率为
P(0) e
距≥t的概率：
t
• 即P(0)为车头时距≥t的概率。于是，车头时
P(h t ) e
t
负指数分布
• 于是，车头时距≥t的概率：
P(h t ) e
• 车头时距<t的概率：
Q VS K
n
n
f
i 1
i 1
i i
N
i
• 其中：n——观测数据分组数； • fi——计算间隔T内到达xi辆车(人)发生的次（频） • •
数； xi——计数间隔T内的到达数或各组的中值； N——观测的总计间隔数。
泊松分布
• 递推公式
P( X 0) e m P( X x) P( X x 1) x
算p、n： • p=(m-S2)/m • n=m/p=m2/(m-S2)(取整数)
二项分布
• 递推公式
P( X 0) （ 1 p) n n x 1 p P( X x) P( X x 1) x 1 p
• 应用条件：车流比较拥挤，自由行驶机会
不多的车流。
• 均值m显著大于方差S2。
n
2 χ 检验
• 确定统计量的临界值 • 当n相当大时，就可以应用χ2分布确定上式统计量 • • •
的临界值，作为取舍H0的依据。 当选定了置信度水平α后，根据自由度DF的值， 可由表8-1查出临界值。 判定统计检验结果 2 比较 的计算值与临界值，
2 2
• 若 ≥ ，则假设H0被接受，即认为随机变量
负指数分布
• 若车辆到达符合泊松分布，则车头时距就
是负指数分布。 • 在记数间隔t内没有车到达的概率为
P(0) e
距≥t的概率：
t
• 即P(0)为车头时距≥t的概率。于是，车头时
P(h t ) e
t
负指数分布
• 于是，车头时距≥t的概率：
P(h t ) e
• 车头时距<t的概率：
Q VS K
第七、八章 三参数的关系及交通流理论
F (t ) 1 e (t ) 其概率分布密度为 f (t ) e
nk
, ( k 0 ,1, 2 ,...)
式中：P—在计数间隔t内到达k辆车的概率； λ—平均到车率(辆/s)；
t —每个计数间隔持续的时间(s)； n —正整数。
3)分布的均值M和方差D分别为：
M=np；
（8-1）
D=np(1-p). （8-2）
由此可得参数p，n的一组估计：
布。求:
1、一个周ห้องสมุดไป่ตู้内到达车辆不超过10辆的概率； 2、使到达车辆不致两次排队的周期能占的最大百分率。
解：1）一个周期内平均到达车辆数为：
m 400 3600 90 10 （辆） ;
所以，一个周期内到达车辆数X不超过10辆
的概率是：
P ( X 10 )
0
10
(10 )
路上横穿车辆连续通过时的车头时距(s), λ为主干道 上车辆平均到达率(辆/s)，Q次为次干道横穿主干道 的交通量(辆/s)；
利用负指数分布可求得下式：
Q次 ( e
0
1 e
e
c c 0
1 e
)；
式中:C ——主干道的饱和流量; Q次——次要车流能横穿主干道的最大流量,这是次要车道能
为使交通流理论的应用紧密跟上理论的发展,一 方面要求理论工作者深入工程实际,另一方面交通工 程技术人员应努力学习,钻研理论并积极应用理论分 巩加速实际问题。
交通流理论是发展中的科学,虽然现在还没有形 成完整的体系,但有很多理论在探讨各种交通现象， 它们是:
(1)
(2)
nk
, ( k 0 ,1, 2 ,...)
式中：P—在计数间隔t内到达k辆车的概率； λ—平均到车率(辆/s)；
t —每个计数间隔持续的时间(s)； n —正整数。
3)分布的均值M和方差D分别为：
M=np；
（8-1）
D=np(1-p). （8-2）
由此可得参数p，n的一组估计：
布。求:
1、一个周ห้องสมุดไป่ตู้内到达车辆不超过10辆的概率； 2、使到达车辆不致两次排队的周期能占的最大百分率。
解：1）一个周期内平均到达车辆数为：
m 400 3600 90 10 （辆） ;
所以，一个周期内到达车辆数X不超过10辆
的概率是：
P ( X 10 )
0
10
(10 )
路上横穿车辆连续通过时的车头时距(s), λ为主干道 上车辆平均到达率(辆/s)，Q次为次干道横穿主干道 的交通量(辆/s)；
利用负指数分布可求得下式：
Q次 ( e
0
1 e
e
c c 0
1 e
)；
式中:C ——主干道的饱和流量; Q次——次要车流能横穿主干道的最大流量,这是次要车道能
为使交通流理论的应用紧密跟上理论的发展,一 方面要求理论工作者深入工程实际,另一方面交通工 程技术人员应努力学习,钻研理论并积极应用理论分 巩加速实际问题。
交通流理论是发展中的科学,虽然现在还没有形 成完整的体系,但有很多理论在探讨各种交通现象， 它们是:
(1)
(2)
交通流三个参数K Q V之间关系
过C点作一条平行于流量坐标轴的线，将曲线分 成两部分，这条线以上的部分，为不拥挤部分，速度 随流量的增加而降低，直至达到通行能力的流量Qm 为止，速度为Vm；这条线以下部分为拥挤部分，流 量和速度都下降。
综合以上三个参数的关系可知：当道路上交通密 度小时，车辆可自由行驶，平均车速高，交通流量不 大；随着交通密度增大，交通流量也增加，但车速下 降；当交通密度增加到最佳密度时，交通流量达到最 大值，即交通流量达到了道路的通行能力，车辆的行 驶形成了车队跟随现象，车速低且均衡；当交通密度 继续增大，即超过了最佳密度，交通流量下降，车速 明显下降，直到车速接近于零，道路出现阻塞，交通 密度达到最大值，即阻塞密度，交通流量等于零。
（2）此时所对应的车速是：
Vm＝Vf/2=1/2*80=40 km／h
例7-2 在长400m的道路上行驶28辆车，速度-密度为直 线关系，V=60-3/4 K， 求：该道路的Vf ，Kj ，Q ，Qm 。 解：V=60-3/4 K=60（1- K/80） Vf=60 km／h K=N/L=28/0.4=70（veh／km）
上式是二次函数关系，可用一条抛物线表示，如 图7－3所示。
图7－3交通量和密度的关系
当交通密度为零时，流量为零，故曲线通过坐标 原点。当交通密度增加，流量增大，直至达到道路的 通行能力，即曲线C点的交通量达到最大值，对应的 交通密度为最佳密度Km；从C点起，交通密度增加， 速度下降，交通量 减少，直到阻塞密度Kj，速度等 于零，流量等于零；由坐标原点向曲线上任一点画矢 径。这些矢径的斜率，表示矢端的平均速度。通过A 点的矢径与曲线相切，其斜率为畅行速度Vf；对于密 度比Km小的点，表示不拥挤情况，而密度比Km大 的点，表示拥挤情况。
参考文献
交通工程学课件
如图4.11所示，当C=0.50 时，间距值的摆动衰减很快；当 C=0.80时，其罢动逐渐减小；C=1.57时，摆动停止衰减 ，其间距基本稳定；当C=1.60 时，摆动幅度逐渐增大 。可见，C=1.57为线性跟驰模型中车头间距从稳定到非 稳定的临界值。 渐近稳定：一列处于跟驰状态的车队仅当C<0.5时，才是 渐近稳定的。 与局部稳定相比较，这里C=0.50时，车头间距的摆动衰减 很快。头车运行中的扰动是以 1/λ(s/辆)的速率沿车队向后传播。当C>0.5时，将以增大变 动幅度传播，增大了车辆间的干扰，当干扰的幅度增大 到使车间距小于一个车长时，则发生追尾事故。图4.12 显示了一列有8辆车的车队，可知，前车改变运行状态后，后车也 要改变。但前后车运行状态的改变不是同步的，而是 延迟的。这是由于驾驶员对于前车运行状态的改变要 有一个反应的过程，这过程包括四个阶段： 感觉阶段——前车运行状态的改变被察觉； 认识阶段——对这一改变加以认识； 判断阶段—— 对本车将要采取的措施做出判断； 执行阶段—— 由大脑到手脚的操纵动作。 这四个阶段所需要的时间称为反应时间。假设反应时间 为△t，前车在t时刻的动作，后车要经过△t在(△t+t)时 刻才能作出相应的动作，这就是延迟性。
1.制约性 在一队汽车中，后车跟随前车运行，出于对旅行时间的考 虑，驾驶员总不愿意落后很多，而是紧随前车前进，这 就是“紧随要求”。从安全的角度考虑，跟驶车辆要满 足两个条件：一是后车的车速不能长时间大于前车的车 速只能在前车速度附近摆动，否则会发生碰撞，这是“ 车速条件”；二是前后车之间必须保持一个安全距离， 即前车刹车时，两车之间有足够的距离，从而有足够的 时间供后车驾驶员做出反应，采取制动措施，这是“间 距条件”。显然，车速高时，制动距离长，安全距离也 应加大。紧随要求、车速条件和间距条件构成了一队汽 车跟驰行驶的制约性，即前车的车速制约着后车的车速 和两车间距。
东大版交通工程学课后习题解答
第一部份：交通工程学课后思考题解答第一章:绪论1-1简述交通工程学的概念、性质、特点、与发展趋势概念：交通工程学是研究交通发生、发展、散布、运行与停住规律，探讨交通调查、计划、设计、监管、管理、安全的理论和有关设施、装备、法律与法规。
协调道路交通中人、车、路与环境之间的彼此关系。
使道路交通加倍安全、高校、快捷、舒适、方便、经济的一门工程技术学科。
性质：是一门兼有自然科学与社会科学双重属性的综合性学科。
特点：系统性、综合性、交叉性、社会性、超前性、动态性发展趋势：智能化和系统化1-2简述我国的交通现状与交通工程学科面临的任务现状：综合运输六点；公路交通三点；城市交通四点任务：即重点研究的那些领域1-3简述城市交通畅通工程的目标和重点任务目标：提高城市交通建设与管理科学化水平。
重点任务：改善道路条件，优化交通结构，强化科学管理，规范交通行为1-4简述交通工程学科的研究范围、重点及作用。
范围：交通特性分析技术、交通调查方式、交通流理论、道路通行能力分析技术、道路交通系统计划理论、交通安全技术、道路交通系统管理技术与管理计划、静态交通系统计划、交通系统的可持续发展计划、交通工程的新理论新方式新技术作用：良好的交通条件与高效的运输系统能增进社会的发展，经济的繁荣，和人们日常生活的正常进行和城市各项功能的发挥、山区开发、旅游开展。
经济方面能扩大商品市场与原材料的来源，降低生产本钱与运输费用，增进工业、企业的发展与区域土地的开发，提高土地价钱与城市的活力，交通的发展还可实现运输的专业化、便捷化、批量化与运费低廉化。
从而有可能更大的范围内合理配置生产要素，同时也可增进全国或地域范围内人口的合理流动。
第二章：交通特性2-1交通特性包括那几个方面？为何要进行分析？意义如何？分析中要注意什么问题？特性：人-车-路大体特性、交通量特性、行车速度特性、交通密度特性、交通流大体特性及其彼此关系、交通要素与环境之间的相关关系。
05交通工程学 第五讲 交通流理论-流密速三参数基本关系
交通工程学基础
Traffic Engineering
叶彭姚 博士
交通运输与物流学院 西南交通大学 2011.3
第五讲 交通流理论
－流密速三参数基本关系 §5-1 交通流特性 §5-2 概率统计模型 §5-3 排队论模型 §5-4 跟驰模型 §5-5 流体动力学模拟
交通流理论概述
交通流理论是交通工程学的理论基础；
拥挤区 不拥挤区 Vm 速度V（Km/h） E
A
Vf
4.1 交通流特性
4.1.3 间断流特征
1. 信号间断处交通流特征
1 车头时距 2 3 4 5 6 7 8
h
t1
t2
t3
t4
t5
车队中的车辆
4.1 交通流特性
4.1.3 间断流特征
2. 关键变量及其定义
饱和车头间距 饱和交通量比率（饱和流率） 启动损失时间：Σ超时 净损失时间：最后一辆车越过停车线至下一 次绿灯启亮之间的时间。
Qm 流量Q（辆/h）
B
Vc=Vm VD D
流量（辆/h）
不拥挤区 A Km 拥挤区 E
Kj
密度K（辆/km）
4.1 交通流特性
4.1.2 连续流特征
2. 数学描述
3）流量与速度的关系 （利用Greenhields线性模型）
Qm 流量Q（辆/h） B Kc=Km D C
KD
流量（辆/h）
它是运用物理学和数学的方法来描述交通特性 的理论，它用分析的方法阐述交通现象及其机 理,使我们能更好地理解交通现象及本质；
研究交通流理论的意义 ——把握交通流运动机理与规律，科学地分析 交通设施设计效果与运营管理系统
Traffic Engineering
叶彭姚 博士
交通运输与物流学院 西南交通大学 2011.3
第五讲 交通流理论
－流密速三参数基本关系 §5-1 交通流特性 §5-2 概率统计模型 §5-3 排队论模型 §5-4 跟驰模型 §5-5 流体动力学模拟
交通流理论概述
交通流理论是交通工程学的理论基础；
拥挤区 不拥挤区 Vm 速度V（Km/h） E
A
Vf
4.1 交通流特性
4.1.3 间断流特征
1. 信号间断处交通流特征
1 车头时距 2 3 4 5 6 7 8
h
t1
t2
t3
t4
t5
车队中的车辆
4.1 交通流特性
4.1.3 间断流特征
2. 关键变量及其定义
饱和车头间距 饱和交通量比率（饱和流率） 启动损失时间：Σ超时 净损失时间：最后一辆车越过停车线至下一 次绿灯启亮之间的时间。
Qm 流量Q（辆/h）
B
Vc=Vm VD D
流量（辆/h）
不拥挤区 A Km 拥挤区 E
Kj
密度K（辆/km）
4.1 交通流特性
4.1.2 连续流特征
2. 数学描述
3）流量与速度的关系 （利用Greenhields线性模型）
Qm 流量Q（辆/h） B Kc=Km D C
KD
流量（辆/h）
它是运用物理学和数学的方法来描述交通特性 的理论，它用分析的方法阐述交通现象及其机 理,使我们能更好地理解交通现象及本质；
研究交通流理论的意义 ——把握交通流运动机理与规律，科学地分析 交通设施设计效果与运营管理系统
第7章 交通流特征参数之间的关系
3600 3600 Qm = = = 2400 （pcu/车道 小时） 1.5 ht
4Qm 4 × 2400 K2 vf = = = 76.8(km / h) Q = v f (K − ) kj 125 Kj K2 K2 Q = v f (K − ) = 76.8( K − ) 125 Kj 聊城大学汽车与交通工程学院
3600 S = ht
注：3600表示每个小时的时间之内，有效通行时 间为3600秒（注意具体情况具体分析）。
聊城大学汽车与交通工程学院
交通工ቤተ መጻሕፍቲ ባይዱ学
信号交叉口间断流的有效通行时间： 信号交叉口间断流的有效通行时间： 1、存在损失时间 启动损失时间（l1） 清尾损失时间（l2） 2、允许通行时间 有效时间＝允许通行时间－启动损失时间－ 有效时间＝允许通行时间－启动损失时间－清 尾损失时间
1000 K= hs
3600 Q= ht
hs Q vs = = 3.6 K ht
聊城大学汽车与交通工程学院
交通工程学
第六节
连续流特征
一.连续流 指没有外部固定因素（如交通信号）影响的不间 断交通流。
聊城大学汽车与交通工程学院
交通工程学
交通量Q、平均区间行车平均速度 、车流密度 K是表征交通流特性的三个基本参数。
1 vm = v f 2
2
不拥挤 Vm
1 Qm = K m vm = K j v f 4
拥挤
Q
聊城大学汽车与交通工程学院
交通工程学
例1：已知某公路上畅行速度vf＝80km/h，阻塞密 度Kj＝100辆/km，速度—密度关系为线性关系。试 问： （1）该路段上期望得到的最大流量是？ （2）此时所对应的速度是多少？ 解： Qm = K m vm = 1 K j v f = 2000
4Qm 4 × 2400 K2 vf = = = 76.8(km / h) Q = v f (K − ) kj 125 Kj K2 K2 Q = v f (K − ) = 76.8( K − ) 125 Kj 聊城大学汽车与交通工程学院
3600 S = ht
注：3600表示每个小时的时间之内，有效通行时 间为3600秒（注意具体情况具体分析）。
聊城大学汽车与交通工程学院
交通工ቤተ መጻሕፍቲ ባይዱ学
信号交叉口间断流的有效通行时间： 信号交叉口间断流的有效通行时间： 1、存在损失时间 启动损失时间（l1） 清尾损失时间（l2） 2、允许通行时间 有效时间＝允许通行时间－启动损失时间－ 有效时间＝允许通行时间－启动损失时间－清 尾损失时间
1000 K= hs
3600 Q= ht
hs Q vs = = 3.6 K ht
聊城大学汽车与交通工程学院
交通工程学
第六节
连续流特征
一.连续流 指没有外部固定因素（如交通信号）影响的不间 断交通流。
聊城大学汽车与交通工程学院
交通工程学
交通量Q、平均区间行车平均速度 、车流密度 K是表征交通流特性的三个基本参数。
1 vm = v f 2
2
不拥挤 Vm
1 Qm = K m vm = K j v f 4
拥挤
Q
聊城大学汽车与交通工程学院
交通工程学
例1：已知某公路上畅行速度vf＝80km/h，阻塞密 度Kj＝100辆/km，速度—密度关系为线性关系。试 问： （1）该路段上期望得到的最大流量是？ （2）此时所对应的速度是多少？ 解： Qm = K m vm = 1 K j v f = 2000
交通工程学道路通行能力课件
34
四、信号交叉口的通行能力
信号交叉口的运行特征 ： 交叉口是两条或两条以上道路相交的区域，车辆由此通过，并转换方 向，其运行路线必须相互交织或交叉， 由色灯信号控制指挥车辆前 进、停止或转向，这就不可避免地要减速、制动、停车或启动、加速、 转向，同时还由于红灯周期性地定时出现，所以必然要导致停车等候 和时间损失。 在交叉口范围内各种车辆混合行驶，转弯时相互穿插，当自行车高峰 时，机动车差不多处于非机动车的包围之中，要实现方向转换是困难 的。
354W W 3 QM—交织段上最大通1行能W力（辆/h）；
l—交织段长度（m）l ；
W—交织段宽度（m）；
e—环交入口引道平均宽度：
e=(e1+e2)/2 （m） ；
P—交织段内交织车辆与全部车辆之比(%)。
27
三、环行交叉口的通行能力
根据经验检验，一般设计通行能力应为沃尔卓普公式计算最大值的 80%，因此沃尔卓普公式应修改为：
8
二、道路通行能力与服务水平
道路通行能力的分类 较长路段畅通无阻的连续行驶车流的通行能力，一般称为路段通行能 力，它是所有道路交通系统都必须考虑的; 在有横向干扰条件下，时通时断、不连续车流的通行能力，如具有平 面信号交叉口的城市道路的通行能力; 在合流、分流或交叉运行状态下的通行能力，如各类匝道收费口及其 附近连接段的通行能力; 交织运行状态下的通行能力，如立体交叉的各类匝道、常规环道上车 流的通行能力。
6
管制条件：是指道路管制设施装备的类型、管理体制的层次，交通信 号的位置、种类、配时等影响通行能力的关键性管制条件，其它还有 停车让路标志、车道使用限制，转弯禁限等措施。 其它条件：有气候、温度、地形、风力、心理等因素。但其中直接影 响通行能力数值的主要因素有：车行道宽度及侧向净空，车行道数量、 交通组成、驾驶员特性、道路纵坡、横向干扰与视距等。
四、信号交叉口的通行能力
信号交叉口的运行特征 ： 交叉口是两条或两条以上道路相交的区域，车辆由此通过，并转换方 向，其运行路线必须相互交织或交叉， 由色灯信号控制指挥车辆前 进、停止或转向，这就不可避免地要减速、制动、停车或启动、加速、 转向，同时还由于红灯周期性地定时出现，所以必然要导致停车等候 和时间损失。 在交叉口范围内各种车辆混合行驶，转弯时相互穿插，当自行车高峰 时，机动车差不多处于非机动车的包围之中，要实现方向转换是困难 的。
354W W 3 QM—交织段上最大通1行能W力（辆/h）；
l—交织段长度（m）l ；
W—交织段宽度（m）；
e—环交入口引道平均宽度：
e=(e1+e2)/2 （m） ；
P—交织段内交织车辆与全部车辆之比(%)。
27
三、环行交叉口的通行能力
根据经验检验，一般设计通行能力应为沃尔卓普公式计算最大值的 80%，因此沃尔卓普公式应修改为：
8
二、道路通行能力与服务水平
道路通行能力的分类 较长路段畅通无阻的连续行驶车流的通行能力，一般称为路段通行能 力，它是所有道路交通系统都必须考虑的; 在有横向干扰条件下，时通时断、不连续车流的通行能力，如具有平 面信号交叉口的城市道路的通行能力; 在合流、分流或交叉运行状态下的通行能力，如各类匝道收费口及其 附近连接段的通行能力; 交织运行状态下的通行能力，如立体交叉的各类匝道、常规环道上车 流的通行能力。
6
管制条件：是指道路管制设施装备的类型、管理体制的层次，交通信 号的位置、种类、配时等影响通行能力的关键性管制条件，其它还有 停车让路标志、车道使用限制，转弯禁限等措施。 其它条件：有气候、温度、地形、风力、心理等因素。但其中直接影 响通行能力数值的主要因素有：车行道宽度及侧向净空，车行道数量、 交通组成、驾驶员特性、道路纵坡、横向干扰与视距等。
交通工程学课件
本章内容
交通系统各要素特性及要素之间相关特性 ■ 2.1三要素（人、车、路）基本特性 ■ 2.2交通量基本特性 ■ 2.3行车速度特性 ■ 2.4交通流基本特性及其相互关系
2.1 人—车—路基本特性
道路交通三要素
■人：出行者、规划设计和管理者等； ■车：小汽车、公共汽车、卡车、摩托车、
人力车（自行车、三轮车）； ■路：道路网（密度、等级、布局），道路
2.1.3 道路基本特性
环形放射的道路网布局
2.1.3 道路基本特性
） 典型的环形放射交通网（莫斯科
西安市道路网
2.1.3 道路基本特性
重庆市道路网
2.1.3 道路基本特性
道路的功能
2.1.4 道路基本特性
由速度及交通量决定
城市道路分类
公路分级
公路行政等级
■ 快速路 ■ 主干道 ■ 次干道 ■ 支路
3）时变化
2.2.2 交通量的时间分布特性
■ 一天24h中，各个小时内交通量变化特性
■ 指标：用某一小时或某一时段交通量占全日交通
量之比表示交通量的时变规律
■ 16h（6：00~22：00） ■ 12h（6：00~18：00） ■ 18h（4：00~22：00） ■ 高峰小时
占全日交通量之比
3）时变化
（线形、宽度、路面质量、交叉口及交通流状况及标志、信号等影响 驾驶人的反应。
■刺激信息
■早显信息——有提前量信息，驾驶人易判断 ■突显信息——外界信息来之突然、易出事故 ■微弱信息——刺激信息量小，易造成判断错误 ■先兆信息——有先兆，驾驶人易察觉 ■潜伏信息——不易直观察觉，易造成判断错误
■反应时间
驾驶人基本特征—视觉特性
■色彩感觉： 红色——刺激性强，易见性高； 黄色——有最高的明亮度； 绿色——温柔、平静，有安全感 蓝色——寒冷感，使人镇静。
交通系统各要素特性及要素之间相关特性 ■ 2.1三要素（人、车、路）基本特性 ■ 2.2交通量基本特性 ■ 2.3行车速度特性 ■ 2.4交通流基本特性及其相互关系
2.1 人—车—路基本特性
道路交通三要素
■人：出行者、规划设计和管理者等； ■车：小汽车、公共汽车、卡车、摩托车、
人力车（自行车、三轮车）； ■路：道路网（密度、等级、布局），道路
2.1.3 道路基本特性
环形放射的道路网布局
2.1.3 道路基本特性
） 典型的环形放射交通网（莫斯科
西安市道路网
2.1.3 道路基本特性
重庆市道路网
2.1.3 道路基本特性
道路的功能
2.1.4 道路基本特性
由速度及交通量决定
城市道路分类
公路分级
公路行政等级
■ 快速路 ■ 主干道 ■ 次干道 ■ 支路
3）时变化
2.2.2 交通量的时间分布特性
■ 一天24h中，各个小时内交通量变化特性
■ 指标：用某一小时或某一时段交通量占全日交通
量之比表示交通量的时变规律
■ 16h（6：00~22：00） ■ 12h（6：00~18：00） ■ 18h（4：00~22：00） ■ 高峰小时
占全日交通量之比
3）时变化
（线形、宽度、路面质量、交叉口及交通流状况及标志、信号等影响 驾驶人的反应。
■刺激信息
■早显信息——有提前量信息，驾驶人易判断 ■突显信息——外界信息来之突然、易出事故 ■微弱信息——刺激信息量小，易造成判断错误 ■先兆信息——有先兆，驾驶人易察觉 ■潜伏信息——不易直观察觉，易造成判断错误
■反应时间
驾驶人基本特征—视觉特性
■色彩感觉： 红色——刺激性强，易见性高； 黄色——有最高的明亮度； 绿色——温柔、平静，有安全感 蓝色——寒冷感，使人镇静。
05交通工程学 第五讲 交通流理论-流密速三参数基本关系
它是运用物理学和数学的方法来描述交通特性 的理论，它用分析的方法阐述交通现象及其机 理,使我们能更好地理解交通现象及本质；
研究交通流理论的意义 ——把握交通流运动机理与规律，科学地分析 交通设施设计效果与运营管理系统
4.1 交通流特性
4.1.1 交通设施种类
连续流设施
间断流设施
4.1 交通流特性
拥挤区 不拥挤区 Vm 速度V（Km/h） E
A
Vf
4.1 交通流特性
4.1.3 间断流特征
1. 信号间断处交通流特征
1 车头时距 2 3 4 5 6 7 8
h
t1
t2
t3
t4
t5
车队中的车辆
4.1 交通流特性
4.1.3 间断流特征
2. 关键变量及其定义
饱和车头间距 饱和交通量比率（饱和流率） 启动损失时间：Σ超时 净损失时间：最后一辆车越过停车线至下一 次绿灯启亮之间的时间。
4.1.1 交通设施种类
连续流设施
间断流设施
无外部因素导致周期 性中断 高速公路、限制出入 的一般公路路段。
由于外部设备导致 交通流周期性中断 一般道路交叉口
4.1 交通流特性
4.1.2 连续流特征
4.1 交通流特性
4.1.2 连续流特征
几个特征变量
(1) (2) (3) (4) (5) 极大流量Qm 临界速度Vm 最佳密度km 阻塞密度kj 畅行速度Vf
交通工程学基础
Traffic Engineering
叶彭姚 博士
交通运输与物流学院 西南交通大学 2011.3
研究交通流理论的意义 ——把握交通流运动机理与规律，科学地分析 交通设施设计效果与运营管理系统
4.1 交通流特性
4.1.1 交通设施种类
连续流设施
间断流设施
4.1 交通流特性
拥挤区 不拥挤区 Vm 速度V（Km/h） E
A
Vf
4.1 交通流特性
4.1.3 间断流特征
1. 信号间断处交通流特征
1 车头时距 2 3 4 5 6 7 8
h
t1
t2
t3
t4
t5
车队中的车辆
4.1 交通流特性
4.1.3 间断流特征
2. 关键变量及其定义
饱和车头间距 饱和交通量比率（饱和流率） 启动损失时间：Σ超时 净损失时间：最后一辆车越过停车线至下一 次绿灯启亮之间的时间。
4.1.1 交通设施种类
连续流设施
间断流设施
无外部因素导致周期 性中断 高速公路、限制出入 的一般公路路段。
由于外部设备导致 交通流周期性中断 一般道路交叉口
4.1 交通流特性
4.1.2 连续流特征
4.1 交通流特性
4.1.2 连续流特征
几个特征变量
(1) (2) (3) (4) (5) 极大流量Qm 临界速度Vm 最佳密度km 阻塞密度kj 畅行速度Vf
交通工程学基础
Traffic Engineering
叶彭姚 博士
交通运输与物流学院 西南交通大学 2011.3
第七章交通流三参数之间的关系
式 表明速度与流量的关系曲 线同样是一条抛物线（图7-4）
v2 Q K j (v ) vf
图7—4 速度与流量的关系
当交通密度为零时，畅行交通流的车速就可能达 到最高车速，如图中曲线的最高点A，就是畅行速度 Vf，而流量等于零。当交通密度等于阻塞密度时，速 度等于零，流量也等于零，因此，曲线通过坐标原点。
对于式（7-6）若另dQ/dK=0，则可求出对应于 Qm的Km值：
km
1 kj 2
从而
Qm K m vm
K mv f 4
第四节 速度和流量的关系
由式
K v v f (1 ) Kj
可得：
v K K j (1 ) vf
代人式Q＝KV，得
v2 Q K j (v ) vf
例7-1已知某公路上畅行速度Vf=80 km/h，阻塞密度Kj =105veh／km，速度一密度符合直线关系式。 求：（1）在该路段上期望得到的最大流量？ （2）此时所对应的车速是多少？ 解：（1）该路段上期望得到的最大流量为： Qm=1/4 KjVf=1/4*80*105= 2100（veh／h）
（2）此时所对应的车速是：
Vm＝Vf/2=1/2*80=40 km／h
例7-2 在长400m的道路上行驶28辆车，速度-密度为直 线关系，V=60-3/4 K， 求：该道路的Vf ，Kj ，Q ，Qm 。 解：V=60-3/4 K=60（1- K/80） Vf=60 km／h K=N/L=28/0.4=70（veh／km）
（3）在速度、密度图上，车辆减少，密度随着变小， 速度增大。当密度趋于零时，速度可达最大值，这时 车辆可畅行无阻，所以Vf是畅行速度。若车辆增多时； 则密度增大，车速随之减小。当密度达到最大值Kj时， 车流受阻即Q = 0。此时的密度Kj称阻塞密度。
7 QVK模型解析
第七章 交通量、速度和密度之间的关系
第一节 三参数之间的关系 第二节 速度-密度的关系 第三节 交通量-密度的关系 第四节 交通量-速度的关系
本节需要掌握：
一、概念：
1_交通流的定 2_交通流理 3_交通流的的参数
的几个特殊值
6_流量-速度- 7_速度-密 8_流量－密 9_流量－
交通流密度很小时: 4、其他模型
K
v v f * e Km
v
v
f
(1
K Kj
)n
主要的速度－密度模型：
格林希尔茨——线性模型
在通常的交通流密度条件下：v v f (1 K K j )
格林柏——对数模型
交通流密度很大时： v vm ln( K j K )
安德伍德——指数模型
K
__
__
hs 1000 / K , K j 1000 / hs , K j 1000 / 8.05 124辆/km 车道
车头间距hs
例题：已知某公路上的自由流速度为Vf=80Km/h，阻塞密度为 Kj=96辆/km，速度与密度关系V=b-aK；试求：
（1）该路段在密度为30辆/km时的路段平均交通量？ （2）该道路的最大交通量为多少，对应的速度和密度值是多少？
（2）交通流参数的概念： 用来描述和反映交通流特征的物理量。
（3）交通流参数包括： 宏观参数：描述交通流整体特征。 例：交通量、速度、密度。 微观参数：个体车辆之间的运行特性。 例：车头时距、车头间距、地点车速。
（4）交通流参数的几个特殊值
自由流速度 （Free-flow Speed）vf
阻塞密度 （Jam Density） Kj
交通流密度很小时：v v f * e Km
第一节 三参数之间的关系 第二节 速度-密度的关系 第三节 交通量-密度的关系 第四节 交通量-速度的关系
本节需要掌握：
一、概念：
1_交通流的定 2_交通流理 3_交通流的的参数
的几个特殊值
6_流量-速度- 7_速度-密 8_流量－密 9_流量－
交通流密度很小时: 4、其他模型
K
v v f * e Km
v
v
f
(1
K Kj
)n
主要的速度－密度模型：
格林希尔茨——线性模型
在通常的交通流密度条件下：v v f (1 K K j )
格林柏——对数模型
交通流密度很大时： v vm ln( K j K )
安德伍德——指数模型
K
__
__
hs 1000 / K , K j 1000 / hs , K j 1000 / 8.05 124辆/km 车道
车头间距hs
例题：已知某公路上的自由流速度为Vf=80Km/h，阻塞密度为 Kj=96辆/km，速度与密度关系V=b-aK；试求：
（1）该路段在密度为30辆/km时的路段平均交通量？ （2）该道路的最大交通量为多少，对应的速度和密度值是多少？
（2）交通流参数的概念： 用来描述和反映交通流特征的物理量。
（3）交通流参数包括： 宏观参数：描述交通流整体特征。 例：交通量、速度、密度。 微观参数：个体车辆之间的运行特性。 例：车头时距、车头间距、地点车速。
（4）交通流参数的几个特殊值
自由流速度 （Free-flow Speed）vf
阻塞密度 （Jam Density） Kj
交通流密度很小时：v v f * e Km
1[1].3+交通流三参数--交通工程改.ppt
![1[1].3+交通流三参数--交通工程改.ppt](https://img.taocdn.com/s3/m/e1b2d253bceb19e8b9f6ba3f.png)
S
s1
s2
s3
s4
2021/3/12
25
二、车道占有率
时间占有率： 在道路的任意路段上，车辆通过时 间的累计值与观测总时间之比（%），其表达式 为：
Rt
1 T
n
ti
i1
式中： Rt —时间占有率； T —观测总时间；
ti —第i 辆车的通过时间； n —观测时间内通过该路段的车辆数。
2021/3/12
36
三、流量与密度的关系
交通流的流量-密度关系是交通流的基本关系，根 据格林希尔茨公式及三参数的基本关系式可得：
Q
KV f
(1
K Kj
)
Vf
(K
K2 Kj
)
2上式对Q 求导，并令：
dQ dK
Vf
2V f Kj
K
0
可求出当：
K K j 时 ，Q最 大 。 2
➢ 当Q≤Qm 、K＞Km 、 V<Vm时，
属于拥挤状态；
➢ 当Q≤Qm 、K≤ Km 、 V≥Vm时， 则属于不拥挤状态。
1959年，格林柏（Greenberg）提出了用于密度很 大时对数模型：
V
Vm
ln(
Kj K
)
格林柏模型 的适用范围
2021/3/12
35
二、速度与密度的关系
1961年安德伍德（Underwood）提出了用于密度 很小时的指数模型：
K
V Vf e Km
安德伍德模型 的适用范围
2021/3/12
式中：N —路段内的车辆数(辆); L —路段长度(km)。
2021/3/12
22
二、车道占有率
由于密度是瞬时值，随观测时间和区间长度而变 化，且反映不出车辆长度和速度的关系，尤其是 在车辆混合行驶时密度的大小并不能明确表示交 通流的状态，这就要引入车道占有率的概念表示 密度。 车道占有率包括空间占有率和时间占有率两种。
s1
s2
s3
s4
2021/3/12
25
二、车道占有率
时间占有率： 在道路的任意路段上，车辆通过时 间的累计值与观测总时间之比（%），其表达式 为：
Rt
1 T
n
ti
i1
式中： Rt —时间占有率； T —观测总时间；
ti —第i 辆车的通过时间； n —观测时间内通过该路段的车辆数。
2021/3/12
36
三、流量与密度的关系
交通流的流量-密度关系是交通流的基本关系，根 据格林希尔茨公式及三参数的基本关系式可得：
Q
KV f
(1
K Kj
)
Vf
(K
K2 Kj
)
2上式对Q 求导，并令：
dQ dK
Vf
2V f Kj
K
0
可求出当：
K K j 时 ，Q最 大 。 2
➢ 当Q≤Qm 、K＞Km 、 V<Vm时，
属于拥挤状态；
➢ 当Q≤Qm 、K≤ Km 、 V≥Vm时， 则属于不拥挤状态。
1959年，格林柏（Greenberg）提出了用于密度很 大时对数模型：
V
Vm
ln(
Kj K
)
格林柏模型 的适用范围
2021/3/12
35
二、速度与密度的关系
1961年安德伍德（Underwood）提出了用于密度 很小时的指数模型：
K
V Vf e Km
安德伍德模型 的适用范围
2021/3/12
式中：N —路段内的车辆数(辆); L —路段长度(km)。
2021/3/12
22
二、车道占有率
由于密度是瞬时值，随观测时间和区间长度而变 化，且反映不出车辆长度和速度的关系，尤其是 在车辆混合行驶时密度的大小并不能明确表示交 通流的状态，这就要引入车道占有率的概念表示 密度。 车道占有率包括空间占有率和时间占有率两种。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对于车流密度比Km小的点，表示不拥挤情况；而 车流密度比Km大的点，表示拥挤情况
7.3 交通量—密度的关系
算例1
假定车辆平均长度为6.1m，在阻塞密度时，单车道车
辆间的平均距离为1.95m，因此车头间距 hd 8.05m ，试
说明流量与密度的关系。
E点
hd 1000 K
阻塞密度值Kj
K j 1 0 0 0h d 1 0 0 08 .0 5 1 2 4辆 km
7.2 速度—密度的关系
速度一密度对数曲线（小密度）
7.2 速度—密度的关系
广义速度—密度模型
V
Vf
(1
K Kj
)n
n——大于零的实数 当n=1时，该式变为直线关系式
7.3 交通量—密度的关系
数学模型
Q KV
VVf
Vf Kj
K KVf (1Kj )
QKV KfV (1K K j)Vf(KK K2 j)
当车流密度小时不适宜使用此模型。
7.2 速度—密度的关系
速度一密度对数曲线（大密度）
7.2 速度—密度的关系
指数模型
当交通密度小时，Underwood提出的指数模型比较
符合实际：
Kj
V Vf (1 e ) Km
K m ——为最大交通量时的密度，辆/km； E ——自然对数的底数；
此模型的缺点是当 K K j 时，V≠0。
Vm = 3 8 .7
C
1.24
32.2
1.86
Q m =KmVm
D
K m=62
3.73
31 62 93 密 度 (辆 /km )
E K j=124
速度—密度的直线关系
7.2 速度—密度的关系
对数关系模型
当车流密度大时，Grenberg提出的对数模型较符合实 际：
V
Vm
ln(Kj K
)
V m ——对应最大交通量的速度，km/h
密 度 K (辆 /km )
交通流量—密度曲线图
7.3 交通量—密度的关系
当车流密度值为零时，交通量为零，密度增大时， 交通量增加，密度到最佳密度Km时，交通量取最大值 Qm。密度再增大，到阻塞密度Kj时，交通量为零。
QKV KfV (1K K j)Vf(KK K2 j)
KKm
1 2Kj
V Vm 12Vt
B点
由图上可知点B的交通量为1800辆，密度为30辆/ km，
速度为60km／h。
D点
D点表示拥挤情况，D点流量为1224辆／h，密度为106.6 辆/h，速度为11.6km/h。
7.4 交通量—速度的关系
不同的速度—密度关系式将产生不同的速度—交通量关系式
V K Kj (1Vf )
Q
K
j
(V
V2 Vf
Qm 14Vf Kj
7.3 交通量—密度的关系
上图中由坐标原点A向曲线上任一点画矢径，矢 径的斜率表示区段平均车速。而其切线的斜率则表示 交通量微小变化时速度的变化：
Q v
K
v Q K
同时，上图中在A点的斜率最大，表示车速最高， 交通量与车流密度均很小，车辆以自由流速度Vf行驶。
7.3 交通量—密度的关系
直线关系模型 1933年，Greenshields提出了KV单段式直线关
系模型：
VabK
当车流密度很大或很小时不适宜使用此模型。
7.2 速度—密度的关系
速 度(km /h)
行 驶 时 ( 间m in/km )
车头间距 hd (m)
A V f =77.4
60
30
15 12 9
0.78
64.4
B
0.93
)
V40ln180/K
Kj 180辆km
Vm 40kmh 时通过的交通量最大
)
7.4 交通量—速度的关系
流量—速度曲线图
7.4 交通量—速度的关系
算例2
已知某公路上畅行速度 Vf 80kmh ，阻塞密度Kj 100辆/km， 速度—密度关系为直线关系。试问：
（1）该路段上期望得到的最大交通量是多少？ （2）此时所对应的车速是多少？
（1）最大交通量：Qm
Vf K 4
j
Qm8041002000辆h
7.3 交通量—密度的关系
特征描述
流 量Q (辆/h) 车 间 时 距ht (s)
Qm =2400 2000
1600 1200
800 400
A
车头间距hd (m)
60 30
15 12
C
B
9 1.5 1.8
Байду номын сангаас
Vt VB Vc=Vm
D 3.0
VD
4.5
不拥挤 拥挤
9.0
E
31
62
93 K j=124
Km
（2）交通量最大时，对应的车速：
Vm
Vf 2
Vm
80 2
40km
h
7.4 交通量—速度的关系
算例3
对某路上的交通流进行观测，发现速度与密度的关 系是对数关系：V40ln180/K，式中车速单位为km/h， 密度单位为：辆/km。试问该路段阻塞密度是多少？车 速为何值时交通流量最大？
V
Vm
ln( K j K
第七章 交通流量、速度和密度 之间的关系
7.1 三参数之间的关系
假设交通流为自由流。在长度为L的路段上有连续行 进的N辆车，其速度V，如下图。由三个参数的定义可 知：
V
A1
2
NB
KN
t L
L
V
QN t
Q
N t
N L
V
Q NV L
Q KV
7.1 三参数之间的关系
交通流量、速度、密度三参数关系图
7.2 速度—密度的关系
7.3 交通量—密度的关系
算例1
假定车辆平均长度为6.1m，在阻塞密度时，单车道车
辆间的平均距离为1.95m，因此车头间距 hd 8.05m ，试
说明流量与密度的关系。
E点
hd 1000 K
阻塞密度值Kj
K j 1 0 0 0h d 1 0 0 08 .0 5 1 2 4辆 km
7.2 速度—密度的关系
速度一密度对数曲线（小密度）
7.2 速度—密度的关系
广义速度—密度模型
V
Vf
(1
K Kj
)n
n——大于零的实数 当n=1时，该式变为直线关系式
7.3 交通量—密度的关系
数学模型
Q KV
VVf
Vf Kj
K KVf (1Kj )
QKV KfV (1K K j)Vf(KK K2 j)
当车流密度小时不适宜使用此模型。
7.2 速度—密度的关系
速度一密度对数曲线（大密度）
7.2 速度—密度的关系
指数模型
当交通密度小时，Underwood提出的指数模型比较
符合实际：
Kj
V Vf (1 e ) Km
K m ——为最大交通量时的密度，辆/km； E ——自然对数的底数；
此模型的缺点是当 K K j 时，V≠0。
Vm = 3 8 .7
C
1.24
32.2
1.86
Q m =KmVm
D
K m=62
3.73
31 62 93 密 度 (辆 /km )
E K j=124
速度—密度的直线关系
7.2 速度—密度的关系
对数关系模型
当车流密度大时，Grenberg提出的对数模型较符合实 际：
V
Vm
ln(Kj K
)
V m ——对应最大交通量的速度，km/h
密 度 K (辆 /km )
交通流量—密度曲线图
7.3 交通量—密度的关系
当车流密度值为零时，交通量为零，密度增大时， 交通量增加，密度到最佳密度Km时，交通量取最大值 Qm。密度再增大，到阻塞密度Kj时，交通量为零。
QKV KfV (1K K j)Vf(KK K2 j)
KKm
1 2Kj
V Vm 12Vt
B点
由图上可知点B的交通量为1800辆，密度为30辆/ km，
速度为60km／h。
D点
D点表示拥挤情况，D点流量为1224辆／h，密度为106.6 辆/h，速度为11.6km/h。
7.4 交通量—速度的关系
不同的速度—密度关系式将产生不同的速度—交通量关系式
V K Kj (1Vf )
Q
K
j
(V
V2 Vf
Qm 14Vf Kj
7.3 交通量—密度的关系
上图中由坐标原点A向曲线上任一点画矢径，矢 径的斜率表示区段平均车速。而其切线的斜率则表示 交通量微小变化时速度的变化：
Q v
K
v Q K
同时，上图中在A点的斜率最大，表示车速最高， 交通量与车流密度均很小，车辆以自由流速度Vf行驶。
7.3 交通量—密度的关系
直线关系模型 1933年，Greenshields提出了KV单段式直线关
系模型：
VabK
当车流密度很大或很小时不适宜使用此模型。
7.2 速度—密度的关系
速 度(km /h)
行 驶 时 ( 间m in/km )
车头间距 hd (m)
A V f =77.4
60
30
15 12 9
0.78
64.4
B
0.93
)
V40ln180/K
Kj 180辆km
Vm 40kmh 时通过的交通量最大
)
7.4 交通量—速度的关系
流量—速度曲线图
7.4 交通量—速度的关系
算例2
已知某公路上畅行速度 Vf 80kmh ，阻塞密度Kj 100辆/km， 速度—密度关系为直线关系。试问：
（1）该路段上期望得到的最大交通量是多少？ （2）此时所对应的车速是多少？
（1）最大交通量：Qm
Vf K 4
j
Qm8041002000辆h
7.3 交通量—密度的关系
特征描述
流 量Q (辆/h) 车 间 时 距ht (s)
Qm =2400 2000
1600 1200
800 400
A
车头间距hd (m)
60 30
15 12
C
B
9 1.5 1.8
Байду номын сангаас
Vt VB Vc=Vm
D 3.0
VD
4.5
不拥挤 拥挤
9.0
E
31
62
93 K j=124
Km
（2）交通量最大时，对应的车速：
Vm
Vf 2
Vm
80 2
40km
h
7.4 交通量—速度的关系
算例3
对某路上的交通流进行观测，发现速度与密度的关 系是对数关系：V40ln180/K，式中车速单位为km/h， 密度单位为：辆/km。试问该路段阻塞密度是多少？车 速为何值时交通流量最大？
V
Vm
ln( K j K
第七章 交通流量、速度和密度 之间的关系
7.1 三参数之间的关系
假设交通流为自由流。在长度为L的路段上有连续行 进的N辆车，其速度V，如下图。由三个参数的定义可 知：
V
A1
2
NB
KN
t L
L
V
QN t
Q
N t
N L
V
Q NV L
Q KV
7.1 三参数之间的关系
交通流量、速度、密度三参数关系图
7.2 速度—密度的关系