平行四边形、菱形、矩形、正方形性质和判定归纳如表
平行四边形、矩形、菱形、正方形定义 性质和判定归纳表
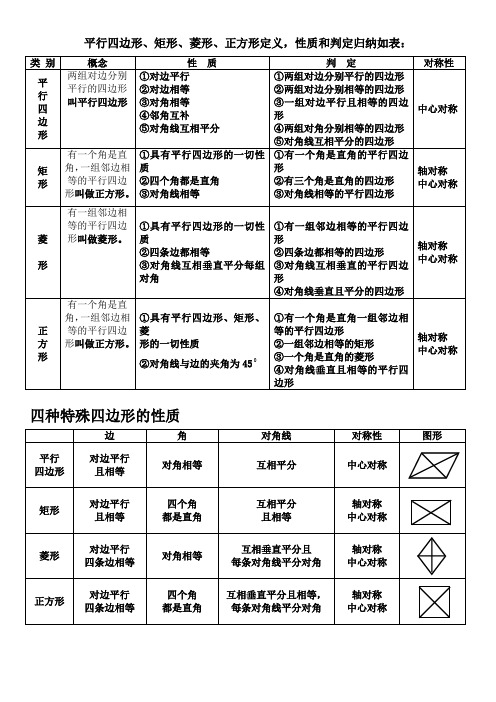
平行四边形、矩形、菱形、正方形定义,性质和判定归纳如表:类别概念性质判定对称性平行四边形两组对边分别平行的四边形叫平行四边形①对边平行②对边相等③对角相等④邻角互补⑤对角线互相平分①两组对边分别平行的四边形②两组对边分别相等的四边形③一组对边平行且相等的四边形④两组对角分别相等的四边形⑤对角线互相平分的四边形中心对称矩形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形的一切性质②四个角都是直角③对角线相等①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形轴对称中心对称菱形有一组邻边相等的平行四边形叫做菱形。
①具有平行四边形的一切性质②四条边都相等③对角线互相垂直平分每组对角①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形④对角线垂直且平分的四边形轴对称中心对称正方形有一个角是直角,一组邻边相等的平行四边形叫做正方形。
①具有平行四边形、矩形、菱形的一切性质②对角线与边的夹角为450①有一个角是直角一组邻边相等的平行四边形②一组邻边相等的矩形③一个角是直角的菱形④对角线垂直且相等的平行四边形轴对称中心对称四种特殊四边形的性质边角对角线对称性图形平行四边形对边平行且相等对角相等互相平分中心对称矩形对边平行且相等四个角都是直角互相平分且相等轴对称中心对称菱形对边平行四条边相等对角相等互相垂直平分且每条对角线平分对角轴对称中心对称正方形对边平行四条边相等四个角都是直角互相垂直平分且相等,每条对角线平分对角轴对称中心对称。
平行四边形的性质和判定 菱形梯形等腰梯形矩形正方形性质和判定

平行四边形的性质和判定菱形梯形等腰梯形矩形正方形性质和判定平行四边形的性质和判定定义:两组对边分别平行的四边形叫做平行四边形.性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分 .判定:①两组对边分别平行的四边形是平行四边形;②两组对边分别相等的四边形是平行四边形;③两组对角分别相等的四边形是平行四边形;④对角线互相平分的四边形是平行四边形;⑤一组对边平行且相等的四边形是平行四边形 .注意:一组对边平行,一组对角相等的四边形是平行四边形;一组对边平行,另一组对边相等的四边形不一定是平行四边形,如:等腰梯形菱形是四边相等的四边形,属於特殊的平行四边形,除了这些图形的性质之外,它还具有以下性质:对角线互相垂直平分;四条边都相等;对角相等,邻角互补;每条对角线平分一组对角.判定:一组邻边相等的平行四边形是菱形对角线互相垂直的平行四边形是菱形四边相等的四边形是菱形依次连接四边形各边中点所得的四边形称为中点四边形。
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形。
菱形的中点四边形是矩形。
菱形面积:对角线相乘后除二或边长乘高;菱形周界为边长的四倍:顺次连接菱形各边中点为矩形正方形是特殊的菱形梯形是指一组对边平行而另一组对边不平行的四边形。
平行的两边叫做梯形的底,其中长边叫下底;不平行的两边叫腰;两底间的距离叫梯形的高。
一腰垂直于底的梯形叫直角梯形,两腰相等的梯形叫等腰梯形。
梯形的性质及判定:一组对边平行且另一组对边不平行的四边形是梯形,但要判断另一组对边不平行比较困难,一般用一组对边平行且不相等的四边形是梯形来判断。
等腰梯形性质:等腰梯形在同一底上的两个底角相等等腰梯形的两条对角线相等等腰梯形判定:1两腰相等的梯形是等腰梯形;2同一底上的两个角相等的梯形是等腰梯形;3对角线相等的梯形是等腰梯形.梯形的体积计算公式:V=〔S1+S2+开根号(S1*S2)〕/3*H注:V:体积;S1:上表面积;S2:下表面积;H:高。
平行四边形等性质判定归纳表

直角三角形斜边上的中线等于斜边的一半。
平行四边形、菱形、矩形、正方形性质和判定归纳表
图形
性 质
判 定
平行四边形
1两组对边分别平行;
2两组对边分别相等;
3两组对角分别相等;邻角互补。
4两条对角线互相平分;
1两组对边分别平行的四边形是平行四边形;
2两组对边分别相等的四边形是平行四边形;
3一组对边平行且相等的四边形是平行四边形;
4两组对角分别相等的四边形是平行四边形;
5对角线互相平分的四边形是平行四边形。
菱形
1菱形的四条边都相等;
2菱形的对角线互相垂直;
3一条对角线平分一组对角。
4菱形面积=对角线乘积× =底×高
1一组邻边相等的平行四边形是菱形;
2对角线互相垂直的平行四边形是菱形;
3四边都相等的四边形是菱形;
矩形
1矩形的四个角都是直角;
2矩形的对角线相等。
1有一个角是直角的平行四边形是矩形;
2对角线相等的平行四边形是矩形;
3有三个角是直角的四边形是都相等;
3正方形的对角线相等,且互相垂直平分;
4对角线与边的夹角为45度。
1一组邻边相等的矩形是正方形;
2有一个角是直角的菱形是正方形;
3对角线相等的菱形是正方形。
4对角线互相垂直的矩形是正方形。
1.3平行四边形,矩形,菱形,正方形的性质和判定

第三节 平行四边形,矩形,菱形,正方形的性质和判定(一)平行四边形的性质和判定 一.教学重难点:重点:平行四边形的性质证明. 难点:分析、综合思考的方法.二.知识点和考点:1.平行四边形的定义2.平行四边形的性质,面积3.平行四边形的判定4.三角形的中位线及其性质三.知识点讲解考点一: 平行四边形的定义考点二:平行四边形的性质(1)平行四边形的对边相等注:在证明题时使用格式是:∵四边形ABCD 是平行四边形,定义:有两组对边分别平行的四边形叫做平行四边形。
记做例1:如图:在中,如果E F ∥AD ,GH ∥CD ,EF 与GH 相交于点O ,那么图中的平行四边形一共有 ( ) A .4个 B 、5个 C 、8个 D 、9个例2:如图,E 、F 分别是边AD 、BC 上的点,并且AF ∥CE ,求证:∠AFB=∠DEC 。
∴AB=DC,AD=BC例1、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE。
例2.平行四边形的周长等于56cm,两邻边长的比为3:1,那么这个平行四边形较长的边长为(2).平行四边形的对角相等注:在证明题时使用格式是:∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D例1.已知中,E、F是对角线AC上的两点,且AE=CF。
求证:∠ADF=∠CBE。
例2、在中,∠A、∠B的度数之比为5:4,则∠C等于()A、 B、 C、 D、(3)、平行四边形的对角线互相平分注:在证明题时使用格式是:∵四边形ABCD是平行四边形∴OA=OC,OB=OD例3.如图,,过其对角线交点O,引一直线交BC于E,交AD于F,若AB=2.4cm,BC=4cm,OE=1.1cm,求四边形ABEF的周长。
例4.如图,已知:中,AC、BD相交于O点,OE⊥AD于E,OF⊥BC于F,求证:OE=OF。
例5.如图,如果的周长之差为8,而AB:AD=3:2,那么的周长为多少?例6.如图,已知的周长为60cm,对角线AC、BD相交于点O,的周长长8cm,求这个四边形各边长.(4)平行四边形的面积如图(1),,也就是边长×高=ah(2)、同底(等底)同高(等高)的平行四边形面积相等。
菱形矩形平行四边形和正方形的判定和定理

菱形矩形平行四边形和正方形的判定和定理好嘞,今天咱们来聊聊菱形、矩形、平行四边形和正方形这几个几何形状,听起来有点儿像数学课上那些晦涩的定义,但其实它们可有趣多了,就像一场几何的聚会,各有各的特色和风采。
先说说正方形吧,正方形简直是几何界的小可爱,四条边一样长,四个角都直得像刚刚打过铅笔的直角,真是一个方方正正的小家伙。
你想啊,正方形的每一边都能相互“打招呼”,彼此对称,简直就像是一个和谐的小家庭,里面的每个成员都能友好相处。
不仅如此,正方形的对角线也是超级好玩,长短一致,交点正好是中心,真是“家有一老,如有一宝”的感觉。
正方形总是给人一种稳稳当当的安全感,想象一下,你的书桌上放着一张正方形的桌子,摆放整齐,工作起来心里也踏实多了。
再说矩形,这家伙有点像正方形的哥哥,四条边也是直的,不过它就喜欢长得不一样,长边短边各有不同,像极了那种总是和朋友们比拼身高的家伙,长得高高瘦瘦的。
矩形的对角线同样是一对好兄弟,长度相等,分担着各自的职责。
不过呢,矩形也常常被调侃,毕竟它的角虽然直,但不如正方形的可爱。
就像学校里的风云人物,有点儿高冷,但其实心里藏着许多故事。
很多时候,矩形在日常生活中扮演着重要角色,像窗户、门这样大方的形状,给我们的生活带来了便利。
说到平行四边形,哎呀,这个家伙可有意思了,四条边也齐刷刷的,不过对边平行,不同于正方形和矩形。
它就像个爱运动的年轻人,灵活多变,斜斜的看着世界,像在向你展示它的独特风采。
平行四边形的对角线不一定相等,但它的面积可不低。
用一个简单的公式,就能算出它的大小。
平行四边形就像是一种风格,不在乎外表,内涵才是最重要的。
就像那些看似不拘一格的人,反而往往更有魅力。
最后得提提菱形,嘿,这可真是个神奇的家伙。
菱形的四条边都是一样长的,就像是个四面体的明星,爱闪闪发光。
对角线相互垂直交叉,这简直像在跳舞,动感十足。
菱形的形状有点像菱角,水中漂浮,别有一番风味。
很多时候,我们会看到它在装饰中闪现,或者在图案中点缀,仿佛在告诉我们,生活需要点儿花样,别太单调。
矩形、菱形、正方形的性质及判定(四边形)

矩形、菱形、正方形的性质及判定一、知识提要1.矩形定义有一个角是直角的平行四边形叫做矩形;性质①矩形的四个角都是直角;②矩形的对角线相等.判定①有一个角是直角的平行四边形叫做矩形;②对角线相等的平行四边形是矩形;③有三个角是直角的四边形是矩形.2.直角三角形斜边的中线等于斜边长的一半.3.菱形定义有一组邻边相等的平行四边形叫做菱形.性质①菱形的四条边都相等;②菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.判定①有一组邻边相等的平行四边形叫做菱形;②对角线互相垂直的平行四边形是菱形;③四边相等的四边形是菱形.4.菱形的面积等于对角线乘积的一半.5.正方形定义四条边都相等、四个角都是直角的四边形是正方形.性质正方形拥有平行四边形、矩形、菱形的所有性质;判定①由一个角是直角的菱形是正方形;②有一组邻边相等的矩形是正方形.二、精讲精练1.矩形ABCD的对角线AC,BD相交于点O,则边与对角线组成的直角三角形的个数是________.2.(2011浙江)如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( ) A.2条B.4条ODC BA60°C .5条D .6条3. 矩形ABCD 中,AB =2BC ,E 为CD 上一点,且AE =AB ,则∠BEC = ___.4. 已知矩形ABCD ,若它的宽扩大2倍,且它的长缩小四分之一,那么新矩形的面积等于原矩形ABCD 面积的__________.5. (2011四川)下列关于矩形的说法中正确的是( )A .对角线相等的四边形是矩形B .对角线互相平分的四边形是矩形C .矩形的对角线互相垂直且平分D .矩形的对角线相等且互相平分6. (2011江苏)在四边形ABCD 中,AB=DC ,AD=BC .请再添加一个条件,使四边形ABCD 是矩形.你添加的条件是_______________(写出一种即可) 7. (2011山东)如图,△ABC 中,AC 的垂直平分线分别交AC 、AB 于点D 、F ,BE ⊥DF 交DF 的延长线于点E ,已知∠A =30°,BC =2,AF =BF ,则四边形BCDE 的面积是( )A .23B .33C .4D .438. 如图,将□ABCD 的边DC 延长到点E ,使CE =DC ,连接AE ,交BC 于点F .(1)求证:△ABF ≌△ECF(2)若∠AFC =2∠D ,连接AC 、BE .求证:四边形ABEC 是矩形.9. (2011江苏)在菱形ABCD 中,AB=5cm ,则此菱形的周长为( )A. 5cmB. 15cmC. 20cmD. 25cm10. (2011河北)如图,已知菱形ABCD ,其顶点A ,B 在数轴对应的数分别为-4和1,则BC =_______.EFDCBAD CBAHFGE ADBC11. 菱形的一边与两条对角线夹角的差是20°,则菱形的各角的度数为___________.12. (2011重庆)如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC =8,BD =6,过点O 作OH ⊥AB ,垂足为H ,则点O 到边AB 的距离OH =_________.13. 已知菱形周长是24cm ,一个内角为60°,则菱形的面积为______.14. 菱形ABCD 中,AE ⊥BC 于E ,若S 菱形ABCD =24cm 2,则AE =6cm ,则菱形ABCD的边长为_______.15. (2011山东)已知一个菱形的周长是20cm ,两条对角线的比是4:3,则这个菱形的面积是( )A .12cm 2B . 24cm 2C . 48cm 2D . 96cm 2 16. 菱形有____条对称轴,对称轴之间具有________的位置关系. 17. 菱形具有而一般平行四边形不具有的性质是( )A .两组对边分别平行B .两组对边分别相等C .一组邻边相等D .对角线相互平分18. (2011四川)如图,点E 、F 、G 、H 分别是任意四边形ABCD 中AD 、BD 、BC 、CA 的中点,当四边形ABCD 的边至少满足__________条件时,四边形EFGH 是菱形.19. (2011浙江)如图,在□ABCD 中,E 、F 分别为边AB 、CD 的中点,BD 是对角线,过点A 作AG ∥DB 交CB 的延长线于点G . (1)求证:DE ∥BF ;(2)若∠G =90°,求证:四边形DEBF 是菱形.F E B C A D 20. (2011湖州)如图,已知E 、F 分别是□ABCD 的边BC 、AD 上的点,且BE =DF . (1)求证:四边形AECF 是平行四边形;(2)若BC =10, BAC =90,且四边形AECF 是菱形,求BE 的长.21. (2011湖南)下列四边形中,对角线相等且互相垂直平分的是( ) A.平行四边形 B.正方形 C.等腰梯形 D.矩形22. 有一组邻边_______并且有一个角是________的平行四边形,叫做正方形. 23. (2010湖北)已知正方形ABCD ,以CD 为边作等边△CDE ,则∠AED 的度数是 .24. 已知正方形ABCD 中,AC ,BD 交于点O ,OE ⊥BC 于E ,若OE =2,则正方形的面积为____.25. 如图,已知,正方形ABCD 的对角线交于O ,过O 点作OE ⊥OF ,分别交AB 、BC 于E 、F ,若AE =4,CF =3,则EF 等于( )A .7B .5C .4D .326. (2011贵州)如图,点E 是正方形ABCD 内一点,△CDE 是等边三角形,连接EB 、EA ,延长BE 交边AD 于点F . (1)求证: △ADE ≌△BCE ; (2)求∠AFB 的度数.FED CBA FE ODCBA三、测试提高【板块一】菱形的性质1. 若菱形两邻角的比为1:2,周长为24 cm ,则较短对角线的长为_____. 【板块二】菱形的判定2. (2011湖南)如图,小聪在作线段AB 的垂直平分线时,他是这样操作的:分别以A 和B 为圆心,大于12AB 的长为半径画弧,两弧相交于C 、D ,则直线CD 即为所求.根据他的作图方法可知四边形ADBC 一定是( ) A .矩形B .菱形C .正方形D .等腰梯形 3. (2011湖北)顺次连接四边形ABCD 各边的中点所得四边形是菱形,则四边形ABCD 一定是( ) A.菱形 B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形【板块三】菱形余矩形的性质4. (2011江苏)菱形具有而矩形不一定具有的性质是( )A .对角线互相垂直B .对角线相等C .对角线互相平分D .对角互补 【板块四】特殊四边形的判定5. 下列命题中,正确命题是( )A .两条对角线相等的四边形是平行四边形;B .两条对角线相等且互相垂直的四边形是矩形;C .两条对角线互相垂直平分的四边形是菱形;D .两条对角线平分且相等的四边形是正方形;四、课后作业1. 矩形ABCD 中,对角线AC ,BD 相交于点O ,∠AOB =60°,若BD =10 cm ,则AD =_____.2. 矩形周长为72cm ,一边中点与对边两个端点连线的夹角为直角,此矩形的长边为_______.3. 矩形的边长为10和15,其中一个内角平分线分长边为两部分,这两部分的长度分别为_________.4. 过矩形ABCD 的顶点D ,作对角线AC 的平行线交BA 的延长线于E ,则△DEB 是( ).A . 不等边三角形B . 等腰三角形C . 等边三角形D . 等腰直角三角形BACD5. 矩形ABCD 的对角线AC 的垂直平分线与边AD ,BC 分别交于E ,F ,则四边形AFCE 是___________.6. 菱形一个内角为120°,平分这个内角的一条对角线长12 cm ,则菱形的周长为_____.7. 若菱形两条对角线长分别为6 cm 和8 cm ,则它的周长是________,面积是_______.8. 菱形的一个角是60°,边长是8 cm ,那么菱形的两条对角线的长分别是_________.9. 已知菱形的一条对角线与边长相等,则菱形的邻角度数分别为_____. 10. 在菱形ABCD 中,AE ⊥BC , AF ⊥CD ,且BE =EC , CF =FD ,则∠AEF 等于_______.11. 如图,小华剪了两条宽为2的纸条,交叉叠放在一起,且它们交角为45°,则它们重叠部分的面积为( ). A.22 B.1 C.332 D.2 12. (2011广东)如图,两条笔直的公路1l 、2l 相交于点O ,村庄C 的村民在公路的旁边建三个加工厂A 、B 、D ,已知AB =BC =CD =DA =5公里,村庄C 到公路1l 的距离为4公里,则村庄C 到公路2l 的距离是( ). A .3公里 B .4公里C .5公里D .6公里13. 正方形的对角线__________且_________,每条对角线平分_____. 14. 如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且AE =AF . 求证:△ACE ≌△ACF .FE BCDA15. (2011山东)如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作直线EF ⊥BD ,分别交AD 、BC 于点E 和点F ,求证:四边形BEDF 是菱形.OFEDCBA。
1.3平行四边形,矩形,菱形,正方形的性质和判定4

苏科
1.3平行四边形,菱形,菱形, 正方形的性质和判定4.
教学目标
• 1.复习菱形的定义;分清菱形与平行四边形 的关系; • 2.会证明菱形的性质,会利用性质解决有关 的数学问题;
动动脑,回忆一下
• 菱形的定义是什么? • 有一组邻边_____的平行四边形叫做菱形; • 根据菱形的定义可知,菱形一定是 ______(图形名称),所以具备这类图形的所 有Hale Waihona Puke 质,而且必定有一组邻边_____;
小结
• 有一组邻边_____的平行四边形叫做菱形; • 性质定理一:菱形的四条边都________; • 性质定理二:菱形的对角线_______,并且每 一条对角线平分_______;
矩形
菱形
平行 四边 形
再回忆一下
• 除了由定义得到的性质,菱形还有哪些性质? • 性质定理一:菱形的四条边都________; • 性质定理二:菱形的对角线_______,并且每 一条对角线平分_______; • 如何证明????
看性质掌握了没有?
• 例一; • 例二;
练练吧
• 练习一; • 练习二; • 练习三;
特殊平行四边形性质及判定方法

特殊平行四边形——菱形、矩形、正方形
【菱形】
定义:有一组邻边相等的平行四边形是菱形
性质:菱形的四条边相等。
菱形的对角线互相垂直。
判定:对角线互相垂直的平行四边形是菱形。
四边相等的四边形是菱形。
有一组邻边相等的平行四边形是菱形。
【矩形】
定义:有一个角是直角的平行四边形叫做矩形。
性质:矩形的四个角都是直角。
矩形的对角线相等。
&&直角三角形斜边上中线等于斜边的一半。
判定:对角线相等的平行四边形是矩形。
有三个角是直角的四边形是矩形。
有一个角是直角的平行四边形叫做矩形。
【正方形】
定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
性质:正方形的四个角都是直角,四条边相等。
正方形的对角线相等且互相垂直平分。
判定:有一组邻边相等的矩形是正方形。
对角线互相垂直的矩形是正方形。
有一个角是直角的菱形是正方形。
对角线相等的菱形是正方形。
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章几个重要的概念
一、两条平行线的距离:
1、定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线的距离。
2、注意:平行线间的距离处处相等。
二、矩形的一条对角线把矩形分成两个直角三角形,与之相联系的性质:
1、直角三角形的两个锐角互余。
2、直角三角形两直角边的平方和等于斜边的平方。
(即勾股定理)
3、直角三角形斜边上的中线等于斜边的一半。
4、直角三角形中30度角所对的直角边等于斜边的一半。
三、三角形中位线
1、定义:
连接三角形两边中点的线段,叫做三角形的中位线
如图,如果D、E、F分别为AB、AC、BC的中点则DE、EF、DF是
三角形的3条中位线。
2、三角形中位线定理:
三角形的中位线平行于第三边(位置关系),
并且等于第三边的一半(数量关系)。
四、梯形中位线定理
1、定义:连接梯形两腰中点的线段叫做梯形的中位线.
2、性质:梯形的中位线平行于两底,并且等于两底和的一半
如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,则
EF∥AD,且EF=(AD+BC)/2。
