弹性力学第七章

其中由于小变形假定，略去了形变的2、3次幂。
物理方程
空间问题的物理方程
可表示为两种形式： ⑴ 应变用应力表示，用于按应力求解方法：
x E1(σx σy σz),
yz
2(1 E
)
yz ,
( x ,y ,z ). (e)
⑵ 应力用应变表示，用于按位移求解方法：
x
E
1
(12
x
),
yz
E
(1 )
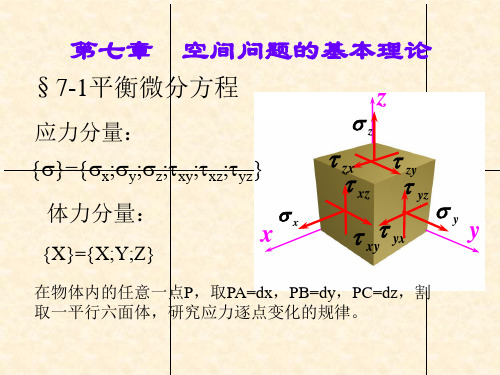
§7-1 平衡微分方程
平衡条件
取出微小的平行六面体，dv d xd yd z，
考虑其平衡条件:
Fx 0,
Fy 0, Fz 0; (a)
Mx 0,
M y 0,
Mz 0. (b)
平衡微分方程
由x 轴向投影的平衡微分方程 F x 0 ,
得
σ x x
yx
y
zx
z
fx
0
,
(x, y, z).
形变中只有 , , z , z , z 0; (a)
位移中只有 u ,uz ,
u 0。
平衡微分方程：
F 0, FZ 0,
σ
z
z
σ
σ
f
0,
σz z
z
z
fz
0.
(b)
而由 F 0, 得出为 σ σ。
几何方程：
其中 u 0， z 0, 几何方程为
所以分别称 Θ1 ,Θ 2 ,Θ 3 为第一、二、 三应力不变量。这些不变量常用于塑性力 学之中。
一点应力状态
6.关于一点应力状态的结论：
(1)6个坐标面上的应力分量完全确定一点 的应力状态。只要6个坐标面上的应力 分量确定了，则通过此点的任何面上的 应力也完全确定并可求出。
(2)一点存在着3个互相垂直的应力主面及 主应力。
空间问题的平衡微分方程精确到三阶 微量 (dxd ydz)。
思考题 z
在图中，若点
o的x向正应力分 量为 σ x ，试表
B dz
示点 A , B 的x向 正应力分量。
dy
y
o dx
A
x
斜面应力
§7-2 物体内任一点的应力状态
在空间问题中，同样需要解决：由直
角坐标的应力分量 σ x … yz…，来求出斜
(c)
因为 x , y , z 轴互相垂直，均为定向， 量纲均为L，所以 x , y , z 坐标具有对等 性，其方程也必然具有对等性。因此，式 (a)的其余两式可通过式(c)的坐标轮换得 到。
平衡微分方程
由3个力矩方程得到3个切应力互等定理，
M x 0 ， yz zy ， (x, y , z) 。 (d)
yz ,
(x ,y , z). ( f )
由物理方程可以导出
1 2 Θ,
（g
E
）
Θ是第一应力不变量，又称为体积应力。
E
1 2
--称为体积模量。
结论
结论：
空间问题的应力，形变，位移等15个未 知函数，它们都是(x ,y ,z)的函数。这些函数 在区域V内必须满足3个平衡微分方程，6个 几何方程及6个物理方程，并在边界上满足3 个应力或位移的边界条件。
标面。所以边界条件也十分简单。
在柱坐标中，坐标分量 , , z 的量
纲、方向性、坐标线的性质不是完全相同 的。因此，相应的方程不具有对等性。
思考题
试由空间轴对称问题的基本方程，简 化导出平面轴对称问题的基本方程。
例题1 试求图示空间弹性体中的应力分量。
(a)正六面体弹性体置于刚体中，上边
界受均布压力q作用，设刚性体与弹性体之
σ 1 , σ 2 , σ 3 （证明见书上）。
5.应力不变量
应力不变量
若从式(c) 求出三个主应力 σ1,σ 2 ,σ3 ，
则式(c)也可以用根式方程表示为，
(σ σ1)(σ σ2 )(σ3 σ ) 0 .
(f )
因式(c) 和( f )是等价的方程，故 σ 的各
幂次系数应相等，从而得出：
代入 p x , p y , p z , 得到：
lσ x m yx n zx lσ ,
m σ y n zy l xy m σ ,
(a )
nσ z
l xz
m yz
nσ.
考虑方向余弦关系式，有
l 2 m2 n2 1.
(b)
结论：式(a) , (b)是求主应力及其方 向余弦的方程。
xy xz
yx
σ y σ
yz
zx zy 0,
σz σ
展开，即得求主应力的方程,
σ3 (σx σy σz)σ2 (σyσz σzσx σxσy y2z z2x x2y)σ (σxσyσz σxy2z σyz2xσzx2y2yzzxxy)0. ( c )
应力主向
3.应力主向
设主应力 σ1 的主向为 l1, m1, n1。代入式 (a)中的前两式，整理后得
(3) 3个主应力包含了此点的最大和最小 正应力。
(4) 一点存在3个应力不变量 Θ1,Θ2 ,Θ3.
(5) 最大和最小切应力为
σ1 σ3 . 2
设σ 1 σ 2 σ 3 ，作用于通过中间
主应力、并且“平分最大和最小正应
力的夹角”的平面上。
几何方程
§7-4 几何方程及物理方程
空间问题的几何方程，可以从平面问 题推广得出：
u , v , w ，则空间问题的位移边界条件
为：
(u )s u , (u,v, w).
(c)
体积应变
体积应变定义为：
d v dv
dv
(d x x d x)(d y y d y )(d z z d z ) d xd yd z
dxd ydz
(1x)(1y)(1z)1
x y z.
(d)
Fx : Fy : Fz : Mx : My : Mz :
a b
a b (τ zx ) z0 d x d y 0,
ab
a b (τ zy ) z0 d x d y 0,
ab
a b (σ z ) z0 d x d y F ; a b
a b (σ z ) z0 y d x d y Fb,
函数。若
x
yz
0
( x,
y, z)，还存在对应的位
移分量，为：
u u0 yz z y,
(x, y, z;u,v, w). (b)
u 0 , v 0 , w 0 --沿x , y , z 向的刚体平移；
x , y , z --绕x , y , z轴的刚体转动。
位移边界条件
若在 su 边界上给定了约束位移分量
由四面体的平衡条件 Fx 0( x, y, z) ，
得出坐标向的应力分量,
px lσx m yx n zx , (x, y, z). (a)
n n
2. 求 p (σ n , n ) 将 p ( px , py , pz ) 向法向 n 投影，即得
σ n lp x mp y np z l2σx m2σy n2σz 2mn yz 2nl zx 2lm xy . (b)
由
p
2
p
2 x
p
2 y
p
2 z
σ
2 n
2 n
,
得
2 n
p
2 x
p
2 y
p
2 z
σ
2 n
.
(c)
n n
从式(b)、(c )可见, 当六个坐标面上的 应力分量确定之后，任一斜面上的应力也 就完全确定了。
应力边界条件
3. 在 sσ 上的应力边界条件
设在 sσ 边界上，给定了面力分量 fx, f y , fz ,
式(d)只用于 sσ边界点上，表示边界面
上的面力与坐标面的应力之间的关系，所 以必须将边界面方程代入式(d)。
斜面应力
§7-3 主应力 最大与最小的应力 1.假设 n 面(l , m , n)为主面，则此斜面上
n 0 , p σn σ. 斜面上沿坐标向的应力分量为：
p x l , p y m , p z n .
x
u x
,
(x, y, z;u,v,w)
(a)
yz
w y
v z
,
(x, y, z;u,v,w)
几何方程
从几何方程同样可得出形变与位移 之间的关系：
⑴ 若位移确定，则形变完全确定。 从数学上看，由位移函数求导数是
完全确定的，故形变完全确定。
几何方程
⑵ 若形变确定，则位移不完全确定。
由形变求位移，要通过积分，会出现待定的
由于面力的主矢量和主矩是给定的， 因此，应力的主矢量和主矩的数值，应等 于面力的主矢量和主矩的数值；
而面力主矢量和主矩的方向，就是 应力主矢量和主矩的方向。应力主矢量 和主矩的正负号和正负方向，则根据应 力的正负号和正负方向来确定。
对于一般的空间问题，列积分的应力 边界条件时，应包括6个条件。对于图示 问题这6个积分的边界条件是：
求主应力
2. 求主应力 σ 将式(a)改写为：
(σ x
xy l
σ )l yx m
(σ y σ)m
zx zy
n n
0, 0,
xzl yz m (σ z σ )n0。
求主应力
上式是求解 l , m , n 的齐次代数方程。由于l , m , n不全为0，所以其系数行列式必须为零，得
σx σ
轴对称问题
§7-5 轴对称问题的基本方程
空间轴对称问题 如果弹性体的几何形状，约束情况和所 受的外力都为轴对称，则应力，形变和位 移也是轴对称的。
采用柱坐标 ( , , z ) 表示。
轴对称问题
对于空间轴对称问题：
所有物理量仅为(ρ,z)的函数。
应力中只有 σ ,σ ,σ z , z , z 0;
则可将微分四面体移动到边界点上，并使斜 面与边界重合。斜面应力分量 ( px , py , pz ) 应 代之为面力分量 ( f x , f y , f z ) ，从而得出空间 问题的应力边界条件:
(lσx myx nzx)s fx , (x, y, z) . (在Sσ上) (d)
注意:
式(b), (c) 用于V内任一点，表示斜面应 力与坐标面应力之间的关系；
εx
1 E
(σ
x
σ
y
σz
)0,
εy
1 E
(σ
y
σ
x
σz
)0,
则可解出：
σ
x
σ
y
1
σ
z
1
q.
例题2
图示的弹性体为 一长柱形体，在顶面 z=0 上有一集中力 F 作用于角点，试写出 z=0 表面上的边界条 件。
aa
P
b
o
b
x
y
z
图7-5
解：本题是空间问题，z=0 的表面是小边 界，可以应用圣维南原理列出应力的边界 条件。即在z=0的表面边界上，使应力的主 矢量和主矩，分别等于面力的主矢量和主 矩，两者数值相等，方向一致。
应力不变量
Θ1
σ1
σ2
σ3
σx
σy
σz
,
Θ2 σ1σ 2 σ 2σ3 σ3σ1 σ yσ z
Θ3
σzσx
σxσ y
τ
2 yz
τ
2 zx
τ
2 xy
,
σ1σ 2σ3 σ xσ yσ z
(g)
σ
x
τ
2 yz
σ
y
τ
2 zx
σ
z
τ
2 xy
2τ yz τ zx τ xy .
式(g)中的各式，左边是不随坐标选择 而变的；而右边各项虽与坐标的选择有 关，但其和也应与坐标选择无关。
yx
m1 l1
zx
n1 l1
(σx
σ1)
0,
(d)
(σ y
σ1)
m1 l1
zy
n1 l1
xy
0.
应力主向
由上两式解出
m1 l1
,
n1 l1
。然后由式(b)得出
l1
1
.
1 ( m1 ) 2 ( n1 ) 2
(e)
l1
l1
再求出 m1 及 n1 。
4. 一点至少存在着三个互相垂直的主应力
第七章 空间问题的基本理论
目录
§7-1 平衡微分方程 §7-2 物体内任一点的应力状态 §7-3 主应力 最大与最小应力 §7-4 几何方程及物理方程 §7-5 轴对称问题的基本方程
在空间问题中，应力、形变和位移等基 本知函数共有15个，且均为x,y,z的函数。
空间问题的基本方程，边界条件，以 及按位移求解和按应力求解的方法，都是 与平面问题相似的。因此，许多问题可以 从平面问题推广得到。
间无摩擦力。
(b)半无限大空间体，其表面受均布压 力q的作用。
q
o
x
q
o
x
z
z
解：图示的(a),(b)两问题是相同的应力 状态：x向与y向的应力、应变和位移都是
相同的，即 σ x σ y 等。
对于(a)，有约束条件 εx εy 0 ；
对于(b)，有对称条件 εx εy 0 。
而两者的 σ z q ，因此，由物理方程：
面(法线为 n ）上的应力。
斜面应力
斜面的全应力p 可表示为两种分量形式： p沿坐标向分量:
p ( px , py , pz ). p沿法向和切向分量:
p (σn , n ).
1. 求 p ( px , py , pz )
px py pz
取出如图的包含斜面
的微分四面体，斜面面积 为ds, 则x面，y面和z面的 面积分别为lds,mds,nds。
u
,
u
,
z
uz
u z
。
z
uz z
,
(c)
物理方程：
应变用应力表示：
1 E
(σ
σ
σ
Z
)，（
,φ,
z
)
z
2(1 E
)
z。
(d)
应力用应变表示：
σ
E
1
( 1 2
)，（ , , z),
(e)
z
E 2(1
) z.
其中
zLeabharlann Baidu
u
u
uz z
。
边界条件： 一般用柱坐标表示时，边界面均为坐