混凝土结构原理3.2混凝土强度理论
混凝土强度理论原理

混凝土强度理论原理一、前言混凝土作为一种重要的建筑材料,广泛应用于各种建筑结构中。
混凝土强度是衡量混凝土质量的重要指标之一。
混凝土强度的理论原理是混凝土学科的重要内容,深入了解混凝土强度理论原理对于提高混凝土的质量、保证工程质量、提高工程安全性具有重要意义。
二、混凝土强度的定义混凝土强度是指混凝土在外力作用下的抵抗能力,即混凝土在承受外力时所能承受的最大应力值。
混凝土强度是由混凝土中的水泥胶体、骨料、空气孔隙等因素共同作用而成的。
混凝土强度通常用抗压强度来表示。
抗压强度是指单位面积的混凝土在受到均匀压力时所能承受的最大压力值。
三、混凝土强度的影响因素混凝土强度受到多种因素的影响,主要包括以下几个方面:1、水胶比:混凝土中水泥胶体与水的比值称为水胶比,水胶比的大小直接影响混凝土的强度。
一般情况下,水胶比越小,混凝土强度越高。
2、骨料:混凝土中的骨料分为粗骨料和细骨料,骨料的种类、质量、形状等因素都会影响混凝土的强度。
一般情况下,骨料的强度越高、形状越好、质量越好,混凝土强度越高。
3、水泥品种:不同品种的水泥在混凝土中的强度表现也不同,例如硅酸盐水泥的强度比普通硅酸盐水泥高。
4、养护条件:混凝土在养护过程中的环境条件直接影响混凝土的强度。
一般情况下,养护环境温度适宜、湿度适宜、养护时间充足,混凝土强度越高。
5、掺合料:混凝土中加入适量的掺合料可以提高混凝土的强度和抗裂性能。
四、混凝土强度的计算方法1、强度试验法:强度试验法是目前混凝土强度计算的主要方法之一。
强度试验法主要分为压缩试验和拉伸试验两种。
其中,压缩试验是目前常用的混凝土强度试验方法,其原理是将试件置于试验机上,在垂直方向施加一定的压力,测量试件的破坏荷载和破坏形态,从而计算出混凝土的抗压强度。
2、理论计算法:理论计算法是通过混凝土的材料力学性质来计算混凝土强度的方法。
理论计算法主要分为弹性理论和塑性理论两种。
其中,弹性理论是最早应用于混凝土强度计算的方法之一,弹性理论认为混凝土在受到外力作用时,只发生弹性变形,即变形与应力之间呈线性关系。
第二章-混凝土结构设计原理
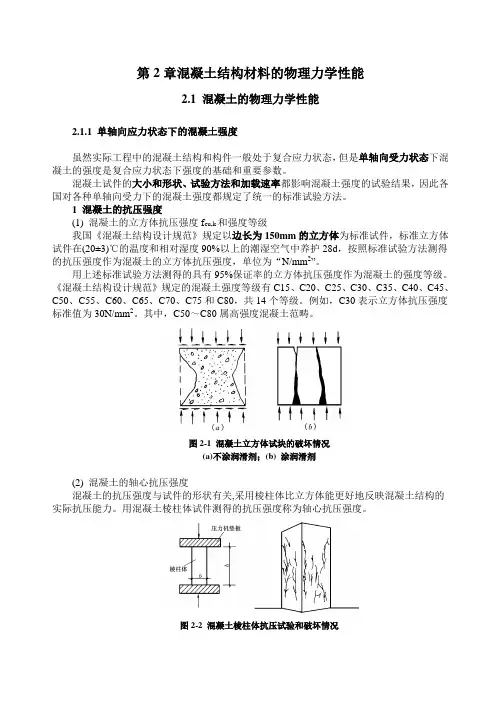
第2章混凝土结构材料的物理力学性能2.1 混凝土的物理力学性能2.1.1 单轴向应力状态下的混凝土强度虽然实际工程中的混凝土结构和构件一般处于复合应力状态,但是单轴向受力状态下混凝土的强度是复合应力状态下强度的基础和重要参数。
混凝土试件的大小和形状、试验方法和加载速率都影响混凝土强度的试验结果,因此各国对各种单轴向受力下的混凝土强度都规定了统一的标准试验方法。
1 混凝土的抗压强度(1) 混凝土的立方体抗压强度f cu,k和强度等级我国《混凝土结构设计规范》规定以边长为150mm的立方体为标准试件,标准立方体试件在(20±3)℃的温度和相对湿度90%以上的潮湿空气中养护28d,按照标准试验方法测得的抗压强度作为混凝土的立方体抗压强度,单位为“N/mm2”。
用上述标准试验方法测得的具有95%保证率的立方体抗压强度作为混凝土的强度等级。
《混凝土结构设计规范》规定的混凝土强度等级有C15、C20、C25、C30、C35、C40、C45、C50、C55、C60、C65、C70、C75和C80,共14个等级。
例如,C30表示立方体抗压强度标准值为30N/mm2。
其中,C50~C80属高强度混凝土范畴。
图2-1 混凝土立方体试块的破坏情况(a)不涂润滑剂;(b) 涂润滑剂(2) 混凝土的轴心抗压强度混凝土的抗压强度与试件的形状有关,采用棱柱体比立方体能更好地反映混凝土结构的实际抗压能力。
用混凝土棱柱体试件测得的抗压强度称为轴心抗压强度。
图2-2 混凝土棱柱体抗压试验和破坏情况我国《普通混凝土力学性能试验方法标准》(GB/T 50081—2002)规定以150mm×150mm×300mm的棱柱体作为混凝土轴心抗压强度试验的标准试件。
《混凝土结构设计规范》规定以上述棱柱体试件试验测得的具有95%保证率的抗压强度为混凝土轴心抗压强度标准值,用符号f ck表示,下标c表示受压,k表示标准值。
《混凝土结构设计原理》电子教案

《混凝土结构设计原理》电子教案第一章:混凝土结构的基本概念1.1 混凝土结构的定义1.2 混凝土结构的特点1.3 混凝土结构的应用范围1.4 混凝土结构的设计原则1.5 混凝土结构的设计流程第二章:混凝土的基本性质2.1 混凝土的组成材料2.2 混凝土的力学性质2.3 混凝土的耐久性2.4 混凝土的变形特性2.5 混凝土的强度理论第三章:混凝土结构的设计方法3.1 结构力学的相关知识3.2 极限状态设计方法3.3 安全系数设计方法3.4 混凝土结构的极限状态方程3.5 混凝土结构的设计计算步骤第四章:梁和板的设计4.1 梁的设计要点4.2 梁的抗弯承载力计算4.3 梁的抗剪承载力计算4.4 板的设计要点4.5 板的抗弯承载力计算第五章:柱和墙的设计5.1 柱的设计要点5.2 柱的轴压承载力计算5.3 柱的抗弯承载力计算5.4 墙的设计要点5.5 墙的抗压承载力计算第六章:混凝土结构的设计规范6.1 国内外主要混凝土结构设计规范简介6.2 设计规范的基本原则和规定6.3 混凝土强度等级和构件尺寸限制6.4 荷载及其组合6.5 结构耐久性和防火要求第七章:钢筋混凝土梁的设计7.1 钢筋混凝土梁的设计流程7.2 抗弯承载力设计7.3 抗剪承载力设计7.4 挠度验算7.5 裂缝宽度验算第八章:钢筋混凝土板的设计8.1 钢筋混凝土板的设计流程8.2 单向板设计8.3 双向板设计8.4 板的翘曲验算8.5 板的构造要求第九章:钢筋混凝土柱和墙的设计9.1 钢筋混凝土柱的设计流程9.2 轴压承载力设计9.3 抗弯承载力设计9.4 抗剪承载力设计9.5 柱和墙的稳定性验算第十章:混凝土结构施工图的解读10.1 施工图的基本构成10.2 结构平面图的解读10.3 结构立面图和剖面图的解读10.4 钢筋图的解读10.5 施工图的变更和修改第十一章:混凝土结构的抗震设计11.1 地震工程基本概念11.2 结构抗震设计原则11.3 地震作用计算11.4 混凝土结构的抗震承载力设计11.5 抗震构造要求第十二章:混凝土结构的加固设计与修复12.1 结构加固的必要性12.2 常见的加固方法12.3 加固设计的计算方法12.4 加固材料的选用12.5 加固施工注意事项第十三章:混凝土结构的经济性分析13.1 结构经济性的重要性13.2 成本分析的基本方法13.3 结构方案的经济比较13.4 材料选择的经济性考虑13.5 施工方案的经济性分析第十四章:计算机在混凝土结构设计中的应用14.1 结构分析软件的介绍14.2 结构分析的基本步骤14.3 参数设置和模型建立14.4 结构分析与设计结果输出14.5 计算机设计在工程实践中的应用案例第十五章:混凝土结构设计的案例分析15.1 案例一:小型混凝土框架结构设计15.2 案例二:高层混凝土剪力墙结构设计15.3 案例三:混凝土连续梁的设计与施工15.4 案例四:混凝土结构的抗震加固设计15.5 案例五:混凝土结构的经济性优化设计重点和难点解析本文档详细介绍了《混凝土结构设计原理》电子教案,共包含十五个章节。
混凝土结构设计原理(第五版)答案2

《混凝土结构设计原理》思考题及习题(参考答案)第3章 按近似概率理论的极限状态设计法思 考 题3.1 结构在规定的时间内,在规定的条件下,完成预定功能的能力称为结构的可靠性。
它包含安全性、适用性、耐久性三个功能要求。
结构超过承载能力极限状态后就不能满足安全性的要求;结构超过正常使用极限状态后就不能保证适用性和耐久性的功能要求。
建筑结构安全等级是根据建筑结构破坏时可能产生的后果严重与否来划分的。
3.2 所有能使结构产生内力或变形的原因统称为作用,荷载则为“作用”中的一种,属于直接作用,其特点是以力的形式出现的。
影响结构可靠性的因素有:1)设计使用年限;2)设计、施工、使用及维护的条件;3)完成预定功能的能力。
结构构件的抗力与构件的几何尺寸、配筋情况、混凝土和钢筋的强度等级等因素有关。
由于材料强度的离散性、构件截面尺寸的施工误差及简化计算时由于近似处理某些系数的误差,使得结构构件的抗力具有不确定的性质,所以抗力是一个随机变量。
3.3 整个结构或构件的一部分超过某一特定状态就不能满足设计指定的某一功能要求,这个特定状态称为该功能的极限状态。
结构的极限状态可分为两类,一类是承载能力极限状态,即结构或构件达到最大承载能力或者达到不适于继续承载的变形状态。
另一类是正常使用极限状态,即结构或构件达到正常使用或耐久性能中某项规定限值的状态。
3.4 建筑结构应该满足安全性、适用性和耐久性的功能要求。
结构的设计工作寿命是指设计规定的结构或结构构件不需进行大修即可按其预定目的使用的时期,它可按《建筑结构可靠度设计统一标准》确定,业主可提出要求,经主管部门批准,也可按业主的要求确定。
结构超过其设计工作寿命并不意味着不能再使用,只是其完成预定功能的能力越来越差了。
3.5 正态分布概率密度曲线主要有平均值μ和标准差σ两个数字特征。
μ越大,表示曲线离纵轴越远;σ越大,表示数据越分散,曲线扁而平;反之,则数据越集中,曲线高而窄。
混凝土结构设计原理

混凝土结构设计原理
绪论
分析方法:有限元方法 软件:ANSYS ADINA MAPLE 桥梁博士
可靠度方面:从经验到概率 - 1950年经验性的允许应力法 -1960年半经验半概率极限状态 -1970年以概率论为基础的极限状态
混凝土结构设计原理
绪论
§0.6 符号体系
采用主体符号或带上、下标的主体符号。如
混凝土结构设计原理
绪论
0.9.2 N+2考核方式:
N: 期中测验40分 小论文10分
2: 笔记10分 期末考试40分
混凝土结构设计原理
绪论
0.9.3 《混凝土结构设计原理》 主要参考资料
3个精品教材(国家级精品课程):
湖南大学 沈蒲生 清华大学 叶列平 西安建筑科技大学 梁兴文
配套复习题及学习辅导:
0.8.3 采用教材
沈蒲生主编,梁兴文副主编. 混凝土结构设计原理 (第2版). 北京:高等教育出版社,2005。
混凝土结构设计原理
绪论Βιβλιοθήκη §0.9 其它内容0.9.1 混凝土结构领域目前主要研究的课题 (需要及时更新)
混凝土材料性能的研究 混凝土材料力学模型 混凝土拉、压、弯、剪、扭构件 耐久性研究(钢筋、混凝土) 预应力混凝土构件的设计及施工方法 结构抗震研究
绪论
0.8.2 学习方法
❖ 熟悉材性,以解释现象; ❖ 熟悉设计方法,以便更好掌握设计原理; ❖ 注意与几门力学的联系与区别; ❖ 重视试验,重视实践经验; ❖ 拓宽专业面,重点在建工、桥梁结构; ❖ 适应采用电子文档的教学,记好笔记; ❖ 及时复习,按时做作业; ❖ 平时成绩(作业、测验)与期末考试的比例为N+2。
混凝土结构设计原理
混凝土结构设计原理答案

第2章-思考题2.1 混凝土立方体抗压强度f cu,k 、轴心抗压强度标准值f ck 和抗拉强度标准值f tk 是如何确定的?为什么f ck 低于f cu,k ?f tk 与f cu,k 有何关系?f ck 与f cu,k 有何关系?答:混凝土立方体抗压强度f cu,k :以边长为150mm 的立方体为标准试件,标准立方体试件在(20±3)℃的温度和相对湿度90%以上的潮湿空气中养护28d ,按照标准试验方法测得的具有95%保证率的立方体抗压强度作为混凝土立方体抗压强度标准值。
轴心抗压强度标准值f ck :以150mm ×150mm ×300mm 的棱柱体作为混凝土轴心抗压强度试验的标准试件,棱柱体试件与立方体试件的制作条件与养护条件相同,按照标准试验方法测得的具有95%保证率的抗压强度作为混凝土轴心抗压强度标准值。
轴心抗拉强度标准值f tk :以150mm ×150mm ×300mm 的棱柱体作为混凝土轴心抗拉强度试验的标准试件,棱柱体试件与立方体试件的制作条件与养护条件相同,按照标准试验方法测得的具有95%保证率的抗拉强度作为混凝土轴心抗拉强度标准值。
(我国轴心抗拉强度标准值是以轴拉试验确定,美国和加拿大是以劈拉实验确定)为什么f ck 低于f cu,k :我国规定的标准试验方法是不涂润滑剂的,试件在加载过程中横向变形就会受到加载板的约束(即“套箍作用”),而这种横向约束对于立方体试件而言可以到达试件的中部;由于棱柱体试件的高度较大,试验机压板与试件之间摩擦力对试件高度中部的横向变形的约束影响较小,所以棱柱体试件的抗压强度标准值f ck 都比立方体抗压强度标准值f cu,k 小,并且棱柱体试件高宽比越大,强度越小。
f tk 与f cu,k 的关系:()0.450.55,20.880.3951 1.645tk cu k c f f δα=⨯-⨯2c α-高强砼的脆性折减系数; δ-变异系数。
混凝土结构设计原理讲解
混凝土结构设计原理讲解一、混凝土结构设计的基本原理混凝土结构设计是指根据工程的要求和使用条件,选定合适的混凝土材料和结构形式,通过计算和分析,确定混凝土各部分的尺寸、配筋、荷载和钢筋的数量等设计要素,以保证结构的安全性、经济性和使用功能。
混凝土结构设计的基本原理主要包括以下三个方面:1.力学基础理论:混凝土结构的设计需要基于力学基础理论,包括静力学、动力学、材料力学、结构力学等方面的知识。
力学基础理论是混凝土结构设计的基石,只有掌握了这些理论,才能进行科学合理的设计。
2.工程经验和规范:混凝土结构设计还需要依据工程经验和规范进行,这些经验和规范包括国家和地方的建筑设计规范、混凝土结构设计手册、混凝土标准等。
这些规范是根据实践经验总结的,具有实用性和可靠性,是混凝土结构设计的重要依据。
3.工程实际情况:混凝土结构设计还需要考虑工程实际情况,包括工程的使用条件、地质环境、气候条件、荷载情况等。
只有综合考虑这些实际情况,才能进行合理的混凝土结构设计。
二、混凝土结构设计中的荷载分析荷载是混凝土结构设计中的重要因素,是指作用在结构上的各种力和力矩,包括静载荷、动载荷和温度荷载等。
荷载分析是混凝土结构设计的第一步,主要包括以下内容:1.荷载种类和大小的确定:荷载的种类和大小是混凝土结构设计的基础,需要根据工程的实际情况进行确定。
常见的荷载有自重荷载、活载荷载、风荷载、地震荷载、温度荷载等。
2.荷载分布形式的确定:荷载分布形式是指荷载在结构上的分布情况,包括集中荷载、均布荷载、三角形荷载、梯形荷载等。
荷载分布形式的不同会对结构的受力情况产生重要影响,需要进行合理的分析和计算。
3.荷载组合的确定:荷载组合是指根据工程实际情况,将各种荷载按照一定的比例组合在一起,进行受力分析和计算。
荷载组合需要根据规范的规定进行,以确保结构具有足够的安全性。
三、混凝土结构设计中的材料力学分析混凝土结构设计中的材料力学分析是指对混凝土材料的力学性能进行分析和计算,主要包括以下内容:1.混凝土的强度计算:混凝土的强度是指其抗压和抗拉的能力,需要根据混凝土的配合比、制作工艺、养护条件等进行计算。
混凝土抗剪强度设计值
混凝土抗剪强度设计值1. 引言混凝土结构是现代建筑中常见的一种结构形式,其承受着重大的荷载和力学作用。
在混凝土结构设计中,抗剪强度是一个重要的设计指标,直接影响着结构的安全性和承载能力。
本文将详细介绍混凝土抗剪强度设计值的概念、计算方法以及与之相关的因素。
2. 混凝土抗剪强度设计值的概念混凝土抗剪强度设计值是指在给定荷载作用下,混凝土材料在抗剪破坏前能够承受的最大剪应力。
它是根据结构使用要求和安全性要求来确定的,并且需要满足国家规范中对于混凝土结构设计的相关要求。
3. 混凝土抗剪强度设计值计算方法混凝土抗剪强度设计值可以通过试验或理论计算来确定。
下面将介绍两种常用的计算方法:3.1 直接试验法直接试验法是通过对混凝土试件进行加载试验,测量其抗剪强度来确定设计值。
该方法需要进行大量的试验,包括不同材料、不同配合比和不同尺寸的试件。
试验结果可以通过统计分析得到设计值。
3.2 理论计算法理论计算法是通过混凝土的力学性质和结构的几何形状等参数,利用力学原理进行计算来确定设计值。
常用的理论计算方法有剪应力理论、塑性抗剪承载力理论和极限平衡理论等。
4. 影响混凝土抗剪强度设计值的因素混凝土抗剪强度设计值受到多种因素的影响,下面将介绍其中几个主要因素:4.1 混凝土材料特性混凝土材料的强度、韧性和粘聚力等特性对抗剪强度有重要影响。
其中水灰比、砂率和骨料种类等是影响混凝土抗剪强度的关键参数。
4.2 结构形式与尺寸结构形式和尺寸对混凝土结构的受力状态有直接影响。
例如,梁、柱、板等结构单元的截面形状和尺寸会影响抗剪强度的设计值。
4.3 荷载类型与大小不同荷载类型和大小对混凝土结构的抗剪性能有不同要求。
例如,静荷载和动荷载对混凝土结构的抗剪强度设计值有不同要求。
4.4 环境条件环境条件如温度、湿度和腐蚀等也会影响混凝土结构的抗剪强度。
特殊环境下需考虑这些因素对设计值的影响。
5. 结论混凝土抗剪强度设计值是混凝土结构设计中一个重要的指标,其计算方法需要根据试验或理论计算来确定。
沈蒲生混凝土结构设计原理三版第二章:混凝土结构设计方法
目 录 上一章 下一章 帮 助
2.4.2 结构的安全等级
{
一级: 一级:重要建筑 二级: 二级:一般建筑 三级: 三级:次要建筑
混凝土结构设计原理
第2章
§2.5
结构的可靠度
主 页 目 录
2.5.1 结构的可靠性
指结构的安全性、适用性、耐久性。 指结构的安全性、适用性、耐久性。
上一章
2.5.2 结构的可靠度
μz 平均值
变异系数 δz µz σz
正态分布
= /
{
Z>0,结构可靠; Z>0 结构可靠; Z<0,结构失效; Z<0 结构失效; 0,极限状态。 Z= 0,极限状态。
混凝土结构设计原理
第2章
2.4.2 结构的可靠指标
现行设计方法以概率理论为基础,用可靠指标度量,采 现行设计方法以概率理论为基础,用可靠指标度量, 用多个分项系数表达。 则可靠指标为: 用多个分项系数表达。设 µz = βσ z,则可靠指标为:
β= µ −µ µz = R2 s 2 σz σR +σs
主 页 目 录 上一章 下一章 帮 助
…2-2
式中: 结构抗力的平均值和标准值; 式中: µR、σ R ––– 结构抗力的平均值和标准值; µs、σ s ––– 作用效应的平均值和标准值。 作用效应的平均值和标准值。
混凝土结构设计原理
第2章
混凝土结构设计原理
第2章
2. 组合值 组合值—— 当有两个或两个以上可变荷载同时作用 时的代表值 。 组合值 = ψc ×标准值 3. 频遇值 频遇值——可变荷载可能出现的较大值 但小于标 可变荷载可能出现的较大值,但小于标 可变荷载可能出现的较大值 准值。计算裂缝变形时用。 准值。计算裂缝变形时用。 频遇值 = ψf ×标准值 t/T<0.1
03 混凝土的基本力学性能-001
2、混凝土的本构关系、强度理论
● 应力张量、Haigh-Westergaad坐标系 4) 八面体应力 主应力空间中,主应力轴等倾的八个面围成一个正八面体 作用在等倾面上的应力成为八面体应力
σ oct = τ oct = 1 I (σ 1 + σ 2 + σ 3 ) = 1 = σ m 3 3 1 3
6)断裂力学本构关系——断裂强度因子、J积分绕过裂纹尖端 7)损伤力学本构关系——考虑材料裂化、刚度降低 σ = ( I − D ) : C0 : ε
2、混凝土的本构关系、强度理论
Saenz 模型
σ = E 0ε E0 ε ε − 1+ 2 E ε + s 0 ε 0
σ 11 σ 12 σ 13 σ x τ xy τ xz = τ σ ij = σ σ σ σ τ 22 23 y yz yz 21 σ 31 σ 32 σ 33 τ zx τ zy σ z
ቤተ መጻሕፍቲ ባይዱ
2) 应力不变量
(σ
ij
− σδ ij ) n j = 0
表层下30mm电镜图
1、混凝土力学性能的微观机制
裂纹形成及过程区
• 混凝土力学性能的离散性
• 混凝土力学性能的离散性
•
混凝土单轴力学性能—循环加卸载
单轴应力-应变曲线是循环加载破坏的包 络曲线 加载应力低于50%fc,一般认为不会出 现疲劳破坏
If we unload in the stress range under 50 percent of fc ', the unloading curve exhibits slight nonlinearity. If reloading takes place, a small characteristic hysteresis loop is formed. However, for unloading from stress at above 50 percent of fc ', the unloading-reloading curves exhibit strong nonlinearity, and a significant degradation of stiffness can also be observed.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.2 混凝土强度理论1.混凝土强度理论模型概况2.古典强度理论(1)最大拉应力理论Rankine(1876)● 强度准则:任一主应力方向最大拉应力达到抗拉强度时破坏 ● 原表达式[]t f ≤1σ ● 等效计算式03cos 2=-+t f r ξθ● 标定方法:单轴抗拉强度 (2)最大拉应变理论Mariotto(1682)● 强度准则:某主方向最大拉应变达到极限拉应变时破坏 ● 原表达式()[][]t Eεσσνσε≤+-=32111● 标定方法:单轴受拉破坏应变 (3)最大剪应力理论Tresca(1864)● 强度准则:最大剪应力达到抗剪强度时破坏 ● 原表达式[]2231max tf =≤-=τσστ● 等效计算式023sin =-⎪⎭⎫ ⎝⎛+k r πθ● 标定方法:单轴抗拉强度(4)平均剪应力理论V on Mises(1913)● 强度准则:统计平均剪应力或八面体剪应力达到极限值时破坏 ● 原表达式()()()[][]t oct f k 3231213232221=≤-+-+-=σσσσσστ ● 等效计算式0222=-k r● 标定方法:单轴抗拉强度(5)摩尔—库仑理论Mohr-Coulomb(1900)● 强度准则:破坏强度不仅取决于最大剪应力,还受剪切面上正应力影响 ● 原表达式στσστk +≤-=031max 2(正应力压为正)● 等效计算式0cos 6sin 3cos 3sin 3sin 2=-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++φφπθπθφξc r r● 标定方法:带正应力作用下的抗剪强度(6)Drucker-Prager 理论(1952)● 强度准则:采用V on Mises 理论的圆形偏平面包络线和Mohr-Coulomb理论的直线子午线组合形成破坏包络面 ● 原表达式oct oct k σττ-=0 ● 等效计算式026=-+k r a ξ● 标定方法:单轴抗压强度、单轴抗拉强度 3.基于实验建立的强度理论 (1)Bresler-Pister(1958)● 强度准则:以二次抛物线子午线和圆形偏平面形成旋转抛物面 ● 表达式2⎪⎪⎭⎫ ⎝⎛+-=c oct coctcoctf c f ba f σστ ● 标定方法:采用单轴抗拉强度t f 、单轴抗压强度c f 、二轴等压强度(c cc f f 28.1=) ● 强度计算式20144.14613.1097.0⎪⎪⎭⎫ ⎝⎛--=c octcoctcoctff f σστ (2)Willam-Warnke (3)(1975)● 强度准则:偏平面包络线由6段椭圆弧曲线组成,各段在00=θ和060=θ处连续;00=θ和060=θ处的值采用不同的值t r 和c r ;根据椭圆方程推导建立偏平面曲线方程:()()()()()()22222222222cos 445cos 42cos 2c t t ccr t t c c t c t c c r r r r r r r r r r r r r r r r -+--+--+-=θθθθ子午线为直线,组合形成直线椭圆组合的破坏包络面。
● 表达式⎪⎪⎭⎫⎝⎛⋅-=c m c mf r f σρθτ11)( ● 标定方法采用单轴抗拉强度t f 、单轴抗压强度c f 、二轴等压强度cc f(3)Reimann (1965)● 强度准则采用抛物线子午线和弧形偏平面包络线组合形成破坏包络面● 表达式c f r b f r a f c c c c c +⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=2ξc r r φ=(4)Ottosen(1977)● 强度准则基于薄膜比拟法,在等边三角形边框上覆盖薄膜,给薄膜施加均匀压力,使其受拉鼓胀,形成的曲面薄膜(由基准面的三角形截面慢慢过度到圆形截面)类似混凝土破坏面,由薄膜的二阶偏微分方程求解得到混凝土的破坏面。
● 表达式011222=-++ccc f I bf J f J a λ当()⎥⎦⎤⎢⎣⎡≤-θλθ3cos cos 31cos 302110k k =时,当()⎥⎦⎤⎢⎣⎡-->-θπλθ3cos cos 313cos 302110k k =时,● 标定采用单轴抗拉强度t f 、单轴抗压强度c f 、二轴等压强度(c cc f f 16.1-=)和常规三轴抗压强度(4,0.5,6021=-==cc f J f I θ)联合确定● 强度准则在Ottosen 模型的基础上,通过两项修正(去除复杂的λ计算式、引入最大主拉应力1σ对混凝土强度的影响),形成组合曲面破坏包络面● 表达式0111222=-+++cccc f I df cf J bf J aσ ● 基本特征是古典强度理论的广义形式当t c f f c d b a ====,0时,为最大主应力理论; 当0===d c a 时,为统计剪应力理论; 当0==c a 时,为Drucker-Prager 理论。
● 标定采用单轴抗拉强度t f 、单轴抗压强度c f 、二轴等压强度(c cc f f 15.1-=)和常规三轴抗压强度(96.1,85.5,60210=-==cc f J f I θ)联合标定。
● 强度计算式012312.01412.99714.00108.211222=-+++c c c cf I f f J f J σ (6)Willam-Warnke (5)(1975)● 强度准则偏平面包络线由6段椭圆弧曲线组成,各段在00=θ和060=θ处连续;00=θ和060=θ处的值采用不同的值t r 和c r ;根据椭圆方程推导建立偏平面曲线方程:()()()()()()22222222222cos 445cos 42cos 2c t t ccr t t c c t c t c c r r r r r r r r r r r r r r r r -+--+--+-=θθθθ子午线为抛物线,组合形成抛物线椭圆组合的破坏包络面。
● 表达式22100,0⎪⎪⎭⎫⎝⎛++==cmc mc mt f a f a a f σστθ 22100,60⎪⎪⎭⎫ ⎝⎛++==cmc mcmcf b f b b f σστθ ● 标定采用单轴抗拉强度c t f f 15.0=、单轴抗压强度c f 、二轴等压强度c cc f f 8.1=和高静水压三轴抗压强度(5.1,67.3,00=-==cmcmf f τσθ;94.1,12.2,600=-==cmcmf f τσθ)联合标定。
● 强度计算式2003785.052553.0081143.0,0⎪⎪⎭⎫⎝⎛--==cm c m c mtf f f σστθ 2007305.076444.011845.0,60⎪⎪⎭⎫ ⎝⎛--==cmc mcmcf f f σστθ (7)Kotsovos(1979)● 强度准则采用Willam-Warnke 的组合椭圆偏平面包络线、幂函数子午线组合形成椭圆组合截面的指数形破坏包络面● 表达式bc oct ctoct f c a f ⎪⎪⎭⎫⎝⎛-==στθ,0,0 ec oct ccoct f c d f ⎪⎪⎭⎫ ⎝⎛-==στθ,0,60 ● 标定不采用强度特征值标定,而直接采用若干实验数据通过最小二乘法拟合得到待定参数。
(8)Podgorski(1985)● 强度准则采用Ottosen 理论的基本形式,将其主应力不变量改为八面体应力描述。
● 表达式02210=++-oct oct oct c P c c ττσ()⎥⎦⎤⎢⎣⎡-=-βθα3cos cos 31cos 1p● 标定采用单轴抗拉强度c t f f 1.0=、单轴抗压强度c f 、二轴等压强度(c cc f f 1.1=)、三轴等拉强度(t ttt f f =),以及剪子午线(1:5.0:0::,301110--==σσσθ)上的二轴受压强度(c cc f f 25.1=)联合标定。
(9)过-王(1990)● 强度准则采用幂函数作为破坏包络面曲线方程 ● 表达式dc b a ⎪⎪⎭⎫ ⎝⎛--=000σστ()()25.15.1sin 5.1cos θθc t c c c +=其中:coctf σσ=0,coctf ττ=● 特点——参数的物理意义a ——当-∞=0σ时,a ==m ax ,00ττ,代表高静水压时偏平面包络线为半径为a 的圆。
b ——当b =0σ时,00=τ,破坏包络面与静水压力轴相交与三轴等拉应力点,可以得到:ttttf f b =c ——偏平面包络线至静水压力轴的距离(半径), 当00=θ时,t c c =,拉子午线半径 当060=θ时,c c c =,压子午线半径d ——子午线幂函数指数,当10<<d 时,在b =0σ处,∞=∂∂0στ,说明子午线切线在b =0σ处与静水压力轴垂直(破坏包络面在b =0σ的切平面)● 标定参数采用单轴抗拉强度c t f f 1.0=、单轴抗压强度c f -、二轴等压强度(c cc f f 28.1-=)、三轴等拉强度(t t t t f f 9.0=),以及常规三轴受压强度(7.2,0.4,600=-==coctcoctf f τσθ),通过迭代计算。
● 强度计算式9297.000009.09638.6⎪⎪⎭⎫ ⎝⎛--=σστc()()25.15.1sin 3319.75.1cos 2445.12θθ+=c● 拉压子午线方程 拉子午线:00=θ,9297.00002445.1209.09638.6⎪⎪⎭⎫ ⎝⎛--=σστt压子午线:060=θ,9297.00003319.709.09638.6⎪⎪⎭⎫ ⎝⎛--=σστt拉压子午线八面体剪应力比值:9297.000002445.123319.7⎪⎪⎭⎫ ⎝⎛--=σσττc t偏平面包络线形状: 当b =0σ时,618.000=ctττ,微凸光滑三角形 当-∞=0σ时,0.100=ctττ,圆形 4. 混凝土强度特征值及及统一标定强度理论表达式混凝土强度准则统一表达式(c oct f σσ=0,c oct f ττ=0)混凝土强度准则统一表达式(c oct f σσ=0,c oct f ττ=0)混凝土强度准则统一表达式(c oct f σσ=0,c oct f ττ=0)5.强度理论的评价。
