矩形菱形正方形练习题.docx
中考数学总复习《矩形、菱形、正方形》专项测试卷含答案
中考数学总复习《矩形、菱形、正方形》专项测试卷含答案学校:___________班级：___________姓名：___________考号：___________A层·基础过关1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是( )A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D2.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是( )A.点O为矩形ABCD的对称中心B.点O为线段AB的对称中心C.直线BD为矩形ABCD的对称轴D.直线AC为线段BD的对称轴3.如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为( )A.20°B.60°C.70°D.80°4.(2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )A.AB=ADB.AC⊥BDC.AC=BDD.∠ACB=∠ACD5.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为( )A.12B.1C.√32D.√36.(2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC=°.7.(2024·龙东)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件,使得菱形ABCD为正方形.8.(2024·遂宁)康康在学习了矩形定义及判定定理1后,继续探究其他判定定理.(1)实践与操作①任意作两条相交的直线,交点记为O;②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA,OB,OC,OD;③顺次连接所得的四点得到四边形ABCD.于是可以直接判定四边形ABCD是平行四边形,则该判定定理是:.(2)猜想与证明通过和同伴交流,他们一致认为四边形ABCD是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.已知:如图,四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.B层·能力提升9.(2024·泸州)如图,在边长为6的正方形ABCD中,点E,F分别是边AB,BC上的动点,且满足AE=BF,AF与DE交于点O,点M是DF的中点,G是边AB上的点,AG=2GB,则OM+1FG的最小值是( )2A.4B.5C.8D.1010.(2024·贵州)如图,在菱形ABCD中,点E,F分别是BC,CD的中点,连接AE,AF.若sin∠EAF=4,AE=5,则AB的长为.511.(2024·天津)如图,正方形ABCD的边长为3√2,对角线AC,BD相交于点O,点E 在CA的延长线上,OE=5,连接DE.(1)线段AE的长为;(2)若F为DE的中点,则线段AF的长为.C层·挑战冲A+12.(2024·济宁)综合与实践某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中,AB>AD且AB足够长)进行探究活动.【动手操作】如图2,第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.第三步,连接GF.【探究发现】根据以上操作,甲、乙两同学分别写出了一个结论.甲同学的结论:四边形AEFD是正方形.乙同学的结论:tan∠AFG=1.3(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.【继续探究】在上面操作的基础上,丙同学继续操作.如图3,第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.第五步,连接FM交GP于点N.根据以上操作,丁同学写出了一个正确结论:FN·AM=GN·AD.(2)请证明这个结论.参考答案A层·基础过关1.在四边形ABCD中,AD∥BC,AB=CD.下列说法能使四边形ABCD为矩形的是(C)A.AB∥CDB.AD=BCC.∠A=∠BD.∠A=∠D2.如图所示,在矩形ABCD中,AB>AD,AC与BD相交于点O,下列说法正确的是(A)A.点O为矩形ABCD的对称中心B.点O为线段AB的对称中心C.直线BD为矩形ABCD的对称轴D.直线AC为线段BD的对称轴3.如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为(C)A.20°B.60°C.70°D.80°4.(2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是(C)A.AB=ADB.AC⊥BDC.AC=BDD.∠ACB=∠ACD5.如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为(D)A.12B.1C.√32D.√36.(2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC=57°.7.(2024·龙东)如图,在菱形ABCD中,对角线AC,BD相交于点O,请添加一个条件AC=BD(答案不唯一),使得菱形ABCD为正方形.8.(2024·遂宁)康康在学习了矩形定义及判定定理1后,继续探究其他判定定理.(1)实践与操作①任意作两条相交的直线,交点记为O;②以点O为圆心,适当长为半径画弧,在两条直线上分别截取相等的四条线段OA,OB,OC,OD;③顺次连接所得的四点得到四边形ABCD.于是可以直接判定四边形ABCD是平行四边形,则该判定定理是:.【解析】(1)∵OA=OC,OB=OD∴四边形ABCD的对角线互相平分∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).答案:对角线互相平分的四边形是平行四边形(2)猜想与证明通过和同伴交流,他们一致认为四边形ABCD是矩形,于是猜想得到了矩形的另外一种判定方法:对角线相等的平行四边形是矩形.并写出了以下已知、求证,请你完成证明过程.已知:如图,四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.【解析】(2)∵四边形ABCD 是平行四边形 ∴AD =BC∴在△BAD 和△ABC 中,{AB =BAAD =BC BD =AC∴△BAD ≌△ABC (SSS) ∴∠BAD =∠ABC ∵AD ∥BC∴∠BAD +∠ABC =180° ∴∠BAD =∠ABC =90°∴四边形ABCD 是矩形(有一个角是直角的平行四边形是矩形).B 层·能力提升9.(2024·泸州)如图,在边长为6的正方形ABCD 中,点E ,F 分别是边AB ,BC 上的动点,且满足AE =BF ,AF 与DE 交于点O ,点M 是DF 的中点,G 是边AB 上的点,AG =2GB ,则OM +12FG 的最小值是(B)A .4B .5C .8D .1010.(2024·贵州)如图,在菱形ABCD 中,点E ,F 分别是BC ,CD 的中点,连接AE ,AF .若sin ∠EAF =45,AE =5,则AB 的长为2√653.11.(2024·天津)如图,正方形ABCD的边长为3√2,对角线AC,BD相交于点O,点E 在CA的延长线上,OE=5,连接DE.(1)线段AE的长为2;.(2)若F为DE的中点,则线段AF的长为√102C层·挑战冲A+12.(2024·济宁)综合与实践某校数学课外活动小组用一张矩形纸片(如图1,矩形ABCD中,AB>AD且AB足够长)进行探究活动.【动手操作】如图2,第一步,沿点A所在直线折叠,使点D落在AB上的点E处,折痕为AF,连接EF,把纸片展平.第二步,把四边形AEFD折叠,使点A与点E重合,点D与点F重合,折痕为GH,再把纸片展平.第三步,连接GF.【探究发现】根据以上操作,甲、乙两同学分别写出了一个结论.甲同学的结论:四边形AEFD是正方形.乙同学的结论:tan∠AFG=1.3(1)请分别判断甲、乙两同学的结论是否正确.若正确,写出证明过程;若不正确,请说明理由.【继续探究】在上面操作的基础上,丙同学继续操作.如图3,第四步,沿点G所在直线折叠,使点F落在AB上的点M处,折痕为GP,连接PM,把纸片展平.第五步,连接FM交GP于点N.根据以上操作,丁同学写出了一个正确结论:FN·AM=GN·AD.(2)请证明这个结论.【解析】(1)甲同学和乙同学的结论都正确,证明如下∵四边形ABCD是矩形∴∠D=∠BAD=90°∵折叠,∴∠D=∠AEF=90°=∠DAE,AD=AE,∴四边形AEFD是正方形;故甲同学的结论正确.过点G作GK⊥AF于点K设AE=2x,则AG=EG=x ∵四边形AEFD是正方形∴∠EAF=45°∴AF=2√2x,AK=KG=√22AG=√22x∴KF=AF-AK=3√22x∴tan∠AFG=KGKF =1 3 ;故乙同学的结论也正确.(2)方法一:过点G作GQ⊥PM,交PM的延长线于点Q∵折叠∴FP=PM,FG=GM,GH=GQ,∠FPG=∠MPG,PH=PQ∵AB∥CD,∴∠FPG=∠PGM∴∠PGM=∠MPG∴PM=GM∴PF=GM=PM=FG∴四边形FGMP是菱形∴∠FNG=90°∵∠GQP=90°=∠FNG,∠FGN=∠GPQ∴△GFN∽△PGQ∴FNGQ =GN PQ∴FN·PQ=GN·GQ∵AM=AG+GM=HF+FP=PH∴AM=PQ∵GQ=GH=AD∴FN·AM=GN·AD.方法二:连接DM,证△ADM∽△NFG也可.。
初中数学 矩形、菱形与正方形测试题含答案
矩形、菱形与正方形测试题一、选择题1．能判定四边形ABCD为平行四边形的题设是（）．（A）AB∥CD，AD=BC; （B）∠A=∠B，∠C=∠D;（C）AB=CD，AD=BC; （D）AB=AD，CB=CD2．在给定的条件中，能画出平行四边形的是（）．（A）以60cm为一条对角线，20cm、34cm为两条邻边;（B）以6cm、10cm为对角线，8cm为一边;（C）以20cm、36cm为对角线，22cm为一边;（D）以6cm为一条对角线，3cm、10cm为两条邻边3．正方形具有而菱形不一定具有的性质是（）（A）对角线互相平分; （B）对角线相等;（C）对角线平分一组对角; （D）对角线互相垂直4．在下列说法中不正确的是（）（A）两条对角线互相垂直的矩形是正方形;（B）两条对角线相等的菱形是正方形;（C）两条对角线垂直且相等的平行四边形是正方形;（D）两条对角线垂直且相等的四边形是正方形5．下列说法不正确的是（）（A）对角线相等且互相平分的四边形是矩形;（B）对角线互相垂直平分的四边形是菱形;（C）一组对边平行且不等的四边形是梯形;（D）一边上的两角相等的梯形是等腰梯形6．不能判定四边形ABCD为平行四边形的题设是（）（A）AB=CD，AD=BC （B）AB//CD（C）AB=CD，AD∥BC （D）AB∥CD，AD∥BC7．四边形ABCD的对角线AC，BD相交于点O，能判定它为正方形的题设是（）（A）AO=CO，BO=DO; （B）AO=CO=BO=DO;（C）AO=CO，BO=DO，AC⊥BD; （D）AO=BO=CO=DO，AC⊥BD8．下列说法不正确的是（）（A）只有一组对边平行的四边形是梯形;（B）只有一组对边相等的梯形是等腰梯形;（C）等腰梯形的对角线相等且互相平分;（D）在直角梯形中有且只有两个角是直角9．如图1，在□ABCD中，MN分别是AB、CD的中点，BD分别交AN、CM于点P、Q，在结论：①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S △ADP=14S ABCD中，正确的个数为（）．（A）1 （B）2 （C）3 （D）4(1) (2) (3)10．如图2，在梯形ABCD中，AD∥CB，AD=2，BC=8，AC=6，BD=8，则梯形ABCD的面积为（）．（A）24 （B）20 （C）16 （D）12二、填空题11．在□ABCD中，AC与BD交于O，则其中共有_____对全等的三角形．12．矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20cm，则其对角线长为_______，矩形的面积为________．13．一个菱形的两条对角线长分别为6cm，8cm，这个菱形的边长为_______，•面积S=______．14．如果一个四边形的四个角的比是3：5：5：7，则这个四边形是_____形．15．如图3，等腰梯形ABCD中，AD∥BC，AB∥DE，BC=8，AB=6，AD=5，则△CDE的周长是________．16．如图4，在正方形ABCD的外侧，作等边△ADE，则∠AEB=_______．(4) (5) (6)17．在长为1.6m，宽为1.2m的矩形铅板上，剪切如图5所示的直角梯形零件（•尺寸单位为mm），则这块铅板最多能剪出______个这样的零件．18．如图6，ABCD中，过对角线交点O，引一直线交BC于E，交AD于F，若AB=2.4cm，BC=4cm，OE=1.1cm，则四边形CDFE周长为________．19．已知等腰梯形的一个锐角等于60•°，•它两底分别为15cm，•49cm，•则腰长为_______．20．已知等腰梯形ABCD中AD∥BC，BD平分∠ABC，BD•⊥DC，•且梯形ABCD•的周长为30cm，则AD=_____．三、计算题21．如图，已知等腰梯形ABCD中，AD∥BC，对角线AC⊥BD，AD=3cm，BC=7cm，•DE•⊥BC 于E，试求DE的长．四、证明题22．如图，已知四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA边上的中点，求证：四边形EFGH是菱形．23．已知如图，梯形ABCD中，AD∥BC，AM=MB，DN=NC．求证：MN∥BC，MN=12（BC+AD）．答案:1．（C） 2．（C） 3．（B） 4．（D） 5．（D）6．（C） 7．（D） 8．（C） 9．（C） 10．（A）11．4 12．40cm 4003cm213．5cm 24cm2 14．直角梯形15．15 16．15° •17．12 18．8.6cm 19．34cm20．如图，作AE⊥BC于E，DF⊥BC于F，∴AD=EF，设BE=x．则AB=2x，DC=2x，FC=x，∴BD平分∠ABC，∴∠DBC=30°．∴DC=12BC，∴BC=4x．∴EF=2x=AD．又∵AB+BC+CD+AD=30，∴4x+6x=30，x=3，∴AD=6（cm）．21．过D点作DF∥AC，交BC的延长线于点F，则四边形ACFD为平行四边形，•所以AC=DF，AD=CF．因为四边形ABCD为等腰梯形，所以AC=BD，所以BD=DF，又已知AC⊥BD，DF∥AC，•所以BD⊥DF，则△BDF为等腰直角三角形．又因为DF⊥BC，所以DE=12BF=12（BC+CF）=12（BC+AD）=12（7+3）=5（cm）．22．证明：∵E、F、G、H分别是AB、BC、CD、DA的中点，∴EF=12AC，HG=12AC，FG=12BD，EH=12BD．∴EF=HG=12AC，FG=EH=12BD．又∵AC=BD，∴EF=HG=FG=EH．∴四边形EFGH是菱形．23．证明：如图，连接AN并延长，交BC的延长线于点E．∵DN=NC，∠1=∠2，∠D=∠3，∴△ADN≌△ECN，∴AN=EN，AD=EC．又AM=MB，∴MN是△ABE的中位线．∴MN∥BC，MN=12BE（三角形中位线定理）∵BE=BC+CE=BC+AD，∴MN=12（BC+AD）．。
(完整word版)矩形菱形正方形练习题及答案
矩形的习题精选一、性质1、下列性中，矩形具有而质平行四边形不一定具有的是（）A、对边相等B、对角相等C、对角线相等D、对边平行2.在矩形ABCD中，∠AOD=130°，则∠ACB=_ _3.已知矩形的一条对角线长是8cm，两条对角线的一个交角为60°，则矩形的周长为______4.矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm，对角线是13cm，那么矩形的周长是____________5.如图所示，矩形ABCD中，AE⊥BD于E，∠BAE=30°，BE=1cm，那么DE的长为_____6、直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积为___7、已知，在Rt△ABC中，BD为斜边AC上的中线，若∠A=35°，那么∠DBC= 。
8、如图，矩形ABCD中，AC与BD交于O点，BE⊥AC于E，CF⊥BD 于F.求证：BE=CF. AB E FO9.如图，△ABC中，∠ACB=90度，点D、E分别为AC、AB的中点，点F在BC延长线上，且∠CDF=∠A，求证：四边形DECF是平行四边形；10.已知:如图，在△ABC中，∠BAC≠90°∠ABC=2∠C，AD⊥AC，交BC或CB的延长线D。
试说明:DC=2AB.11、在△ABC中，∠C=90O，AC=BC，AD=BD，PE⊥AC于点E，PF ⊥BC于点F。
求证：DE=DF二、判定1、下列检查一个门框是否为矩形的方法中正确的是（C ）A．测量两条对角线，是否相等B．测量两条对角线，是否互相平分C．用曲尺测量门框的三个角，是否都是直角D．用曲尺测量对角线，是否互相垂直2、平行四边形ABCD，E是CD的中点，△ABE是等边三角形，求证：四边形ABCD是矩形3、在平行四边形ABCD中，对角线AC、BD相交于O，EF过点O，且AF⊥BC，求证：四边形AFCE是矩形4、平行四边形ABCD中，对角线AC、BD相交于点Ｏ，点Ｐ是四边形外一点，且PA⊥PC，PB⊥PD，垂足为Ｐ。
中考数学专题训练：矩形、菱形、正方形(附参考答案)
中考数学专题训练：矩形、菱形、正方形（附参考答案）1．下列命题正确的是( )A ．正方形的对角线相等且互相平分B ．对角互补的四边形是平行四边形C ．矩形的对角线互相垂直D ．一组邻边相等的四边形是菱形2．如图，D ，E ，F 分别是△ABC 各边的中点，则以下说法错误的是( )A ．△BDE 和△DCF 的面积相等B ．四边形AEDF 是平行四边形C ．若AB ＝BC ，则四边形AEDF 是菱形D ．若∠A ＝90°，则四边形AEDF 是矩形3．如图，在正方形ABCD 中，E ，F 分别是AB ，BC 的中点，CE ，DF 交于点G ，连接AG .下列结论：①CE ＝DF ；②CE ⊥DF ；③∠AGE ＝∠CDF .其中正确的结论是( )A ．①②B ．①③C ．②③D ．①②③4．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，E 为BC 的中点，连接EO 并延长交AD 于点F ，∠ABC ＝60°，BC ＝2AB .下列结论：①AB ⊥AC ；②AD ＝4OE ；③四边形AECF 是菱形；④S △BOE ＝14S △ABC .其中正确结论的个数是( )A ．4B ．3C ．2D ．15．如图，在矩形ABCD中，AB＝6 cm，BC＝9 cm，点E，F分别在边AB，BC上，AE＝2 cm，BD，EF交于点G.若G是EF的中点，则BG的长为______cm.6．如图，在菱形ABCD中，AC，BD为菱形的对角线，∠DBC＝60°，BD＝10，点F为BC的中点，则EF的长为_____．7．已知四边形ABCD是正方形，点E在边DA的延长线上，连接CE交AB于点G，过点B作BM⊥CE，垂足为点M，BM的延长线交AD于点F，交CD的延长线于点H.(1)如图1，求证：CE＝BH；(2)如图2，若AE＝AB，连接CF，在不添加任何辅助线情况下，请直接写出图2中的四个三角形(△AEG除外)，使写出的每个三角形都与△AEG全等．8．如图，在菱形ABCD中，E，F，G，H分别是AB，BC，CD，AD上的点，且BE ＝BF＝CG＝AH.若菱形的面积等于24，BD＝8，则EF＋GH＝_____．9．如图，在矩形ABCD中，点E在DC上，DE＝BE，AC与BD相交于点O，BE与AC相交于点F.(1)若BE平分∠CBD，求证：BF⊥AC；(2)找出图中与△OBF相似的三角形，并说明理由；(3)若OF＝3，EF＝2，求DE的长度．10．(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G.求证：△ADE∽△DCF.【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC 到点H，使CH＝DE，连接DH.求证：∠ADF＝∠H.【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．参考答案1．A 2．C 3．A 4．D5．√13 6．5 7．(1)证明略 (2)略8．6解析：如图，连接AC ，交BD 于点O ，∵四边形ABCD 是菱形，BD ＝8，∴AB ＝BC ＝AD ＝CD ，AC ⊥BD ，AO ＝OC ＝12AC ，BO ＝OD ＝12BD ＝4. ∵S 菱形ABCD ＝12AC ·BD ＝24，∴AC ＝6，∴AO ＝3，∴AB ＝√AO 2+BO 2＝5＝AD .∵BE ＝BF ＝CG ＝AH ，∴AE ＝CF ＝DH ＝DG ，∴BE AE ＝BF CF ，∴EF ∥AC .同理可得GH ∥AC ，设BE ＝BF ＝CG ＝AH ＝a ，则有DH ＝5－a ，∵EF ∥AC ，∴△BEF ∽△BAC ，∴BE AB ＝EF AC ，即a 5＝EF 6，∴EF ＝65a ，同理可得DH DA ＝GH CA ，即5−a 5＝GH 6，∴GH ＝6－65a ，∴EF ＋GH ＝6.9．(1)证明略(2)与△OBF相似的三角形有△ECF，△BAF，理由略(3)DE＝3＋√1910．(1)证明：∵四边形ABCD是矩形，∴∠C＝∠ADE＝90°，∴∠CDF＋∠DFC＝90°.∵AE⊥DF，∴∠DGE＝90°，∴∠CDF＋∠AED＝90°，∴∠AED＝∠DFC，∴△ADE∽△DCF.(2)证明：∵四边形ABCD是正方形，∴AD＝DC，AD∥BC，∠ADE＝∠DCF＝90°.∵AE＝DF，∴Rt△ADE≌Rt△DCF(HL)，∴DE＝CF.∵CH＝DE，∴CF＝CH.∵点H在BC的延长线上，∴∠DCH＝∠DCF＝90°.又∵DC＝DC，∴△DCF≌△DCH(SAS)，∴∠DFC＝∠H.∵AD∥BC，∴∠ADF＝∠DFC，∴∠ADF＝∠H.(3)解：如图3，延长BC至点G，使CG＝DE＝8，连接DG，∵四边形ABCD是菱形，∴AD＝DC，AD∥BC，∴∠ADE＝∠DCG，∴△ADE≌△DCG(SAS)，∴∠DGC＝∠AED＝60°，AE＝DG. ∵AE＝DF，∴DG＝DF，∴△DFG是等边三角形，∴FG＝DF＝11.∵CF＋CG＝FG，∴CF＝FG－CG＝11－8＝3，即CF的长为3.。
矩形、菱形、正方形练习题
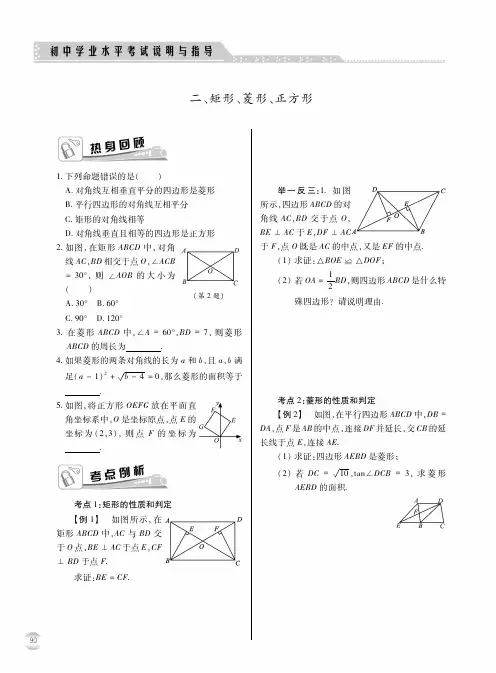
（第１ 题） （第２ 题）
２． 如图，在菱形ＡＢＣＤ中，Ｅ 是ＡＢ 边上一点，且
有下列结论： ∠Ａ ＝ ∠ＥＤＦ ＝ ６０°．
①ＡＥ ＝
； ＢＦ ②△ＤＥＦ 是等边三角形；③△ＢＥＦ 是等
腰三角形；④∠ＡＤＥ ＝ ∠ＢＥＦ． 其中结论正 ９１
确的个数是（ ）
Ａ． ３ Ｂ． ４ Ｃ． １ Ｄ． ２
．
考点２：菱形的性质和判定 【例２】 如图，在平行四边形ＡＢＣＤ 中，ＤＢ ＝ ＤＡ，点Ｆ 是ＡＢ 的中点，连接ＤＦ 并延长，交ＣＢ 的延 长线于点Ｅ，连接ＡＥ． （１）求证：四边形ＡＥＢＤ 是菱形；
（２）若ＤＣ ＝ 槡， １０ ｔａｎ∠ＤＣＢ ＝ ３，求菱形 ＡＥＢＤ 的面积．
考点１：矩形的性质和判定
△ＡＤＥ 绕点Ｅ 旋转１８０°，得到
（２）求证：四边形ＣＢＥＧ 是正方形．
，连接 ， △ＣＦＥ
ＡＦ ＣＤ．
（１）求证：四边形ＡＤＣＦ
是菱形；
（２）若ＢＣ ＝ ，８ ＡＣ ＝ ６，求四边形ＡＢＣＦ 的周
长．
考点３：正方形的性质与判定 【例３】 如图，在正方形 ＡＢＣＤ 中，Ｅ 为ＣＤ 边上一点，Ｆ 为 ＢＣ 延长线上一点，且ＣＥ ＝ ＣＦ． （１）求证：△ＢＣＥ ； ≌△ＤＣＦ （２）若∠ＦＤＣ ＝ ，求 ３０° ∠ＢＥＦ 的度数．
５． 如图，在矩形纸片ＡＢＣＤ
中，ＡＢ ＝ ，４ ＢＣ ＝ ６， 将
△ＡＢＣ 沿ＡＣ 折叠，使点Ｂ
落在点Ｅ 处，ＣＥ 交ＡＤ 于
点Ｆ，则ＤＦ 的长等于 （第５ 题）
．
６． 如图，已知正方形ＡＢＣＤ 的边 长为５，点Ｅ，Ｆ 分别在ＡＤ，ＤＣ 上， ， 与 相交 ＡＥ ＝ ＤＦ ＝ ２ ＢＥ ＡＦ 于点Ｇ，点Ｈ 为ＢＦ 的中点，连 接ＧＨ，则ＧＨ 的长为 ． （第６ 题）
(完整word版)矩形菱形正方形练习题及答案
矩形的习题精选性质1、下列性中，矩形具有而质平行四边形不一定具有的是（）A、对边相等B、对角相等C、对角线相等D、对边平行2. 在矩形ABCD 中，/ AOD=130 °，则/ ACB=_ _3•已知矩形的一条对角线长是8cm，两条对角线的一个交角为60 °,则矩形的周长为_______4•矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86cm，对角线是13cm，那么矩形的周长是 _______________ 5•如图所示，矩形ABCD中，AE丄BD于E,/ BAE=30BE=1cm，那么DE的长为_______6、直角三角形斜边上的高与中线分别是5cm和6cm，则它的面积为7、已知，在Rt△ ABC中，BD为斜边AC上的中线，若/A=35 °，那么 / DBC=&如图，矩形ABCD中，AC与BD交于O点，BE丄AC于E, CF丄BD于F.求证：BE=CF.9•如图，△ ABC 中，/ ACB=90度，点D 、E 分别为AC 、AB 的中点，点 F 在BC 延长线上，且/ CDF= / A ，求证：四边形DECF 是平行四边形；F c B10.已知：如图，在△ ABC 中，/ BAC 工90°/ ABC=2 / C , AD 丄 AC ，交11、在厶 ABC 中，/ C=90O , AC=BC , AD=BD , PE 丄 AC 于点 E , PF、判定1、下列检查一个门框是否为矩形的方法中正确的是（ C ） C .用曲尺测量门框的三个角， 是否都是直角 是否互相垂直2、平行四边形 ABCD , E 是CD 的中点，△ ABE 是等边三角形，求证:四边形ABCD 是矩形BC 或CB 的延长线 D 。
试说明：DC=2AB.丄BC 于点F 。
求证：DE=DFA .测量两条对角线，是否相等 是否互相平分B .测量两条对角线，D .用曲尺测量对角线,A3、在平行四边形 ABCD 中，对角线 AC 、BD 相交于O , EF 过点0,且4、平行四边形 ABCD 中，对角线AC 、BD 相交于点O,点P 是四边形外 一点，且PA 丄PC , PB 丄PD ，垂足为P 。
(完整版)矩形菱形与正方形测试题及答案
第19章 矩形、菱形与正方形测试题一、选择题（每小题3分，共30分）1、关于四边形ABCD ①两组对边分别平行；②两组对边分别相等；③有一组对边平行且相等；④对角线AC 和BD 相等；以上四个条件中可以判定四边形ABCD 是平行四边形的有（ ）。
（A ） 1个 （B ）2个 （C ）3个 （D ）4个2、若顺次连结四边形ABCD 各边中点所得四边形是矩形，则四边形ABCD 必定是（ ）A 、菱形B 、对角线相互垂直的四边形C 、正方形D 、对角线相等的四边形 3、如图1，大正方形中有2个小正方形，如果它们的面积分别是S 1、S 2，那么S 1、S 2的大小关系是（ ）A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定 4、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为（ ）A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 2 5、如图2，菱形花坛 ABCD 的边长为 6m ，∠B ＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长（粗线部分）为（ ） A.123m B.20m C.22m D.24m6、如图3，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是( ) A ．3B ．23C ．5D ．257、如图4，在宽为20m ，长为30m 的矩形地面上修建两条同样宽的道路，余下部分作为耕地. 根据图中数据，计算耕地的面积为( )A ．600m 2B ．551m 2C ．550 m 2D ．500m 28、如图5，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD 的面积比是 （ ）A.3∶4B.5∶8C.9∶16D.1∶29、如图6，矩形ABCD 中，DE ⊥AC 于E ，且∠ADE ：∠EDC=3：2，则∠BDE 的度数为 （ ）A 、36oB 、9oC 、27oD 、18o图41m1m30m 20mFEDCBA图3图2图110、如图7，是由两个正方形组成的长方形花坛ABCD ，小明从顶点A 沿着花坛间小路直到走到长边中点O ，再从中点O 走到正方形OCDF 的中心O 1，再从中心O 1走到正方形O 1GFH 的中心O 2，又从中心O 2走到正方形O 2IHJ 的中心O 3，再从中心O 3走2走到正方形O 3KJP 的中心O 4，一共走了31 2 m ，则长方形花坛ABCD 的周长是（ ）A.36 mB.48mC.96 mD.60 m二、填空题（每小题3分，共30分）11，如图8, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于＿＿＿.12，如图9，过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ，那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2（填“＞”或“＜”或“＝”）.13，如图10，四边形ABCD 是正方形，P 在CD 上，△ADP 旋转后能够与△ABP ′重合，若AB ＝3，DP ＝1，则PP ′＝＿＿＿.14，已知菱形有一个锐角为60°，一条对角线长为6cm ，则其面积为＿＿＿cm 2. 15，如图11，在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为＿＿＿.16，如图12，四边形ABCD 的两条对角线AC 、BD 互相垂直，A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC ＝8，BD ＝10，那么四边形A 1B 1C 1D 1的面积为＿＿＿.17，如图13，□ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，AB CD 图5图7图12 A 1 B 1C 1D 1 D AB C D A B C E F 图13 D CB A 图8 图10图9 KN M Q C B图11 E D C BA 图6点A 正好落在CD 上的点F ，若△FDE 的周长为8，△FCB 的周长为22，则FC 的长为＿＿＿.18，将一张长方形的纸对折,如图14所示，可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕，那么对折四次可以得到 条折痕，如果对折n 次，可以得到 条折痕.19、如图15，已知AB ∥DC ，AE ⊥DC ，AE ＝12，BD ＝15，AC ＝20, 则梯形ABCD 的面积为＿＿＿.20、在直线l 上依次摆放着七个正方形(如图16所示).已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4，则S 1＋S 2＋S 3＋S 4＝＿＿＿.三、解答题21、（8分）如图17，把一张长方形ABCD 的纸片沿EF 折叠后，ED 与BC 的交点为G ，点D 、C 分别落在D ′、C ′的位置上，若∠EFG=55°，求∠AEG 和∠EGB 的度数。
矩形、菱形与正方形-专题训练(含答案)(可编辑修改word版)
3矩形、菱形与正方形专题训练(含答案)班级姓名成绩一、选择题(每小题3 分，共30 分)1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B′ 处，若AE＝2，DE ＝6，∠EFB＝60°，则矩形ABCD 的面积是( )A．12 B．24 C．12 D．16第1 题图第2 题图第3 题图第4 题图2.如图，菱形ABCD 中，∠B＝60°，AB＝4，则以AC 为边长的正方形ACEF 的周长为( ) A．14 B．15 C．16 D．173.如图，将矩形ABCD 沿对角线BD 折叠，使点C 与点C′重合．若AB＝2，则C′D 的长为( ) A．1 B．2 C．3 D．44.如图，在△ABC 中，AC＝BC，点D，E 分别是边AB，AC 的中点．将△ADE 绕点E 旋转180°得△CFE，则四边形ADCF 一定是( )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD 的周长为16 cm，AC，BD 相交于点O，OE⊥AC 交AD 于点E，则△DCE 的周长为( )A．4 cm B．6 cm C．8 cm D．10 cm第6 题图第9 题图第10 题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( )A．3∶1 B．4∶1 C．5∶1 D．6∶138.用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9.如图，边长为6 的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( )A．16 B．17 C．18 D．1910.如图，F 为正方形ABCD 的边AD 上一点，CE⊥CF 交AB 的延长线于点E，若正方形ABCD 的面积为64，△CEF 的面积为50，则△CBE 的面积为( )A．20 B．24 C．25 D．26二、填空题(每小题3 分，共24 分)11.如图所示，在菱形ABCD 中，∠ADC＝72°，AD 的垂直平分线交对角线BD 于点P，垂足为点E，连结CP，则∠CPB＝度．第11 题图第12 题图第14 题图第15 题图12.如图，四边形ABCD 的两条对角线AC，BD 互相垂直，A1，B1，C1，D1分别是四边形ABCD 各边中点，如果AC＝8，BD＝10，则四边形A1B1C1D1的面积为．13.矩形的对角线相交成的角中，有一个角是60°，这个角所对的边长为20 cm，则其对角线长为-_，矩形的面积为．14.如图，四边形ABCD 是菱形，对角线AC 和BD 相交于点O，AC＝4 cm，BD＝8 cm，则这个菱形的面积是cm2.15.如图，矩形ABCD 中，点E，F 分别是AB，CD 的中点，连结DE 和BF，分别取DE，BF 的中点M，N，连结AM，CN，MN，若AB＝2 2，BC＝2 3，则图中阴影部分的面积为．,第16 题图第17 题第18 题图16.如图，▱ABCD 的对角线相交于点O，请你添加一个条件，使▱ABCD 是矩形．17.如图，正方形ABCD 中，对角线AC，BD 交于点O，E 点在BC 上，EG⊥OB，EF⊥OC，垂足分别为点G，F，AC＝10，则EG＋EF＝．18.如图，在平面直角坐标系中，矩形OABC 的顶点A，C 的坐标分别为(10，0)，(0，4)，点D是OA 的中点，点P 在BC 上运动，当△ODP 是腰长为5 的等腰三角形时，点P 的坐标为．三、解答题(共66 分)19．(6 分)如图，已知矩形ABCD 中，E是AD 上一点，F是AB 上一点，EF⊥EC 且EF＝EC，DE＝4 cm，矩形ABCD 的周长为32 cm，求AE 的长．20．(8 分)如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M，与BD 相交于点O，与BC 相交于点N，连结BM，DN.(1)求证：四边形BMDN 是菱形；(2)若AB＝4，AD＝8，求MD 的长．21．(8 分)如图所示，矩形ABCD 中，AE⊥BD 于点E，∠DAE∶∠BAE＝3∶1，求∠BAE 和∠EAO的度数．22．(10 分)如图，已知菱形ABCD 中，AB＝AC，E，F 分别是BC，AD 的中点，连结AE，CF. (1)证明：四边形AECF 是矩形；(2)若AB＝8，求菱形ABCD 的面积．23．(12 分)如图，已知四边形ABCD 是平行四边形，DE⊥AB，DF⊥BC，垂足分别是点E，F，并且DE＝DF，求证：(1)△ADE≌△CDF；(2)四边形ABCD 是菱形．24．(10 分)在四边形ABCD 中，AB＝CD，M，N，P，Q 分别是AD，BC，BD，AC 的中点，求证：MN 与PQ 互相垂直平分．参考答案一、选择题(每小题3 分，共30 分)1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B′ 处，若AE＝2，DE ＝6，∠EFB＝60°，则矩形ABCD 的面积是( D )A．12 B．24 C．12 D．16第1 题图第2 题图第3 题图第4 题图2.如图，菱形ABCD 中，∠B＝60°，AB＝4，则以AC 为边长的正方形ACEF 的周长为( C ) A．14 B．15 C．16 D．173.如图，将矩形ABCD 沿对角线BD 折叠，使点C 与点C′重合．若AB＝2，则C′D 的长为( B ) A．1 B．2 C．3 D．44.如图，在△ABC 中，AC＝BC，点D，E 分别是边AB，AC 的中点．将△ADE 绕点E 旋转180°得△CFE，则四边形ADCF 一定是( A )A．矩形B．菱形C．正方形D．梯形5．由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是( B )A．平行四边形B．矩形C．菱形D．正方形6．如图，▱ABCD 的周长为16 cm，AC，BD 相交于点O，OE⊥AC 交AD 于点E，则△DCE 的周长为( C )A．4 cm B．6 cm C．8 cm D．10 cm第6 题图第9 题图第10 题图7．菱形的周长为8 cm，高为1 cm，则菱形两邻角度数比为( C )A．3∶1 B．4∶1 C．5∶1 D．6∶18.用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是( D )A．①④⑤B．②⑤⑥C．①②③D．①②⑤9.如图，边长为6 的大正方形中有两个小正方形，若两个小正方形的面积分别为S1，S2，则S1＋S2的值为( B )A．16 B．17 C．18 D．1910.如图，F 为正方形ABCD 的边AD 上一点，CE⊥CF 交AB 的延长线于点E，若正方形ABCD 的面积为64，△CEF 的面积为50，则△CBE 的面积为( B )A ．20B ．24C ．25D ．26二、填空题(每小题 3 分，共 24 分)11. 如图所示，在菱形 ABCD 中，∠ADC ＝72°，AD 的垂直平分线交对角线 BD 于点 P ，垂足为点E ，连结 CP ，则∠CPB ＝ 72 度．第 11 题图 第 12 题图 第 14 题图 第 15 题图12. 如图，四边形 ABCD 的两条对角线 AC ，BD 互相垂直，A 1，B 1，C 1，D 1 分别是四边形 ABCD各边中点，如果 AC ＝8，BD ＝10，则四边形 A 1B 1C 1D 1 的面积为 20 ．13. 矩形的对角线相交成的角中，有一个角是 60°，这个角所对的边长为 20 cm ，则其对角线长为40_cm ，矩形的面积为 400_cm 2 ．14. 如图，四边形 ABCD 是菱形，对角线 AC 和 BD 相交于点 O ，AC ＝4 cm ，BD ＝8 cm ，则这个菱形的面积是 16 cm 2.15. 如图，矩形 ABCD 中，点 E ，F 分别是 AB ，CD 的中点，连结 DE 和 BF ，分别取 DE ，BF 的中点 M ，N ，连结 AM ，CN ，MN ，若 AB ＝2，BC ＝2，则图中阴影部分的面积为 2 ．,第 16 题图 第 17 题 第 18 题图16. 如图，▱ABCD 的对角线相交于点 O ，请你添加一个条件 AO ＝BO (答案不唯一)，使▱ABCD是矩形．17. 如图，正方形 ABCD 中，对角线 AC ，BD 交于点 O ，E 点在 BC 上，EG ⊥OB ，EF ⊥OC ，垂足分别为点 G ，F ，AC ＝10，则 EG ＋EF ＝ 5 ．18. 如图，在平面直角坐标系中，矩形 OABC 的顶点 A ，C 的坐标分别为(10，0)，(0，4)，点 D是O A 三、解答题(共 66 分)19．(6 分)如图，已知矩形 ABCD 中，E 是 AD 上一点，F 是 AB 上一点，EF ⊥EC 且 EF ＝EC ，DE ＝4 cm ，矩形 ABCD 的周长为 32 cm ，求 AE 的长．解：∵∠AFE＋∠AEF＝∠AEF＋∠CED＝90°，∴∠AFE＝∠DEC.又∵∠A＝∠D＝90°，EF＝EC，∴△AEF≌△DCE，∴AE＝CD.设AE＝x，则CD＝x，∴AD＋CD＝1×32，即x＋4＋x＝16，2∴x＝6.即AE＝6 cm20．(8 分)如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M，与BD 相交于点O，与BC 相交于点N，连结BM，DN.(1)求证：四边形BMDN 是菱形；(2)若AB＝4，AD＝8，求MD 的长．解：(1)∵MN 是BD 的垂直平分线，∴BO＝DO，∠BON＝∠DOM＝90°.∵四边形ABCD 是矩形，∴AD∥BC，∴∠BNO＝∠DMO，∴△BON≌△DOM(AAS)，∴OM＝ON.∵OB＝OD，∴四边形BMDN 是平行四边形．∵MN⊥BD，∴▱BMDN 是菱形(2)设MD＝x，则MB＝x，MA＝8－x，在Rt△ABM 中，∵BM2＝AM2＋AB2，∴x2＝(8－x)2＋42，解得x＝5.∴MD 的长为521．(8 分)如图所示，矩形ABCD 中，AE⊥BD 于点E，∠DAE∶∠BAE＝3∶1，求∠BAE 和∠EAO 的度数．解：提示：由∠DAE∶∠BAE＝3∶1，求出∠BAE＝22.5°，而∠ABD＝90°－∠BAE＝90°－22.5°＝67.5°，∵∠BAO＝∠ABD＝67.5°，∴∠EAO＝∠BAO－∠BAE＝67.5°－22.5°＝45°22．(10 分)如图，已知菱形ABCD 中，AB＝AC，E，F 分别是BC，AD 的中点，连结AE，CF.(1)证明：四边形AECF 是矩形；(2)若AB＝8，求菱形ABCD 的面积．解：(1)∵四边形ABCD 是菱形，∴AB＝BC，又∵AB＝AC，∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE⊥BC(等边三角形三线合一)，∠AEC＝90°.同理，CF⊥AD.∵E，F 分别是BC，AD 的中点，∴AF＝1AD，EC＝1BC.2 2∵四边形ABCD 是菱形，∴AD 綊BC，∴AF 綊EC，∴四边形AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形)．又∵∠AEC＝90°，∴四边形AECF 是矩形(有一个角是直角的平行四边形是矩形) (2)在Rt△ABE 中，∵AE＝＝4，∴S 菱形ABCD＝8×4＝3223．(12 分)如图，已知四边形ABCD 是平行四边形，DE⊥AB，DF⊥BC，垂足分别是点E，F，并且DE＝DF，求证：(1)△ADE≌△CDF；(2)四边形ABCD 是菱形．解：证明：(1)∵四边形ABCD 是平行四边形，∴∠A＝∠C，又∵DE＝DF，DE⊥AB，DF⊥BC，∴∠DEA＝∠DFC＝90°，∴△ADE≌△CDF(AAS) (2)由(1)知AD＝DC，又∵四边形ABCD 是平行四边形，∴四边形ABCD 是菱形24．(10 分)在四边形ABCD 中，AB＝CD，M，N，P，Q 分别是AD，BC，BD，AC 的中点，求证：MN 与PQ 互相垂直平分．解：证明：连结MP，NQ，PN，MQ，∵PM 綊1AB，同理NQ 綊1AB，∴PM 綊NQ，∴四边形MPNQ2 2为平行四边形，又∵PN 綊1CD，而CD＝AB，∴PN＝PM，2∴四边形MPNQ 为菱形，∴MN 与PQ 互相垂直平分。
2024学年八年级数学经典好题专项(矩形、菱形、正方形)练习(附答案)
2024学年八年级数学经典好题专项（矩形、菱形、正方形）练习一、选择题1、菱形不具备的性质是( )A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形2、如图，菱形ABCD 中，∠D ＝150°，则∠1＝( )A ．30°B ．25°C ．20°D ．15°（2题） （3题） （4题）3、如图，在▱ABCD 中，AB ＝BC ，下列结论错误的是( )A ．四边形ABCD 是菱形B ．AB ＝ADC ．AO ＝OC ，BO ＝OD D ．∠BAD ＝∠ABC4、如图所示，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为( )A ．2 3B ．3 3C ．4 3D ．35、如图，菱形ABCD 中，AB=15，∠ADC=120°，则B、D 两点之间的距离为（ ）A．15 B．3215 C．7.5 D．315（5题） （7题） （8题） （9题）6、菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（ ）A．8cm 和cm B．4cm 和cm C．8cm 和cm D．4cm 和cm7、如图，菱形ABCD 的对角线AC ，BD 的长分别为6 cm ，8 cm ，则这个菱形的周长为( )A ．5 cmB ．10 cmC ．14 cmD ．20 cm8、如图，在菱形ABCD 中，∠BAD ＝80°，AB 的垂直平分线交对角线AC 于点F ，垂足为点E ，连接DF ，则∠CDF 等于( )A ．50°B ．60°C ．70°D ．80°9、如图．剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）A．∠ABC=∠ADC,∠BAD=∠BCD B．AB=BC C．AB=CD ,AD=BC D．∠DAB+∠BCD=180º10、如图，在平面直角坐标系中，四边形OABC 为菱形，O(0，0)，A(4，0)，∠AOC ＝60°，则对角线交点E 的坐标为( )A ．(2， 3 )B ．( 3 ，2)C ．( 3 ，3)D ．(3， 3 )（10题） （11题） （12题） （13题）二、填空题11、如图，在△ABC 中，点D ，E ，F 分别在边BC ，AB ，CA 上，且DE ∥CA ，DF ∥BA.小聪认为如果AD平分∠BAC ，那么四边形AEDF 是菱形，小聪的说法 ．(填“正确”或“不正确”)12、在菱形ABCD 中，对角线AC 、BD 相交于点O ，若∠ABC ＝140°，则∠BAD ＝________°，∠ABD ＝________°，∠BCA ＝________°；13、如图，菱形ABCD 的边长为2 cm ，E 是BC 的中点，且AE ⊥BC ，则菱形ABCD 的面积为_____.14、如图，P 是菱形ABCD 的对角线AC 上一点，PE ⊥AD 于点E ，且PE ＝3 cm ，则点P 到AB 的距离为__ __ cm.（14题） （15题） （17题） （20题）15、如图，在菱形ABCD 中，AB ＝5，AO ＝3，点E 在BC 的延长线上，∠E ＝12∠ABC ，DE ＝16、菱形ABCD 的周长为48cm，∠BAD：∠ABC=1：2，则BD=_____，菱形的面积是______．17、如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，若AC ＝8 cm ，BD ＝6 cm ，则该菱形的面积为________cm 2，周长为________cm.18、已知菱形ABCD 的面积为24 cm 2，若对角线AC ＝6 cm ，则这个菱形的边长为____ cm.19、四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为_________20、如图，点P 是边长为1的菱形ABCD 对角线AC 上的一个动点，点M ，N 分别是AB ，BC 边的中点，则MP ＋PN 的最小值是______.三、解答题21、已知：如图，在△ABC 中，CD 平分∠ACB 交AB 于点D ，DE ∥AC 交BC 于点E ，DF ∥BC 交AC于点F. 四边形DECF 是菱形吗？为什么？22、如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝8 cm，BD＝6 cm，DH⊥AB于H.(1)求菱形ABCD的面积；(2)求DH的长．23、如图，在菱形ABCD中，对角线AC与BD相交于点O，BD＝12 cm，AC＝6 cm.求菱形的周长．24、已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD.（1）求证：四边形AODE是矩形；（2）若AB=6，∠BCD=120°，求四边形AODE的面积.25、如图，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF.求证：(1)△ABF≌△DAE；(2)DE＝BF＋EF.26、已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1＝∠2.(1)若CE＝1，求BC的长；(2)求证：AM＝DF＋ME.参考答案一、选择题1、菱形不具备的性质是( B )A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形2、如图，菱形ABCD 中，∠D ＝150°，则∠1＝( D )A ．30°B ．25°C ．20°D ．15°3、如图，在▱ABCD 中，AB ＝BC ，下列结论错误的是( D )A ．四边形ABCD 是菱形B ．AB ＝ADC ．AO ＝OC ，BO ＝OD D ．∠BAD ＝∠ABC4、如图所示，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 的周长为( B )A ．2 3B ．3 3C ．4 3D ．35、如图，菱形ABCD 中，AB=15，∠ADC=120°，则B、D 两点之间的距离为（ A ）A．15 B．3215 C．7.5 D．3156、菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（C ）A．8cm 和cm B．4cm 和cm C．8cm 和cm D．4cm 和cm7、如图，菱形ABCD 的对角线AC ，BD 的长分别为6 cm ，8 cm ，则这个菱形的周长为(D )A ．5 cmB ．10 cmC ．14 cmD ．20 cm8、如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为点E，连接DF，则∠CDF等于( B )A．50° B．60° C．70° D．80°9、如图．剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（ ）A．∠ABC=∠ADC,∠BAD=∠BCD B．AB=BC C．AB=CD ,AD=BC D．∠DAB+∠BCD=180º解析：∵四边形ABCD是用两张等宽的纸条交叉重叠放在一起而组成的图形，∴AB∥CD，AD∥BC, ∴四边形ABCD是平行四边形（对边相互平行的四边形是平行四边形）．过点A分别作BC，CD边上的高为AE，AF，连接AC，则AE=AF(两纸条相同，纸条宽度相同)，∴在平行四边形ABCD中．S△ABC=S△ACD，即BC•AE=CD•AF，∴BC=CD，AB=BC．故B中结论成立；∴平行四边形ABCD为菱形（邻边相等的平行四边形是菱形），∴∠ABC=∠ADC，∠BAD=∠BCD（菱形的对角相等），故A中结论成立；AB=CD，AD=BC（平行四边形的对边相等），故C中结论成立：当四边形ABCD是矩形时，有∠DAB+∠BCD=180º．故D中结论不一定成立，故选D．10、如图，在平面直角坐标系中，四边形OABC为菱形，O(0，0)，A(4，0)，∠AOC＝60°，则对角线交点E的坐标为( D )A．(2， 3 ) B．( 3 ，2) C．( 3 ，3) D．(3， 3 )二、填空题11、如图，在△ABC中，点D，E，F分别在边BC，AB，CA上，且DE∥CA，DF∥BA.小聪认为如果AD平分∠BAC，那么四边形AEDF是菱形，小聪的说法正确．(填“正确”或“不正确”)12、在菱形ABCD中，对角线AC、BD相交于点O，若∠ABC＝140°，则∠BAD＝________°，∠ABD＝________°，∠BCA＝________°；答案：40，70，2013、如图，菱形ABCD的边长为2 cm，E是BC的中点，且AE⊥BC，则菱形ABCD的面积为__2 3 cm2 ____.14、如图，P是菱形ABCD的对角线AC上一点，PE⊥AD于点E，且PE＝3 cm，则点P到AB的距离为__3 __ cm.15、如图，在菱形ABCD中，AB＝5，AO＝3，点E在BC的延长线上，∠E＝12∠ABC，DE＝816、菱形ABCD的周长为48cm，∠BAD：∠ABC=1：2，则BD=_____，菱形的面积是______．217、如图，在菱形ABCD中，对角线AC、BD相交于点O，若AC＝8 cm，BD＝6 cm，则该菱形的面积为________cm2，周长为________cm.答案：24，2018、已知菱形ABCD的面积为24 cm2，若对角线AC＝6 cm，则这个菱形的边长为__5 __ cm.19、四边形ABCD是菱形，∠BAD＝60°，AB＝6，对角线AC与BD相交于点O，点E在AC上，若OE＝3，则CE的长为___43或23______20、如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边的中点，则MP＋PN的最小值是__1 ____.三、解答题21、已知：如图，在△ABC中，CD平分∠ACB交AB于点D，DE∥AC交BC于点E，DF∥BC交AC于点F. 四边形DECF是菱形吗？为什么？解：四边形DECF是菱形．理由如下：∵DE∥FC，DF∥EC，∴四边形DECF为平行四边形．由AC∥DE，知∠2＝∠3. ∵CD平分∠ACB，∴∠1＝∠2，∴∠1＝∠3，∴DE＝EC，∴平行四边形DECF为菱形．22、如图，四边形ABCD是菱形，对角线AC和BD相交于点O，AC＝8 cm，BD＝6 cm，DH⊥AB于H.(1)求菱形ABCD的面积；(2)求DH的长．解：(1)∵四边形ABCD 是菱形，AC ＝8 cm ，BD ＝6 cm ，∴S 菱形ABCD ＝12ACꞏBD ＝12×6×8＝24(cm 2)．(2)∵四边形ABCD 是菱形，∴AC ⊥BD ，OA ＝OC ＝12＝4 cm ，OB ＝OD ＝3 cm ，∴在直角三角形AOB 中，AB ＝OB 2＋OA 2＝32＋42＝5 cm ，∴DH ＝S 菱形ABCD AB ＝4.8 cm.23、如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，BD ＝12 cm ，AC ＝6 cm.求菱形的周长．解：∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝12AC ，BO ＝12 BD.∵AC ＝6 cm ，BD ＝12 cm ， ∴AO ＝3 cm ，BO ＝6 cm.在Rt △ABO 中，由勾股定理，得AB ＝AO 2＋BO 2＝32＋62＝3 5 cm ，∴菱形的周长＝4AB=4×3 5 =12 5 cm.24、已知：如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，DE ∥AC ，AE ∥BD.（1）求证：四边形AODE 是矩形；（2）若AB=6，∠BCD=120°，求四边形AODE 的面积.解答：（1）证明：∵DE ∥AC ，AE ∥BD ，∴四边形AODE 是平行四边形，∵在菱形ABCD 中，AC ⊥BD ，∴ AOD=90 , ∴平行四边形AODE 是是矩形；（2）∵∠BCD=120°，AB ∥CD ，∴∠ABC=180°‐120°=60°，∵AB=BC ，∴△ABC 是等边三角形，∴OA=21×6=3, OD=OB=6×23=33,∴四边形AODE 的面积=OA ∙OD=9325、如图，在菱形ABCD 中，点P 是BC 边上一点，连接AP ，点E ，F 是AP 上的两点，连接DE ，BF ，使得∠AED ＝∠ABC ，∠ABF ＝∠BPF .求证：(1)△ABF ≌△DAE ；(2)DE ＝BF ＋EF .证明：(1)∵四边形ABCD 是菱形，∴AB ＝AD ，AD ∥BC . ∴∠BP A ＝∠DAE .∵∠ABC ＝∠AED ，∴∠BAF ＝∠ADE .∵∠ABF ＝∠BPF ，∠BP A ＝∠DAE ，∴∠ABF ＝∠DAE .∵AB ＝DA ，∴△ABF ≌△DAE (ASA)．(2)∵△ABF ≌△DAE ， ∴BF ＝AE ，AF ＝DE .∵AF ＝AE ＋EF ＝BF ＋EF ，∴DE ＝BF ＋EF .26、已知：如图，在菱形ABCD 中，F 为边BC 的中点，DF 与对角线AC 交于点M ，过M 作ME ⊥CD 于点E ，∠1＝∠2.(1)若CE ＝1，求BC 的长；(2)求证：AM ＝DF ＋ME.(1)解：∵四边形ABCD 是菱形，∴AB ∥CD ，∴∠1＝∠ACD ，∵∠1＝∠2，∴∠ACD ＝∠2，∴MC ＝MD ，∵ME ⊥CD ，∴CD ＝2CE ， ∵CE ＝1，∴CD ＝2，∴BC ＝CD ＝2(2)证明：如图，∵F 为边BC 的中点，∴BF ＝CF ＝12BC ，∴CF ＝CE ，在菱形ABCD 中，AC 平分∠BCD ，∴∠ACB ＝∠ACD ，在△CEM 和△CFM 中，∵⎩⎪⎨⎪⎧CE ＝CF ，∠ACB ＝∠ACD ，CM ＝CM ，∴△CEM ≌△CFM(SAS)，∴ME ＝MF ，延长AB 交DF 的延长线于点G ， ∵AB ∥CD ，∴∠G ＝∠2， ∵∠1＝∠2，∴∠1＝∠G ，∴AM ＝MG ，在△CDF 和△BGF 中，∵⎪⎩⎪⎨⎧=∠=∠∠=∠FC FB DFC GFB G 2,∴△CDF ≌△BGF(AAS)，∴GF ＝DF ， 由图形可知，GM ＝GF ＋MF ，∴AM ＝DF ＋ME。
第19章矩形、菱形和正方形单元测试2021-2022学年华东师大版数学八年级下册(word 含答案)
第19章矩形、菱形和正方形单元测试一.单选题（共10题；共30分）1.取四边形ABCD的各边中点E、F、G、H，依次连结EFGH得到四边形EFGH，现知四边形EFGH是菱形，则四边形ABCD的对角线( )A. 相等B. 相等且平分C. 垂直D. 垂直且平分2.四边形ABCD的对角线AC，BD相交于点O，能判定它为正方形的是（）A. AO=CO，BO=DOB. AO=CO=BO=DOC. AO=CO，BO=DO，AC⊥BDD. AO=BO=CO=DO，AC⊥BD3.如图，矩形ABCD中，AE⊥BD垂足为E，若∠DAE=3∠BAE，则∠EAC的度数为（）A. 67.5°B. 45°C. 22.5°D. 无法确定4.如图，菱形OABC的顶点O在坐标系原点，顶点A在x轴上，∠B=120°，OA=2，将菱形OABC绕原点O顺时针旋转105°至OA′B′C′的位置，则点B′的坐标为（）A. （，）B. （，）C. （2，﹣2）D. （，﹣）5.如图，在平面直角坐标系中，四边形ABCO是正方形，已知点C的坐标为（，1），则点B的坐标为（）A. （﹣1，+1）B. （﹣1，1）C. （1，+1）D. （﹣1，2）6.下列性质中，正方形具有而菱形不一定具有的性质是（）A. 四条边相等B. 对角线互相平分C. 对角线相等D. 对角线互相垂直7.菱形具有而矩形不具有的性质是（）A. 对角线互相平分B. 四条边都相等C. 对角相等D. 邻角互补8.在平面中，下列说法正确的是（）．A. 四边相等的四边形是正方形B. 四个角相等的四边形是矩形C. 对角线相等的四边形是菱形D. 对角线互相垂直的四边形是平行四边形9.如图，ABCD、AEFC都是矩形，而且点B在EF上，这两个矩形的面积分别是S1，S2，则S1，S2的关系是（）A. S1＞S2B. S1＜S2C. S1=S2D. 3S1=2S210.如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是（）A. 90°B. 80°C. 70°D. 60°二.填空题（共8题；共24分）11.如图，已知AD∥BC，AB∥CD，AB=4，BC=6，EF是AC的垂直平分线，分别交AD、AC于E、F，连结CE，则△CDE的周长是________ ．12.如图，由四个直角边分别为5和4的全等直角三角形拼成“赵爽弦图”，其中阴影部分面积为________．13.如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB=2，BC=3，则图中阴影部分的面积为________．14.设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去…根据以上规律，第n个正方形的边长a n=________．15.在四边形ABCD中，∠A=∠B=∠C=∠D，则四边形ABCD是________．16.正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=x+1和x轴上，则点B n的坐标是________ .17.（如图所示）两个长宽分别为7cm、3cm的矩形如图叠放在一起，则图中阴影部分的面积是________．18.如图，正方形ABCD的边长为4，延长CB至点M，使BM=2，过点B作BN⊥AM，垂足为N，O是对角线AC，BD的交点，连接ON，则ON的长为________．三.解答题（共6题；共36分）19.如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．求四边形AEBD的面积．20.如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE等于多少时，四边形CEDF是矩形；②当AE等于多少时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）21.如图所示，在菱形ABCD中，∠BAD=120°，AB=4．求：（1）对角线AC，BD的长；（2）菱形ABCD的面积．22.在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF的值。
(完整版)矩形菱形正方形习题含答案
1. 在一次数学活动课上，张明同学将矩形ABCD 沿直线CE 折叠，顶点B 恰好落在AD 边上F 点处，如图所示，已知8CD =cm ，5BE =cm ，则AD = cm ．2.如图，在菱形ABCD 中，60B ∠=o，点E F ，分别从点B D ，出发以同样的速度沿边BC DC ，向点C 运动．给出以下四个结论：①AE AF =②CEF CFE ∠=∠③当点E F ，分别为边BC DC ，的中点时，AEF △是等边三角形④当点E F ，分别为边BC DC ，的中点时，AEF △的面积最大．上述结论中正确的序号有 ．（把你认为正确的序号都填上）3如图，四边形ABCD 为正方形，ADE △为等边三角形．AC 为正方形ABCD 的对角线，则EAC ∠= 度． 4.如图，过正方形ABCD 的顶点B 作直线l ，过A C ，作l 的垂线，垂足分别为 E F ，．若1AE =，3CF =，则AB 的长度为 ．5如图，正方形ABCD 的边长为4，MN BC ∥分别交AB CD ，于点M N ，，在MN 上任取两点P Q ，，那么图中阴影部分的面积是 ．1. 如图，在菱形ABCD 中，对角线AC BD ，相交于点O E ，为AB 的中点，且OE a =，则菱形ABCD 的周长为（ ） A ．16a B ．12a C ．8a D ．4a 2. 菱形的两条对角线的长分别是6和8 ，则这个菱形的周长是（ ） A ．24 B ．20C ．10D ．53. 如图，在四边形ABCD 中，AD BC ∥，90D ∠=o，若再添加一个条件，就能推出四边形ABCD 是矩形，你所添加的条件是 ．（写出一种情况即可） 4. 如图，在正方形ABCD 中，E 为AB 边的中点，G ，F 分别为AD ，BC 边上的点，若1=AG ，2=BF ，︒=∠90GEF ，则GF 的长为 ．ＦＤ Ａ ＥＣlD M N DD C FG5.如图，在正方形纸片ABCD 中，对角线AC BD ，交于点O ，折叠正方形纸片 ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后，折痕DE 分别交AB AC ，于点E G ，，连结GF ．下列结论：①112.5AGD ∠=o；② tan 2AED ∠=；③AGD OGD S S =△△；④四边形AEFG 是菱形；⑤2BE OG =．则其中正确结论的序号是 ．6. 菱形ABCD 中，AE 垂直平分BC ，垂足为E ，4cm AB =．那么，菱形ABCD 的面积是 ，对角线BD 的长是 ．7. 如图，菱形ABCD 中，∠BAD =60º ，M 是AB 的中点，P 是对角线AC 上的一个动点，若PM +PB 的最小值是3，则AB 长为 ． 8. 将一正方形按如图方式分成n 个全等矩形，上、下各横排两个，中间竖排若干个，则n 的值为 A ．12 B ．10 C ．8 D ．6 9. 如图，矩形ABCD 的周长为20cm ，两条对角线相交于O 点，过点O 作AC 的垂线EF ，分别交AD BC ，于E F ，点，连结CE ，则CDE △的周长为（ ）A ．5cmB ．8cmC ．9cmD ．10cm10. 如果菱形的周长是8cm ，高是1cm ，那么这个菱形两邻角的度数比为（ ） A ．1:2 B ．1:4 C ．1:5 D ．1:611. 如图，四边形ABCD 为矩形纸片．把纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF ．若6CD =，则AF 等于（ ） Ａ．43 Ｂ．33Ｃ．42Ｄ．812.如图，在菱形ABCD 中，对角线AC BD ，分别等于8和6，将BD 沿CB 的方向平移，使D 与A 重合，B 与CB 延长线上的点E 重合，则四边形AECD 的面积等于（ ）A ．36B ．48C ．72D ．96ADEBPB CAD MOD EＢＦ ＣＥＤ ＡABDE O6如图，点P 是正方形ABCD 的对角线BD 上一点，连结PA 、PC ． （1）证明：PAB PCB ∠=∠；（2）在BC 上取一点E ，连结PE ，使得PE PC =，连结AE ，判断PAE △的形状，并说明理由．7如图，在□ABCD 中，EF ∥BD ，分别交BC 、CD 于点P 、Q ，分别交AB 、AD 的延长线于点E 、F ．已知BE=BP ．求证：（1）∠E=∠F ．（2）□ABCD 是菱形．8如图1，在ABC △中，点P 为BC 边中点，直线a 绕顶点A 旋转，若点B P 、在直线a 的异侧，BM ⊥直线a 于点M ，CN ⊥直线a 于点N ，连接.PM PN 、 （1）延长MP 交CN 于点E （如图2），①求证：BPM CPE △≌△；②求证：PM PN =；（2）若直线a 绕点A 旋转到图3的位置时，点B P 、在直线a 的同侧，其它条件不变.此时PM PN =还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变，请直接判断四边形MBCN 的形状及此时PM PN =还成立吗？不必说明理由.D C B A P图1 图2 图39已知：如图，在正方形ABCD 中，点E 、F 分别在BC 和CD 上，AE = AF ．（1）求证：BE = DF ；（2）连接AC 交EF 于点O ，延长OC 至点M ，使OM = OA ，连接EM 、FM ．判断四边形AEMF 是什么特殊四边形？并证明你的结论．证明：（1）10如图，在正方形ABCD 中，G 是BC 上的任意一点（G 与B C 、两点不重合），E F 、是AG 上的两点（E F 、与A G 、两点都不重合），若AF BF EF =+，12∠=∠，请判断线段DE 与BF 有怎样的位置关系，并证明你的结论.11如图，ABC △中，点O 是边AC 上一个动点，过O 作直线MN BC ∥，设MN 交BCA ∠的平分线于点E ，交BCA ∠的外角平分线于点F ．（1）探究：线段OE 与OF 的数量关系并加以证明；（2）当点O 在边AC 上运动时，四边形BCFE 会是菱形吗？若是，请证明，若不是，则说明理由； （3）当点O 运动到何处，且ABC △满足什么条件时，四边形AECF 是正方形？12如图①，四边形ABCD 是正方形， 点G 是BC 上任意一点，DE ⊥AG 于点E ，BF ⊥AG 于点F . （1） 求证：DE －BF = EF ．（2） 当点G 为BC 边中点时， 试探究线段EF 与GF 之间的数量关系， 并说明理由．（3） 若点G 为CB 延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE 、BF 、EF 之间A D BEFOCM2 ABCDEFG 1A F N D CB M E O（图）的数量关系（不需要证明）．13如图，将矩形纸片ABCD 沿其对角线AC 折叠，使点B 落到点B '的位置，AB '与CD 交于点E ． （1）试找出一个与AED △全等的三角形，并加以证明； （2）若83AB DE P ==，，为线段AC 上任意一点，PG AE ⊥于G ，PH EC ⊥于H ．试求PG PH +的值，并说明理由．14已知：如图，菱形ABCD 中，E F ，分别是CB CD ，上的点，且BE DF =． （1）求证：AE AF =．（2）若60B ∠=o，点E F ，分别为BC 和CD 的中点．求证：AEF △为等边三角形．15如图1，四边形ABCD 是正方形，G 是CD 边上的一个动点(点G 与C 、D 不重合)，以CG 为一边在正方形ABCD 外作正方形CEFG ，连结BG ，DE ．我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系：（1）①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系； ②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．ABDEF A DEFBG C图①CB GAD图②ABC D PG HE B ′16如图-1，已知P 为正方形ABCD 的对角线AC 上一点（不与A 、C 重合），PE ⊥BC 于点E ，PF ⊥CD 于点F ．（1） 求证：BP =DP ；（2） 如图-2，若四边形PECF 绕点C 按逆时针方向旋转，在旋转过程中是否总有BP =DP ？若是，请给予证明；若不是，请用反例加以说明；（3） 试选取正方形ABCD 的两个顶点，分别与四边形PECF 的两个顶点连结，使得到的两条线段在四边形PECF 绕点C 按逆时针方向旋转的过程中长度始终相等，并证明你的结论 ．17已知：如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为点D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为点E ，（1）求证：四边形ADCE 为矩形；（2）当△ABC 满足什么条件时，四边形ADCE 是一个正方形？并给出证明．17（1）证明：在△A BC 中， AB ＝AC ，AD ⊥BC ．∴ ∠BAD ＝∠DAC ． 2分∵ AN 是△ABC 外角∠CAM 的平分线， ∴ MAE CAE ∠=∠．∴ ∠DAE ＝∠DAC ＋∠CAE ＝⨯21180°＝90°．4分又 ∵ AD ⊥BC ，CE ⊥AN ， ∴ ADC CEA ∠=∠＝90°， ∴ 四边形ADCE 为矩形．5分（2）说明：①给出正确条件得1分，证明正确得3分．②答案只要正确均应给分．例如，当AD ＝12BC 时，四边形ADCE 是正方形． 6分图-2图-1 AM NE证明：∵ AB ＝AC ，AD ⊥BC 于D ．∴ DC ＝12BC ．7分 又 AD ＝12BC ，∴ DC ＝AD ． 8分 由（1）四边形ADCE 为矩形，∴ 矩形ADCE 是正方形． 9分 16⑴ 解法一：在△ABP 与△ADP 中，利用全等可得BP =DP . 2分 解法二：利用正方形的轴对称性，可得BP =DP . 2分 ⑵ 不是总成立 . 3分 当四边形PECF 绕点C 按逆时针方向旋转，点P 旋转到BC 边上时，DP >DC >BP ，此时BP =DP 不成立. 5分说明：未用举反例的方法说理的不得分. ⑶ 连接BE 、DF ，则BE 与DF 始终相等. 6分 在图8-1中，可证四边形PECF 为正方形， 7分 在△BEC 与△DFC 中，可证△BEC ≌△DFC . 从而有 BE =DF . 8分15（1）①BG DE BG DE =⊥， 2分 ②BG DE BG DE =⊥，仍然成立 1分在图（2）中证明如下∵四边形ABCD 、四边形ABCD 都是正方形 ∴ BC CD =，CG CE =， 90BCD ECG ∠=∠=o∴BCG DCE ∠=∠1分 ∴BCG DCE △≌△ （SAS ）1分∴BG DE = CBG CDE ∠=∠又∵BHC DHO ∠=∠ 90CBG BHC ∠+∠=o∴90CDE DHO ∠+∠=o∴90DOH ∠=o∴BG DE ⊥14证明：(1)∵四边形ABCD 是菱形， ∴AB =AD ，B D ∠=∠， 又∵BE =DF∴ABE △≌ADF △ ∴AE =AF (2)连接AC∵AB =BC ，60B ∠=︒ ∴ABC ∆是等边三角形， E 是BC 的中点∴AE ⊥BC ， ∴906030BAE ︒∠=︒-=︒，同理30DAF ∠=︒ ∵120BAD ∠=︒∴60EAF BAD BAE DAF ∠=∠-∠-∠=︒又∵AE =AF∴AEF △是等边三角形． 13解：（1）AED CEB '△≌△证明：Q 四边形ABCD 为矩形，90B C BC AD B B D ''∴==∠=∠=∠=，°， 又B EC DEA '∠=∠Q ， ∴AED CEB '△≌△．（2）由已知得：EAC CAB ∠=∠且CAB ECA ∠=∠ EAC ECA ∴∠=∠ 835AE EC ∴==-=在ADE △中，4AD = 延长HP 交AB 于M 则PM AB ⊥ PG PM ∴=4PG PH PM PH HM AD ∴+=+===12（1） 证明：∵ 四边形ABCD 是正方形， BF ⊥AG ， DE ⊥AG ∴ DA =AB ，∠BAF + ∠DAE = ∠DAE + ∠ADE = 90° ∴ ∠BAF = ∠ADE ∴ △ABF ≌ △DAE ∴ BF = AE ， AF = DE ∴ DE －BF = AF －AE = EFA DE F BG C图①（2）EF = 2FG 理由如下：∵ AB ⊥BC ， BF ⊥AG ， AB =2 BG ∴ △AFB ∽△BFG ∽△ABG∴2===FGBFBF AF BF AB ∴ AF = 2BF ， BF = 2 FG由（1）知，AE = BF ，∴ EF = BF = 2 FG（3） 如图 DE + BF = EF------------------------------------------------ 11解：（1）OE OF =． 其证明如下：∵CE 是ACB ∠的平分线，12∴∠=∠．∵MN BC ∥，∴13∠=∠． ∴23∠=∠． ∴OE OC =． 同理可证OC OF =． ∴OE OF =． 3分（2）四边形BCFE 不可能是菱形，若BCFE 为菱形，则BF EC ⊥，而由（1）可知FC EC ⊥，在平面内过同一点F 不可能有两条直线同垂直于一条直线． 3分（3）当点O 运动到AC 中点时，OE OF =，OA OC =，则四边形AECF 为Y，要使AECF 为正方形，必须使EF AC ⊥．∵EF BC ∥，∴AC BC ⊥，∴ABC △是以ACB ∠为直角的直角三角形， ∴当点O 为AC 中点且ABC △是以ACB ∠为直角的直角三角形时， 四边形AECF 是正方形．------------------------------------------------10根据题目条件可判断.DE BF ∥证明如下：∵四边形ABCD 为正方形，∴ 290AB AD BAF ∠+∠==，°． ∵,AF AE EF =+又,AF BF EF =+ ∴AE BF =，∵12,∠=∠∴().ABF DAE SAS △≌△5分∴AFB DEA ∠=∠，BAF ADE ∠=∠.∴290ADE ∠+∠=°.∴90AED BFA ∠=∠=°. ∴.DE BF ∥9分------------------------------------------------ 9证明：（1）∵四边形ABCD 是正方形，∴AB ＝AD ,∠B = ∠D = 90°． ∵AE = AF ，AF N D CB M EO （图） 1 2 54 3 6∴Rt Rt ABE ADF △≌△． ∴BE ＝DF ．4分（2）四边形AEMF 是菱形．∵四边形ABCD 是正方形， ∴∠BCA = ∠DCA = 45°，BC = DC ． ∵BE ＝DF ，∴BC －BE = DC －DF . 即CE CF =． ∴OE OF =． ∵OM = OA ，∴四边形AEMF 是平行四边形． ∵AE = AF ，∴平行四边形AEMF 是菱形．8分------------------------------------------------ 8（1）证明：①如图2.BM Q ⊥直线a 于点M ，CN ⊥直线a 于点N ，90BMN CNM ∴∠=∠=°．BM CN ∴∥．MBP ECP ∴∠=∠．又P Q 为BC 边中点， .BP CP ∴=又BPM CPE ∠=∠Q ， BPM CPE ∴△≌△ 3分②BPM CPE Q △≌△12PM PE PM ME ∴=∴=∴在Rt MNE △中，12PN ME =PM PN ∴=5分 （2）成立.如图3.6分证明：延长MP 与NC 的延长线相交于点E .BM Q ⊥直线a 于点M ，CN ⊥直线a 于点N ， 90180BMN CNM BMN CNM ∴∠=∠=∴∠+∠=°．°．BM CN MBP ECP ∴∴∠=∠∥．．7分又P Q 为BC 中点，BP CP ∴=． 又Q BPM CPE ∠=∠，BPM CPE ∴△≌△． 12PM PE PM ME ∴=∴=．．则在Rt MNE △中，12PN ME =．∴PM PN =．10分 （3）四边形MBCN 是矩形. 11分 PM PN =成立.12分AD BE FOC-----------------------------------------------7证明：（1）在□ABCD 中，BC AD ∥ ∴1F ∠=∠ ∵BE BP = ∴1E ∠=∠ ∴E F ∠=∠ （2）∵BD EF ∥ ∴23E F ∠=∠∠=∠， ∵E F ∠=∠ ∴23∠=∠ ∴AB AD = ∴□ABCD 是菱形6（1）∵在正方形ABCD 中，BD 是对角线， ∴AB CB ABD CBD =∠=∠，． 又∵BP BP =， ∴ABP CBP △≌△．∴PA PC PAB PCB =∠=∠，． ··········································································································· 3分 （2）如图，PAE △是等腰直角三角形，理由如下： ···································································· 4分 ∵PE PC =， ∴PEC PCB ∠=∠． 又∵PAB PCB ∠=∠， ∴PAB PEC ∠=∠．∵E 是BC 上一点,180PEB PEC ∠+∠=o, ∴180PAB PEB ∠+∠=o．DCEBAPADFQ CPEB 1 2 3图2 图3∵在四边形ABEP 中，36090PAB ABC PEB APE ABC ∠+∠+∠+∠=∠=o o，， ∴90APE ∠=o． ∵PA PC PE PC ==，， ∴PA PE =．∴PAE △是等腰直角三角形． ·································································· 7分（其他方法酌情给分）1.102. ①②③3. 1054.5. 81. 2. B 3. 90A ∠=o或AD BC =或AB CD ∥ 4. 3 5. ①④⑤ 6. 27. 8. C 9. D 10. C 11. A 12. A。
中考复习《矩形、菱形、正方形》测试题(含答案)
中考复习《矩形、菱形、正方形》测试题（含答案）一、选择题(每题4分，共24分)1．[2015·泸州]菱形具有而平行四边形不具有的性质是(D) A．两组对边分别平行B．两组对角分别相等C．对角线互相平分D．对角线互相垂直2．[2015·衢州]如图28－1，已知某菱形花坛ABCD的周长是24 m，∠BAD＝120°，则花坛对角线AC的长是(B)A．6 3 m B．6 m图28－1 C．3 3 m D．3 m【解析】易知△ABC为等边三角形，所以AC＝AB＝6 m.3．[2015·益阳]如图28－2，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是(D) A．∠ABC＝90°B．AC＝BDC．OA＝OB D．OA＝AD图28－2 图28－34．[2014·福州]如图28－3，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为(C) A．45°B．55°C．60°D．75°【解析】∵四边形ABCD是正方形，∴AB＝AD，又∵△ADE 是等边三角形， ∴AE ＝AD ＝DE ，∠DAE ＝60°， ∴AB ＝AE ，∴∠ABE ＝∠AEB ，∠BAE ＝90°＋60°＝150°， ∴∠ABE ＝(180°－150°)÷2＝15°， 又∵∠BAC ＝45°， ∴∠BFC ＝45°＋15°＝60°.5．[2015·临沂]如图28－4，四边形ABCD 为平行四边形，延长AD 到E ，使DE ＝AD ，连结EB ，EC ，DB .添加一个条件，不能使四边形DBCE 成为矩形的是 (B) A ．AB ＝BEB ．BE ⊥DCC ．∠ADB ＝90°D ．CE ⊥DE【解析】 因为四边形ABCD 为平行四边形，所以AD 綊BC ，因为DE ＝AD ，所以DE 綊BC所以四边形EDBC 为平行四边形，A ．假若AB ＝BE ，因为AB ＝BE ，AD ＝DE ，BD ＝BD ，所以△ADB ≌△EDB ，所以∠BDE ＝90°，所以四边形EDBC 为矩形； B ．假若BE ⊥DC ，可得四边形EDBC 为菱形；C ．假若∠ADB ＝90°，所以∠EDB ＝90°，所以四边形EDBC 为矩形；D ．假若CE ⊥DE ，所以∠DEC ＝90°，所以四边形EDBC 为矩形，故选B. 6．[2015·日照]小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件①AB ＝BC ，②∠ABC ＝90°，③AC ＝BD ，④AC ⊥BD 中选两个作为补充条件，使▱ABCD 成为正方形(如图28－5)现有下列四种选法，你图28－4图28－5认为其中错误的是(B)A．①②B．②③C．①③D．②④【解析】此题考查正方形的判定，即在▱ABCD的基础上，需要再同时具备矩形和菱形的特征．①是菱形的特征；②是矩形的特征；③是矩形的特征，④是菱形的特征．而B中都是矩形的特征，故选B.二、填空题(每题4分，共20分)7．[2015·铜仁]已知一个菱形的两条对角线长分别为6 cm和8 cm，则这个菱形的面积为__24__cm2.8．[2014·衡阳]如图28－6，在矩形ABCD中，∠BOC＝120°，AB＝5，则BD的长为__10__．9．[2015·上海]已知E是正方形ABCD的对角线AC上一点，图28－6 AE＝AD，过点E作AC的垂线，交边CD于点F，那么∠F AD＝__22.5__度．10．[2014·淄博]已知▱ABCD，对角线AC，BD相交于点O，请你添加一个适当的条件，使▱ABCD成为一个菱形．你添加的条件是__AB＝BC或AC⊥BD等__．11．[2014·资阳]如图28－7，在边长为4的正方形ABCD中，E是AB边上的一点，且AE＝3，点Q为对角线AC上的动点，则△BEQ周长的最小值为__6__．图28－7【解析】如答图，连结BD，DE，∵四边形ABCD是正方形，∴点B与点D关于直线AC对称，∴DE的长即为BQ＋QE的最小值，∵DE＝BQ＋QE＝5，∴△BEQ周长的最小值＝DE＋BE＝5＋1＝6.三、解答题(共20分)12．(10分)[2015·安顺]如图28－8，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于图28－8F.(1)求证：AE＝DF；(2)若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．证明：(1)∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∴AE＝DF；(2)若AD平分∠BAC，四边形AEDF是菱形，理由如下：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形，∵AD平分∠BAC，∴∠EAD＝∠F AD，∵AE∥DF，∴∠EAD＝ADF，∠DAF＝∠FDA，∴AF＝DF，∴平行四边形AEDF为菱形．13．(10分)[2015·青岛]已知：如图28－9，在△ABC中，AB ＝AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E.(1)求证：△ABD≌△CAE；图28－9(2)连结DE ，线段DE 与AB 之间有怎样的位置和数量关系？请证明你的结论． 解：(1)证明：∵AB ＝AC ，AD 是BC 边上的中线， ∴AD ⊥BC ，BD ＝CD . ∵AE ∥BC ，CE ⊥AE ， ∴四边形ADCE 是矩形， ∴AD ＝CE .在Rt △ABD 与Rt △CAE 中， ⎩⎪⎨⎪⎧AD ＝CE ，AB ＝CA ，∴△ABD ≌△CAE (HL )；(2)DE ∥AB ，DE ＝AB .证明如下： 如答图所示，∵四边形ADCE 是矩形， ∴AE ＝CD ＝BD ，AE ∥BD ， ∴四边形ABDE 是平行四边形， ∴DE ∥AB ，DE ＝AB .14．(10分)[2014·扬州]如图28－10，已知Rt △ABC ，∠ABC ＝90°，先把△ABC 绕点B 顺时针旋转90°后至△DBE ，再把△ABC 沿射线AB 平移至△FEG ，DE ，FG 相交于点H .(1)判断线段DE ，FG 的位置关系，并说明理由； (2)连结CG ，求证：四边形CBEG 是正方形． 解：(1)DE ⊥FG ，理由如下：由题意得∠A ＝∠EDB ＝∠GFE ，∠ABC ＝∠DBE ＝90°，第13题答图图28－10∴∠BDE＋∠BED＝90°.∴∠GFE＋∠BED＝90°，∴∠FHE＝90°，即DE⊥FG；(2)证明：∵△ABC沿射线AB平移至△FEG，∴CB∥GE，CB＝GE.∴四边形CBEG是平行四边形．∵∠ABC＝∠GEF＝90°，∴四边形CBEG是矩形．∵BC＝BE，∴四边形CBEG是正方形．15．(10分)[2015·南京]如图28－11，AB∥CD，点E，F分别在AB，CD上，连结EF，∠AEF，∠CFE的平分线交于点G，∠BEF，∠DFE的平分线交于点H.(1)求证：四边形EGFH是矩形；(2)小明在完成(1)的证明后继续进行了探索，过G作MN∥EF，分别交AB，CD于点M，N，过H作PQ∥EF，分别交AB，CD交于点P，Q，得到四边形MNQP.此时，他猜想四边形MNQP是菱形，请在下列框图中补全他的证明思路．小明的证明思路由AB∥CD，MN∥EF，易证四边形MNQP是平行四边形，要证▱MNQP是菱形，只要证MN＝NQ.由已知条件__FG平分∠CFE__，MN∥EF，可证NG＝NF，故只要证GM＝FQ，即证△MEG≌△QFH，易证__GE＝FH__，__∠GME ＝∠FQH__.故只要证∠MGE＝∠QFH.易证∠MGE＝∠GEF，∠QFH＝∠EFH，__∠GEF＝∠EFH__，即可得证．图28－11解：(1)证明：∵EH平分∠BEF.∴∠FEH＝12∠BEF，∵FH平分∠DFE，∴∠EFH＝12∠DFE，∵AB∥CD，∴∠BEF＋∠DFE＝180°，∴∠FEH＋∠EFH＝12(∠BEF＋∠DFE)＝12×180°＝90°，又∵∠FEH＋∠EFH＋∠EHF＝180°，∴∠EHF＝180°－(∠FEH＋∠EFH)＝180°－90°＝90°，同理可证，∠EGF＝90°，∵EG平分∠AEF，∴∠FEG＝12∠AEF，∵EH平分∠BEF，∴∠FEH＝12∠BEF，∵点A，E，B在同一条直线上．∴∠AEB＝180°，即∠AEF＋∠BEF＝180°.∴∠FEG＋∠FEH＝12(∠AEF＋∠BEF)＝12×180°＝90°，即∠GEH＝90°.∴四边形EGFH是矩形；(2)本题答案不唯一，下列解法供参考．例如，FG平分∠CFE；GE＝FH；∠GME ＝∠FQH；∠GEF＝∠EFH.16．(6分)[2015·资阳]若顺次连结四边形ABCD四边的中点，得到的图形是一个矩形，则四边形ABCD一定是(D) A．矩形B．菱形C．对角线相等的四边形D．对角线互相垂直的四边形17．(10分)如图28－12，在菱形ABCD中，边长为10，∠A＝60°.顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；…；按此规律继续下去，则四边形A2B2C2D2的周长是__20__；四边形A2 016B2 016C2 016D2 016的周长是__521 005__．图28－12。
菱形矩形正方形练习题
（第10F ABCDH EG① ②③④⑤矩形、菱形与正方形 练习题一、选择题1.如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重叠无缝隙）．若①②③④四个平行四边形面积的和为14cm 2，四边形ABCD 面积是11cm 2，则①②③④四个平行四边形周长的总和为（ ） （A ）48cm（B ）36cm （C ）24cm（D ）18cm2.图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），……，则第n 个图形的周长是（A ）2n （B ）4n （C ）12n + （D ）22n +3.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2，则S 1+S 2的值为A.17B.17C.18D.19 4.如图，点O 是矩形ABCD 的中心，E 是AB 上的点，沿CE 折叠后，点B 恰好与点O 重合，若BC =3，则折痕CE 的长为 A.2 3 B.332C. 3D.6 5. （2011浙江衢州，1,3新颜，如图为一农村民居侧面截图，屋坡AF AG 、分别架在墙体的点B 、点C 处，且AB AC =,侧面四边形BDEC 为矩形，若测得100FAG ∠=︒，则FBD ∠=( )A. 35°B. 40°C. 55°D. 70°6.如图，在矩形ABCD 中，对角线AC ，BD 交于点O ．已知∠AOB = 60°，AC ＝16，则图中长度为8的线段有( ) A ．2条B ．4条C ．5条D ．6条图1图2图3……A CD 图2…A 1 A A 2 A 3B B 1B 2B 3CC 2 C 1C 3 DD 2D 1 D 3 第10题图（第7题图）ECBA7.如图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( ) A ．1B ．2C ．3D ．48..如图2，小聪在作线段AB 的垂直平分线时，他是这样操作的：分别以A和B 为圆心，大于12AB 的长为半径画弧，两弧相交于C 、D ，则直线CD 即为所求．根据他的作图方法可知四边形ADBC 一定‧‧是‧A ．矩形B ．菱形C ．正方形D ．等腰梯形9.. 已知一个菱形的周长是20cm ，两条对角线的比是4∶3，则这个菱形的面积是（ ） A ．12cm2B ． 24cm 2C ． 48cm 2D ． 96cm 210. 如图，矩形纸片ABCD 中，已知AD=8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF=3，则AB 的长为（ ） A ．3 B ．4 C ．5 D ．611 如图,四边形ABCD 中,AC=a,BD=b,且AC ⊥BD,顺次连接四边形ABCD 各边中点,得到四边形A 1B 1C 1D 1,再顺次连接四边形A 1B 1C 1D 1各边中点,得到四边形A 2B 2C 2D 2……,如此进行下去,得到四边形A n B n C n D n .下列结论正确的有( )①四边形A 2B 2C 2D 2是矩形; ②四边形A 4B 4C 4D 4是菱形;③四边形A 5B 5C 5D 5的周长4b a +; ④四边形A n B n C n D n 的面积是12+n abA.①②B.②③C.②③④D.①②③④ 12.在菱形ABCD 中，AB=5cm ，则此菱形的周长为（ ）A. 5cmB. 15cmC. 20cmD. 25cm13.如图，△ABC 中，AC 的垂直平分线分别交AC 、AB 于点D 、F ，BE ⊥DF 交DF 的延长线于点E ，已知∩A ＝30°，BC ＝2，AF ＝BF,则四边形BCDE 的面积是（ ）A ．23B ．33C ．4D ．43 14. 下列关于矩形的说法中正确的是A ．对角线相等的四边形是矩形B ．对角线互相平分的四边形是矩形C ．矩形的对角线互相垂直且平分D ．矩形的对角线相等且互相平分B（第17题图）EDD′CBAABCD第5题图1413121115．菱形具有而矩形不一定具有的性质是 ( )A ．对角线互相垂直B ．对角线相等C ．对角线互相平分D ．对角互补 二、填空题1.将矩形ABCD 沿AE 折叠，得到如图所示图形。
(完整版)矩形、菱形与正方形-专题训练(含答案)
矩形、菱形与正方形专题训练（含答案）班级_________ 姓名 __________ 成绩 ___________、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（ ）A . 12B . 24C . 12 .'3D . 16 .'3第1题图 第2题图 第3题图 第4题图2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（） A . 14 B . 15C . 16D . 173. 如图， 将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，则CD 的长为（） A. 1 B . 2C . 3D . 44. 如图， 在厶ABC 中，AC =BC , 占 八D ,E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰疋是 ( )A.矩形 B . 菱形 C . 正方形 D .梯形5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是（ ）6.如图，?ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点 丘，则厶DCE 的周 长为（）A •平行四边形B •矩形C •菱形D .正方形A . 4 cmB . 6 cmC .第6题图 第9题图7•菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为BC10 cmA F DE&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等腰三角形，⑥等边三角形，一定能拼成的图形是（）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9. 如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S i, S2,则S i + S2的值为（）A . 16B . 17 C. 18 D . 1910. 如图，F为正方形ABCD的边AD上一点，CE丄CF交AB的延长线于点E,若正方形ABCD 的面积为64,A CEF的面积为50,则厶CBE的面积为（）A . 20B . 24C . 25D . 26二、填空题（每小题3分，共24分）11. 如图所示，在菱形ABCD中，/ ADC = 72 ° AD的垂直平分线交对角线BD于点P,垂足为点E,连结CP,则/ CPB = _______ 度.1)第11题图第12题图第14题图第15题图12 .如图，四边形ABCD的两条对角线AC, BD互相垂直，A1, B1, C1, D1分别是四边形ABCD 各边中点，如果AC= 8, BD = 10,则四边形A1B1C1D1的面积为—.13 .矩形的对角线相交成的角中，有一个角是60°这个角所对的边长为20 cm,则其对角线长为___________ -_,矩形的面积为__________________ .14 .如图，四边形ABCD是菱形，对角线AC和BD相交于点O, AC = 4 cm, BD = 8 cm,则这个菱形的面积是_____ c m2.AC , BD 交于点 O , E 点在BC 上，EG 丄OB , EF 丄OC ,垂足，使?ABCD 是矩形.17 .如图，正方形 ABCD 中，对角线第18题图15 .如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的 中点M , N ,连结AM , CN , MN ,若AB = 2 2, BC = 2 '3,则图中阴影部分的面积为，第16题O ,请你添加一个条件16 .如图,分别为点G , F, AC= 10,则EG + EF = ______ .18. 如图，在平面直角坐标系中，矩形OABC的顶点A, C的坐标分别为(10, 0), (0, 4),点D是OA的中点，点P在BC上运动，当△ ODP是腰长为5的等腰三角形时，点P的坐标为三、解答题(共66分)19. (6分)如图，已知矩形ABCD中，E是AD上一点，F是AB上一点，EF丄EC且EF = EC, DE =4 cm，矩形ABCD的周长为32 cm,求AE的长.20. (8分)如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O,与BC相交于点N,连结BM , DN.(1)求证：四边形BMDN是菱形；⑵若AB= 4, AD = 8,求MD的长.21 . （8 分）如图所示，矩形ABCD 中，AE丄BD 于点E,/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.22. （10分）如图，已知菱形 ABCD 中，AB = AC , E , F 分别是BC , AD 的中点，连结 AE , CF. （1）证明：四边形 AECF 是矩形； ⑵若AB = 8,求菱形 ABCD 的面积.参考答案一、选择题（每小题3分，共30分）1.如图，把矩形ABCD 沿EF 翻折，点B 恰好落在AD 边的B 处，若AE = 2, DE = 6, / EFB = 60 ° 则矩形ABCD 的面积是（D ） A . 12B . 24C . 12D . 164 / 9DE 丄AB , DF 丄BC ,垂足分另U 是点 E , F ，并且DE = DF ，求证： (1)△ ADECDF ; (2)四边形 ABCD 是菱形.24. (10分)在四边形 ABCD 中，AB = CD , M , N , P , Q 分别是AD , BC , BD , AC 的中点，求证:MN 与PQ 互相垂直平分.23. （12分）如图，已知四边形 ABCD 是平行四边形,6.如图，？ABCD 的周长为16 cm , AC , BD 相交于点 O , 0E 丄AC 交AD 于点 丘，则厶DCE 的周 长为（C ）7.菱形的周长为 8 cm ,高为1 cm ,则菱形两邻角度数比为 （C ） A . 3 : 1B . 4 : 1C . 5 : 1D . 6 : 1&用两块完全相同的直角三角形拼下列图形：①平行四边形，②矩形，③菱形，④正方形，⑤等 腰三角形，⑥等边三角形，一定能拼成的图形是 （D ）A .①④⑤B .②⑤⑥C .①②③D .①②⑤9.如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为 S 1, S 2,则S 1 +S 2的值为（B ） A . 16B . 17C . 18D . 19的面积为64,^ CEF 的面积为50,则厶CBE 的面积为（B）2 . 如图，菱形ABCD 中，/ B = 60 ° AB = 4,则以AC 为边长的正方形 ACEF 的周长为（C ） A . 14 B . 15C . 16D . 173. 如图， 将矩形 ABCD 沿对角线 BD 折叠，使点 C 与点 C 重合.若AB = 2，贝U CD 的长为（B ） A . 1 B . 2C . 3D . 44. 如图，在厶ABC 中，AC =BC , 点D , E 分别是边AB , ,AC 的中点. 将厶 ADE 绕点E 旋转180 得厶CFE ，则四边形 ADCF •宀曰(A )定是A.矩形 B . 菱形C .正方形D .梯形A •平行四边形B •矩形C •菱形D .正方形 A . 4 cmB . 6 cmC .第6题图10 .如图, F 为正方形 ABCD 的边AD 上一点, CE 丄CF 交AB 的延长线于点 E ,若正方形 ABCD第4题图第1题图 第2题图 第3题图 5•由菱形的两条对角线的交点向各边引垂线，以各垂足为顶点的四边形是 （B BC第9题图10 cm二、填空题(每小题3分，共24分)11.如图所示，在菱形 ABCD 中，/ ADC = 72 ° AD 的垂直平分线交对角线 BD 于点P ,垂足为点 E ,连结 CP ,则/ CPB =72 度.第11题图 第12题图 第14题图 第15题图12. 如图，四边形 ABCD 的两条对角线 AC , BD 互相垂直，A 1, B 1, C 1, D 1分别是四边形 ABCD 各边中点，如果 AC = 8, BD = 10,则四边形 A 1B 1C 1D 1的面积为 _20_. 13. 矩形的对角线相交成的角中，有一个角是 _40 cm ，矩形的面积为_400 cm 2 .14. 如图，四边形 ABCD 是菱形，对角线 AC 和BD 相交于点O , AC= 4 cm , BD = 8 cm ,则这个菱形的面积是_16 cm 2.15. 如图，矩形 ABCD 中，点E , F 分别是 AB , CD 的中点，连结 DE 和BF ，分别取 DE , BF 的是矩形. 17.如图，正方形 ABCD 中，对角线 AC , BD 交于点O , E 点在BC 上, EG 丄OB , EF 丄OC ,垂足 分别为点 G , F , AC = 10,则 EG + EF = 5 . 18.如图，在平面直角坐标系中，矩形 OABC 的顶点A , C 的坐标分别为(10, 0), (0, 4),点D 是 OA 的中点，点P 在BC 上运动，当△ ODP 是腰长为5的等腰三角形时，点 P 的坐标为 _(8, 4), (3, 4)或(2, 4)_. 三、解答题(共66分)19. (6分)如图，已知矩形 ABCD 中，E 是AD 上一点，F 是AB 上一点，EF 丄EC 且EF = EC , DE =4 cm ，矩形ABCD 的周长为32 cm ，求AE 的长.B . 24C . 25D . 2660°这个角所对的边长为 20 cm ,则其对角线长为中点M , N ,连结AM , CN , MN ，若，第16题图16.如图, ?ABCD 的对角线相交于点 O ,请你添加一个条件AO = BO (答案不唯一)，使?ABCD第17题AB = 2, BC = 2，则图中阴影部分的面积为2解：I/ AFE + / AEF = / AEF + / CED = 90° /•/ AFE = / DEC . 又•••/ A = / D = 90° EF = EC ,•••△ AEF◎△ DCE AE = CD.1设 AE = x ，贝U CD = x , • AD + CD = 2x32，即 x + 4 + x = 16, •- x = 6.即卩 AE = 6 cm⑴求证：四边形 BMDN 是菱形； ⑵若AB = 4, AD = 8,求MD 的长.解：(1) •/ MN 是 BD 的垂直平分线，• BO = DO , / BON =/ DOM = 90° •••四边形 ABCD 是矩形，• AD // BC ，• / BNO = / DMO , • △ BON ◎△ DOM (AAS), • OM = ON.v OB = OD , •四边形 BMDN 是平行四边形.•/ MN 丄BD , • ?BMDN 是菱形(2)设 MD = x ，贝U MB = x , MA = 8-x ，在 Rt △ ABM 中，T BM 2= AM 2+ AB 2, • x 2= (8- x)2 + 42,解得 x = 5.「. MD 的长为 521 . （8 分）如图所示，矩形 ABCD 中，AE 丄 BD 于点 E ，/ DAE :/ BAE = 3 : 1，求/ BAE 和/ EAO 的度数.解：提示：由 / DAE :/ BAE = 3 ： 1 ,求出 / BAE = 22.5 ° 而/ABD = 90°— / BAE = 90° — 22.5° = 67.5°•••/ BAO = / ABD = 67.5 ° •••/ EAO = Z BAO — / BAE = 67.5。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矩形 A 组题1 、⑴矩形ABCD中， AC与BD相交于点O，如果AC=8㎝，那么BD=________ ，OB=________ ；⑵有三个角是直角的四边形是________________ ；对角线___________的平行四边形是矩形；2 、如图，平行四边形ABCD 中，∠ BAD=90 °，对角线AC 、BD 相交于点O，则∠ ___=∠_______=∠ _______=_________=90 ° ,△ ABC 与三角形 __________ 重叠（只需写出一个）。
所以AC=___________ ，既矩形的四角都是_________ ，矩形的对角线____________ 。
A DOBC3 、已知：平行四边形ABCD 的对角线AC 、BD 相交于点O，且 AC=BD ，则四边形 ABCD是__________,理由是 ________________________ ；OA=OB=OC ，由此可以得出直角三角形斜边上的中线等于 ____________________.4、矩形具有而一般平行四边形不具有的性质是（） .A 对角线相等B对边相等 C 对角相等 D 对角线互相平分5、下面说法中正确的是（）（可能有多个答案） .A有一个角是直角的四边形是矩形. B 两条对角线相等的四边形是矩形.C两条对角线互相垂直的四边形是矩形.D四个角都是直角的四边形是矩形.E 对角线互相平分且相等F 对角线垂直且相等6、已知平行四边形 ABCD 中对角线 AC ，BD 相交于 o，△ AOB 是等边三角形，求∠ BAD 的度数。
解：∵△ AOB是等边三角形（∵四边形ABCD 是平行四边形（∴AC=_____ （∴平行四边形ABCD 是矩形（∴∠ BAD ＝ 90°（），∴ OA=_____=_____ （），∴ AC=2OA,BD=2BO），（））））7、下列各判定矩形的说法是否正确？为什么？（ 1）对角线相等的四边形是矩形（ 2）对角线互相平分且相等的四边形是矩形（ 3）有一个角是直角的四边形是矩形（ 4）有四个角是直角的四边形是矩形（ 5）四个角都相等的四边是矩形（ 6）对角线相等，且有一个直角的四边形是矩形（ 7）一组邻边垂直，一组对边平行且相等的四边形是矩形（ 8）对角线相等且互垂直的四边形的矩形8、某居民小区搞绿化，要在一块矩形空地上建花坛，现征集设计方案。
要求设计的图案由圆和正方形组成(圆和正方形个数不限)，并且使整个矩形地成轴对称图形。
请在矩形中画出你的设计方案。
B组题9 、已知矩形的两条对角线相交所成的锐角为60°，其较短的一边与一条对角线之和为15㎝，求矩形的对角线长。
A E D10、如图，矩形 ABCD 中， E 为 AD 中点，∠ BEC 为直角，矩形 ABCD 的周长是20，B C 求 AD 、 AB 的长。
11 、 (难 ) 已知：如图，ABCD 中， M 为 BC 中点，∠ MAD= ∠ MDA求证：四边形是 ABCD 是矩形。
ADB MCC组题14、如图，将矩形 ABCD 沿着直线 BD 折叠使点 C 落在点 C＇处， BC ＇交 AD 于 E，AD=8 ， AB=4 ， BE=5, 求△ BED 的面积。
C'A EDBC菱形 A 组题A1 、___＿＿＿＿＿＿ ___的平行四边形叫做菱形。
木工做菱形窗棂时总要保持四条边框一样长，道理是_____________＿＿B O D2、如图，在菱形 ABCD 中，对角线 AC 、BD 相交于点 O,则有（ 1）图中的等腰三角形有 __________________, 直角三角形有C_________________,（ 3）△ AOD 与那几个三角形可以重叠______________________ ，由此可以得出菱形的对角线__________________, 每一条对角线________________.（ 4）菱形是轴对称图形，它的对称轴是 _________ ；菱形是中心对称图形，它的对称中心是_____________3、（ 1）如图，在菱形 ABCD 中， AB=5,OA=4,OB=3, 则菱形的周长是＿＿＿＿两条对角线的长是＿＿＿＿＿＿；（ 2）菱形的一条对角线与一条边长相等，则菱形相邻两个内角的D Ao度数分别为＿＿＿＿C B ；4 、已知菱形的对角线长分别为12m 和 16m ，则面积是 ()，一个边长为20 m ，菱形的高为 () 。
5 、选择题：⑴下列条件中，能判定一个四边形为菱形的条件是()A 、对角线互相平分的四边形B、对角线互相垂直且平分的四边形C、对角线相等的四边形 D 、对角线相等且互相垂直的四边形⑵下列性质中，菱形具有而矩形不一定具有的性质是()A 、对边平行且相等； B、对角线互相平分；C、内角和等于外角和； D、每一条对角线都是它的对称轴6、如图，在菱形 ABCD 中，∠ BAD=2 ∠ B， AC=5 ㎝，说明△ ABC 等边三角形并求菱形的周长。
AB DC A7、如图 ,AD 是△ ABC 的角平分线。
DE ∥ AC 交1 AB 于 E， DF∥ AB 交 AC 于 F 。
说明：四边形AEDF 是菱形证明：∵＿＿＿＿＿＿＿＿＿＿＿＿＿＿（）∴四边形 AEDF 是平行四边形（）E F∵AD 是△ ABC 的角平分线（）∴＿＿＿＿＿＿＿＿＿＿（角平分线的定义）B C ∵DE ∥ AC （）∴＿＿＿＿＿＿＿＿＿＿＿＿＿＿（）D∴＿＿＿＿＿＿＿＿＿＿＿＿＿＿（ 等量代换 ）∴＿＿＿＿＿＿＿＿＿＿（ 等角对等边）∴ 平行四边形AEDF 是菱形（）B 组题8、近几年，某城市流行一种衣帽架，它是用木条(四长四短 )构成的几个连续的菱形(如图 )，每一个顶点处都有一个挂钩 ( 连在轴上 )，不仅美观，而且实用。
你能根据形状，说出它的好处和固定方法吗？AB9、(难 )如图， 菱形 ABCD 的边长为 2，高 AE 平分 BC 。
求： ⑴菱形面积； ⑵两对角线的长。
ABDCC 组题110、 (难 )如图，△ ABC 中， AB=AC ， AD 是角平分线， E 为 AD 延长线上一点， CF//BE 交 AD 于 F ，连接 BF 、 CE ，求证：四边形 BECF 是菱形。
AFBCDEA11、(难 )已知菱形 ABCD 中，AC 与 BD 相交 O 点，若∠ BDC = 30,菱形的周长为 20 厘米，求最短对角线长BO DC正方形 A 组题1、⑴正方形具有_________、 ___________、 ____________的一切性质。
有一个角是直角的__________是正方形，有一组邻边相等的_________是正方形。
⑵如下图，四边形ABCD 是正方形，两条对角线相交于点O ， OA=2 ，则∠ AOB=________, ∠ OAB=________,BD =____________,AC=__________.A DOB C∠ ABD=________, 、∠ DAC=________, 、⑶上图中等腰三角形的个数是（） A.4 个 B.5 个C.6个 D.8 个（ 4 ）正方形ABCD 的对角线交于点O ，与△ AOB全等的三角形有_____________________________ ；这些三角形都是_______三角形； (注：能完全重合的两个图形称为全等图形)（5 ）正方形既是 __________ 图形，又是 __________图形，它有 __________条对称轴；2、判断。
（ 1）正方形一定是矩形。
（）（ 2）正方形一定是菱形。
（）（ 3）菱形一定是正方形。
（）（ 4）矩形一定是正方形。
（）（ 5）正方形、矩形、菱形都是平行四边形。
（）3、在下列性质中，平行四边形具有的是__________，矩形具有的是_________ ，菱形具有的是 __________ ，正方形具有的是____________。
（1）四边都相等；（2）对角线互相平分；（3）对角线相等；（4）对角线互相垂直；（5）四个角都是直角；（6）每条对角线平分一组对角；（7）对边相等且平行；（8）有两条对称轴。
4、在图⑴中有________个正方形， _________个矩形；在图⑵中有 ________个正方形， __________个矩形；⑴⑵5、现有一块正方形的蛋糕，请切两刀形状相同且面积相等的 4 块，请设计三种不同的分法。
6、正方形两条对角线的和为8cm ，它的面积为____________.7、如图，在△ＡＢＣ中，∠ＡＣＢ＝ 90°，ＣＤ平分∠ＡＣＢ，ＤＥ⊥ＢＣ，ＤＦ⊥ＡＣ，垂足分别Ｅ，Ｆ，试说明四边形ＣＦＤＥ为正方形ＥＣＢＦＤＡ8、如图， E 为正方形ABCD 对角线 BD 上的一点，且BE=BC ，试求∠ DCE 的大小A DE9、请用两种方法将一个正方形分割成9 个小正方形。
C 组题10 、 (难 )在正方形ABCD中， E在BC上， BE=2 ， CE=1 ， P 在BD上，则PE和PC的长度之和最小可达到_____________A DGFBE C11 、(难 ) 如图，点 E、F 在正方形 ABCD的边 BC 、CD 上， BE=CF. AE 与 BF 相等吗？为什么？AE 与 BF 是否垂直？说明你的理由。