苏教版必修四3.2《二倍角的三角函数》word学案
苏教版数学高一-必修4导学案 3.2二倍角的三角函数(1)学生版
课题：§3.2二倍角的三角函数（一） 总第____课时 班级_______________姓名_______________【学习目标】 1．掌握二倍角的正弦、余弦、正切公式，能用上述公式进行简单的求值、化简、恒等证明；2．引导学生发现数学规律，让学生体会化归这一基本数学思想在发现中所起的作用，培养学生的创新意识.【重点难点】学习重点：二倍角公式的推导及简单应用.学习难点：理解倍角公式，用单角的三角函数表示二倍角的三角函数.【学习过程】一、自主学习与交流反馈：问题1：请说出两角和与差的正弦、余弦、正切公式；问题2：若α=β，则以上公式变为什么形式？二、知识建构与应用：倍角公式：sin2α = 2sin αcos α； （S 2α）cos2α = cos 2α – sin 2α； （C 2α）tan2α = 2tan α1 - tan 2α .（T 2α） 说明：①“二倍角”的意义是相对的，如：4α是8α的二倍角； ②观察公式特征：“倍角”与“二次”的关系；③利用三角函数关系式22sin cos 1αα+=，可将余弦的倍角公式变形为：22cos 22cos 112sin ααα=-=-， 22cos 2cos sin ααα=-，2cos 22cos 1αα=-，2cos 212sin αα==-统称为“升幂公式”；类似地也有公式： 21cos 2cos2αα+=，21cos 2sin 2αα-= 称为“降幂公式”，这两个形式今后常用；④注意公式成立的条件，特别是二倍角的正切公式成立的条件：,()242k k k Z πππαπα≠+≠+∈． 三、例题例1 已知),2(,1312sin ππαα∈=，求sin 2α，cos2α，tan 2α的值。
变式：已知),2(,1312sin ππαα∈=，求sin α2、cos α2及tan α2的值.例2归纳： 1 + sin α = _____； 1 - sin α = _______； 1 + cos α = ______； 1 - cos α = ______. 例3 求证：θθθθθtan 2cos 2sin 12cos 2sin 1=++-+四、巩固练习1．利用倍角公式求下列各式的值． ① sincos 88ππ= ； ②22cos sin 88ππ-= ； ③ 1－ 15sin 22= ；④15tan 115tan 22-= .⑤ 1 - sin80° = __________.2．已知08,0,,sin 2,cos 22πsin .αααα⎛⎫=∈ ⎪⎝⎭求的值．3．已知的值．求αα2tan ,21tan =4．证明：①2sin()cos()sin 2ππααα+-=； ②22cos cos 212=-+θθ； ③αααsin 2sin 2cos 1=-； ④A A A 2tan 2cos 12cos 1=+-.。
苏教版数学高一必修4教案 3.2《二倍角的三角函数》(2)
3.2 二倍角的三角函数 (2)一、教学目标1．运用公式进行化简、求值、证明，增强学生灵活运用数学知识和逻辑推理能力；2．能运用公式解决一些简单的实际问题；3．培养学生观察、推理的思维能力．二、教学重难点教学重点 二倍角公式的简单应用。
教学难点 二倍角的理解及其灵活运用（公式的逆向运用及变式训练）。
三、教学方法建构主义认为：教学应当用情节、背景真实的问题引导出所学的内容，通过营造解决问题的环境，启发学生积极思考和自主探究。
基于本节课的特点：二倍角三角函数公式是和角公式的特例，着重采用的教学方法是引导发现法．即：通过创设生动逼真和符合数学教学内容的问题情境，激发学生对数学问题的兴趣，帮助他们形成学习动机；提示新旧数学知识之间的联系线索，帮助学生建构当前所学数学知识的意义．四、教学过程一、复习引入二倍角公式：sin22sin cos ααα=； 22cos 2cos sin ααα=-；22tan tan 21tan ααα=-； 2cos 22cos 1αα=-；2cos 212sin αα=-．（1）二倍角公式的作用在于用单角的三角函数来表达二倍角的三角函数，它适用于二倍角与单角的三角函数之间的互化问题．（2）二倍角公式为仅限于2α是α的二倍的形式，尤其是“倍角”的意义是相对的（3）熟悉“倍角”与“二次”的关系（括角—降次，缩角—升次）．（4）特别注意公式的三角表达形式，且要善于变形：221cos 21cos 2cos ,sin 22αααα+-== 这两个形式今后常用． 二、数学运用1. 例题.例1 化简222sin ()sin ()sin 66ππααα-++-。
法一: 由倍角公式2cos 212sin αα=-,得21cos 2sin 2αα-=, 对原式进行降幂化简,角由单角变为倍角． 这里用到了21cos 2sin 2αα-=,它和21cos 2cos 2αα+=，21cos2tan 1cos2ααα-=+统称为降幂公式．法二: 两角和差的正弦展开．例2 求证: sin 50(13tan10)1+=例3 求函数44sin cos cos y x x x x =+-的最小正周期和最小值,并写出该函数在[]0,π上的单调递增区间．注:解决三角函数问题,首先用公式进行化简,再按要求进行求解．例4 已知11tan(),tan ,,(0,),2.27αββαβπαβ-==-∈-求的值 这是一个由函数值求角的问题,这就需要求出这个角的某个三角函数值,并需要判断这个角所在的范围．2. 练习．（1）证明①B A B A A 2cos 2cos )(sin B (cos 22=--+）②θθθ2cos )tan 1(cos 22=-（2）求函数y=的最小值x x x x cos sin 2sin cos 22+-（3）11tan ,tan ,273αβαβαβ==+已知且，都是锐角，求的值. （4）扇形AOB 的半径为1，中心角为60，PQRS 是扇形内接矩形，问P 在怎样的位置时，矩形PQRS 的面积最大，并求这个最大值．三、课堂小结1．在解决三角函数式的化简问题时，经常从以下三个方面来考虑：一看函数式中所涉及的角之间的关系；二看函数式中所涉及的三角函数的名称之间的关系；三看所涉及的函数的幂．遵循的原则是：不同角化同角，不同名化同名，高次降低次．2．若所要化简或证明的三角函数式中含有多个名称的三角函数，我们常用的方法是将正切化为正弦、余弦，若是有常数和分式相加，我们采取的措施是通分，而后再化简．。
苏教版高中数学必修四新课程第课时二倍角的三角函数导学案(1)
总 课 题 二倍角的三角函数 总课时 第36课时 分 课 题二倍角的三角函数（2）分课时 第 2 课时教学目标 灵活运用二倍角公式进行三角恒等变换。
重点难点记住二倍角公式，运用二倍角公式进行求值、化简和证明。
在运用当中如何正确恰当运用二倍角公式。
引入新课1、=α2sin ； =α2cos = = ；=α2tan _______________ ；=α2cos ；=α2sin 。
2、化简：)125cos 125)(sin 125cos 125(sin ππππ-+= ； ︒︒75sin 15sin =125tan2125tan 12ππ-= 例题剖析例1、化简απαπα222sin )6(sin )6(sin -++-。
例2 、求证：1)10tan 31(50sin =︒+︒例3、在半圆形钢板上截取一块矩形材料，怎样截取能使这个矩形的面积最大？巩固练习1、化简：（1）2)15cos 15(sin ︒+︒ （2）125cos 12sin 22ππ+；（3）︒-︒+10sin 20cos 22 （4）θθtan 11tan 11+--2、证明：（1）B A B A B A 2cos 2cos )(sin )(cos 22=--+（2）θθθ2cos )tan 1(cos 22=-3、已知31tan ,71tan ==βα, 且α,β都是锐角，求βα2+的值。
4、试说明x y x y 2sin 2sin ==与图象之间有什么关系？课堂小结灵活运用二倍角公式进行三角恒等变换课后训练班级：高一（ ）班 姓名__________一、基础题 1、已知x sin =215-，则)42(sin 2π-x 的值等于______________.2、若)2,0(πα∈，则化简α2cos 21212121--= 3、若0cos cos sin sin =+βαβα，则ββααcos sin cos sin +的值为_____________. 4、用αsin 表示α3sin 。
高中数学 第36课时(二倍角的三角函数2)教学案 苏教版必修4 学案
江苏省南京市溧水县高中数学 第36课时《二倍角的三角函数2》教学案 苏教版必修4总 课 题 二倍角的三角函数总课时 第36课时 分 课题 二倍角的三角函数（2）分课时第 2 课时教学目标 灵活运用二倍角公式进行三角恒等变换。
重点难点记住二倍角公式，运用二倍角公式进行求值、化简和证明。
在运用当中如何正确恰当运用二倍角公式。
引入新课1、=α2sin ； =α2cos = = ；=α2tan _______________ ；=α2cos ；=α2sin 。
2、化简：)125cos 125)(sin 125cos 125(sin ππππ-+= ；︒︒75sin 15sin = 125tan2125tan 12ππ-=例题剖析例1、化简απαπα222sin )6(sin )6(sin -++-。
例2 、求证：1)10tan 31(50sin =︒+︒例3、在半圆形钢板上截取一块矩形材料，怎样截取能使这个矩形的面积最大？巩固练习1、化简：（1）2)15cos 15(sin ︒+︒ （2）125cos 12sin 22ππ+；（3）︒-︒+10sin 20cos 22（4）θθtan 11tan 11+--2、证明：（1）B A B A B A 2cos 2cos )(sin )(cos 22=--+（2）θθθ2cos )tan 1(cos 22=-3、已知31tan ,71tan ==βα, 且α,β都是锐角，求βα2+的值。
4、试说明x y x y 2sin 2sin ==与图象之间有什么关系？课堂小结灵活运用二倍角公式进行三角恒等变换 课后训练班级：高一（ ）班 姓名__________ 一、基础题 1、已知x sin =215-，则)42(sin 2π-x 的值等于______________. 2、若)2,0(πα∈，则化简α2cos 21212121--= 3、若0cos cos sin sin =+βαβα，则ββααcos sin cos sin +的值为_____________. 4、用αsin 表示α3sin 。
高中数学 32二倍角的三角函数学案 苏教版必修4 学案
3.2 二倍角的三角函数一、 学习内容、要求及建议二、预习指导 1. 预习目标(1)推导二倍角公式的思想和方法；(2)二倍角公式以及余弦的二倍角公式的变形(升、降幂公式)的记忆和应用； (3)和差角公式、二倍角公式综合应用. 2. 预习提纲(1)阅读课本P105思考如何推导二倍角正弦、余弦、正切公式，并探究三倍角正弦、余弦、正切公式，并填空：sin 2=； cos 2===；tan 2=(所有tan 有意义)注意“倍角”的相对性.(2)阅读课本P107的降幂公式并学会运用降幂公式解题(如P106例3的解法1)，阅读课本P107的例4，学会公式灵活运用.(3)探究：求sin10sin30sin50sin 70的值. 3. 典型例题 (1) 熟悉公式 例1 已知1312cos -=α，)23,(ππα∈，求α2sin ，α2cos ，α2tan 的值. 分析：先利用同角三角函数的关系求出αsin ，再分别套用二倍角正弦、余弦公式，注意角的X 围.解：∵1312cos -=α，)23,(ππα∈∴135)1312(1sin 2-=---=α. ∴169120)1312()135(2cos sin 22sin =-⋅-⋅==ααα 1691191)1312(21cos 22cos 22=--=-=αα，1191202cos 2sin 2tan ==ααα (2) 应用二倍角公式进行化简、求值、证明等 例2 已知21)tan(=-βα，71tan -=β，),0(,πβα∈，求βα-2.分析：先求αtan ，再求α2tan ，最后求)2tan(βα-，注意βα-2的X 围.解：∵βαβαβαtan tan 1tan tan )tan(+-=-，∴)71(tan 1)71(tan 21-⋅+--=αα，解得31tan =α ∴43)31(1312tan 1tan 22tan 22=-⋅=-=ααα ∴1)71(431)71(43tan 2tan 1tan 2tan )2tan(=-⋅+--=+-=-βαβαβα ∵),0(,πβα∈，031tan >=α，071tan <-=β，∴),2(),2,0(ππβπα∈∈∴)2,(ππβ--∈- 又∵0432tan >=α∴)2,0(2πα∈，∴)0,(2πβα-∈-∴432πβα-=-.例3 已知xxx x x tan 1sin 22sin ,4745,53)4cos(2-+<<=+求πππ的值．分析：(1)先降幂，再用和差角公式展开,(2)条件展开为关于“x x sin cos -”的条件，对需要求值的式子先化简，对“切”化成“弦”，对“x 2sin ”用二倍角公式，注意“x x sin cos -”、 “x x sin cos +” 、“x x cos sin 2”这三者的关系. 解：由53)4cos(=+πx 得523sin cos =-x x ，两边平方得：2518cos sin 21=-x x ，∴257cos sin 2=x x ，∵4745ππ<<x ∴2)cos (sin sin cos x x x x +-=+=5242571cos sin 21-=+-=+-x x ∴xx x tan 1sin 22sin 2-+=xx x x x cos sin 1sin 2cos sin 22-+=x x x x x x sin cos )sin (cos cos sin 2-+⋅=523)524(257-⋅=7528-. 例4 求值：(1)178cos 174cos 172cos17cosππππ； (2)sin 6sin 42sin 66sin 78；(3)tan 70cos103sin10tan 702cos 40+-.分析：(1)由这些角中后一角为前一角的两倍，联想到用正弦的二倍角公式；(2)这是4个正弦的积，且它们的角之间难以看出明显的关系.仿(1)将部分正弦化为余弦，用类似(1)的方法解题；(3)注意到20与40的关系，选择恰当的公式向“同角”方向努力.解：(1)原式=17sin 2178cos 174cos 172cos17cos17sin244ππππππ=17sin16178cos174cos 172cos 172sin 23πππππ =17sin 16178cos 174cos 174sin 22ππππ=17sin 16178cos 178sin 2πππ=16sin1171616sin17ππ= (2)原式=sin 6cos 48cos 24cos12=442cos 6sin 6cos12cos 24cos 482cos 6=32sin12cos12cos 24cos 4816cos 6=sin 9616cos 6=sin 84116sin 8416= (3)原式=tan 70(cos103sin10)2cos 40+-=cos 202sin 402cos 40sin 20⋅-=cos 204sin 20cos 202cos 40sin 20⋅-=224cos 202(2cos 201)2--=(3) 升幂、降幂公式的应用降幂公式22cos 1sin 2αα-=，22cos 1cos 2αα+=特点：降幂同时扩角，当遇到αα22cos ,sin 且不需要“平方”时，常考虑该公式.升幂公式αα2sin 22cos 1=-，αα2cos 22cos 1=+特点：升幂同时缩角，当遇到αcos 1±时，常考虑该公式.例5 化简：θθθθθcos 22)2cos 2)(sincos sin 1(+-++，(0,)∈分析：分母显然用升幂公式，分子中的“1”可与θsin 结合换成12cos 2sin22=+θθ同时对θsin 用二倍角公式；也可把“1”与θcos 结合用升幂公式同时对θsin 也用二倍角公式，公式选择的主要依据依然是“同角”.解：原式=2cos 4)2cos 2)(sin 2cos 22cos 2sin2(22θθθθθθ-+=2cos )2cos 2(sin 2cos 22θθθθ-=2coscos 2cos θθθ⋅-∵),0(πθ∈∴)2,0(2πθ∈∴02cos >θ∴原式=θcos - 例6 (1)已知21sin sin =+βα，31cos cos =+βα，求2cos 2βα-的值；(2)求函数1)12(cos )12(sin 22--++=ππx x y 的最大值．分析：(1)∵2)cos(12cos 2βαβα-+=-∴只要求)cos(βα-，将已知两等式平方相加即可；(2)∵12π不是特殊角∴应先降幂扩角，再用和差角公式展开.解：(1)将21sin sin =+βα，31cos cos =+βα分别平方并相加得： 3613)cos cos sin (sin 22=++βαβα，即7259)cos(-=-βα. ∴144132725912)cos(12cos 2=-=-+=-βαβα.(2)1)12(cos )12(sin 22--++=ππx x y =12)62cos(12)62cos(1--+++-ππx x=)2sin 212cos 232sin 212cos 23(21x x x x +-+=x 2sin 21∴21max =y 4. 自我检测 (1)已知sin:sin8:52=，则cos 的值为______________．(2)等腰三角形的一个底角的正弦为53，则这个三角形的顶角的正切为_________． (3)不查表求值：=-125sin 1211sin 22ππ． (4)计算：13sin 50+=．(5)化简：sin 2sincos 2cos 1+++=__________．(6)求值：(1)24coscoscos 777πππ⋅⋅；(2))10tan 31(40cos+.(7)求证：函数222()cos cos ()cos ()33f x x x x =+++-是常数函数．三、 课后巩固练习A 组1．已知sin 26cos 5x x =，则cos2x 的值等于___________． 2．已知1sin 2x =，则sin 2()4x π-=．3．已知02x π-<<，4cos 5x =，则tan 2x 等于_________． 4．函数22cos sin 2y x x =+的最小值是_____________________．5．已知的值等于则x x 2sin ,135)4sin(-=-π__________． 6．求值：(1)224cos 1533-+︒； (2) 44sin 67.5cos 67.5- ； (3) 111tan151tan15-+-.7．已知sin()sin()44ππαα-+=，且α为锐角，求sin 2α的值．8．已知sin cos 3αα+=，0απ<<，求cos 2α的值． 9. 若1tan 4tan θθ+=,则sin 2θ=.10. 若42ππθ⎡⎤∈⎢⎥⎣⎦，,sin 2=8θ,则sin θ=.11(1sin cos )(sincos )αααα++-2παπ<<)．B 组121sin 20--为___________． 13．已知 ααα则角,532cos ,542sin-==是第____象限角. 14. 设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则)122sin(π+a 的值为．15. 已知1cos 21sin cos ααα-=，1tan()3βα-=-，则tan(2)βα-=．16．求值：（1）=080cos 40cos 20cos ； （2）=+++167sin 165sin 163sin 4sin4444ππππ． 17．已知sin14cos14a=+，2142b =-2c =，则a 、b 、c 按从小到大的顺序排列为．18．函数sin cos 1sin cos 1x x y x x +=-的值域是____________________．19．函数1sin cos sin 22x x x +-的值域为．20．函数11()cos 22cos 22f x x x =-+在区间2[,]3πθ-上的最大值为1，则θ的最小值是．21．已知函数()2sin()cos f x x x π=-. (1)求()f x 的最小正周期；(2)求()f x 在区,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.22．(1)2sin 13cos17sin13cos17︒+︒-︒︒(2)2sin 15cos15sin15cos15︒+︒-︒︒(3)2sin 18cos12sin18cos12︒+︒-︒︒(4)2sin (18)cos 48sin(18)cos 48-︒+︒--︒︒(5)2sin (25)cos55sin(25)cos55-︒+︒--︒︒ Ⅰ 试从上述五个式子中选择一个,求出这个常数；Ⅱ 根据(Ⅰ)的计算结果,将该同学的发现推广三角恒等式,并证明你的结论. 23．设函数2()cos(2)sin 3f x x x =++.(1) 求函数()f x 的最大值和最小正周期； (2) 设,,A B C 为ABC 的三个内角，若1cos 3B =，1()24c f =-，且C 为锐角，求sin A .24. 已知函数2()=sin (2+)+sin(2)+2cos 133f x x x x ππ--,x R ∈.(Ⅰ)求函数()f x 的最小正周期； (Ⅱ)求函数()f x 在区间[,]44ππ-上的最大值和最小值.25. 已知向量(1sin 2,sin cos )a x x x =+-，(1,sin cos )b x x =+，函数()f x a b =⋅． （1）求()f x 的最大值及相应的x 的值；（2）若8()5f θ=，求cos 2(2)4πθ-的值． C 组26．若42x ππ<<，则函数3tan 2tan y x x =的最大值为．27．已知函数2()2cos cos f x x x x =+.（1）求函数()f x 在[,]63ππ-上的值域； （2）在△ABC 中，若()2,2sin cos()cos()f C B A C A C ==--+，求tan A 的值. 28．设函数2()sin()2cos 1468x xf x πππ=--+． (1)求()f x 的最小正周期；(2)若函数()y g x =与()y f x =的图像关于直线1x =对称，求当4[0,]3x ∈时()y g x =的最大值．29．已知sin sin 1+=，cos cos 0+=，试求cos 2cos 2+的值．30．已知2244x y +=，求22441t x xy y =+-+的最大值和最小值．四、 学习心得五、 拓展视野课本112111=P 向我们介绍了正弦函数与余弦函数的叠加函数x B x A x f cos sin )(+=(A ，B 不全为0)，并指出该函数可以改写成)sin()(22θ++=x B A x f ，其中22cos BA A +=θ，22sin BA B +=θ，一般地，我们把公式xB x A cos sin +)sin(22θ++=x B A (22cos BA A +=θ，22sin BA B +=θ)称为辅助角公式.下面我们来看它的两个应用：例1 求函数)80sin(5)20sin(300+++=x x y 的最大值.解：23)20cos(521)20sin(5)20sin(300⋅++⋅+++=x x x y =)20cos(235)20sin(21100+++x x =)20sin()235()211(022θ+++x =)20sin(70θ++x (其中1411cos =θ，1435sin =θ)∴7max =y 例2 求函数xxy cos 2sin 3+=的值域.解：将xxy cos 2sin 3+=变形为y x y x 2cos sin 3=-，∴y x y 2)sin(32=++θ(其中233cos y+=θ，23sin yy +-=θ)即232)sin(yy x +=+θ，∵1sin(≤+θx ∴1322≤+yy ，解得11≤≤-y∴函数xxy cos 2sin 3+=的值域为[-1，1].。
高中数学 第35课时(二倍角的三角函数1)教学案 苏教版必修4 学案
某某省某某市溧水县高中数学 第35课时《二倍角的三角函数1》教学案 苏教版必修4总 课题二倍角的三角函数 总课时 第35课时分 课题 二倍角的三角函数（1）分课时第1课时 教学目标 能记住二倍角公式，会运用二倍角公式进行求值、化简和证明，同时懂得这一公式在运用当中所起到的用途。
培养观察分析问题的能力，寻找数学规律的能力，同时注意渗透由一般到特殊的化归的数学思想及问题转化的数学思想。
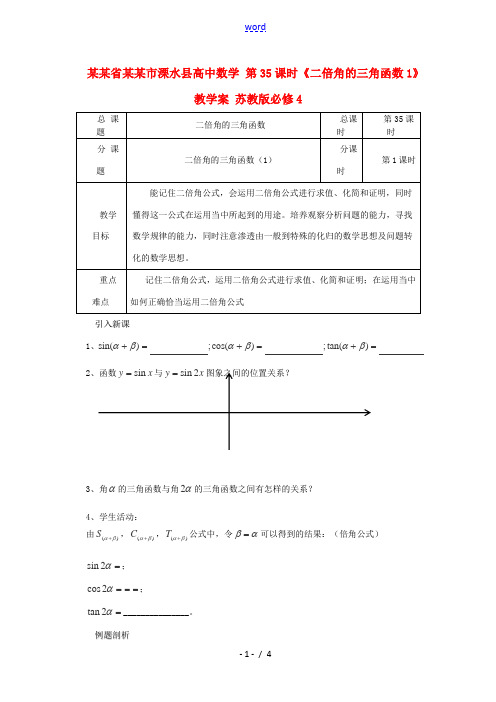
重点难点 记住二倍角公式，运用二倍角公式进行求值、化简和证明；在运用当中如何正确恰当运用二倍角公式 引入新课1、=+=+=+)tan(;)cos(;)sin(βαβαβα2、函数x y sin =与x y 2sin =图象之间的位置关系？3、角α的三角函数与角α2的三角函数之间有怎样的关系？4、学生活动：由)(βα+S ，)(βα+C ，)(βα+T 公式中，令αβ=可以得到的结果：（倍角公式） =α2sin ；=α2cos ==；=α2tan _______________。
例题剖析O xy例1、已知1312sin =α，),2(ππα∈，求ααα2tan 2cos 2sin ，，的值。
例2、求证：θθθθθtan 2cos 2sin 12cos 2sin 1=++-+。
例3、不查表，求下列各式的值。
（1）︒︒15cos 15sin （2）8sin 8cos 22ππ- （3）︒-︒5.22tan 15.22tan 22 （4）︒-75sin 212巩固练习1、求下列各式的值：（1）8cos 8sin ππ=；（2）16cos 16sin 22ππ-=；（3）=︒-︒15tan 115tan 22； （4）=︒-15sin 212；（5）=12cos 24cos 48cos 48sin 8ππππ。
2、已知，，542cos 532sin -==αα 则角α的终边在第___________象限。
3、已知)2,0(8.0sin παα∈=，，求αα2cos 2sin ，的值。
苏教版高中数学必修四《二倍角的三角函数》教案2
二倍角的三角函数教学目标：掌握二倍角的正弦、余弦、正切公式，能用上述公式进行简单的求值、化简、恒等证明；引导学生发现数学规律，让学生体会化归这一基本数学思想在发现中所起的作用，培养学生的创新意识.教学重点：二倍角公式的推导及简单应用.教学难点：理解倍角公式，用单角的三角函数表示二倍角的三角函数.教学过程：Ⅰ.课题导入前一段时间，我们共同探讨了和角公式、差角公式，今天，我们继续探讨一下二倍角公式.我们知道，和角公式与差角公式是可以互相化归的.当两角相等时，两角之和便为此角的二倍，那么是否可把和角公式化归为二倍角公式呢?请同学们试推.先回忆和角公式sin(α＋β)＝sinαcosβ＋cosαsinβ当α＝β时，sin(α＋β)＝sin2α＝2sinαcosα即：sin2α＝2sinαcosα(S2α)cos(α＋β)＝cosαcosβ－sinαsinβ当α＝β时cos(α＋β)＝cos2α＝cos2α－sin2α即：cos2α＝cos2α－sin2α(C2α)tan(α＋β)＝tanα＋tanβ1－tanαtanβ当α＝β时，tan2α＝2tanα1－tan2αⅡ.讲授新课同学们推证所得结果是否与此结果相同呢?其中由于sin2α＋cos2α＝1，公式C2α还可以变形为：cos2α＝2cos2α－1或：cos2α＝1－2sin2α同学们是否也考虑到了呢?另外运用这些公式要注意如下几点：(1)公式S 2α、C 2α中，角α可以是任意角；但公式T 2α只有当α≠π2 ＋kπ及α≠π4 ＋k π2 (k ∈Z )时才成立，否则不成立(因为当α＝π2 ＋kπ，k ∈Z 时，tan α的值不存在；当α＝π4 ＋k π2 ，k ∈Z 时tan2α的值不存在).当α＝π2 ＋kπ(k ∈Z )时,虽然tan α的值不存在，但tan2α的值是存在的，这时求tan2α的值可利用诱导公式：即：tan2α＝tan2(π2 ＋kπ)＝tan(π＋2kπ)＝tan π＝0(2)在一般情况下，sin2α≠2sin α例如：sin π3 ＝32≠2sin π6 ＝1；只有在一些特殊的情况下，才有可能成立［当且仅当α＝kπ(k ∈Z )时，sin2α＝2sin α＝0成立］.同样在一般情况下cos2α≠2cos αtan2α≠2tan α(3)倍角公式不仅可运用于将2α作为α的2倍的情况，还可以运用于诸如将4α作为2α的2倍，将α作为 α2 的2倍，将 α2 作为 α4 的2倍，将3α作为 3α2的2倍等等.下面，来看一些例子：［例1］已知sin α＝513 ，α∈(π2 ，π)，求sin2α，cos2α，tan2α的值.解：∵sin α＝513 ，α∈(π2 ，π)∴cos α＝－1－sin 2α ＝－1－（513 ）2 ＝－1213∴sin2α＝2sin αcos α＝2×513 ×(－1213 )＝－120169 ，cos2α＝1－2sin 2α＝1－2×(513 )2＝119169 ，tan2α＝sin2αcos2α ＝－120169 ×169119 ＝－120119 .练习题：1.已知cos α＝m ，α在第二象限，求sin2α，cos2α，tan2α的值.解：∵cos α＝m ，α在第二象限.∴sin α＝1－cos 2α ＝1－m 2∴sin2α＝2sin αcos α＝21－m 2 ·m ＝2m 1－m 2cos2α＝2cos 2α－1＝2m 2－1tan2α＝sin2αcos2α ＝2m 1－m 2 2m 2－1或由tan α＝sin αcos α ＝1－m 2 mtan2α＝2tan α1－tan 2α ＝2m 1－m 2 2m 2－12.化简cos(θ＋15°)＋cos(θ－15°)－32cos2θ分析：由于观察到此式中的角出现了θ＋15°、θ－15°与2θ，另外还出现了二次式，所以要用二倍角余弦公式的变形式达到降“次”及统一角的目的.解：cos(θ＋15°)＋cos(θ－15°)－32cos2θ＝1＋cos[2(θ＋15°)]2 ＋1＋cos[2(θ－15°)]2 －32cos2θ＝1＋12 ［cos(2θ＋30°)＋cos(2θ－30°)］－32cos2θ＝1＋12 ［cos2θcos30°－sin2θsin30°＋cos2θcos30°＋sin2θsin30°］－32cos2θ＝1＋12 ×2cos2θcos30°－32cos2θ ＝1＋32cos2θ－32cos2θ＝1评述：二倍角公式的等价变形：sin 2α＝1－cos2α2 ，cos 2α＝1＋cos2α2 ，可以进行“升(降)幂”的变换，即可将“二次式”与“一次式”互化.［例2］若270°＜α＜360°，化简：12 ＋12 12 ＋12 cos2α解：∵cos2α＝2cos 2α－1，cos α＝2cos 2α2 －1 ∴12 ＋12 12 ＋12 cos2α＝12 ＋12 12 ＋12 （2cos 2α－1） ＝12 ＋12 cos 2α 又∵270°＜α＜360° 135°＜α2 ＜180°∴原式＝12 ＋12 cos α ＝12 ＋12 （2cos 2α2 －1） ＝cos 2α2 ＝－cos α2［例3］求sin10°sin30°sin50°sin70°的值.解：sin10°＝cos80° sin50°＝cos40°sin70°＝cos20°∴原式＝12 cos80°cos40°cos20°＝12 ×cos80°cos40°cos20°sin20°sin20° ＝12 ×cos80°cos40°sin40°×12 sin20°＝12 ×cos80°sin80°×12 ×12 sin20° ＝12 ×sin160°×12 ×12 ×12 sin20° ＝116［例4］求证：8cos 4θ＝cos4θ＋4cos2θ＋3证明：8cos 4θ＝8(cos 2θ)2＝8(1＋cos2θ2 )2＝2(cos 22θ＋2cos2θ＋1) ＝2(1＋cos4θ2)＋4cos2θ＋2＝cos4θ＋4cos2θ＋3 Ⅲ.课堂练习课本1、2、3、4.Ⅳ.课时小结理解并掌握二倍角公式以及推导，能正确运用二倍角的正弦、余弦、正切公式进行简单三角函数式的化简、求值与恒等式证明.二倍角公式是由和角公式由一般化归为特殊而来的，要注重这种基本数学思想方法，学会怎样去发现数学规律.Ⅴ.课后作业课本习题 1、2、3、4。
高中数学 3.2 二倍角的三角函数教案2 苏教版必修4
第2课时二倍角的三角函数的应用(教师用书独具)●三维目标1．知识与技能(1)能用倍角公式推导出半角公式．(2)能运用三角函数的公式进行简单的恒等变换．(3)会用三角函数解决一些简单的实际问题．2．过程与方法让学生由倍角公式导出半角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣；通过例题讲解，总结方法，通过做练习，巩固所学知识．3．情感、态度与价值观通过本节的学习，使学生对三角函数各个公式之间有一个全新的认识；理解掌握三角函数各个公式的各种变形，增强学生灵活运用数学知识的能力、逻辑推理能力和综合分析能力，提高逆用思维的能力．●重点难点重点：角的和、差、倍公式的综合应用．难点：运用所学公式解决简单的实际问题．(教师用书独具)●教学建议关于半角公式的教学教学时，建议教师从让学生回忆二倍角的三个余弦公式出发，提出问题“如何用角θ的三角函数值，表示角θ2的三角函数值”．在此基础上，让学生自主归纳探究，并总结出半角公式，然后结合半角公式的特点，师生共同总结出公式记忆方法，最后通过典型例题及题组训练熟悉并掌握半角公式．整个教学立足于体现一种“以思导学”的知识生成过程．●教学流程 创设问题情境，引导学生推导出降幂公式与半角公式，并总结公式的特点及作用.⇒通过例1及其互动探究，使学生掌握利用降幂公式进行三角函数式的化简与证明的方法.⇒通过例2及其变式训练，使学生掌握利用和、差、倍角公式研究函数的性质的解题方法.⇒通过例3及其变式训练，使学生掌握解决三角函数实际应用问题的思路及方法.⇒归纳整理，进行课堂小结，整体认识本节课所学知识.⇒完成当堂双基达标，巩固所学知识并进行反馈矫正.已知cos α的值，如何求sin α2的值？【提示】 由cos α＝1－2sin2α2得sin2α2＝1－cos α2，∴sin α2＝± 1－cos α2.(1)降幂公式①sin 2α2＝1－cos α2； ②cos 2α2＝1＋cos α2； ③tan 2α2＝sin2α2cos2α2＝1－cos α1＋cos α.(2)半角公式①sin α2＝± 1－cos α2；②cos α2＝±1＋cos α2； ③tan α2＝±1－cos α1＋cos α＝sin α1＋cos α＝1－cosαsin α.化简cos 2(θ＋15°)＋cos 2(θ－15°)－32cos 2θ. 【思路探究】 此式中出现了θ＋15°，θ－15°与2θ，要达到角的统一，需将角θ＋15°，θ－15°向角2θ进行转化，因此，可考虑降幂公式．【自主解答】 cos 2(θ＋15°)＋cos 2(θ－15°)－32cos 2θ ＝1＋cos[2θ＋15°]2＋1＋cos[2θ－15°]2－32cos 2θ＝1＋12[cos(2θ＋30°)＋cos(2θ－30°)]－32cos 2θ＝1＋12(cos 2θcos 30°－sin 2θsin 30°＋cos 2θcos 30°＋sin 2θsin 30°)－32cos 2θ ＝1＋12×2cos 2θcos 30°－32cos 2θ＝1＋32cos 2θ－32cos 2θ＝1.1．应用降幂公式可将“二次式”转化为“一次式”．2．三角函数式的化简，一般从减少角的种类、减少函数的种类、改变函数运算的结构入手，常采用化弦法、化切法、异角化同角、异次化同次、异名化同名等方法，达到化简的目的．如将本例改为“sin 2(θ＋15°)＋sin 2(θ－15°)＋32cos 2θ”，如何化简？ 【解】 原式＝1－cos 2θ＋30°2＋1－cos 2θ－30°2＋32cos 2θ＝1－12[cos(2θ＋30°)＋cos(2θ－30°)]＋32cos 2θ＝1－12()2cos 2θ·cos 30°＋32cos 2θ＝1－3cos 2θ＋3cos 2θ＝1.利用和、差、倍角公式研究函数的性质求函数f (x )＝53cos 2x ＋3sin 2x －4sin x cos x ，x ∈[π4，7π24]的最小值，并求其单调减区间．【思路探究】化简f x 的解析式→fx ＝A sin ωx ＋φ＋B →ωx ＋φ的范围→求最小值，单调减区间【自主解答】 f (x )＝53·1＋cos 2x 2＋3·1－cos 2x2－2sin 2x＝33＋23cos 2x －2sin 2x＝33＋4(32cos 2x －12sin 2x )＝33＋4(sin π3cos 2x －cos π3sin 2x )＝33＋4sin(π3－2x )＝33－4sin(2x －π3)，∵π4≤x ≤7π24， ∴π6≤2x －π3≤π4. ∴sin(2x －π3)∈[12，22]．∴当2x －π3＝π4，即x ＝7π24时，f (x )取最小值为33－2 2.∵y ＝sin(2x －π3)在[π4，7π24]上单调递增，∴f (x )在[π4，7π24]上单调递减．1．研究函数性质的一般步骤： (1)对函数式化简；(2)借用函数图象，运用数形结合法研究函数的性质． 2．对三角函数式化简的常用方法： (1)降幂化倍角； (2)升幂角减半；(3)利用f (x )＝a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)(其中tan φ＝ba)，化同名函数．(2013·济宁高一检测)已知函数f (x )＝2cos 2x ＋23sin x cos x ＋3，x ∈R . (1)求函数f (x )的最小正周期；(2)求函数f (x )在(0，π3]上的最小值与最大值．【解】 (1)f (x )＝2cos 2x ＋23sin x cos x ＋3＝cos 2x ＋3sin 2x ＋4＝2sin(2x ＋π6)＋4.所以函数f (x )的最小正周期T ＝2π2＝π.(2)∵0＜x ≤π3，∴π6＜2x ＋π6≤5π6，当x ＝π3时，2x ＋π6＝5π6，函数f (x )取得最小值为5.当x ＝π时，2x ＋π＝π，函数f (x )取得最大值为6.点P 在直径AB ＝1的半圆上移动，过P 作圆的切线PT ，且PT ＝1，∠PAB ＝α，问α为何值时，四边形ABTP 的面积最大？【思路探究】 首先根据题意画出图形，然后根据圆的几何性质和四边形面积的求法，将四边形的面积表示为三角函数的形式，最后利用三角函数的性质解决．【自主解答】 如图，∵AB 为直径，∴∠APB ＝90°， PA ＝cos α，PB ＝sin α.又PT 切圆于P 点， ∴∠TPB ＝∠PAB ＝α， ∴S四边形ABTP＝S △PAB ＋S △TPB ＝12PA ·PB ＋12PT ·PB sin α＝12sin αcos α＋12sin 2α＝14sin2α＋1－cos 2α4＝14(sin 2α－cos 2α)＋14＝24sin(2α－π4)＋14. ∵0＜α＜π2，∴－π4＜2α－π4＜3π4.∴当2α－π4＝π2，即当α＝3π8时，四边形ABTP 的面积最大，最大为1＋24.解决实际问题时，应首先设定主变量角α以及相关的常量与变量，建立含有角α的三角函数的关系式，再利用三角变换、三角函数的性质等进行求解．一般地，求最值的问题需利用三角函数的有界性来解决．某工人要从一块圆心角为45°的扇形木板中割出一块一边在半径上的内接长方形桌面，若扇形的半径长为1 m ，求割出的长方形桌面的最大面积为________．【解析】 如图，连结 OC，设∠COB＝θ，则 0°＜θ＜45°，OC＝1，∵AB＝OB－OA＝cos θ－AD＝cos θ－BC＝cos θ－sin θ，∴S 矩形 ABCD＝AB·BC＝(cos θ－sin θ)sin θ ＝－sin2θ＋sin θcos θ＝－12(1－cos 2θ)＋12sin 2θ1 ＝2(sin2θ＋cos2θ)－12＝ 22cos(2θ－π4 )－12， 当 2θ－π4 ＝0， 即 θ＝π8 时，Smax＝ 22－1(m2)，∴割出的长方形桌面的最大面积为2－1 2m2.【答案】2－1 2m211三角函数式化简时忽视角的范围致误已知3π 2 ＜α＜2π，化简12＋1212＋21cos α.【错解】11 2＋211 2＋2cosα＝ 12＋121＋cos 2α＝12＋12cos2α211 α ＝ 2＋2cos 2 ＝α 1＋cos 22＝cos2α4 ＝cos α4 .【错因分析】 上述错解在于运用倍角公式从里到外去根号时，没有顾及角的范围而选 择正、负号，只是机械地套用公式．【防范措施】 应根据三角函数式的值的符号去掉绝对值，因此在去掉三角函数式的绝 对值符号时，要注意角的范围问题．12【正解】12＋1221＋12cos α11 ＝ 2＋21＋cos α 2＝12＋12cos2α2＝ 12＋12|cos α2 |.因为32π＜α＜2π，所以34π＜α2 ＜π，α 所以 cos 2 ＜0，所以原式＝12－21cosα 2＝1－cosα 22＝sin2α4 ＝|sinα 4 |.因为32π＜α＜2π，所以38π＜α4 ＜π2 ，αα所以 sin 4 ＞0，所以原式＝sin 4 .(1)二倍角余弦公式变形用来升幂降幂，应灵活掌握：sin2α＝1－co2s 2α，cos2α＝1＋cos 22α.(2)解决有关的化简、求值、证明时注意二倍角公式的综合运用．(3)对于三角函数在实际问题中的应用，其求解策略为引入恰当的辅助角，建立有关辅助角的三角函数表达式，并利用和、差、倍角公式进行化简整理．由于引入辅助角的恰当与13否直接影响该题的计算量，故求解时多注意分析题设，恰当引入．1．若 cosα＝13，且 α∈(0，π)，则 sinα 2 的值为________．【解析】 ∵α∈(0，π)，∴α2 ∈(0，π2 )，∴sin α2 ＝1－cos 2α＝13＝ 33.【答案】3 32．已知 cosα＝－35，且 π＜α＜32π，则 cosα 2 ＝________.【解析】 ∵π＜α＜32π，∴π2 ＜α2 ＜34π，α1＋cos α∴cos 2 ＝－2 ＝－31－552 ＝－ 5 .5 【答案】 － 53．已知 tanα 2 ＝3，则 cosα＝________.α 【解析】 由 tan 2 ＝1－cos 1＋cosα α＝3 可得：1－cos 1＋cosα α＝9，则 cosα＝－45.【答案】 －451＋sin θ＋cos θsinθ2 －cosθ 24．化简：2＋2cos θ(0＜θ＜π)．【解】 原式142sinθ 2 cosθ2 ＋2cos2θ2θθsin 2 －cos 2＝4cos2θ2cosθ 2＝sin2θ2 －cos2θ2 |cos θ2 |－cos θ2 cos θ ＝ |cos θ2 | .∵0＜θ＜π，∴0＜θ2 ＜π2 .θ ∴cos 2 ＞0.∴原式＝－cos θ.一、填空题 1．sinπ8 ＝________.【解析】 sinπ8 ＝1－cosπ4 2＝1－2 22＝2－ 22.【答案】2－ 2 22.－23＋43cos2 15°＝________.【解析】 原式＝－23＋43×1＋co2s 30°＝－23＋23＋23cos 30°＝ 33.【答案】3 33．5π<θ<6π，cosθ2 ＝a，则θ sin 4 ＝________.15【解析】 ∵5π<θ<6π，∴5π4 <θ4 <32π，∴sinθ4 <0.sin θ4 ＝－θ 1－cos 22 ＝－1－2 a.【答案】 －1－a 24．函数 f(x)＝2cos x(sin x＋cos x)的最小正周期为________．【解析】 f(x)＝2cos x(sin x＋cos x)＝2cos xsin x＋2cos2x＝sin 2x＋cos 2x＋1＝ 2sin(2x＋π4 )＋1.故最小正周期为 T＝2π 2 ＝π. 【答案】 π5. 2＋2cos 8＋2 1－sin 8的化简结果是________．【解析】 原式＝2|cos 4|＋2|sin 4－cos 4|.∵54π＜4，∴cos 4＜0，sin 4＜cos 4.∴原式＝－2cos 4＋2cos 4－2sin 4＝－2sin 4.【答案】 －2sin 46．在△ABC 中，角 A、B、C 满足 4sin2A＋2 C－cos 2B＝72，则角 B 的度数为________．【解析】在 △ ABC中 ， A ＋ B ＋ C ＝ 180° ， 由4sin2A＋C 2－cos2B＝7 2，得4·1－cos 2 A＋C －2cos2B＋1＝72，∴4cos2B－4cos B＋1＝0.∴cos B＝12，B＝60°.【答案】 60°7．(2013·四川高考)设 sin 2α＝－sin α，α∈(π2 ，π)，则 tan 2α 的值是________．【解析】 ∵sin 2α＝－sin α，∴2sin αcos α＝－sin α.∵α∈(π2 ，π)，sin α≠0，∴cos α＝－12.又∵α∈(π2 ，π)，∴α＝23π，∴tan2α＝tan4π3π＝tan(π＋ 3 )＝tanπ 3＝3.【答案】 3 8．设 f(x)＝2s1i＋n cπo2s－2xx＋sin x＋a2sin(x＋π4 )的最大值为 2＋3，则常数 a＝________. 【解析】 f(x)＝1＋22ccooss2xx－1＋sin x＋a2sin(x＋π4 )＝cos x＋sin x＋a2sin(x＋π4 )16＝ 2sin(x＋π4 )＋a2sin(x＋π4 )＝( 2＋a2)sin(x＋π4 )．依题意有 2＋a2＝ 2＋3，∴a＝± 3.【答案】 ± 3 二、解答题 9．设 π＜θ＜2π，cos θ2 ＝a，求(1)sin θ 的值；(2)cos θ 的值；(3)sin2θ4 的值．【解】 (1)∵π＜θ＜2π，∴π2 ＜θ2 ＜π， 又 cos θ2 ＝a，θ ∴sin 2 ＝1－cos2θ2 ＝ 1－a2，∴sin θ＝2sin θ2 cos θ2 ＝2a 1－a2.(2)cos θ＝2cos2θ2 －1＝2a2－1.θ (3)sin2θ4 ＝1－c2os 2 ＝1－2 a.10．若 π＜α＜32π，化简1＋sin α＋1＋cos α－ 1－cos α1－sin α.1＋cos α＋ 1－cos α【解】 ∵π＜α＜3π 2 ，∴π2 ＜α2 ＜34π，αα∴cos 2 ＜0，sin 2 ＞0.sinα2 ＋cosα 22sinα2 －cosα 22∴原式＝αα＋αα2|cos 2 |－ 2|sin 2 | 2|cos 2 |＋ 2|sin 2 |sinα2 ＋cosα 22＝αα－ 2 sin 2 ＋cos 2sinα2 －cosα 22＋αα2 sin 2 －cos 2ααααsin 2 ＋cos 2 sin 2 －cos 2α＝－＋ 22＝－ 2cos 2 .11．(2013·山东高考)设函数 f(x)＝ 23－ 3sin2ωx－sin ωxcos ωx(ω＞0)，且 y＝f(x)图象的一个对称中心到最近的对称轴的距离为π4 .(1)求 ω 的值； (2)求 f(x)在区间[π，32π]上的最大值和最小值．17【解】(1)f(x)＝3 2－3sin2ωx－sin ωxcos ωx3 ＝2－1－cos3·22ωx 1 －2sin2ωx＝3 2 cos2ωx－12sin2ωx＝－sin(2ωx－π3 )．π 因为图象的一个对称中心到最近的对称轴的距离为 4 ，又 ω＞0，所以22π ω＝4×π4 .因此 ω＝1.(2)由(1)知 f(x)＝－sin(2x－π3 )．当 π≤x≤3π 2 时，53π≤2x－π3 ≤8π3 .所以－ 23≤sin(2x－π3 )≤1.因此－1≤f(x)≤ 23.故 f(x)在区间[π，3π 2 ]上的最大值和最小值分别为 23，－1.(教师用书独具)18已知 sin θ＋cos θ＝2sin α，sin2β＝sin θcos θ，求证：2cos 2α＝cos 2β. 【思路探究】 观察问题的条件和结论，发现被证的等式中不含角 θ，因此从已知条 件中消去角 θ，问题即得证．【自主解答】 由题意，得2sin α＝sin θ＋cos θ，①sin2β＝sin θcos θ. ②①2－②×2，得 4sin2α－2sin2β＝1.变形为 1－2sin2β＝2－4sin2α，则有 cos 2β＝2cos 2α.对于给定条件的三角恒等式的证明，常用的方法有直推法和代入法．将条件角转化为 结论角后，由条件等式直接推到结论等式，就是直推法；有时从条件等式中解出关于某个角 的某个三角函数值，代入结论等式便消去某个角，从而将问题转化为三角恒等式的证明问题， 这就是代入法的基本思想方法．19已知 cos θ＝1c＋oscoαs ＋αccooss ββ，求证：tan2θ2 ＝tan2α2 tan2β2 .【证明】∵11－ ＋ccooss θθ＝22csoisn22θθ22 ＝tan2θ2 ，同理有11－ ＋ccooss αα＝tan2α2 ，1－cos 1＋cosββ＝tan2β2 ，cos α＋cos β∴tan2θ2 ＝11－＋ccoossθ 1－1＋cos αcos β θ＝ cos α＋cos β1＋1＋cos αcos β1＋cos αcos β－cos α－cos β ＝1＋cos αcos β＋cos α＋cos β＝1－cos α 1＋cos α1－cos β 1＋cos β＝tan2α2 tan2β2 .20。
高中数学新苏教版精品教案《苏教版高中数学必修4 3.2 二倍角的三角函数》7
二倍角的三角函数一、教学目标：1、知识与技能（1）能由两角和的公式推导出二倍角公式，理解化归思想在公式推导中的作用。
（2）能用二倍角公式进行简单的三角函数式的化简、求值、求角及三角恒等证明。
（3）通过推导二倍角公式，激发学生分析、探求的学习态度，强化学生参与意识，培养学生综合分析能力，增强学习数学的兴趣。
2、过程与方法让学生自己由两角和的正弦、余弦、正切公式推导出二倍角公式，领会从一般到特殊的数学思想，体会公式所蕴含的和谐美，激发学生学习数学的兴趣，通过例题讲解，总结方法，通过做题，巩固所学二倍角公式。
3、情感态度价值观通过本节的学习，使学生对三角的恒等变换有一个全新的认识，熟练掌握三角各个公式的正用，逆用和变形，提高学生灵活运用公式、逻辑推理的能力和综合分析能力。
二、教学重、难点教学重点：熟记二倍角公式，运用二倍角公式求值、化简。
教学难点：在解题过程中如何正确灵活运用二倍角公式及变形。
三、学法与教学工具学法：（1）自主和探究性学习：让学生默写已学的两角和的公式，通过观察思考推导出二倍角的公式，领会从一般到特殊的数学思想，体会公式之间的联系，激发学习数学的兴趣，提高数学素养。
（2）反馈学习法：通过做题来检测知识的掌握情况，查漏补缺，做到活学活用，融会贯通，举一反三。
教学用具：多媒体四、教学过程：（1）回顾两角和与差的正弦、余弦、正切公式（默写公式）=-=+=-=+=-=+)tan()tan()cos()cos()sin()sin(βαβαβαβαβαβα（2）推导二倍角公式思考： 当βα=时，你能否推导出sin 2,cos 2,tan 2ααα？ααααααααααααααααααtan tan 1tan tan )tan(sin sin cos cos )cos(sin cos cos sin )sin(-+=+-=++=+（3）二倍角公式Z k k k R R∈+≠+≠-=∈-=∈=,4,42,tan 1tan 22tan ,sin cos 2cos ,cos sin 22sin 222ππαππαααααααααααα注意：记住每个公式的特点，尤其理解这里的“倍角”的意义是相对以及角的范围。
苏教版数学高一苏教版必修4学案3.2二倍角的三角函数
课堂导学三点剖析1.二倍角公式应用初步 【例1】（1）求cos12πcos 125π的值； （2）求cos20°·cos40°·cos80°； （3）求︒-︒10cos 310sin 1的值.思路分析：本题主要涉及给角求值问题，应充分利用倍角公式及变形形式，抓住题目中各角之间的关系.解：（1）cos 12πcos 125π=cos 12πsin 12π =21·2cos 12πsin 12π=21sin 6π=41. （2）原式=︒︒•︒•︒•︒20sin 280cos 40cos 20cos 20sin 2=︒︒•︒•︒20sin 480cos 40cos 40sin 2=8120sin 8160sin 20sin 880cos 80sin 2=︒︒=︒︒•︒.（3）︒-︒10cos 310sin 1=︒︒︒-︒10cos 10sin 10sin 310cos=︒•︒•︒-︒10cos 10sin 221)10sin 2310cos 21(2 =.420sin )1030sin(4=︒︒-︒•温馨提示对于这类给角求值的问题，应首先观察题目中各角之间的关系.（1）根据12π、125π两角互余，将cos125π换成sin 12π，再配以系数2即可逆用二倍角公式求值；（2）由于各角之间具有倍数关系，40°=2×20°，80°=2×40°，故分子分母同乘以sin20°，便可逆用二倍角公式求值；（3）由结构特点看应先通分，分子正好逆用两角差的正弦公式，分母逆用二倍角公式，约分后即可求值. 2.二倍角公式的变形应用 【例2】设sin （4π-x ）=135,0＜x ＜4π,求)4cos(2cos x x +π的值.思路分析：注意到角之间的关系，2x 是x 的二倍角，4π-x 与4π+x 互为余角，4π是特殊角. 解法1：∵0＜x ＜4π,∴0＜4π-x ＜4π, ∴cos(4π-x)=)4(sin 12x --π=1312)135(12=-. 又cos （4π+x ）=sin(4π-x)=135,∴原式=)4sin()]4(2sin[x x --ππ=)4sin()4cos()4sin(2x x x ---πππ=2cos(4π-x)=1324.解法2：cos2x=cos 2x-sin 2x=(cosx+sinx)·(cosx-sinx)=2sin(x+4π)·2cos(x+4π) =2sin(x+4π)cos(x+4π).∴原式=)4cos()4cos()4sin(2πππ+++x x x =2sin(x+4π)=2cos(4π-x).后面同解法一.温馨提示仔细分析角与角的关系，如4π-x 与4π+x 互为余角；2x 是x 的倍角，且cos2x=sin(2π±2x)=sin ［2（4π±x ）］.分析角的关系，往往是解题的突破口. 3.二倍角变形应用【例3】（1）化简8cos 228sin 12+++；（2）设α∈（π23，2π），化简.cos 21212121α2++解：（1）原式=4cos 44cos 4sin 2122++=2|sin4+cos4|+2|cos4|. 因为4∈（π，π23），所以sin4＜0,cos4＜0. 故原式=-2（sin4+cos4）-2cos4 =-2sin4-4cos4=-2（sin4+2cos4）. （2）因为α∈（π23，2π），所以cosα＞0，cos 2α＜0. 故，原式=.2cos |2cos |2cos cos 2121cos 212122ααααα-===+=+ 温馨提示（1）带有根号的化简问题，首先要去掉根号，想办法将根号内的式子化成完全平方式，即三角函数中常用的解题技巧：“变次”，其中用到了二倍角正弦和余弦的两个重要的变形：1±sinα=（sin2α±cos 2α）2，1±cosα=2cos 22α. （2）脱掉根号时要注意符号问题，如2cos 1=+α|cos2α|，利用α所在的象限，判断cos2α的正负，然后去掉绝对值符号. 各个击破 类题演练1 化简.（1）cos72°·cos36°； （2）cosα·cos2α·cos 22α·cos 32α·…·cos 12-n α. 思路分析：对于（1）要注意72°=2×36°；对于（2）要注意12222--⨯=k k a a （k=1，2，…，n ）.注意到以上的特点，可同乘除一个恰当的因式，然后用倍角公式解之.解：（1）cos36°·cos72°=︒︒•︒•︒36sin 272cos 36cos 36sin 2=︒︒=︒︒•︒36sin 4144sin 36sin 472cos 72sin 2=41. （2）原式同乘除因式sin12-n α，然后逐次使用倍角公式解得原式=12sin22sin -n nαα.变式提升1 已知θ∈（45π，23π），|cos2θ|=51，则sinθ的值是（ ） A.510-B.510C.55-D.515-思路分析：∵θ∈（45π，23π）， ∴si nθ＜0，且2θ∈（25π，3π），∴cos2θ＜0.∵|cos2θ|=51，∴cos2θ=51-.由cos2θ=1-2sin 2θ，得sin 2θ=22cos 1θ-=53，∴sinθ=515-. 答案：D 类题演练2已知sinα+cosα=31,且0＜α＜π,求sin2α、cos2α、tan2α的值. 解：∵sinα+cosα=31,∴sin 2α+cos 2α+2sinαcosα=91,∴sin2α=-98且sinαcosα=94-＜0.又∵0＜α＜π,sinα＞0,∴cosα＜0,∴sinα-cosα＞0.∴sinα-cosα=3172sin 1=-α, ∴cos 2α=cos 2α-sin 2α=(cosα+sinα)(cosα-sinα)=31×(217-)=917-.tan2α=171782cos 2sin =αα.变式提升2 化简ααααα2sin )1cos )(sin 1cos (sin +--+.解法1：原式=αααααααααcos 2cos2sin4)2sin 22cos2sin2)(2sin 22cos2sin2(22•+-=αααααααcos 2cos 2sin )2sin 2)(cos 2sin2(cos••+-=αααααcos 2cos2sin)2sin 2(cos 22••-=2tan cos 2cos 2sincos ααααα=••.解法2：原式=ααααα2sin ]cos 1()][sin cos 1([sin -+--=ααα2sin )cos 1(sin 22--=αααα2-+-sin cos cos 21sin 22=ααααααsin cos 1cos sin 2cos 2cos 22-=-=2tan2cos2sin22sin 22αααα=•.类题演练3︒--︒+100cos 1100cos 1等于( )A.-2cos5°B.2cos5°C.-2sin5°D.2sin5° 解析：原式=︒+---︒+50sin 211150cos 2122 =)50sin 50(cos 250sin 250cos 2︒-︒=︒-︒=2（22cos50°-22sin50°） =2sin （-5°）=-2sin5°，故选C. 答案：C 变式提升3已知函数f （x ）=cos 4x-2sinxcosx-sin 4x. （1）求f （x ）的最小正周期； （2）若x ∈[0，2π],求f （x ）的最大值、最小值. 解：（1）因为f （x ）=cos 4x-2sinxcosx-sin 4x=（cos 2x+sin 2x ）（cos 2x-sin 2x ）-sin2x =cos2x-sin2x=2cos （2x+4π），所以f （x ）的最小正周期T=22π=π. （2）因为0≤x≤2π，所以4π≤2x+4π≤π45.当2x+4π=4π时，cos （2x+4π）取得最大值22；当2x+4π=π时，cos （2x+4π）取得最小值-1. 所以f （x ）在[0，4π]上的最大值为1，最小值为2-.。
苏教版高中数学必修四第课时二倍角的三角函数导学案
1、=+=+=+)tan(;)cos(;)sin(βαβαβα 2、函数x y sin =与x y 2sin =图象之间的位置关系？3、角α的三角函数与角α2的三角函数之间有怎样的关系？4、学生活动：由)(βα+S ，)(βα+C ，)(βα+T 公式中，令αβ=可以得到的结果：（倍角公式）=α2sin ；=α2cos = = ； =α2tan _______________。
例题剖析例1、已知1312sin =α，),2(ππα∈，求ααα2tan 2cos 2sin ，，的值。
例2、求证：θθθθθtan 2cos 2sin 12cos 2sin 1=++-+。
例3、不查表，求下列各式的值。
Oxy（1）︒︒15cos 15sin （2）8sin 8cos 22ππ- （3）︒-︒5.22tan 15.22tan 22（4）︒-75sin 212巩固练习1、求下列各式的值： （1）8cos8sinππ= ；（2）16cos 16sin 22ππ-= ；（3）=︒-︒15tan 115tan 22 ；（4）=︒-15sin 212 ；（5）=12cos24cos48cos48sin8ππππ。
2、已知，，542cos 532sin-==αα则角α的终边在第___________象限。
3、已知)2,0(8.0sin παα∈=，，求αα2cos 2sin ，的值。
4、已知21tan =α，求)22tan(απ+的值5、证明：（1）ααπαπ2sin )cos()sin(2=-+（2）12cos cos 22=-θθ（3）αααsin 2sin 2cos 1=-（4）2tan cos 1cos 12AA A =+-课堂小结 记住二倍角公式，运用二倍角公式进行求值、化简和证明课后训练班级：高一（ ）班 姓名__________一、基础题1、求下列各式的值：（1）0367cos 03112sin '︒'︒= ； （2）︒-︒15cos 15sin 22= ； （3）2112sin 2-π= ；（4）︒-750cos 212= ．2、化简： （1）8cos 8sin 22ππ-= ；（2）2sin 2cos 44αα-=（3）245tan 1245tan2ππ-= ； （4）︒+︒︒-︒15cos 15sin 15cos 15sin = ．3、若21cos sin =+αα，则=α2sin ______________。
二倍角的三角函数学案
二倍角的三角函数(1)学案教学目标：1. 知识： 让学生自己由和角公式推导出倍角公式，了解他们的内在联系；2. 能力： 会利用倍角公式进行求值运算，培养运算能力和逻辑推导能力；3. 情感态度价值观： 领会从一般到特殊的化归数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣。
教学重点：二倍角公式的推导及简单应用.教学难点：倍角公式的形成以及公式的应用教学过程一：问题情境问题1：两角和与差的正弦、余弦、正切公式是什么？你能写出来吗？sin()αβ+=cos()αβ+=tan()αβ+=问题2：若α＝β，结果会如何，你能得出什么结论？试一试！二：学生活动（三名学生板演正弦、余弦、正切二倍角公式的推导过程）sin2α＝2sin α cos αcos2α＝cos 2α－sin 2αtan2α＝2tan α1－tan 2α注：（1）倍角的意义是相对的，如：24αα是的二倍角,224ππαα--是的二倍角，遇到三倍角等名称时，“三”字不能省去。
（如有兴趣可求sin3α=sin(2)αα+）（2）公式S 2α、C 2α中，角α可以是任意角；但公式T 2α只有当α≠π2 ＋kπ及α≠π4 ＋k π2(k ∈Z )时才成立，否则不成立(因为当α＝π2 ＋kπ，k ∈Z 时，tan α的值不存在；当α＝π4 ＋k π2，k ∈Z 时tan2α的值不存在).三：学前质疑问题3：你能给出公式的变形吗？升幂公式：cos2α＝cos 2α－sin 2α，cos2α＝2cos 2α－1，cos2α＝1－2sin 2α降幂公式：22cos2cos2cos ,sin 1+α1-αα=α=22注：要保持平衡。
即降幂要扩角，升幂要缩角四：数学应用题型一:求值例1：口答()222(1)sin cos 88(2)sin cos 12122tan1531tan 15ππππ-===-。
ex1:22log sinlog cos 1212ππ+的值为例2：已知sin α＝513 ，α∈(π2，π)，求sin2α，cos2α，tan2α的值.（课本P1 06例一）变式 1：已知：1sin ,sin 2()24x x π=-求题型二：化简(((13 4= = = =题型三：证明例3求证：1sin2cos2tan1sin2cos2θθθθθ+-=++（课本例2，交流给出不同的证法）注:指导思想------把不同的角化成相同的角。
高中数学3.2 二倍角的三角函数(一) 教案(苏教版必修4)
第 6 课时： 3.2 二倍角的三角函数（一）【三维目标】：一、知识与技能1. 能从两角和的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式，了解它们的内在联系；理解化归思想在推导中的作用。
2. 能正确运用（顺向、逆向、变形运用）二倍角公式求值、化简、证明，增强学生灵活运用数学知识和逻辑推理能力；3.揭示知识背景，引发学生学习兴趣，激发学生分析、探求的学习态度，强化学生的参与意识，并培养学生综合分析能力.4.结合三角函数值域求函数值域问题。
二、过程与方法1.让学生自己由和角公式而导出倍角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣；通过例题讲解，总结方法.通过做练习,巩固所学知识.2.通过公式的推导，了解它们的内在联系，从而培养逻辑推理能力；通过综合运用公式，掌握有关技巧，提高分析问题、解决问题的能力。
三、情感、态度与价值观1.通过本节的学习，使同学们对三角函数各个公式之间有一个全新的认识；理解掌握三角函数各个公式的各种变形，增强学生灵活运用数学知识、逻辑推理能力和综合分析能力.提高逆用思维的能力.2.引导学生发现数学规律,培养学生思维的严密性与科学性等思维品质.【教学重点与难点】：重点：二倍角的正弦、余弦、正切公式以及公式的变形，二倍角公式的简单应用；难点：二倍角的理解及其灵活运用（公式的逆向运用及变式训练）。
【学法与教学用具】：1. 学法：(1)自主+探究性学习：让学生自己由和角公式导出倍角公式，领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣。
(2)反馈练习法：以练习来检验知识的应用情况，找出未掌握的内容及其存在的差距.2. 教法：本节课采用观察、赋值、启发探究相结合的教学方法，运用现代多媒体教学手段，进行教学活动，通过设置问题引导学生观察分析，使学生在独立思考的基础上进行合作交流，在思考、探索和交流的过程中获得倍角公式；（通过设置问题让学生理解二倍角公式是由和角公式由一般化归为特殊而来的）对于二倍角公式的灵活运用，采用讲、练结合的方式进行处理，让学生从实例中去理解,从而能灵活地运用二倍角公式解题。
高中数学 3.2 二倍角的三角函数教案1 苏教版必修4(1)
3.2二倍角的三角函数第 1 课时 二倍角的三角函数(教师用书独具)●三维目标 1．知识与技能 能从两角和的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式．了解它们 的内在联系，并能运用上述公式进行简单的恒等变换． 2．过程与方法 通过公式的推导过程，使学生认识整个公式体系的形成过程，领会体现出的数学基本思 想和方法，从而提高数学素质． 3．情感、态度与价值观 通过公式推导，了解它们的内在联系和知识的发展过程，体会一般与特殊的关系与转化， 培养学生辩证唯物主义观点． ●重点难点 重点：二倍角公式的推导及运用． 难点：二倍角公式的灵活运用．(教师用书独具)●教学建议 1．关于二倍角公式推导的教学 教学时，建议教师先复习和角公式 T(α＋β)，S(α＋β)，C(α＋β)，然后令 α＝β，利用特殊 化的推理方式，让学生自主推导出二倍角公式；在此基础上借助同角三角函数关系，引导学 生得出 C2α 的其他两种形式．通过公式推导，让学生进一步体会公式间的密切联系，提高学 生熟练应用公式解题的能力． 2．关于二倍角公式应用的教学 教学时，建议教师处理好以下两点： (1)强调“倍角”的相对性，打破学生习惯认为只有 α 与 2α 才具有二倍角关系． (2)通过例题教学让学生熟悉公式的正向、逆向和变形运用，特别是余弦公式的变式较 多，教学中应适当通过题目强化训练． ●教学流程创设问题情境，引出问题，如何用α的三角函数表示出sin 2α，cos 2α与tan 2α？⇒ 引导学生结合公式S α＋β 、C α＋β 及T α＋β 推导出倍角公式，并探究二倍角余弦公式的变形.⇒通过例1及其变式训练，使学生掌握灵活运用倍角公式进行求值的方法.⇒1通过例2及其变式训练，使学生掌握利用倍角公式解决给值求值问题的求解策略及方法.⇒通过例3及其变式训练，使学生掌握三角函数式的化简方法及要求.⇒归纳整理，进行课堂小结，整体认识本节课所学知识.⇒完成当堂双基达标，巩固所学知识并进行反馈矫正.课标解读1.能利用两角和的正弦、余弦、正切公式导出二倍角的正弦、余弦、正切公式，了解它们的内在联系． 2.会借助同角三角函数的关系导出 C2α的另两种表示形式．(难点) 3.能利用二倍角公式进行简单的化简、求值和证明．(重点)倍角公式【问题导思】 1．如何利用两角和的正弦和余弦公式推导出 sin 2α，cos 2α？ 【提示】 sin 2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α， 即 sin 2α＝2sin αcos α. cos 2α＝cos(α＋α)＝cos2α－sin2α，即 cos 2α＝cos2α－sin2α. 2．如何利用两角和的正切公式推导出 tan 2α？ 【提示】 tan 2α＝tan(α＋α)＝12－tatnanα2α，即 tan 2α＝12－tatnanα2α. (1)sin 2α＝2sin_αcos_α(S2α)； (2)cos 2α＝cos2α－sin2α(C2α)； (3)tan 2α＝12－tatnanα2α(T2α).二倍角的余弦公式的变形【问题导思】 你还能得到二倍角的余弦公式其他变形吗？【提示】 利用 sin2α＋cos2α＝1，公式 C2α 可变形为 cos 2α＝2cos2α－1 或 cos 2α ＝1－2sin2α.cos 2α＝2cos2α－1，cos 2α＝1－2sin2α.求下列各式的值． π 3π (1)cos 8 cos 8 ； (2)12－cos2 π8 ；利用倍角公式求值2(3)tan1π2－tan1π； 12(4)cos 20°cos 40°cos 80°.【思路探究】 (1)中两角互余，故可以转化为同角正余弦的积的形式．(2)中的角的倍角为特殊角，故可以用降幂公式解决．(3)式可化为正切倍角公式的形式．(4)中可用公式的变形：cos α＝s2isnin2αα来解决．【自主解答】(1)cosπ8 cos38π＝cosπ8 sinπ 8＝12sin π4 ＝ 42.(2)12－cos2 π8 ＝12(1－2cos2π8 )＝－12cos π4 ＝－ 42.π1tan2π 12－11－tan2π121 －2(3)tan 12－ π＝πtan 12 tan 12＝－2·2tanπ 12＝－2× tanπ＝ 6＝－2 3 33.(4)cos 20°cos 40°cos 80°＝2ssiinn 4200°°·2ssiinn 8400°°·s2isnin16800° °＝18.1．解答本类题关键是抓住公式及其变形式的特征，观察分析题目中具有的与公式相似 的结构特征，从而找到解题的切入点．2．对于倍角公式应做到灵活运用，即根据所给式子的特点构造出倍角形式，正用、逆 用或变形用倍角公式进行化简和求值．求下列各式的值： 2tan 15°(1)1－tan215°；(2)sin 10°sin 30°sin 50°sin 70°.2tan 15°3【解】 (1)1－tan215°＝tan 30°＝ 3 .(2)∵sin 10°sin 50°sin 70°＝sin20°sin 50°sin 2cos 10°70°＝sin20°cos 20°sin 2cos 10°50°＝sin44c0o°s s1i0n°50°＝sin40°cos 40° 4cos 10°sin 80° 1 ＝8cos 10°＝8，∴sin 10°sin 30°sin 50°sin 70°＝116.给值求值(1)已知 sin α＋cos α＝13，0＜α＜π，求 sin 2α 的值；(2)已知 cos α＝－45，α∈(π2 ，π)，tan(π－β)＝12，求 tan(α－2β)的值．3【思路探究】 (1)将已知等式两边平方，利用同角三角函数的基本关系求解；(2)已知 α 的余弦值和范围可求出 tan α 的值，利用诱导公式可求出 tan β 的值，然后利用倍角 公式求出 tan 2β 的值，结合两角差的正切公式求解．【自主解答】 (1)sin α＋cos α＝13两边同时平方，得 sin2α＋2sin αcos α＋cos2α＝19，因为 sin2α＋cos2＝1，所以 2sin αcos α＝sin 2α＝－89.(2)由已知条件得 sin α＝ 1－cos2α＝1－4 －52＝35，tanα＝csoisnα3 α＝－4，由 tan β＝－tan(π－β)＝－12得 tan 2β＝12－tatnanβ2β＝ －11＝－43， 1－4所以tan(α－2β)＝1t＋antaαn －αttaann2β 2β34－4－ －3＝341＋ －4 × －37 ＝24.对于给值求值问题，注意寻找已知式与未知式的联系，有以下两种解题方向： (1)有方向地将已知式或未知式化简，使关系明朗化； (2)寻找角之间的关系，看是否适合相关公式的使用，注意常见角的变换和角之间的二 倍关系．已知 sin(π4 －x)＝153，0＜x＜π4 ，求coscoπs4 ＋2xx 的值．【解】sin π2 ＋2x原式＝ cosπ4 ＋x2sin ＝π4 ＋x ·cos cos π4 ＋xπ4 ＋x＝2sin(π4 ＋x)．∵sin(π4 －x)＝cos(π4 ＋x)＝153，且 0＜x＜π4 ，∴π4 ＋x∈(π4 ，π2 )，∴sin(π4 ＋x)＝1－cos2π4 ＋x12 ＝13，∴原式＝2×1132＝1234.化简：11＋ ＋ssiinn4α－cos 4α＋cos44αα.三角函数式的化简【思路探究】 本题主要考查二倍角公式的应用．基本思路是能化简成使该分式的分子 与分母有公因式进行约分，解法有两种：一是将 sin 4α＝2sin 2αcos 2α，cos 4α＝42cos22α－1，cos 4α＝1－2sin22α 代入进行化简；二是将 sin 4α＝2sin 2αcos 2α，1＋cos 4α＝2cos22α，1－cos 4α＝2sin22α 代入进行化简．【自主解答】 法一 原式1＋2sin 2αcos 2α－1＋2sin22α ＝1＋2sin 2αcos 2α＋2cos22α－1＝22scions2α 2αcos 2α＋sin 2α sin 2α＋cos 2α＝tan 2α.法二原式＝1－cos 4α 1＋cos 4α＋sin 4α ＋sin 4α2sin22α＋2sin 2αcos 2α ＝2cos22α＋2sin 2αcos 2α＝22scions2α 2αcos 2α＋sin 2α cos 2α＋sin 2α＝tan 2α.1．三角函数的化简有四个方向，即分别从“角”“函数名”“幂”“形”着手分析， 消除差异．2．对三角函数式化简结果的一般要求： (1)函数种类最少； (2)项数最少； (3)函数次数最低； (4)能求值的求出值； (5)尽量使分母不含三角函数； (6)尽量使分母不含根式．化简：(1)1＋t1an θ－1－t1an θ；2cos2α－1(2) 2tanπ4 －αsin2π4 ＋α.1－tan θ － 1＋tan θ 【解】 (1)原式＝ 1＋tan θ 1－tan θcos 2α(2)原式＝ 2tanπ4 －αcos2π2 －π4 －α2tan θ ＝－1－tan2θ＝－tan2θ.cos 2α＝ 2tanπ4 －αcos2π4 －α＝ 2sincos 2α π4 －α cosπ4 －α＝ sincos 2α 2×π4 －2α＝ccooss 22αα＝1.选择公式不恰当致误5已知 cos α＋sin α＝ 33(0＜α＜π)，求 cos 2α 的值． 【错解】 ∵(cos α＋sin α)2＝1＋2sin αcos α＝13， ∴sin 2α＝－23，∴cos 2α＝±1－sin22α＝±5 3.【错因分析】 利用二倍角公式的变形形式 cos 2α＝± 1－sin22α时，忽略了 α 角 的取值范围，导致错解．【防范措施】 在三角恒等变换中，运用不同的公式有不同的解题过程，若在解题过程 中选择恰当的公式，则能使解题过程更严密，不容易出错．【正解】 ∵(cos α＋sin α)2＋(sin α－cos α)2＝2， ∴(cos α－sin α)2＝2－13＝53，∴cosα－sinα＝±15 3.∵cos α＋sin α＝ 33， ∴(cos α＋sin α)2＝13，sin αcos α＝－13. ∵0＜α＜π 且 sin αcos α＝－13＜0， ∴sin α＞0，cos α＜0，∴cosα－sinα＝－15 3.∴cos 2α＝(cos α－sin α)(cos α＋sin α)＝－ 315× 33＝－ 35.6对二倍角公式的理解及二倍角公式的应用形式 (1)对于“二倍角”应该有广义上的理解，如：8α 是 4α 的二倍角；6α 是 3α 的二倍 角；4α 是 2α 的二倍角；3α 是32α 的二倍角；α2 是α4 的二倍角；α3 是α6 的二倍角；…… 又如 α＝2·α2 ，α2 ＝2·α4 ，…. (2)公式正用 从题设条件出发，顺着问题的线索，正用三角公式，通过对信息的感知、加工、转换， 运用已知条件和推算手段逐步达到目的． (3)公式逆用 异向转移，逆用公式，这种在原有基础上的变通是创新意识的体现．应用时要求对公式 特点有一个整体感知． 主要形式有 2sin αcos α＝sin 2α，sin αcos α＝12sin 2α，cos α＝2ssiinn2αα， cos2α－sin2α＝cos 2α，1－2ttaann2αα＝tan 2α.71．计算 1－2sin2 22.5°的结果等于________．【解析】1－2sin222.5°＝cos45°＝2 2.2 【答案】 22．(2012·济宁高一检测)已知 x∈(－π2 ，0)，cos x＝45，则 tan 2x＝________.【解析】 ∵x∈(－π2 ，0)，cos x＝45，∴sin x＝－35，∴tan x＝－34， ∴tan 2x＝12－tatnanx2x＝－274. 【答案】 －274 3．计算：(1)2sin 37.5°·cos 37.5°＝________； (2)sin267.5°－cos267.5°＝________；tan 7.5° (3)1－tan27.5°＝________.【解析】(1)2sin 37.5°cos 37.5°＝sin 75°＝6＋ 42.(2)sin267.5°－cos267.5°＝－cos 135°＝ 22.tan 7.5° 1 2tan 7.5° 12－ 3(3)1－tan27.5°＝2·1－tan27.5°＝2tan 15° ＝ 2 .6＋ 22 2－ 3【答案】 (1) 4(2) 2 (3) 2xx4．已知 sin 2－2cos 2＝0.(1)求 tan x 的值；(2)求 2coscos 2x π4 ＋x·sin的值． x【解】 (1)由 sin x2－2cos x2＝0⇒ tan x2＝2，x ∴tan x＝12－tatnan222x＝12－×222＝－43.(2)原式＝ 2cos2x－sin2x 22cos x－ 22sin x sin xcos x－sin x cos x＋sin x cos x＋sin x＝cos x－sin x sin x＝ sin x8＝ta1n x＋1＝(－34)＋1＝14.一、填空题 1．cos21π2－sin2π12＝________.【解析】 原式＝cos(2×1π2)＝cos π6 ＝ 23.【答案】3 22．计算 sin 105°cos 75°的值为________．【解析】 sin 105°cos 75°＝sin(180°－75°)cos 75°＝sin 75°cos 75°＝12sin11150°＝2sin 30°＝4.【答案】1 43．若 sin α＝13，则 cos 2α＝________.【解析】 cos 2α＝1－2sin2α＝1－2×(13)2＝79.【答案】7 94．若 tan(α＋π4 )＝3＋2 2，则1－sicnos2α2α＝________.【解析】 由 tan(α＋π4 )＝11＋－ttaann αα＝3＋2 2，得 tan α＝ 22，1－cos 2α2sin2α∴ sin 2α ＝2sin αcosα＝tanα＝22.【答案】2 25．已知 tan 2θ＝－2 2，π＜2θ＜2π，则 tan θ 的值为________． 2tan θ【解析】 由题意得1－tan2θ＝－2 2，解得 tan θ＝－ 22或 tan θ＝ 2.又 π＜2θ＜2π，则π2 ＜θ＜π，所以有 tan θ＝－ 22.【答案】－2 26．已知 tanθ2 ＝3，则11－ ＋ccoossθ＋sin θ＋sinθθ＝________.9【解析】θ2sin2θ2 ＋sin θ2sin2θ2 ＋2sinθ 2 cosθ 2∵ tan2＝ 3 ， ∴ 原 式 ＝2cos2θ2 ＋sinθ ＝ 2cos2θ2 ＋2sinθ 2 cosθ＝ 2tan2θ2 ＋tanθ 2θθ ＝tan 2 ＝3.1＋tan 2【答案】 3 7．θ 是第三象限角，sin4θ＋cos4θ＝59，则 sin 2θ＝________.【解析】 sin4θ＋cos4θ＝(sin2θ＋cos2θ)2－2sin2θcos2θ＝1－12sin22θ＝59， ∴sin 22θ＝89，又 θ 为第三象限角， ∴sin θ<0，cos θ<0，∴sin2θ＝2sinθcosθ>0，∴sin2θ＝232 .22 【答案】 3 8．若 sin 2α＝45，则 tan2α＋tan12α＝________. 【解析】 tan2α＋tan12α＝scions22αα＋csoisn22αα＝ssiinn4α2α＋cocso2sα4αsin2α＋cos2α 2－2sin2αcos2α 1－12sin22α＝14sin22α＝ 14sin22α1 1－2×4 5217＝1 4×4 52 ＝4.17 【答案】 4 二、解答题9．(2013·巢湖市质检)已知 cos x＝－2 5 5，x∈(－π，0)． (1)求 sin 2x 的值； (2)求 tan(2x＋π4 )的值．【解】(1)∵cosx＝－2 5 5，x∈(－π，0)，∴sinx＝－5 5，∴sin 2x＝2sin xcos x＝45.(2)由(1)得，tanx＝scionsx1 x＝2，∴tan2x＝12－tatnanx2x＝43，10∴tan(2x ＋π4)＝tan 2x ＋tanπ41－tan 2x tanπ4＝－7.10．已知sin 22α＋sin 2αcos α－cos 2α＝1，α∈(0，π2)，求sin α及tan α的值．【解】 由题意得sin 22α＋sin 2αcos α＝1＋cos 2α＝2cos 2α，∴2sin 2αcos 2α＋sin αcos 2α－cos 2α＝0.∵α∈(0，π2)，∴cos α≠0，∴2sin 2α＋sin α－1＝0， 即(2sin α－1)(sin α＋1)＝0.∵sin α＋1≠0，∴2sin α－1＝0，∴sin α＝12.∵0＜α＜π2，∴α＝π6，∴tan α＝33.11．已知函数f (x )＝2sin(π－x )cos x . (1)求f (x )的最小正周期；(2)求f (x )在区间[－π6，π2]上的最大值和最小值．【解】 (1)∵f (x )＝2sin(π－x )cos x ＝2sin x cos x ＝sin 2x ，∴函数f (x )的最小正周期为π.(2)由－π6≤x ≤π2⇒－π3≤2x ≤π，∴－32≤sin 2x ≤1， ∴f (x )在区间[－π6，π2]上的最大值为1，最小值为－32.(教师用书独具)求证：3－4cos 2A ＋cos 4A 3＋4cos 2A ＋cos 4A＝tan 4A .【思路探究】 从左边入手，从角的构成看，化4A 为2A ，再化为A ，从函数名称构成看，化弦为切．从左、右两边的结构看，将左边分式化简为右边的整式形式．【自主解答】 ∵左边＝3－4cos 2A ＋2cos 22A －13＋4cos 2A ＋2cos 22A －1＝(1－cos 2A 1＋cos 2A )2＝(2sin 2A 2cos 2A)2＝(tan 2A )2＝tan 4A ＝右边，∴3－4cos 2A ＋cos 4A 3＋4cos 2A ＋cos 4A ＝tan 4A .证明恒等式问题的两个原则：(1)观察式子两端的结构形式，一般是从复杂到简单，如果两端都比较复杂，就将两端都化简，即采用“两头凑”的思想．(2)证明的一般步骤是：先观察，找出角、函数名称、式子结构等方面的差异，然后本着“复角化单角”、“异名化同名”、变换式子结构‘变量集中’”等原则，设法消除差异，达到证明的目的．求证：1＋sin 4θ－cos 4θ2tan θ＝1＋sin 4θ＋cos 4θ1－tan 2θ. 【证明】 要证1＋sin 4θ－cos 4θ2tan θ＝1＋sin 4θ＋cos 4θ1－tan 2θ， 只需证1＋sin 4θ－cos 4θ1＋sin 4θ＋cos 4θ＝2tan θ1－tan 2θ. 上式：左边＝1－cos 4θ＋sin 4θ1＋cos 4θ＋sin 4θ＝2sin 22θ＋2sin 2θcos 2θ2cos 22θ＋2sin 2θcos 2θ ＝2sin 2θsin 2θ＋cos 2θ2cos 2θsin 2θ＋cos 2θ＝tan 2θ＝2tan θ1－tan 2θ＝右边． ∴原等式成立．。
江苏省新马高级中学高中数学必修四启发性学案：3.2二倍角(1)
第三章 三角恒等变换第4节 二倍角的三角函数（1）主备人：赵海 做题人：张俊 审核人：刘主任一．学习目标:1.掌握二倍角的正弦、余弦、正切公式.2.能用公式进行简单的化简、求值.二．课堂活动：活动一：（目标：二倍角的正弦、余弦、正切公式的推导）在公式()S αβ+,()C αβ+，()T αβ+中，令βα=，得到相应的一组公式： sin 2α= . 2a Scos2α= . 2a Ctan 2α= . 2T α2C α还可以变形为cos2α= . cos2α= . 活动二：（目标：二倍角的正弦、余弦、正切公式的运用）例1. 设5,,sin 213παπα⎛⎫∈= ⎪⎝⎭，求sin 2,cos 2,tan 2ααα的值.例2．（1）证明：1sin 4cos 411sin 4cos 4tan 2ααααα++=+- （2）o o o o cos20cos40cos60cos80(3)若tan 3θ=,求sin 2cos2θθ-思考感悟____________________________________________________________________________________________________________________________________________________ 活动三：（目标：理解倍角概念）例3.（1）已知)40(135)4sin(πθθπ<<=-，求)4cos(,2cos θπθ+的值。
（2）已知33cos ()4522πππαα⎛⎫+=<< ⎪⎝⎭，求α2sin 。
思考感悟____________________________________________________________________________________________________________________________________________________三．小结反思__________________________________________________________________________________________________________________________________四．巩固练习：1、sincos 88ππ= .2、2coscos 55ππ= .3、01sin10= .4、已知()00001sin(45)sin(45),90,1806ααα+-=∈，求sin 4α= .5、0000sin10sin30sin50sin 70= .6、已知353sin(),cos()41345παπβ+=-=，3,4444πππαβπ-<<<<，求[]c o s2-αβ（）的值.。
苏教版高中数学必修4《二倍角的三角函数(第1课时)》参考学案
总 课 题 二倍角的三角函数 分 课 题 二倍角的三角函数（1）教学目标 能记住二倍角公式，会运用二倍角公式进行求值、化简和证明，同时懂得这一公式在运用当中所起到的用途。
培养观察分析问题的能力，寻找数学规律的能力，同时注意渗透由一般到特殊的化归的数学思想及问题转化的数学思想。
重点难点记住二倍角公式，运用二倍角公式进行求值、化简和证明；在运用当中如何正确恰当运用二倍角公式引入新课 1、=+=+=+)tan(;)cos(;)sin(βαβαβα2、函数x y sin =与x y 2sin =图象之间的位置关系？3、角α的三角函数与角α2的三角函数之间有怎样的关系？4、学生活动：由)(βα+S ，)(βα+C ，)(βα+T 公式中，令αβ=可以得到的结果：（倍角公式） =α2sin ；=α2cos = = ； =α2tan _______________。
例题剖析例1、已知1312sin =α，),2(ππα∈，求ααα2tan 2cos 2sin ，，的值。
O x y例2、求证：θθθθθtan 2cos 2sin 12cos 2sin 1=++-+。
例3、不查表，求下列各式的值。
（1）︒︒15cos 15sin （2）8sin 8cos 22ππ- （3）︒-︒5.22tan 15.22tan 22 （4）︒-75sin 212巩固练习1、求下列各式的值：（1）8cos 8sin ππ= ；（2）16cos 16sin 22ππ-= ；（3）=︒-︒15tan 115tan 22 ； （4）=︒-15sin 212 ；（5）=12cos 24cos 48cos 48sin8ππππ 。
2、已知，，542cos 532sin -==αα 则角α的终边在第___________象限。
3、已知)2,0(8.0sin παα∈=，，求αα2cos 2sin ，的值。
4、已知21tan =α，求)22tan(απ+的值5、证明： （1）ααπαπ2sin )cos()sin(2=-+（2）12cos cos 22=-θθ（3）αααsin 2sin 2cos 1=- （4）2tan cos 1cos 12A A A =+-课堂小结 记住二倍角公式，运用二倍角公式进行求值、化简和证明。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、学习目标
1、让学生自己由和角公式而导出倍角公式，了解它们的内在联系；
2、会利用倍角公式进行求值运算，培养运算和逻辑推理能力；
3、领会从一般化归为特殊的数学思想，体会公式所蕴涵的和谐美，激发学生学数学的兴趣。
二、学习重点
倍角公式的形成，及公式的变形形式的运用。
三、学习难点 倍角公式的形成，及公式的变形形式的运用。
四、学习过程
问题1：两角和与差的正弦、余弦、正切公式是什么？
问题2：若β=α，结果会如何，你能得出什么结论？
α2S ：
α2C ：
α2T ：
问题3：你能利用同角三角函数公式对α2C 进行变形吗？
总结：公式α2S 、α2C 、α2T 叫做 ，简称 。
注意：（1）这里的“倍角”，实际上专指“二倍角”，遇到“三倍角”等名称时，“三”字等不能省去。
（2）倍角公式是和角公式的特例。
（3）倍角公式中的“倍角”的意义是相对的，如：4α是8α
的二倍角。
（4）倍角公式的公式特征：“倍角”与“二次”的关系。
试一试：不查表，求值：
（1）sin 2230cos 2230''⋅= ； （2）=-π18cos 22
； （3）=π-π8
cos 8sin 22 ；（4）= 40cos 20cos 10sin 。
例1：已知)0,2
(135cos παα-∈=且，求sin 2α，cos 2α，tan 2α的值。
例2：化简απ
απ
α222sin )3(cos )3(cos -++-。
例3：证明下列恒等式
（1）θθθθθtan 2cos 2sin 12cos 2sin 1=++-+； （2）1)10tan 3(40sin =- 。
例4：求函数2sin (sin cos )y x x x =+的最小正周期，以及最值。
例5：在半圆形钢板上截取一块矩形材料，怎样截取使这个矩形面积最大？
五、巩固练习
1、化简（1； （2；
（3； （4。
2、求值（1）sin15cos15= ；
（2）(cos sin )(cos sin )12121212
ππππ-+= ； （3）22cos 112π
-= ； （4）22tan
22.51tan 22.5-= ； （5）8sin cos cos cos 48482412
ππππ= ； （6） 15tan 50tan 50tan 25tan 25tan 15tan ++= 。
3、已知θ为第三象限角，且9
5cos sin 44=
+θθ，求sin 2α，cos 2α，tan 2α。
4、已知函数21sin cos 12y x x x =++，x R ∈。
求（1）最小正周期；（2）函数的最大值，以及取最大值时，自变量x 的集合。