固体物理计算题
固体物理学-试题及答案

得
分
二、简答与作图题(每题10分,共20分)
1、在考虑晶格振动对晶体热容的贡献时,爱因斯坦模型和德拜模型分别是怎样的?并定性说明二者的结果.
2、画体心立方晶格结构的金属在(100),(110),(111)面上原子排列。
2、体心立方晶体结构中原子球的排列方式为(ABAB,ABCABC),六角密排晶体结构中原子球的排列方式为(ABAB,ABCABC)。
3、在简立方晶体结构中,与(100)、(110)、(111)晶面等效的晶面数分别为,,。
4、固体结合的类型一般有:离子键结合、、、范德瓦尔斯键结合等.
5、固体的热容量在常温附近遵守杜珑-帕蒂定律,即等于;在低温下,固体的热容量随温度降低而(升高,降低)。
3、解:,,5分;,5分。
4、解:一维晶格的能带E(k) = ε0−β − 2γcos(ka),10分;电子速度,5分;在边界,,,5分.
4、(无机非金属专业选作)解:第一能带,5分;第二能带,5分;第三能带,5分;第四能带,5分。
课程考试试题纸
课程名称:
固体物理学
考试方式:
闭卷
印刷份数:
学院:
任课教师:
专业年级:
题பைடு நூலகம்
号
一
二
三
四
五
六
七
八
总分
阅卷
教师
得
分
……………………………………………………………………………………………………
得
分
一、填空题(每小题2分,共30分)
1、对简立方晶体结构,立方体边长为a,其最近邻的原子数为,最近邻原子的间距为。次近邻的原子数为,次近邻原子的间距为。
本科阶段固体物理期末重点计算题完整版

本科阶段固体物理期末重点计算题HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】第一章 晶体结构1. 氯化钠与金刚石型结构是复式格子还是布拉维格子,各自的基元为何?写出这两种结构的原胞与晶胞基矢,设晶格常数为a 。
解:氯化钠与金刚石型结构都是复式格子。
氯化钠的基元为一个Na +和一个Cl -组成的正负离子对。
金刚石的基元是一个面心立方上的C原子和一个体对角线上的C原子组成的C原子对。
由于NaCl 和金刚石都由面心立方结构套构而成,所以,其元胞基矢都为:相应的晶胞基矢都为:2. 六角密集结构可取四个原胞基矢123,,a a a 与4a ,如图所示。
试写出13O A A '、1331A A B B 、2255A B B A 、123456A A A A A A 这四个晶面所属晶面族的晶面指数()h k l m 。
解:(1).对于13O A A '面,其在四个原胞基矢上的截矩分别为:1,1,12-,1。
所以,其晶面指数为()1121。
(2).对于1331A A B B 面,其在四个原胞基矢上的截矩分别为:1,1,12-,∞。
所以,其晶面指数为()1120。
(3).对于2255A B B A 面,其在四个原胞基矢上的截矩分别为:1,1-,∞,∞。
所以,其晶面指数为()1100。
(4).对于123456A A A A A A 面,其在四个原胞基矢上的截矩分别为:∞,∞,∞,1。
所以,其晶面指数为()0001。
3. 如将等体积的硬球堆成下列结构,求证球体可能占据的最大体积与总体积的比为:简立方:6π;面心立方:6;六角密集:6;金刚石:16。
证明:由于晶格常数为a ,所以:(1).构成简立方时,最大球半径为2m aR =,每个原胞中占有一个原子,(2).构成体心立方时,体对角线等于4倍的最大球半径,即:4m R ,每个晶胞中占有两个原子,(3).构成面心立方时,面对角线等于4倍的最大球半径,即:4m R ,每个晶胞占有4个原子,(4).构成六角密集结构时,中间层的三个原子与底面中心的那个原子恰构成一个正四面体,其高则正好是其原胞基矢c 的长度的一半,由几何知识易知3m R =c 。
固体物理习题参考答案

固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。
固体物理期末试题及答案

固体物理期末试题及答案一、选择题(每题5分,共20分)1. 下列关于晶体的说法,错误的是:A. 晶体具有规则的几何外形B. 晶体内部原子排列是无序的C. 晶体具有各向异性D. 晶体具有固定的熔点答案:B2. 电子在金属中的自由运动是金属导电的主要原因,这种现象称为:A. 金属键B. 离子键C. 共价键D. 范德华力答案:A3. 半导体材料的导电性介于导体和绝缘体之间,这是因为:A. 半导体材料中的电子不能自由移动B. 半导体材料中的电子在特定条件下才能自由移动C. 半导体材料中的电子数量少于导体D. 半导体材料中的电子数量多于绝缘体答案:B4. 根据泡利不相容原理,一个原子轨道中最多可以容纳的电子数是:A. 1个B. 2个C. 4个D. 8个答案:B二、填空题(每题5分,共20分)1. 晶体的三种基本类型是________、________和________。
答案:单晶体、多晶体、非晶体2. 根据能带理论,固体中的能带可以分为________和________。
答案:导带、价带3. 固体物理中,费米能级是指在绝对零度时,电子占据的最高能级,其对应的温度是________。
答案:0K4. 根据德布罗意波理论,物质粒子也具有波动性,电子的波长与其动量成________关系。
答案:反比三、简答题(每题10分,共30分)1. 简述布拉格定律及其在晶体结构分析中的应用。
答案:布拉格定律是指当X射线或电子波以一定角度入射到晶体表面时,如果满足nλ=2d*sinθ的条件,其中n为整数,λ为波长,d为晶面间距,θ为入射角,那么会发生衍射现象。
这个定律在晶体结构分析中非常重要,因为它允许科学家通过测量衍射角来确定晶体的晶面间距和晶体结构。
2. 解释什么是超导现象,并简述其应用。
答案:超导现象是指某些材料在低于临界温度时,电阻突然降为零的现象。
这意味着在超导状态下,电流可以在材料内部无损耗地流动。
超导现象的应用非常广泛,包括但不限于磁悬浮列车、粒子加速器中的超导磁体、以及医疗成像设备如MRI。
固体物理题库-zzk-第一至第五章
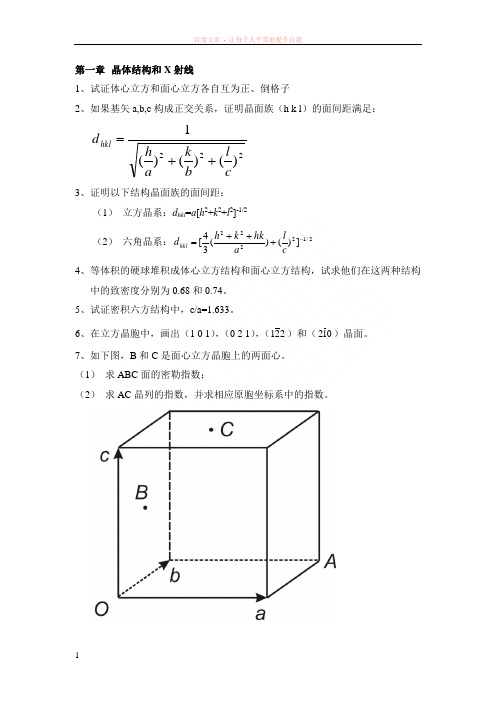
第一章 晶体结构和X 射线1、试证体心立方和面心立方各自互为正、倒格子2、如果基矢a,b,c 构成正交关系,证明晶面族(h k l )的面间距满足:222)()()(1c l b k a hd hkl ++=3、证明以下结构晶面族的面间距:(1) 立方晶系:d hkl =a [h 2+k 2+l 2]-1/2(2) 六角晶系:2/12222])()(34[-+++=c l ahk k h d hkl 4、等体积的硬球堆积成体心立方结构和面心立方结构,试求他们在这两种结构中的致密度分别为0.68和0.74。
5、试证密积六方结构中,c/a=1.633。
6、在立方晶胞中,画出(1 0 1),(0 2 1),(221)和(012)晶面。
7、如下图,B 和C 是面心立方晶胞上的两面心。
(1) 求ABC 面的密勒指数;(2) 求AC 晶列的指数,并求相应原胞坐标系中的指数。
8、六角晶胞的基矢为.,223,223k c c j a i a b j a i a a =+-=+=求其倒格子基矢。
9、求晶格常数为a 的面心立方和体心立方晶体晶面族(h 1 h 2 h 3)之间的面间距(指导p30,10)。
10、讨论六角密积结构,X 光衍射的消光条件。
11、求出体心立方、面心立方的几何因子和消光条件。
12、原胞和晶胞的区别?13、倒空间的物理意义?14、布拉格衍射方程,原子和几何结构因子在确定晶格结构上分别起何作用?15、什么是布拉格简单格子,什么是复式格子?第二章 自由电子气1、设有一个长度为L 的一维金属线,它有N 个导电电子,若把这些导电电子看成自由电子气,试求:(1) 电子的状态密度(2) 绝对零度下的电子费米能级,以及费米能级随温度的变化关系。
(3) 电子的平均能量。
(4) 电子的比热。
2、二维电子气的能态密度2)( πm E N =,证明费米能 ]1ln[/2-=T mk n B F b eT k E π 3、求出一维金属中自由电子的能态密度、费米能级、电子的平均动能以及一个电子对于比热的贡献。
固体物理重点计算题

固体物理重点计算题1.3、证明:⾯⼼⽴⽅的倒格⼦是体⼼⽴⽅;体⼼⽴⽅的倒格⼦是⾯⼼⽴⽅。
证明:(1)⾯⼼⽴⽅的正格⼦基⽮(固体物理学原胞基⽮):123()2()2()2a a j k a a i k a a i j ?=+??=+=+由倒格⼦基⽮的定义:1232()b a a π=?Ω31230,,22(),0,224,,22a a a aaa a a a a Ω=??==,223,,,0,()224,,022i j k a a aa a i j k a a ?==-++213422()()4a b i j k i j k a aππ∴=??-++=-++同理可得:232()2()b i j k ab i j k aππ=-+=+- 即⾯⼼⽴⽅的倒格⼦基⽮与体⼼⽴⽅的正格基⽮相同。
所以,⾯⼼⽴⽅的倒格⼦是体⼼⽴⽅。
(2)体⼼⽴⽅的正格⼦基⽮(固体物理学原胞基⽮):123()2()2()2a a i j k a a i j k a a i j k ?=-++?? =-+=+-由倒格⼦基⽮的定义:1232()b a a π=?Ω3123,,222(),,2222,,222a a a a a a aa a a a a a -Ω=??=-=-,223,,,,()2222,,222i j k a a a aa a j k a a a ?=-=+-213222()()2a b j k j k a aππ∴=??+=+同理可得:232()2()b i k ab i j aππ=+=+ 即体⼼⽴⽅的倒格⼦基⽮与⾯⼼⽴⽅的正格基⽮相同。
所以,体⼼⽴⽅的倒格⼦是⾯⼼⽴⽅。
1.5、证明倒格⼦⽮量112233G h b h b h b =++垂直于密勒指数为123()h h h 的晶⾯系。
证明:因为33121323,a a a a C A C B h h h h =-=-,112233G h b h b h b =++ 利⽤2i j ij a b πδ?=,容易证明123123h h h h h h G C A G C B ?=?=所以,倒格⼦⽮量112233G h b h b h b =++垂直于密勒指数为123()h h h 的晶⾯系。
固体物理40题

1. 设晶体中的每个振子的零点振动能.试用德拜模型求晶体的零点振动能.证明:根据量子力学零点能是谐振子所固有的,与温度无关,故T=0K 时振动能0E 就是各振动模零点能之和。
()()()000012mE E g d E ωωωωωω==⎰将和()22332s V g v ωωπ=代入积分有402339168m m s V E N v ωωπ==,由于098m B D B D k E Nk ωθθ==得 一股晶体德拜温度为~210K ,可见零点振动能是相当大的,其量值可与温升数百度所需热能相比拟.2. 试画出二维长方格子的第一、第二布里渊区.3. 证明:在磁场中运动的布洛赫电子,在K 空间中,轨迹面积A n 和在r 空间的轨迹面积S n之间的关系A n= (qB hc)2S n()d k d rc qv B q B dt dt⋅=-⨯=--⋅解: dk qB dr dt c dt∴=⋅ t k qBr c两边对积分,即 =22()()n n A r c S k qB∴== 4. 证明:面心立方晶格的倒格子为体心立方. 解:面心立方晶格的基矢为()()()a a aa j ,b ,c 222k i k i j =+=+=+ 则面心立方原胞体积3V []4a abc ⋅⨯==a 2bc V π*⨯=面心立方倒格矢 ()()2384a i k i j a π=⋅+⨯+()ai j k π-++2=()b a i j k π*=-+2同理: ,()ac i j k π*=+-2 a b c ***显然,,为体心立方原胞基矢,因此面心立方晶格倒格子为体心立方 5. 证明:根据倒格子的定义证明简单立方格子体积与其倒格子体积成反比解:设简单立方晶格常数为a ,则基矢为a ,b ,c ,V a ai a j ak ===3体积=其倒格矢2312b 2a a i V aππ⨯==,3122b 2a a j V a ππ⨯==,1232b 2a a k V a ππ⨯== 则倒格子体积()31232[]V b b b Vπ*=⋅⨯=6. 是否存在与库伦力无关的晶型,为什么?答:不存在与库仑力无关的晶型,因为①共价结合中电子虽不能脱离电负性 的原子,但靠近的两个原子各给出一个电子,形成电子共有的形状,位于两原子之间通过库仑力把两个原子结合起来。
固体物理习题与及解答

固体物理习题与及解答固体物理习题与及解答⼀、填空题1. 晶格常数为a 的⽴⽅晶系 (hkl>晶⾯族的晶⾯间距为/a该(hkl>晶⾯族的倒格⼦⽮量hkl G ρ为 k al j a k i a h ρρρπππ222++ 。
2. 晶体结构可看成是将基元按相同的⽅式放置在具有三维平移周期性的晶格的每个格点构成。
3. 晶体结构按晶胞形状对称性可划分为 7 ⼤晶系,考虑平移对称性晶体结构可划分为 14 种布拉维晶格。
4. 体⼼⽴⽅[]{})(ex p 1l k h i f S hkl ++-+=π,其衍射消光条件是奇数=++l k h 。
5. 与正格⼦晶列[hkl]垂直的倒格⼦晶⾯的晶⾯指数为(hkl> ,与正格⼦晶⾯[hkl] 。
6. 由N 个晶胞常数为a 的晶胞所构成的⼀维晶格,其第⼀布⾥渊区边界宽度为a /2π,电⼦波⽮的允许值为 Na /2π的整数倍。
7. 对于体积为V,并具有N 个电⼦的⾦属, 其波⽮空间中每⼀个波⽮所占的体积为 ()V /23π,费M 波⽮为 3/123???? ??=V N k F π。
8. 按经典统计理论,N 个⾃由电⼦系统的⽐热应为 B Nk 23 ,⽽根据量⼦统计得到的⾦属三维电⼦⽓的⽐热为F B T T Nk /22π,⽐经典值⼩了约两个数量级。
9.在晶体的周期性势场中,电⼦能带在布⾥渊区边界将出现带隙,这是因为电⼦⾏波在该处受到布拉格反射变成驻波⽽导致的结果。
10. 对晶格常数为a的简单⽴⽅晶体,与正格⽮R=a i+2a j+2a k正交的倒格⼦晶⾯族的⾯指数为 (122> , 其⾯间距为.11. 铁磁相变属于典型的⼆级相变,在居⾥温度附近,⾃由能连续变化,但其⼀阶导数<⽐热)不连续。
12. 晶体结构按点对称操作可划分为 32 个点群,结合平移对称操作可进⼀步划分为 230 个空间群。
13.等径圆球的最密堆积⽅式有六⽅密堆74%。
14. ⾯⼼⽴⽅⾯⼼⽴⽅⼩;原⼦形状因⼦反映⼀个原⼦对于衍射能⼒⼤⼩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a 基矢 a 1 ( i j k ) 2 a a2 ( i j k) 2 a a3 ( i j k ) 2
原胞体积
1 3 V a1 ( a 2 a 3 ) a 2
—— 原胞中只包含一个原子
• 面心立方 ( face-centered cubic; fcc ) , 例如 ,Cu等 。
1
2
3
1.5 证明:倒格子矢量G h b h b h b 垂直于密勒指数 1 1 2 2 3 3 为 ( h1h2 h3 ) 的晶面系
因为
a i b j 2 ij
a1 a 3 a2 a3 CA , CB h1 h3 h2 h3
1 d a( ) cos( qa)dq M 2
1 2
M
2
代入上式可得模式密度 L 12 1 ( ) ( ) a M 1
2L
2 a 0 2
1 sin( qa) 2
0 m
晶格振动的量子化、声子
• 声子与光子非常相类,不同的是: 声子具 有纵向振动模。可以证明, 与光子一样, 声子服从玻色统计分布, 为玻色子。它既 可以产生, 也可以消灭。 • 晶格振动能量是量子化的:
一维晶格振动格波
m
a
a
0
a
a
一维双原子晶格
• 在光学支与声学支之间存在一间隙, 即晶 格不能传播这样的波, 因此, 双原子晶格 起到带通机械滤波器的作用。
[2 1/m 1+1/m 2)] ( (2 m 1) /
1/2 1/2
空隙
光学支
(2 m 2)1/2 /
3N KBT 3N KB 近似常数 NO
E 3N
h e h ( q ) / k BT 1
3 Vk B T 3 E 3k B T 2 2 3v 3 p
xm
0
x 3dx ex 1
e E / T 2 CV 3R ( ) T ( e E / T 1) 2
E
3 Vk B T 3 CV 3k B 2 2 3v 3 p
xm
0
e x x 4 dx ( e x 1) 2
近似常数 T
近似常数 T3 law
第四章 能带理论
根据布洛赫定理
电子的波函数 晶格周期性函数
( r Rn ) e
i k R n
( r ) —— 布洛赫函数
(r ) e
i k r
uk ( r )
• 合力:
f ma
d 2 un m 2 ( 2un un 1 un 1 ) dt
(3-1)
一维晶格振动格波
• 在列出(3-1)式时已假设晶格中足够长, t忽 ) unq Ae i ( qna 略边界, 故以试探解(行波) 代 入(3-1)式, i ( t nqa) 2 i ( t nqa) iqa iqa m e e (2 e e )
uk ( r R) uk ( r )
4.1一维周期场中电子的波函数 k ( x) 满足Bloch定理,若晶格常数为a的电子波函数为:
(a) k ( x) sin x
a
(b) k ( x) i cos (c) k ( x)
3 x a
l
f ( x la)
• 简单晶体的体心立方 ( body-centered cubic bcc ) , 例如,Li,K
体心立方堆积
体心立方结构单元
体心立方
• 其特点有: • 晶胞基矢 a b c , 并且 a a i ; b a j ; c a k . • 其原胞基矢由从一顶点指向另外三个体心点的 矢量构成:
R l1 a1 l2 a 2 l3 a 3
Lattice Translation Vector Translation Vector 基矢 Primitive Cell 原胞
( l1 , l2 , l3 )
li为整数。
conventional cell 晶胞 (nonprimitive cell 非初基单胞 )
Multiply up to integers: (8 3 4) [if necessary]
倒易点阵、倒格矢、波失(倒)空间
证明:体心立方晶格的倒格子是面心立方; 面心立方晶格的倒格子是体心立方 倒格子定义
b 1 2
a 2 a3
a1 a 2 a 3
b 2 2
固体物理复习
第一章 晶体结构
• • • • 通过本章学习重点内容: 晶体结构中的一些常用术语 晶格类型 几种晶体结构
Terms about Crystal Structures
Lattice 晶格 Lattice point Basis Bravais Lattice 布喇菲格子 格点 基元 格矢
声学支
a
0
a
q
一维双原子晶格
a
声学支
a
光学支
格波的态密度函数
格波的态密度函数g(),又称为模式密度数,其定义为 在附 近单位频率间隔内的格波总数
求:一维单原子点振动的声子谱密度 解:
( )
,并作图。
一维单原子点振动的色散曲线如下图所示
d
a
dq
dq
2 同理 b 2 2 (i k) a a1a 2 a 3 a 1 a 2 2 b 3 2 ( i j) a a a a
a 3 a1
可见由 b 1 , b 2 , b 3 为基矢构成的格子为面心立方格子
倒格子基矢
2 a a b 1 2 ( i j k) ( i j k) 2 a1 a 2 a 3 2 2 2 a 2 ( i j k)( i j k) ( j k) 4 a a 2 a3
第三章 晶格振动与晶体的热学特性
1.讨论晶格振动时的物理框架是牛顿力学还是量子力学?
答:牛顿力学+量子力学修正,所以又可称为半经典理论。
2.讨论晶格振动时采用了哪些近似条件? 答:采用了近邻近似和简谐近似。 3.什幺是近邻近似和简谐近似? 近邻近似:在晶格振动中,只考虑最近邻的原子间的相互 作用; 简谐近似:在原子的互作用势能展开式中,只取到二阶项 。
a a1 ( i j k ); 2
a a 2 ( i j k ); 2
a a3 ( i j k ) 2
• 其体积为 a 3 • 配位数=8。
2
;
a1 a3
a2
a2 a1
简单立方晶胞
c
b a
a3
体心立方晶胞与惯用原胞
3) 体心立方晶格 由立方体的中心到三个顶点引三个基矢
4.晶体中一个原胞中有n个原子组成,有3支声学波和 3n-3支光学波
一维晶格振动格波
u n-1 u n u n+1
n-1
n
n+1 n+2
一维晶格振动格波
• 考虑第n个粒子的受力情况, 它只受最近 邻粒子的相互作用, 即分别受到来自第n1个粒子及第n+1个粒子的弹性力: f n1 (un un1 ) f n1 (un un1 )
若只取第一布x ika i cos e i cos (b) k ( x a) i cos a a a 3 5 所以电子的波失为
a a a 若只取第一布里渊区 k 则 k a a a
(c)
l l
§1-2 常见的晶体结构及其 原胞、晶胞
• 简单晶体的简单立方(simple cubic, sc),例如氧 、硫固体
简单立方堆积
简单立方结构单元
简单立方
• 其特点有: 三个基矢互相垂直( a b c ), 重复间距相等, 为a, 亦称晶格常数; 3 • 其晶胞=原胞; 体积= a ; • 配位数(第一近邻数) =6。
a
k
则
a
k
a
k
,
,
,..........
试求电子在这些态的波失。
解:根据Bloch定理 k ( x a) e
(a) k ( x a) sin
jka
k ( x) 可得:
( x a)
a
sin
x
a
e jka sin
x
a
3 5 所以电子的波失为 k , , ,.......... a a a
a a 2 ( i k ); 2
a a3 ( i j) 2
a3 4 ; • 其体积= • 配位数=12。 •
a 1 a 2 60
• 找出在单胞轴a,b,c上,以点阵常数量 度的截距,这些轴可以是初基的或是非 初基的。
• 取这些截距的倒数,然后划成与之具有 同样比率的三个整数,一般是化成三个 最小的整数。将结果括在括号里(hkl)。
• 利用 ,即:
2
4 2 qa sin ( ) m 2
e
iqa
e
iqa
2 cosqa
1 cos 2 sin2
