河南省商丘市高考数学二模试卷(文科)
河南省商丘市高三第二次模拟考试文科综合试题(扫描版).pdf

商丘市2013年高三第二次模拟考试 文科综合能力测试参考答案1.B2.B3.B4.D5.C6.A7.D8.D9.B 10.B 11.D 12.A 13.B 14.C 15.C 16.D 17.C 18.B19.A 20.C 21.B 22.A 23.C 24.D 25.D 26.B 27.C 28.A 29.C 30.D 31.B 32.D 33.B 34.A35.C 36.(20分) (1)西(南)部为山地(多火山);东(北)部为平原(多沼泽);地势西南高东北低(6分) ()沿海、沿河流分布 地形平坦;水源充足;交通便利(8分) ()加强自主创新,树立品牌意识;产业结构调整与升级,大力发展高端加工业与第三产业(如服务业);加强市场营销,占领国际市场。
(6分)(1)新疆纬度较高,靠近冬季风的源地(2分),冬季风开始的早,影响时间长(2分)。
()()同意(2分):理由:工业强省可加快城市化进程,提高城市化水平;可提供就业机会解决剩余劳动力问题;可快速增加经济收入,提升本省在全国的位次;本省资源丰富,劳动力廉价,工业成本较低,有传统工业得天独厚的发展条件。
(分)() 不同意(2分)理由:本省基础设施不完善,发展工业投入大;工业会污染环境,无法保存原生态的旅游条件;发展工业会导致资源过度开采,使资源过早枯竭;人才、资金不足,无法满足现代工业的基本要求(分)()“三个代表”重要思想和科学发展观的内在要求。
(每点2分,共10分) (2)①文化对人的影响来自特定的文化环境,文化影响人的交往行为和交往方式、实践活动、认识活动和思维方式。
加强廉政文化建设,为党的建设创造良好的文化环境,对党的领导干部及党员的交往行为和交往方式、实践活动、认识活动和思维方式都会产生非常重要的积极影响。
(3分) ②文化对人的影响具有潜移默化和深远持久的特点。
加强廉政文化建设,有助于党的领导干部和党员自觉树立科学“三观”,增强辨别是非的能力,避免走上违法犯罪的道路。
河南省2020届高三第二次模拟考试卷 文科数学(二)(PDF版,答案解析)

成立.
(1)求实数 k 的值;
(2)若 m 1 , n 1 且求证 f (m) f (n) 10 ,求证: 9 1 16 .
2
2
mn 3
二模测试卷 第 7 页(共 8 页)
二模测试卷 第 8 页(共 8 页)
高三第二次模拟考试卷
文科数学(二)答 案
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.【答案】C
B.若 1 x 1,则 x2 1
C.若 x 1或 x 1,则 x2 1
D.若 x 1或 x 1,则 x2 1
4焦点分别为 F1 ,F2 ,过 F2 且垂直于长轴的直线交椭圆于 A, B 两点,
则 △ABF1的周长为( )
A. 4
B. 6
C. 8
D.16
为
cos2
2asin (a
0)
,过点
P(1, 2)
的直线 l
的参数方程为
x
1
2t 2 ( t 为参数),l
y
2
2t 2
与 C 交于 A , B 两点.
(1)求 C 的直角坐标方程和 l 的普通方程;
(2)若 PA , AB , PB 成等比数列,求 a 的值.
23.(12 分)已知定义在 R 上的函数 f (x) 2x k 2 x , k N* .存在实数 x0 使 f (x0 ) 2
∴△ABF1的周长为| AF1 | | BF1 | | AB | (| AF1 | | AF2 |) (| BF1 | | BF2 |) 8 ,
故选 C. 5.【答案】A
【解析】因为平面向量 a (1, 3) , b (2, 0) ,
河南省商丘市高三数学下学期第二次模拟考试试题文(扫描版)

河南省商丘市2016届高三数学下学期第二次模拟考试试题文(扫描版)商丘市2016年第二次模拟考试参考答案高三数学(文科)一、选择题(每小题5分,共60分)B C D A B C C A D B A D 二、填空题(每小题5分,共20分)(13) 12 (14)45 (15) 73 (16) 34π 三、解答题(本大题共6小题,共70分)(17)解:(Ⅰ)设等比数列{}n a 的公比为q ,∵33S a +,55S a +,44S a +成等差数列, ∴ 2(55S a +)=(33S a +)+(44S a +),………………………………… 2分∴534a a =,因此,25314a q a ==, …………………………………………4分 ∴12q =±, ∵数列{}n a 不是递减数列,∴12q =-, ……………………………………5分∴11*313()(1),222n n n n a n --=-=-∈N . …………………………………… 6分 (Ⅱ)∵1133(1)(1)22n n n n n nn a b n -+⋅=-⨯-=,…………………………………………7分∴231233()2222n n nT =++++ , …………………………………………… 8分∴23111213()22222n n n n nT +-=++++ , ……………………………………10分 以上两式相减得:1211111113()3(1)2222222n n n n n n nT ++=+++-=-- ,∴126(1)2n n n T ++=-.………………………………………………………………12分(18) 解:(I )由频率分布直方图可得,损失不少于6000元的居民共有(0.00003 + 0.00003)×2000×50 = 6户,…………………………………………1分损失为6000~8000元的居民共有0.00003×2000×50 = 3户, (2)分损失不少于8000元的居民共有0.00003×2000×50 = 3户,……………………3分因此,记损失为6000~8000元的3个居民为,,A B C ,损失不少于8000元的3居民为,,D E F .6户中抽2户的组合为,,,,,,,,,,,,,,.AB AC AD AE AF BC BD BE BF CD CE CF DE DF EF共15种,其中同一分组的有,,,,,.AB AC BC DE DF EF 共6种,………………5分 所以这两户在同一分组的概率为62155p ==. ……………………………………6分…………………… 8分K2=50×(30×6-9×5)239×11×35×15= 40501001= 4.046 >3.841.……………………………10分所以有95℅以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否4000元有关.……………………………………………………………………………………12分 (19)解:(Ⅰ)证明:连AC 交BD 于O ,四边形ABCD 为菱形,∴AC BD ⊥, …………1分∵⊥AE 平面ABCD ,⊂BD 平面ABCD ,∴AE BD ⊥, (2)分又∵AAE AC =⋂,∴⊥BD 平面EA ,……………………………4分由于⊂AF 平面EACF ,∴AF BD ⊥,又∵BE AF ⊥,BBE BD =⋂,∴⊥AF 平面B D E .………………6分(Ⅱ)由(Ⅰ)⊥AF 平面BDE ,EO BDE ⊂平面,得AF EO ⊥, ……………………………7分 ∴CAF AEO ∠=∠,AC FCAE AO CAF AEO ==∠=∠tan tan ,……8分 ∴21=FC .………………………………………9分 所求多面体的体积为B A V VV --=+113=33ACEF ACEF S OB S OD ⋅+⋅=分 (20)解:(Ⅰ)由题意212=p ,则1=p ,故抛物线方程为x y 22=,…………………………2分由0522p NF x =+=,则4,2200==y x , ∵00>y ,∴20=y ,所以(2,2)N . (4)分(Ⅱ)由题意知直线的斜率不为0,则可设直线l 的方程为b ty x +=,联立方程组⎩⎨⎧+==bty x xy 22,得0222=--b ty y .设两个交点211(,)2y A y ,222(,)2y B y (122,2y y ≠±≠±),则2480t b ∆=+>122y y t+=,122y y b =-,………………………………6分由122212122242(2)(2)2222NA NB y y k k y y y y --⋅=⋅==-++--整理得 32+=t b ,此时,0)64(42>++=∆t t 恒成O立,……………………8分故直线l 的方程可化为)2(3+=-y t x ,从而直线l 过定点(3,2)E -, 因为(2,2)M -,所以,M E 所在直线平行x轴,所以△MAB的面积2)2(64212221++=++=-=t t t y y ME S …10分当2t =-时有最小值为2,此时直线'l 的方程为012=++y x .…………12分解法二:(Ⅱ)当l 的斜率不存在时,:2l x =(舍) 或3x =,△MAB的面积S =5分当斜率存在时,设:l y kx b =+,22222(22)0y xk x kb x b y kx b⎧=⇒+-+=⎨=+⎩ ,212122222,kb b x x x x k k-+==,121222,by y y y k k+==, …………………………………………………7分由122212122242(2)(2)2222NA NB y y k k y y y y --⋅=⋅==-++--,整理得 226(52)4032k b k b b k +-+-=⇒=--或22b k =--(舍) (8)分点M到直线的距离d =,22AB k k ==, ……………9分12S AB d =⋅==. ………………10分综上,所以△MAB 的面积最小值为2, 此时12k =-,直线'l 的方程为012=++y x . ………………………12分(21)解:(I )()f x 的定义域为(0,)+∞,2()x af x x-'= , ………………………………2分①若0,a ≤ 则()0f x '>,()f x 在(0,)+∞上单调递增; …………………3分②若0a >,当(0,)x a ∈时,()0f x '<,()f x 在(0,)a 单调递减, 当(,)x a ∈+∞时,()0f x '>,()f x 在(,)a +∞单调递增. (5)分综上0a ≤时,()f x 的递增区间为(0,)+∞;0a >时,()f x 的递减区间为(0,)a ,递增区间为(,)a +∞.………………………………………………………………6分(II ) 11(1,2)ln 1x m x x ∈-<- 等价于1ln (1)ln x x m x x --<-, 即(1,2)x ∈,不等式(1)ln 10mx m x x -+-+>恒成立, (8)分令()(1)ln 1g x mx m x x =-+-+, 则1ln (1)1()ln 1mx m mx x m x mg x m x x x+-+-+-'=+-=, 令()ln (1)1h x mx x m x m =+-+-,则()ln 21h x m x m '=+-, ①当0m ≤时,(1,2)x ∈时,()0h x '<,∴()h x 在(1,2)上单调递减,()(1)0,h x h <=∴(1,2)x ∈,()0g x '<,()g x 在(1,2)上单调递减,∴(1,2)x ∈,()(1)0,g x g <=与(1,2)x ∈,()0g x >矛盾,此种情况不可能. …9分②当102m <<时,由()h x '在(1,2)上单调递增,且(1)210h m '=-<, ∴一定存在00,(1,2)x x ∈,使得0(1,)x x ∈时,()0h x '<, ∴()h x 在0(1,)x 上单调递减,0(1,)x x ∈时,()(1)0,h x h <= ∴0(1,)x x ∈,()0g x '<,()g x 在0(1,)x 上单调递减, ∴0(1,)x x ∈,()(1)0,g x g <= 与(1,2)x ∈时,()0g x >矛盾,此种情况不可能. …………………………………10分③当12m ≥时,(1,2)x ∈,()0h x '>,()h x 在(1,2)上单调递增,()(1)0,h x h >=∴(1,2)x ∈,()0g x '>,()g x 在(1,2)上单调递增, ∴(1,2)x ∈,()(1)0,g x g >=恒成立, ……………………………………………11分综上可知m的范围为1,2⎡⎫+∞⎪⎢⎣⎭.………………………………………………12分 (22)解:(Ⅰ)因为CA 为⊙O 的切线,所以B EAC ∠=∠.…………………………………1分因为DC 是ACB ∠的平分线,所以ACD DCB ∠=∠………………………2分所以B DCB EAC ACD ∠+∠=∠+∠,即ADF AFD ∠=∠………………3分因为90DAE ∠=︒,所以1(180)452ADF DAE ∠=︒-∠=︒………………5分 (Ⅱ)因为B EAC ∠=∠,ACB ECA ∠=∠,所以ACE ∆∽BCA ∆,所以AC AEBC AB=,……………………………………7分在ABC ∆中,又因为AC AB =,所以30B ACB ∠=∠=︒, (8)分分 (23)解:(Ⅰ)∵圆C 的极坐标方程为4sin()6πρθ=-,∴214sin()4cos )62πρρθρθθ=-=-.……………………………2分 又∵222x y ρ=+,cos ,sinx y ρθρθ==,∴222x yx +=-, ∴圆C 的普通方程为2220x y x++-=………………………………5分(Ⅱ)设zy =+,由圆C 的方程2220xy x ++-=,即22(1)(4x y ++=, ∴圆C 的圆心是(1-,半径是2, 将112x y t ⎧=-⎪⎪⎨⎪=⎪⎩, 代入z y =+得z t=-,……………………7分又∵直线l 过点(1C -,圆C 的半径是2,∴22t -≤≤, (8)分∴22t -≤-≤,即z y =+的取值范围是[2,2]-.…………………………………………10分(24)解:(Ⅰ)当2a =,12)(+≥x x f ,即122+-≥-x x ,即⎩⎨⎧≥-+-≥-02122x x x 或⎩⎨⎧<-+-≥-02122x x x ,………………………………………3分 解得{}1-≥x x . …………………………………………………………………5分(Ⅱ)37)2(2-+≥a x x f 可化为37)2(2-≥-a x x f ,令()(2)7g x f x x =-, 3()2()(2)72()2a x a x g x f x x x a x a a x x ⎧-≥⎪⎪=-=-+=⎨⎪-<⎪⎩, …………………………6分 因为(,)2a x ∈-∞,()g x 单调递减,(,)2a x ∈+∞,()g x 单调递增; 所以当2ax =时,()g x 有最小值,min ()()22a a g x g ==,………………………………8分 若使原命题成立,只需232a a ≥-,……………………………………………………………………9分 解得(]2,0∈a .………………………………………………………………………………………………………10分。
河南省商丘市2024年数学(高考)部编版第二次模拟(评估卷)模拟试卷

河南省商丘市2024年数学(高考)部编版第二次模拟(评估卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题已知点在抛物线上,设的焦点为,线段的中点在的准线上的射影为,且,则向量的夹角的最大值为( )A.B .C .D .第(2)题已知,,(为自然对数的底数),则( )A .B .C .D .第(3)题已知直角的直角顶点在圆上,若点,,则的取值范围为( )A.B .C .D .第(4)题执行如图所示的程序框图,当输入的的值为4时,输出的的值为2,则空白判断框中的条件可能为( ).A .B .C .D .第(5)题已知函数,,将函数的图象经过下列哪种可以与的图象重合( )A .向左平移个单位B .向左平移个单位C .向右平移个单位D .向右平移个单位第(6)题已知O 为坐标原点,抛物线C :的焦点为F ,过抛物线C 上一点A (点A 在第一象限)作C 的准线的垂线,垂足为B ,若,则点A 到直线的距离为( )A .B .C .D .第(7)题某地质勘探单位从甲、乙、丙、丁、戊5人中选取2人到某矿区进行地质勘探,则甲被选中的概率为( )A.B .C .D .第(8)题下列关于函数的结论错误的是( )A.的图像关于点对称B .的图像关于直线对称C.存在使得D .在上的零点之和为二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)定义为数列的“优值”.已知某数列的“优值”,前n项和为,下列关于数列的描述正确的有()A.数列为等差数列B.数列为递增数列C.D.,,成等差数列第(2)题已知,是互不重合的直线,,是互不重合的平面,下列四个命题中正确的是()A.若,,,,则B.若,,,则C.若,,,则D.若,,,则第(3)题已知,则下列有关函数在上零点的说法正确的是()A.函数有5个零点B.函数有6个零点C.函数所有零点之和大于2D.函数正数零点之和小于4三、填空(本题包含3个小题,每小题5分,共15分。
河南省商丘市2024年数学(高考)部编版第二次模拟(培优卷)模拟试卷

河南省商丘市2024年数学(高考)部编版第二次模拟(培优卷)模拟试卷一、单项选择题(本题包含8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题设函数在上存在导函数,对于任意的实数,都有,当时,,若,则实数的取值范围是A.B.C.D.第(2)题复数(i为虚数单位)的虚部是A.-1B.1C.-i D.i第(3)题对于实数,规定表示不大于的最大整数,那么使不等式成立的的取值范围是()A.B.C.D.第(4)题设集合,则()A.B.C.D.第(5)题已知函数是定义在上的偶函数,当时,,则函数的零点个数A.B.C.D.第(6)题已知是虚数单位,a,,,则复数的模为()A.5B.C.2D.4第(7)题已知集合,,则()A.B.C.D.第(8)题已知函数的定义域为,当时,,且对任意的实数,等式成立,若数列满足,且,则下列结论成立的是A.B.C.D.二、多项选择题(本题包含3小题,每小题6分,共18分。
在每小题给出的四个选项中,至少有两个选项正确。
全部选对的得6分,选对但不全的得3分,有选错或不答的得0分) (共3题)第(1)题有6本不同的书,按下列方式进行分配,其中分配种数正确的是()A.分给甲、乙、丙三人,每人各2本,有15种分法B.分给甲、乙、丙三人,一人4本,另两人各1本,有180种分法C.分给甲、乙每人各2本,分给丙、丁每人各1本,有180种分法D.分给甲、乙、丙、丁四人,两人各2本,另两人各1本,有1080种分法第(2)题下列说法中,正确的命题是()A.以模型去拟合一组数据时,为了求出回归方程,设,将其变换后得到线性方程,则的值分别是和.B.在线性回归模型拟合中,若相关系数的绝对值越小,则样本的线性相关性越强.C.在回归分析中,决定系数的值越大,说明残差平方和越大.D.在具有线性相关关系的两个变量的统计数据所得的回归直线方程中,,则.第(3)题在锐角中,角所对的边分别为,且,则下列结论正确的有()A.B.的取值范围为C.的取值范围为D.的最小值为三、填空(本题包含3个小题,每小题5分,共15分。
河南省商丘市高考数学二模试卷(文科)
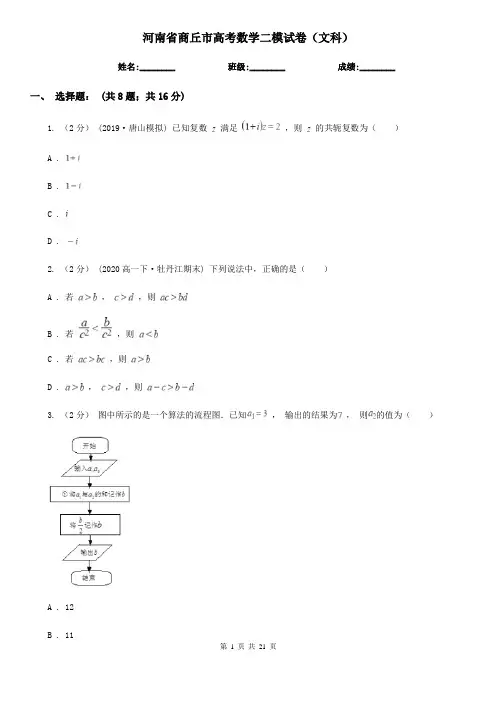
河南省商丘市高考数学二模试卷(文科)姓名:________班级:________成绩:________一、 选择题: (共 8 题;共 16 分)1. (2 分) (2019·唐山模拟) 已知复数 满足,则 的共轭复数为( )A.B.C.D.2. (2 分) (2020 高一下·牡丹江期末) 下列说法中,正确的是( )A.若,,则B.若 C.若,则 ,则D.,,则3. (2 分) 图中所示的是一个算法的流程图.已知, 输出的结果为 , 则 的值为( )A . 12 B . 11第 1 页 共 21 页C . 10 D.94. (2 分) (2019 高三上·浙江月考) 已知 , 为实数,则,是A . 充分不必要条件B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件的( )5. (2 分) 如图是函数 y=sin(ωx+φ)(ω>0,0<φ< )在区间[﹣ , ]上的图象,将该图象向右 平移 m(m>0)个单位后,所得图象关于直线 x= 对称,则 m 的最小值为( )A. B. C. D. 6. (2 分) (2020·厦门模拟) 某三棱锥的三视图如图所示,其中网格纸上小正方形的边长为 1,则该几何体 的外接球的表面积为( ).第 2 页 共 21 页A. B. C. D.7. (2 分) (2017 高二上·海淀期中) “”是“直线与圆相切”的( ).A . 充分而必要条件B . 必要而不充分条件C . 充分必要条件D . 既不充分也不必要条件8. (2 分) (2016 高一下·枣阳期中) 式子 σ(a,b,c)满足 σ(a,b,c)=σ(b,c,a)=σ(c,a,b), 则称 σ(a,b,c)为轮换对称式.给出如下三个式子:①σ(a,b,c)=abc; ②σ(a,b,c)=a2﹣b2+c2; ③σ (A,B,C)=cosC•cos(A﹣B)﹣cos2C(A,B,C 是△ABC 的内角).其中,为轮换对称式的个数是( )A.0B.1C.2D.3二、 填空题: (共 6 题;共 6 分)9. (1 分) (2020·盐城模拟) 已知集合,集合,则________.10. (1 分) (2018 高一下·通辽期末) 已知变量 ,则 的最大值是________ .满足的约束条件为,且目标函数为11. (1 分) (2020 高二上·厦门月考) 已知 、 是椭圆短轴上的两个顶点,点是椭圆上不同于短轴端点的任意一点,点 与点 关于 轴对称,则下列四个命题中,其中正确的是第 3 页 共 21 页________.①直线与的斜率之积为定值;②;③△的外接圆半径的最大值为;④直线与的交点 的轨迹为双曲线.12.(1 分)(2019 高三上·武汉月考) 如图,圆形纸片的圆心为 ,半径为,该纸片上的正方形的中心为 , 、 、 、 为圆 上点,,,,分别是以 ,, , 为底边的等腰三角形,沿虚线剪开后,分别以 , , , 为折痕折起,,,,使得 、 、 、 重合,得到四棱锥.当该四棱锥体积取得最大值时,正方形的边长为________ .13. (1 分) (2019 高三上·桂林月考) 已知双曲线虚轴的一个端点到它的一条渐近线的距离为 ,则双曲线的离心率为________. 14. (1 分) (2017 高一下·定州期末) 若过定点 M(﹣1,0)且斜率为 k 的直线与圆 x2+4x+y2﹣5=0 在第一象限内的部分有交点,则 k 的取值范围是________.三、 解答题: (共 6 题;共 60 分)15. (10 分) (2018 高二上·湛江月考) 在锐角 .中,分别为角所对的边,且(1) 确定角 的大小;第 4 页 共 21 页(2) 若,且的面积为,求的周长.16. (10 分) (2015 高二上·孟津期末) 已知二次函数 y=f(x)的图象过坐标原点,其导函数 f′(x)=6x ﹣2,数列{an}前 n 项和为 Sn , 点(n,Sn)(n∈N*)均在 y=f(x)的图象上.(1) 求数列{an}的通项公式;(2) 设,Tn 是数列{bn}的前 n 项和,求当对所有 n∈N*都成立 m 取值范围.17. (15 分) (2019 高二下·珠海期末) 某育种基地对某个品种的种子进行试种观察,经过一个生长期培养后,随机抽取 株作为样本进行研究.株高在及以下为不良,株高在到之间为正常,株高在及以上为优等.下面是这 个样本株高指标的茎叶图和频率分布直方图,但是由于数据递送过程出现差错,造成图表损毁.请根据可见部分,解答下面的问题:(1) 求 的值并在答题卡的附图中补全频率分布直方图;(2) 通过频率分布直方图估计这 株株高的中位数(结果保留整数);(3) 从育种基地内这种品种的种株中随机抽取 2 株,记 概率,求随机变量 的分布列(用最简分数表示).表示抽到优等的株数,由样本的频率作为总体的18. (10 分) (2018 高三上·龙泉驿月考) 如图,在三棱柱侧面底面.中,,,第 5 页 共 21 页(1) 求证:平面;(2) 若,,,求棱柱的体积.19. (5 分) (2017 高一下·景德镇期末) 已知 m>1,直线 l:x﹣my﹣ F2 分别为椭圆 C 的左、右焦点.=0,椭圆 C:+y2=1,F1、(Ⅰ)当直线 l 过右焦点 F2 时,求直线 l 的方程;(Ⅱ)设直线 l 与椭圆 C 交于 A、B 两点,△AF1F2 , △BF1F2 的重心分别为 G、H.若原点 O 在以线段 GH 为 直径的圆内,求实数 m 的取值范围.20. (10 分) (2017·莆田模拟) 设函数 f(x)=xex﹣ax(a∈R,a 为常数),e 为自然对数的底数.(1) 若函数 f(x)的任意一条切线都不与 y 轴垂直,求 a 的取值范围;(2) 当 a=2 时,求使得 f(x)+k>0 成立的最小正整数 k.第 6 页 共 21 页一、 选择题: (共 8 题;共 16 分)答案:1-1、 考点:参考答案解析: 答案:2-1、 考点:解析: 答案:3-1、 考点:解析:第 7 页 共 21 页答案:4-1、 考点:解析: 答案:5-1、 考点: 解析:答案:6-1、第 8 页 共 21 页考点:解析: 答案:7-1、 考点: 解析:答案:8-1、 考点: 解析:第 9 页 共 21 页二、 填空题: (共 6 题;共 6 分)答案:9-1、 考点:解析: 答案:10-1、 考点: 解析:第 10 页 共 21 页答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:三、解答题: (共6题;共60分)答案:15-1、答案:15-2、考点:解析:答案:16-1、答案:16-2、考点:解析:答案:17-1、答案:17-2、答案:17-3、考点:解析:答案:18-1、答案:18-2、考点:解析:考点:解析:答案:20-1、答案:20-2、。
河南省商丘市2017-2018高三第二次模拟考试文科数学答案
商丘市2018年高三第二次模拟考试数学(文科)参考答案一、选择题(每小题5分,共60分)(1) C (2)B (3)D (4) A (5) C (6)B(7) A (8)B (9)D (10) D (11) C (12)A二、填空题(每小题5分,共20分)(13)1- (14)1 (15)336 (16)3三、解答题(共70分)(17)(本小题满分12分) 解:(Ⅰ)证明:∵ A B C π++=,sin+)2sin cos()A C A A B =+(, ∴sin 2sin cos B A C =-……………………………………………………………………1分 在ABC ∆中,由正弦定理得,2cos b a C =-,…………………………………………3分∵34C π=,∴b =, 则2222b a a a ==⋅…………………………………………………………………………5分 ∴,,2a b a 成等比数列; ………………………………………………………………………6分(Ⅱ) 1sin 224S ab C ===,则ab =,…………………………………………7分由(Ⅰ)知,b = ,联立两式解得2,a b ==,…………………………………………………………9分由余弦定理得,2222cos 4822()202c a b ab C =+-=+-⨯⨯-= …………11分∴c =12分(18)(本小题满分12分)解:(Ⅰ) 这100个数据的平均值约为2.250.04 2.350.26 2.450.30 2.550.28⨯+⨯+⨯+⨯ 2.650.10 2.750.02 2.47+⨯+⨯=…4分 (Ⅱ)重量落在[2.40,2.70)中的概率约为0.300.280.100.68++=,…………………………6分所以某陶瓷厂生产这样的工艺品5000件中,估计重量落在[2.40,2.70)中的件数估计为 50000.68=3400⨯(件)……………………………………………………………………8分(Ⅲ)记第一组的4件工艺品为1234,,A A A A ,,第六组2件工艺品为12,B B ,从中抽取两件共有: 111221223132414212131423243412,,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A A A A A A A A A A A A B B ,共有15种取法,……………………………………………………………………………10分 其中分别来自第一第六组的有:1112212231324142,,,,,,,A B A B A B A B A B A B A B A B 共有8种, 所以所求概率815P = 答:一个来自第一组,一个来自第六组的概率为815.…………………………………12分 (19)(本小题满分12分)(Ⅰ)解:三棱柱111C B A ABC -中,所以AB B A =11.因为12AB AA ==,所以1112A B AA ==.又因为06011=∠B AA ,.连接1AB ,所以△11B AA 是边长为2的正三角形. …………………………………1分因为E 是棱11B A 的中点,所以11B A AE ⊥,且AE =又AB B A //11,所以AB AE ⊥ ………………………………………………………2分又侧面⊥11A ABB 底面ABC ,且侧面11ABB A I 底面AB ABC =, 又⊂AE 侧面11ABB A ,所以⊥AE 底面ABC ,……………………………………4分 所以三棱柱111C B A ABC -的体积为112222ABC V S AE AB AC AE ∆=⋅=⋅⋅=⨯⨯=;………………………6分 (Ⅱ)在直线1AA 上存在点P ,使得//CP 平面AEF .…………………………………………7分 证明如下:连接BE 并延长,与1AA 的延长线相交,设交点为P .连接CP .因为11//A B AB ,故11PA A E PE PB PA AB==………………………………………8分 由于E 为棱11A B 的中点,所以112A E AB =,故有PE EB =………………9分 又F 为棱BC 的中点,故EF 为BCP ∆的中位线,所以//EF CP ……10分又EF ⊂平面AEF ,CP ⊄平面AEF , 所以//CP 平面AEF .……11分故在直线1AA 上存在点P ,使得//CP 平面AEF .此时,211==AA PA ,所以124AP AA==…………………………12分(20)(本小题满分12分)解:(Ⅰ)依题意,1224PF PF a +==,故2a =.…………………………………………1分将-1⎫⎪⎪⎝⎭代入椭圆22214x y b +=中, 解得23b =,………………………………………………………………………3分故椭圆C 的方程为:22143x y +=.………………………………………………4分 (Ⅱ)由题知直线l 的斜率必存在,设l 的方程为(4)y k x =-.设点11()M x y ,,22()N x y ,,则11()G x y -,, 联立22(4)3412y k x x y =-⎧⎨+=⎩,得22234(4)12x k x +-=. 即2222(34)3264120k x k x k +-+-=,则0∆>,21223234k x x k +=+,2122641234k x x k -=+………………………………………6分 由题可得直线NG 方程为211121()y y y y x x x x ++=--,…………………………………7分 又∵11(4)y k x =-,22(4)y k x =-.∴直线NG 方程为211121(4)(4)(4)()k x k x y k x x x x x -+-+-=--,……………………8分 令0y =,整理得2122111212112124424()88x x x x x x x x x x x x x x x --+-+=+=+-+- 22222264123224343432834k k k k k k -⨯-⨯++=-+22222434132243234k k k k -+==--+,1C C即直线NG 过点(10),.…………………………………………………………………10分又∵椭圆C 的右焦点坐标为2(10)F ,, ∴三点G ,2F ,N 在同一直线上. ……………………………………………………11分 ∴ 存在实数λ,使得22GF F N λ=……………………………………………………12分(21)(本小题满分12分)解: (Ⅰ)当1m =时,+12()(1)x f x x e x =-+,111()(1)22x x x f x e x e x xe x +++'∴=+-+=+=+1(2)x x e +…………………………………………………………………1分∴切线的斜率(-1)3k f '==-,又(-1)1f =-,…………………………………2分 故切线的方程为13(+1)y x +=-,即340x y ++=………………………………………………………………………3分 (Ⅱ)(,),x ∈-∞+∞且+1+1+1()(1)2(2)x x x f x e x e mx x e m '=+-+=+,(i )当0m ≥时,+10x e >,+120x e m ∴+>∴当0x >时,()0f x '>;当0x <时,()0f x '<.故()f x 在区间(,0)-∞上单调递减,在区间(0,)+∞上单调递增;……………………5分(ii )当02e m -<<,()0f x '=有两个实数根120,(2)-1x x ln m ==-, 且12x x >,故0x >时,()0f x '>;(2)-10ln m x -<<时,()0;f x '<(2)-1x ln m <-时,()0f x '>.故()f x 在区间(,(2)-1)(0,)ln m -∞-+∞,上均为单调增函数, 在区间((2)-1,0)ln m -上为减函数. ……………………………………………………………7分 综上所述,当0m ≥时,()f x 在(,0)-∞上单调递减,在(0,)+∞上单调递增; 当02e m -<<时,()f x 在(,(2)-1)ln m -∞-、(0,)+∞上单调递增,在((2)-1,0)ln m -上单调递减.……………………………………………………………………………………………8分(Ⅲ)当0m >时,由(Ⅱ)知,min ()(0).f x f e ==-……………………………………9分 又224()3g x x m x '=+-.m ≥ 06m <≤,()0.g x '∴>()g x ∴在(]0,2上为增函数.max ()82262g x m m ∴=--=-.………………………………………………………10分 依题意有min max ()().62.f x g x m e ≤∴-≥-……………………………………………11分 032e m ∴<≤+ 故m 的取值范围为03+2e ⎛⎤ ⎥⎝⎦,.……………………………………………………………12分 (22)(本小题满分10分)解:(Ⅰ)依题意,直线1l的直角坐标方程为y =,………………………………1分 直线2l的直角坐标方程为y =.…………………………………………2分因为4cos 2sin ρθθ=+,∴24cos 2sin ρρθρθ=+,∴2242x y x y +=+, 即22(2)(1)5x y -+-=,………………………………………………………4分∴曲线C的参数方程为21x y αα⎧=+⎪⎨=+⎪⎩,(α为参数). …………………5分 (Ⅱ)联立64cos 2sin πθρθθ⎧=⎪⎨⎪=+⎩,,得到||1OM =,同理||2ON =………7分 又6MON π∠=,所以1||||sin 2MON S OM ON MON =⋅∠=△即OMN ∆……………………………………………………10分 (23)(本小题满分10分) 解:(Ⅰ)依题意,431()|2|2|1|12342x x f x x x x x x x -<⎧⎪=-+-=⎨⎪->⎩,,,≤≤,,,……………………………2分 故不等式()4f x >的解集为8(0)3⎛⎫-∞+∞ ⎪⎝⎭,,.………………………………5分 (Ⅱ)由(Ⅰ)可得,当1x =时,()f x 取最小值1,…………………………………7分2()274f x m m >-+对于x ∈R 恒成立,∴2min ()274f x m m >-+,即22741m m -+<,…………………………………8分∴22730m m -+<, 解之得132m <<,……………………………………………………………………9分 ∴实数m 的取值范围是132(,).……………………………………………………10分。
河南省商丘市高三第二次模拟模拟考试题(数学文)
河南省商丘市高三第二次模拟模拟考试题(数学文)姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分第1小题:评卷人得分已知全集U=R,集合A={x|lgx≤0},B={x|≤1},则CU(A∪B)=(A)(-∞,1)(B)(1 ,+∞)(C)(-∞,1] (D)[1,+∞)【答案解析】B第2小题:若i为虚数单位,图中复平面内点Z表示复数z,则此复平面内表示复数的点是(A)E(B)F (C)G(D)H【答案解析】D第3小题:已知数列{}是等差数列,其前n项和为,若=2,且S5=30,则S8l【答案解析】C第6小题:已知向量a与b的夹角为60°,且|a|=2,|b|=1,则向量a与a+2b的夹角等于(A)30°(B)60°(C)90°(D)150°【答案解析】A第7小题:如果执行右面的程序框图,那么输出的s为(A)3(B)(C)(D)-2【答案解析】C第8小题:设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(5)=(A)5(B)(C)1 (D)0【答案解析】B第9小题:如图是函数y=Asin(ωx+)(A&(*);0,ω&(*);0,||&(*);)在一个周期内的图象,M、N分别是最大、最小值点,且·=0,则A·ω的值为(A)(B)(C)(D)【答案解析】C第10小题:设函数f(x)=则函数g(x)=f(x)-的零点个数为(A)4(B)3(C)2(D)1【答案解析】B第11小题:已知F1、F2分别是双曲线C:(a&(*);0,b&(*);0)的左、右焦点,过点F2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M,且∠F1MF2=90°,则双曲线的离心率为(A)(B)(C)2(D)3【答案解析】C第12小题:设函数f(x)(x∈R)的导函数为(x),满足(x)&(*);f(x),则当a&(*);0时,f(a)与f(0)的大小关系为(A)f(a)&(*);f(0)(B)f(a)&(*);f(0)(C)f(a)=f(0)(D)不能确定【答案解析】A第13小题:在平面直角坐标系中,不等式组表示的平面区域为M,M的边界所围成图形的外接圆的面积是36π,那么实数a的值为__________.【答案解析】4第14小题:已知三棱锥S-ABC中,SA⊥面ABC,AB⊥BC,SA=AB=1,BC=,则此三棱锥外接球的体积为________.【答案解析】第15小题:已知数列{}满足a1=l,+=(n∈N﹡),=+·4+·+…+·,类比课本中推导等比数列前n项和公式的方法,可求得5-=_____.【答案解析】第16小题:下列正确结论的序号是__________.①连续函数f(x)在区间(a,b)上有零点的充要条件为f(a)·f(b)&(*);0;②若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=x+2,则f(1)+(1)=3;③对&(*);0,不等式+-a&(*);0恒成立,则实数a的取值范围为(-∞,2);④若f(x)=+++2x+1,则f(2)的值用二进制表示为111101.【答案解析】②④。
河南省商丘市高三数学第二次模拟考试试题 文
数 学(文科)本试卷分试题卷和答题卷两部分,试题卷共4页.答题卷共6页。
请按要求把答案涂、写在答题卷规定的范围内,超出答题框或答在试题卷上的答案无效。
满分为150分。
考试时间为120分钟。
考试结束只收答题卷。
第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A ={1,2},则满足A ∪B ={1,2,3}的集合B 的个数为A .1B .3C .4D .82.复数211i i -3(+)(i 是虚数单位)的实部是 A .-32 B .12 C .12 D .323.在等差数列{n a }中,前n 项的和为n S ,若2a 8=6+a 11,则S 9=A .27B .36C .45D .544.已知m >0,且mcos α-sin 5(α+ϕ),则tan ϕ=A .-2B .-12C .12D .2 5.已知f (x )是定义在R 上的奇函数,它的最小正周期为T ,则f (-2T )的值为 A .-2T B .0 C .2T D .T 6.同时随机掷两颗骰子,则至少有一颗骰子向上的点数小于4的概率为A .19 B .89C .14D .34 7.一个几何体的三视图如右图所示,则该几何体的体积为A .33B .33C .536D .38.函数f (x )=3x -21()2x -的零点所在区间为A .(-1,0)B .(0,1)C .(1,2)D .(2,3)9.某程序框图如图所示,该程序运行后输出的s 值为A .102B .410C .614D .163810.等比数列{n a }中,a 1=2,a 8=4,f (x )=x (x -a 1)(x -a 2)…(x -a 8),()f x '为函数f (x )的导函数,则(0)f '=A .0B .62C .92D .12211.一个六棱柱的底面是正六边形,其侧棱垂直于底面.已知该六棱柱,底面周长为3,则这个球的体积为A .43πB .83π C .163π D .323π 12.已知抛物线2y =2px (p >0)上一点M (1,m )(m >0)到其焦点的距离为5,双曲线2x a-2y =1的左顶点为A ,若双曲线的一条渐近线与直线AM 平行,则实数a 的值是 A .125B .19C .15D .13 第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.设实数x ,y 满足不等式组1,1,0,y x x y ⎧⎪⎨⎪⎩+≤y -≤≥则2y x +的取值范围是________. 14.若直线y =kx -1与圆21x 2+y =相交于P ,Q 两点,且∠POQ =120°(其中O 为原点),则k =___________.15.已知△ABC 及其平面内一点P 满足PA +PB +PC =0,若实数λ满足AB +AC =λAP .则λ=__________.16.若命题“a ∃∈[1,3],使a 2x +(a -2)x -2>0”为假命题,则实数x 的取值范围是________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,且bcosC=(3a—c)cosB.(Ⅰ)求cosB的值;(Ⅱ)若BA·BC=2,且b=2,求a和c的值.18.(本小题满分12分)如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,侧面APD为等腰直角三角形,PA⊥PD,平面PAD⊥底面ABCD,E为侧棱PC上不同于端点的一点.(Ⅰ)求证:PA⊥DE:(Ⅱ)设AD=2BC=2,CD3,求三棱锥D-PBC的高.19.(本小题满分12分)为征求个人所得税法修改建议,某机构对当地居民的月收入调查10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500))。
河南省商丘市2018届高三第二次模拟考试文科数学试题(解析卷)
河南省商丘市2017-2018高三第二次模拟考试试题文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}290A x x =-≤,集合{}10B x x =->,则A B =( )A. ()1,3B. (]1,3C. [)3,1-D. ()3,1-【答案】C 【解析】由题得{|33}A x x =-≤≤,{|1}B x x =<,{|33}{x|x<1}A B x x ∴⋂=-≤≤⋂,={|31}x x -≤<,故选C.2. 复数352z i =+(i 是虚数单位)的共轭复数z =( ) A. 2i + B. 2i -C. 2i --D. 2i -+【答案】B 【解析】由题得()()()225251051052,222215i i i z i i i i +++=====+--++所以共轭复数2z i =-,故选B. 3. 设函数()()()2212log 02x x f x x x ⎧-≥⎪=⎨<<⎪⎩,若()3f m =,则实数 m 的值为( ) A. -2 B. 8 C. 1 D. 2【答案】D 【解析】当m≥2时,2213,4,2,2, 2.m m m m m -=∴=∴=±≥∴=当0<m<2时,32log 3,28,02,.m m m m φ=∴==<<∴∈综上所述m=2,故选D.4. 已知平面向量()()1,2,,1a b k =-=,且a b ⊥,则a b +在a 上的投影为( )A.B. 2C.D. 1【答案】A 【解析】因为a b ⊥,所以(1)210, 2.k k -⨯+⨯=∴=所以(1,3),a b += 所以221310,5,a b a +=+==所以a b ⊥在a 上的投影为()cos 105a b a a b a b aα+⋅+=⋅==+故选A.5. 设1F 和2F 为双曲线()222210,0x y a b a b-=>>的两个焦点,若点()120,2,,P b F F 是等腰直角三角形的三个顶点,则双曲线的离心率为( )A. 2B.7C.3D.3【答案】C 【解析】因为点()120,2,,P b F F 是等腰直角三角形的三个顶点,所以2b=c,所以2222222222444,4(),34,,,33c b c c a c c a e e a =∴-=∴=∴=∴=∴=故选C.6. 已知数列{}n a 满足()*111,2n n a a a n N +=-≥∈,则( ) A. 21n a n ≥+ B. 2n S n ≥C. 12n n a -≥ D. 12n n S -≥【答案】B 【解析】由题得21324312,2,2,,2,n n a a a a a a a a --≥-≥-≥-≥213243112(1),2(1),2 1.n n n n a a a a a a a a n a a n a n -∴-+-+-++-≥-∴-≥-∴≥-1231231,3,5,,21,13521n n a a a a n a a a a n ∴≥≥≥≥-∴++++≥++++-,2(121).2n nS n n ∴≥+-=故选B. 点睛:类比想象是数学想象的一种,看到1(n n a a f n +-=),我们要想到累加法,这里不是等式,是不等式,我们也可以累加得到21n a n ≥-,再利用累加得到2n S n ≥.7. 执行如图的程序框图,若输入的是9k =,则输出的S =( )A. 10B. 15C. 21D. 28【答案】A 【解析】运行程序如下:n=1,s=1,1<9,n=2,s=3;3<9.n=3,s=6, 6<9,n=4,s=10,10>9,s=10. 故选A.8. 将函数()sin 06y x πωω⎛⎫=+> ⎪⎝⎭的图象向右平移3π个单位后,得到()y g x =,()g x 为偶函数,则ω的最小值为( ) A. 1 B. 2C.12D.32【答案】B 【解析】 将函数()sin 06y x πωω⎛⎫=+> ⎪⎝⎭的图象向右平移3π个单位后,得到()sin[()]sin[]3636w y g x w x wx ππππ==-+=-+,由于函数g(x)为偶函数,所以min +31,3(1)1 2.362w k w k w ππππ-+=∴=--∴=-⨯--=,故选B. 9. 函数f (x )=ln|11xx+-|的大致图象是( )A. B.C. D.【答案】D 【解析】 因为()()11lnln 11x xf x f x x x-+-==-=-+-,所以函数()f x 是奇函数,图象关于原点对称,可排除,A C ;由()2ln30f =>,可排除B ,故选D.【方法点晴】本题通过对多个图象的选择考查函数的图象与性质,属于中档题. 这类题型也是近年高考常见的命题方向,该题型的特点是综合性较强较强、考查知识点较多,但是并不是无路可循.解答这类题型可以从多方面入手,根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.10. 已知正方形ABCD 如图所示,其中AC ,BD 相交于O 点,E ,F ,G ,H ,I ,J 分别为AD ,AO ,DO ,BC ,BO ,CO 的中点,阴影部分中的两个圆分别为ABO ∆与CDO ∆的内切圆,若往正方形ABCD 中随机投掷一点,则该点落在图中阴影区域内的概率为( )A.1(22)π+-B.1(422)π+-C.1(642)π+-D.1(622)π+-【答案】C 【解析】依题意,不妨设2AO =,则四边形EFOG 与四边形HIOJ 的面积之和为2S =,两个内切圆的面积之和为((2'222122S ππ=⨯⨯-=-,故所求概率((212821164284P π+-+-==,故选C.11. 某几何体的三视图如图所示,则该几何体的体积为( )A. 3πB. 2πC.53π D.43π【答案】C 【解析】由三视图可知,原几何体左边是半边圆柱,圆柱上面是14个球,几何体右边是一个圆锥,且圆锥的顶点和球心重合.所以几何体的体积为2311421243ππ⋅⨯+⨯⨯ 211512.233ππ+⨯⨯⨯⨯=故选C. 12. 定义在R 上的函数()f x 满足:()()()1,05f x f x f >'=+,()f x '是()f x 的导函数,则不等式()() 41x e f x -> (其中e 为自然对数的底数)的解集为( )A . ()0,∞+ B. ()(),03,-∞+∞ C. ()(),01,-∞⋃+∞ D. ()3,+∞【答案】A 【解析】 设g(x)=()()1x e f x -,()(()1)()(()()1),()()1,()0,x x x g x e f x e f x e f x f x f x f x g x ∴=-+=+-+>''∴'>''所以函数g(x)R 上单调递增.因为()05f =,所以g(0)=4,因为()()14xe f x ->,所以g(x)>g(0),所以x>0.故选A.点睛:构造函数,再研究函数的性质,再利用函数的性质解题,是函数里的一个常用技巧.本题就利用了这个技巧,先构造函数g(x)=()()1xe f x -,再分析函数g(x)的单调性和特殊点,最后利用函数的性质解答.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若x ,y 满足1203220x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩,则3z x y =-的最小值为__________.【答案】1- 【解析】 【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论.【详解】作出不等式组1203220x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩对应的平面区域,如图,由3z x y =-得3y x z =-, 平移直线3y x z =-,由图象可知当直线3y x z =-经过点()0,1时, 直线3y x z =-的纵截距z -最大,z 最小,3z x y =-的最小值为3011⨯-=-.故答案为1-.【点睛】本题主要考查线性规划中,利用可行域求目标函数的最值,属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.14. 已知球的表面积为8π,此球面上有,,A B C三点,且2AB AC BC ===,则球心到平面ABC 的距离为__________. 【答案】1 【解析】因为球的表面积为8π,所以248,R R ππ=∴=因为2AB AC BC ===,所以三角形ABC 为直角三角形,因此球心到平面ABC 的距离为球心到BC1= .点睛:涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解. 15. “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲,1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2018这2017个整数中能被2除余1且被3除余1的数按由小到大的顺序排成一列,构成数列{}n a ,则此数列的项数为__________. 【答案】336 【解析】因为这些整数能被2除余1且被3除余1,所以这些数组成的数列的通项61,n a n =+1612018,62017,336.6n n n +≤∴≤∴≤设所以此数列的项数为336. 故填336.16. 过圆()227:19M x y ++=的圆心M 的直线与抛物线2:4C y x =相交于,A B 两点,且3MB MA =,则点A 到圆M 上任意一点的距离的最小值为__________.【答案】3【解析】设221212(,),(,),44y y A y B y由题得212112122123300,1144MA MB y y y y y y y k k y y =⎧⎪=⎧⎪--∴∴==⎨⎨=⎩⎪++⎪⎩不妨设1110,(3y y A MA >∴=∴∴==所以点A 到圆M r ==故填3. 点睛:本题的难点在于探究解题的思路,根据数形结合可得点A 到圆M 上任意一点的距离的最小值为|MA|-r,所以要求点A 的坐标,所以要找到关于点A ,B 的两个方程即可,从哪里找到方程,一个是3MB MA =,一个是MA MB k k =.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,若()()sin 2sin cos A C A A B +=+,且34C π=. (1)求证:,,2a b a 成等比数列; (2)若ABC ∆的面积是2,求c 边的长.【答案】(1)证明见解析;(2)【解析】试题分析:(1)第(1)问,一般利用正弦定理化简()()sin 2sin cos A C A A B +=+ 得到b = ,再证明,,2a b a 成等比数列.(2)第(2)问,先计算出2,a b ==,再利用余弦定理求出c 的长. 试题解析:(1)证明:∵ A B C π++=,()sin +)2sin cos A C A A B =+(, ∴sin 2sin cos B A C =-在ABC ∆中,由正弦定理得,2cos b a C =-,∵34C π=,∴b =, 则2222b a a a ==⋅ ∴,,2a b a 成等比数列;(2) 1sin 22S ab C ===,则ab =,由(1)知,b =,,联立两式解得2,a b == ,由余弦定理得,2222cos 4822202c a b ab C ⎛=+-=+-⨯⨯-= ⎝⎭,∴25c =.18. 唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史,某陶瓷厂在生产过程中,对仿制100件工艺品测得其重量(单位:kg ) 数据,将数据分组如下表:(1)统计方法中,同一组数据常用该组区间的中点值(例如区间[)2.20,2.30的中点值是2.25)作为代表.据此,估计这100个数据的平均值;(2)根据样本数据,以频率作为概率,若该陶瓷厂生产这样的工艺品5000件,试估计重量落在[)2.40,2.70中的件数;(3)从第一组和第六组6件工艺品中随机抽取2个工艺品,求一个来自第一组,一个来自第六组的概率. 【答案】(1)2.47 ;(2)3400;(3)815. 【解析】试题分析:(1)第(1)问,直接利用平均数的公式求解. (2)第(2)问,根据频率的公式估计重量落在[)2.40,2.70中的件数.(3)第(3)问,利用古典概型的概率公式求解.试题解析:(1) 这100个数据的平均值约为2.250.04 2.350.26 2.450.30 2.550.28⨯+⨯+⨯+⨯… 2.650.10 2.750.02 2.47+⨯+⨯=.(2)重量落在[)2.40,2.70中的概率约为0.300.280.100.68++=,所以某陶瓷厂生产这样的工艺品5000件中,估计重量落在[)2.40,2.70中的件数估计为50000.68=3400⨯(件).(3)记第一组的4件工艺品为1234,,A A A A ,,第六组2件工艺品为12,B B ,从中抽取两件共有:111221223132414212131423243412,,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A A A A A A A A A A A A B B ,共有15种取法,其中分别来自第一第六组的有:1112212231324142,,,,,,,A B A B A B A B A B A B A B A B 共有8种,所以所求概率815P =,答:一个来自第一组,一个来自第六组的概率为815. 19. 如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,1,2AC AB AC AB AA ⊥===,1160AA B ∠=︒,,E F 分别为棱11,A B BC 的中点(1)求三棱柱111ABC A B C -的体积;(2)在直线1AA 上是否存在一点P ,使得//CP 平面AEF ?若存在,求出AP 的长;若不存在,说明理由.【答案】(1)23(2)4. 【解析】【详解】试题分析:(1)第(1)问,先证明AE ⊥底面ABC,计算出△ABC 的面积,再利用柱体的体积公式求三棱柱111ABC A B C -的体积.(2)第(2)问,先假设在直线1AA 上存在点P ,使得CP||平面AEF ,再找到点P 的位置,再求AP 的长. 试题解析:(1)三棱柱111ABC A B C -中,所以11A B AB =. 因为12AB AA ==,所以1112A B AA ==. 又因0160AA B ∠=,连接1AB ,所以△11AA B 是边长为2的正三角形. 因为E 是棱11A B 的中点,所以11AE A B ⊥,且3AE =又11||AB A B ,所以AE AB ⊥又侧面11ABB A ⊥底面ABC ,且侧面11ABB A 底面ABC=AB ,又AE ⊂侧面11ABB A ,所以AE ⊥底面ABC ,所以三棱柱111ABC A B C -的体积为112232322ABC V S AE AB AC AE ∆=⋅=⋅⋅=⨯⨯⨯=;(2)在直线1AA 上存在点P ,使得CP||平面AEF .证明如下:连接BE 并延长,与1AA 的延长线相交,设交点为P .连接CP .因为11//A B AB ,故11=PA A EPE PB PA AB= 由于E 为棱11A B 的中点,所以112A E AB =,故有PE EB =又F 为棱BC 的中点,故EF 为BCP ∆的中位线,所以//EF CP 又EF ⊂平面AEF ,CP平面AEF , 所以//CP 平面AEF .故在直线1AA 上存在点P ,使得//CP 平面AEF. 此时,12PA AA ==,所以124AP AA == .20. 已知椭圆()2222:10x y C a b a b +=>>的左右焦点分别为12,F F ,若椭圆上一点261P ⎫-⎪⎪⎝⎭满足124PF PF +=,过点()4,0R 的直线l 与椭圆C 交于两点M N 、.(1)求椭圆C 的方程;(2)过点M 作x 轴的垂线,交椭圆C 于G ,求证:存在实数λ,使得22GF F N λ=.【答案】(1)22143x y +=;(2)证明见解析. 【解析】试题分析:(1)第(1)问,由124PF PF +=得到a=2,再把点1P ⎫-⎪⎪⎝⎭的坐标代入椭圆方程,解方程组即得椭圆的方程.(2)第(2)问,设l 的方程为()4y k x =-.设点()11M x y ,,()22N x y ,,再求出NG 的方程,证明直线NG 过点()10,,即可证明 存在实数λ,使得22GF F N λ=. 试题解析:(1)依题意,1224PF PF a +==,故2a =.将-13⎛⎫ ⎪ ⎪⎝⎭代入椭圆22214x y b +=中,解得23b =,故椭圆C 的方程为:22143x y +=.(2)由题知直线l 的斜率必存在,设l 的方程为()4y k x =-.设点()11M x y ,,()22N x y ,,则()11G x y -,, 联立()2243412y k x x y ⎧=-⎨+=⎩,得()22234412x k x +-=. 即()2222343264120kxk x k +-+-=,则0∆>,21223234k x x k +=+,2122641234k x x k-=+ 由题可得直线NG 方程为()211121y y y y x x x x ++=--,又∵()114y k x =-,()224y k x =-. ∴直线NG 方程为()()()()211121444k x k x y k x x x x x -+-+-=--,令0y =,整理得()212121221111212244488x x x x x x x x x x x x x x x -+--+=+=+-+-22222264123224343432834k k k k kk -⨯-⨯++=-+ 22222434132243234k k k k -+==--+, 即直线NG 过点()10,. 又∵椭圆C 的右焦点坐标为()210F ,, ∴三点G ,2F ,N 在同一直线上. ∴ 存在实数λ,使得22GF F N λ= .点睛:存在实数λ,使得22GF F N λ=,就是证明G,2F N ,三点共线,要就是证明直线NG 过定点(1,0).所以解答本题的关键是读懂命题转化命题.21. 已知函数()()121x f x x e mx +=-+,其中m 为常数且2m e >-.(1)当1m =时,求曲线()y f x =在点()()1,1P f --处的切线方程; (2)讨论函数()y f x =的单调性;(3)当06m <≤时,()(]34,0,2g x x mx x x=--∈,若存在(]12,0,2x R x ∈∈,使()()12f x g x ≤成立,求实数m 的取值范围.【答案】(1)340x y ++=;(2),当0m ≥时,()f x 在(),0-∞上单调递减,在()0,∞+上单调递增; 当02m e-<<时,()f x 在()()(),ln 21,0,m -∞--+∞上单调递增,在()()ln 21,0m --上单调递减;(3)0,32e ⎛⎤+ ⎥⎝⎦. 【解析】试题分析:(1)第(1)问,先求导,再利用导数的几何意义,求出切线的斜率,最后写出直线的点斜式方程,化简即可. (2)第(2)问,对m 分类讨论,求出函数()y f x =的单调性.(3)第(3)问,由题得()()min max f x g x ≤,再求出()()min max f x g x 和代入化简即得m 的取值范围.试题解析:(1)当1m =时,()()+121x f x x ex =-+,()()111122x x x f x e x e x xe x +++∴=+-+='+=()+12x x e+∴切线的斜率()-13k f ='=-,又()-11f =-,故切线的方程为()13+1y x +=-, 即340x y ++=.(2)(),,x ∈-∞+∞且()()()+1+1+1122x x x f x e x e mx x e m =+-+=+',(i )当0m ≥时,+10x e >,+120x e m ∴+>∴当0x >时,()0f x '>;当0x <时,()0f x '<.故()f x 在区间(),0-∞上单调递减,在区间()0,+∞上单调递增; (ii )当02em -<<,()0f x '=有两个实数根()120,2-1x x ln m ==-, 且12x x >,故0x >时,()0f x '>;()2-10ln m x -<<时,()0;f x '< ()2-1x ln m <-时,()0f x '>.故()f x 在区间()()(),2-10,ln m -∞-+∞,上均为单调增函数, 在区间()()2-1,0ln m -上为减函数.综上所述,当0m ≥时,()f x 在(),0-∞上单调递减,在()0,+∞上单调递增; 当02em -<<时,()f x 在()(),2-1ln m -∞-、()0,+∞上单调递增,在()()2-1,0ln m -上单调递减. (3)当0m >时,由(2)知,()()min 0.f x f e ==-又()2243g x x m x =+-' .m ≥ 06m <≤,()0.g x ∴'>()g x ∴在(]02,上为增函数. ()max 82262g x m m ∴=--=-.依题意有()()min max .62.f x g x m e ≤∴-≥-032e m ∴<≤+故m 的取值范围为03+2e ⎛⎤⎥⎝⎦,. 点睛:存在(]12,0,2x R x ∈∈,使()()12f x g x ≤成立,即()()min max f x g x ≤,因为不等式两边的自变量不同.如果是存在x 使得f(x)<g(x)恒成立,就不能等价于()()min max f x g x ≤,因为不等式两边的自变量都是x ,这种情况一般移项转化成[f(x)-g(x)]的最小值小于零. 这两种命题要学会区分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.选修4-4:坐标系与参数方程 22. 已知曲线C的极坐标方程为4cos 2sin ρθθ=+,直线()1:6l R πθρ=∈,直线()2:3lR πθρ=∈.以极点O 为原点,极轴为x 轴正半轴建立平面直角坐标系.(1)求直线12,l l 的直角坐标方程以及曲线C 的参数方程;(2)已知直线1l 与曲线C交于,O M两点,直线2l 与曲线C 交于,O N 两点,求OMN ∆的周长.【答案】(1)3y x =,y =;21x y αα⎧=⎪⎨=+⎪⎩;(2)3+. 【解析】 【分析】(1)直接利用转换关系式,把参数方程直角坐标方程和极坐标方程之间进行转换. (2)利用(1)的结论,建立方程组,进一步利用余弦定理求出结果. 【详解】(1)解:直线1:()6l R πθρ=∈,所以:直线1l 的直角坐标方程为3y x =, 直线2:()3l R πθρ=∈.所以:直线2l 的直角坐标方程为y = 曲线C 的直角坐标方程为22(2)(1)5x y -+-=,所以:曲线C 的参数方程为21x y αα⎧=+⎪⎨=+⎪⎩(α为参数);(2)解:联立64cos 2sin πθρθθ⎧=⎪⎨⎪=+⎩,得到||1OM =+,同理||2ON = 又6MON π∠=,所以根据余弦定理可得MN =所以周长3l =+.【点睛】本题考查的知识要点:参数方程直角坐标方程和极坐标方程之间的转换,方程组的应用和余弦定理的应用,主要考查学生的运算能力和转化能力,属于基础题型. 选修4-5:不等式选讲23. 已知函数()221f x x x =-+-. (1)求不等式()4f x >的解集;(2)若不等式()2274f x m m >-+对于x ∀∈R 恒成立,求实数m 的取值范围.【答案】(1)8(0)3⎛⎫-∞+∞ ⎪⎝⎭,,;(2)1|32m m ⎧⎫<<⎨⎬⎩⎭【解析】试题分析:(1)绝对值函去绝对值得到分段函数()43122112342x x f x x x x x x x ,,,,,,-<⎧⎪=-+-=≤≤⎨⎪->⎩,得()4f x >的解集为()803⎛⎫-∞⋃+∞ ⎪⎝⎭,,;(2)由题意得,()2min 274f x m m >-+,即22741m m -+<,解得132m <<. 试题解析:(1)依题意,()43122112342x x f x x x x x x x ,,,,,,-<⎧⎪=-+-=≤≤⎨⎪->⎩故不等式()4f x >的解集为()803⎛⎫-∞⋃+∞ ⎪⎝⎭,, (2)由(1)可得,当1x =时,()f x 取最小值1,()2274f x m m >-+对于x R ∈恒成立,∴()2min 274f x m m >-+,即22741m m -+<,∴22730m m -+<,解之得132m <<,∴实数m 的取值范围是1|32m m ⎧⎫<<⎨⎬⎩⎭点睛:绝对值函数基本处理技巧就是去绝对值,得到分段函数,本题中再进行分段解不等式,得到答案;任意型恒成立问题得到()2min 274f x m m >-+,由分段函数分析得到()min 1f x =,所以22741m m -+<,解得答案.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省商丘市高考数学二模试卷(文科)
姓名:________ 班级:________ 成绩:________
一、选择题 (共12题;共24分)
1. (2分)(2020·漳州模拟) 复数满足,则()
A .
B .
C .
D .
2. (2分)设全集U={x|x<4,x∈N},A={0,1,2},B={2,3},则B∪∁UA等于()
A . {3}
B . {2,3}
C . ∅
D . {0,1,2,3}
3. (2分)设6件产品中有4件合格品2件不合格品,从中任意取2件,则其中至少一件是不合格品的概率为()
A . 0.4
B . 0.5
C . 0.6
D . 0.7
4. (2分) (2016高二上·和平期中) 设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=()
A . 5
B . 7
C . 9
D . 11
5. (2分) (2016高二下·东莞期末) 已知函数f(x)= 在点(1,2)处的切线与f (x)的图象有三个公共点,则b的取值范围是()
A . [﹣8,﹣4+2 )
B . (﹣4﹣2 ,﹣4+2 )
C . (﹣4+2 ,8]
D . (﹣4﹣2 ,﹣8]
6. (2分) (2018高二下·温州期中) 椭圆与双曲线有相同的焦点坐标,则
()
A . 3
B .
C . 5
D .
7. (2分)(2020·江西模拟) 已知是球O的内接三棱锥,球O的半径为2,且,,
,则点A到平面的距离为()
A .
B .
C .
D .
8. (2分)(2017·上高模拟) 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近于圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的(四舍五入精确到小数点后两位)的值为()(参考数据:sin15°=0.2588,sin75°=0.1305)
A . 3.10
B . 3.11
C . 3.12
D . 3.13
9. (2分)设,若函数在上单调递增,则的取值范围是()
A .
B .
C .
D .
10. (2分) (2019高二上·惠州期末) 函数的极大值为()
A .
B . 6
C .
D . 7
11. (2分)(2017·揭阳模拟) 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的体积为()
A .
B . 1
C . 2
D .
12. (2分) (2019高一上·东至期中) 若函数单调递增,则实数的取值范围是()
A .
B .
C .
D .
二、填空题 (共4题;共4分)
13. (1分)已知向量,若,则 ________.
14. (1分) (2016高一下·雅安期末) 若变量x、y满足约束条件:,则y﹣2x的最大值为________.
15. (1分)(2012·辽宁理) 已知等比数列{an}为递增数列,且a52=a10 , 2(an+an+2)=5an+1 ,则数列{an}的通项公式an=________.
16. (1分)已知双曲线的方程为,点是其左右焦点,是圆上的一点,点在双曲线的右支上,则的最小值是________.
三、解答题 (共7题;共65分)
17. (10分) (2019高三上·郑州期中) 在中,点在边上,,,
.
(1)若的面积为3,求;
(2)若,求 .
18. (10分)如图所示的空间几何体中,四边形是边长为2的正方形,平面
,,,, .
(1)求证:平面平面;
(2)求平面与平面所成的锐二面角的余弦值.
19. (5分) (2017高二下·肇庆期末) 某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表,若成绩120分以上(含120分)为优秀.
分数区间甲班频率乙班频率
[0,30)0.10.2
[30,60)0.20.2
[60,90)0.30.3
[90,120)0.20.2
[120,150]0.20.1
优秀不优秀总计
甲班
乙班
总计
k0 2.072 2.706 3.841 5.024 6.6357.87910.828
P(K2≥k0)0.150.100.050.0250.0100.0050.001(Ⅰ)求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成上面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关?
20. (10分)(2017·鄂尔多斯模拟) 设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A∈C,已知以F 为圆心,FA为半径的圆F交l于B,D两点;
(1)若∠BFD=90°,△ABD的面积为,求p的值及圆F的方程;
(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.
21. (10分)已知函数在处的切线方程为 .
(1)求,的值;
(2)求的单调区间与极值.
22. (10分)(2017·郴州模拟) 在平面直角坐标系xoy中,曲线C的参数方程为(θ为参
数),直线l的参数方程为(t为参数)以坐标原点O为极点,x轴的正半轴为极轴的极坐标系.(1)写出直线l的普通方程以及曲线C的极坐标方程;
(2)若直线l与曲线C的两个交点分别为M,N,直线l与x轴的交点为P,求|PM|•|PN|的值.
23. (10分) (2020高二上·安徽月考)
(1)已知 , , ,试比较与的大小;
(2)求证:.
参考答案一、选择题 (共12题;共24分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、
14-1、
15-1、
16-1、
三、解答题 (共7题;共65分) 17-1、
17-2、
18-1、18-2、
19-1、
20-1、
20-2、
21-1、21-2、22-1、
22-2、23-1、23-2、。
