生活中的轴对称PPT教学课件
合集下载
《生活中的轴对称》PPT课件

成一个整体,那么它就成了一个
轴对称图形。
第十五页,共19页。
下图是由小正方形组成的 L 形图,请你在 图中添画一个小正方形,使它成为轴对 称图形,并画出对称轴。
第十六页,共19页。
通过今天的学习,你有什么 收获与体会?
第十七页,共19页。
作业 P50 1,2,3,4
(做在书上)
第十八页,共19页。
第十三页,共19页。
观察下图中的每组图案,你发现了什么?
每一组图片中都有两个图形,并且沿一条直线 对折后,这两个图形完全重合,我们就说这两个 图形成轴对称,这条直线就是对称轴。两个图 形中的对应点(即对折后两图形中互相重合的点 叫对称点。
第十四页,共19页。
请说出两个图形成轴对称与轴对称图形的区别
区别:(1)轴对称是说两
联系:(1)定义中都有一条直
个图形的位置关系,轴对称
线都要沿着这条直线折叠重合。
图形是说一个具有特殊形状
的图形。
(2)如果把轴对称图形沿着对
(2)轴对称涉及两个图形, 称轴分成两部分,那么这两个图
轴对称图形是对一个图形说的。 形就是关于这条直线成轴对称,
反过来如果把两个成对称图形看
做完练习有 何感受?
有的图形的对称轴这么多哇! 以后找对称轴我可得 好好 想想呀
第十一页,共19页。
你能找出下图中各图形的对称轴 吗?如果能,请在图上画出来。
第十二页,共19页。
• 你能举出日常生活中常见 的轴对称图形的例子吗?
如果想不出,不要紧,可 以先看看我们的周围有没 有?再想一想外面有没有?
做一做
1.请你画出书上P48图15-1各个图形的对称轴
2. 按图示的步骤用纸剪出一个葫芦形状的图形 思考:通过练习,你对轴对称图形有了那些更深 刻的感受?
《生活中的轴对称》课件(教学设计)

1、下面的图形是轴对称图形吗?如果是, 有几条对称轴?
每组图案中的两个图形有什么 关系?
定义:把一个图形 沿着某一条直线折 叠,如果它能够与 另一个图形重合, 那么就说这两个图 形关于这条直线成 轴对称.这条直线 叫对称轴,折叠后 重合的点叫做对称 点.
对称轴
A
B
A′
B′
C
C′
练一练:
1、举例:举出生活中常见的两个图形 成轴对称的例子. 2、操作:将一张纸对折,中间夹进复 写纸,在纸上任意画出一个多边形, 展开后观察印出的两个多边形是否关 于折痕成轴对称?它的对称轴是什么? 请画出来.
1、观察下列各种图形,判断是不是轴对称图形? 并找出该轴对称图形的对称轴?
2、观察下图中的每组图案,你能找出成轴 对称的图形吗?
(1) (2)
(4) (3)
通过今天的学习,你有什么 收获与体会?
教材分析
教法学法
教学过程
设计说明
1、课本82页习题1至4.
2、为班级设计一个班徽(要求设计的图案是轴对 称图形或成轴对称,并有一定的寓意)
比一比
轴对称图形
区 别
两个图形成轴对称
一个图形
两个图形的位置关系
沿某条直线对折后都能完全重合 联 系 都有对称轴、对称点
找一找
找出下列图形中的对应点、对应线段、对应角
A A D E H
B B C C
G F
对应线段,对应角各有什么关系?
轴对称图形(或关于某条直线对称的两个图形) 的性质: 1.沿对称轴对折后的两部分(或两个图形)完全重合. 2.对应线段相等,对应角相等.
4、归纳“对应线段相等,对应
活动1:试一试
将一张纸对折,然后从折叠处任意剪 出一个图形,展开后观察它有什么特征?
北师大版七年级下册数学《利用轴对称进行设计》生活中的轴对称PPT教学课件

利用轴对称变换设计美丽图案
轴对称变换:
像上面那样,由一个平面图 形得到它的轴对称图形叫作轴对称 变换.
典例精析
例1 如图,已知△ABC和直线l,作出与△ABC关于 直线l对称的图形.
l
A A′
C B
C′ B′
∴△A′B′C′即为所求.
例2 某居民小区搞绿化,要在一块长方形空地(如 下图)上建花坛,现征集设计方案,要求设计的图案 由圆和正方形组成(圆与正方形的个数不限),并且 使整个矩形场地成轴对称图形.请在下边长方形中 画出你的设计方案.
是轴对称图形.
走进生活,动手创作
观察图案: (1)它们是轴对称图形吗? (2)生活中这些图案可以代表什么含义? (3)自己设计一个轴对称图案,并说明你的设计意图.
利用两个圆、两条线段、两个三角形设计 一个轴对称图案,并说明你的设计意图和要表 达的含义.
当堂练习
1. 如图给出了一个图案的一半,其中的虚线 l 是这个
解:如图所示.
做一做
取一张长30厘米、宽6厘米的纸条,将它每3厘米一 段,一反一正像“手风琴”那样折叠起来,并在折 叠好的纸上画出字母E.用小刀把画出的字母E挖去, 拉开“手风琴”,你就可以得到一条以字母E为图 案的花边.
在上面的活动中,如果先把纸条纵向对折,再 折成“手风琴”,然后继续上面的步骤,此时 会得到怎样的花边?它是轴对称图形吗?
(1)你会得到怎样的图案?先猜一猜,再做一做.
(2)你能说明为什么会得到这样的图案吗?应用学过 的轴对称知识试一试.
两次对折折出了2条对称轴,因此图案中一定有2条对称轴.
(3)如果将正方形按上面方式对折3次,然后沿圆 弧剪开,去掉较小部分,展开后结果又会怎样?
三次对折折出了4条对称轴,因此图案中一定有4条对称轴. (4)当纸对折2次后,剪出的图案至少部分的面积相等. (2)答案不唯一,如图所示:
《生活中的轴对称》课件

利用等腰三角形证明轴对称
总结词
通过构造等腰三角形,利用等腰三角形的性 质证明轴对称。
详细描述
首先,在轴对称图形中,选取两个对应点, 并连接它们与对称轴的垂直线段。然后,利 用这些垂直线段构造一个等腰三角形,利用 等腰三角形的性质证明这个三角形是等腰的 。最后,根据等腰三角形的性质,可以证明 轴对称的存在。
05
轴对称的证明方法
利用全等三角形证明轴对称
总结词
通过构造全等三角形,利用全等三角形 的性质证明轴对称。
VS
详细描述
首先,在轴对称图形中,选取两个对应点 ,并连接它们与对称轴的垂直线段。然后 ,利用这些垂直线段构造两个全等三角形 ,利用全等三角形的性质证明这两个三角 形是全等的。最后,根据全等三角形的性 质,可以证明轴对称的存在。
自然界中的轴对称
总结词
自然界中存在着许多轴对称的例子,如蝴蝶、花朵和树木等 。
详细描述
自然界中的许多生物都呈现出轴对称的特点。例如,蝴蝶的 翅膀、花朵的花瓣和树木的枝干等。这些对称性不仅使生物 看起来更加美观,而且有助于提高生物的生存能力和适应环 境的能力。
艺术作品中的轴对称
总结词
艺术作品中的轴对称是指通过中轴线的两侧呈现对称的艺术表现形式,包括绘画、雕塑和摄影等。
对称性分类
根据轴对称的特点,可以将几何图形分为中心对称、轴对称和旋转对称等不同类型,每种类型都 具有独特的性质和表现形式。
02
轴对称的应用
建筑中的轴对称
总结词
建筑中的轴对称是指建筑物的设计通过中轴线两侧呈现对称的特点,给人以平衡 、稳定和美的感受。
详细描述
在建筑设计中,轴对称是一种常见的形式,尤其在古典建筑中。例如,古希腊的 帕特农神庙、巴黎的凯旋门和北京的天坛都是典型的轴对称建筑。这种设计不仅 使建筑看起来更加庄重、典雅,而且增强了建筑的稳定性和视觉效果。
轴对称--完整版课件
BC=10cm,那么△BCD的周长是
_______cm.
26cm
A
E D
B
C
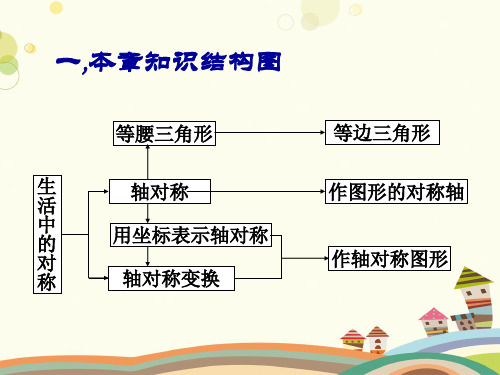
一,本章知识结构图
等腰三角形
等边三角形
生 活
轴对称
作图形的对称轴
中 的
用坐标表示轴对称
对
作轴对称图形
称
轴对称变换
轴对称的性质
•对应点所连的线段的中垂线就是 对称轴 •对应线段相等,对应角相等
轴对称变换
准确做图形对称轴的方法
因为对称轴垂直平分每对对应点所连接 的线段,所以只要找一对对应点,用圆规 作出对应点所连线段的垂直平分线即可。
8、已知,如图: AB=AC AD=DC=BC
则∠A=
Байду номын сангаас
360
A
D
B
C
9.在△ABC中,AB=AC,DE 为AB的垂直 A 平分线,D为垂足,交AC与E,若AB=8cm, △ABC的周长为21cm,求△BCE的周长.
D E
10.如图∠ ABC=70°, ∠ A=50°
B
C
AB的垂直平分线交AC于D,则∠DBC=___.
A
E
B
D
C
11 如图, ∠ABC、∠ACB的平分线相 交于F,过F作DE//BC交AB于D,交AC于E, 若AB=9cm, AC=8cm,则△ADE的周长是 多少? A
AB=AD+DB=AD+DF D F E AC=AE+EC=AE+EF
B
C
13、如图,在△ABC中,AB=AC=16cm,
AB的垂直平分线交AC于D,如果
利用轴对称变换作图1
作出三角形关于直线L对称的图形
七年级 下册 数学 PPT课件 精品课 第5章生活中的轴对称 角平分线的性质

(来自《点拨》)
知2-练
1 【中考·怀化】如图,OP为∠AOB的平分线, PC⊥OA,PD⊥OB,垂足分别是C,D,则下列 结论错误的是( B ) A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
(来自《典中点》)
知2-练
2 如图,在△ABC中,∠C=90°,AC=BC, AD平分∠CAB交BC于D,DE⊥AB于E,若 AB=6 cm,则△DBE的周长是( A ) A.6 cm B.7 cm C.8 cm D.9 cm
7.如图所示,D是∠ACG的平分线上的一点. DE⊥AC, DF⊥CG,垂足分别为E,F.试说明:CE=CF.
解:∵CD是∠ACG的平分线, DE⊥AC,DF⊥CG,
∴DE=DF. 在Rt△CDE和Rt△CDF中,
CD DE
CD, DF,
∴Rt△CDE≌Rt△CDF(HL),
∴CE=CF.
总结
因为∠AEB=∠AOB=90°, 所以∠OAF+∠AFO=90°,∠OBD+∠AFO=90°. 所以∠OAF=∠OBD. 又因为OA=OB,∠AOF=∠BOD=90°, 所以△AOF≌△BOD(ASA). 所以AF=BD. 所以BD=2AE.
返回
方 法 4 截取作对称图形法
4.如图,在△ABC中,AD平分∠BAC,∠C= 2∠B.
即为所求.
(来自《点拨》)
知识点 2 角的平分线的性质
做一做
(1)在一张纸上任意画∠AOB,沿角的
两边将角剪下,将这个角对折,使 角的两边重合,折痕就是∠AOB的 平分线. (2)在∠AOB的角平分线上任意取一点C,分别折出过点C 且与∠AOB的两边垂直的直线,垂足分别为D,E,将 ∠AOB再次对折, 线段CD与CE能重合吗? 改变点C的位置,线段CD和CE还相等吗?
《生活中的轴对称》课件

《生活中的轴对称》PPT课件
生活中的轴对称
什么是轴对称
- 轴对称是一种图形的特征, 左右或上下对称。
- 通过一个轴线将图形分为两 个完全相同的部分。
- 轴对称中的基本概念如轴线 和对称中ቤተ መጻሕፍቲ ባይዱ。
轴对称的应用
- 生活中的轴对称:自然界中 的形状和生物体。
- 建筑物中的轴对称:古代建 筑和现代建筑的设计。
- 艺术中的轴对称:绘画、雕 塑和摄影中的艺术创作。
轴对称的实践
- 用手绘制轴对称图形:练习 构图和对称性。
- 制作一个轴对称的模型:用 纸板和其他材料创建。
- 判断物体是否是轴对称的: 观察和分析图像和实物。
轴对称的重要性
轴对称在日常生活中 的应用
家居摆放、服装设计、厨房烹 饪。
轴对称在科学研究中 的作用
1 轴对称是生活中随处 2 轴对称在各个领域中 3 希望通过本课程能够
可见的重要概念
都有广泛的应用和发
更好地认识和理解轴
无论是自然界还是人类创
展前景
对称的意义和作用
造的事物,轴对称都扮演
从日常生活到工业制造,
通过学习和实践,提升对
着重要角色。
轴对称的应用潜力仍有很
轴对称的认知和创造能力。
多待发掘。
物理学、化学、生物学和天文 学。
轴对称在工业制作中 的重要性
汽车制造、电子产品、品牌标 志。
轴对称的发展趋势
新材料的开发和使用
研发更轻、更坚固的材料,推动 轴对称设计的创新。
机器人应用轴对称的机制
利用轴对称技术改进机器人的运 动和操作。
未来轴对称技术的发展方向
探索更高级的轴对称概念和应用 场景。
结论
生活中的轴对称
什么是轴对称
- 轴对称是一种图形的特征, 左右或上下对称。
- 通过一个轴线将图形分为两 个完全相同的部分。
- 轴对称中的基本概念如轴线 和对称中ቤተ መጻሕፍቲ ባይዱ。
轴对称的应用
- 生活中的轴对称:自然界中 的形状和生物体。
- 建筑物中的轴对称:古代建 筑和现代建筑的设计。
- 艺术中的轴对称:绘画、雕 塑和摄影中的艺术创作。
轴对称的实践
- 用手绘制轴对称图形:练习 构图和对称性。
- 制作一个轴对称的模型:用 纸板和其他材料创建。
- 判断物体是否是轴对称的: 观察和分析图像和实物。
轴对称的重要性
轴对称在日常生活中 的应用
家居摆放、服装设计、厨房烹 饪。
轴对称在科学研究中 的作用
1 轴对称是生活中随处 2 轴对称在各个领域中 3 希望通过本课程能够
可见的重要概念
都有广泛的应用和发
更好地认识和理解轴
无论是自然界还是人类创
展前景
对称的意义和作用
造的事物,轴对称都扮演
从日常生活到工业制造,
通过学习和实践,提升对
着重要角色。
轴对称的应用潜力仍有很
轴对称的认知和创造能力。
多待发掘。
物理学、化学、生物学和天文 学。
轴对称在工业制作中 的重要性
汽车制造、电子产品、品牌标 志。
轴对称的发展趋势
新材料的开发和使用
研发更轻、更坚固的材料,推动 轴对称设计的创新。
机器人应用轴对称的机制
利用轴对称技术改进机器人的运 动和操作。
未来轴对称技术的发展方向
探索更高级的轴对称概念和应用 场景。
结论
生活中的轴对称图形ppt课件

23
用一用 在纸的一侧上滴几滴墨水,将纸迅速对折、 压平,并用手指压出清晰的折痕,再将纸打开后 铺平,观察所得到的图案,位于折痕两侧墨水图 案彼此之间有什么关系?它的对称轴是什么呢?
位于折痕两侧墨水图案成轴对称 ,对称轴为 折痕所在直线.
24
做一做 将一张矩形纸对折,然后用笔尖扎出“17”这个
数字,将纸打开后铺平,
36
37
38
你们知道 猴子为什么捞 不到月亮吗?
39
你见过这些现象吗?
40
41
42
43
在生活中,为了证实人的身 份,经常需要提取人的指纹, 俗称“按手印”。
如图,想一想,取下的指纹 与按手印的手指上的指纹完 全一样吗?它们有什么关系? 动手试一试,对比一下,然 后民同学交流。
①形状和大小相同;
(第一组)
21
议一议 我们再看图10.1.3中的两组图形,它们有什 么共同点?
(第二组)
22
议一议 我们再看图10.1.3中的两组图形,它们有什 么共同点?
D
D1
像这样,把一个图形沿着某一条直线翻折过去,如果 它能够与另一个图形重合,那么就说这两个图形成轴对 称,这条直线就是对称轴,两个图形中的对应点(即两 个图形重合时互相重合的点)叫做对称点.
轴对称图形是对一个图形说的。
33
轴对称与轴对称图形的区别和联系:
联系:
(1)定义中都有一条直线,都要沿这条直 线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部 分,那么这两个图形就是关于这条直 线成轴对称;反过来,如果把两个成 轴对称的图形看成一个整体,那么它 就是一个轴对称图形。
34
练习:
1、在下列图形中,是轴对称图形的是( C )
用一用 在纸的一侧上滴几滴墨水,将纸迅速对折、 压平,并用手指压出清晰的折痕,再将纸打开后 铺平,观察所得到的图案,位于折痕两侧墨水图 案彼此之间有什么关系?它的对称轴是什么呢?
位于折痕两侧墨水图案成轴对称 ,对称轴为 折痕所在直线.
24
做一做 将一张矩形纸对折,然后用笔尖扎出“17”这个
数字,将纸打开后铺平,
36
37
38
你们知道 猴子为什么捞 不到月亮吗?
39
你见过这些现象吗?
40
41
42
43
在生活中,为了证实人的身 份,经常需要提取人的指纹, 俗称“按手印”。
如图,想一想,取下的指纹 与按手印的手指上的指纹完 全一样吗?它们有什么关系? 动手试一试,对比一下,然 后民同学交流。
①形状和大小相同;
(第一组)
21
议一议 我们再看图10.1.3中的两组图形,它们有什 么共同点?
(第二组)
22
议一议 我们再看图10.1.3中的两组图形,它们有什 么共同点?
D
D1
像这样,把一个图形沿着某一条直线翻折过去,如果 它能够与另一个图形重合,那么就说这两个图形成轴对 称,这条直线就是对称轴,两个图形中的对应点(即两 个图形重合时互相重合的点)叫做对称点.
轴对称图形是对一个图形说的。
33
轴对称与轴对称图形的区别和联系:
联系:
(1)定义中都有一条直线,都要沿这条直 线折叠重合;
(2)如果把轴对称图形沿对称轴分成两部 分,那么这两个图形就是关于这条直 线成轴对称;反过来,如果把两个成 轴对称的图形看成一个整体,那么它 就是一个轴对称图形。
34
练习:
1、在下列图形中,是轴对称图形的是( C )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、在Rt△ABC中,BD是角平分线,DE⊥AB, 垂足为E,DE与DC相等吗?为什么?
解:DE=DC ∵ 在Rt⊿ABC中(已知)
∴ ∠C=90°(垂直定义)
E A ∵ DE⊥AB(已知) D 又∵BD是∠B的平分线(已知) ∴DE=DC(角平分线的性质)
B
C
想一想
已如知图D,是 在B△CA的 BC中中点 ,AD,是D∠EBAAC的B与 平E分,
AA
(1)角是轴对称图形吗?
如果是,请找出它的 对称轴;
(2)在上述的操作过程中,
你发现了哪些线段相等?
说说你的理由。
在折痕上另取一点,
再试一试。
O
角是轴对称图形,
角的对称轴是 角的平分线 所在的直线。
B E
CC
DBΒιβλιοθήκη AACE=CD角的平分线上的点 到这个角的两边的距离 相等。
下面用我们学过的知识证明发现:
线D,DFE⊥AACB与 于点F,E,且 DFB⊥EACC于F点. F,那么图 中请相说等明 的A线D段平有分 哪些B?说AC明的理理 由.由.
做一做
用尺规作角的平分线 已知:∠AOB 求作:射线OC,使∠AOC= ∠BOC
A
O B
我来设计
如图,直线a,b,c表示三条相交叉的公路,A.B.C 表示公路的交叉点.若在△ABC内部修建一处加 油站,使加油站到三条公路a,b,c的距离相等,则加 油站应建在何处.
如图,已知AO平分∠BAC,OE⊥AC,
试
OD⊥AB 。则OE=OD吗?请说明理由。
一
答:相等。
试
∵ AO平分∠BAC
∴ ∠EAO= ∠DAO ∵ OE⊥AB,OD⊥AC
C E
∴ ∠AEO= ∠ADO
∠AEO= ∠ADO
∴由 ∠EAO= ∠DAO
A
O
D
B
AO=AO
得⊿ AEO≌⊿ ADO(AAS)
∴OE=OD
A
c
b
B
a
C
通过今天这节课你有什么收获?
(1)角是轴对称图形。
(2) 角平分线上的点到这个角的两 边的距离相等。
作业:P7习题1.2
补充:画一个角,画出它的对称轴后过 对称轴上的任意一个点画对称轴的垂线, 所构成的图形有什么特征?(可先折再 画并与本节课的内容对比。)
2
做一做
(1)在一张纸上任意画一个角∠AOB 沿角的两边剪下, 将这个角对折,使角的两边重合。
(2) 在折痕(即角平分线) 上任意取一点C;
(3) 过点C折OA边的垂线,
得到新的折痕CD,
其中点D是折痕与OA
的交点,即垂足。
O
(4) 将纸打开,新的折痕 与OB 的交点为 E 。
E AB
B CC
D
B
