工程力学11-1-动力学习题课及作业习题解答
大学《工程力学》课后习题解答-精品
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
工程力学课后习题答案第一部分

⼯程⼒学课后习题答案第⼀部分(a) (b) 习题1-1图 (a) (b) 习题1-2图D R(a-1)C(a-2) D R F(a-3)(b-1) ⼯程⼒学教程第⼀卷第⼀篇⼯程静⼒学第1章引论1-1 图a 、b 所⽰,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同⼀⽅F 分别对两坐标系进⾏分解和投影,并⽐较分⼒与⼒的投影。
解:(a ),图(c ):11 s i n c o s j i F ααF F += 分⼒:11 cos i F αF x = , 11 s i n j F αF y = 投影:αcos 1F F x = ,αs i n 1F F y =讨论:?= 90°时,投影与分⼒的模相等;分⼒是⽮量,投影是代数量。
(b ),图(d ):分⼒:22)tan sin cos (i F ?ααF F x -= ,22sin sin j F ?αF y =投影:αcos 2F F x = , )cos(2α?-=F F y 讨论:?≠90°时,投影与分量的模不等。
1-2 试画出图a 、b(c )22x (d )习题1-3图⽐较:图(a-1)与图(b-1)不同,因两者之F R D 值⼤⼩也不同。
1-3 试画出图⽰各物体的受⼒图。
或(a-2)B (a-1) (b-1)F Ay (c-1) 或(b-2) (e-1) (f-1)'A (f-2) 1O (f-3) Ax F'(b-3)E D (a-3)习题1-4图习题1-5图B (b-2)(b-1) Ax F 1-4 图a 所⽰为三⾓架结构。
⼒F 1作⽤在B 铰上。
杆AB 不计⾃重,杆BD 杆⾃重为W 。
试画出图b 、c 、d 所⽰的隔离体的受⼒图,并加以讨论。
1-5 试画出图⽰结构中各杆的受⼒图。
F F'F 1(d-2)y B 21 F (b-2) (b-3) F y B 2A F A B1B F习题1-8图F 'CB C(c) F(a) 'F(a)1-6 图⽰刚性构件ABC 由销钉A 和拉杆GH ⽀撑,在构件的点C 作⽤有⼀⽔平⼒F 。
工程力学(高教第3版)习题解答:第11章 组合变形
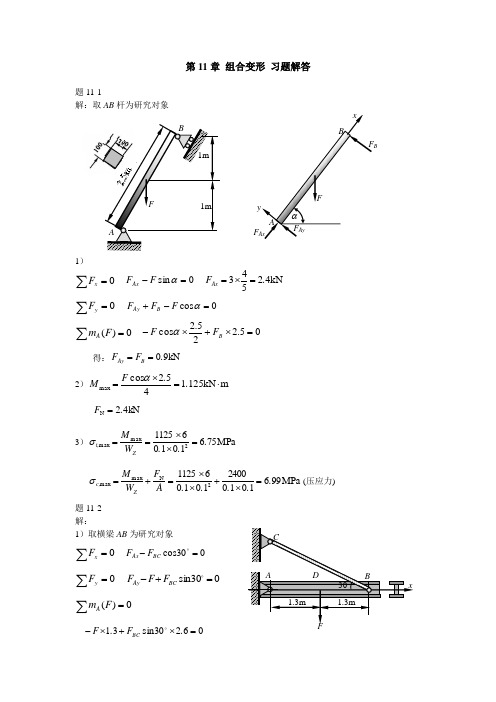
1mF1mB A 第11章 组合变形 习题解答题11-1解:取AB 杆为研究对象1)∑=0xF 0sin =-αF F Ax kN 42543.F Ax =⨯= ∑=0yF0cos =-+αF F F B Ay∑=0)(F m A 05.225.2cos =⨯+⨯-B F F α 得:kN 90.F F B Ay == 2)m kN 1251452cos max ⋅=⨯=..F M αkN 42N .F = 3)MPa 7561010611252max max ...W M Z t,=⨯⨯==σ MPa 996101024001010611252N max max .....A F W M Z c,=⨯+⨯⨯=+=σ(压应力) 题11-2解:1)取横梁AB 为研究对象∑=0xF 030cos =- BC Ax F F ∑=0yF030sin =+- BC Ay F F F ∑=0)(F mA06230sin 31=⨯+⨯-.F .F BCB1.3mx1.3mF ADC30F AxF AyFF Bαx y AB得:kN 30=BC F kN 26=Ax F kN 15=Ay F2)作内力图(略) 知:kN 26max N =Fm kN 5194max ⋅==.lF M3)查表得:N O 18工字钢 2cm 75630.A = 3cm 185=Z W则:MPa 91131075630102610185105194363Nmax max max ...A F W M σZ =⨯⨯+⨯⨯=+=--<MPa 160][=σ横梁强度足够题11-3 解:1) kN 15N ==F Fm kN 64015⋅=⨯=⨯=.e F M因 ][max σσ≤+=A FW M2)先按][max σσ≤=WM进行设计则633103532π106⨯≤⨯d 得:mm 5120.d = 3)代入拉弯组合应力公式校核MPa 2436120504π10151205032π1062333max ...A F W M =⨯⨯+⨯⨯=+=σ%6.3][][max =-σσσ<5%所以取 d =mm 5120.题11-4 解:1)内力分析kN 100N ==F F30m kN 502⋅=⨯=a aF M 2)应力分析6692max 10610)200(1805010)200(180650⨯≤⨯-⨯+⨯-⨯⨯⨯=+=--a a a AF W M σ得:mm 439.a ≤ 所以允许mm 439max .a =题11-5解:受力图略1)计算截面形心和ZC Imm 555381135138)553(113...y C =⨯⨯+⨯⨯⨯++⨯⨯=42323mm 6103138)51555(1238113)55558(12113.....I ZC =⨯⨯-+⨯+⨯⨯-+⨯=2)内力分析F F =N 310)55.526(-⨯+=F M3)确定夹紧力F410300][1055.563max ,⨯=≤⨯⨯+=-t ZC t I M A F σσ 得:N 400=F410600][1045.863max ,⨯=≤⨯⨯+-=-c ZC c I M A F σσ 得:N 7622.F =所以 N 400max =F题11-61)柱子受压弯组合,危险点为K 和K ′点(见图中所示)。
工程力学课后习题答案-工程力学实验课后题答案之欧阳化创编

欧阳化创编 2021..02.12工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得:N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得:PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4图示为一拔桩装置。
工程力学第十一章习题解答

工程力学第十一章习题解答题目:一物体质量为10kg,在水平地面上以10m/s的初速度开始运动,若物体受到一个恒力F=20N的作用,且与运动方向相反,求物体在力作用下停止前所经过的距离。
解答过程:一、问题分析根据牛顿第二定律,力等于质量乘以加速度,即F=ma。
本题中,物体受到一个恒力F=20N的作用,且与运动方向相反,因此加速度a为负值。
我们需要求解物体在力作用下停止前所经过的距离。
二、解题步骤1. 求加速度a根据牛顿第二定律,F=ma,代入已知数据,得到加速度a:a = F/m = -20N / 10kg = -2m/s²2. 求物体停止前所经过的时间t由于物体初速度v0=10m/s,加速度a=-2m/s²,根据速度-时间关系式v=v0+at,我们可以求解物体停止前的时间t:0 = 10m/s - 2m/s² tt = 10m/s / 2m/s² = 5s3. 求物体在力作用下停止前所经过的距离s根据位移-时间关系式s=v0t + 1/2at²,代入已知数据,求解物体在力作用下停止前所经过的距离s:s = 10m/s 5s + 1/2 (-2m/s²) (5s)²s = 50m - 25ms = 25m三、答案验证根据动能定理,物体在运动过程中,动能的变化等于外力做的功。
物体从初始速度10m/s减速到0,动能变化为:ΔK = 1/2 m (v² - v0²) = 1/2 10kg (0 - 100m²/s²) = -500J外力做的功为:W = F s = 20N 25m = 500J由于动能变化等于外力做的功,所以我们的答案是正确的。
四、总结本题主要考查了牛顿第二定律、速度-时间关系式、位移-时间关系式和动能定理的应用。
通过求解加速度、时间和距离,我们得到了物体在力作用下停止前所经过的距离为25m。
工程力学 第二版 (范钦珊 唐静静 著) 高等教育出版社 课后答案 第11章 压杆的稳定性问题

角钢(连结成一整体)。试确定梁与柱的工作安全因 数。
解:1.查型钢表得
习题 11-12 图
No.16aI:Iz = 1130cm4,Wz = 141cm3 2No. 63×63×5: A = 2 × 6.143 = 12.286 cm2
i y = 1.94cm I y = 2 × 23.17 = 46.34 cm
采用,欧拉公式计算临界力
FPcr = σ cr A =
轴的工作安全因数
2 π E
λ2
=
所以,轴不安全。
11-11 图示正方形桁架结构,由五根圆截面钢杆组成,
连接处均为铰链,各杆直径均为 d=40 mm,a=1 m。材料 均为 Q235 钢,E=200 GPa,[n]st=1.8。试;
网
ww w
.k hd 案
μ =1
co
界力。
m
11-5
图示 a、b、c、d 四桁架的几何尺寸、圆杆的横截面直径、材料、加力点及加力
方向均相同。关于四桁架所能承受的最大外力 FPmax 有如下四种结论,试判断哪一种是正确 的。 (A)FPmax(a)=FPmax(c)<FPmax(b)=FPmax(d); (B)FPmax(a)=FPmax(c)=FPmax(b)=FPmax(d); (C)FPmax(a)=FPmax(d)<FPmax(b)=FPmax(c);
案
对于 A3 钢, λ P = 102,
λs = 61.6 。因此,第一杆为大柔度杆,第二杆为中柔度杆,
网
i μl λ2 = 2 i μl λ3 = 3 i
λ1 =
=
ww w
FPcr = ( a − bλ ) A = (304 − 1.12 × 62.5) × 10 3 ×
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学课后习题答案_范钦珊(合订版)

Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向,杆与水平面的夹角为 30°,碾子重量为 250 N。试比较这两种情形 下,碾子越过台阶所需力 F 的大小。
习题 1-10 图
即 (d + 3) sinθ = 2(4.5 − d ) sinθ 2 d +3=9−d
d =3
(2)
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2-2 解图
∴ F 点的坐标为(-3, 0) 合力方向如图所示,作用线过 B、F 点;
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
nb2返回总目录下一章11ebook工程力学静力学与材料力学习题详细解答教师用书第2章范钦珊唐静静200612181第2章力系的简化21由作用线处于同一平面内的两个力f和2f所组成平行力系如图所示
eBook
工程力学
(静力学与材料力学)
习题详细解答
(教师用书) (第 1 章)
范钦珊 唐静静
2006-12-18
FC C
A FA
习题 1-3e 解 1 图
C
BF
FB
FAx A
FAy
习题 1-3b 解 1 图
A FA
FB
α C
B
D
FD 习题 1-3d 解 1 图
D
F
C
F'c
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杆 r
五个未知量,可解得:
N1 mg
B
Ff
C
•
mg
N2
轮
12
N1
92 26
mg
,杆
3 2g 26 r
,轮
3g 13r
,
Ff
3 26 mg , N2
35 mg 26
2.杆运动到铅垂位置时 补充运动学方程:由 va ve vr
va ve cos
ve 3r杆 va r轮
轮
2杆
vr ve sin r杆(*)
FOy
(m
m1)g
maC
m1aA
(m
m1)g
3(m 2m1)2 2(m 3m1)
g
4
习题20-12 已知细长杆AB长2l ,B端置于光滑水平 面,A端系有长l ,质量不计的柔绳,杆于图示初始 位置无初速释放。求:绳子运动到铅垂位置时,杆 两端所受的约束力。
解:绳子运动到铅垂时,杆上端受绳的拉力,下端受 地面支持力。系统仅有重力作功—机械能守恒。
T1
1 2
J
杆 2
O杆
1 2
m1vA2
1 2
(1 3
ml 2 )杆2
1 2
m1(l杆 )2
(
1 6
m
1 2
m1 )l
2 2 杆
O
mgl
V1 2 m1gl
杆
T1 V1 T0 V0
杆
3(m 2m1)g () (m 3m1)l
A
3
画出铅垂位置系统整体受力图:
对固定点O的动量矩定理:dLO dt
杆
A
3r
轮
几何关系:
2r
tan r 1 ;cos 2 ;sin 1
2r 2
3
3
机械能守恒:T1 V1 T2 V2
ve
•
B
r
C vr
va
取C点为势能零点。
13
轮 2杆 vr ve sin r杆(*)
几何关系: tan r 1 ;cos 2 ;sin 1
2r 2
3
3
机械能守恒:T1 V1 T2 V2
工程力学A (下)
动力学习题解答1 (第20章:20-9,20-12,20-14,20-16)
北京理工大学理学院力学系 韩斌
20
习题20.9 均质细杆OA质量为m,长度为l ,以铰链A
与质量为m1,半径 r 的均质圆盘中心相连,不计摩擦,系 统于图示水平位置无初速释放,求杆OA转至铅垂位置
时,杆的角速度,角加速度及O处的约束力。 解:注意杆与圆盘是铰接,从约束
对a动a 点Ca,en建动a系e固连a于r杆AaBC,
r轮 0 2r杆 ? 0
(e 杆 0)
ar 0,
r轮 2r杆
轮 2杆 (1)
分别取杆和轮为分离体, 画出受力图
杆 r
r
r
B
ar
A
轮
2r
C
•
aa
ae
ae
11
运动学关系: 轮 2杆 (1)
对杆列定点A动量矩定理: 1
3
m2r 2 杆
FB
l
cos
(1)
y方向质心运动定理: maCy mg FT FB (2)
运动学补充
g 2l cos
(3)
方程: 几何关系:
aCy
a
n A
2
v
2 A
2l
g 2
(4)
sin
3 1 , cos2 3
2
2
(5)
3l
解得:
FT
3 4
1 mg 6 3
27 2 36
3 mg()
FB
3 4
1 63
mg
27 2 36
3 mg()
B
lA 2l
9
习题20-14
已知AB杆长2r,质量m;圆盘半径r,质量m,初 始位置AC垂直,∠BAC=45ο 求:在重力作用下, 初始瞬时位置时和AB垂直时,杆AB的角加速度及 地面对圆盘的约束力。
rA
r
B
2r
rC •
10
解: 1.初始瞬时
系统静止: vC 0, 杆 0, 轮 0 设角加速度如图,找出 杆,轮之间的运动学关系:
O
A
FAy
条件分析: 杆为定轴转动, 盘为一般平面运动。 受力分析:画出圆盘受力图
A FAx 圆盘对质心动量矩守恒:
LA J AA LA0 J AA0 0 m1g A 0 圆盘平移!
仅重力作功,机械能守恒:
2
以O点所在平面为势能零点,系统初始静止:
T0 V0 0
O
A
设杆转至铅垂位置时角速度为杆 :
M
(e) O
0
LO
1 3
ml 2杆
m1(l杆 ) l
1 3
(m
3m1)l 2杆
aC
OFOy
F杆Ox C
m g
dLO dt
1 3
(m
3m1
)l
2
杆
0
杆 0
A aA
aC
l 2
杆2
()
aA l杆2 ()
m1g
由系统整体的质心运动定理:
FOx 0
FOy (m m1)g maC m1aA
AB杆运动到铅直位置时, AB杆瞬时平动,以地面为 势能零点,则由机械能守恒 原理:
V0 T0 V1 T1
B
lA
A
3l
2l
B
5
由机械能守恒原理: V0 T0 V1 T1
3 V0 mg 2 l, T0 0
V1 mg
3 1l, 2
T1
1 2
mvC 2
得 vC gl
vA vC gl
7
又
aC
1 2
(aA
aB )
1 2
(aAn
aA
aB )
沿y方向投影,得: aCy
a
n A
2
v
2 A
2l
g 2
(4)
几何关系: sin 3 1 , cos2 3
2
2
(5)
aA
vA
FT
aAn
A
vBaBFBBvCaB A
Hale Waihona Puke mg3lBlA 2l
8
对质心的动量矩定理:1
12
m2l 2
FT
mg
2 2
r
N1r
(2)
对圆盘列对质心的动量矩定理:
1 2
mr 2 轮
Ff
r
(3)
对圆盘列质心运动定理:
maCx
Fx
mr N1
2 2
Ff
2 2
N1
Ff
(4)
maCy Fy
N2 mg N1
2 0 2
(5)
FAy
A
FAx
N1
上述5个方程中,共有
r
r
轮 ,杆 , N1, N2 , Ff
取C点为势能零点 T1 0
V1 mg
2r 2
T2
1 2
m(2r)2 3
杆2
1( 3 22
mr
2 )轮2
13 6
mr 2杆2
V2 mg ( 2r r)
运动?a学B补充vaA2方An/ l 程a:?A由A2a,lB BA 两 点a0Bn的A 加速 A度B 关 0系故a
n BA
0
✓ ✓✓ ✓
y方向: 0 2l
v
2 A
2l 2 cos
g 2l cos
(3)
cos
vA2 l
aAvA
FT
vBaBFBBvCaB A
mg
aAn
A
3l
B
lA 2l
对质心的动量矩定理: 1 m2l2
12
FT
FB l cos
(1)
y方向质心运动定理:
maCy mg FT FB (2)
注意:对动点A
vC
或B列动量矩定 vB FB
vA
FT
A
mg
3l
B
理容易出错!
B
lA 2l
6
对质心的动量矩定理:1
12
m2l 2
FT
FB
l
cos
(1)
y方向质心运动定理: maCy mg FT FB (2)
