结构在移动荷载作用下的计算共39页文档
合集下载
框架结构在水平荷载下的计算反弯点法和值法详解

A
B
Ma
4i a
2ib
6i l
Mb
4i b
2i a
6i l
a
b
l
V 6i a 6ib 12i
l
l
l2
37
第三十七页,共69页。
计算转角和位移的关系 – 节点 A 、B 处
Ma
4i a
2i b
6i l
V 6i a 6ib 12i
l
l
l2
M 0
A:
4(i3 i4 ic ic ) 2(i3 i4 ic ic )
i1、 i2
与柱A端相交的梁的线刚度 为
i3、 i4
i1
ic B
i2
i3
ic i4
A
ic
34
第三十四页,共69页。
35
第三十五页,共69页。
第三十六页,共69页。
ui D
B
hi
A
C
36
柱 AB 剪力与 相邻梁 、柱杆端的侧移△及转角 相关
因此需求出转角和位移的关系 预备公式 : 转角位移方程
A、B 端均为刚结的杆端
端部的转角就很小,此时忽略节点转角的存在,对框架 内力计算影响不大。
由此也可以看出,反弯点法是有一定的适用范围 的,即框架梁、柱的线刚度之比应不小于3。
5
第五页,共69页。
水平荷载作用下框架 的变形情况:
第六页,共69页。
当梁刚度无限大 时,水平荷载作用 下框架的变形情况 :节点转角为0,各 节点水平位移相同 。
V1k
h1 3
Mb c1k
V1k
2h1 3
上部各层柱,上下 柱端弯矩相等
Mt cjk
结构力学二6-移动荷载作用下的结构计算

§6—1 影响线的概念 1. 问题的提出
工程结构除了承受固定荷载作用外,还要受到移动荷 载的作用。例如:见图。 在移动荷载作用下,结构的反力 和内力将随着荷载位置的移动而变化,在结构设计中,必
须求出移动荷载作用下反力和内力的最大值。
为了解决这个问题,需要研究荷 载移动时反力和内力的变化规律。然 而不同的反力和不同截面的内力变化 规律各不相同,即使同一截面,不同 的内力变化规律也不相同,解决这个 复杂问题的工具就是影响线。
截面C的最大弯矩。 A
C
解:作Mc影响线
首 其根先次据考再虑考上车虑述队车两右队行调
将头种重向车临左后行界轮驶位置。置于将,顶重可点车。后 轮分置按别于式影算(响出6—线相6顶)应计点的算。 15
故有故其有M,M右故这 它C1m这13C行:1又情0a015505值x00是500=×1是况时7151。611临5010一也00.M×00200界经2052临不35C5+11.位112比值7155界必23355000500置+0位考较大×置虑得,,。
其他行97.03驶×8+位25.20置5×+不73.0必8×8考+ 虑。
0.75=1962kN·m
15m 40m
3·75 6·25 9·38 7·88
70kN 30 100 50
6m
45 4
B
25m
2·25 0·75 70 30
15
42
27
集中荷载 P=1沿结构移动时,对某量值产生的影响,然后
据叠加原理可进一步研究各种移动荷载对该量值的影响。
例如:见图。这样所得的图形就表示了 P=1在梁上
移动时反力 RA的变化规律,这一图形就称为反力 RA的 影响线。
工程结构除了承受固定荷载作用外,还要受到移动荷 载的作用。例如:见图。 在移动荷载作用下,结构的反力 和内力将随着荷载位置的移动而变化,在结构设计中,必
须求出移动荷载作用下反力和内力的最大值。
为了解决这个问题,需要研究荷 载移动时反力和内力的变化规律。然 而不同的反力和不同截面的内力变化 规律各不相同,即使同一截面,不同 的内力变化规律也不相同,解决这个 复杂问题的工具就是影响线。
截面C的最大弯矩。 A
C
解:作Mc影响线
首 其根先次据考再虑考上车虑述队车两右队行调
将头种重向车临左后行界轮驶位置。置于将,顶重可点车。后 轮分置按别于式影算(响出6—线相6顶)应计点的算。 15
故有故其有M,M右故这 它C1m这13C行:1又情0a015505值x00是500=×1是况时7151。611临5010一也00.M×00200界经2052临不35C5+11.位112比值7155界必23355000500置+0位考较大×置虑得,,。
其他行97.03驶×8+位25.20置5×+不73.0必8×8考+ 虑。
0.75=1962kN·m
15m 40m
3·75 6·25 9·38 7·88
70kN 30 100 50
6m
45 4
B
25m
2·25 0·75 70 30
15
42
27
集中荷载 P=1沿结构移动时,对某量值产生的影响,然后
据叠加原理可进一步研究各种移动荷载对该量值的影响。
例如:见图。这样所得的图形就表示了 P=1在梁上
移动时反力 RA的变化规律,这一图形就称为反力 RA的 影响线。
结构的位移计算和刚度
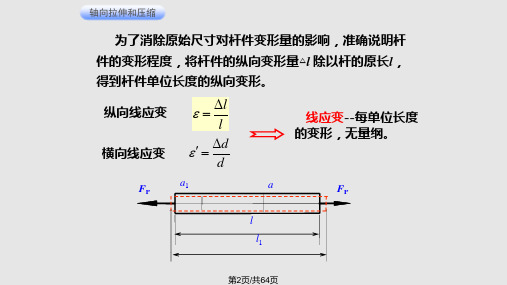
结构位移计算
M 1
A
求A截面角位 移的虚拟状态
FP 1C
E
D
A
F
B
求C点水平位移的虚拟状态
M 1
C
M 1
A
求两截面相对角 位移的虚拟状态
1l
C
E
D
M 1
A
B
F 1l
BE=l
求BE杆转角 BE 的虚拟状态
第21页/共64页
结构位移计算
1l
C
M 1
1l
E
D
M 1
A 1l F 1l B
AE=BE=l 求AE、BE两杆相对转角的虚拟状态
0
D
2 2
1
2
B
1 2
解:1. 建立虚设状态;
2. 分别求两种状态各杆轴力;
3. 由公式计算位移:
CV
F N FNPl EA
1 EA
1 2
F 2
l
2
1 EA
2 2
1 2 Fl 1.914 Fl
2 EA
EA
2F 2
2l 2
第33页/共64页
结构位移计算
l
2 2
F
F
A
2
2 2 F
F F
轴向拉伸和压缩
为了消除原始尺寸对杆件变形量的影响,准确说明杆 件的变形程度,将杆件的纵向变形量△l 除以杆的原长l, 得到杆件单位长度的纵向变形。
纵向线应变 横向线应变
l
l d
d
线应变--每单位长度 的变形,无量纲。
FP
a1
a
FP
l l1
第2页/共64页
轴向拉伸和压缩
结构力学第六章 力法

34
四、n次超静定结构的力法典型方程
i1X1 i2 X 2 in X n iP 0(i 1、2、、n)
符号意义同前。 求解内力(作内力图)的公式:
M M1X1 M2X2 Mn Xn M P
FQ FQ1X1 FQ2 X2 FQn Xn FQP
FN FN1 X1 FN 2 X 2 FNn X n FNP 作内力图可以延用第三章的作法:由M→FQ→FN。
通常做法:拆除原结构的所有多余约束,代之 以多余力X,而得到静定结构。
规则: 1)去掉或切断一根链杆,相当于去掉一个约束; 2)去掉一个简单铰,相当于去掉两个约束; 3)去掉一个固定支座或切断一根梁式杆,相当于去 掉三个约束; 4)在梁式杆上加一个简单铰,相当于去掉一个约束。
10
例: a)
X1
X2
37
2、列 力法方程
1211XX11
12 X 2 22 X 2
1P 2P
0 0
(B 0) (C 0)
讨论方程和系数的物理意义。
q
A
D
Δ1P B
C
A
X1=1
δ11 δ21
D
B
C
A
δ12
X2=1 δ22
D
B C
38
位移方程(力法方程)
ΔφB=0 ——B左右截面相对转角等于零。 ΔφC=0 —— C左右截面相对转角等于零。
d)
原结构
X2
X1
X1
X2
n=2
13
e)
原结构
X1 X1 n=1
f)
原结构
n=3
X1
X3
X2
特别注意:不要把原结
构拆成几何可变体系。此
四、n次超静定结构的力法典型方程
i1X1 i2 X 2 in X n iP 0(i 1、2、、n)
符号意义同前。 求解内力(作内力图)的公式:
M M1X1 M2X2 Mn Xn M P
FQ FQ1X1 FQ2 X2 FQn Xn FQP
FN FN1 X1 FN 2 X 2 FNn X n FNP 作内力图可以延用第三章的作法:由M→FQ→FN。
通常做法:拆除原结构的所有多余约束,代之 以多余力X,而得到静定结构。
规则: 1)去掉或切断一根链杆,相当于去掉一个约束; 2)去掉一个简单铰,相当于去掉两个约束; 3)去掉一个固定支座或切断一根梁式杆,相当于去 掉三个约束; 4)在梁式杆上加一个简单铰,相当于去掉一个约束。
10
例: a)
X1
X2
37
2、列 力法方程
1211XX11
12 X 2 22 X 2
1P 2P
0 0
(B 0) (C 0)
讨论方程和系数的物理意义。
q
A
D
Δ1P B
C
A
X1=1
δ11 δ21
D
B
C
A
δ12
X2=1 δ22
D
B C
38
位移方程(力法方程)
ΔφB=0 ——B左右截面相对转角等于零。 ΔφC=0 —— C左右截面相对转角等于零。
d)
原结构
X2
X1
X1
X2
n=2
13
e)
原结构
X1 X1 n=1
f)
原结构
n=3
X1
X3
X2
特别注意:不要把原结
构拆成几何可变体系。此
2 结构的荷载和作用

22
第二十二页,共四十七页。
地震 震 (dìzhèn) 害
23
第二十三页,共四十七页。
地震造成的破碎带,引起地表沉陷、隆起(lónɡ qǐ)、裂缝、液化等地表破坏
24
第二十四页,共四十七页。
局部地形改观(gǎiguān)引起铁轨
变形
25
第二十五页,共四十七页。
汶
萨
川
尔
地
瓦
震
多
(dì
(sà
zhè
短,量值可能很大。
例如:地震作用、爆炸力、船只(chuánzhī)或漂流物撞击力等。
【思考】施工荷载、设备及家具自重属于何种作用?
6
第六页,共四十七页。
2、按随空间位置的变异(biànyì)分类
(1)固定(gùdìng) 作用 ——在结构上出现的空间位置固定不变,但其量值可能具有随机
性。 例如:结构自重(zìzhòng)、固定设备自重(zìzhòng)、屋顶水箱重量等。
砂粒的振动(zhèndòng)
砂土液化(yèhuà)试验
28
第二十八页,共四十七页。
承载力不足(bùzú)
变形(biàn xíng)过大
29
第二十九页,共四十七页。
座落在活断层上的一座二层小学(xiǎoxué)教学楼被完全摧 毁
30
第三十页,共四十七页。
楼房底层空旷,结构(jiégòu)不合理,房屋整体倾斜,二楼成了一
34
第三十四页,共四十七页。
常用(chánɡ yònɡ) 术语
92%的地震发生在地壳中,
其余的发生在地幔上
部。
地球内部发生地震的地方叫震源(zhènyuán); 震源深度
震源在地面上的投影点称为(chēnɡ wéi)震中; 震中距
吊车梁设计PPT课件

Wnx 2
W’ny—吊车梁上翼缘截面对 y轴的净截面抵抗矩。
第30页/共54页
带制动梁的吊车梁 A点最不利
Mx My f
Wnx 1 Wny 1
Wny1—制动梁截面对其 形心轴y1的净截面抵抗矩。
第31页/共54页
带制动桁架的吊车梁
A点最不利
Mx Wnx
M
' y
Wn'y
N1 An
f
An—吊车梁上翼缘及腹板15第t3w2的页/共净54截页面面积之和。
21计算项目计算力吊车台数组合轻中级吊车重级吊车吊车梁及制动结构的强度和稳定按实际情况不多于两台轮压处腹板局部压应力腹板局部稳定不多于两台吊车梁和制动结构的疲劳强度一台最大吊车吊车梁的竖向挠一台最大吊车计算力及吊车台总数组合表22计算项目计算力吊车台数组合轻中级吊车重级吊车制动结构的水平挠度一台最大吊车梁上翼缘制动结构与柱的连接按实际情况不多于两台柱间支撑处吊车按实际情况不多于两台计算力及吊车台总数组合表23273吊车梁的内力计算吊车荷载为移动荷载确定最不利轮压位置计算最大内力采用影响线法根据影响线法计算弯矩时的吊车的最不利轮距布置为
制动结 构形式
正应力σ 上翼缘处
下翼缘处
剪应力τ
腹板计算高 度边缘的局 腹板计算高度边缘的折算 部压应力 应力
σc
无制动 结构
制动梁
制动桁 架
Mx Wnx 1
My Wn'y
f
Mx Wnx
My Wn'y 1
f
Mx Wnx
M
' y
Wn&梁 轮压影响范围内
Mx
f
Vmax S w I xtw
1.35F fv lztw
f
W’ny—吊车梁上翼缘截面对 y轴的净截面抵抗矩。
第30页/共54页
带制动梁的吊车梁 A点最不利
Mx My f
Wnx 1 Wny 1
Wny1—制动梁截面对其 形心轴y1的净截面抵抗矩。
第31页/共54页
带制动桁架的吊车梁
A点最不利
Mx Wnx
M
' y
Wn'y
N1 An
f
An—吊车梁上翼缘及腹板15第t3w2的页/共净54截页面面积之和。
21计算项目计算力吊车台数组合轻中级吊车重级吊车吊车梁及制动结构的强度和稳定按实际情况不多于两台轮压处腹板局部压应力腹板局部稳定不多于两台吊车梁和制动结构的疲劳强度一台最大吊车吊车梁的竖向挠一台最大吊车计算力及吊车台总数组合表22计算项目计算力吊车台数组合轻中级吊车重级吊车制动结构的水平挠度一台最大吊车梁上翼缘制动结构与柱的连接按实际情况不多于两台柱间支撑处吊车按实际情况不多于两台计算力及吊车台总数组合表23273吊车梁的内力计算吊车荷载为移动荷载确定最不利轮压位置计算最大内力采用影响线法根据影响线法计算弯矩时的吊车的最不利轮距布置为
制动结 构形式
正应力σ 上翼缘处
下翼缘处
剪应力τ
腹板计算高 度边缘的局 腹板计算高度边缘的折算 部压应力 应力
σc
无制动 结构
制动梁
制动桁 架
Mx Wnx 1
My Wn'y
f
Mx Wnx
My Wn'y 1
f
Mx Wnx
M
' y
Wn&梁 轮压影响范围内
Mx
f
Vmax S w I xtw
1.35F fv lztw
f
结构在移动荷载作用下的计算
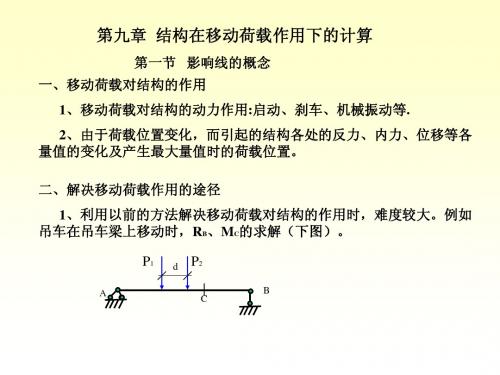
∑M
NFD影响线 (分析例题9-3,讨论书后思考题) 分析例题 ,讨论书后思考题)
K
=0
R A a N FD r2 = 0
∴ N FD = a RA r2
第六节 影响线的应用 一、当荷载位置固定时,求某量值的大小 当荷载位置固定时, 1、集中荷载位置固定时,求某量值的大小 、集中荷载位置固定时,
影响线: (三)NFD影响线: 1、作1-1截面,令P=1在截面左 、 截面, 截面 在截面左 侧移动,研究其右半部: 侧移动,研究其右半部:
∑M
K
=0
RB (l + a ቤተ መጻሕፍቲ ባይዱ + N FD r2 = 0
∴ N FD l+a = RB r2
2、作1-1截面,令P=1在截面右 、 截面, 截面 在截面右 侧移动,研究其左半部: 侧移动,研究其左半部:
P=1
A
δX P=1 δP
B
代替A支座作用 以X代替 支座作用,结构仍能维持平 代替 支座作用, 使其发生虚位移,依虚位移原理: 衡。使其发生虚位移,依虚位移原理: XδX+P δP=0 δ X=-PδP/δX=- δP/δX - δ δ - δ 令 δX=1, 则X=-δP , -
结论:为作某量值的影响线, 结论:为作某量值的影响线,只需将与该量值相应的联系 去掉,并以未知量X代替;而后令所得的机构沿X的正方 去掉,并以未知量 代替;而后令所得的机构沿 的正方 代替 向发生单位位移, 向发生单位位移,则由此所得的虚位移图即为所求量值的 影响线。 影响线。
S=∫q 1ydx=qω x
x2
(2)
MC影响线 综合以上两种情况,当荷载位置固定时, 综合以上两种情况,当荷载位置固定时,求某量值的大小按下 式计算: 式计算: S=∑ piyi+qω
移动模架现浇梁施工

第38页/共43页
质量保证措施
(1) 提高质量意识,加强质量教育。
(2) 加强技术培训和技术指导工作
(3)健全完善各种工程质量检查验收签证制度, 严格执行各项质量检验程序,通过全方位、全 过程的质量控制,确保质量目标的实现。
(4) 加强质量常规性的检查,建立质量检查程 序。 坚持质量工作四大检查制度:开工前检 查、施工中检查、隐蔽工程检查、定期质量检 查。
榀/对 4/2
推进平车
台
4
横梁
节/榀 各2/15
外模系统(贴不锈钢板) 段/部 9/2
内模系统
段
52
前支撑横梁
节/榀 2/1
C型梁(含两侧悬挂行走装置) 节/榀 3/1
后横梁
榀
1
重量
单位 重量
T 270
T 80
T 70
T 24
T 45
T 148
T 70
T
5
T 25
T 11
附注 最重节28T
分为左右两Leabharlann 分• 检查时要求必须要有监理及指挥部专业技术人员参加。检验合格表必须有项目负责人及监理工程师签字方 可进行下一工序。
第23页/共43页
设备预压 • (1)试验采用砂袋堆载方法逐级加载,直至加至混凝土荷载的 1.05倍 • (2)荷载布置:堆载时根据砼箱梁腹板与顶底板处荷载不同,
应尽量保证移动模架系统的受力与实际浇筑混凝土时一致。 • (3)持荷72小时。 • (4)观测设备各构件、零部件的变形量和沉降量,并做好记录
第41页/共43页
It ’s over!
Thank you!!!
第42页/共43页
感谢您的观看!
第43页/共43页
质量保证措施
(1) 提高质量意识,加强质量教育。
(2) 加强技术培训和技术指导工作
(3)健全完善各种工程质量检查验收签证制度, 严格执行各项质量检验程序,通过全方位、全 过程的质量控制,确保质量目标的实现。
(4) 加强质量常规性的检查,建立质量检查程 序。 坚持质量工作四大检查制度:开工前检 查、施工中检查、隐蔽工程检查、定期质量检 查。
榀/对 4/2
推进平车
台
4
横梁
节/榀 各2/15
外模系统(贴不锈钢板) 段/部 9/2
内模系统
段
52
前支撑横梁
节/榀 2/1
C型梁(含两侧悬挂行走装置) 节/榀 3/1
后横梁
榀
1
重量
单位 重量
T 270
T 80
T 70
T 24
T 45
T 148
T 70
T
5
T 25
T 11
附注 最重节28T
分为左右两Leabharlann 分• 检查时要求必须要有监理及指挥部专业技术人员参加。检验合格表必须有项目负责人及监理工程师签字方 可进行下一工序。
第23页/共43页
设备预压 • (1)试验采用砂袋堆载方法逐级加载,直至加至混凝土荷载的 1.05倍 • (2)荷载布置:堆载时根据砼箱梁腹板与顶底板处荷载不同,
应尽量保证移动模架系统的受力与实际浇筑混凝土时一致。 • (3)持荷72小时。 • (4)观测设备各构件、零部件的变形量和沉降量,并做好记录
第41页/共43页
It ’s over!
Thank you!!!
第42页/共43页
感谢您的观看!
第43页/共43页
