上海市闸北区2015届高三下学期期中练习(二模)数学理试题
上海市闸北区2015届高三下学期期中练习物理试题及答案

28.( 7 分)某同学做“用单摆测定重力加速度”的实验,实验步骤如下:
I.选取一个摆线长约 1m 的单摆,把线的上端用铁夹固定在铁架台上,把铁架台放在实验桌边,使 铁夹伸到桌面以外,让摆球自由下垂。
________ kg·m/s,球棒的动量变化量为 ________
kg· m/s。
22B.已知地球质量约为某一星球质量的 6 倍,地球半径约为该星球半径的 1.5 倍,则该星球表面的
重力加速度约为 _________ m/s2,航天器在该星球表面附近绕其做匀速圆周运动的速率约为
________
m/s。(地球表面重力加速度 g 为 10m/s2,地球半径 R≈ 6.4× 106m)
度为 ρ,大气压强为 po)
25.如图( 1),正三角形金属线框水平放置,总电阻为 1Ω,边长为 3m,处在两个半径均为 1m 的圆
形匀强磁场区域中。线框顶点与右侧圆中心重合,线框底边中点与左侧圆中心重合。磁感应强度
B1
垂直水平面向外,大小不变, B2 垂直水平面向里,大小随时间变化, B1、B2 的值如图( 2)。则 t=0.6s
b、 c、d 所示。下列说法正确的是
(
A .若已知小方格的边长,可求得平抛的初速度
B .若已知小方格的边长,可求得频闪周期
C .若已知小方格的边长和当地的重力加速度,可求得
速度
) a、b、 c、 d 任
一 点的
D .若已知小方格的边长和频闪周期,可以求得当地的重力加速度
18.如图,两同心圆环 A 、 B 置于同一水平面上,其中 B 为均匀带负电绝缘环, A 为导体环。当 B
(
)
(
)
3.下列说法符合历史事实的是
(
2015年上海中考数学二模19-23题

2015年宝山嘉定联合模拟考试数学试卷三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)先化简,再求值:xx x x x x x x 124122222++---+- ,其中13-=x .20.(本题满分10分)解方程组:⎩⎨⎧=--=+.,0658222y xy x y x ②①21.(本题满分10分,每小题满分各5分)某住宅小区将现有一块三角形的绿化地改造为一块圆形的绿化地如图6.已知原来三角形绿化地中道路AB 长为216米,在点B 的拐弯处道路AB 与BC 所夹的B ∠为︒45,在点C 的拐弯处道路AC 与BC 所夹的C ∠的正切值为2(即2tan =∠C ),如图7. (1)求拐弯点B 与C 之间的距离; (2)在改造好的圆形(圆O )绿化地中,这个圆O 过点A 、C ,并与原道路BC 交于点D ,如果点A 是圆弧(优弧)道路DC 的中点,求圆O 的半径长.A .OB C D 图7 图622.(本题满分10分,每小题满分各5分)已知一水池的容积V (公升)与注入水的时间t (分钟)之间开始是一次函数关系,表(1)求这段时间时关于的函数关系式(不需要写出函数的定义域);(2)从t 为25分钟开始,每分钟注入的水量发生变化了,到t 为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.23.(本题满分12分,每小题满分各6分)如图8,已知△ABC 和△ADE 都是等边三角形,点D 在边BC 上,点E 在边AD 的右侧,联结CE .(1)求证:︒=∠60ACE ;(2)在边AB 上取一点F ,使BD BF =,联结DF 、EF .求证:四边形CDFE 是等腰梯形.图8崇明县2014学年第二学期教学质量调研测试卷(2)九年级数学三、解答题(本大题共7题,满分78分)19.(本题满分10分) 先化简,再求值:2122121x x x x x x +-÷+--+,其中6tan302x =︒-. 20.(本题满分10分)解方程组:222230x y x xy y -=⎧⎨--=⎩ 21.(本题满分10分,第(1)小题5分、第(2)小题5分) 在Rt ABC ∆中,90BAC ∠=︒,点E 是BC 的中点, AD BC ⊥,垂足为点D .已知9AC =,3cos 5C =. (1)求线段AE 的长; (2)求sin DAE ∠的值.(第21题图)CABED22.(本题满分10分,第(1)小题4分,第(2)小题6分)周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y (km)与小明离家时间x (h)的函数图像.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.(1)小明骑电动自行车的速度为千米/小时,在甲地游玩的时间为小时;(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?23.(本题满分12分,每小题各6分)如图,ABC ∆中,2BC AB =,点D 、E 分别是BC 、AC 的中点,过点A 作AF BC ∥交线段DE 的延长线于点F ,取AF 的中点G ,联结DG ,GD 与AE 交于点H . (1)求证:四边形ABDF 是菱形; (2)求证:2DH HE HC =⋅.(第22题图))A BDHG FEC(第23题图)2014学年奉贤区调研测试九年级数学三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 计算:1o )12(45cos 22218-++--+.20.(本题满分10分)解不等式组:⎪⎩⎪⎨⎧-≤-+<-x x x x 2371211513)(,将其解集在数轴上表示出来,并写出这个不等式组的最小整数解......21.(本题满分10分,每小题满分各5分)已知:如图,在△ABC 中,AB=AC =6,BC =4,AB 的垂直 平分线交AB 于点E ,交BC 的延长线于点D . (1)求∠D 的正弦值; (2)求点C 到直线DE 的距离.CBA(第21题图)EDS22.(本题满分10分)某学校组织为贫困地区儿童捐资助学的活动,其中七年级捐款总数为1000元,八年级捐款总数比七年级多了20%.已知八年级学生人数比七年级学生人数少25名,而八年级的人均捐款数比七年级的人均捐款数多4元.求七年级学生人均捐款数.23.(本题满分12分,每小题满分各6分)已知:如图,在四边形ABCD中,AB//CD,点E是对角线AC上一点,∠DEC=∠ABC,且CACECD⋅=2.(1)求证:四边形ABCD是平行四边形;(2)分别过点E、B作AB和AC的平行线交于点F,联结CF,若∠FCE=∠DCE,求证:四边形EFCD是菱形.B(第23题图)A黄浦区2015年九年级学业考试模拟考数学试卷三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:.20. (本题满分10分)解方程组:21. (本题满分10分,第(1)满分7分,(2)小题满分3分)温度通常有两种表示方法:华氏度(单位:)与摄氏度(单位:).已知华氏度数y与摄氏度数x 之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.(1)选用表格中给出的数据,求y 关于x 的函数解析式(不需要写出该函数的定义域); (2)已知某天的最低气温是,求与之对应的华氏度数.)1134811-+-+-2222, 1. x y x y ⎧-=-⎨-=⎩①②FC 5-C22. (本题满分10分,第(1)、(2)小题满分各5分)如图5,在梯形ABCD 中,AD //BC ,AB ⊥BC ,已知AD =2,,梯形ABCD 的面积是9.(1)求AB 的长;(2)求的值.23. (本题满分12分,第(1),(2)小题满分各6分)如图6,在正方形ABCD 中,点E 在对角线AC 上,点F 在边B C 上,联结BE 、DF ,DF 交对角线AC 于点G ,且DE =DG . (1)求证:AE =CG ;(2)求证:BE //DF .4cot 3ACB ∠=tan ACD ∠图5图6F2014学年金山区第二学期期中质量检测 初三数学试卷三、(本题共有7题,满分78分) 19.(本题满分10分)化简:(12122+---+x x x x x x )22)1(1-+÷x x x20.(本题满分10分)解方程组⎩⎨⎧=-+-=+-04440122y xy x y x21.(本题满分10分)如图,点P 表示某港口的位置,甲船在港口北偏西30方向距港口50海里的A 处,乙船在港口北偏东45方向距港口60海里的B 处,两船同时出发分别沿AP 、BP 方向匀速驶向港口P ,1小时后乙船在甲船的正东方向处,已知甲船的速度是10海里/时,求乙船的速度.东第21题图22.(本题满分10分)为了解本区初中学生的视力情况,教育局有关部门采用抽样调查的方法,从全区2万名中学生中抽查了部分学生的视力,分成以下四类进行统计注:(4.3—4.5之间表示包括4.3及4.5)根据图表完成下列问题:(1) 填完整表格及补充完整图一;(2) “类型D ”在扇形图(图二)中所占的圆心角是度; (3) 本次调查数据的中位数落在类型内;(4) 视力在5.0以下(不含5.0)均为不良,那么全区视力不良的初中学生估计人 .AB视力 类型 图二 第22题图23.(本题满分12分)已知:如图,在中ABC Rt ∆中,︒=∠90ACB ,BC AC =,点E 在边AC 上,延长BC 至D点,使CD CE =,延长BE 交AD 于F ,过点C 作CG //BF ,交AD 于点G ,在BE 上取一点H ,使DCG HCE ∠=∠. (1)求证:ACD BCE ∆≅∆; (2) 求证:四边形FHCG 是正方形.G FE D BAC第23题图H静安、青浦区2014学年第二学期教学质量调研九年级数学2015.4三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)化简:))(111(222x x x x x +---,并求当02133-=x 时的值.20.(本题满分10分)求不等式组⎪⎩⎪⎨⎧+≥++<-12)132(6,34)1(7x x x x 的整数解.21.(本题满分10分,第(1)小题满分4分,第(2)小题满分6分)如图,在直角坐标系xOy 中,反比例函数图像与直线2-=x y 相交于横坐标为3的点A . (1)求反比例函数的解析式;(2)如果点B 在直线2-=x y 上,点C 在反比例函数图像上,BC //x 轴,BC = 4,且BC 在点A 上方,求点B 的坐标.22.(本题满分10分)甲乙两人各加工30个零件,甲比乙少用1小时完成任务;乙改进操作方法,使生产效率提高了一倍,结果乙完成30个零件的时间比甲完成24个零件所用的时间少1小时.问甲乙两人原来每小时各加工多少个零件.23.(本题满分12分,第小题满分6分)如图,在梯形ABCD 中,AB //CD ,AD =BC ,E 是CD 的中点,BE 交AC 于F ,过点F 作FG ∥AB ,交AE 于点G .(1) 求证:AG=BF ;(2) 当CF CA AD ⋅=2时,求证:AC AG AD AB ⋅=⋅.E D CG FAB(第23题图)闵行区2014学年第二学期九年级质量调研考试数学试卷三、解答题:(本大题共7题,满分78分)19.(本题满分10分).20.(本题满分10分)解方程:22212,320.x yx x y y+=⎧⎨-+=⎩21.(本题满分10分,其中每小题各5分)如图,已知在△ABC中,AB AC==,sin B∠=D为边BC的中点.E为边BC延长线上一点,且CE = BC.联结AE,F为线段AE的中点.求:(1)线段DF的长;(2)∠CAE的正切值.AB CD EF(第21题图)22.(本题满分10分,其中每小题各5分)货车在公路A 处加满油后,以每小时60千米的速度匀速行驶,前往与A 处相距360千米的B 处.下表记录的是货车一次加满油后油箱内剩余油量y (升)与行驶时间x (时)之间关系:(范围);(2)在(1)的条件下,如果货车的行驶速度和每小时的耗油量都不变,货车行驶4小时后到达C 处,C 的前方12千米的D 处有一加油站,那么在D 处至少加多少升油,才能使货车到达B 处卸货后能顺利返回D 处加油?(根据驾驶经验,为保险起见,油箱内剩余油量应随时不少于10升)23.(本题满分12分,其中每小题各6分)如图,已知在梯形ABCD 中,AD // BC ,∠A = 90º,AB = AD .点E 在边AB 上,且DE ⊥CD ,DF 平分∠EDC ,交BC 于点F ,联结CE 、EF . (1)求证:DE = DC ; (2)如果2BE BF BC =⋅,求证:∠BEF =∠CEF .(第23题图)A BCDEF浦东新区初三教学质量检测数学试卷 (2015.4.21)三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)化简并求值:12)111(22+-÷-+x x x x ,其中12+=x . 20.(本题满分10分)解不等式组:⎪⎩⎪⎨⎧->--≥+,1262,6325x x x x 并写出它的非负整数解.21.(本题满分10分,其中每小题各5分)已知:如图,在△ABC 中,D 是边BC 上一点,以点D 为圆心、CD 为半径作半圆,分别与边AC 、BC 相交于点E 和点F .如果AB =AC =5,cos B =54,AE =1. 求:(1)线段CD 的长度;(2)点A 和点F 之间的距离.C(第21题图)22.(本题满分10分)小张利用休息日进行登山锻炼,从山脚到山顶的路程为12千米.他上午8时从山脚出发,到达山顶后停留了半小时,再原路返回,下午3时30分回到山脚.假设他上山与下山时都是匀速行走,且下山比上山时的速度每小时快1千米,求小张上山时的速度.23.(本题满分12分,其中每小题各6分)如图,已知在平行四边形ABCD中,AE⊥BC,垂足为点E,AF⊥CD,垂足为点F.(1)如果AB=AD,求证:EF∥BD;(2)如果EF∥BD,求证:AB=AD. AB C DEF (第23题图)普陀区2014学年度第二学期初三质量调研数学试卷三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:()121245sin 13210+--︒+--.20.(本题满分10分)解方程组:2230240x y ,x xy y .-=⎧⎨-+-=⎩21.(本题满分10分)已知:如图7,在平面直角坐标系xOy 中,直线1122y x =+与x 轴交于点A ,在第一象限内与反比例函数图像交于点B ,BC 垂直于x 轴,垂足为点C ,且OC =2AO .求(1)点C 的坐标;(2)反比例函数的解析式.图722.(本题满分10分)本市为了给市容营造温馨和谐的夜间景观,准备在一条宽7.4米的道路上空利用轻轨桥墩,安装呈大中小三个同心圆的景观灯带(如图8-1所示). 如图8-2,已知EF 表示路面宽度,轻轨桥墩的下方为等腰梯形ABCD ,且AD ∥EF ,DC AB =,∠=ABC 37°.在轻轨桥墩上设有两处限高标志,分别表示等腰梯形的下底边到路面的距离为2.9米和等腰梯形的上底边到路面的距离为3.8米.大圆直径等于AD ,三圆半径的比等于1∶2∶3.试求这三个圆形灯带的总长为多少米?(结果保留π)(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)23.(本题满分12分)如图9,在△ABC 中,点D 、E 分别在边BC 、AC 上,BE 、AD 相交于点G ,EF ∥AD 交BC 于点F ,且2BF BD BC = ,联结FG . (1)求证:FG ∥CE ;(2)设BAD C ∠=∠,求证:四边形AGFE 是菱形.图9CG FEDBADA图图2.93.8B2015年松江区初中毕业生学业模拟考试数学试卷三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:323112---÷-+x x x x )(20.(本题满分10分)解方程组:⎩⎨⎧=--=+0548322y xy x y x21.(本题满分10分)某品牌电动车经销商一月份销售该品牌电动车100辆,二月份的销售量比一月份增加10%,二月份每辆电动车的售价比一月份每辆电动车的售价低80元,二月份的销售总额比一月份销售总额多12200元,问一月份每辆电动车的售价是多少?22.(本题满分10分,每小题各5分)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,且CD =24,点M 在⊙O 上,MD 经过圆心O ,联结MB .(1)若BE =8,求⊙O 的半径; (2)若∠DMB=∠D ,求线段OE 的长.23.(本题满分12分,每小题各6分)如图,已知在正方形ABCD 中,点E 在CD 边上,过C 点作AE 的垂线交于点F ,联结DF ,过点D 作DF 的垂线交AF 于点G ,联结BG . (1)求证:△ADG ≌△CDF ;(2)如果E 为CD 的中点,求证:BG ⊥AF .A(第23题图)EGDFB(第22题图)2014学年第二学期徐汇区学习能力诊断卷初三数学试卷(时间100分钟满分150分)2015.4 三.(本大题共7题,19~22每题10分,23、24每题10分,25题14分,满分78分)19.化简并求值:22256()32x x xxx x x-+⋅+--,其中x=.20.解方程组:2222699,440. x xy yx y x y⎧++=⎪⎨--+=⎪⎩21.某公司市场营销部的某营销员的个人月收入与该营销员每月的销售量成一次函数关系,其图像如图所示.根据图像提供的信息,解答下列问题:(1)求营销员的个人月收入y元与该营销员每月的销售量x万件(x≥0)之间的函数关系式;(2)若两个月内该营销员的销售量从2万件猛增到5万件,月收入两个月大幅度增长,且连续两个月的月收入的增长率是相同的,试求这个增长率 1.414≈,保留到百分位);AD22.如图,在Rt △ABC 中,∠CAB =90º,sin C=35,AC =6,BD 平分∠CBA 交AC 边于点D . 求:(1)线段AB 的长; (2)tan ∠DBA 的值23.已知:如图,正方形ABCD ,BM 、DN 分别是正方形的两个外角平分线,∠MAN =45°, 将∠MAN 绕着正方形的顶点A 旋转,边AM 、AN 分别交两条角平分线于点M 、N ,联结MN .(1)求证:ABM ADN ∆∆ ;(2)联结BD ,当∠BAM 的度数为多少时,四边形BMND 为矩形,并加以证明.杨浦区2014学年度第二学期初三质量调研数 学 试 卷一、 解答题(第19~22题每题10分,第23~24题每题12分,第25题14分,满分78分) 19.(本题满分10分)计算:0111)2cos30()12-︒+.20.(本题满分10分) 解方程组:223240.xy x xy y =⎧⎨-+-=⎩21. (本题满分10分)如图,在一笔直的海岸线 上有A 、B 两个观察站,A 在B 的正东方向,A 与B 相距2千米。
2015年上海市十三校联考高考数学二模试卷(理科)含详解

2015年上海市十三校联考高考数学二模试卷(理科)一、填空题(本大题满分56分)本大题共有14题,每个空格填对4分,否则一律得零分.1.(4分)幂函数y=x(m∈N)在区间(0,+∞)上是减函数,则m=.2.(4分)函数的定义域是.3.(4分)在△ABC中,已知BC=8,AC=5,三角形面积为12,则cos2C=.4.(4分)设i为虚数单位,若关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,则m=.5.(4分)若椭圆的方程为+=1,且此椭圆的焦距为4,则实数a=.6.(4分)若一个圆锥的侧面展开如圆心角为120°、半径为3 的扇形,则这个圆锥的表面积是.7.(4分)若关于x的方程lg(x2+ax)=1在x∈[1,5]上有解,则实数a的取值范围为.8.(4分)《孙子算经》卷下第二十六题:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?.(只需写出一个答案即可)9.(4分)在极坐标系中,某直线的极坐标方程为ρsin(θ+)=,则极点O 到这条直线的距离为.10.(4分)设口袋中有黑球、白球共7 个,从中任取两个球,令取到白球的个数为ξ,且ξ的数学期望Eξ=,则口袋中白球的个数为.11.(4分)如图所示,一个确定的凸五边形ABCDE,令x=•,y=•,z=•,则x、y、z 的大小顺序为.12.(4分)设函数f(x)的定义域为D,D⊆[0,4π],它的对应法则为f:x→sin x,现已知f(x)的值域为{0,﹣,1},则这样的函数共有个.13.(4分)若多项式(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,则a1+a3+…+a2015=.14.(4分)在平面直角坐标系中有两点A(﹣1,3)、B(1,),以原点为圆心,r>0为半径作一个圆,与射线y=﹣x(x<0)交于点M,与x轴正半轴交于N,则当r变化时,|AM|+|BN|的最小值为.二、选择题(本大题满分20分)本大题共有4题,每题有且仅有一个正确答案,选对得5分,否则一律得零分.15.(5分)若非空集合A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若A⊊B,则命题α是命题β的()条件.A.充分非必要B.必要非充分C.充分必要D.既非充分又非必要16.(5分)用反证法证明命题:“已知a、b∈N+,如果ab可被 5 整除,那么a、b 中至少有一个能被5 整除”时,假设的内容应为()A.a、b 都能被5 整除B.a、b 都不能被5 整除C.a、b 不都能被5 整除D.a 不能被5 整除17.(5分)实数x、y满足x2+2xy+y2+4x2y2=4,则x﹣y的最大值为()A.B.C.D.218.(5分)直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是()A.[,]B.[2﹣2,2+2]C.[,]D.[3﹣2,3+2]三、解答题(本大题满分74分)本大题共5题,解答下列各题须写出必要的步骤.19.(12分)已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.20.(14分)已知数列{b n}满足b1=1,且b n+1=16b n(n∈N),设数列{}的前n 项和是T n.(1)比较T n+12与T n•T n+2的大小;(2)若数列{a n}的前n项和S n=2n2+2n+2,数列{c n}=a n﹣log d b n(d>0,d≠1),求d的取值范围使得{c n}是递增数列.21.(14分)某种波的传播是由曲线f(x)=Asin(ωx+φ)(A>0)来实现的,我们把函数解析式f(x)=Asin(ωx+φ)称为“波”,把振幅都是A 的波称为“A 类波”,把两个解析式相加称为波的叠加.(1)已知“1 类波”中的两个波f1(x)=sin(x+φ1)与f2(x)=sin(x+φ2)叠加后仍是“1类波”,求φ2﹣φ1的值;(2)在“A 类波“中有一个是f1(x)=Asinx,从A类波中再找出两个不同的波f2(x),f3(x),使得这三个不同的波叠加之后是平波,即叠加后f1(x)+f2(x)+f3(x),并说明理由.(3)在n(n∈N,n≥2)个“A类波”的情况下对(2)进行推广,使得(2)是推广后命题的一个特例.只需写出推广的结论,而不需证明.22.(16分)设函数f(x)=ax2+(2b+1)x﹣a﹣2(a,b∈R).(1)若a=0,当x∈[,1]时恒有f(x)≥0,求b的取值范围;(2)若a≠0且b=﹣1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.23.(18分)设有二元关系f(x,y)=(x﹣y)2+a(x﹣y)﹣1,已知曲线Γ:f (x,y)=0(1)若a=2时,正方形ABCD的四个顶点均在曲线上Γ,求正方形ABCD的面积;(2)设曲线Γ与x轴的交点是M、N,抛物线Γ′:y=x2+1与y轴的交点是G,直线MG与曲线Γ′交于点P,直线NG与曲线Γ′交于Q,求证:直线PQ过定点,并求出该定点的坐标.(3)设曲线Γ与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线Γ在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Y i(i=1,2,…,255),将Y i中的所有元素相加(若iY中只有一个元素,则其是其自身)得到255个数y1,y2,…,y255求所有的正整数n的值,使得y1n+y2n+…+y255n是与变数a及变数x i(i=1,2,…8)均无关的常数.2015年上海市十三校联考高考数学二模试卷(理科)参考答案与试题解析一、填空题(本大题满分56分)本大题共有14题,每个空格填对4分,否则一律得零分.1.(4分)幂函数y=x(m∈N)在区间(0,+∞)上是减函数,则m= 0.【考点】4U:幂函数的概念、解析式、定义域、值域;4Y:幂函数的单调性、奇偶性及其应用.【专题】11:计算题;51:函数的性质及应用;59:不等式的解法及应用.【分析】根据幂函数的性质,可得m2+2m﹣3<0,解不等式求得自然数解,即可得到m=0.【解答】解:由幂函数y=x m2+2m﹣3在(0,+∞)为减函数,则m2+2m﹣3<0,解得﹣3<m<1.由于m∈N,则m=0.故答案为:0.【点评】本题考查幂函数的性质,主要考查二次不等式的解法,属于基础题.2.(4分)函数的定义域是(0,1] .【考点】33:函数的定义域及其求法;4K:对数函数的定义域.【专题】11:计算题.【分析】令被开方数大于等于0,然后利用对数函数的单调性及真数大于0求出x的范围,写出集合区间形式即为函数的定义域.【解答】解:∴0<x≤1∴函数的定义域为(0,1]故答案为:(0,1]【点评】求解析式已知的函数的定义域应该考虑:开偶次方根的被开方数大于等于0;对数函数的真数大于0底数大于0小于1;分母非0.3.(4分)在△ABC中,已知BC=8,AC=5,三角形面积为12,则cos2C=.【考点】HR:余弦定理.【专题】11:计算题.【分析】先通过BC=8,AC=5,三角形面积为12求出sinC的值,再通过余弦函数的二倍角公式求出答案.【解答】解:∵已知BC=8,AC=5,三角形面积为12,∴•BC•ACsinC=12∴sinC=∴cos2C=1﹣2sin2C=1﹣2×=故答案为:【点评】本题主要考查通过正弦求三角形面积及倍角公式的应用.属基础题.4.(4分)设i为虚数单位,若关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,则m=1.【考点】A1:虚数单位i、复数.【专题】5N:数系的扩充和复数.【分析】把n代入方程,利用复数相等的条件,求出m,n,即可.【解答】解:关于x的方程x2﹣(2+i)x+1+mi=0(m∈R)有一实根为n,可得n2﹣(2+i)n+1+mi=0所以,所以m=n=1,故答案为:1.【点评】本题考查复数相等的条件,考查计算能力,是基础题.5.(4分)若椭圆的方程为+=1,且此椭圆的焦距为4,则实数a=4或8.【考点】K4:椭圆的性质.【专题】5D:圆锥曲线的定义、性质与方程.【分析】首先分两种情况:①焦点在x轴上.②焦点在y轴上,分别求出a的值即可.【解答】解:∵椭圆的焦距为4.∴2c=4,即c=2∵在椭圆中,a2=b2+c2①焦点在x轴上时:10﹣a﹣(a﹣2)=4解得:a=4.②焦点在y轴上时a﹣2﹣(10﹣a)=4解得:a=8故答案为:4或8.【点评】本题考查的知识要点:椭圆方程的两种情况:焦点在x轴或y轴上,考察a、b、c的关系式,及相关的运算问题.6.(4分)若一个圆锥的侧面展开如圆心角为120°、半径为3 的扇形,则这个圆锥的表面积是4π.【考点】LE:棱柱、棱锥、棱台的侧面积和表面积.【专题】5F:空间位置关系与距离.【分析】易得圆锥侧面展开图的弧长,除以2π即为圆锥的底面半径,圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长,把相关数值代入即可求解.【解答】解:圆锥的侧面展开图的弧长为:=2π,∴圆锥的底面半径为2π÷2π=1,∴此圆锥的表面积=π×(1)2+π×1×3=4π.故答案为:4π.【点评】本题考查扇形的弧长公式为;圆锥的侧面展开图的弧长等于圆锥的底面周长,圆锥的表面积的求法.7.(4分)若关于x的方程lg(x2+ax)=1在x∈[1,5]上有解,则实数a的取值范围为﹣3≤a≤9.【考点】51:函数的零点.【专题】11:计算题;51:函数的性质及应用.【分析】由题意,x2+ax﹣10=0在x∈[1,5]上有解,可得a=﹣x在x∈[1,5]上有解,利用a=﹣x在x∈[1,5]上单调递减,即可求出实数a的取值范围.【解答】解:由题意,x2+ax﹣10=0在x∈[1,5]上有解,所以a=﹣x在x∈[1,5]上有解,因为a=﹣x在x∈[1,5]上单调递减,所以﹣3≤a≤9,故答案为:﹣3≤a≤9.【点评】本题主要考查方程的根与函数之间的关系,考查由单调性求函数的值域,比较基础.8.(4分)《孙子算经》卷下第二十六题:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?23,或105k+23(k为正整数)..(只需写出一个答案即可)【考点】F4:进行简单的合情推理.【专题】5M:推理和证明.【分析】根据“三三数之剩二,五五数之剩三,七七数之剩二”找到三个数:第一个数能同时被3和5整除;第二个数能同时被3和7整除;第三个数能同时被5和7整除,将这三个数分别乘以被7、5、3除的余数再相加即可求出答案.【解答】解:我们首先需要先求出三个数:第一个数能同时被3和5整除,但除以7余1,即15;第二个数能同时被3和7整除,但除以5余1,即21;第三个数能同时被5和7整除,但除以3余1,即70;然后将这三个数分别乘以被7、5、3除的余数再相加,即:15×2+21×3+70×2=233.最后,再减去3、5、7最小公倍数的整数倍,可得:233﹣105×2=23.或105k+23(k为正整数).故答案为:23,或105k+23(k为正整数).【点评】本题考查的是带余数的除法,简单的合情推理的应用,根据题意下求出15、21、70这三个数是解答此题的关键.[可以原文理解为:三个三个的数余二,七个七个的数也余二,那么,总数可能是三乘七加二,等于二十三.二十三用五去除余数又恰好是三]9.(4分)在极坐标系中,某直线的极坐标方程为ρsin(θ+)=,则极点O 到这条直线的距离为.【考点】Q4:简单曲线的极坐标方程.【专题】5S:坐标系和参数方程.【分析】由直线的极坐标方程为ρsin(θ+)=,展开并利用即可得出直角坐标方程,再利用点到直线的距离公式即可得出.【解答】解:由直线的极坐标方程为ρsin(θ+)=,展开为,化为x+y﹣1=0,∴极点O到这条直线的距离d==.故答案为:.【点评】本题考查了直线的极坐标方程化为直角坐标方程、点到直线的距离公式、两角和差的正弦公式,考查了推理能力与计算能力,属于基础题.10.(4分)设口袋中有黑球、白球共7 个,从中任取两个球,令取到白球的个数为ξ,且ξ的数学期望Eξ=,则口袋中白球的个数为3.【考点】CH:离散型随机变量的期望与方差.【专题】5I:概率与统计.【分析】设口袋中有白球x个,由已知得ξ的可能取值为0,1,2,由Eξ=,得×,由此能求出口袋中白球的个数.【解答】解:设口袋中有白球x个,由已知得ξ的可能取值为0,1,2,P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,∵Eξ=,∴×,解得x=3.∴口袋中白球的个数为3.故答案为:3.【点评】本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.11.(4分)如图所示,一个确定的凸五边形ABCDE,令x=•,y=•,z=•,则x、y、z 的大小顺序为x>y>z.【考点】9O:平面向量数量积的性质及其运算;9S:数量积表示两个向量的夹角.【专题】5A:平面向量及应用.【分析】根据向量的数量积公式分别判断x,y,z的符号,得到大小关系.【解答】解:由题意,x=•=AB×ACcos∠BAC>0,y=•=AB×ADcos∠BAD≈AB×ACcos∠BAD,又∠BAD>∠BAC所以cos∠BAD<cos∠BAC,所以x>y>0z=•=AB×AEcos∠BAE<0,所以x>y>z.故答案为:x>y>z.【点评】本题考查了向量的数量积的公式;属于基础题.12.(4分)设函数f(x)的定义域为D,D⊆[0,4π],它的对应法则为f:x→sin x,现已知f(x)的值域为{0,﹣,1},则这样的函数共有1395个.【考点】3C:映射.【专题】51:函数的性质及应用;5J:集合.【分析】分别求出sinx=0,x=0,π,2π,3π,4π,sinx=,x=,x=,x=,x=,sinx=1,x=,x=利用排列组合知识求解得出这样的函数共有:(C+C)()()即可.【解答】解:∵函数f(x)的定义域为D,D⊆[0,4π],∴它的对应法则为f:x→sin x,f(x)的值域为{0,﹣,1},sinx=0,x=0,π,2π,3π,4π,sinx=,x=,x=,x=,x=,sinx=1,x=,x=这样的函数共有:(C+C)()()=31×15×3=1395故答案为:1395【点评】本题考查了映射,函数的概念,排列组合的知识,难度不大,但是综合性较强.13.(4分)若多项式(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,则a1+a3+…+a2015=0.【考点】DA:二项式定理.【专题】5P:二项式定理.【分析】根据等式,确定a1=﹣2000×2001+2001×2000=0,a3=0,a5=0,…,即可得出结论.【解答】解:根据(1﹣2x+3x2﹣4x3+…﹣2000x1999+2001x2000)(1+2x+3x2+4x3+…+2000x1999+2001x2000)=a0x4000+a1x3999+a2x3998+…+a3999x+a4000,可得x1999•x2000的系数a1=﹣2000×2001+2001×2000=0,a3=0,a5=0,…,所以a1+a3+a5+…+a2011+a2013+a2015=0,故答案为:0.【点评】本题考查二项式定理的运用,考查学生分析解决问题的能力,属于中档题.14.(4分)在平面直角坐标系中有两点A(﹣1,3)、B(1,),以原点为圆心,r>0为半径作一个圆,与射线y=﹣x(x<0)交于点M,与x轴正半轴交于N,则当r变化时,|AM|+|BN|的最小值为2.【考点】IR:两点间的距离公式.【专题】11:计算题;35:转化思想;5M:推理和证明.【分析】由题意,设M(a,﹣a)(a<0),则r=﹣2a,N(﹣2a,0).可得|AM|+|BN|=+,设2a=x,进而可以理解为(x,0)与(﹣,)和(﹣1,)的距离和,即可得出结论.【解答】解:由题意,设M(a,﹣a)(a<0),则r=﹣2a,N(﹣2a,0).∴|AM|+|BN|=+设2a=x,则|AM|+|BN|=+,可以理解为(x,0)与(﹣5,)和(﹣1,)的距离和,∴|AM|+|BN|的最小值为(﹣5,)和(﹣1,﹣)的距离,即2.故答案为:2.【点评】本题考查两点间距离公式的应用,考查学生分析解决问题的能力,有难度.二、选择题(本大题满分20分)本大题共有4题,每题有且仅有一个正确答案,选对得5分,否则一律得零分.15.(5分)若非空集合A中的元素具有命题α的性质,集合B中的元素具有命题β的性质,若A⊊B,则命题α是命题β的()条件.A.充分非必要B.必要非充分C.充分必要D.既非充分又非必要【考点】29:充分条件、必要条件、充要条件.【专题】5J:集合;5L:简易逻辑.【分析】可举个例子来判断:比如A={1},B={1,2},α:x>0,β:x<3,容易说明此时命题α是命题β的既非充分又非必要条件.【解答】解:命题α是命题β的既非充分又非必要条件;比如A={1},α:x>0;B={1,2},β:x<3;显然α成立得不到β成立,β成立得不到α成立;∴此时,α是β的既非充分又非必要条件.故选:D.【点评】考查真子集的概念,以及充分条件、必要条件、既不充分又不必要条件的概念,以及找一个例子来说明问题的方法.16.(5分)用反证法证明命题:“已知a、b∈N+,如果ab可被 5 整除,那么a、b 中至少有一个能被5 整除”时,假设的内容应为()A.a、b 都能被5 整除B.a、b 都不能被5 整除C.a、b 不都能被5 整除D.a 不能被5 整除【考点】FC:反证法.【专题】5M:推理和证明.【分析】反设是一种对立性假设,即想证明一个命题成立时,可以证明其否定不成立,由此得出此命题是成立的.【解答】解:由于反证法是命题的否定的一个运用,故用反证法证明命题时,可以设其否定成立进行推证.命题“a,b∈N,如果ab可被5整除,那么a,b至少有1个能被5整除.”的否定是“a,b都不能被5整除”.故选:B.【点评】反证法是命题的否定的一个重要运用,用反证法证明问题大大拓展了解决证明问题的技巧.17.(5分)实数x、y满足x2+2xy+y2+4x2y2=4,则x﹣y的最大值为()A.B.C.D.2【考点】7F:基本不等式及其应用.【专题】56:三角函数的求值.【分析】x2+2xy+y2+4x2y2=4,变形为(x+y)2+(2xy)2=4,设x+y=2cosθ,2xy=2sinθ,θ∈[0,2π).化简利用三角函数的单调性即可得出.【解答】解:x2+2xy+y2+4x2y2=4,变形为(x+y)2+(2xy)2=4,设x+y=2cosθ,2xy=2sinθ,θ∈[0,2π).则(x﹣y)2=(x+y)2﹣4xy=4cos2θ﹣4sinθ=5﹣4(sinθ+)2≤5,∴x﹣y.故选:C.【点评】本题考查了平方法、三角函数代换方法、三角函数的单调性,考查了推理能力与计算能力,属于中档题.18.(5分)直线m⊥平面α,垂足是O,正四面体ABCD的棱长为4,点C在平面α上运动,点B在直线m上运动,则点O到直线AD的距离的取值范围是()A.[,]B.[2﹣2,2+2]C.[,]D.[3﹣2,3+2]【考点】MK:点、线、面间的距离计算.【专题】5F:空间位置关系与距离.【分析】确定直线BC与动点O的空间关系,得到最大距离为AD到球心的距离+半径,最小距离为AD到球心的距离﹣半径.【解答】解:由题意,直线BC与动点O的空间关系:点O是以BC为直径的球面上的点,所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离,最大距离为AD到球心的距离(即BC与AD的公垂线)+半径=2+2.最小距离为AD到球心的距离(即BC与AD的公垂线)﹣半径=2﹣2.∴点O到直线AD的距离的取值范围是:[2﹣2,2+2].故选:B.【点评】本题考查点、线、面间的距离计算,考查学生分析解决问题的能力,属于中档题,解题时要注意空间思维能力的培养.三、解答题(本大题满分74分)本大题共5题,解答下列各题须写出必要的步骤.19.(12分)已知正四棱柱ABCD﹣A1B1C1D1,底面边长为,点P、Q、R分别在棱AA1、BB1、BC上,Q是BB1中点,且PQ∥AB,C1Q⊥QR(1)求证:C1Q⊥平面PQR;(2)若C1Q=,求四面体C1PQR的体积.【考点】LF:棱柱、棱锥、棱台的体积;LW:直线与平面垂直.【专题】5F:空间位置关系与距离;5G:空间角.【分析】(1)由已知得AB⊥平面B1BCC1,从而PQ⊥平面B1BCC1,进而C1Q⊥PQ,又C1Q⊥QR,由此能证明C1Q⊥平面PQR.(2)由已知得B1Q=1,BQ=1,△B1C1Q∽△BQR,从而BR=,QR=,由C1Q、QR、QP两两垂直,能求出四面体C1PQR 的体积.【解答】(1)证明:∵四棱柱ABCD﹣A1B1C1D1是正四棱柱,∴AB⊥平面B1BCC1,又PQ∥AB,∴PQ⊥平面B1BCC1,∴C1Q⊥PQ,又已知C1Q⊥QR,且QR∩QP=Q,∴C1Q⊥平面PQR.(2)解:∵B1C1=,,∴B1Q=1,∴BQ=1,∵Q是BB1中点,C1Q⊥QR,∴∠B1C1Q=∠BQR,∠C1B1Q=∠QBR,∴△B1C1Q∽△BQR,∴BR=,∴QR=,∵C1Q、QR、QP两两垂直,∴四面体C1PQR 的体积V=.【点评】本小题主要考查空间线面关系、线面垂直的证明、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.20.(14分)已知数列{b n}满足b1=1,且b n+1=16b n(n∈N),设数列{}的前n 项和是T n.(1)比较T n+12与T n•T n+2的大小;(2)若数列{a n}的前n项和S n=2n2+2n+2,数列{c n}=a n﹣log d b n(d>0,d≠1),求d的取值范围使得{c n}是递增数列.【考点】82:数列的函数特性;8H:数列递推式.【专题】11:计算题;54:等差数列与等比数列.【分析】(1)由数列递推式可得数列{b n}为公比是16的等比数列,求出其通项公式后可得,然后由等比数列的前n项和求得T n,再由作差法证明T n+12>T n•T n+2;(2)由S n=2n2+2n+2求出首项,进一步得到n≥2时的通项公式,再把数列{a n},{b n}的通项公式代入c n=a n﹣log d b n=4n+(4﹣4n)log d2=(4﹣4log d2)n+4log d2,然后由一次项系数大于0求得d的取值范围.【解答】解:(1)由b n+1=16b n,得数列{b n}为公比是16的等比数列,又b1=1,∴,因此,则=,∵T n+12﹣T n•T n+2=.于是T n+12>T n•T n+2;(2)由S n=2n2+2n+2,当n=1时求得a1=S1=6;当n≥2时,=4n.a1=6不满足上式,∴a n=.当n=1时,c1=a1﹣log d b1=6﹣log d1=6,当n≥2时,可得c n=a n﹣log d b n=4n+(4﹣4n)log d2=(4﹣4log d2)n+4log d2,要使数列{c n}是递增数列,则,解得:0<d<1或d>4.综上,d∈(0,1)∪(4,+∞).【点评】本题考查了等比关系的确定,考查了数列的函数特性,考查了对数不等式的解法,是中档题.21.(14分)某种波的传播是由曲线f(x)=Asin(ωx+φ)(A>0)来实现的,我们把函数解析式f(x)=Asin(ωx+φ)称为“波”,把振幅都是A 的波称为“A 类波”,把两个解析式相加称为波的叠加.(1)已知“1 类波”中的两个波f1(x)=sin(x+φ1)与f2(x)=sin(x+φ2)叠加后仍是“1类波”,求φ2﹣φ1的值;(2)在“A 类波“中有一个是f1(x)=Asinx,从A类波中再找出两个不同的波f2(x),f3(x),使得这三个不同的波叠加之后是平波,即叠加后f1(x)+f2(x)+f3(x),并说明理由.(3)在n(n∈N,n≥2)个“A类波”的情况下对(2)进行推广,使得(2)是推广后命题的一个特例.只需写出推广的结论,而不需证明.【考点】F1:归纳推理;GP:两角和与差的三角函数.【专题】15:综合题;57:三角函数的图像与性质;5M:推理和证明.【分析】(1)根据定义可求得f1(x)+f2(x)=(cosφ1+cosφ2)sinx+(sinφ1+sinφ2)cosx,则振幅是=,由=1,即可求得φ1﹣φ1的值.(2)设f2(x)=Asin(x+φ1),f3(x)=Asin(x+φ2),则f1(x)+f2(x)+f3(x)=0恒成立,可解得cosφ1=﹣,可取φ2=(或φ2=﹣等),证明f1(x)+f2(x)+f3(x)=0.(3)由题意可得f1(x)=Asinx,f2(x)=Asin(x+),f3(x)=Asin(x+),…,从而可求f n(x)=Asin(x+),这n个波叠加后是平波.【解答】解:(1)f1(x)+f2(x)=sin(x+φ1)+sin(x+φ2)=(cosφ1+cosφ2)sinx+(sinφ1+sinφ2)cosx,振幅是=则=1,即cos(φ1﹣φ2)=﹣,所以φ1﹣φ2=2kπ±,k ∈Z.(2)设f2(x)=Asin(x+φ1),f3(x)=Asin(x+φ2),则f1(x)+f2(x)+f3(x)=Asinx+Asin(x+φ1)+Asin(x+φ2)=Asinx(1+cosφ1+cosφ2)+Acosx(sinφ1+sinφ2)=0恒成立,则1+cosφ1+cosφ2=0且sinφ1+sinφ2=0,即有:cosφ2=﹣cosφ1﹣1且sinφ2=﹣sinφ1,消去φ2可解得cosφ1=﹣,若取φ1=,可取φ2=(或φ2=﹣等),此时,f2(x)=Asin(x+),f3(x)=Asin(x+)(或f3(x)=Asin(x﹣)等),则:f1(x)+f2(x)+f3(x)=A[sinx+(sinx+cosx)+(﹣sinx﹣cosx)]=0,所以是平波.(3)f1(x)=Asinx,f2(x)=Asin(x+),f3(x)=Asin(x+),…,f n(x)=Asin(x+),这n个波叠加后是平波.【点评】本题主要考查了两角和与差的正弦函数公式的应用,考查了归纳推理的常用方法,综合性较强,考查了转化思想,属于中档题.22.(16分)设函数f(x)=ax2+(2b+1)x﹣a﹣2(a,b∈R).(1)若a=0,当x∈[,1]时恒有f(x)≥0,求b的取值范围;(2)若a≠0且b=﹣1,试在直角坐标平面内找出横坐标不同的两个点,使得函数y=f(x)的图象永远不经过这两点;(3)若a≠0,函数y=f(x)在区间[3,4]上至少有一个零点,求a2+b2的最小值.【考点】3H:函数的最值及其几何意义;53:函数的零点与方程根的关系.【专题】15:综合题;51:函数的性质及应用.【分析】(1)求出a=0的解析式,再由一次函数的单调性,得到不等式,即可得到范围;(2)b=﹣1时,y=a(x2﹣1)﹣x﹣2,当x2=1时,无论a取任何值,y=﹣x﹣2为定值,y=f(x)图象一定过点(1,﹣3)和(﹣1,﹣1),运用函数的定义即可得到结论;(3)由题意,存在t∈[3,4],使得at2+(2b+1)t﹣a﹣2=0,即(t2﹣1)a+(2t)b+t﹣2=0,由点到直线的距离意义可知≥=,由此只要求,t∈[3,4]的最小值.【解答】解:(1)当a=0时,f(x)=(2b+1)x﹣2,当x∈[,1]时恒有f(x)≥0,则f()≥0且f(1)≥0,即b﹣≥0且2b﹣1≥0,解得b≥;(2)b=﹣1时,y=a(x2﹣1)﹣x﹣2,当x2=1时,无论a取任何值,y=﹣x﹣2为定值,y=f(x)图象一定过点(1,﹣3)和(﹣1,﹣1)由函数定义可知函数图象一定不过A(1,y1)(y1≠﹣3)和B(﹣1,y2)(y2≠﹣1);(3)由题意,存在t∈[3,4],使得at2+(2b+1)t﹣a﹣2=0即(t2﹣1)a+(2t)b+t﹣2=0,由点到直线的距离意义可知≥=,由此只要求,t∈[3,4]的最小值.令g(t)=,t∈[3,4]设u=t﹣2,u∈[1,2],则g(t)=f(u)==∴u=1,即t=3时,g(t)取最小值,∴t=3时,a2+b2的最小值为.【点评】本题考查不等式的恒成立问题转化为求函数的值域问题,主要考查一次函数的单调性,运用主元法和直线和圆有交点的条件是解题的关键.23.(18分)设有二元关系f(x,y)=(x﹣y)2+a(x﹣y)﹣1,已知曲线Γ:f (x,y)=0(1)若a=2时,正方形ABCD的四个顶点均在曲线上Γ,求正方形ABCD的面积;(2)设曲线Γ与x轴的交点是M、N,抛物线Γ′:y=x2+1与y轴的交点是G,直线MG与曲线Γ′交于点P,直线NG与曲线Γ′交于Q,求证:直线PQ过定点,并求出该定点的坐标.(3)设曲线Γ与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线Γ在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Y i(i=1,2,…,255),将Y i中的所有元素相加(若iY中只有一个元素,则其是其自身)得到255个数y1,y2,…,y255求所有的正整数n的值,使得y1n+y2n+…+y255n是与变数a及变数x i(i=1,2,…8)均无关的常数.【考点】KH:直线与圆锥曲线的综合.【专题】5E:圆锥曲线中的最值与范围问题.【分析】(1)令f(x,y)=(x﹣y)2+2(x﹣y)﹣1=0,解得x﹣y=﹣1±,由于f(x,y)表示两条平行线,之间的距离是2,为一个正方形,即可得出面积S.(2):在曲线C中,令y=0,则x2+ax﹣1=0,设M(m,0),N(n,0),则mn=﹣1,G(0,1),则直线MG:y=﹣x+1,NG:y=﹣x+1.分别与抛物线方程联立可得P,Q.直线PQ的方程为:,令x=0,可得y=3,因此直线PQ过定点(0,3).(3)令y=0,则x2+ax﹣1=0,则mn=﹣1,即点R(u,v)在曲线xy=﹣1上,又曲线C:f(x,y)=0.恒表示平行线x﹣y=,A(x1,x2),B(x3,x4)关于直线y=﹣x对称,即x1+x2+x3+x4=0,同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,集合X={x1,x2,…,x8}的所有非空子集设为Y i=1,2,…,255),取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,=0,对X的其它子集,把它们配成集合“对”(Y p,Y q),Y p∪Y q=X,Y p∩Y q=∅,这样的集合“对”共有127对,且对每一个集合“对”都满足y p+y q=0.可以利用扇形归纳法证明:对于Y p的元素和y p与Y q的元素和y q,当n为奇数时,=0.即可得出.【解答】解:(1)令f(x,y)=(x﹣y)2+2(x﹣y)﹣1=0,解得x﹣y=﹣1±,∴f(x,y)=0表示两条平行线,之间的距离是2,此为一个正方形的一个边长,其面积S=4.(2)证明:在曲线C中,令y=0,则x2+ax﹣1=0,设M(m,0),N(n,0),则mn=﹣1,G(0,1),则直线MG:y=﹣x+1,NG:y=﹣x+1.联立,解得P,同理可得Q.∴直线PQ的方程为:令x=0,则y===3,因此直线PQ过定点(0,3).(3)令y=0,则x2+ax﹣1=0,则mn=﹣1,即点R(u,v)在曲线xy=﹣1上,又曲线C:f(x,y)=(x﹣y)2+a(x﹣y)﹣1=0.恒表示平行线x﹣y=,如图所示,A(x1,x2),B(x3,x4)关于直线y=﹣x对称,则=,即x1+x2+x3+x4=0,同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,集合X={x1,x2,…,x8}的所有非空子集设为Y i,取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,=0,对X的其它子集,把它们配成集合“对”(Y p,Y q),Y p∪Y q=X,Y p∩Y q=∅,这样的集合“对”共有127对,且对每一个集合“对”都满足y p+y q=0.以下证明:对于Y p的元素和y p与Y q的元素和y q,当n为奇数时,=0.先证明:n为奇数时,x+y能够整除x n+y n,用数学归纳法证明.1°当n=1时,成立;2°假设当n=k(奇数)时,x+y能够整除x k+y k,则当n=k+2时,x k+2+y k+2=x k+2﹣x k y2+x k y2+y k+2=x k(x2﹣y2)+y2(x k+y k),因此上式可被x+y整除.由1°,2°可知:n为奇数时,x+y能够整除x n+y n.又∵当n为奇数时,=(y p+y q)M,其中M是关于y p,y q的整式,∵Y p∪Y q=X,Y p∩Y q=∅,∴每一个集合“对”(Y p,Y q)都满足y p+y q=0.则一定有=(x+y)M=0,M∈N*,于是可得y1n+y2n+…+y255n=0是常数.【点评】本题考查了平行直线系、直线的交点、一元二次方程的根与系数的关系、集合的性质、中点坐标公式、对称性、扇形归纳法,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.。
2015年高考数学全国卷二理科(完美版)
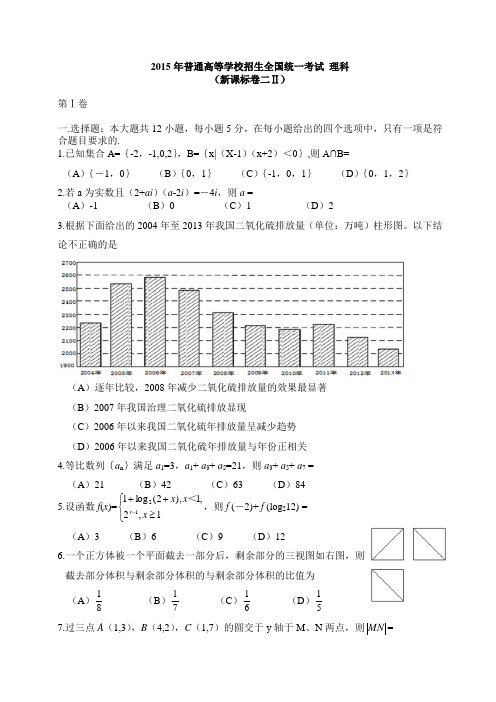
2015年普通高等学校招生全国统一考试 理科(新课标卷二Ⅱ)第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={-2,-1,0,2},B={x|(X-1)(x+2)<0},则A∩B=(A ){-1,0} (B ){0,1} (C ){-1,0,1} (D ){0,1,2}2.若a 为实数且(2+ai )(a -2i )=-4i ,则a =(A )-1 (B )0 (C )1 (D )23.根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图。
以下结论不正确的是(A )逐年比较,2008年减少二氧化硫排放量的效果最显著(B )2007年我国治理二氧化硫排放显现(C )2006年以来我国二氧化硫年排放量呈减少趋势(D )2006年以来我国二氧化硫年排放量与年份正相关4.等比数列{a n }满足a 1=3,a 1+ a 3+ a 5=21,则a 3+ a 5+ a 7 =(A )21 (B )42 (C )63 (D )845.设函数f (x )=⎩⎨⎧≥++-1,2,1),2(log 112x x x x <,则f (-2)+ f (log 212) =(A )3 (B )6 (C )9 (D )126.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的与剩余部分体积的比值为(A )81 (B )71 (C )61 (D )51 7.过三点A (1,3),B (4,2),C (1,7)的圆交于y 轴于M 、N 两点,则MN=(A )26 (B )8 (C )46 (D )108.右边程序抗土的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”。
执行该程序框图,若输入a,b 分别为14,18,则输出的a=(A )0(B )2(C )4(D )149.已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体 积的最大值为36,则球O 的表面积为(A )36π (B )64π (C )144π (D )256π10.如图,长方形ABCD 的边AB=2,BC=1,O 是AB 的中点,点P 沿着边BC ,CD 与 DA 运动,∠BOP=x 。
2015年高考理科数学试题全国卷2及解析word完美版

2015年高考全国新课标卷Ⅱ理科数学真题一、选择题1、已知集合A={–2,–1,0,1,2},B={x|(x –1)(x+2)<0},则A∩B=() A .{–1,0} B .{0,1} C .{–1,0,1} D .{0,1,2}2、若a 为实数,且(2+ai)(a –2i)=–4i ,则a=() A .–1 B .0 C .1 D .23、根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图,以下结论中不正确的是()A .逐年比较,2008年减少二氧化硫排放量的效果最显着B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫排放量呈减少趋势D .20064、已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则A .21 B .42 C .63 D .84 5、设函数f(x)=,则f(–2)+f(log 212)=() A .3 B .6 C .9 D .12 6.一个正方体被一个平面截去一部分后,分体积的比值为()A .B .C .D .7、过三点A .2 8、如上左2a=() A .0 9、已知A ,C 为该球上的动点,若三棱锥O –ABC 的体积最大值为36A .36π.256π10、如上左O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记∠BOP=x x 的函数,则y=f(x)的图像大致为()A .B .C .D . 11、已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,△ABM 为等腰三角形,且顶角为120°,则E 的离心率为()A .B .2C .D .12、设函数f’(x)是奇函数f(x)(x R)的导函数,f(–1)=0,当x>0时,xf’(x)–f(x)<0,则使得f(x)>0成立的x 的取值范围是() A .(–∞,–1)∪(0,1) B .(,0)∪(1,+∞)C .(–∞,–1)∪(–1,0) D .(,1)∪(1,+∞) 二、填空题13、设向量a,b 不平行,向量λa+b 与a+2b 平行,则实数λ=. 14、若x ,y 满足约束条件,则z=x+y 的最大值为.15、(a+x)(1+x)4的展开式中x 的奇数次幂项的系数之和为32,则a=.16、设S n 是数列{a n }的前n 项和,且a 1=–1,a n+1=S n S n+1,则S n =________________. 三、解答题17、△ABC 中,D 是BC 上的点,AD 平分∠BAC,△ABD 面积是△ADC 面积的2倍. (1)求.(2)若AD=1,DC=,求BD 和AC 的长.18.某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机抽查了20个用户,得到用户对产品的满意度评分如下: A 地区:62738192958574645376 78869566977888827689B 地区:73836251914653736482 93486581745654766579(1)均值及分散程度(记事件C :“A 地区用户的满意等级高于B 19、如图,长方形ABCD –A 1B 1C 1D 1中,AB=16,BC=101F=4.过点E ,F 的平面α(1)在途中画出这个正方形(不必说明画法和理由(2)求直线AF 与α平面所成角的正弦值.20、已知椭圆C :9x 2+y 2=M 2(m>0).直线l A ,B ,线段AB 的中点为M .(1)(2)若l l 的21、设函数(1)证明:(2)2)|≤e –1,求m 的取值范围.22、[选修4ABC 内一点,⊙O 与△ABC 的底边BC 交于M ,N E ,F 两点. (1)(2)若AG EBCF 的面积. 23、[选修4xOy 中,曲线C 1:(t 为参数,t≠0),其中0≤α<π. 在以O C 2:ρ=2sinθ,C 3:ρ=2cosθ. (1)求C 2与C (2)若C 1与C 2相交于点A ,C 1与C 3相交于点B ,求|AB|的最大值24、[选修4–5:不等式选讲]设a ,b ,c ,d 均为正数,且a+b=c+d ,证明: (1)若ab>cd ,则+>+;(2)+>+是|a –b|<|c –d|的充要条件. 2015年高考全国新课标卷Ⅱ理科数学真题 一、选择题1、答案:A .∵(x–1)(x+2)<0,解得–2<x<1,∴B={x|–2<x<1},∴A∩B={–1,0}.2、答案:B .∵(2+ai)(a–2i)=(2a+2a)+(a 2–4)i=–4i ,∴a 2–4=–4,解得a=0.3、答案:D .由柱形图得,从2006年以来,我国二氧化硫排放量呈下降趋势,故年排放量与年份负相关.4、答案:B .∵a 1+a 3+a 5=a 1+a 1q 2+a1q 4=3(1+q 2+q 4)=21,∴1+q 2+q 4=7,整理得(q 2+3)(q 2–2)=0.解得q 2=2,∴a 3+a 5+a 7=a 1q 2+a 1q 4+a 1q 6=a 1q 2(1+q 2+q 4)=3×2×7=42. 5、答案:C .∵f(–2)=1+log 2(2+2)=3,()222log 121log 3log 412log 1222f -+-==222log 3log 2log 6226+===,∴f(–2)+f(log 212)=9.6、答案:D .如图所示截面为ABC ,设边长为a ,则截取部分体积为S △ADC ·|DB|=a 3, 所以截去部分体积与剩余部分体积的比值为=.7、答案:C .由题可得,解得,所以圆方程为x 2+y 2–2x+4y –20=0,令x=0,解得y=–2±2, 所以|MN|=|–2+2–(–2–2)|=4. 8、答案:B .输入a=14,b=18.第一步a≠b 成立,执行a>b ,不成立执行b=b –a=18–14=4; 第二步a≠b第三步a≠b 第四步a≠b 第四步a≠b 第五步a≠b 9、答案:C 点C 到平面10、答案:当点P 在CD 当x=时,从点P B . 11、答案:过点M 作, 12、答案:因为当x>0 又因为函数且g(–, 二、填空题131415、答案:所以Ca+Ca+C+C+C=32,解得a=3.16、答案:–.∵a n+1=S n+1–S n =S n S n+1,∴–=1.即–=–1,∴{}是等差数列, ∴=–(n –1)=–1–n+1=–n ,即S n =–. 三、解答题17、答案:(1);(2)|BD|=,|AC|=1.(1)如图,由题意可得S △ABD =|AB||AD|sin ∠BAD,S △ADC =|AC||AD|sin ∠CAD, ∵S △ABD =2S △ADC ,∠BAD=∠DAC,∴|AB |=2|AC|,∴==. (2)设BC 边上的高为h ,则S △ABD =|BD|·h=2S △ADC =2××h ,解得|BD|=,设|AC|=x ,|AB|=2x ,则cos ∠BAD=,cos ∠DAC=.∵cos∠DAC=cos ∠BAD ,∴=,解得x=1或x=–1(舍去).∴|AC|=1. 18、(1)如图所示.通过茎叶图可知A 地区的平均值比B 地区的高,A地区的分散程度大于B地区.(2)记事件不满意为事件A1,B1,满意为事件A2,B2,非常满意为事件A3,B3.则由题意可得P(A1)=,P(A2)=,P(A3)=,P(B1)=,P(B2)=,P(B3)=,则P(C)=P(A2)P(B1)+P(A3)(P(B1)+P(B2))=×+×(+)=.19、(1)如图所示(2)建立空间直角坐标系.由题意和(1)可得A(10,0,0),F(0,4,8),E(10,4,8),G(10,10,0),则向量AF=(–10,4,8),EF=(–10,0,0),EG=(0,6,–8).设平面EFHG的一个法向量为n=(x,y,z),则,即,解得x=0,令y=4,z=3,则n=(0,4,3).所以直线AF与α平面所成角的正弦值为sinθ=|cos<AF,n>|===.20、(1)设直线l的方程为y=kx+b(k≠0),点A(x1,y1),B(x2,y2),则M(,),联立方程,消去y整理得(9+k2)x2+2kbx+b2–m2=0(*),∴x1+x2=–,y1+y2=k(–)+2b=,∴kOM ·kAB=·k=·(–)·k=–9.k=4±,有21∴∴,所以此时当令e–m–2m 在而.当当22则∵.在在Rt△AEO中,sin∠OAE===.∴∠OAE=60°,∵∠OAE=∠OAF=∠EAF,AE=AF,∴∠EAF=2∠OAE=60°,∴△AEF、△ABC是等边三角形.连接OM,∴OM=2.∵OD⊥MN,∴MD=ND=MN=.在Rt△ODM中,OD===1,∴AD=OA+AD=4+1=5.在Rt△ADB中,AB===.∴四边形EBCF的面积为S△ABC –S△AEF=×()2–×(2)2=.23、(1)将曲线C2,C3化为直角坐标系方程C2:x2+y2–2y=0,C3:x2+y2–2x=0.联立,解得或.所以交点坐标为(0,0),(,).(2)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),其中0≤α<π.∵A的极坐标为(2sinα,α),B的极坐标为(2cosα,α).∴|AB|=|2sinα–2 cosα|=4|sin(α–)|.当α=时,|AB|取得最大值,最大值为4.24、(1)由题意可得(+)2=a+b+2,(+)2=c+d+2,∵ab>cd,∴>,而a+b=c+d,∴(+)2>(+)2,即+>+.(2)+>+,即a+b+2>c+d+2,∴>,∴ab>cd,∴–4ab<–4cd,∴(a+b)2–4ab<(c+d)2–4cd,∴(a–b)2<(c–d)2,∴|a–b|<|c–d|.。
(完整)2015年上海各区二模18题汇总,推荐文档

黄埔18. 如图4-1,点P是以r为半径的圆O外一点,点在线段OP上,若满足,则称点是点P关于圆O的反演点.如图4-2,在Rt△AB O中,,AB=2,BO=4,圆O的半径为2,如果点、分别是点A、B关于圆O的反演点,那么的长是▲.奉贤18.如图,已知钝角三角形ABC,∠A=35°,OC为边AB上的中线,将△AOC绕着点O顺时针旋转,点C落在BC边上的点处,点A落在点处,联结,如果点A、C、在同一直线上,那么∠的度数为▲;虹口徐汇18.如图,已知扇形AOB的半径为6,圆心角为90°,E是半径OA上一点,F是上一点.将扇形AOB沿EF对折,使得折叠后的圆弧恰好与半径OB相切于点G,若OE=5,则O到折痕EF的距离为▲ .静安、青浦区18.如图,⊙O1的半径为1,⊙O2的半径为2,O1O2=5,⊙O分别与⊙O1外切、与⊙O2内切,那么⊙O半径的取值范围是▲ .宝山嘉定18.在矩形中,,点在边上,联结,△沿直线翻折后点落到点,过点作,垂足为点,如图5,如果,那么▲.18.如图,在△ABC中,AB=AC=5cm,BC=6cm,BD平分∠ABC,BD交AC于点D.如果将△ABD沿BD翻折,点A落在点A′处,那么△D A′C的面积为_______________cm2.长宁18.如图,△ABC≌△DEF(点A、B分别与点D、E对应),AB=AC=5,且juxingABCD4BC=6,△ABC固定不动,△DEF运动,并满足点E在BC边从B向C移动(点E不与B、C重合),DE始终经过点A,EF与AC边交于点M,当△AEM 是等腰三角形时,BE= ▲ .18.如图,在中,,,点是的中点,将沿着直线EF折叠,使点与点重合,折痕交于点,交于点,那么的值为▲.闵行18.如图,已知在Rt△ABC中,∠C = 90º,AC = BC = 1,点D在边BC上,将△ABC沿直线AD翻折,使点C落在点C′处,联结AC′,直线AC′与边CB的延长线相交于点F.如果∠DAB=∠BAF,那么BF =▲ .浦东新区18.如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于▲.普陀区18.如图6,在矩形纸片中,<.点、分别在边、上,沿直线将四边形翻折,点恰好与点重合.如果此时在原图中△与△的面积比是1︰3,那么的值等于▲.杨浦18.如图,钝角△ABC中,tan∠BA C=,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C,处,点B落在点B,处,若C、B、B,恰好在一直线上,则A B的长为▲ .闸北18.在矩形中,,,把矩形沿直线翻折,点落在边上的点处,若,那么的长等于▲。
2015年上海市闸北区中考数学二模试卷
2015年上海市闸北区中考数学二模试卷参考答案与试题解析一、选择题(共6小题,每小题4分,满分24分)1.(4分)(2015•闸北区二模)﹣8的立方根是()A.2 B.﹣2 C.±2 D.【考点】M228 算术平方根、立方根【难度】容易题【分析】利用立方根的定义:∵(﹣2)3=﹣8,∴﹣8的立方根是﹣2.故选B【解答】B【点评】本题主要考查了平方根和立方根的概念.如果一个数x的立方等于a,即x的三次方等于a(x3=a),那么这个数x就叫做a的立方根,也叫做三次方根.读作“三次根号a”其中,a叫做被开方数,3叫做根指数.2.(4分)下列属于最简二次根式的是()A. B.C.D.【考点】M223 最简二次根式【难度】容易题【分析】A、,无法化简,故是最简二次根式,故本选项正确;B、,被开方数中含有分母;故本选项错误;C、,被开方数中含有分母,故本选项错误;D、所以本二次根式的被开方数中含有没开的尽方的数;故本选项错误;故选:A.【解答】A.【点评】本题考查了最简二次根式的定义.在判断最简二次根式的过程中要注意:(1)在二次根式的被开方数中,只要含有分数或小数,就不是最简二次根式;(2)在二次根式的被开方数中的每一个因式(或因数),如果幂的指数大于或等于2,也不是最简二次根式.3.(4分)(2015•闸北区二模)下列方程中,有实数根的是()A.=﹣2 B.x2+1=0 C.=1 D.x2+x+1=0【考点】M242 一元二次方程的根的判别式M253 分式方程M254 无理方程【难度】容易题【分析】A、方程=﹣2没有实数解,所以A选项错误;B、△=0﹣4<0,方程没有实数解,所以B选项错误;C、去分母得1=x+1,解得x=0,经检验x=0是原方程的解,所以C选项正确;D、△=14<0,方程没有实数解,所以D选项错误.故选C.【解答】C.【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了分式方程和无理方程.4.(4分)(2015•闸北区二模)在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC 相交于点E.如果DE过重心G点,且DE=4,那么BC的长是()A.5 B.6 C.7 D.8【考点】M33L 三角形重心、内心、外心M33H 比例的性质M33M 相似三角形性质、判定【难度】容易题【分析】如图,连结AG并延长交BC于F,根据三角形重心性质得=2,又DE∥BC得△ADE∽△ABC,根据相似三角形的性质得=,然后利用比例的性质计算BC=6.故选B.【解答】B.【点评】本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查了相似三角形的判定与性质.均属于中考常考知识点,考生要注意掌握!5.(4分)(2015•闸北区二模)饭店为某公司提供“白领午餐”,有12元、15元、18元三种价格的套餐可供选择,每人限购一份.本周销售套餐共计500份,其中12元的占总份数的20%,15元的卖出180份,其余均为18元的,那么所购买的盒饭费用的中位数和众数分别是()A.15元和18元B.15元和15元C.18元和15元D.18元和18元【考点】M524 中位数、众数M522 平均数、方差和标准差【难度】容易题【分析】12元的份数有500×20%=100(份),18元的份数有500﹣100﹣180=220(份),∵本周销售套餐共计500份,∴所购买的盒饭费用的中位数是第250和251个数的平均数,∴中位数是15元;18元出现的次数最多,则众数是18元;故选A.【解答】A.【点评】此题考查了众数与中位数,众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.6.(4分)(2015•闸北区二模)如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC 的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH 为2.1米.求放水后水面上升的高度是()A.0.55 B.0.8 C.0.6 D.0.75【考点】M346 等腰梯形的性质与判定M364 解直角三角形M365 仰角、俯角、坡度、坡角【难度】中等题【分析】如图;过点E作EM⊥GH于点M,∵水渠的横断面是等腰梯形,∴GM=×(GH﹣EF)=×(2.1﹣1.2)=0.45,∵斜坡AD的坡度为1:0.6,∴EM:GM=1:0.6,∴EM:0.45=1:0.6,∴EM=0.75,故选:D.【解答】D.【点评】此题考查了解直角三角形的应用,用到的知识点是坡度、等腰三角形的性质,关键是根据题意画出图形,作出辅助线,构造直角三角形.二、填空题(共12小题,每小题4分,满分48分)7.(4分)(2015•闸北区二模)计算:2﹣2=.【考点】M213 整数指数幂的运算【难度】容易题【分析】根据负整数指数幂的定义:a﹣p=(a≠0,p为正整数)求解得2﹣2==,故答案为.【解答】.【点评】本题考查了负整数指数幂的定义,解题时牢记定义是关键,此题比较简单,易于掌握.8.(4分)(2015•闸北区二模)用科学记数法表示:3402000=.【考点】M123 近似计算以及科学记数法【难度】容易题【分析】确定a×10n(1≤|a|<10,n为整数)中n的值是易错点,由于3402000有7位,所以可以确定n=7﹣1=6.则3402000=3.402×106.故答案为:3.402×106.【解答】3.402×106.【点评】此题考查科学记数法,用科学记数法表示一个数的方法是(1)确定a:a是只有一位整数的数;(2)确定n:当原数的绝对值≥10时,n为正整数,n等于原数的整数位数减1;当原数的绝对值<1时,n为负整数,n的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零).9.(4分)化简分式:=.【考点】M215 分式的基本性质M217 因式分解【难度】容易题【分析】先把分母因式分解,然后进行约分即原式==.故答案为.【解答】.【点评】本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.10.(4分)(2015•闸北区二模)不等式组的解集是.【考点】M236 解一元一次不等式(组)【难度】容易题【分析】由①得:x>﹣2,由②得:x≥3,∴不等式组的解集是x≥3.故答案为x≥3.【解答】x≥3.【点评】本题主要考查对不等式的性质,解一元一次不等式,解一元一次不等式组等知识点的理解和掌握,能根据不等式的解集找出不等式组的解集是解此题的关键.11.(4分)(2015•闸北区二模)方程x+=0的解是.【考点】M254 无理方程【难度】容易题【分析】本题含根号,计算比较不便,因此可先对方程两边平方变形为:x=x2即x2﹣x=0 ∴(x﹣1)x=0 ∴x=0或x=1∵x=1时不满足题意.∴x=0.故答案为0.【点评】本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的提点灵活选用合适的方法.本题运用的是因式分解法和平方法.12.(4分)(2015•闸北区二模)已知反比例函数y=(k≠0)图象过点(﹣1,﹣3),在每个象限内,自变量x的值逐渐增大时,y的值随着逐渐.(填“减小”或“增大”)【考点】M124 实数大小比较M414 用待定系数法求函数关系式M432 反比例函数的的图象、性质【难度】容易题【分析】设反比例函数的解析式为y=(k≠0),∵反比例函数图象过点(﹣1,﹣3),∴把(﹣1,﹣3)代入得3=k>0,根据反比例函数图象的性质可知它在每个象限内y随x的增大而减小,故答案为:减小;【解答】减小;【点评】考查了反比例函数的性质,解答此题的关键是要熟知反比例函数图象的性质及用待定系数法求反比例函数的解析式.反比例函数图象的性质:(1)当k>0时,反比例函数的图象位于一、三象限;(2)当k<0时,反比例函数的图象位于二、四象限.13.(4分)(2015•闸北区二模)文件夹里放了大小相同的试卷共12张,其中语文4张、数学2张、英语6张,随机从中抽出1张,抽出的试卷恰好是数学试卷的概率为.【考点】M511 事件M512 概率的计算【难度】容易题【分析】由文件夹里放了大小相同的试卷共12张,其中语文4张、数学2张、英语6张,直接利用概率公式求解即随机从中抽出1张,抽出的试卷恰好是数学试卷的概率为:=.故答案为:.【解答】.【点评】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.14.(4分)(2015•闸北区二模)某品牌汽车经过两次连续的调价,先降价10%,后又提价10%,原价10万元的汽车,现售价万元.【考点】M122 实数的运算【难度】容易题【分析】根据题意得:10×(1﹣10%)×(1+10%)=9.9(万元),则现售价为9.9万元.故答案为:9.9.【解答】9.9.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.15.(4分)(2015•闸北区二模)如图,在正方形ABCD中,如果AC=3,=,=,那么|﹣|=.【考点】M382 向量的加法与减法M383 实数与向量的乘法M384 向量的线性运算M344 平行四边形(包括矩形、菱形、正方形)的判定与性质M339 等腰三角形的性质和判定M33D 直角三角形的性质和判定M33E 勾股定理M361 锐角的三角比的概念(正切、余切、正弦、余弦)M362 特殊角的锐角三角函数值【难度】中等题【分析】首先由在正方形ABCD中,如果AC=3,可利用锐角三角函数求得AB=BC=3又由=,=,可得﹣=﹣=,则|﹣|=||=BC=3.故答案为:3.【解答】3.【点评】此题主要考查了平面向量的知识,属于中考常考知识点,解题时要注意掌握三角形法则的应用.16.(4分)(2015•闸北区二模)某公园正在举行郁金香花展,现从红、黄两种郁金香中,各抽出6株,测得它们离地面的高度分别如下(单位cm):红:54、44、37、36、35、34;黄:48、35、38、36、43、40;已知它们的平均高度均是40cm,请判断哪种颜色的郁金香样本长得整齐?.(填“红”或“黄”)【考点】M122 实数的运算M123 近似计算以及科学记数法M124 实数大小比较M522 平均数、方差和标准差【难度】中等题【分析】先根据方差公式S2=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2]分别求出红颜色和黄颜色的方差,然后进行比较,即:红颜色的郁金香的方差是:[(54﹣40)2+(44﹣40)2+(37﹣40)2+(36﹣40)2+(35﹣40)2+(34﹣40)2]≈49.67,黄颜色的郁金香的方差是:[(48﹣40)2+(35﹣40)2+(38﹣40)2+(36﹣40)2+(43﹣40)2+(40﹣40)2]≈29.67,∵S2红>S2黄,∴黄颜色的郁金香样本长得整齐;故答案为:黄.【解答】黄.【点评】本题考查方差的定义与意义:一般地设n个数据,x1,x2,…x n的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(x n﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.17.(4分)(2015•闸北区二模)已知⊙O的直径是10,△ABC是⊙O的内接等腰三角形,且底边BC=6,求△ABC的面积是.【考点】M339 等腰三角形的性质和判定M33O 三角形面积M33E 勾股定理M354 圆的有关性质M357 正多边形与圆【难度】较难题【分析】从圆心在三角形内部和外部两种情况讨论,当圆心在三角形内部时,0B=5,BD=3,根据勾股定理,OD=4,则AD=9,S△ABC=×6×9=27,当圆心在三角形外部时,0B=5,BD=3,根据勾股定理,OD=4,则AD=1,S△ABC=×6×1=3,故答案为:3或27.【解答】3或27.【点评】本题考查的是垂径定理、等腰三角形的性质和勾股定理,正确运用定理和性质是解题的关键,注意分情况讨论思想的运用.18.(4分)(2015•闸北区二模)如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比=.【考点】M33M 相似三角形性质、判定M361 锐角的三角比的概念(正切、余切、正弦、余弦)M373 图形的翻折与轴对称图形【难度】中等题【分析】根据△BED与△ABC相似和△ABC沿BD折叠,点C恰巧落在边AB上的C′处,求出∠A=∠DBA=∠DBC=30°,设BC为x,利用三角函数求出则AC=x,BD=x,=.则:故答案为:.【解答】.【点评】本题主要考查的是相似三角形的性质和翻折变换等知识点,考生要注意理解并灵活运用,对于本题掌握相似三角形的对应角相等和锐角三角函数的应用是解题的关键.三、解答题(共7小题,满分78分)19.(10分)(2015•闸北区二模)计算:﹣|cos45°﹣1|+(﹣2015)0+3.【考点】M122 实数的运算M125 绝对值M213 整数指数幂的运算M226 二次根式的加、减、乘、除及其混合运算M227 分数指数幂M362 特殊角的锐角三角函数值【难度】容易题【分析】根据零指数幂、分数指数幂和特殊角的三角函数值得到原式=﹣|﹣1|+1+,然后分母有理化和去绝对值后合并即可.【解答】解:原式=﹣|﹣1|+1+ (3)=2﹣+﹣1+1+ (6)=2+. (10)【点评】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和分数指数幂.20.(10分)(2015•闸北区二模)解方程组:.【考点】M233 二元一次方程(组)的概念、解法M255 简单的二元二次方程(组)M217 因式分解【难度】中等题【分析】把①化为x=±2y,把②化为x+y=±2,重新组成方程组,解二元一次方程组即可.【解答】解:,由①得,x=±2y, (2)由②得,x+y=±2, (4)则,,, (7)解得,,,,. (10)【点评】本题考查的是二元二次方程组的解法,把二元二次方程根据平方差公式和完全平方公式进行变形化为两个二元一次方程是解题的关键.21.(10分)(2015•闸北区二模)已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的倍,甲到达目的地C点的同时乙恰好到达终点D处.(1)求tan∠ECD的值;(2)求线段AB及BC的长度.【考点】M33E 勾股定理M344 平行四边形(包括矩形、菱形、正方形)的判定与性质M361 锐角的三角比的概念(正切、余切、正弦、余弦)M241 一元二次方程的概念、解法【难度】容易题【分析】(1)设ED=a,则EC=a,在Rt△EDC中根据勾股定理用a表示出DC的长,在Rt△ABE中,根据BE2=AB2+AE2求出a的值,故可得出ED及CD的长,由锐角三角函数的定义即可得出结论;(2)由(1)中,DE=a,CD=3a,a=2可得出DE=2,CD=6,再根据四边形ABCD是矩形,BE=AD即可得出结论.【解答】解:(1)设ED=a,则EC=a, (1)在Rt△EDC中,∵DC===3a,∴BE=AE+ED=8+a. (3)在Rt△ABE中,∵BE2=AB2+AE2,即(8+a)2=(3a)2+82,解得a=2,∴ED=2,CD=6, (5)∴tan∠ECD===. (6)(2)∵由(1)知,DE=a,CD=3a,a=2,∴DE=2,CD=6. (8)∵四边形ABCD是矩形,BE=AD,AE=8,∴AB=CD=6,BC=AD=AE+DE=8+2=10. (10)【点评】本题主要考查的是勾股定理,矩形的性质、判定等知识点;熟知勾股定理即是在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.22.(10分)(2015•闸北区二模)某公司的物流业务原来由A运输队承接,已知其收费标准(公里)的函数解析式;(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式;(不需写出定义域)(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?【考点】M124 实数大小比较M422 一次函数的的图象、性质M423 一次函数的关系式M424 一次函数的应用【难度】容易题【分析】(1)根据表可知:当运输路程跑80公里时,收费200元,所以每公里收费为2.5元,即可得出;(2)根据题意得出等量关系,列出函数解析式即可。
上海市闸北区2015年高三第二学期期中(高考等级考二模)学科质量检测地理试题及答案
闸北区2014~2015学年度第二学期教学质量检测高三地理试卷2015.04考生注意:1、试卷满分150分,考试时间120分钟。
2、本考试分设试卷和答题纸。
试卷包括选择题和综合分析题。
3、答题前,务必在答题纸上填写姓名、学校、考场和座位号、班级。
作答必须涂或写在答题纸上,在试卷上作答一律不得分。
选择题的作答必须涂在答题纸上相应的区域,综合分析题的作答必须写在答题纸上与试卷题号对应的位置。
一、选择题(共60分,每小题2分,每小题只有一个正确答案)(一)大气圈是地球的保温被、地球生命的保护伞。
1.大气对地面具有保温作用,是因为其能够A.吸收并放射长波辐射B.吸收短波辐射放射长波辐射C.吸收并放射短波辐射D.吸收长波辐射放射短波辐射2.大气臭氧层遭破坏将导致A.极光现象增多,危害人类与生物B.扰乱电离层,影响地面短波通讯C.大量紫外线进入地表,危害人类与生物D.大气失去保温作用,加剧昼夜温差3.下列关于对流层和平流层特征的叙述中,正确的是A.对流层是航空最佳飞行层B.对流层高度随季节发生变化C.因臭氧层的存在,平流层气温随高度变化而增加D.平流层天气复杂多变(二)读下面人口金字塔图,第六次人口普查显示,与1982年相比,我国农村人口构成发生了明显变化。
4.我国农村人口的变化特点是女男女男我国人口金字塔图A .总人口持续减少,男女比例失衡B .总人口持续减少,老年人口快速增加C .总人口维持不变,少年儿童占比下降D .总人口维持不变,劳动力人口有所增加 5.造成这一变化的主要原因是A .农村生活水平快速提高B .人们生育观念的转变C .我国城镇化率快速提高D .大量适龄劳动人口外出务工(三)读澳大利亚简图,十八世纪墨累—达令盆地开始种植小麦,饲养绵羊,现已成为澳大利亚主要的农产品输出地。
随着农业的发展,该地区出现了一系列环境问题。
6.墨累—达令盆地地区的农业地域类型属于A .旱作农业B .牧场畜牧业C .高度发达的商品化混合农业D .游牧畜牧业 7.该地区农业发展面临的主要限制性因素是A .地形B .土壤C .气候D .水源 8.该地区面临的主要环境问题可能是①土地盐碱化 ②河水流量增多,河口附近侵蚀作用增强 ③水生动植物大量繁殖 ④湿地萎缩,牧草生长不良A .①④B .②③C .③④D .①② (四)右图三是我国某地区气温、降水量和蒸发量年内分布示意图。
2015上海二模 上海市普陀区2015届高三4月质量调研(二模)数学(理)试题 Word版含答案
2015届普陀区高三二模数学试卷(理科)2015.04一、填空题(共14题,每题4分,满分56分)1.不等式01xx >-的解集为 . 2.若1m i i i+=+(i 为虚数单位),则实数m = . 3.若函数()()sin sin 022x xf x ωπωω+=>的最小正周期为π,则ω= .4.集合{{}2,4,R A x y B x y x x ====∈,则AB .5. 若0x π≤≤,则函数sin cos 32y x x ππ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭的单调递增区间为 .6.如图,若6OFB π∠=,6OF FB ⋅=-,则以OA 为长半轴,OB 为短半轴,F 为左焦点的椭圆的标准方程为 .7.函数())1f x x =≤,若函数()2g x x ax =+是偶函数,则()f a = .8.一个圆锥与一个球的体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为 .9.已知直线l 和曲线Γ的极坐标方程分别为()sin cos 1ρθθ-=和1ρ=,若l 和Γ相交于两点,A B ,则AB = .10.如图,机车甲、乙分别停在A B ,处,且=10AB km ,甲的速度为4千米/小时,乙的速度是甲的12,甲沿北偏东60︒的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为 千米.11.一个袋子中有7个除颜色外完全相同的小球,其中5个红色,2个黑色.从袋中随机地取出3个小球.其中取到黑球的个数为ξ,则E ξ= (结果用最简分数作答). 12.若正方形ABCD 的边长为1,且,,,AB a BC b AC c ===则326a b c +-= . 13.已知复数12,z z 满足11z ≤,21Re 1z -≤≤,21Im 1z -≤≤,若12z z z =+,则z 在复平面上对应的点组成的图形的面积为.6第题图北AC B ∙D6010第题图14.R x ∈,用记号()N x 表示不小于实数的最小整数,例如()2.53N =,(1N =-,()11N =;则函数()()13122f x N x x =+-+的所有零点之和为 . 二、选择题(共4题,每题5分,满分20分)15. ,,a b c 表示直线,α表示平面,下列命题正确的是( )A.若//a b ,//a α,则//b αB. 若a ⊥b , b ⊥α,则a ⊥αC. 若a ⊥c ,b ⊥c ,则//a bD.若a ⊥α,b ⊥α,则//a b16.”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( ) A.充分非必要条件 B.必要非充分条件 C.充要条件 D.非充分非必要条件 17.在*22)()nn N x∈的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( )A.第2项B.第3项C.第4项D.第5项18.已知,,,m n i j 均为正整数,记,i j a 为矩阵1,21,2,22,,1,2,12m m n mn n n m a a a a A a a a ⨯⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭中第i 行、第j 列的元素,且,,11i j i j a a ++=,2,1,,2i j i j i j a a a ++=+(其中2i n ≤-,2j m ≤-);给出结论:①5,6134a =;②2,12,22,2m a a a m +++=;③1,,12nn m n ma a +⎛⎫=+- ⎪⎝⎭④若m 为常数,则,23lim 3n m n m a →∞+=.其中正确的个数是( )A.0个B.1个C.2个D.3个 三、解答题(本大题共5题,写出必要的文字说明与步骤) 19.(本题满分12分,第1小题6分,第2小题6分) 已知函数()2cos f x x =,()1cos 2g x x x =. (1)若直线x a =是函数()y f x =的图像的一条对称轴,求()2g a 的值; (2)若02x π≤≤,求()()()h x f x g x =+的值域.20.(本题满分14分,第1小题6分,第2小题8分) 在正方体1111ABCD A B C D -中,E 是棱1DD 的中点.(1)求直线BE 与平面11ABB A 所成角的大小(结果用反三角函数表示)(2)在棱1C D 上是否存在一点F ,使得1//BF 平面1A BE ,若存在,指明点F 的位置,若不存在,请说明理由.20.(本题满分14分,第1小题6分,第2小题8分) 已知函数()2x f x =的反函数为1()f x -(1)若11()(1)1f x f x ----=,求实数x 的值;(2)若关于x 的方程()(1)0f x f x m +--=在区间[]0,2内有解,求实数m 的取值范围;22.(本题满分16分,第1小题4分,第2小题7分,第3小题5分)如图,射线,OA OB 所在的直线的方向向量分别为()11,d k =,()()21,0d k k =->,点P 在AOB ∠内,PM OA ⊥于M ,PN OB ⊥于N ;(1)若1k =,31,22P ⎛⎫⎪⎝⎭,求OM 的值;(2)若()2,1P ,OMP ∆的面积为65,求k 的值; (3)已知k 为常数,,M N 的中点为T ,且1MONS k=,当P 变化时,求动点T 轨迹方程;23.(本题满分18分,第1小题4分,第2小题6分,第3小题8分)A1A B 1B C1C D1D E已知数列{}n a 的前n 项和为n S ,且0n a >,()*1N 4nn n a S n ⎛⎫⋅=∈ ⎪⎝⎭(1)若()21log n n n b S a =+⋅,求数列{}n b 的前n 项和n T ; (2)若02n πθ<<,2tan n n n a θ⋅=,求证:数列{}n θ为等比数列,并求出其通项公式;(3)记12311112222n n c a a a a =-+-+-++-,若对任意的*N n ∈,n c m ≥恒成立,求实数m 的取值范围.2015届普陀区高三二模数学试卷(理科)答案2015.04一、填空题(共14题,每题4分,满分56分)1.不等式01xx >-的解集为 ()0,1 . 2.若1m i i i+=+(i 为虚数单位),则实数m 1- . 3.若函数()()sin sin 022x xf x ωπωω+=>的最小正周期为π,则ω=2 .4. 集合{{}2,4,R A x y B x y x x ====∈,则AB []0,1 .5. 若0x π≤≤,则函数sin cos 32y x x ππ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭的单调递增区间为536ππ⎡⎤⎢⎥⎣⎦, . 6.如图,若6OFB π∠=,6OF FB ⋅=-,则以OA 为长半轴,OB 为短半轴,F 为左焦点的椭圆的标准方程为 22182x y += .7.函数())1f x x =≤,若函数()2g x x ax =+是偶函数,则()f a = 1 . 8.一个圆锥与一个球的体积相等且圆锥的底面半径是球半径的2倍,若圆锥的高为1,则球的表面积为 4π .9.已知直线l 和曲线Γ的极坐标方程分别为()sin cos 1ρθθ-=和1ρ=,若l 和Γ相交于两点,A B ,则AB =10.如图,机车甲、乙分别停在A B ,处,且=10AB km ,甲的速度为4千米/小时,乙的速度是甲的12,甲沿北偏东60︒的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为千米. 11.一个袋子中有7个除颜色外完全相同的小球,其中5个红色,2个黑色.从袋中随机地取出6第题图北AC B ∙D6010第题图3个小球.其中取到黑球的个数为ξ,则E ξ=67(结果用最简分数作答). 12.若正方形ABCD 的边长为1,且,,,AB a BC b AC c ===则326a b c +-= 5 . 13.已知复数12,z z 满足11z ≤,21Re 1z -≤≤,21Im 1z -≤≤,若12z z z =+,则z 在复平面上对应的点组成的图形的面积为 12π+ .14.R x ∈,用记号()N x 表示不小于实数的最小整数,例如()2.53N =,(1N =-,()11N =;则函数()()13122f x N x x =+-+的所有零点之和为 4- . 二、选择题(共4题,每题5分,满分20分)15. ,,a b c 表示直线,α表示平面,下列命题正确的是( D ) A.若//a b ,//a α,则//b α B. 若a ⊥b , b ⊥α,则a ⊥αC. 若a ⊥c ,b ⊥c ,则//a bD.若a ⊥α,b ⊥α,则//a b16.”直线与抛物线相切”是“直线与抛物线只有一个公共点”的( A ) A.充分非必要条件 B.必要非充分条件 C.充要条件D.非充分非必要条件 17. 在*22)()n n N x ∈的展开式中,若第五项的系数与第三项的系数之比为56:3,则展开式中的常数项是( B )A.第2项B.第3项C.第4项D.第5项18.已知,,,m n i j 均为正整数,记,i j a 为矩阵1,21,2,22,,1,2,12m m n mn n n m a a a a A a a a ⨯⎛⎫⎪ ⎪= ⎪ ⎪ ⎪⎝⎭中第i 行、第j 列的元素,且,,11i j i j a a ++=,2,1,,2i j i j i j a a a ++=+(其中2i n ≤-,2j m ≤-);给出结论:①5,6134a =;②2,12,22,2m a a a m +++=;③1,,12nn m n ma a +⎛⎫=+- ⎪⎝⎭④若m 为常数,则,23lim 3n m n m a →∞+=.其中正确的个数是( B )A.0个B.1个C.2个D.3个 三、解答题(本大题共5题,写出必要的文字说明与步骤) 19.(本题满分12分,第1小题6分,第2小题6分) 已知函数()2cos f x x =,()1cos 2g x x x =. (1)若直线x a =是函数()y f x =的图像的一条对称轴,求()2g a 的值; (2)若02x π≤≤,求()()()h x f x g x =+的值域.解:(1)()21cos2cos 2xf x x +==, 其对称轴为2,,2k x k x k Zππ==∈, 因为直线线x a =是函数()y f x =的图像的一条对称轴, 所以,2k a k Z π=∈, 又因为()122g x x =,所以()()()1122=22g a g k k ππ==+ 即()122g a =. (2)由(1)得 ()()()1cos2212sin 216h x f x g x x x x π=+=+⎛⎫=++ ⎪⎝⎭1710,,2,,sin 2,2266662x x x ππππ⎡⎤⎡⎤⎛⎫⎡⎤∈∴+∈+∈- ⎪⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎣⎦所以()h x 的值域为122⎡⎤⎢⎥⎣⎦,.20.(本题满分14分,第1小题6分,第2小题8分) 在正方体1111ABCD A B C D -中,E 是棱1DD 的中点.(1)求直线BE 与平面11ABB A 所成角的大小(结果用反三角函数表示)(2)在棱11C D 上是否存在一点F ,使得1//BF 平面1A BE ,若存在,指明点F 的位置,若不存在,请说明理由.解:(1) (2)存在,F 在棱11C D 的中点.(提示:用空间向量)21.(本题满分14分,第1小题6分,第2小题8分) 已知函数()2x f x =的反函数为1()f x -(1)若11()(1)1f x f x ----=,求实数x 的值;(2)若关于x 的方程()(1)0f x f x m +--=在区间[]0,2内有解,求实数m 的取值范围;解:(1)23x =(2)92⎡⎤⎢⎥⎣⎦.22.(本题满分16分,第1小题4分,第2小题7分,第3小题5分) 如图,射线,OA OB 所在的直线的方向向量分别为()11,d k =,()()21,0d k k =->,点P 在AOB ∠内,PM OA ⊥于M ,PN OB ⊥于N ;(1)若1k =,31,22P ⎛⎫⎪⎝⎭,求OM 的值;(2)若()2,1P ,OMP ∆的面积为65,求k 的值; (3)已知k 为常数,,M N 的中点为T ,且1MONS k=,当P 变化时,求动点T 轨迹方程;解:(1(2)1122k =或; (3)设()()()1122,,,,,M x kx N x kx T x y -,120,00x x k >>>,,A1A B 1B C1C D1D E设直线OA 的倾斜角为α,则22tan ,sin21kk kαα==+,根据题意得 ()12112222x x x y x x k x x k y y x x OM x k ON x +⎧=⎪⎪⎧=+-⎪⎪⎪⎪=⇒⎨⎨⎪⎪=-=⎪⎪⎩⎪=⎪⎩ 代入11sin22MON S OM ON k α∆==化简得动点T 轨迹方程为22211k x y x k ⎛⎫-=≥ ⎪⎝⎭.23.(本题满分18分,第1小题4分,第2小题6分,第3小题8分) 已知数列{}n a 的前n 项和为n S ,且0n a >,()*1N 4nn n a S n ⎛⎫⋅=∈ ⎪⎝⎭(1)若()21log n n n b S a =+⋅,求数列{}n b 的前n 项和n T ; (2)若02n πθ<<,2tan n n n a θ⋅=,求证:数列{}n θ为等比数列,并求出其通项公式;(3)记12311112222n n c a a a a =-+-+-++-,若对任意的*N n ∈,n c m ≥恒成立,求实数m 的取值范围. 解:(1)*12,N n b n n =-∈ (2)由tan 2tan 2n nn n n n a a θθ⋅==得代入()*1N 4nn n a S n ⎛⎫⋅=∈ ⎪⎝⎭得12tan n n nS θ=,当2n ≥时,111112tan 2tan n n n n n n n a S S θθ---=-==, 因为tan 2n n n a θ=,代入上式整理得()1tan tan 2n n θθ-=,02nπθ<<所以1112,02n n n n θθθθ--==≠的常数. 当1n =时,111111111,,0,tan 1,424n a S a a a a πθθ⎛⎫=⋅=>∴===⎪⎝⎭所以数列{}n θ是等比数列,首项为4π,公比为12,其通项公式为 11*11,N 422n n n n πθπ-+⎛⎫⎛⎫==∈ ⎪⎪⎝⎭⎝⎭(3)由(2)得*11tan ,N 22n n n a n π+=∈,它是个单调递减的数列, 所以 11111,0,2222n n n n a a a a a ≤=-≤∴-=-123111122222n n n c a a a a nS =-+-+-++-=-对任意的*N n ∈,n c m ≥恒成立,所以()min n m c ≤. 由111110222n n n n n c c n n S S a ++++⎛⎫---=- ⎝-≥⎪⎭=知,1n n c c +≥ 所以数列{}n c 是单调递增的,n c 最小值为10c =,()min 0n m c ≤= 因此,实数m 的取值范围是(],0-∞.。
上海市闸北区高三数学下学期期中练习试题理(含解析)
上海市闸北区2015届高三数学下学期期中练习试题 理(含解析)一、填空题:(60分)本大题共有10题,要求在答题纸相应题序的空格内直接填写结果,每 个空格填对得6分,否则一律得零分.1.设幂函数()f x 的图象经过点()8,4,则函数()f x 的奇偶性为____________. 【答案】偶函数考点:幂函数的定义、函数的奇偶性.2.设复数122,12z i z i =+=+,在复平面的对应的向量分别为,OA OB ,则向量AB 对应的复数所对应的点的坐标为____________. 【答案】(1,1)- 【解析】试题分析:∵复数122,12z i z i =+=+,∴(2,1)OA =,(1,2)OB =,∴(1,1)AB OB OA =-=-,∴向量AB 对应的复数所对应的点的坐标为(1,1)-. 考点:向量的减法.3.已知定义域为R 的函数()y f x =的图象关于点()1,0-对称,()y g x =是()y f x =的反函数,若120x x +=,则()()12g x g x +=___________. 【答案】-2 【解析】试题分析:∵函数()y f x =的图象关于点()1,0-对称,()y g x =是()y f x =的反函数,∴()y g x =关于点(0,1)-对称,∵120x x +=,∴21x x =-,∴()()()()12112g x g x g x g x +=+-=-.考点:反函数、函数的对称性.4.一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c ,其中,,(0,1)a b c ∈.已知投篮一次得分的期望是2,则ab 的最大值是____________.【答案】16【解析】试题分析:由题意可得:∵投篮一次得分的期望是2,∴232b a +=,∴211321(23)()6626a b ab b a +=⨯≤=,当且仅当23b a =时取“=”. 考点:期望、均值定理.5.设⎪⎩⎪⎨⎧∈≥∈≤≤=-.N ,3,31,N ,21,21n n n n a n n n 数列{}n a 的前n 项和为n S ,则=∞→n n S lim ___________.【答案】5518考点:极限、等比数列的前n 项和.6.设函数⎩⎨⎧<+≥+-=.0,4,0,66)(2x x x x x x f 若存在互不相等的实数123,,x x x 满足123()()()f x f x f x ==,则123x x x ++的取值范围是_____________.【答案】(1,6)- 【解析】试题分析:∵存在互不相等的实数123,,x x x 满足123()()()f x f x f x ==,∴170x -<<,236x x +=,∴12316x x x -<++<.考点:函数图象.7.若二项式nx⎛⎝展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________. 【答案】47【解析】试题分析:∵展开式中只有第四项的系数最大,∴展开式共7项,∴6n =,∴3662166r r rr rr T C xC x --+==, 当展开式中的项为有理项,则0,2,4,6r =,∴47P =. 考点:二项式定理、概率.8.从双曲线()222210,0x y a b a b -=>>的左焦点F 引圆222x y a +=的切线,切点为T ,延长FT 交双曲线右支于点P ,若M 是线段FP 的中点,O 为坐标原点,则MO MT -的值是____________. 【答案】b a - 【解析】试题分析:将点P 置于第一象限,设1F 是双曲线的右焦点,连接1PF ,∵M 、O 分别为FP 、1FF 的中点,∴11||||2MO PF =,又由双曲线定义得,1||||2PF PF a -=,||FT b ==,故1111||||||||||(||||)||22MO MT PF MF FT PF PF FT b a -=-+=-+=-.考点:双曲线的简单性质. 9.已知集合(){},,U x y x R y R =∈∈,(){},M x y x y a =+<,()(){},P x y y f x ==,现给出下列函数:①a y x -=;② log a y x = ;③ ()sin y x a =+;④ cos y ax =.若01a <<时,恒有U P C M P =,则所有满足条件的函数()f x 的编号是___________.【答案】①②④ 【解析】试题分析:∵{(,)|||||}U C M x y x y a =+≥,当01a <<时,U P C M P =,∴()(){},UP x y y f x CM ==⊆,如图所示:结合图形可得满足条件的函数图象应位于曲线x y a +=()a x a -≤≤的上方. ①中,,0x R y ∈>,满足||||x y a +≥,故①正确;②中,0,log a x y x R >=∈,满足||||x y a +≥,故②正确;③中的函数不满足条件,如0,4x πα==时,y =,不满足||||x y a +≥;④中,11x R y ∈-≤≤,满足||||x y a +≥,故④正确;故答案为①②④.考点:绝对值不等式的解法、对数函数的值域与最值、余弦函数的定义域和值域.10.把正整数排列成如图()a 的三角形数阵,然后擦去第偶数行中的所有奇数、第奇数行中的所有偶数,可得到如图()b 的三角形数阵,现将图()b 中的正整数按从小到大的顺序构成一个数列{}n a ,若2015k a =,则__________.k =1 1234 2 456789 5 7 9 10 11 12 13 14 15 16 10 12 14 16 17 18 19 20 21 22 23 24 25 17 19 21 23 25 26 27 28 29 30 31 32 33 34 35 36 26 28 30 32 34 36 ()a ()b 【答案】1030 【解析】试题分析:由题意,图a 中第n 行有21n -个数,前n 行有21212n n n +-⨯=个数,由于45452025⨯=,故2015是第45行的倒数第11个数,由图b 知各行数字个数等于行数,故前45行共有1454510352+⨯=, 由于最后一个数是奇数,按图b 规则知,2015是第45行倒数第6个数,故103551030k =-=. 考点:归纳推理.二、选择题(15分)本大题共有3题,每题都给出四个结论,其中有且只有一个结论是正确 的,必须把答题纸上相应题序内的正确结论代号涂黑,选对得5分,否则一律得零分. 11.下列命题中,正确的个数是……………………………………………………………【 】 (1)直线上有两个点到平面的距离相等,则这条直线和这个平面平行; (2)a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; (3)直四棱柱是直平行六面体;(4)两相邻侧面所成角相等的棱锥是正棱锥.A. 0B. 1C. 2D. 3 【答案】B 【解析】试题分析:①错误,如果这两个点在该平面的异侧,则直线与平面相交;②若,a b 是异面直线,则经过a 且与b 平行的平面有且仅有一个,根据异面直线的定义以及线面平行的判定定理可以判断②正确;③直四棱柱,它的底面不一定是平行四边形,故直四棱柱不一定是直平行六面体,故③错误;④,两相邻侧面所成角相等的棱锥不一定底面是正多边形,所以不一定是正棱锥,所以④错,综上得:四个命题中只有②正确. 考点:命题的真假.12.在极坐标系中,关于曲线:4sin 3C πρθ⎛⎫=- ⎪⎝⎭的下列判断中正确的是……………【 】A.曲线C 关于直线56πθ=对称B.曲线C 关于直线3πθ=对称 C.曲线C 关于点2,3π⎛⎫⎪⎝⎭对称 D.曲线C 关于极点()0,0对称 【答案】A 【解析】试题分析:曲线:4sin 3C πρθ⎛⎫=-⎪⎝⎭转化为直角坐标方程为:22(1)(4x y -+=,所以圆心坐标为(1,,转化为极坐标为11(2,)6π,过极点的对称轴为:y =,即56πθ=,所以A 正确. 考点:简单曲线的极坐标方程.13.已知O 是正三角形ABC 内部的一点,230OA OB OC ++=,则O A C ∆的面积与OAB ∆的面积之比是…………………………………………………………………………………【 】 A.32 B. 23C. 2D. 1 【答案】B 【解析】试题分析:∵230OA OB OC ++=,∴220OA OC OB OC +++=,如图,D 、E 分别是对应边的中点,由平行四边形法则知2OA OC OE +=,224OB OC OD +=,故2OE OD =,由于正三角形ABC ,故22113323AOC ADC ABC ABC S S S S ∆∆∆∆==⨯⨯=,又D 、E 是中点,所以O 到AB 的距离是正三角形ABC 高的一半,所以12AOB ABC S S ∆∆=⨯,∴OAC ∆的面积与OAB ∆的面积之比为23.考点:向量在几何中的应用、三角形中的几何计算、三角形五心.三、解答题(本题满分75分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤.14.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,AB 是圆柱体1OO 的一条母线,已知BC 过底面圆的圆心O ,D 是圆O 上不与点,B C 重合的任意一点,5AB =,5BC =,3CD =. (1)求直线AC 与平面ABD 所成角的大小;(2)将四面体ABCD 绕母线AB 旋转一周,求ACD ∆的三边在旋转过程中所围成的几何体的体积.【答案】(1);(2)15π. 【解析】试题分析:本题主要考查了直线与平面之间所成角、棱柱、棱锥、棱台的体积,考查空间想象能力、运算能力和推理论证能力. 第一问,欲求直线AC 与平面ABD 所成的角,先证出CD ⊥平面ABD ,从而得出CAD ∠为直线AC 与平面ABD 所成的角,最后在Rt ADC ∆中,求解即可;第二问,由题意可知,所求体积是两个圆锥体的体积之差,只须分别求出这两个锥体的体积后求它们的差即得.试题解析:(1)∵点D 以BC 为直径的圆上,∴BD DC ⊥,∵AB ⊥平面BDC ,DC ⊂平面BDC ,∴AB DC ⊥,∴CD ⊥平面ABD ,∴CAD ∠为直线AC 与平面ABD 所成的角,在Rt ADC ∆中,sin10CD CAD AC ∠===,∴arcsin 10CAD ∠=,即直线AC 与平面ABD 所成的角为arcsin10. (2)由题意可知,所求体积是两个圆锥体的体积之差,2211125805545153333ABC ABD V V V πππππ=-=∙∙-∙∙=-=圆锥圆锥,故所求体积为15π.考点:直线与平面所成的角、棱柱、棱锥、棱台的体积、平面与圆柱面的截线. 15.(本题满分13分,第(1)小题5分,第(2)小题8分)如图所示,某市拟在长为8km 道路OP 的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM ,该曲线段为函数()sin 0,0y A x A ωω=>>[]()0,4x ∈的图像,且图像的最高点为(3,S ,赛道的后一部分为折线段MNP ,且120MNP ∠=.(1)求M 、P 两点间的直线距离; (2)求折线段赛道MNP 长度的最大值.【答案】(1)5;(2. 【解析】试题分析:本题主要考查三角函数图象及其性质、两点间距离公式、正弦定理、三角函数的最值等基础知识,考查学生的分析问题解决问题的能力、读图能力、计算能力.第一问,利用最高点(3,S 得到A =S 的横坐标,得到134T =,得到ω,最后得到点(4,3)M ,(8,0)P ,利用两点间距离公式计算MP ;第二问,在MNP ∆中,利用正弦定理,将NP 和MN 用θ角表示,再将表达式化简,利用两角和的正弦公式化简,利用θ的取值范围求最值. 试题解析:解法一:(1)依题意,有A =……………………………………………1分又34T =, 而2T πω=, 6πω∴= ……………………………1分6y x π∴=当4x =时,233y π==,()4,3M ∴,又()8,0P5MP ∴= ………………………………………3分(2)在MNP ∆中,120MNP ∠=,5MP =.设PMN θ∠=,则060θ<<. ……………………………………1分 由正弦定理得()sin120sin sin 60MP NP MNθθ==-,3NP θ∴=,()603MN θ=-, ……………………………3分故()()10360sin 60333NP MN θθθ+=+-=+……3分 060θ<<,∴当30θ=时,折线段赛道MNP 最长. ……………………2分解法二 :(1)同解法一.(2)在MNP ∆中,120MNP ∠=, 5.MP =由余弦定理得2222MN NP MN NP COS MNP MP +-⋅⋅∠=, 即2225MN NP MN NP ++⋅=; …………………………3分故()22252MN NP MN NP MN NP +⎛⎫+-=≤ ⎪⎝⎭,从而()23254MN NP +≤…4分即MN NP +≤,当且仅当MN NP =时等号成立. ………………2分 亦即,设计为MN NP =时,折线段赛道MNP 最长.注:本题第(2)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方法,还可设计为:①N ⎝⎭;②N ⎝⎭;③点N 在线段MP 的垂直平分线上等.考点:三角函数图象及其性质、两点间距离公式、正弦定理、三角函数的最值. 16.(本题满分14分,第(1)小题5分,第(2)小题9分)已知圆()221:18C x y ++=,点()21,0C ,点Q 在圆1C 上运动,2QC 的垂直平分线交1QC 于点P .(1)求动点P 的轨迹W 方程;(2)过点10,3S ⎛⎫- ⎪⎝⎭且斜率为k 的动直线l 交曲线W 于,A B 两点,在y 轴上是否存在定点D ,使以AB 为直径的圆恒过这个点?若存在,请求出点D 的坐标;若不存在,请说明理由.【答案】(1)2212x y +=;(2)点D 的坐标为()0,1. 【解析】试题分析:本题主要考查椭圆的标准方程、定义及其几何性质、直线与椭圆的相交问题、向量的数量积等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由垂直平分线得2PQ PC =,计算出2112PC PC C C +>,利用椭圆的定义知点P 的轨迹为椭圆,从而得到椭圆的标准方程;第二问,将直线与椭圆方程联立,消参,利用韦达定理得12x x +、12x x ,假设存在定点D ,则由题意可得0DA DB ∙=恒成立,即得到221818096150m m m ⎧-=⎪⎨+-=⎪⎩,所以1m =,从而得到点D 的坐标. 试题解析:(1)2QC 的垂直平分线交1QC 于点P ,2PQ PC ∴=.………………1分2111122PC PC PQ PC QC C C +=+==>=,所以动点P 的轨迹W 是以点1C 、2C 为焦点的椭圆.…………………………2分设椭圆的标准方程为22221x y a b +=()0a b >>,则2a =,22c =,2221b a c =-=,故椭圆的标准方程为2212x y +=…………………………………………………………2分 (2)直线l的方程为13y kx =-,联立直线和椭圆的方程得221132y kx x y ⎧=-⎪⎪⎨+=⎪⎪⎩,即()2291212160k x kx +--=,易知点10,3S ⎛⎫- ⎪⎝⎭在椭圆内部,所以直线l 与椭圆必交于两点. (1)分设()()1122,,,A x y B x y ,则()()121222416,312912k x x x x k k +==-++,……………………2分假设在y 轴上存在定点()0,D m 满足题设,则()()1122,,,DA x y m DB x y m =-=-. 因为以AB 为直径的圆恒过点D ,则()()1122,,0DB x y DA m x y m ⋅=-⋅-=.……………………2分 即()()()12120*x x y m y m +--=,因为112211,33y kx y kx =-=-,所以(*)变为()()()12122121212121221213111333x x y m y m x x y y m y y m kx m kx kx x x kx m ⎛⎫⎛⎫+-⎛⎫=+--=+-++⋅---+-+ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭ ()()()()()2121222222189121133186199521m k m k x x k x m m x m m k +⎛⎫=+--+-+++++= ⎝⎭+⎪.………3分由假设得对于任意的k ∈R ,0DA DB ⋅=恒成立,即221818096150m m m ⎧-=⎪⎨+-=⎪⎩,解得1m =. 因此,在y轴上存在点D ,点D 的坐标为()0,1………………………………………………3分 考点:椭圆的标准方程、定义及其几何性质、直线与椭圆的相交问题、向量的数量积. 17.(本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)设函数()y f x =的定义域为D ,值域为A ,如果存在函数()x g t =,使得函数()y f g t =⎡⎤⎣⎦的值域仍是A ,那么称()x g t =是函数()y f x =的一个等值域变换.(1)判断下列函数()x g t =是不是函数()y f x =的一个等值域变换?说明你的理由;①()2log ,0f x x x =>,()1,0x g t t t t==+>; ②()21,f x x x x R =-+∈,()2,tx g t t R ==∈.(2)设函数()y f x =的定义域为D ,值域为A ,函数()g t 的定义域为1D ,值域为1A ,那么“1D A =”是否为“()x g t =是()y f x =的一个等值域变换”的一个必要条件?请说明理由;(3)设()2log f x x =的定义域为[]2,8x ∈,已知()2231mt t n x g t t -+==+是()y f x =的一个等值域变换,且函数()y f g t =⎡⎤⎣⎦的定义域为R ,求实数m n 、的值.【答案】(1)①不是,②是;(2)详见解析;;(3)55m n ⎧=⎪⎪⎨⎪=⎪⎩.【解析】试题分析:本题主要考查函数的值域、配方法、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,①2()log f x x =的值域为R ,而21(())log ()y f g t t t==+的值域为[1,)+∞,值域不相同,所以不是等值域变换;②2()1f x x x =-+利用配方法求值域为3,4⎡⎫+∞⎪⎢⎣⎭,而()2213(2)21224t tt f g t ⎛⎫=-+=-+⎡⎤ ⎪⎣⎦⎝⎭利用配方法求值域与前面()f x 的值域相同;第二问,通过举反例证明不必要性;第三问,通过()x g t =是()f x 的一个等值域变换,将题目转化为()x g t =的值域为[2,8],转化为恒成立问题,解出m 和n 的值.试题解析:(1)①不是……………………………………………………………………2分②()221331244f x x x x ⎛⎫=-+=-+≥ ⎪⎝⎭,即()f x 的值域为3,4⎡⎫+∞⎪⎢⎣⎭,当t ∈R 时,()21332244t f g t ⎛⎫=-+≥⎡⎤ ⎪⎣⎦⎝⎭,即()y f g t =⎡⎤⎣⎦的值域仍为3,4⎡⎫+∞⎪⎢⎣⎭,所以()x g t = 是()f x 的一个等值域变换.………………………………………………2分(2)不必要性的反例: ()[)2,,0,x x D B f ===∞+R ()()1121,,1,t g t D B =-==-+∞R此时1B D ⊂,但()()221tf g t =-⎡⎤⎣⎦的值域仍为[)0,B =+∞,即()()21t g t x =-∈R 是()()2f x x x =∈R 的一个等值域变换.(反例不唯一)………………3分 (3)()2log f x x =定义域为[]2,8,因为()x g t =是()f x 的一个等值域变换,且函数()f g t ⎡⎤⎣⎦的定义域为R ,所以()22,13t mt x g t t t n +==+-∈R 的值域为[]2,8,……………………2分()()22222328213811mt t n t mt t n t t -+≤≤⇔+≤-+≤++,……………………………………1分 所以,恒有()()()()12289422094880m m n m n ⎧<<⎪∆=---=⎨⎪∆=---=⎩,………………………………………………3分解得55m n ⎧=⎪⎪⎨⎪=+⎪⎩.……………………………………………………………………3分考点:函数的值域、配方法、恒成立问题.18.(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分) 我们把一系列向量()1,2,,i a i n =按次序排成一列,称之为向量列,记作{}n a ,已知向量列{}na 满足:()1,11=a ,()()11111,,2nn n n n n n ax y x y x y ----==-+()2n ≥. (1)证明:数列{}n a 是等比数列;(2)设2l o g n n n c a a =⋅,问数列{}n c 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由;(3)设n θ表示向量1n a -与n a 间的夹角,若2nn n b θπ=,对于任意正整数n ,不等式()11log 122a ab +>-恒成立,求实数a 的范围. 【答案】(1)证明详见解析;(2)数列{}n c 中存在最小项,最小项是325322c -=-⋅;(3)()1..【解析】试题分析:本题主要考查等比数列的定义、分组求和、数列的单调性等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,根据向量的模的计算公式列出||n a ,再化简,得到12n n a a -=,从而利用等比数列的定义,得数列{}na 是等比数列;第二问,先利用向量的夹角公式计算出n θ,代入到nb 中,再计算n S ,利用分组求和法计算结果;第三问,先利用向量的夹角公式,先求出n θ代入n b 2n=,利用数列{}n T 的单调性,求出222122n n n +++++的最小值,即转化为()31log 1212a -<,解出a 的取值范围. 试题解析:(1)()()22221122n n a x y x y x y a -=-++=+= ∴数列{}n a 是等比数列 ………………………………………………3分(2)12222n nn a --⎛== ⎭, 22222nn n c --∴=⋅ ………………2分 假设 {}n c 中的第 n 项最小,由 1c =,20c =,210.c c ∴≤< 当3n ≥时,有0n c <,又由1n n c c +≤可得()()212222122222n nn n -+--+-⋅≤⋅,即12221n n --≥-,22112nn -⎛⎫≥ ⎪-⎝⎭. 2670n n -+≥,3n ≥3n ≤,5n ∴≥.…………2分即有567c c c <<<;由1n n c c +≥,得35n ≤≤,又210c c ≤<,541c c c ∴<<<;………………2分故数列{}n c 中存在最小项,最小项是325322c -=-⋅………………………………1分(3)112cos n n n n na a a a θ--⋅==⋅, 4n πθ∴=…………1分24n n b ∴=……………………………………1分不等式化为:()32221log 121222a n n n +++>-++对任意正整数n 恒成立.设222122n T n n n=++++. 又()122222021*******n n T T n n n n n +-=+-=->+++++, 数列{}n T 单调递增……………………………………………………2分()1min 1n T T ∴==,要使不等式恒成立,只要()311log 122a >-,……1分120a ->, 102a ∴<<,212a a-> ,01a ∴<< 所以,使不等式对于任意正整数恒成立的a 的取值范围是()1.…………2分 考点:等比数列的定义、分组求和、数列的单调性.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海市闸北区2015年高三第二学期期中练习数学(理科)试卷考生注意:1. 本次测试有试题纸和答题纸,解答必须在答题纸上,写在试题纸上的解答无效.2. 答卷前,考生务必在答题纸上将姓名、学校、考试号,以及试卷类型等填写清楚,并在规定区域内贴上条形码.3. 本试卷共有18道试题,满分150分.考试时间120分钟.一、填空题(60分)本大题共有10题,要求在答题纸相应题序的空格内直接填写结果,每个空格填对得6分,否则一律得零分.1. 设幂函数()f x 的图像经过点()8,4,则函数()f x 的奇偶性为____________.2. 设复数122,12z i z i =+=+,在复平面的对应的向量分别为,OA OB ,则向量AB对应的复数所对应的点的坐标为____________.3. 已知定义域为R 的函数()y f x =的图像关于点()1,0-对称,()y g x =是()y f x =的反函数,若120x x +=,则()()12g x g x +=___________.4. 一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c ,其中,,(0,1)a b c ∈.已知投篮一次得分的期望是2,则ab 的最大值是____________.5. 设⎪⎩⎪⎨⎧∈≥∈≤≤=-.N ,3,31,N ,21,21n n n n a n n n 数列{}n a 的前n 项和为n S ,则=∞→n n S lim ___________.6. 设函数⎩⎨⎧<+≥+-=.0,4,0,66)(2x x x x x x f 若存在互不相等的实数123,,x x x 满足123()()()f x f x f x ==,则123x x x ++的取值范围是_____________.7.若二项式nx ⎛⎝展开式中只有第四项的系数最大,则这个展开式中任取一项为有理项的概率是____________.8. 从双曲线()222210,0x y a b a b-=>>的左焦点F 引圆222x y a +=的切线,切点为T ,延长FT 交双曲线右支于点P ,若M 是线段FP 的中点,O 为坐标原点,则MO MT -的值是____________. 9. 已知集合(){},,U x y x R y R =∈∈,(){},M x y x y a =+<,()(){},P x y y f x ==,现给出下列函数:①a y x -=;②log a y x = ;③()sin y x a =+;④cos y ax =.若01a <<时,恒有U P C M P = ,则所有满足条件的函数()f x 的编号是___________.10. 把正整数排列成如图()a 的三角形数阵,然后擦去第偶数行中的所有奇数、第奇数行中的所有偶数,可得到如图()b 的三角形数阵,现将图()b 中的正整数按从小到大的顺序构成一个数列{}n a ,若2015k a =,则__________.k =1 12 3 4 2 4 5 6 7 8 9 5 7 9 10 11 12 13 14 15 16 10 12 14 16 17 18 19 20 21 22 23 24 25 17 19 21 23 25 26 27 28 29 30 31 32 33 34 35 36 26 28 30 32 34 36 ()a ()b二、选择题(15分)本大题共有3题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把答题纸上相应题序内的正确结论代号涂黑,选对得5分,否则一律得零分. 11. 下列命题中,正确的个数是……………………………………………………………【 】(1) 直线上有两个点到平面的距离相等,则这条直线和这个平面平行; (2) a 、b 为异面直线,则过a 且与b 平行的平面有且仅有一个; (3) 直四棱柱是直平行六面体;(4) 两相邻侧面所成角相等的棱锥是正棱锥.A 、0B 、1C 、2D 、3 12. 在极坐标系中,关于曲线:4sin 3C πρθ⎛⎫=-⎪⎝⎭的下列判断中正确的是……………【 】 A 、曲线C 关于直线56πθ=对称 B 、曲线C 关于直线3πθ=对称 C 、曲线C 关于点2,3π⎛⎫⎪⎝⎭对称 D 、曲线C 关于极点()0,0对称13. 已知O 是正三角形ABC 内部的一点,230OA OB OC ++=,则OAC ∆的面积与OAB ∆的面积之比是…………………………………………………………………………………【 】 A 、32 B 、23C 、2D 、 三、解答题(本题满分75分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤.14. (本题满分12分,第(1)小题5分,第(2)小题7分)如图,AB 是圆柱体1OO 的一条母线,已知BC 过底面圆的圆心O , D 是圆O 上不与点,B C 重合的任意一点,5AB =,5BC =,3CD =.(1)求直线AC 与平面ABD 所成角的大小;(2)将四面体ABCD 绕母线AB 旋转一周,求ACD ∆的三边在旋 转过程中所围成的几何体的体积.15. (本题满分13分,第(1)小题5分,第(2)小题8分)如图所示,某市拟在长为8km 道路OP 的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM ,该曲线段为函数()sin 0,0y A x A ωω=>>[]()0,4x ∈的图像,且图像的最高点为(3,S ,赛道的后一部分为折线段MNP ,且120MNP ∠= .(1)求M 、P 两点间的直线距离;(2)求折线段赛道MNP 长度的最大值.16. (本题满分14分,第(1)小题5分,第(2)小题9分)已知圆()221:18C x y ++=,点()21,0C ,点Q 在圆1C 上运动,2QC 的垂直平分线交1QC 于点P .(1)求动点P 的轨迹W 方程;(2)过点10,3S ⎛⎫- ⎪⎝⎭且斜率为k 的动直线交曲线W 于,A B 两点,在y 轴上是否存在定点D ,使以AB 为直径的圆恒过这个点?若存在,请求出点D 的坐标;若不存在,请说明理由.17. (本题满分18分,第(1)小题4分,第(2)小题5分,第(3)小题9分)设函数()y f x =的定义域为D ,值域为A ,如果存在函数()x g t =,使得函数()y f g t =⎡⎤⎣⎦的值域仍是A ,那么称()x g t =是函数()y f x =的一个等值域变换.(1)判断下列函数()x g t =是不是函数()y f x =的一个等值域变换?说明你的理由;① ()2log ,0f x x x =>,()1,0x g t t t t==+>; ② ()21,f x x x x R =-+∈,()2,tx g t t R ==∈.(2)设函数()y f x =的定义域为D ,值域为A ,函数()g t 的定义域为1D ,值域为1A ,那么“1D A =”是否为“()x g t =是()y f x =的一个等值域变换”的一个必要条件?请说明理由;(3)设()2log f x x =的定义域为[]2,8x ∈,已知()2231mt t n x g t t -+==+是()y f x =的一个等值域变换,且函数()y f g t =⎡⎤⎣⎦的定义域为R ,求实数m n 、的值.18. (本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)我们把一系列向量()1,2,,i a i n = 按次序排成一列,称之为向量列,记作{}n a,已知向量列{}n a 满足:()1,11=a ,()()11111,,2n n n n n n n a x y x y x y ----==-+ ()2n ≥.(1)证明:数列{}n a是等比数列;(2)设2log n n n c a a =⋅,问数列{}n c 中是否存在最小项?若存在,求出最小项;若不存在,请说明理由;(3)设n θ表示向量1n a - 与n a 间的夹角,若2n nn b θπ=,对于任意正整数n ,不等式()1log 122a a +++>- 恒成立,求实数a 的范围.理科答案一. 填空题1、偶函数;2、()1,1-3、2-4、165、55186、()1,6-7、478、b a - 9、①②④ 10、1030 二. 选择题11、B 12、A 13、B 三.解答题 14、(1) ………………………………………………………5分 (2)15π ………………………………………………………………7分15、解(1)依题意,有A = …………………………………………1分 又34T =, 而2T πω=, 6πω∴= ………………………1分6y x π∴=当4x =时,233y π==,()4,3M ∴,又()8,0P5MP ∴== ………………………………………3分(2)解:法一:在MNP ∆中,120MNP ∠= ,5MP =.设PMN θ∠=,则060θ<< .……………………………………1分由正弦定理得()sin120sin sin 60MP NP MNθθ==-,NP θ∴=,()60MN θ=- ,……………………………………………………3分故())6060NP MN θθ+=+-=+ ……3分060θ<< ,∴当30θ= 时,折线段赛道MNP ……………2分 解法二 : (2)在MNP ∆中,120MNP ∠= , 5.MP = 由余弦定理得2222MN NP MN NP COS MNP MP +-⋅⋅∠=,即2225MN NP MN NP ++⋅=;…………………………3分故()22252MN NP MN NP MN NP +⎛⎫+-=≤ ⎪⎝⎭,从而()23254MN NP +≤…4分即MN NP +≤MN NP =时等号成立.………………2分亦即,设计为MN NP =时,折线段赛道MNP最长为3310.注:本题第(2)问答案及其呈现方式均不唯一,除了解法一、解法二给出的两种设计方法,还可设计为:①N ;②N;③点N 在线段MP 的垂直平分线上等.16、(1)2QC 的垂直平分线交1QC 于点P ,2PQ PC ∴=.………………1分211122PC PC PQ PC QC C +=+===,所以动点P 的轨迹W 是以点1C 、2C 为焦点的椭圆.…………………………2分设椭圆的标准方程为22221x y a b +=()0a b >>,则2a =,22c =,2221b a c =-=,故椭圆的标准方程为2212x y +=…………………………………………………………2分 (2) 直线l 的方程为13y kx =-,联立直线和椭圆的方程得221132y kx xy ⎧=-⎪⎪⎨+=⎪⎪⎩,即 ()2291212160k x kx +--=,易知点10,3S ⎛⎫- ⎪⎝⎭在椭圆内部,所以直线l 与椭圆必交于两点. …1分设()()1122,,,A x y B x y ,则()()121222416,312912k x x x x k k +==-++,……………………2分 假设在y 轴上存在定点()0,D m 满足题设,则()()1122,,,DA x y m DB x y m =-=-. 因为以AB 为直径的圆恒过点D ,则()()1122,,0DB x y DA m x y m ⋅=-⋅-= .……………………2分 即()()()12120*x x y m y m +--=,因为112211,33y kx y kx =-=-,所以(*)变为()()()12122121212121221213111333x x y m y m x x y y m y y m kx m kx kx x x kx m ⎛⎫⎛⎫+-⎛⎫=+--=+-++⋅---+-+ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭()()()()()2121222222189121133186199521m k m k x x k x m m x m m k +⎛⎫=+--+-+++++=⎝⎭+⎪.………3分 由假设得对于任意的k ∈R ,0DA DB ⋅= 恒成立,即221818096150m m m ⎧-=⎪⎨+-=⎪⎩,解得1m =. 因此,在y 轴上存在点D ,点D 的坐标为()0,1………………………………………………3分17、(1)①不是……………………………………………………………………2分②()221331244f x x x x ⎛⎫=-+=-+≥ ⎪⎝⎭,即()f x 的值域为3,4⎡⎫+∞⎪⎢⎣⎭,当t ∈R 时,()21332244t f g t ⎛⎫=-+≥⎡⎤ ⎪⎣⎦⎝⎭,即()y f g t =⎡⎤⎣⎦的值域仍为3,4⎡⎫+∞⎪⎢⎣⎭,所以()x g t = 是()f x 的一个等值域变换.………………………………………………2分(2)不必要性的反例: ()[)2,,0,x x D B f ===∞+R ()()1121,,1,t g t D B =-==-+∞R此时1B D ⊂,但()()221tf g t =-⎡⎤⎣⎦的值域仍为[)0,B =+∞,即()()21t g t x =-∈R 是()()2f x x x =∈R 的一个等值域变换.(反例不唯一)………………3分 (3)()2log f x x =定义域为[]2,8,因为()x g t =是()f x 的一个等值域变换,且函数()f g t ⎡⎤⎣⎦的定义域为R ,所以()22,13t mt x g t t t n+==+-∈R 的值域为[]2,8,……………………2分()()22222328213811mt t n t mt t n t t -+≤≤⇔+≤-+≤++,……………………………………1分 所以,恒有()()()()12289422094880m m n m n ⎧<<⎪∆=---=⎨⎪∆=---=⎩,………………………………………………3分解得55m n ⎧=⎪⎪⎨⎪=⎪⎩.……………………………………………………………………3分18、(==∴数列{}n a 是等比数列………………………………………………3分(21222nn--=,22222nnnc--∴=⋅………………2分假设{}nc中的第n项最小,由1c=,2c=,210.c c∴≤<当3n≥时,有0nc<,又由1n nc c+≤可得()()212222122222nn nn-+--+-⋅≤⋅,即12221nn--≥-,22112nn-⎛⎫≥⎪-⎝⎭.2670n n-+≥,3n≥+或3n≤(舍),5n∴≥.…………2分即有567c c c<<< ;由1n nc c+≥,得35n≤≤,又210c c≤<,541c c c∴<<<;………………2分故数列{}n c中存在最小项,最小项是325322c-=-⋅………………………………1分(3) 11cos n nnn na aa aθ--⋅==⋅4nπθ∴=……………………………………1分24nnb∴=………………………………………………………………1分不等式化为:()32221log121222an n n+++>-++对任意正整数n恒成立.设222122nTn n n=++++.又 ()122222212112122n nT Tn n n n n+-=+-=->+++++,数列{}n T单调递增……………………………………………………2分()1min1nT T∴==,要使不等式恒成立,只要()311log122a>-,……1分120a->,12a∴<<,212a a->,01a∴<<-所以,使不等式对于任意正整数恒成立的a的取值范围是()1.…………2分。
