公差模型和公差分析方法的研究
统计公差分析方法概述

统计公差分析方法概述公差分析是设计和制造过程中的重要环节,用于评估产品的尺寸和形状的变化并确定其质量要求。
它帮助确定制造过程中允许的变化范围,以确保产品的功能和性能满足设计要求。
下面是公差分析方法的概述:1.公差概念和术语:公差是表示产品尺寸和形状变异的一种度量,是设计要求和制造能力之间的差异。
了解公差的基本概念和术语对于进行有效的公差分析非常重要。
例如,公差带、公差上限、公差下限、公差等级等。
2.公差链:公差链是将不同部件的公差延伸到整个产品装配中的一种方法。
通过分析公差链,可以确定整个装配的总体公差,并评估其对产品性能的影响。
公差链分析通常采用功能环或冗余环的方法。
3.公差配合:公差配合是指零件之间在装配时的相互作用。
公差配合分析可以确定零件之间的配合方式,并对其作用进行评估。
常见的公差配合包括配合间隙、过盈配合和间隙配合等。
4. 公差分析工具:公差分析通常使用一些专门的工具来辅助。
例如,一维公差分析工具(如Matlab、Excel等)用于分析单个尺寸的公差,根据统计数据计算出尺寸的上下限。
使用二维和三维CAD软件进行公差堆叠分析,可以在装配设计阶段模拟零件堆叠时产生的误差变化。
5.公差分配:公差分配是将总体公差分配给不同的零件以实现装配要求的过程。
公差分配通常基于设计要求、制造能力和装配要求等考虑因素。
公差分配需要根据装配关系和功能要求来确定每个零件的公差。
6.公差检验:公差分析的最后一步是进行公差检验,以确保产品的尺寸和形状在规定的公差范围内。
公差检验可以通过测量和检测工具来进行,例如卡尺、测量仪器、投影仪等。
公差检验是确保产品质量和性能的关键步骤。
7.公差优化:公差优化是指通过优化公差的分配和设计来最小化产品的尺寸和形状变化,以提高产品的质量和性能。
公差优化可以通过使用计算机辅助设计(CAD)软件和专业的公差优化工具来实现。
总之,公差分析是设计和制造中的关键环节,有助于确保产品质量和性能满足要求。
公差分析

分析目的
分析目的
公差分析目的公差分析作为面向制造和装配的产品设计中非常有用的工具,可以帮助机械工程师实现以下目 的:
1)合理设定零件的公差以减少零件的制造成本。
2)判断零件的可装配性,判断零件是否在装配过程中发生干涉。 3)判断零件装配后产品关键尺寸是否满足外观、质量以及功能等要求。 4)优化产品的设计,这是公差分析非常重要的一个目的。当通过公差分析发现产品设计不满足要求时,一般 有两种方法来解决问题。其一是通过精密的零件公差来达到要求,但这会增加零件的制造成本;其二是通过优化 产品的设计(例如,增加装配定位特征)来满足产品设计要求,这是最好的方法,也是公差分析的意义所在。
5)公差分析除了用于产品设计中,还可用于产品装配完成后,当产品的装配尺寸不符合要求时,可以通过公 差分析来分析制造和装配过程中出现的问题,寻找问题的根本原因。
分析步骤
分析步骤
公差分析具体的步骤包括: 1)定义公差分析的目标尺寸和判断标准。 2)定义尺寸链。 3)判断尺寸的正负。 4)将非双向对称公差转化为双向对称公差。 5)公差分析的计算。 6)判断和优化。
计算模型
计算模型
常用的公差分析的计算模型有两种,一是极值法,二是均方根法。 1)极值法 极值法是考虑零件尺寸最不利的情况,通过尺寸链中尺寸的最大值或最小值来计算目标尺寸的值。 2)均方根法 均方根法是统计分析法的一种,顾名思义,均方根法是把尺寸链中的各个尺寸公差的平方之和再开根即得到 目标尺寸的公差。
谢谢观看
公差分析
定义和分配零件和产品的公差
01 分析目的
03 计算模型
目录
02 分析步骤
基本信息
公差分析是指在满足品功能、性能、外观和可装配性等要求的前提下,合理地定义和分配零件和产品的公 差,优化产品设计,从而以最小的成本和最高的质量制造产品。公差分析是面向制造和装配的产品设计中非常重 要的一个环节,对于降低产品成本、提高产品质量具有重大影响。
统计公差分析方法概述
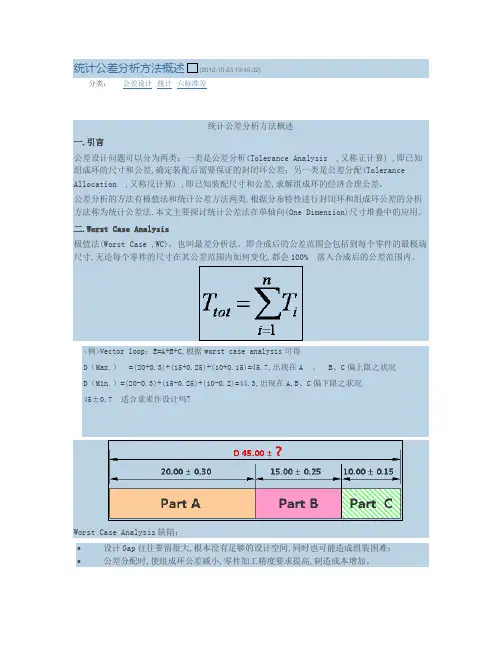
统计公差分析方法概述(2012-10-23 19:45:32)分类:公差设计统计六标准差统计公差分析方法概述一.引言公差设计问题可以分为两类:一类是公差分析(Tolerance Analysis ,又称正计算) ,即已知组成环的尺寸和公差,确定装配后需要保证的封闭环公差;另一类是公差分配(Tolerance Allocation ,又称反计算) ,即已知装配尺寸和公差,求解组成环的经济合理公差。
公差分析的方法有极值法和统计公差方法两类,根据分布特性进行封闭环和组成环公差的分析方法称为统计公差法.本文主要探讨统计公差法在单轴向(One Dimension)尺寸堆叠中的应用。
二.Worst Case Analysis极值法(Worst Case ,WC),也叫最差分析法,即合成后的公差范围会包括到每个零件的最极端尺寸,无论每个零件的尺寸在其公差范围内如何变化,都会100% 落入合成后的公差范围内。
<例>Vector loop:E=A+B+C,根据worst case analysis可得D(Max.)=(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A、B、C偏上限之状况D(Min.)=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况45±0.7适合拿来作设计吗?Worst Case Analysis缺陷:•设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难;•公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。
以上例Part A +Part B+ Part C,假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平,则每个部材的不良机率为1-0.9973=0.0027;在组装完毕后所有零件都有缺陷的机率为:0.0027^3=0.000000019683。
这表明几个或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。
球面滚子R位置公差分析及检测方法探讨

的。下 面 就 以对 称 滚 子
产品图
d ( h ・、 = 一 /
)。 :。4() (. . m 一5 0 tm ) 0
为例 ,对球面滚子 尺位置的测量方法进行分析讨论 。
根据大量规格滚子的计算 ,结合生产 实际 ,拟制了 球面滚子成品的 弦高公差 ,滚 子尺 寸  ̄ 0 m以下 弦高 3m 公差为 0~+ .0 m,滚子尺寸 + 0 m 以上弦高为 0 0 35m 3m + .0 00 1一 +00 5 m . 0 m。使用 球 面滚 子 半径 尺 检查 仪
图 3 用要求滚子对仪表 图4 测量滚子 R弦高
为 D 5 ,本仪器是 比较 法机 械测 量仪 器 ,主要 用于 钢 01 球 、滚子直径 、圆度 误 差 的测量 ,D 5 0 1测量 最 大直 径
使用中操作不合理 ,滚子外径 尺位 置公差往往超过工艺
要求 ,因为在外 径 曲率 合格 的 条件 下 ,R位置 有公
滚子的测量长度 £ 等于 减去稍大于两倍滚子两端
倒角 ,以便 于测量点大于倒角进行测量 ,取 L = 2X , L一
3= 5— 3 ( m) 2=1. ( m) 4 6= 9 m ,L/ 95 m
所 以
日数值控制在图样要求 的
公差 h=±0 0 m 范 围 .5 m 内,就是球面滚子 位置
这种测量方法也适用于不对称滚 子 ,即将 不对称滚
子取对称的测 量点 即可 应用该 测量 方法 。当 日有一 个 △ 变化量时 ,R圆弧 的平移会引起滚子 的两端处直径发 生变化 ,一端 直径增大而另一端 直径 减小 。因此 ,控制
R4 , 只要求滚子对仪表 ( 图 3 是用要求 滚子对 33 用 见 ) 仪表 ,图 4是测量滚子 尺弦高 。
公差数据处理与分析技巧

公差数据处理与分析技巧公差数据处理与分析技巧公差是指在制造过程中,由于各种原因造成的产品尺寸、形状、位置等方面的偏差。
准确地处理和分析公差数据对于确保产品质量和满足设计要求至关重要。
下面将介绍一些公差数据处理与分析的技巧。
首先,对于公差数据的处理,我们需要进行数据的收集和整理。
在制造过程中,我们需要收集每个产品的测量数据,包括尺寸、形状、位置等方面的数据。
这些数据需要按照一定的规范进行整理和记录,以便后续的分析和处理。
其次,我们需要对公差数据进行统计和分析。
统计分析能够帮助我们了解产品的制造过程中存在的问题,并找到解决问题的方法。
常用的统计分析方法包括均值、标准差、概率分布等。
通过对公差数据的统计分析,我们可以了解产品的尺寸偏差的分布情况,以及存在的异常情况。
此外,我们还需要进行公差数据的可视化处理。
可视化处理可以帮助我们更直观地了解公差数据的分布情况和变化趋势。
常用的可视化处理方法包括绘制直方图、散点图、箱线图等。
通过对公差数据的可视化处理,我们可以更加清楚地了解产品的尺寸偏差的分布情况,以及存在的异常情况。
最后,我们需要对公差数据进行合理的解释和应用。
在处理和分析公差数据的过程中,我们需要根据产品的设计要求和使用环境,对公差数据进行合理的解释。
通过合理解释公差数据,我们可以为产品的制造过程提供合理的指导和改进措施。
综上所述,公差数据处理与分析技巧对于确保产品质量和满足设计要求至关重要。
通过对公差数据的收集、整理、统计、分析和可视化处理,我们可以更好地了解产品的尺寸偏差情况,为产品的制造过程提供合理的指导和改进措施。
公差数据处理与分析技巧不仅可以提高产品的质量,还可以提高制造效率,降低成本,提升企业的竞争力。
公差分析的方法与比较

公差分析的方法與比較PSBU-RDD4-MDD 工程師朱誠璞 alex.chu@2002/11/14 PM 04:32 version 1.1A.公差分析的傳統方法( I)----Worst Case 法首先,必須解釋在公差分析時所用的兩種方法: 公差合成與公差分配.而在以下兩個例子中用來運算公差範圍的數學方法為 Worst Case 法,這是傳統的做法 :1.公差的合成(使用Worst Case 法運算)Part A 與 Part B 必須接合在一起,合成後的尺寸與公差範圍會是如何呢?在這個例子中,可以得到一個很直觀的結果------當Part A 與 Part B相接後所得到的 Part A+B 長度和公差範圍都是Part A + Part B 的結果.也就是說:合成後的公差範圍會包括到每個零件的最極端尺寸,無論每個零件的尺寸在其公差範圍內如何變化,都會 100% 落入合成後的公差範圍內.聽起來相當合理,不是嗎?稍後會解釋這樣做的缺點.2.公差的分配(使用Worst Case 法運算)現在 Part A+B 必須放入 Part C 的開口處,而開口的尺寸與公差如圖所示,那麼 Part A 與 B 的分別的公差範圍又應該是多少呢?我們以最簡單的方法 : 平均分配給其中所有的零件,所以 Part A 與 B 各得50 %,當然也可以按照其他的比例來調整,並沒有絕對的優劣之分.B. Worst Case法的問題1.控制公差範圍難以被控制在設計的需求範圍中.由於 Worst Case 法合成時要求100 % 的可以容許單一零件的公差變化,會造成合成後的公差範圍變的較大,對設計者而言,是非常容易造成零件組裝後相互干涉或間隙過大.在以上的例子中,如果要將 Part A+B 放入 Part C 時,會發生過緊干涉的情況,因為 Part C 最窄只有 10.75 mm,但是 Part A+B 卻可能有 11.50 mm的情況則有 0.75 mm 的干涉;另一方面,當 Part C 最寬11.25 mm,而 Part A+B 為10.5 mm 的最小值時,又有 0.75 mm的間隙產生.由此可知公差範圍過大所造成的難以控制的缺點.2.決定公差範圍的過程缺乏客觀及合邏輯的程序以此類方式決定的公差範圍尺寸,必須仰賴設計者的經驗,且必須經過多次的試作才可真正決定;若生產條件改變:如更換生產廠商,模具修改…等,皆有可能使原訂之公差範圍無法達成,而被迫放寬或產生大量不良品的損失.3.公差範圍與產品生產的品質水準無關對生產者而言,公差範圍越大越容易生產,同時品質要求也較低;但對設計者而言,公差範圍給定越大,品質水準低,則越難達成功能上的需求;由於此種矛盾的情況無法以此方式解決,造成設計者與生產者的衝突.C.其他的公差分析方法 ---基礎知識由於上述的缺點,使得Worst Case法只能被視為一種粗略的近似方法;以下將介紹兩種較接近真實世界的公差分析方法,但是,我們必須先有一些基礎知識才能瞭解這些方法的運作方式.1.何謂不可調整的公差範圍?在做任何的公差分析前,必須清楚的定義哪些是可由設計者調整的,而哪些又不是;在這裡,我們認為只有兩種是不可以被更改的:a.機械上的製造公差範圍:例如各種工具機的精度不同,如果以CNC加工的精度來要求鈑金零件,則勢必吃力不討好.b.客戶或規範上要求的公差範圍例如1U rack mount 機殼的高度,ATX主機板的孔位;特別是有相容性問題發生時.2.何謂常態分佈曲線?我們以一個簡單的例子說明:在一群人中身高與人數的分佈情況.簡單的說,就是中等身材的人應該最多,很高或很矮的人很少;在統計學中會利用這條曲線來模擬真實的情況並藉此進行下一步的分析,當我們在對於工廠所生產出來的一批產品,測量相同的一個尺寸,我們也會得到類似的分佈曲線;例如量測1000件長度為10mm的零件,正常狀況下一定會得到長度為10 mm的零件數目最多;而長度是20 mm或 1 mm 的零件出現的機會應該是微乎其微.在數學定義上,只要知道兩個條件就可以畫出這條曲線,如圖所示:在未來的討論中我們會利用下面的兩項特性進行分析:a.中間值 µ :曲線的對稱軸的位置,這決定了整條曲線的位置b.標準差σ :由中間值到曲線的曲率正負號改變點的距離,這決定了曲線的分散或集中程度.這些特性的來源,其實就是在微積分中,以此曲線的方程式求導數為0所得的解(參照附錄A的說明),有興趣的人可以到這個網頁進一步了解: /CE597N/1997F/students/michael.a.kropins ki.1/project/tutorial3.何謂 “6-σ” ?在我們運用常態分佈曲線來模擬並分析真實的情況時,如果我們加入上限及下限,且運用於品質管制的領域時,而被提出的一種品質水準的規範: “在一批生產出來的產品中,如其允收上限與下限的範圍是其常態分佈曲線σ的6倍,則可確保有 99.9999998 % 的產品是合格的.” 此種方式稱為 6-σ的品質水準要求,如下圖,這是一個簡單的表示方法 :D. 傳統的公差分析方法 ( II )---統計公差分析法我們一樣使用合成與分配的兩個例子來解釋:1.合成:我們一樣用前面所提的例子來看,現在實際上我們要做的是如何疊加這兩條曲線:毫無疑問的,疊加以後,我們還是會得到一條類似的曲線,但是疊加後的上下限應該在那裡??由常態分佈曲線的數學特性(參照附錄A的說明),我們有一個很方便的數學式:Tasm = √(T12+ T22+ T32+ T42+…….) T 代表上限或下限的公差, 所以結果是 :Tasm = √( 0.22+0.32) = 0.36055128... ~ 0.361我們可以知道合成後的情況應該是: 11+/- 0.361 mm.2.分配:同樣道理,用於分配時,可以得到的結果之一:Tasm = 0.25 = √(T12+ T22) Æ T1 = T2= 0.176776695…~ 0.177 也就是說: Part A = 5 +/- 0.177Part B =6 +/- 0.177E.比較兩種傳統公差分析的問題與改善方法:首先我們比較 Worst case 與統計公差法所得的結果:第一,我們可以看出公差合成後所得的公差範圍明顯縮小了,對設計者而言,較小的公差範圍意味著較準確的組裝與配合,所以累積下來的誤差也會減少,可以得到較佳的設計.第二,在公差分配的情況時,每個零件所得到的公差範圍變大了,對製造者而言,較大的公差範圍意味著較容易製作及控制生產品質,十分有利於製造者.所以,統計公差法顯然優於 Worst Case 法,但是是否完全解決了問題呢?答案是“ NO “,統計公差仍然會發生相同的問題,由其是在疊加或分析的零件很多時,請參照附錄C所提的例子,我們依舊需要進行Try and Error 的過程,以求得設計和製造上的平衡點;在這篇文章中利用加入 weight factor的方法修改原有公差以其放大或縮小原有公差範圍來達成設計及製造的需求.另一方面,統計公差法,仍然無法與實際生產的品質有任何關聯,所以仍舊會發生,同樣的公差範圍下,甲廠商可以達成,乙廠商卻叫苦連天的情況.F.新的公差分析方法( I )---加入 6-σ概念的統計公差分析法為了修正上一節所提到的問題,我們導入 6-σ品質水準的概念進入公差分析的過程中,這樣可以取得一個在理論(設計者)與實際(生產者)都可接受的一個平衡點.首先我們必須加入一個條件: 就是生產者的品質水準是滿足 6-σ的要求.(如果不滿足就不行嗎?當然不是,我們會在後面再檢討這個條件.)1.合成:仍舊是最早的例子,但是現在應該是這樣的分佈狀況,以滿足剛剛的加入條件:由上圖,可以得知 : T1= 0.2 = 6σ1 Æσ1 =0.2/6 =0.03333…~0.03333T2=0.3 =6σ2 Æσ2 = 0.3/6 = 0.05為什麼要求個別零件的σ值呢? 因為對於一個疊加後的常態分佈曲線而言,它的σ值與個別零件的σ值正好有以下的關係(參照附錄A的說明):σasm = √(σ12+σ22+σ32+σ42+….)所以我們可以得到合成後的σ值:σasm =√( 0.033332 + 0.052) = 0.06007….~0.06007請注意,合成後的依然要遵守6-σ品質水準的概念,所以:Tasm = 6σasm = 6 x 0.06007 = 0.36042合成後的情況應該是: 11+/- 0.36042 mm.2.分配:同樣的方法,公差分配時,得到的結果:Tasm = 0.25 = 6σasmσasm =0.041666~0.04167 =√(σ12+σ22) Æσ1 =σ2= 0.02946… ~ 0.0295T1=T2= 6 x 0.0295 = 0.177也就是說: Part A = 5 +/- 0.177Part B =6 +/- 0.177G..兩種統計公差方法的比較:我們會馬上發現兩種方法的結果是完全相同的!也就是說在使用統計方式計算的公差範圍是事實上,就是完全要求生產者的品質水準是符合 6-σ的結果,那麼使用新方法又有什麼優點呢?其實在工廠端要求的品質水準並非完全都是要到 6-σ如此之高的地步,以Sun Microsystem 為例,在模具驗收時,成品的製程水準至少需要Cpk = 1.33,也就是說大約是 4-σ ,( 我們會在下一節中解釋 Cpk的意義,以及對我們的影響)而使用新方法,設計者可以自由的調整所需要的品質水準,並且反映到公差範圍之中,而達到一個生產者與設計者都可以接受的平衡點,以下就是調整過的例子:生產 part A 的廠商有 4-σ的品質水準,所以:T1= 0.2 = 4σ1 Æσ1 =0.2/4 =0.05生產 part B 的廠商仍為 6-σ的品質水準,所以:T2=0.3 =6σ2 Æσ2 = 0.3/6 = 0.05所以我們可以得到合成後的σ值:σasm =√( 0.052 + 0.052) = 0.0707…~0.0707組裝時的品質水準要達到 6-σ :Tasm = 6σasm = 6 x 0.0707= 0.4242所以合成後的設計尺寸與公差應為: 11 +/- 0.4242在這裡隱藏了一個很重要的觀念: 以統計和 6-σ的方法應用於公差範圍的決定,可使設計者( RD ) 與品管 (QC) 使用相同的標準與語言去解決生產的問題,以上面的例子而言,當生產 part A 的廠商只有4-σ的生產水準時, σ值會變大則組裝後的公差範圍就應隨之變大;反過來說,當廠商生產品質高時, σ值會變小,我們就會獲得組裝後較小的公差變化範圍,這與品管人員的努力方向是一致的,且設計者也可以確知自己的設計是否會過嚴苛或過於寬鬆.此外使用此種方式具有相當大的彈性,可以針對不同的品質要求,而有不同的結果,而且一切都有理可循,不必完全倚靠經驗.H.新的公差分析方法( I )---完整的 6-σ公差分析法在前面所舉的例子中,我們所用的都是完美的常態分佈曲線,但是實際生產時我們所面對的卻不見得是如此理想的狀況:也就是說,分佈曲線的中心與設計者所定的中心存在一個偏移量 K,在這種狀況下我們要計算σ值,就必須藉由 Cp 和 Cpk (製程能力指標)來做轉換:Cp的定義:Cpk的定義:一般實務上,品管人員都會掌握Cp或 Cpk 值的變化,藉以評估生產的品質差異,所以在取得實際生產的品質資料時,得到Cp和 Cpk 值的機會較大且符合真正的情況.在這裡留個小小的問題: Cpk = 1.33 ,K=0時, part A 的σ值為何?而其餘的運算皆與上一節所提的相同,在這裡不再重覆計算.I.理論與實務----ADCATS Tolerance Spreadsheets以上所提到的理論基礎,全部來自於這個網頁: /home.html 這是美國猶他州( Utah ) Brigham Young University 機械工程學系的Dr. Ken Chase 所建立的,他發表過許多以電腦輔助做公差分析的論文, PTC( 參數科技)的 CE/Tol,是目前少數能做 3D公差分析的軟體,就是由這位教授的學生開發完成的,CE/Tol訓練教材的分析範例就是來自 Chase 教授的論文.在網頁中提供了一個 excel sheet, 就是實際運用上述理論的產物,請到這裡下載: CATS 1D Tolerance Stack-up :/WWW/ADCATS/software/實際上我們已運用於 Sun Microsystem 的 project 中,在機殼設計所碰到的問題中,1D的分析就幾乎可以含蓋全部的狀況;此外使用它的優點在於此 sheet並非由我們發展,而由客觀的第三者提供,我們不必花費太多精力與客戶溝通分析進行的理論,再者此sheet 免費,也無需軟體購買成本.J.附錄.A. 這些理論都應該在此附上證明,這部份將於最近完成.B. CATS 1D 的power point file.C. “Tolerance Allocation Methods for Designers” ADCATS Report No.99-6 Dr.Kenneth W. Chase 1999。
第4部分:公差分析指南
22
DFMA
谢 谢 !
23
3.当公差分析的结果不满足要求时:
DFMA
减少尺寸链的长度; A为54.00±0.20,C为25.00±0.15,D为28.50±0.15
优化的设计
18
四. 公差分析指南
3.当公差分析的结果不满足要求时:
DFMA
使用定位特征; 好处:
定位特征可以提供较精密的尺寸公差 定位特征的尺寸可以放置于比较容易进行尺寸管控的区域 使用定位特征时可以减少和避免对其他尺寸的公差要求,只需严格管控定 位特征的相关尺寸,就可以满足产品设计要求 因为定位特征精度高,使用定位特征有利于减少零件之间的尺寸公差累积
DFMA
制造工艺能力决定了公差分析中公差的设定; 二维图纸中公差标注与公差分析中的公差一致; 对公差分析中的尺寸需要进行制程管控;
制造工艺 能力
公差分析中 公差的设定
二维图样零 件公差标注
零件尺寸 制程管控
15
四. 公差分析指南
3.当公差分析的结果不满足要求时: 不推荐的做法:
DFMA
调整尺寸链中的尺寸公差大小; 降低目标尺寸判断标准;
100±0.20
3
一. 公差分析的介绍
2.公差的本质:
DFMA
公差是产品设计和产品制造的桥梁和纽带,是保证产品以优异的质量、 优良的性能和较低的成本进行制造的关键。
设计 功能 性能 外观 可装配性 设计限制 稳健性设计 设计意图 产品质量 客户满意
公差
制造 制造费用 装配费用 制造方法选择 机器 夹具 检验 不良率 返工率
推荐的做法:
减少尺寸链的长度; 使用定位特征;
公差分析常用方法
公差分析常用方法
公差分析是一种用于研究产品或系统各种要素之间相互连锁关系的方法。
它可用于确定导致产品或系统性能差异的主要因素,并寻找改进的机会。
下面是一些常用的公差分析方法:
1. 传递函数法:传递函数法是一种将产品或系统的总体公差在各个部件或要素上分配的方法。
通过将总体公差按照一定的比例分配给各个部件,以满足产品或系统性能的需求。
2. 采用最小二乘法(Least Square Method):最小二乘法是一种通过最小化观测值和理论值之间的差异平方和,来确定最接近真实值的方法。
在公差分析中,可以使用最小二乘法来评估产品或系统的总体公差和各个部件之间的关系。
3. 驱动因子公差分析(Driver Factor Analysis):驱动因子公差分析是一种通过识别产品或系统的主要性能驱动因子,来优化公差分配的方法。
通过将更多的公差分配给主要驱动因子,可以显著改善产品或系统的性能。
4. 公差优化:公差优化是一种通过最小化总体公差,以满足产品或系统性能要求的方法。
通过分析各个部件之间的相互关系,可以确定最佳的公差分配方案。
5. 敏感度分析:敏感度分析是一种评估产品或系统对公差变化的敏感程度的方法。
通过分析不同参数的变化对产品或系统性能的影响,可以确定哪些部件或要
素对总体公差的变化最为敏感。
以上是常用的公差分析方法,具体选择哪种方法取决于产品或系统的特点和分析目的。
公差分析方法现状与展望
公差分析方法现状与展望
一、公差分析方法的现状
公差分析(tolerance analysis)是一种系统工程分析方法,它的目的是通过对允许的尺寸公差和位置公差进行分析,从而确定系统的有效变化范围,预测和识别系统可能出现的问题。
工业产品在研发、制造和安装过程中,存在着工艺模具公差、零部件尺寸公差、组装公差等一系列公差问题,系统的有效性受到公差设计的影响。
因此,公差分析方法的发展一直是系统工程研究的热点和重点,受到国内外学者的关注。
目前,关于公差分析方法的研究主要集中在四个方面:(1)概念方法和数学模型的建立;(2)集成化设计实现;(3)应用方法的发展;(4)数据与公差库的完善。
1.1概念方法和数学模型的建立
关于公差分析的概念方法和模型,先前一直基于传统的几何学概念和基于规则的数学解法,如基于图形加、减法、基于椭圆形和多边形的规则数学解法等。
这些方法只能处理尺寸公差或是基于空间的组装公差,无法处理系统约束关系的问题,而且还存在时间复杂度高、计算量大的问题。
公差分析
三.统计公差分析法 由制造观点来看,零件尺寸之误差来自于制程之变异,此变异往往呈现统计分布的型态,因此设计的公差规格常被视为统计型态。 统计公差方法的思想是考虑零件在机械加工过程中尺寸误差的实际分布,运用概率统计理论进行公差分析和计算,不要求装配过程中 100 %的成功率(零件的100 %互换) ,要求在保证一定装配成功率的前提下,适当放大组成环的公差,降低零件(组成环) 加工精度,从而 减小制造和生产成本。 在多群数据的线性叠加运算中,可以进行叠加的是『变异』值。
Worst Case Analysis缺陷: 设计Gap往往要留很大,根本没有足够的设计空间,同时也可能造成组装困难; 公差分配时,使组成环公差减小,零件加工精度要求提高,制造成本增加。 以上例Part A +Part B+ Part C,假设A、B、C三个部材,相对于公差规格都有3σ的制程能力水平,则每个部材的不 良机率为1-0.9973=0.0027;在组装完毕后所有零件都有缺陷的机率为:0.0027^3=0.000000019683。这表明几个 或者多个零件在装配时,同一部件的各组成环,恰好都是接近极限尺寸的情况非常罕见。
四.方和根法 计算公式(平方相加开根号)
假设每个尺寸的 Ppk 指标是1.33并且制程 是在中心
比较Worst case与统计公差法 公差合成后所得的公差范围缩小了,对设计者而言,较小的公差范围意味着较准确的组装与配合,累积 下来的误差也会减少。 在公差分配的情况时,每个零件所得到的公差范围变大了,对制造者而言,较大的公差范围意味着较容 易制作及控制生产质量,有利于制造者。
<例>Vector loop:E=A+B+C,根据worst case analysis可得 D(Max.) =(20+0.3)+(15+0.25)+(10+0.15)=45.7,出现在A 、 B、C偏上限之状况 D(Min.)=(20-0.3)+(15-0.25)+(10-0.2)=44.3,出现在A,B、C偏下限之状况 45±0.7 适合拿来作设计吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
生产现场S H O P S O L U T I O N S金属加工汽车工艺与材料 A T&M2009年第7期50机械装配过程中,在保证各组成零件适当功能的前提下,各组成零件所定义的、允许的几何和位置上的误差称为公差。
公差的大小不仅关系到制造和装配过程,还极大影响着产品的质量、功能、生产效率以及制造成本。
公差信息是产品信息库中的重要内容,公差模型就是为表示公差信息而建立的数学及物理模型,它是进行公差分析的理论基础。
公差分析或称偏差分析,即通过已知零部件的尺寸分布和公差,考虑偏差的累积和传播,以计算装配体的尺寸分布和装配公差的过程。
公差分析的目的在于判断零部件的公差分布是否满足装配功能要求,进而评价整个装配的可行性。
早期公差分析方法面向的是一维尺寸公差的分析与计算。
Bjorke 则将公差分析拓展到三维空间。
Wang 、C h a s e 、P a b o n 、H o f f m a n 、Lee 、Turner 、Tsai 、Salomons 、Varghese 、Connor 等许多学者也分别提出了各自的理论和方法开展公差分析的研究。
此后,人工智能、专家系统、神经网络、稳健性理论等工具被引入公差分析领域当中,并分别构建了数学模型以解决公差分析问题。
1 公差模型公差模型可分为零件层面的公差信息模型和装配层面的公差拓扑关系模型。
Shan 提出了完整公差模型的建模准则,即兼容性和可计算性准则。
兼容性准则是指公差模型满足产品设计过程的要求,符合ISO 和ASME 标准,能够完整表述所有类型的公差。
可计算性准则是指公差模型可实现与CAD 系统集成、支持过/欠约束、可提取隐含尺寸信息、可识别公差类型,以检查公差分配方案的可行性等。
目前已经提出了很多公差模型表示法,但每一种模型都是基于一些假设,且只部分满足了公差模型的建模准则,至今尚未出现统一的、公认的公差模型。
以下将对几种典型的公差模型加以介绍和评价。
1.1 尺寸树模型Requicha 最早研究了零件层面的公差信息表示,并首先提出了应用于一维公差分析的尺寸树模型。
该模型中,每一个节点是一个水平特征,节点间连线表示尺寸,公差值附加到尺寸值后。
由于一维零件公差不考虑旋转偏差,所有公差都可表示为尺寸值加公差值的形式。
该模型对于简单的一维公差分析十分有效,但却使尺寸和公差的概念模糊不清,而且没有考虑到形状和位置公差的表示。
1.2 漂移公差带模型Requicha 从几何建模的角度,于20世纪80年代提出了漂移公差带模型以定义形状公差。
在这个模型中,形状公差域定义为空间域,公差表面特征需位于此空间域中,同时采用边界表示法(Breps )建立传统的位置和尺寸公差模型。
对于表面特征和相关公差信息则运用偏差图(VGraph )来表示。
VGraph 主要是作为一种分解实体表面特征的手段,将实体的边界部分定义为特征,公差信息则封装在特征的属性中。
漂移公差带模型很好地表达了轮廓公差,轮廓公差包含了所有实际制造过程中的偏差。
该模型提供了公差的通用理论且易于实现,但是不能区分不同类型的形状公差。
1.3 矢量空间模型Hoffmann 提出了矢量空间模型,Turner 扩展了这一模型。
矢量空间模型首先需要定义公差变量、设计变量和模型变量。
公差变量表示零件名义尺寸的偏差。
设计变量由设计者确定,用以表示最终装配体的多目标优化函数。
模型变量是控制零件各个公差的独立变量。
由公差模型和公差分析方法的研究讨论了目前工程设计、制造中具有代表性的公差模型的建模、描述和分析的方法。
在此基础上,对于面向刚性件和柔性件装配的公差分析方法的研究现状分别进行了综述和评价,通过对比说明各种分析方法的算法、应用范围及不足。
最后,展望了公差模型和公差分析方法的研究方向及其发展动态。
奇瑞汽车股份有限公司 葛宜银 李国波生产现场2009年第7期51汽车工艺与材料 A T&M于旋转偏差是非线性的,Turner 用模型变量表示旋转偏差旋转方向上的矢量顶点,以便将彼此相关的公差转换成各自独立的模型变量。
矢量空间模型具有以下特点。
(1) 模型变量必须独立,否则就不能保证各个公差彼此独立和矢量的可叠加性。
(2) 矢量空间模型需要定义大量模型变量,即使是一个简单的零件,例如平面上两个圆的尺寸公差,也需要定义至少36个模型变量。
(3) 为把公差约束转换成模型变量,需要对公差约束做一些线性化近似处理,因此可能会在特定环境下出现难以预料的计算误差。
矢量空间模型仅用于进行公差分析,而不能用于识别尺寸链。
对于复杂装配体的多维装配,也不宜运用矢量空间模型进行公差分析。
1.4 虚拟边界模型Srinivasan 和Jayaraman 首先为零件定义一个虚拟边界,并限定该零件位于这个边界的半空间内,然后将虚拟边界变换为公差属性子集的形式。
虚拟边界实际上是满足公差定义的零件偏差的极值边界,所以虚拟边界模型可用于极值公差分析,但不适用于尺寸链复杂的装配体。
1.5 最大实体边界模型Parratt 提出最大实体(MMP)的概念,用以定义在指定公差允许的条件下零件的最大实体。
这与虚拟边界的概念相似,因为零件的MMP 边界也就是虚拟边界模型中的虚拟边界。
MMP 模型对于处理公差带漂移、公差分析、路径规划以及零部件存在偏差的情况下的运动学建模等方面有很大的优势。
1.6 TTRS 模型很多学者基于机构学理论,分别提出利用自由度(DOF )方法为公差建模。
Bourdet 在计算机辅助检测方面研究成果的基础上,利用自由度方法,提出了TTRS (与工艺和拓扑相关表面)理论。
Riviere 定义TTRS 为,一个TTRS 是同一实体上因功能原因而彼此联系的表面。
TTRS 理论可很好地表示零件层面的公差信息和装配层面的公差拓扑关系。
经过十几年的发展,TTRS 理论已发展为较为成熟且广泛应用的公差表示方法。
2 面向刚性装配的公差分析方法基于零部件在装配时偏差值的处理方式不同,一些学者将公差分析方法分为极值法、统计公差法和蒙特卡罗模拟法。
此外,许多学者从不同数学模型出发,分别提出了各自的公差分析方法。
这些装配公差分析方法具有共同的特点:以刚性零件为研究对象,其装配偏差的累积仅由零件几何和运动关系确定。
下面对几种具有代表性的面向刚性装配的公差分析方法加以论述。
2.1 极值法极值公差法又称为代数和法。
这种方法在计算装配公差时,假定各零件的尺寸同时处于极限值。
极值法的计算方法为T Y =Σ αi T i (1)式中,T Y 、T i 分别为封闭环(Y )、第i 个组成环的公差;αi 表示零件i 的偏差。
极值法计算公差主要适用于以下方面。
(1) 要求保证完全互换、公差等级较高、组成环环数较少的尺寸链。
(2) 要求保证完全互换、公差等级中等、组成环环数较多的尺寸链,如枪械等一般军工产品。
(3) 公差比较宽松、没有必要进行十分准确计算的尺寸链。
极值法计算简单且计算量小,但是按照这种方法确定的零件公差偏小,常常导致产品成本升高。
2.2 统计公差法统计公差法在计算装配公差时,假定各零件公差服从正态分布,装配公差与零件公差之间是线性关系,通过假设使得实际情况得到了简化。
其计算公式是: T Y =Z [Σ(αi T i /Z i )2]0.5 (2)式中,Z 、Z i 分别为Y 和第i 个变量的偏差系数。
统计公差分析方法由于考虑了零件尺寸的统计分布,对实际产品制造过程的建模更接近于实际。
与极值法相比,统计公差法可得到更接近于实际的装配公差的估计,并允许零件有较宽的公差带。
线性情况在机械装配中较为普遍并且计算简单,因此这种方法应用广泛。
2.3 Monte Carlo 模拟法Monte Carlo 模拟法是一种统计试验法,根据每个尺寸的实际分布,利用随机数发生器生成相应的伪随机数,然后计算设计函数的值。
当得到一定数量的样本后,根据统计公式计算出统计函数的各阶矩,从而获得有关装配函数的统计特性。
Monte Carlo 模拟法在非线性设计函数中,是最常用和最简单的一种公差分析方法,且已被广泛用于VSA 系列软件包中。
Monte Carlo 方法虽然能够处理由装配关系或零件的弹性变形所引起的非线性装配函数,但该方法仍存在以下缺陷。
(1) 蒙特卡罗方法的精度正比于样本量的平方根,因此为保证计算的正确性,需要大量的统计样本ni =1i =1n生产现场S H O P S O L U T I O N S金属加工汽车工艺与材料 A T&M 2009年第7期52进行多次重复运算,计算次数一般在20万次以上,导致计算时间过长。
(2) 如果装配函数中各分量的均值或方差发生改变,需要重新进行运算。
文献提出利用基于数论网格点集的数论序贯优化算法改进Monte Carlo 方法。
与Monte Carlo 方法产生的随机点集相比,数论网格点集的分布更为均匀。
序贯优化算法在保证获得全局最优解的同时,还显著减少了计算量。
2.4 田口试验法20世纪50年代初,日本电讯研究所(ECL )以田口为首的一批研究人员为改进产品和系统质量、提高生产率,提出了田口试验法。
它将所有对试验结果有影响的一系列因素在试验中加以考察、进行比较,然后进行水平组合,是试验设计中的一种有效方法。
试验设计的目的在于寻求试验因素的适宜水平组合,实现质量系统的相对优化。
基于田口试验法的公差分析方法符合产品的实际设计过程,计算简单,对设计函数不必求偏导数,因而具有较为广泛的应用空间。
但它要求组成环数目不能太多,一般应用于组成环数目小于10的场合。
2.5 泰勒级数展开法当可以计算出设计函数各阶偏导数的情况下,可以采用泰勒级数展开法,将函数Y 展开,再计算出Y 的各阶中心矩。
这种方法需要计算偏导数,计算复杂。
2.6 其他公差分析方法文献提出了稳健设计理论在公差分析中的应用。
稳健性是指因素状态发生微小波动对因变量影响的不敏感性。
基于这一思想,对产品的性能、质量和成本综合考虑做出最佳设计,这种工程设计方法为稳健设计。
因此减小产品对制造尺寸波动的敏感性,可提高产品的稳健性和可制造性。
文献根据并行公差设计原则,利用对加工环境进行历史统计得出的各种加工方法的工序能力,提出了基于制造环境的统计公差分析法,为保证设计质量提供了有利的依据。
此外,还有基于可靠度的公差分析法、矩方法、数值积分方法等。
3 面向柔性件装配的公差分析方法1980年,Takezawa 根据对汽车柔性薄板件装配测量数据的回归研究指出,基于刚体假设的偏差累积理论难以适用于柔性薄板冲压件的装配,其装配体偏差可以小于零件偏差,并接近于刚性较大的零件。
20世纪90年代初,美国密西根大学将有限元和统计理论相结合,率先开始了有关柔性件装配公差分析的系统性理论研究。
