c6狭义相对论基础c
6狭义相对论基础141204

又 (1) 所以
(2)
将(2)式与前边的(1)式联立,有
所以
2. 洛仑兹变换 将四个求得的a11, a12, a21, a22系数代入设定的变换式,有
(正变换) 从S系变换到S系
从S系变换到S系(逆变换)
说明
(1) 洛仑兹变换中x是x和t的函数,t是x和t的函数,而且都与 S系和S系的相对运动速度u有关,揭示出时间、空间、物 质运动之间的关系.
由长度收缩公式
l cos 45 u c 1 l 'cos 30
2
解得
l cos 45 u c 1 l 'co s 30
2
4.3.3 时间的相对性 y' S' 固有时间0:在相对观测者静止 y S 的惯性系中同一地点先后发生的 两个事件之间的时间间隔。
t ' t 先出球,后击球 ---- 先后顺序颠倒
光速不服从经典力学的速度变换定理
乙
§4.2 狭义相对论的基本假设与洛伦兹变换
主要内容:
1. 狭义相对论的两个基本假设 2. 洛伦兹变换
4.2.1 狭义相对论的两个基本假设 1. 相对性原理 物理定律在所有惯性系中都具有相同的形式.
2. 光速不变原理 在所有惯性系中,光在真空中的传播速率具有相同的值c .
麦克斯韦 物 伽利略 … 牛顿 … … 1831-1879 1642-1722 理 1564-1642 学 电磁学 关 力学 键 概 念 的 热力学 发 展 1900 1800 1600 1700
以牛顿力学和麦克斯韦电磁场理论为代表的经典物理学,到20世 纪初,已经取得了空前的成就。人类对物质世界的认识,已从宏观 低速物体的运动规律逐渐扩展到高速传播的电磁波(包括光波)的 场物质运动规律。
基础物理狭义相对论基础
L2
S
P
A
L1
干涉条纹
实验结果:条纹无移动(零结果 )。以太不存在,光速与参考系 无关。
12
M2
“我的实验 竟然对相对 论这个怪物 的诞生起了 作用,我对 此感到十分 遗憾。”
s
G
M1
u
T
迈克尔逊-莫雷实验原理图
理论值 N 0.4 实验精度 N 0.01
实验值 N 0.01
爱因斯坦对麦克尔逊-莫雷实验的评价: “还在学生时代,我就在想这个问题了。我知道迈克耳 逊实验的奇怪结果。我很快得出结论:如果我们承认麦克 尔逊的零结果是事实,那么地球相对以太运动的想法就是 错误的。这是引导我走向狭义相对论的最早的想法。”
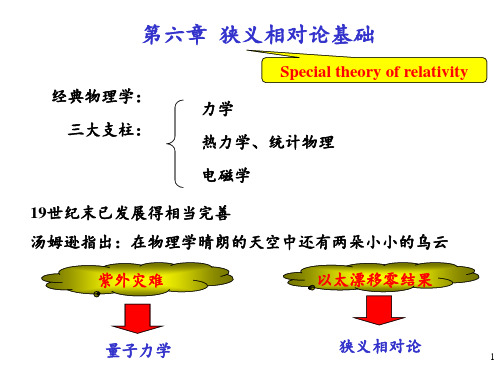
第六章 狭义相对论基础
Special theory of relativity 经典物理学: 三大支柱:
力学
热力学、统计物理 电磁学
19世纪末已发展得相当完善 汤姆逊指出:在物理学晴朗的天空中还有两朵小小的乌云 紫外灾难 以太漂移零结果
量子力学
狭义相对论
1
Albert Einstein
1879 –1955
6狭义相对论基础

6狭义相对论基础第六章狭义相对论基础本章讨论⾼速运动时的运动学和动⼒学主要内容:狭义相对论的基本假设同时性的相对性洛仑兹变换式运动时钟变慢和长度缩短洛仑兹速度变换相对论性质量和动量相对论性能量相对论性⼒和加速度间关系第⼀部分相对论运动学(§1-§6)§1.⼒学相对性原理和伽⾥略变换⼀.⼒学相对性原理原理:⽜顿⼒学规律在⼀切惯性系中形式相同,或⼀切惯性系对⼒学规律平权。
由相对性原理可知,不可能通过⼒学实验来确定所在参考系的运动(伽⾥略实验)。
⼆. 伽⾥略变换运动描述的相对性和⼒学规律的普适性,要求给出不同惯性系对同⼀对象描述的⼒学量间的变换关系,以与⼒学相对性原理在理论上⾃洽。
伽⾥略变换式是在⽜顿绝对时空观基础上给出的时空坐标变换关系式。
事件的时空坐标:每个参考系中各有静⽌于其中的尺度和⼀系列的同步钟,某⼀事件发⽣的时空坐标就⽤该参考系中的尺和当地钟测量。
设S'系相对S系以u沿x轴匀速运动,两参考系的y与y'、z与z'轴平⾏,x与x'轴重合,t = t' =0时,原点O、O'重合。
对事件P,其在S'系和S系中的时空坐标间变换关系如下:x '= x- uty' = yz' = zt' = t上述⼀组变换式称为伽⾥略变换式.显然,这是认为时间和长度的测量与参考系(运动)⽆关,即绝对时空观的结果。
由此还可导出质点速度间的变换关系: u v v -='该式称为伽⾥略速度相加定理。
讨论:设S 系为惯性系,对其中的质点有 a m F =S '系为另⼀惯性系,由伽⾥略变换知,其中质点的加速度 a a =' , ⽜顿⼒学观点:质量和⼒与参考系(运动)⽆关,即 m m F F ='=', ,故在S '系中有 a m F ''='伽⾥略变换与⽜顿定律的不变性相协调,亦即与由⽜顿定律导出的⼒学规律的不变性相协调。
大学物理第6章 狭义相对论基础

x '1 o o' x 1 z z'
l0
x '2 x ' x2 x
中测得棒有 多长?
设 在S系中某时刻 t 同时测得棒两端坐 标为x1、x2,则S系中测得棒长 l= x - x , l 与l 的关系为:
2 1 0
( x ut ) ( x ut ) l x x u 1 c x x l u u 1 1 c c
2
逆 变 换
x ( x ut )
u t (t x) c
2
y y z z
注意
u c 时, u c 1
转换为伽利略变换式.
§6.4 同时性的相对性
同时的相对性
事件 1 :车厢后壁接收器接收到光信号. 事件 2 :车厢前壁接收器接收到光信号.
12
x
时间延缓 :运动 的钟走得慢 .
注意 1 时间延缓是一种相对效应 . 2 时间的流逝不是绝对的,运动 将改变时间的进程.(例如新陈代谢、放 射性的衰变、寿命等 ) 3
u c 时,Δt Δt .
狭义相对论的时空观
(1) 两个事件在不同的惯性系看来, 它们的空间关系是相对的,时间关系也 是相对的,只有将空间和时间联系在一 起才有意义. (2)时—空不互相独立,而是不可分 割的整体. (3)光速 C 是建立不同惯性系间时空 变换的纽带.
2 2
讨论
S系
u Δt Δx c Δt ' 1
2 2
S′系 ------不同时
1 Δx 0 Δt 0
同时不同地
2 Δx 0 Δt 0
同地不同时 ------不同时
讨论
u Δt Δx c Δt ' 1
物理第六章狭义相对论基础PPT课件

第18页/共51页
洛仑兹坐标变换式
正变换
逆变换
x
x ut
1
u2 c2
y y
z z
t
t
u c2
x
2
1 u2 c 第19页/共51页
x x' ut '
1
u2 c2
y y
z z
t
t'
u c2
x'
1
u2 c2
令 u
c
正变换
1 1 2
逆变换
x x ut x x ut
y y
第2页/共51页
v ' a'
正变换:
把S′系的各量用S系的各量表示。
y
y’
u
P(x, y, z, t)
ut o
o’ z
z’
坐标变换
x' x ut y' y z' z t' t
x’
x’
x x
速度变换
加速度变换
vx vx u
vy vy
a' a
vz vz
——伽利略变换式
第3页/共51页
o
x1
第14页/共x251页 x
l x2 x1 ut
Δt是B′、A′相继通过 x1这两个事件之间的固有时。
l和l ' 之间有什么关系呢?
在S′系,棒静止,由于S系向左运动,x1这一点相继经过B′和A′端。
y
u
o
y
u
o o′ y′
o′
y′
A’
A′ x1
x1经过A′和B′两事件之间的时间间隔,在S’ 系中测量为:
狭义相对论基础PPT教学课件

1
u2 =5 c2
1-(9103 / 3108 )2
4.999999998m
差别很难测出。
若 u = o.98 c
l l0
1
u2 c2
=5
1-(0.98)2 1 m
相差5倍!
例2、试从π介子在其中静止的参照系来考虑π介子的平 均寿命。
解:从π介子的参照系看来,实验室的运动速率为 u=0.99c, 实验室中测得的距离是 l=52m 为固有长度 , 在π介子参照系中测量此距离应为:
小结
前言:
类型:港口,车站,航空港 影响因素:经济,社会,技术,自然
港
概念:具有一定面积的水域和陆域,供船舶
口 出入和停泊、货物和旅客集散的场所
的
建
区位选择:
自然条件:航行,停泊,筑港
设 经济和社会条件:腹地,城市
上 海 港
(1)是 ____上的港,兼作____港,主要港区 沿_____分布。
的 (2)_____是中国经济_____地区,包括
讨论 1) 同时性的相对性是光速不变原理的直接结果
2) 相对效应(总之;沿两个惯性系相对运动方向发生的两个
事件,在其中一个惯性系中表现为同时的,在另一惯性系中观 察,则总是在前一惯性系运动的后方的那一个事件先发生。)
3) 当速度 u 远远小于 c 时,两个惯性系结果相同
2.时间膨胀
y′
S ′系中, A ′处有光源闪光 M′
爱因斯坦
1)爱因斯坦的相对性理论 是牛顿理论的发展
一切物 理规律
力学 规律
2) 光速不变与伽利略变换 革命性
与伽利略的速度相加原理针锋相对
3) 观念上的变革
时间标度 牛顿力学 长度标度
第六章 狭义相对论基础

——同时的相对性
用洛伦兹变换式说明同时性的相对性。
S系 S 系
A( x1 ,0,0, t1 )和B( x2 ,0,0, t2 ) A( x1 ,0,0, t1 )和B( x2 ,0,0, t2 )
t u t 2 x c 2 1 2 1 u c u t 2 2 x2 c t2 1 u 2 c2
固有长度:棒静止时测得的它的长度叫棒的静长或 1 固有长度 .(最长)
注意
长度收缩是一种相对效应, 此结果反之亦然 . 当 u c 时 l l .
u 9 103 m / s的速率相对 例6.3 固有长度为5m的飞船以 于地面匀速飞行时,从地面上测量,它的长度是多少?
l 5m 固有长度
消去 x'
1
x' k ( x ut )
x ut u 2 1 ( ) c
消去
x
u t 2 x c t 2 2 1 u c
u t 2 x c t 2 2 1 u c
洛仑兹变换式
S S 正变换
x x ut 1 u 2 c2
1
u c
(B )Vt
V 2 ( D)Ct 1 ( ) C
( C)
6.5 在S系中观察到在同一地点发生两个事件,第二事件 S 发生在第一事件之后2s,在 系中观察到第二事件在第一 事件后3s发生。求在 S 系中这两个事件的空间距离。
1
自然和自然规律隐藏在黑暗之中, 上帝说“让牛顿降生吧”, 一切就有了光明; 但是,光明并不久长,
1
魔鬼又出现了, 上帝咆哮说:“让爱因斯坦降生吧”, 就恢复到现在这个样子。
牛顿: Newton
爱因斯坦: Einstein
《狭义相对论的基本原理》 讲义

《狭义相对论的基本原理》讲义在物理学的发展历程中,狭义相对论无疑是一座重要的里程碑。
它彻底改变了我们对时间和空间的理解,对现代物理学的发展产生了深远的影响。
接下来,让我们一同深入探讨狭义相对论的基本原理。
一、相对性原理相对性原理是狭义相对论的首要基本原理。
它指出,物理规律在所有惯性参考系中都是相同的。
这意味着,无论我们处于何种匀速直线运动的惯性参考系中,进行物理实验和观察所得到的结果应该遵循相同的物理规律。
为了更好地理解相对性原理,我们可以想象这样一个场景:在一辆匀速直线行驶的火车上,有一个人在做一个物理实验,比如测量光在真空中的传播速度。
同时,在地面上也有一个人在做同样的实验。
按照相对性原理,他们所得到的测量结果应该是完全一致的,不会因为火车的运动状态而有所不同。
相对性原理打破了传统的绝对时空观。
在牛顿力学中,存在着一个绝对静止的参考系,而狭义相对论则否定了这种绝对静止的存在,强调了参考系的相对性。
二、光速不变原理光速不变原理是狭义相对论的另一个核心基本原理。
它表明,真空中的光速在任何惯性参考系中都是恒定不变的,与光源和观察者的相对运动状态无关。
这一原理与我们日常生活中的经验似乎有所冲突。
通常,当我们观察一个运动的物体时,它的速度会因为我们自身的运动状态而发生变化。
但对于光来说,情况却完全不同。
无论我们是朝着光源运动,还是背离光源运动,或者光源本身在运动,我们测量到的光速始终是一个恒定的值,约为 299792458 米/秒。
为了验证光速不变原理,科学家们进行了许多实验。
其中,迈克尔逊莫雷实验是一个重要的例证。
这个实验试图测量地球在以太中运动时对光速的影响,但结果却发现光速没有任何变化,这为狭义相对论的提出奠定了实验基础。
三、时间膨胀狭义相对论带来的一个令人惊讶的结果是时间膨胀。
当一个物体以接近光速的速度运动时,相对于静止的观察者,运动物体上的时间会变慢。
这可以通过一个简单的思想实验来理解。
假设在地球上有一个精确的时钟,同时在一艘高速飞行的宇宙飞船上也有一个相同的时钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习十六 狭义相对论(一)
1、惯性系S 和S'的坐标原点在0'==t t 时重合,有一事件发生在S'系中的时空坐标为s t z y x 8100.8',0',10',60'-⨯====。
若S'系相对于S 系以速度u =0.6c 沿'x x -轴正方向运动,则该事件在S 系中测量时X = ;Y = ;Z = ;t = 。
25.111
,6.0c u 2
=-===
βγβ
0'z z ,m 10'y y m 93'ct 'x x =====+)β=γ( s 105.2'x c 't t 7-⨯=+)β=γ( 2.一飞船静止在地面上测量时的长度为20m ,当它以0.8c 在空中竖直向上匀速直线飞行时,地面上的观察者测得
其长度为 ;若宇航员举一次手需2.4s 时,则地面观察者测得他举手的时间是 。
67.111,8.0c u 2
=-===
βγβ s 4't t m 121'L L 2=⨯==-=γΔΔβ
3.( 3 )S'系以速度u =0.6c 相对于S 系沿'x x -轴正向运动,0'==t t 时,0'x x ==。
事件A 发生在S 系中的x 1=50m ,t 1=2.0⨯10-7
秒;事件B 发生在S 系中的x 2=10m ,t 2=3.0⨯10-7
秒。
则S'系中的观察者测得两事件A 、B 的时间间隔为: (1)1.0⨯10-7
秒;(2)1.25⨯10-7
秒;(3)2.25⨯10-7
秒;(4)0.8⨯10-7
秒。
25.111
,6.0c u 2
=-===
βγβ)x c t t',....x c t t'222111β=γ()β=γ(-- s 1025.2)]x (x c
)t t ([t't'7121212-⨯=----β
(=γ
4.( 3 )某不稳定粒子的固有寿命是1.0⨯10-6秒,在实验室参照系中测得它的速度为2.0⨯108m/s ,则此粒子从产生到湮灭能飞行的距离为:(1)149m (2)200m (3)268m (4)402m 解:u 't 和已知Δ ,-1t 't 2
β
ΔΔ= m 268t u x ==ΔΔ
5.长为4m 的棒静止在S'系中'''x y o 平面内,并与x ’轴成300角,S'系以速度u =0.5c 相对于S 系沿'x x -轴正向运动。
0'==t t 时,两坐标的原点重合,求S /
系中的观察者测得此棒的长度和它与x ’轴的夹角。
解:由已知条件可知: Δx ’=L ’cos θ, Δy ’=L ’sin θ
3
2x y tg L 4
13
y x L y'y 1x'x 2
2
2=
==
+==-=ΔΔθΔΔΔΔβΔΔ
6.在惯性系S 中,有两个事件A 、B 同时发生在X 轴上相距 X B -X A =1.0⨯103m 的两地。
从相对于S 系沿'x x -轴正向作匀速 运动的S'系中观测,事件A 和事件B 不是同时发生的,时间 间隔为5.77⨯10-6秒。
求S'系观测这两个事件的空间间隔是多 少?哪一个事件先发生? 解: (1) 由 )β=γ(x c t t'-
得:01c 10)]x (x c )t t ([t't'23
A B A B A B <-⨯-=----β
ββ(=γ 即:t B ’小,B 先发生.
(2) 考虑正负:62
3A B 1077.51c 10t't'-⨯-=-⨯-
=-ββ 2,23==∴γβ
m 100.2)]t (t )x x ([x'x'31212A B ⨯=----c β(=γ
S
)
(S '
相对静止S )
(S '相对静止A x B
x
练习十七 狭义相对论(二)
1.在相对论中,粒子质量与速度的关系是 2
201c
v m m -=
,动量2
201v v p c
v m m -=
= ,动能202k c m mc E -=, 总能
量2
mc E =。
2.正方形的本征体积为125m 3,静质量为125kg 当它沿着与某一棱边平行的方向相对于S 以速率V =0.8c 运动时,S 系中的观察者测得它的体积是 ;质量是 ;密度是 。
解:已知 x ’=y ’=z ’=5m, m 0=125kg, β=0.8
3
2m
75xyz v z'z ,y'y ,m 31x'x =====-=β
32
2
0m /kg 78.2v
m kg
3.2081===-
=
ρc v m m
3.( )电子的静质量m 0=9.1⨯10-31kg ,当它具有2.6⨯105ev 的动能时,增加的质量与静质量之比为: (1)0.1; (2)0.2; (3)0.5; (4)0.9。
由 202k c m mc E -=得:508.0m m m kg
10
63.4c /E m m 0
31
2
k 0=-⨯==-- 4.( )静质量为M 的静止粒子自发地分裂成静质量和速度分别为m 1、v 1和m 2、v 2的两部分。
按照相对论,有: (1)M >m 1+m 2;(2)M =m 1+m 2;(3)M <m 1+m 2。
解:由能量守恒得:Mc 2=m 1c 2+E k1+m 2c 2+E k2>(m 1+m 2)c 2所以 M >m 1+m 2
5.设电子的静质量为m 0光速为c 0(1).把电子的速率从V 1=0.6c 加速到V 2=0.8c ,需作多少功?(2)电子从静止通过1.0⨯106伏特的电势差后,它的质量、速率和动量分别是多少? 解: (1) 20202
2
1
22
2
212220212022k1k2c m 12
5
c m )1111(
c m c m )c m c m ()c m c m (E E W =
--
-=-=---=-=c v c v (2)kg 10691.2m c
qu
m qu c m mc E 3002202-⨯=+=
=-=Δ 由 m/s kg 107.53mv p s /m 108.2c 941.0v :122-82
20⋅⨯==⨯==-=
得c
v m m
6.粒子以多大的速度运动时,它的相对论动量是经典动量的两倍;如果粒子的动能与它的静能相等,粒子的速率
又是多少?
解: (1) 相对论动量:s m c v c
v c
v m m /106.2866.02
111v v p 82
22
20⨯===-∴
-=
=
(2) 202000k 2,2E c m mc E E E E E ===-=所以所以 即:
02
2021m c
v m =- s m c v /106.2866.08⨯==
S。
