初二数学(人教版)全等三角形的性质与判定的综合运用第二课时练习题
人教版 初中数学八年级上册 12.2全等三角形的判定 同步练习(含答案)

人教版初中数学八年级上册12.2全等三角形的判定同步练习(含答案)一、选择题(本大题共8道小题)1. 如图,AD=AE,若利用“SAS”证明△ABE△△ACD,则需要添加的条件是()A.AB=ACB.△B=△CC.△AEB=△ADCD.△A=△B2. 下列三角形中全等的是()A.△△ B.△△ C.△△ D.△△3. 如图,小强画了一个与已知△ABC全等的△DEF,他画图的步骤是:(1)画DE =AB;(2)在DE的同旁画△HDE=△A,△GED=△B,DH,EG相交于点F,小强画图的依据是()A.ASA B.SASC.SSS D.AAS4. 如图所示,△C=△D=90°,若要用“HL”判定Rt△ABC与Rt△ABD全等,则可添加的条件是()A.AC=AD B.AB=ABC.△ABC=△ABD D.△BAC=△BAD5. 如图,点B,F,C,E在一条直线上,AB△ED,AC△FD,那么添加下列一个条件后,仍无法判定△ABC△△DEF的是()A.AB=DE B.AC=DFC.△A=△D D.BF=EC6. 如图所示,P是△BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA△△PF A的依据是()A.HL B.ASA C.SSS D.SAS7. 在Rt△ABC和Rt△DEF中,△C=△F=90°,下列条件不能判定Rt△ABC△Rt△DEF的是()A.AC=DF,△B=△E B.△A=△D,△B=△EC.AB=DE,AC=DF D.AB=DE,△A=△D8. 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角△ABC=35°,则右边的滑梯与地面的夹角△DFE等于()A.60° B.55° C.65° D.35°二、填空题(本大题共4道小题)9. 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于点H,请你添加一个适当条件:________,使△AEH△△CEB.10. 如图,在△ABC中,AD△BC于点D,要使△ABD△△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,已知AD=BC,AB=CD,若△C=40°,则△A=________°.12. 如图K-10-10,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,ED 与AB相交于点G.若△ACD=40°,则△AGD=________°.三、解答题(本大题共2道小题)13. 如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.14. 如图,C是线段BD的中点,AB=EC,△B=△ECD.求证:△ABC△△ECD.人教版初中数学八年级上册12.2全等三角形的判定同步练习-答案一、选择题(本大题共8道小题)1. 【答案】A2. 【答案】A[解析] △△符合证明三角形全等的判定方法“SAS”.△△中相等的角所对的边不相等,所以不可能全等.故选A.3. 【答案】A4. 【答案】A5. 【答案】C[解析] 选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;选项C中添加△A=△D不能判定△ABC△△DEF,故本选项符合题意;选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.故选C.6. 【答案】A7. 【答案】B[解析] 选项A,D均可由“AAS”判定Rt△ABC△Rt△DEF,选项C 可由“HL”判定Rt△ABC△Rt△DEF,只有选项B不能判定Rt△ABC△Rt△DEF.8. 【答案】B [解析] 在Rt△ABC 和Rt△DEF 中,⎩⎨⎧BC =EF ,AC =DF ,△Rt△ABC△Rt△DEF(HL). △△DEF =△ABC =35°.△△DFE =90°-35°=55°.二、填空题(本大题共4道小题)9. 【答案】AH =CB (符合要求即可)【解析】∵AD ⊥BC ,CE ⊥AB ,垂足分别为点D 、E ,∴∠BEC =∠AEC =90°,在Rt △AEH 中,∠EAH =90°-∠AHE ,在Rt △HDC 中,∠ECB =90°-∠DHC ,∵∠AHE =∠DHC ,∴∠EAH =∠ECB ,∴根据AAS 添加AH =CB 或EH =EB ;根据ASA 添加AE =CE.可证△AEH ≌△CEB.故答案为:AH =CB 或EH =EB 或AE =CE 均可.10. 【答案】AB =AC 11. 【答案】40[解析] 如图,连接DB.在△ADB 和△CBD 中,⎩⎨⎧AD =CB ,AB =CD ,DB =BD ,△△ADB△△CBD(SSS). △△A =△C =40°.12. 【答案】40[解析] 在△ABC 和△DEC 中,⎩⎨⎧CA =CD ,AB =DE ,BC =EC ,△△ABC△△DEC(SSS). △△A =△D.又△△AFG =△DFC ,△△AGD =△ACD =40°.三、解答题(本大题共2道小题)13. 【答案】证明:∵CE ∥DF ,∴∠ACE =∠FDB ,(2分)在△ACE 和△FDB 中,⎩⎨⎧EC =BD∠ACE =∠FDB AC =FD,∴△ACE ≌△FDB(SAS ),(5分) ∴AE =FB.(7分)14. 【答案】证明:△C 是线段BD 的中点,△BC =CD.在△ABC 与△ECD 中,⎩⎨⎧BC =CD ,△B =△ECD ,AB =EC ,△△ABC△△ECD.。
人教版八年级上 第十二章 《三角形全等的性质和判定的综合应用》练习题
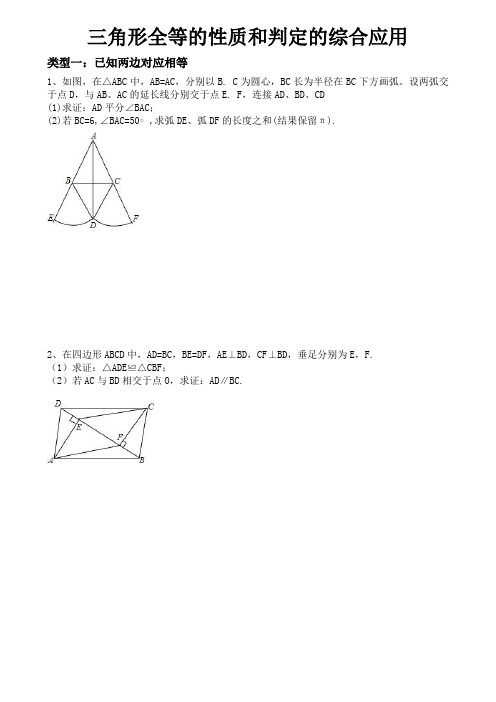
三角形全等的性质和判定的综合应用类型一:已知两边对应相等1、如图,在△ABC中,AB=AC,分别以B. C为圆心,BC长为半径在BC下方画弧。
设两弧交于点D,与AB、AC的延长线分别交于点E. F,连接AD、BD、CD(1)求证:AD平分∠BAC;(2)若BC=6,∠BAC=50∘,求弧DE、弧DF的长度之和(结果保留π).2、在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AD∥BC.3、如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=90∘,且BC=CE,AB=DE.求证:△ABC≌△DEC.类型二:已知两角对应相等4、如图,点A. C. D. B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.5、已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线,求证:AB=DC.类型三:已知一角一边对应相等6、如图所示,AB=DB,∠ABD=∠CBE,∠E=∠C,求证:DE=AC.7、已知如图,点F. A. E. B在一条直线上,∠C=∠F,BC∥DE,AB=DE求证:AC=DF.8、如图,∠ACB=90∘,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是多少?类型四:两次应用全等9、如图,在△ABC与△DCB中,AC与BD交于点E,且∠BAC=∠CDB,∠ACB=∠DBC,分别延长BA与CD交于点F,求证:BF=CE。
10、已知:如图,D是△ABC中BC边上一点,且AD⊥BC,E是AD上的一点,EB=EC,求证:∠BAE=∠CAE.。
八年级数学上册 12 全等三角形综合训练(二)全等三角形习题课件 (新版)新人教版

21.如图,在△ABC中,D是BC的中点,过点D的直线GF交AC于点F, 交AC的平行线BG于点G,DE⊥DF交AB于点E,连接EG,EF. (1)求证:BG=CF; (2)求证:EG=EF; (3)请你判断BE+CF与EF的大小关系,并证明你的结论.
7.如图,在△ABC中,D,E分别是边AC,BC上的点,若 △ADB≌△EDB≌△EDC,则∠C的度数为( D ) A.15° B.20° C.25° D.30°
8.如图,AC平分∠BAD,CM⊥AB于点M,CN⊥AN,且BM=DN, 则∠ADC与∠ABC的关系是(B ) A.相等 B.互补 C.和为150° D.和为165°
解:∵Rt△ABC≌Rt△DBF,∴∠A=∠D,AB=DB,BC=BF,∴ AF=DC,又∵∠AFG=∠DCG=90°,∴△AFG≌△DCG,∴FG= CG,又∵GF⊥FB,GC⊥CB,∴BG 平分∠ABD.∵∠D=28°,∴∠ ABD=90°-∠D=62°,∴∠GBF=12∠ABD=31°
20.如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线 AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G. (1)求证:BF=CG; (2)若AB=9,AC=7,求AF的长.
解:(1)由AAS可证 (2)∵∠1=∠2,∴∠AEB=∠CFA,∵∠1=∠ABE+∠BAE,∠BAE +∠CAF=∠BAC,∠1=∠BAC,∴∠CAF=∠ABE,又∵AB=CA, ∴△ABE≌△CAF(AAS) (3)6 点拨:∵在等腰三角形ABC中,AB=AC,CD=2BD,∴△ABD 与△ADC等高,底边比值为1∶2,∴△ABD与△ADC面积比为1∶2, ∵△ABC的面积为9,∴△ABD与△ADC面积分别为3,6.同(2)可证 △ABE≌△CAF(AAS),∴△ABE与△CAF面积相等,∴△ABE与 △CDF的面积之和为△ADC的面积,∴△ABE与△CDF的面积之和为6
部编版人教数学八年级上册12.2 第2课时 三角形全等的判定SAS 同步训练习题(含答案)

前言:
该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的同步训练习题助力考生查漏补缺,在原有基础上更进一步。
(最新精品同步训练习题)
第2课时三角形全等的判定(SAS)
[学生用书P27]
1.如图12-2-18所示,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需要加上条件( )
图12-2-18
A.AD=BC
B.AC=BD
C.∠C=∠D
D.OA=OB
2.如图12-2-19所示,BE=CD,AE=AD,∠1=∠2,∠2=100°,∠BAE =60°,则∠CAE的度数为( )
图12-2-19
A.20°B.30°C.40°D.50°
3.如图12-2-20,点B,E,C,F在同一直线上,AB=DE,BE=CF.请你添加一个条件:____(只需添加一个即可),使△ABC≌△DEF.
图12-2-20
4.[2016·泸州]如图12-2-21,C是线段AB的中点,CD=BE, CD∥BE.求证:∠D=∠E.
图12-2-21
5.如图12-2-22,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.
图12-2-22
6.[2015·杭州]如图12-2-23,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.。
人教版八年级数学(上册)12.2三角形全等的判定(第2课时) 课时习题(附参考答案)

12.2三角形全等的判定(第2课时)1.判断:①两边及其一角对应相等的两三角形全等.()②两边及其夹角对应相等的两三角形全等.()③两边及其一边的对角对应相等的两个三角形全等()④顶角和一腰对应相等的两个等腰三角形全等()2.在△ABC和△DEF中,已知AC=DF,BC=EF,要使△ABC≌△DEF,还需条件是( )A.∠A=∠DB.∠C=∠FC.∠B=∠ED.∠C=∠D3.如图所示,已知AD∥BC则∠1=∠2,理由是,又知AD=BC,AC 是公共边,则△ACD≌△ABC,理由是,则∠BAC=∠DCA,理由是,即AB∥DC,理由是 .4.已知:AB=AC,AD=AE,∠1=∠2,求证:①△ABD≌△ACE②∠E=∠B5.如图所示,已知EF∥BC,EF=BC,AF=CD,求证:△EFD≌△BCA.6.已知如图所示:AB=AC,DB=DC.求证:①△ABD≌△ACD.②BE=CE.参考答案1.错对错对2.B3.两直线平行,内错角相等.SAS;全等三角形对应角相等;内错角相等两直线平行.4.证明:∵∠1=∠2,∴∠BAD=∠CAE.△ABD与△ACE中,AB=AC, ∠BAD=∠CAE,AD=AE,∴△ABD≌△ACE.5.证明:∵EF∥BC,∴∠F=∠C,△EDF与△BCA中,EF=BC, ∠F=∠C,AF=CD,, ∴△EDF≌△BCA 6.证明在△ABD与△ACD中.AB=AC,DB=DC,AD=AD,∴△ABD≌△ACD.∴∠CAD=∠BAD在△ACE与△ABE中.AB=AC,∠CAD=∠BAD,AE=AE∴△ACE≌△ABE,即BE=CE.。
人教版八年级数学上册 12.2 全等三角形的判定 课时训练(含答案)

人教版八年级数学上册12.2 全等三角形的判定课时训练一、选择题1. 如图,已知AB=DE,∠B=∠E,为了直接用“ASA”说明△ABC≌△DEF,则需要添加的条件是()A.BC=EF B.∠A=∠DC.∠C=∠F D.AC=DF2. 如图所示,∠C=∠D=90°,若要用“HL”判定Rt△ABC与Rt△ABD全等,则可添加的条件是()A.AC=AD B.AB=ABC.∠ABC=∠ABD D.∠BAC=∠BAD3. 下列三角形中全等的是()A.①②B.②③C.③④D.①④4. 如图,已知AB=AD,若利用SSS证明△ABC≌△ADC,则需要添加的条件是()A.AC=ACB.∠B=∠DC.BC=DCD.AB=CD5. 如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件()A.∠B=∠D B.∠C=∠EC.∠1=∠2 D.∠3=∠46. 如图,点B,E,C,F在同一直线上,AB∥DE,∠A=∠D,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是()A.BE=CF B.∠ACB=∠FC.AC=DF D.AB=DE7. 如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有()A.1对B.2对C.3对D.4对8. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PF A的依据是()A.HL B.ASA C.SSS D.SAS9. 已知△ABC的六个元素,下列甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是()A.只有乙B.只有丙C.甲和乙D.乙和丙10. 如图,点B,E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是()A.BC=FD,AC=EDB.∠A=∠DEF,AC=EDC.AC=ED,AB=EFD.∠A=∠DEF,BC=FD二、填空题11. 如图,AB=DE,∠1=∠2,添加一个适当的条件,使△ABC≌△DEC,则需添加的条件是__________(不添加任何辅助线,填一个即可).12. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.13. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN 的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=°.14. 如图所示,AE=AD,∠B=∠C,BE=4,AD=5,则AC=.15. 如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.有下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是.三、解答题16. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放正,沿AC画一条射线AE,则AE就是角平分线,请你说明其中的道理.17. 如图,BM平分∠ABC,D是BM上一点,过点D作DE⊥AB于点E,DF⊥BC于点F,P是BM上的另一点,连接PE,PF.(1)若∠EDF=124°,求∠ABC的度数;(2)求证:PE=PF.18. 如图所示,在一条笔直的海岸线上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸线的距离相等吗?为什么?19. 如图,AD∥BC,AB⊥BC于点B,连接AC,过点D作DE⊥AC于点E,过点B作BF⊥AC于点F.(1)若∠ABF=63°,求∠ADE的度数;DE=BF+EF.20. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下.如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC、BD相交于O,OD⊥CD,垂足为D.已知AB=20米,请根据上述信息求标语CD的长度.人教版 八年级数学上册 12.2 全等三角形的判定 课时训练-答案一、选择题 1. 【答案】B2. 【答案】A3. 【答案】A[解析] ①②符合证明三角形全等的判定方法“SAS”.③④中相等的角所对的边不相等,所以不可能全等.故选A.4. 【答案】C5. 【答案】C[解析] 还需添加条件∠1=∠2.理由:∵∠1=∠2,∴∠1+∠EAC =∠2+∠EAC ,即∠BAC =∠DAE. 在△ABC 和△ADE 中,⎩⎨⎧AB =AD ,∠BAC =∠DAE ,AC =AE ,∴△ABC ≌△ADE(SAS).6. 【答案】B7. 【答案】C[解析] ①∵BE ⊥AC ,CF ⊥AB ,∴∠CFB =∠BEC =90°.在Rt △BCF 和Rt △CBE 中,⎩⎨⎧CF =BE ,BC =CB ,∴Rt △BCF ≌Rt △CBE(HL).②∵BE ⊥AC ,CF ⊥AB ,∴∠AFC =∠AEB =90°.在△ABE 和△ACF 中,⎩⎨⎧∠AEB =∠AFC ,∠A =∠A ,BE =CF ,∴△ABE ≌△ACF(AAS). ③设BE 与CF 相交于点O. ∵BE ⊥AC ,CF ⊥AB , ∴∠OFB =∠OEC =90°.∵△ABE ≌△ACF ,∴AB =AC ,AE =AF. ∴BF =CE.在△BOF 和△COE 中,⎩⎨⎧∠OFB =∠OEC ,∠BOF =∠COE ,BF =CE ,∴△BOF ≌△COE(AAS).8. 【答案】A9. 【答案】D10. 【答案】C[解析] A .添加BC=FD ,AC=ED ,可利用“SAS”判定△ABC ≌△EFD ;B .添加∠A=∠DEF ,AC=ED ,可利用“ASA”判定△ABC ≌△EFD ; C .添加AC=ED ,AB=EF ,不能判定△ABC ≌△EFD ;D .添加∠A=∠DEF ,BC=FD ,可利用“AAS”判定△ABC ≌△EFD.二、填空题11. 【答案】答案不唯一,如∠B =∠E12. 【答案】AB =AC13. 【答案】125[解析] 由题意可得AD 平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°. 14. 【答案】915. 【答案】①②③[解析] 由△ABO ≌△ADO ,得AB=AD ,∠AOB=∠AOD=90°,∠BAC=∠DAC.又因为AC=AC ,所以△ABC ≌△ADC ,则CB=CD.所以①②③正确.三、解答题16. 【答案】解:在△ABC 与△ADC 中,⎩⎨⎧AB =AD ,BC =DC ,AC =AC ,∴△ABC ≌△ADC(SSS).∴∠BAC =∠DAC ,即AE 平分∠BAD.17. 【答案】解:(1)∵DE ⊥AB ,DF ⊥BC , ∴∠DEB =∠DFB =90°. ∵∠EDF =124°,∴∠ABC =360°-90°-90°-124°=56°.(2)证明:∵BM 平分∠ABC ,DE ⊥AB ,DF ⊥BC , ∴∠ABM =∠CBM ,DE =DF.∵∠BDE =90°-∠ABM ,∠BDF =90°-∠CBM , ∴∠BDE =∠BDF. ∴∠EDP =∠FDP.在△EDP 和△FDP 中,⎩⎨⎧DE =DF ,∠EDP =∠FDP ,DP =DP ,∴△EDP ≌△FDP(SAS).∴PE =PF.18. 【答案】解:相等.理由:设AD ,BC 相交于点O.∵∠CAD=∠CBD ,∠COA=∠DOB , ∴由三角形内角和定理,得∠C=∠D. 由已知得∠CAB=∠DBA=90°. 在△CAB 和△DBA 中,∴△CAB ≌△DBA. ∴CA=DB.∴海岛C ,D 到观测点A ,B 所在海岸线的距离相等.19. 【答案】解:(1)∵AD ∥BC ,AB ⊥BC , ∴∠ABC =∠BAD =90°. ∵DE ⊥AC ,BF ⊥AC , ∴∠BFA =∠AED =90°.∴∠ABF +∠BAF =∠BAF +∠DAE =90°. ∴∠DAE =∠ABF =63°.∴∠ADE =27°.(2)证明:由(1)得∠DAE =∠ABF ,∠AED =∠BFA =90°.在△DAE 和△ABF 中,⎩⎨⎧∠DAE =∠ABF ,∠AED =∠BFA ,AD =BA ,∴△DAE ≌△ABF(AAS). ∴AE =BF ,DE =AF.∴DE =AF =AE +EF =BF +EF.20. 【答案】解:∵AB ∥CD ,OD ⊥CD , ∴OB ⊥AB ,∵相邻两平行线间的距离相等, ∴OB =OD.(3分)在△ABO 与△CDO 中,⎩⎨⎧∠ABO =∠CDOOB =OD∠AOB =∠COD, ∴△ABO ≌△CDO(ASA ),(6分) ∴CD =AB =20(米).(7分)。
人教八年级数学上册第12章三角形全等判定》同步练习及(含答案)(2)

人教八年级数学上册第12章三角形全等判定》同步练习及〖含答案〗(2)一﹨选择题1. 如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件( )A.∠1=∠2B.∠B=∠CC.∠D=∠ED.∠BAE=∠CAD2. 能判定△ABC≌△A′B′C′的条件是〖〗A.AB=A′B′,AC=A′C′,∠C=∠C′B. AB=A′B′,∠A=∠A′,BC=B′C′C. AC=A′C′,∠A=∠A′,BC=B′CD. AC=A′C′,∠C=∠C′,BC=B′C3. 如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是( )A. AB∥CDB. AD∥BCC. ∠A=∠CD. ∠ABC=∠CDA4.〖2013•铁岭〗如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是〖〗A.BC=EC,∠B=∠E B.BC=EC,AC=DCC.BC=DC,∠A=∠D D.AC=DC,∠A=∠D5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC﹨BD相交于点O,则图中全等三角形共有〖〗A.1对 B.2对 C.3对 D.4对6.在△ABC和CBA'''∆中,∠C=C'∠,b-a=ab'-',b+a=ab'+',则这两个三角形〖〗A. 不一定全等B.不全等C. 全等,根据“ASA”D. 全等,根据“SAS”第1题第3题图第4题图第5题图7.如图,已知AD 是△ABC 的BC 边上的高,下列能使△ABD ≌△ACD 的条件是〖 〗A .AB=ACB .∠BAC=90°C .BD=ACD .∠B=45°8.如图,梯形ABCD 中,AD ∥BC ,点M 是AD 的中点,且MB=MC ,若AD=4,AB=6,BC=8,则梯形ABCD 的周长为〖 〗A .22B .24C .26D .28 二﹨填空题9. 如图,已知BD=CD ,要根据“SAS ”判定△ABD ≌△ACD ,则还需添加的条件是.10.如图,AC 与BD 相交于点O ,若AO=BO ,AC =BD ,∠DBA=30°,∠DAB=50°, 则∠CBO= 度.11.如图,点B ﹨F ﹨C ﹨E 在同一条直线上,点A ﹨D 在直线BE 的两侧,AB ∥DE ,BF =CE ,请添加一个适当的条件: ,第9题图第7题图第8题图第10题图第11题图使得AC =DF .12.如图,已知AD AB =,DAC BAE ∠=∠,要使 ABC △≌ADE △,可补充的条件是 〖写出一个即可〗. 13.如图,OA=OB ,OC=OD ,∠O=60°,∠C=25°,则 ∠BED= 度.14. 如图,若AO=DO ,只需补充 就可以根据SAS 判定△AOB ≌△DOC.15. 如图,已知△ABC ,BA=BC ,BD 平分∠ABC ,若∠C=40°,则∠ABE 为度.16.在Rt △ABC 中,∠ACB=90°,BC=2cm ,CD ⊥AB ,在AC 上取一点E ,使EC=BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF=5cm ,则 AE= cm .40︒D CBAE17. 已知:如图,DC=EB ,EC=BA ,DC ⊥AC , BA ⊥AC ,垂足分别是C ﹨A ,则AE 与DE 的位置关系是 .ACE B 0CEDB A第13题图第14题图第12题图第15题图第16题图第17题图D18. △ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是 .三﹨解答题19. 如图,点A﹨F﹨C﹨D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.20.已知:如图,点A﹨B﹨C﹨D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE=∠DBF.21.如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.22. 如图,AB=AC,点E﹨F分别是AB﹨AC的中点,求证:△AFB≌△AEC.23.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。
人教版八年级上册12.2全等三角形的性质与判定的综合运用(第二课时)课件

∴CF=DF. ∴点F是CD的中点.
例 如图,点A ,B ,C ,D在一条直线上,且AB=CD, 若∠1=∠2,EC=FB.求证:∠E=∠F.
E
F
H
1
2
AB
CD
∵∠ABC=∠BCD=180°,
分析: 要证∠E=∠F. ②有公共边,公共边一定是对应边,有公共角的,公共角
求证:AB=DE, AC=DF.
课后作业 1. 如图,AC,BD交与点O, AC=BD, AB=CD.
求证:(1)∠C=∠B (2)OA=OD.
2. 如图, AB=AC, AE=AD, ∠1= ∠2. 求证: BD=CE.
D
C
O
A
B
A
12
B
C
E
D
同学们,再见!
A
??
B F
在△ABC和△DEF中,
B E,
BC EF,
ACB DFE,
C
?
E
?
D
∴△ABC≌△DEF (ASA).
∴AB=DE , AC=DF.
课堂小结
证明题的分析思路: ①要证什么 ②已有什么 ③还缺什么 ④推导条件
课堂小结 全等三角形,是证明两条线段或两个角相等的重要方法 之一,证明时:
P
?
D
34
C
找到已知和求证 间的联系
证明: 在△ABC和△DBC中,
1 2, BC BC, 3 4,
B
在△ABP和△DBP中,
AB DB,
1
2,
12 P
A ??D
34
BP
BP,
C
∴△ABP≌△DBP(SAS).
∴△ABC≌△DBC(ASA) . ∴PA=PD.
