全等三角形的判定与性质专题训练
专题06 三角形综合的压轴真题训练(解析版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学选择、填空压轴真题汇编专题06三角形综合的压轴真题训练一.全等三角形的判定与性质1.(2022•淄博)如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为()A.6B.7C.8D.9【答案】B【解答】解:如图,连接AI,BI,CI,DI,过点I作IT⊥AC于点T.∵I是△ABD的内心,∴∠BAI=∠CAI,∵AB=AC,AI=AI,∴△BAI≌△CAI(SAS),∴IB=IC,∵∠ITD=∠IED=90°,∠IDT=∠IDE,DI=DI,∴△IDT≌△IDE(AAS),∴DE=DT,IT=IE,∵∠BEI=∠CTI=90°,∴Rt△BEI≌Rt△CTI(HL),∴BE=CT,设BE=CT=x,∵DE=DT,∴10﹣x=x﹣4,∴x=7,∴BE=7.故选:B.2.(2022•湘西州)如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是()A.24B.22C.20D.18【答案】B【解答】解:∵CG∥AB,∴∠B=∠MCG,∵M是BC的中点,∴BM=CM,在△BMH和△CMG中,,∴△BMH≌△CMG(ASA),∴HM=GM,BH=CG,∵AB=6,AC=8,∴四边形ACGH的周长=AC+CG+AH+GH=AB+AC+GH=14+GH,∴当GH最小时,即MH⊥AB时四边形ACGH的周长有最小值,∵∠A=90°,MH⊥AB,∴GH∥AC,∴四边形ACGH为矩形,∴GH=8,∴四边形ACGH的周长最小值为14+8=22,故选:B.3.(2022•南充)如图,正方形ABCD边长为1,点E在边AB上(不与A,B 重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论是.(填写序号)【答案】①②③【解答】解:∵四边形ABCD是正方形,∴BA=BC,∠ABC=90°,∵∠A1BA2=∠ABC=90°,∴∠ABA1=∠CBA2,∵BA1=BA2,∴△ABA1≌△CBA2(SAS),故①正确,过点D作DT⊥CA1于点T,∵CD=DA1,∴∠CDT=∠A1DT,∵∠ADE=∠A1DE,∠ADC=90°,∴∠ADE+∠CDT=45°,∵∠CDT+∠DCT=90°,∠DCT+∠BCA1=90°,∴∠CDT=∠BCA1,∴∠ADE+∠BCA1=45°,故②正确.连接P A,AC.∵A,A1关于DE对称,∴P A=PA1,∴P A1+PC=PA+PC≥AC=,∴P A1+PC的最小值为,故③正确,过点A1作A1H⊥AB于点H,∵∠ADE=30°,∴AE=A1E=AD•tan30°=,∴EB=AB﹣AE=1﹣,∵∠A1EB=60°,∴A1H=A1E•sin60°=×=,∴=×(1﹣)×=,故④错误.故答案为:①②③.4.(2022•朝阳)等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD 为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为.【答案】3或.【解答】解:如图,E点在AD的右边,∵△ADE与△ABC都是等边三角形,∴AC=AB,AE=AD,∠DAE=∠BAC=60°,∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,即∠CAE=∠BAD.在△CAE和△BAD中,,∴△CAE≌△BAD(SAS),∴CE=BD=2,∵BD=2CD,∴CD=1,∴BC=BD+CD=2+1=3,∴等边三角形ABC的边长为3,如图,E点在AD的左边,同上,△BAE≌△CAD(SAS),∴BE=CD,∠ABE=∠ACD=60°,∴∠EBD=120°,过点E作EF⊥BC交CB的延长线于点F,则∠EBF=60°,∴EF=BE=CD,BF=BE=CD,∴CF=BF+BD+CD=CD,在Rt△EFC中,CE=2,∴EF2+CF2=CE2=4,∴+=4,∴CD=或CD=﹣(舍去),∴BC=,∴等边三角形ABC的边长为,故答案为:3或.5.(2022•日照)如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P 是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是.【答案】2【解答】解:方法一:∵将线段P A绕点P顺时针旋转60°得到线段PF,∴∠APF=60°,PF=PA,∴△APF是等边三角形,∴AP=AF,如图,当点F1在x轴上时,△P1AF1为等边三角形,则P1A=P1F1=AF1,∠AP1F1=60°,∵AO⊥P1F1,∴P1O=F1O,∠AOP1=90°,∴∠P1AO=30°,且AO=4,由勾股定理得:P1O=F1O=,∴P1A=P1F1=AF1=,∴点F1的坐标为(,0),如图,当点F2在y轴上时,∵△P2AF2为等边三角形,AO⊥P2O,∴AO=F2O=4,∴点F2的坐标为(0,﹣4),∵tan∠OF1F2===,∴∠OF1F2=60°,∴点F运动所形成的图象是一条直线,∴当OF⊥F1F2时,线段OF最短,设直线F1F2的解析式为y=kx+b,则,解得,∴直线F1F2的解析式为y=x﹣4,∵AO=F2O=4,AO⊥P1F1,∴F1F2=AF1=,在Rt△OF1F2中,设点O到F1F2的距离为h,则×OF1×OF2=×F1F2×h,∴××4=××h,解得h=2,即线段OF的最小值为2;方法二:如图,在第二象限作等边三角形AOB,连接BP、AF,过点B作BP′⊥x轴于点P′,∵将线段P A绕点P顺时针旋转60°得到线段PF,∴∠APF=60°,PF=PA,∴△APF是等边三角形,∴AP=AF,∠PAF=60°,∵△AOB是等边三角形,∴AB=AO=OB=4,∠BAO=60°,∴∠BAP=60°+∠OAP=∠OAF,在△BAP和△OAF中,,∴△BAP≌△OAF(SAS),∴BP=OF,∵P是x轴上一动点,∴当BP⊥x轴时,BP最小,即点P与点P′重合时BP=BP′最小,∵∠BOP′=30°,∠BP′O=90°,∴BP′=OB=×4=2,∴OF的最小值为2,故答案为2.二.勾股定理6.(2022•内江)勾股定理被记载于我国古代的数学著作《周髀算经》中,汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.图②由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD、正方形EFGH、正方形MNXT的面积分别为S1、S2、S3.若正方形EFGH的边长为4,则S1+S2+S3=.【答案】48【解答】解:设八个全等的直角三角形的长直角边为a,短直角边是b,则:S1=(a+b)2,S2=42=16,S3=(a﹣b)2,且:a2+b2=EF2=16,∴S1+S2+S3=(a+b)2+16+(a﹣b)2=2(a2+b2)+16=2×16+16=48.故答案为:48.7.(2022•常州)如图,在Rt△ABC中,∠C=90°,AC=9,BC=12.在Rt △DEF中,∠F=90°,DF=3,EF=4.用一条始终绷直的弹性染色线连接CF,Rt△DEF从起始位置(点D与点B重合)平移至终止位置(点E与点A 重合),且斜边DE始终在线段AB上,则Rt△ABC的外部被染色的区域面积是.【答案】21【解答】解:如图,连接CF交AB于点M,连接CF′交AB于点N,过点F 作FG⊥AB于点H,过点F′作F′H⊥AB于点H,连接FF′,则四边形FGHF′是矩形,Rt△ABC的外部被染色的区域是梯形MFF′N.在Rt△DEF中,DF=3,EF=4,∴DE===5,在Rt△ABC中,AC=9,BC=12,∴AB===15,∵•DF•EF=•DE•GF,∴FG=,∴BG===,∴GE=BE﹣BG=,AH=GE=,∴F′H=FG=,∴FF′=GH=AB﹣BG﹣AH=15﹣5=10,∵BF∥AC,∴==,∴BM=AB=,同法可证AN=AB=,∴MN=15﹣﹣=,∴Rt△ABC的外部被染色的区域的面积=×(10+)×=21,故答案为:21.8.(2022•武汉)如图,在Rt△ABC中,∠ACB=90°,AC>BC,分别以△ABC的三边为边向外作三个正方形ABHL,ACDE,BCFG,连接DF.过点C作AB的垂线CJ,垂足为J,分别交DF,LH于点I,K.若CI=5,CJ=4,则四边形AJKL的面积是.【答案】80【解答】解:过点D作DM⊥CI,交CI的延长线于点M,过点F作FN⊥CI 于点N,∵△ABC为直角三角形,四边形ACDE,BCFG为正方形,过点C作AB的垂线CJ,CJ=4,∴AC=CD,∠ACD=90°,∠AJC=∠CMD=90°,∠CAJ+∠ACJ=90°,BC=CF,∠BCF=90°,∠CNF=∠BJC=90°,∠FCN+∠CFN=90°,∴∠ACJ+∠DCM=90°,∠FCN+∠BCJ=90°,∴∠CAJ=∠DCM,∠BCJ=∠CFN,∴△ACJ≌△CDM(AAS),△BCJ≌△CFN(AAS),∴AJ=CM,DM=CJ=4,BJ=CN,NF=CJ=4,∴DM=NF,∴△DMI≌△FNI(AAS),∴DI=FI,MI=NI,∵∠DCF=90°,∴DI=FI=CI=5,在Rt△DMI中,由勾股定理可得:MI===3,∴NI=MI=3,∴AJ=CM=CI+MI=5+3=8,BJ=CN=CI﹣NI=5﹣3=2,∴AB=AJ+BJ=8+2=10,∵四边形ABHL为正方形,∴AL=AB=10,∵四边形AJKL为矩形,∴四边形AJKL的面积为:AL•AJ=10×8=80,故答案为:80.三.等腰直角三角形(共2小题)9.(2022•宜宾)如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE =90°,点D是BC边上的动点(不与点B、C重合),DE与AC交于点F,连结CE.下列结论:①BD=CE;②∠DAC=∠CED;③若BD=2CD,则=;④在△ABC内存在唯一一点P,使得PA+PB+PC的值最小,若点D 在AP的延长线上,且AP的长为2,则CE=2+.其中含所有正确结论的选项是()A.①②④B.①②③C.①③④D.①②③④【答案】B【解答】解:如图1中,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=EC,∠ADB=∠AEC,故①正确,∵∠ADB+∠ADC=180°,∴∠AEC+∠ADC=180°,∴∠DAE+∠DCE=180°,∴∠DAE=∠DCE=90°,取DE的中点O,连接OA,OA,OC,则OA=OD=OE=OC,∴A,D,C,E四点共圆,∴∠DAC=∠CED,故②正确,设CD=m,则BD=CE=2m.DE=m,OA=m,过点C作CJ⊥DF于点J,∵tan∠CDF===2,∴CJ=m,∵AO⊥DE,CJ⊥DE,∴AO∥CJ,∴===,故③正确.如图2中,将△BPC绕点B顺时针旋转60°得到△BNM,连接PN,∴BP=BN,PC=NM,∠PBN=60°,∴△BPN是等边三角形,∴BP=PN,∴P A+PB+PC=AP+PN+MN,∴当点A,点P,点N,点M共线时,PA+PB+PC值最小,此时∠APB=∠APC =∠BPC=120°,PB=PC,AD⊥BC,∴∠BPD=∠CPD=60°,设PD=t,则BD=AD=t,∴2+t=t,∴t=+1,∴CE=BD=t=3+,故④错误.故选:B.10.(2022•绵阳)如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC =45°,AC与BD交于点E,若AB=2,CD=2,则△ABE的面积为.【答案】【解答】解:过点D作DF⊥AC于点F,∵AC⊥BC,∠ABC=45°,∴AC=BC=AB=2,∵∠ADC=90°,CD=2,∴AD=,∵,∴DF=,∴AF=,∴CF=,∵DF∥BC,∴△DEF∽△BEC,∴,即,∴EF=,∴AE=,∴.故答案为:.11.(2022•安徽)已知点O是边长为6的等边△ABC的中心,点P在△ABC 外,△ABC,△PAB,△PBC,△PCA的面积分别记为S0,S1,S2,S3.若S1+S2+S3=2S0,则线段OP长的最小值是()A.B.C.3D.【答案】B【解答】解:如图,不妨假设点P在AB的左侧,+S△ABC=S△PBC+S△P AC,∵S△P AB∴S1+S0=S2+S3,∵S1+S2+S3=2S0,∴S1+S1+S0=2,∴S1=S0,∵△ABC是等边三角形,边长为6,∴S0=×62=9,∴S1=,过点P作AB的平行线PM,连接CO延长CO交AB于点R,交PM于点T.∵△P AB的面积是定值,∴点P的运动轨迹是直线PM,∵O是△ABC的中心,∴CT⊥AB,CT⊥PM,∴•AB•RT=,CR=3,OR=,∴RT=,∴OT=OR+TR=,∵OP≥OT,∴OP的最小值为,当点P在②区域时,同法可得OP的最小值为,如图,当点P在①③⑤区域时,OP的最小值为,当点P在②④⑥区域时,最小值为,∵<,故选:B.12.(2022•温州)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连结CF,作GM⊥CF于点M,BJ⊥GM于点J,AK⊥BJ于点K,交CF于点L.若正方形ABGF与正方形JKLM的面积之比为5,CE=+,则CH的长为()A.B.C.2D.【答案】C【解答】解:设CF交AB于点P,过C作CN⊥AB于点N,如图:设正方形JKLM边长为m,∴正方形JKLM面积为m2,∵正方形ABGF与正方形JKLM的面积之比为5,∴正方形ABGF的面积为5m2,∴AF=AB=m,由已知可得:∠AFL=90°﹣∠MFG=∠MGF,∠ALF=90°=∠FMG,AF =GF,∴△AFL≌△FGM(AAS),∴AL=FM,设AL=FM=x,则FL=FM+ML=x+m,在Rt△AFL中,AL2+FL2=AF2,∴x2+(x+m)2=(m)2,解得x=m或x=﹣2m(舍去),∴AL=FM=m,FL=2m,∵tan∠AFL====,∴=,∴AP=,∴FP===m,BP=AB﹣AP=m﹣=,∴AP=BP,即P为AB中点,∵∠ACB=90°,∴CP=AP=BP=,∵∠CPN=∠APF,∠CNP=90°=∠FAP,∴△CPN∽△FPA,∴==,即==,∴CN=m,PN=m,∴AN=AP+PN=m,∴tan∠BAC====,∵△AEC和△BCH是等腰直角三角形,∴△AEC∽△BCH,∴=,∵CE=+,∴=,∴CH=2,故选:C.13.(2022•湖州)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是()A.4B.6C.2D.3【答案】C【解答】解:如图所示:∵BM=NC=4,BN=CP=2,且∠B=∠C=90°,∴△BMN≌△CNP(SAS),∴MN=NP,∠BMN=∠CNP,∵∠BMN+∠BNM=90°,∴∠BNM+∠CNP=90°,∴∠MNP=90°,∴△NMP为等腰直角三角形,根据题意得到点P的轨迹为圆弧,当MP为直径时最长,在Rt△BMN和Rt△NCP中,根据勾股定理得:MN=NP==2,则PM==2.故选:C.14.(2022•苏州)如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为()A.B.C.D.【答案】C【解答】解:过C作CD⊥x轴于点D,CE⊥y轴于点E,如图:∵CD⊥x轴,CE⊥y轴,∠DOE=90°,∴四边形EODC是矩形,∵将线段AB绕点A按逆时针方向旋转60°得到线段AC,∴AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴AB=AC=BC,∵A(0,2),C(m,3),∴CE=m=OD,CD=3,OA=2,∴AE=OE﹣OA=CD﹣OA=1,∴AC===BC=AB,在Rt△BCD中,BD===,在Rt△AOB中,OB===,∵OB+BD=OD=m,∴+=m,化简变形得:3m4﹣22m2﹣25=0,解得m=或m=﹣(舍去),∴m=,故选:C.三.等腰直角三角形(共1小题)15.(2022•成都)如图,在△ABC中,按以下步骤作图:①分别以点B和C 为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN 交边AB于点E.若AC=5,BE=4,∠B=45°,则AB的长为.【答案】7【解答】解:设MN交BC于D,连接EC,如图:由作图可知:MN是线段BC的垂直平分线,∴BE=CE=4,∴∠ECB=∠B=45°,∴∠AEC=∠ECB+∠B=90°,在Rt△ACE中,AE===3,∴AB=AE+BE=3+4=7,故答案为:7.四.等边三角形的性质(共2小题)16.(2022•张家界)如图,点O是等边三角形ABC内一点,OA=2,OB=1,OC=,则△AOB与△BOC的面积之和为()A.B.C.D.【答案】C【解答】解:将△AOB绕点B顺时针旋转60°得△CDB,连接OD,∴OB=BD,∠OBD=60°,CD=OA=2,∴△BOD是等边三角形,∴OD=OB=1,∵OD2+OC2=12+()2=4,CD2=22=4,∴OD2+OC2=CD2,∴∠DOC=90°,+S△BCD=S△BOD+S△COD=×∴△AOB与△BOC的面积之和为S△BOC12+=,故选:C.17.(2022•鄂州)如图,在边长为6的等边△ABC中,D、E分别为边BC、AC 上的点,AD与BE相交于点P,若BD=CE=2,则△ABP的周长为.【答案】【解答】解:∵△ABC是等边三角形,∴AB=BC,∠ABD=∠C=60°,在△ABD和△BCE中,∴△ABD≌△BCE(SAS),∴∠BAD=∠CBE,∴∠APE=∠ABP+∠BAD=∠ABP+∠CBE=∠ABD=60°,∴∠APB=120°,在CB上取一点F使CF=CE=2,则BF=BC﹣CF=4,∴∠C=60°,∴△CEF是等边三角形,∴∠BFE=120°,即∠APB=∠BFE,∴△APB∽△BFE,∴==2,设BP=x,则AP=2x,作BH⊥AD延长线于H,∵∠BPD=∠APE=60°,∴∠PBH=30°,∴PH=,BH=,∴AH=AP+PH=2x+=x,在Rt△ABH中,AH2+BH2=AB2,即(x)2+(x)2=62,解得x=或﹣(舍去),∴AP=,BP=,∴△ABP的周长为AB+AP+BP=6++=6+=,故答案为:.五.含30度角的直角三角形(共1小题)18.(2022•十堰)【阅读材料】如图①,四边形ABCD中,AB=AD,∠B+∠D=180°,点E,F分别在BC,CD上,若∠BAD=2∠EAF,则EF=BE+DF.【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形ABCD.已知CD=CB=100m,∠D=60°,∠ABC=120°,∠BCD=150°,道路AD,AB上分别有景点M,N,且DM=100m,BN=50(﹣1)m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少m (结果取整数,参考数据:≈1.7).【答案】370【解答】解:解法一:如图,延长DC,AB交于点G,过点N作NH⊥AD于H,∵∠D=60°,∠ABC=120°,∠BCD=150°,∴∠A=360°﹣60°﹣120°﹣150°=30°,∴∠G=90°,∴AD=2DG,Rt△CGB中,∠BCG=180°﹣150°=30°,∴BG=BC=50,CG=50,∴DG=CD+CG=100+50,∴AD=2DG=200+100,AG=DG=150+100,∵DM=100,∴AM=AD﹣DM=200+100﹣100=100+100,∵BG=50,BN=50(﹣1),∴AN=AG﹣BG﹣BN=150+100﹣50﹣50(﹣1)=150+50,Rt△ANH中,∵∠A=30°,∴NH=AN=75+25,AH=NH=75+75,由勾股定理得:MN===50(+1),∴AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.解法二:如图,延长DC,AB交于点G,连接CN,CM,则∠G=90°,∵CD=DM,∠D=60°,∴△DCM是等边三角形,∴∠DCM=60°,由解法一可知:CG=50,GN=BG+BN=50+50(﹣1)=50,∴△CGN是等腰直角三角形,∴∠GCN=45°,∴∠BCN=45°﹣30°=15°,∴∠MCN=150°﹣60°﹣15°=75°=∠BCD,由【阅读材料】的结论得:MN=DM+BN=100+50(﹣1)=50+50,∵AM+AN﹣MN=100+100+150+50﹣50(+1)=200+100≈370(m).答:路线M→N的长比路线M→A→N的长少370m.故答案为:370.六.等腰直角三角形(共2小题)19.(2022•长沙)如图,在△ABC中,按以下步骤作图:①分别以点A、B为圆心,大于AB的长为半径画弧,两弧交于P、Q两点;②作直线PQ交AB于点D;③以点D为圆心,AD长为半径画弧交PQ于点M,连接AM、BM.若AB=2,则AM的长为()A.4B.2C.D.【答案】B【解答】解:由作图可知,PQ是AB的垂直平分线,∴AM=BM,∵以点D为圆心,AD长为半径画弧交PQ于点M,∴DA=DM=DB,∴∠DAM=∠DMA,∠DBM=∠DMB,∵∠DAM+∠DMA+∠DBM+∠DMB=180°,∴2∠DMA+2∠DMB=180°,∴∠DMA+∠DMB=90°,即∠AMB=90°,∴△AMB是等腰直角三角形,∴AM=AB=×2=2,故选:B.20.(2022•河南)如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,点D 为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P 的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为.【答案】或【解答】解:如图:∵∠ACB=90°,AC=BC=2,∴AB=AC=4,∵点D为AB的中点,∴CD=AD=AB=2,∠ADC=90°,∵∠ADQ=90°,∴点C、D、Q在同一条直线上,由旋转得:CQ=CP=CQ′=1,分两种情况:当点Q在CD上,在Rt△ADQ中,DQ=CD﹣CQ=1,∴AQ===,当点Q在DC的延长线上,在Rt△ADQ′中,DQ′=CD+CQ′=3,∴AQ′===,综上所述:当∠ADQ=90°时,AQ的长为或,故答案为:或.。
初中数学 三角形全等的判定专题训练题
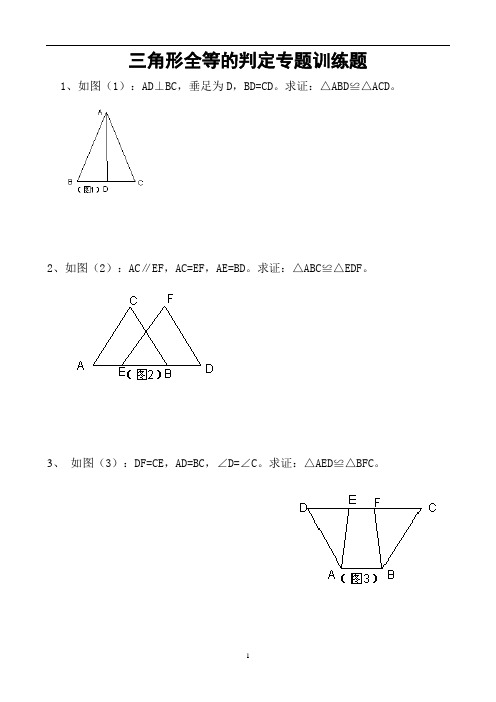
三角形全等的判定专题训练题1、如图(1):AD⊥BC,垂足为D,BD=CD。
求证:△ABD≌△ACD。
2、如图(2):AC∥EF,AC=EF,AE=BD。
求证:△ABC≌△EDF。
3、如图(3):DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
4、如图(4):AB=AC,AD=AE,AB⊥AC,AD⊥AE。
求证:(1)∠B=∠C,(2)BD=CE(5)在一次数学课上,李老师在黑板上画出图6,并写下了四个等式①AB = DC ②BE =CE③∠B =∠C④∠BAE =∠CDE..要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形;请你试着完成李老师提出的要,并说明理由。
(写出一种即可)已知:求证:△AED是等腰三角形5、如图(5):AB⊥BD,ED⊥BD,AB=CD,BC=DE。
求证:AC⊥CE。
6、如图(6):CG=CF,BC=DC,AB=ED,点A、B、C、D、E在同一直线上。
求证:(1)AF=EG,(2)BF∥DG。
7、如图(7):AC⊥BC,BM平分∠ABC且交AC于点M、N是AB的中点且BN=BC。
求证:(1)MN平分∠AMB,(2)∠A=∠CBM。
8、如图(8):A、B、C、D四点在同一直线上,AC=DB,BE∥CF,AE∥DF。
求证:△ABE≌△DCF。
9、如图(9)AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
求证:AM是△ABC的中线。
(6)复习“全等三角形”的知识时李老师布置了一道作业题“如图①已知:在△ABC 中,AB=AC,P 是△ABC 内部任意一点,将AP 绕A 顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP;则BQ=CP..”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP 之后,将点P 移到等腰三角形ABC 之外,原题中的条件不变,发现“BQ=CP”仍然成立..请你就图②给出证明。
三角形全等判定专题训练题

三角形全等判定专题训练题1.给定三角形ABC,AD垂直于BC,垂足为D,且BD=CD。
证明△ABD≌△ACD。
2.给定平行四边形ABCD,AC=EF,AC平行于EF,且F在AD上。
证明△ABC≌△EDF。
3.给定三角形ABC和DEF,DF=CE,AD=BC,∠D=∠C。
证明△AED≌△BFC,其中AE=BD。
4.给定等腰直角三角形ABC,AB=AC,AD=AE,AB垂直于AC,AD垂直于AE。
证明∠B=∠C且BD=CE。
6.给定四边形ABCDE,CG=CF,BC=DC,AB=ED,且A、B、C、D、E在同一直线上。
证明AF=EG且BF平行于DG。
7.给定三角形ABC,AC垂直于BC,___平分∠ABC,且交AC于点M,N是AB的中点,且BN=BC。
证明___平分∠AMB且∠A=∠___。
8.给定四边形ABCD,AC=DB,BE平行于CF,AE平行于DF。
证明△ABE≌△DCF。
9.给定三角形ABC,AE和BC相交于点M,F在AM上,BE平行于CF,且BE=CF。
证明AM是△ABC的中线。
10.给定四边形ABCD,且∠BAC=∠DAE,∠ABD=∠ACE,BD=CE。
证明AB=AC。
11.给定三角形ABC和△DBC,且∠1=∠2,∠3=∠4,P是BC上的任意一点。
证明PA=PD。
12.给定四边形ABCD,AB平行于CD,OA=OD,且F、D、O、A、E在同一直线上,AE=DF。
证明EB平行于CF。
13.给定三角形ABC和△EDC,且△ABC≌△EDC。
证明BE=AD。
14.给定等腰直角三角形ABC,AC=BC,AE是BC的中线,CF⊥AE于F,BD⊥CB交CF的延长线于点D。
证明AB=BD。
15、证明:由图可知,∠BAC=90°,且AB=2AC,因此由勾股定理可得BC=√5AC,而DE=AC,BF=2AC,EF=BC-AC=√5AC-AC=(√5-1)AC,因此AE=AC+EF=2AC+(√5-1)AC=(1+√5)AC,所以△ABC≌△AED。
2024年中考全等三角形的性质与判定专题训练

E B C A DF 2024年中考全等三角形的性质与判定专题训练1.如图,AB =AD ,CB =CD .求证:∠B =∠D .2.如图,点A 、E 、B 、D 在同一条直线上,AE=DB ,AC=DF ,AC ∥DF.请探索BC 与EF 有怎样的位置关系?并说明理由。
3.如图,点B 、D 、C 、F 在同一直线,AB =EF ,∠B =∠F ,BD =CF ,试说明△ABC ≌△EFD .4. 如图,点E ,F 在线段BD 上,已知AF ⊥BD ,CE ⊥BD ,AD=CB ,DE=BF .求证:△AFD ≌△CEB .5.如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.(1)求证:△ABE≌△DCE;(2)当AB=5时,求CD的长.6.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.7.如图,在矩形ABCD中,点E,F在对角线BD上.请添加一个条件,使得结论“AE=CF”成立,并加以证明.8.如图,已知点E在AB上,点C在AD,AB=AC,AD=AE。
求证:BE=CD。
9.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF求证:(1) △ABC≌△DEF(2)AB∥DE9.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:AB=DE.11.如图,已知点B,C,D,E在一条直线上,AB∥FC,AB=FC,BC=DE.求证:AD∥FE.12.如图,∠A =∠D =90°,AC =DB ,AC 、DB 相交于点O .求证:AB =CD .13.已知:如图,AE 和BD 相交于点,,C AC EC BC DC ==;求证:.AB ED =14.已知如图:点C E B F ,,,在同一直线上,∠C=∠F,AC DF =, BF CE =.求证:DEF ABC ∆≅∆。
15.如图,AD∥BC,点E 是CD 的中点,BE 的延长线与AD 的延长线交于点F .则△BCE 和△FDE 全等吗?为什么?A FB EC D16.如图,为一块直角三角板,将CA绕点C顺时针旋转,使得点A落在边AB上的点D处.(1)过点C作于点E,求证:△ACE∽△ABC(2)求BD的长.。
中考数学复习之全等三角形的性质与判定,考点过关与基础练习题

21.三角形全等➢知识过关1.全等三角形:能够完全重合的两个三角形叫全等三角形.2.全等三角形的性质:全等三角形的_________相等,________相等.3.全等三角形的判定定理:(1)一般三角形有________,_________,________,_________(2)直角三角形还有___________4.角平分线的性质及判定(1)角平分线上的点到角两边的______相等.(2)角的内部到角两边的________相等的点在角的平分线上.➢考点分类考点1探究三角形的全等条件例1如图,若△ABC≌△ADE,则下列结论中一定成立的是()A.AD=DC B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED 考点2全等三角形的性质与判定例2如图,∠1=∠2,AB=AE,添加一个条件,使得△ABC≌△AED.考点3角平分线的性质及判定例3如图所示,已知△ABD≌△CFD,AD⊥BC于D.(1)求证:CE⊥AB;(2)已知BC=7,AD=5,求AF的长.➢真题演练1.如图,若△ABC≌△ADE,则下列结论中一定成立的是()A.AD=DC B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED 2.如图,△ABC≌△DEC,点E在线段AB上,∠B=75°,则∠BCE的度数为()A.30°B.35°C.40°D.45°3.如图,N,C,A三点在同一直线上,N,B,M三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM的度数等于()A.10°B.20°C.30°D.40°4.如图,在△ABC中,∠BCA=90°,CA=CB,AD为边BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于点E.有下列结论:①△ADC≌△CEB;②DF =EF;③F为EG的中点;④∠ADC=∠BDF;⑤G为CF的中点.其中正确的结论有()个.A.4B.3C.2D.15.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,则下列结论不正确的是()A.△ABD≌△ACE B.∠ACE+∠DBC=45°C.BD⊥CE D.∠BAE+∠CAD=200°6.如图,△ABC,△CDE是等边三角形,C为线段AE上一点,则以下五个结论正确的个数有()个.①△CEB≌△CDA②AD=BE③∠AOE=120°④CM=CN⑤OC平分∠BCDA.2B.3C.4D.57.如图,已知:AC=BC,DC=EC,∠ACB=∠ECD=90°,现有下列结论:①△BDC≌△AEC;②若∠EBD=38°,则∠AEB=128°;③BD=AE;④AE所在的直线⊥BD.其中正确的有()A.1个B.2个C.3个D.4个8.下列结论中,正确的有①对顶角相等;②两直线平行,同旁内角相等;③面积相等的两个三角形全等;④有两边和一个角分别对应相等的两个三角形全等;⑤钝角三角形三条高所在的直线交于一点,且这点在钝角三角形外部.()A.2个B.3个C.4个D.5个9.△ABC中,AB=AC=12厘米,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v为厘米/秒.10.如图,△ABC为等边三角形,F,E分别是AB,BC上的一动点,且AF=BE,连结CF,AE交于点H,连接BH.给出下列四个结论:△△AHF=60°;△若BH=HC,则AE平分△BAC;△S四边形BEHF>S△AHC;△若BH△CF,则CH=2HA.其中正确的结论有(填写所有正确结论的序号).11.如图,已知△ABF≌△CDE.(1)若∠B=40°,∠DCF=30°,求∠EFC的度数;(2)若BD=10,EF=4,求BF的长.12.如图,线段AD、BE相交于点C,且△ABC≌△DEC,点M、N分别为线段AC、CD的中点.求证:(1)ME=BN;(2)ME∥BN.➢课后作业1.如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F(点E不与A,B重合),给出以下五个结论中正确的有()①△PF A≌△PEB;②EF=AP;③△PEF是等腰直角三角形;④S四边形AEPF=12S△ABC.A.1个B.2个C.3个D.4个2.如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D,E为BC边上的两点,且∠DAE=45°,连接EF,BF,下列结论:①△AED≌△AEF;②BF=CD;③BE+DC>DE;④BE2+DC2=DE2.其中正确的有()A.1个B.2个C.3个D.4个3.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,如图,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.正确的个数有()A.1个B.2个C.3个D.4个4.已知:如图,△ABC中,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BDC=∠AED;③AE=AD=EC;④S四边形ABCE=BF×EF.其中正确的个数是()A.1个B.2个C.3个D.4个5.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC;⑤若AF=2,则DE=4.其中正确的有()个.A.①②④B.①②④⑤C.①②⑤D.①②③⑤6.如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC边上的动点,DE与CM相交于点F且∠DME=90°.则下列5个结论:(1)图中共有两对全等三角形;(2)△DEM是等腰三角形;(3)∠CDM=∠CFE;(4)AD+BE =AC;(5)四边形CDME的面积发生改变.其中正确的结论有()个.A.2B.3C.4D.57.如图,B、C(O),E四点在同一条直线上,∠B=∠E=90°,AB=CE,请添加一个适当的条件,使得△ABC≌△OEF(只需写一个,不添加辅助线)8.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=11,DE=7,则BE的长为.9.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.(1)当α=150°时,试判断△AOD的形状,并说明理由;(2)探究:当α为多少度时,△AOD是等腰三角形,请说明理由.10.已知,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H.(1)如图1,求证:∠BCE=∠CAD;(2)如图2,过点B作BG⊥AD于G.直接写出图中所有的全等三角形.11.如图,在Rt△ABC中,∠ACB=90°,AC=BC,AE⊥CE,BF⊥CE于点F.(1)求证:△AEC≌△CFB;(2)若AE=5,EF=7,求AB的长.12.如图,在等边△ABC的边AC,BC上各取一点D,E,使AD=CE,AE,BD相交于点O.(1)求证:△ABD≌△CAE;(2)求∠BOE的度数.13.如图:AB=AC,AD=AE,∠CAB=∠EAD,F为BD和CE的交点.(1)求证:BD=CE;(2)连接AF,求证:AF平分∠BFE.14.如图,△ABC和△CDE均为等边三角形,且A,D,E在同一条直线上,连接BD,BE.(1)求证:BE=AD;(2)若∠DBE=90°,求证:AD=12 DE.15.如图,△ACD、△BCE都是等边三角形,BD分别与AE、AC相交于点M、N.(1)证明:BD=AE;(2)求∠AMN的度数.➢冲击A+如图1,半径为3的⊙O中任作一个圆内接△ABC,D为劣弧AC上一动点,连接DA,DB,DC且DB,AC相交于点E.(1)求证:△ADE∽△BCE;(2)如图2,当BD过圆心O时,有DE=1,∠AEB=60°,求此时AC的长;(3)如图3,当D运动到某一位置时,过E作直线垂直于BC,垂足为F,与AD边交于点G,恰有AG=EG,若AB+CD=8,且CD<AB,求此时CD的长.。
全等三角形的判定精选练习题(分SSS、SAS、AAS、ASA、HL分专题)

D CB A 全等三角形的判定(一)(SSS )1、如图1,AB=AD ,CB=CD ,∠B=30°,∠BAD=46°,则∠ACD 的度数是( )A.120°B.125°C.127°D.104°2、如图2,线段AD 与BC 交于点O ,且AC=BD ,AD=BC ,•则下面的结论中不正确的是( ) A.△ABC ≌△BAD B.∠CAB=∠DBA C.OB=OC D.∠C=∠D3、在△ABC 和△A 1B 1C 1中,已知AB=A 1B 1,BC=B 1C 1,则补充条件____________,可得到△ABC ≌△A 1B 1C 1.4、如图3,AB=CD ,BF=DE ,E 、F 是AC 上两点,且AE=CF .欲证∠B=∠D ,可先运用等式的性质证明AF=________,再用“SSS ”证明______≌_______得到结论.5、如图,已知AB=CD ,AC=BD ,求证:∠A=∠D .6、如图,AC 与BD 交于点O ,AD=CB ,E 、F 是BD 上两点,且AE=CF ,DE=BF.请推导下列结论:⑴∠D=∠B ;⑵AE ∥CF .7、已知如图,A 、E 、F 、C 四点共线,BF=DE ,AB=CD.⑴请你添加一个条件,使△DEC ≌△BFA ; ⑵在⑴的基础上,求证:DE ∥BF.全等三角形的判定(SAS)1、如图1,AB ∥CD ,AB=CD ,BE=DF ,则图中有多少对全等三角形( )A.3B.4C.5D.62、如图2,AB=AC ,AD=AE ,欲证△ABD ≌△ACE ,可补充条件( ) A.∠1=∠2 B.∠B=∠C C.∠D=∠E D.∠BAE=∠CAD3、如图3,AD=BC ,要得到△ABD 和△CDB 全等,可以添加的条件是( ) A.AB ∥CD B.AD ∥BC C.∠A=∠C D.∠ABC=∠CDA4、如图4,AB 与CD 交于点O ,OA=OC ,OD=OB ,∠AOD=________,•根据_________可得到△AOD ≌△COB ,从而可以得到AD=_________.5、如图5,已知△ABC 中,AB=AC ,AD 平分∠BAC ,请补充完整过程说明△ABD ≌△ACD 的理由. ∵AD 平分∠BAC , ∴∠________=∠_________(角平分线的定义). 在△ABD 和△ACD 中,∵____________________________, ∴△ABD ≌△ACD ( ) 6、如图6,已知AB=AD ,AC=AE ,∠1=∠2,求证∠ADE=∠B.7、如图,已知AB=AD ,若AC 平分∠BAD ,问AC 是否平分∠BCD ?为什么?8、如图,在△ABC 和△DEF 中,B 、E 、F 、C ,在同一直线上,下面有4个条件,请你在其中选3个作为题设,余下的一个作为结论,写一个真命题,并加以证明. ①AB=DE ;②AC=DF ;③∠ABC=∠DEF ;④BE=CF.9、如图⑴,AB ⊥BD ,DE ⊥BD ,点C 是BD 上一点,且BC=DE ,CD=AB .⑴试判断AC 与CE 的位置关系,并说明理由.⑵如图⑵,若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第⑴问中AC 与BE 的位置关系还成立吗?(注意字母的变化)全等三角形(三)AAS 和ASA【知识要点】1.角边角定理(ASA ):有两角及其夹边对应相等的两个三角形全等.2.角角边定理(AAS ):有两角和其中一角的对边对应相等的两个三角形全等. 【典型例题】例1.如图,AB ∥CD ,AE=CF ,求证:AB=CD例2.如图,已知:AD=AE ,ABE ACD ∠=∠,求证:BD=CE.例3.如图,已知:ABD BAC D C ∠=∠∠=∠.,求证:例4.如图已知:AB=CD ,AD=BC ,O 是BD 中点,过O AE=CF.例5.如图,已知321∠=∠=∠,AB=AD.求证:BC=DE.例6.如图,已知四边形ABCD 中,AB=DC ,AD=BC ,点F 在AD 交于O ,请问O 点有何特征?【经典练习】 1.△ABC 和△C B A '''中,C B C B A A ''='∠=∠,',C C '∠=∠2.如图,点C ,F 在BE 上,,,21EF BC =∠=∠3.在△ABC 和△C B A ''' ) ①A A '∠=∠B B '∠=∠,BC =C A C A ''='③A A '∠=∠B B '∠=∠,AC =C A B A ''=' A . 1个B. 2个C. 3个D. 4个4.如图,已知MB=ND ,NDC MBA ∠=∠,下列条件不能判定是△ABM ≌△CDN 的是( )A . N M ∠=∠ B. AB=CD C . AM=CN D. AM ∥CN 5.如图2所示, ∠E =∠F =90°,∠B =∠C ,AE =AF ,给出下列结论:①∠1=∠2 ②BE=CF ③△ACN ≌△ABM ④CD=DN其中正确的结论是__________________。
人教版八年级数学上册专题(三) 全等三角形判定与性质的综合运用

类型三:证明两直线平行
4.如图,AC和BD相交于点O,OA=OC,OB=OD.求证:AB∥CD.
解:在△DOC 与△BOA 中,O∠CD=OOC= A,∠BOA, OD=OB,
∴△DOC≌△BOA(SAS),∴∠D=∠B,∴AB∥CD
类型四:证明两直线互相垂直 5.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点, 将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别 与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证 明你的猜想. 解:BE=EC,BE⊥EC,证明:∵AC=2AB,D是AC的中点,∴AB= AD=CD,∵∠EAD=∠EDA=45°,∴∠EAB=∠EDC=135°,∵EA= ED,∴△EAB≌△EDC(SAS),∴∠AEB=∠DEC,EB=EC,∴∠BED+ ∠DEC=∠BED+∠AEB=90°,∴BE⊥EC
3.如图,AC⊥AD,BC⊥BD,OE⊥CDபைடு நூலகம்AC=BD.求证:DE=CE.
解:∵AC⊥AD,BC⊥BD,∴∠A=∠B=90°,在 Rt△ADC 和 Rt△BCD 中,DACC==CBDD,,∴Rt△ADC≌Rt△BCD(HL),∴∠ACD
=∠BDC,在 Rt△ODE 和 Rt△OCE 中,∠∠OOEDDE==∠∠OOECCE=,90°,∴ OE=OE,
∴∠A=∠D
类型二:证明两线段相等 2.如图,在四边形ABCD中,AD∥BC,∠A=90°,BD=BC, CE⊥BD于点E.求证:AD=BE. 解:∵AD∥BC,∴∠ADB=∠DBC,又CE⊥BD,∴∠BEC=90°, 又∵∠A=90°,∴∠A=∠BEC,又BD=CB,∴△ABD≌△ECB(AAS), ∴AD=BE
(完整版)全等三角形的性质与判定(SSS、SAS、ASA、AAS)练习题

全等三角形的性质与判定(SSS 、SAS 、ASA 、AAS )练习题1. 如图,在△ABC 中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C=2. 如图,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′B ′交AC 于点D ,若∠A ′DC=90°,则∠A=1题图 2题图 3题图 4题图3. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO=4. 如图,△ABC ≌△ADE,BC 的延长线过点E ,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠DEF=5. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,求DE 的长.6. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC,垂足分别是E 、F ,连接EF,交AD 于G ,试判断AD 与EF的关系,并证明你的结论。
7. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
8. 如图,AD=BD,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?E F C D BEGB E FEF C AB A'B'BCD D B'AHE9. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC,点G 在CE 的延长线上,CG=AB,求证:AG ⊥AF10. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB,连结AD 、AG.试判断AD 与AG 的关系如何?并证明之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形判定与性质专题训练
一、全等三角形实际应用问题
1如图,要测量河两岸相对的两点A、B间的距离,先在过B点的AB的垂线L上取两点C、D,使CD=BC,再在过D点的垂线上取点E,使A、C、E在一条直线上,ED=AB这时,测ED的长就得AB得长,判定△ACB≌△ECD的理由是()
A. SAS
B. ASA
C. SSS D .AAS
2.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是()
A.PO B.PQ C.MO D.MQ
3、如图所示,将两根钢条AA′,BB′的中点O连在一起,使A A′,BB′可以绕着点O自由转动,就做成了一个测量工具,则A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是()A、SSS B、SAS C、ASA D、HL
4、如图:工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,得到∠AOB的平分线OP,做法中用到三角形全等的判定方法是()
A、SSS
B、SAS
C、ASA
D、HL
5、如图,有两个长度相等的滑梯靠在一面墙上.已
知左边滑梯的高度AC与右边滑梯水平方向的长度
DF相等,则这两个滑梯与地面的夹角∠ABC+∠DFE= 度
6、如图,小明把一块三角形的玻璃打碎成了三块,
现在要到玻璃店去配一块完全一样的玻璃,那么最
省事的办法是:( )
A、带①去,
B、带②去
C、带③去
D、①②③都带去
二、证两次全等相关问题
1:如图:已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证: CF=DF
2:如图已知AD∥BC,AB∥CD BF=DE,求证:AE=CF,
3:如图AB⊥AC,AD⊥AE AB=AD,BC=DE,求证AM=AN
三、探索两线段的关系问题
1.如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE交CD于点F,试探索线段BE与AD的关系,并证明。
2、如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。
试探索线段EC与BF的关系,并证明。
A
E
B M
C
F
3、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。
试探索线段AM与AN的关系,并证明。
B
4、如图,已知:△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
猜想BE与AC的关系并证明。
A
E F
D
B C
四、探索三线段的数量关系问题
1.在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .
(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;
(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
2、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE
3.如图,AC平分∠BAD,CM⊥AB于M,∠ADC+∠ABC=180°.
求证:AB+AD=2AM.
五、构造全等三角形问题
1.如图,在△ABC中,BD=DC,∠1=∠2,求证:AD 平分∠BAC.
2·如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,则AB与AC+BD相等吗?请说明理由
3如图:AD 为 △ABC 的中线, 求证:21(AB-AC )<AD <2
1(AB+AC )
A
B C D E
4.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC,交AC于F,求证:AE=CF。
