费马原理
费马原理
则易知当i’=i时，QO+OP为光程最短的路径。
§4 费马原理
Q
第一章 光和光的传播
h1
i1
x
p x n1
O
折射定律
过Q、P点作与Σ面 垂直的平面Π 平面Π内的光程比该 平面外的光程短
Q’ M
h i2 2
P
P’
n2
2
QP p
2
(QOP ) n1QO n2OP n1 h1 x 2 n2 h2 ( p x) 2
2
l
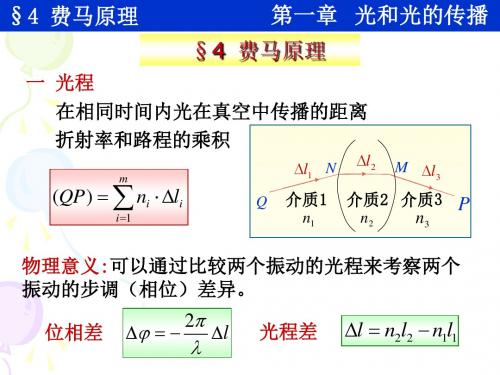
光程差
l n2l2 n1l1
§4 费马原理
二 费马原理的表述
第一章 光和光的传播
（1）定义：两点间的实际路径就是光程(或所需传 播时间)平稳的路径 极小值(常见)
(QP ) ndl 0
( L)
P
Q
极大值(个别) 常数值(物—象等光程性)
l1
（2）由费马原理推导几何 光学三定律
① 直线传播定律 ② 反射定律
Q
N l 2
M l3
介质1 n1
介质2 介质3 n2 n3
P
③ 折射定律
§4 费马原理
第一章 光和光的传播
• （1）光的直线传播定律 在均匀介质中，两点间光程最短的路径 是直线。
§4 费马原理
第一章 光和光的传播
Q点发出的光经 反射面Σ到达P点 P’ 是 P 点关于 Σ 面的对称点。 直线QP’与反射 面Σ交于O点。 P，Q，O三 点确定平面Π。
费马原理的内容
费马原理的内容
费马原理最早由法国科学家皮埃尔·德·费马在1660年提出,又名“最短光时”原理。
费马原理：光沿着所需时间为平稳的路径传播.（所谓的平稳是数学上的变分概念,可以简单理解为一阶导数为零,它可以是极大值、极小值甚至是拐点.多数情况是极小值.宇宙学中指的时空透镜就是极大值,椭圆状镜面的表面则是拐点.）
光程 s=n l(n 为光所在介质的折射率,l为几何路程) 又因为 n=c/v 和
l=vt 所以得到 s=ct. 由此可见,光在某种介质中的光程等于同一时间内光在真空中所走的几何路程。
费马原理指出,光从一点传播到另一点,其间无论经过多少次折射和反射,光程为极值.也就是说,光是沿着光程为极值（极大值、极小值或常量）的路径传播的。
费马原理为几何光学中的基本原理，费马原理也被称为最短时间原理。
通过费马原理可以推导斯涅尔定律、反射定律和光线传播定律。
以及有关各种光学器件的定理也可以从费马原理或上述定律中推导出来。
费马原理的精确表示：在光运动的各种情形下，光会沿着一阶变量为0的路径传播。
这种表述较最短时间原理相比更为准确，在反射定律的例子中，光沿着入射角等于出射角的路径传播。
可是依据最短时间，光线并没有沿着最短的路径传播，毕竟两点之间线段最短。
因此在存在约束的条件下，“在光运动的各种情形下，光会沿着一阶变量为0的路径传播”此表述更为精确。
通过费马原理可以推导出光沿着直线传播，因为相同的一束光在同一种介质内的传播速度相同，所以若这一束光要从点A传播至点B，则根据两点之间线段最短得到光线将沿着此先短传播。
费马原理
t [l] nl [l] ct cc
2. 光程表示光在介质中通过真实路程所需时间内,在真 空中所能传播的路程。
◆ 分区均匀介质:
k
[l] 1 k
[l] nili
i 1 nili
◆ 连续介质:
[l] ndl (l)
二.费马原理的表述及讨论
空间中两点间的实际光线路 径是所经历光程的平稳路径
即
[ A1P1F ] [ A2P2F ]
讨论：如果将点光源置于焦点处，由光的可逆性可知， 光源发出的光线经抛物面镜反射后成为平行于光轴的平 行光束。
例二 折射率分别为n1 ，n2的两种介质的界面为 ，
在折射率为 n1的介质中有一点光源S，它与界面顶点 O相距为d。设S发出的球面波经界面折射后成为平面
利用梯度折射率介质中光线的弯曲,可以表解释蜃景的 现象
例一 一束平行于光轴的光线入射到抛物面镜上反射后，
会聚于焦点F。试证所有这些光到达焦点上光程相等。
分析：
M
A1 A2
P1
Q1
P2
Q2
F 为抛物面的焦点，MN为其准线
F
抛物线性质
N
P1F P1Q1 P2F P2Q2
则 A1P1 P1F A2P2 P2F
三.费马原理的应用
1. 根据直线是两点间最短距离这一几何公理,对于真空 或均匀介质,费马原理可直接得到光线的直线传播定律。
2. 费马原理只涉及光线传播路径,并未涉及到光线的 传播方向。若路径AB的路径取极值，则其逆路径BA的 光程也取极值——包含了光的可逆性。
3. 由费马原理导出光的反射定律
AB的光程为
(x n2d )2 n1 n2
d 2n12 /(n1 n2 )2
费马最短时间原理
费马最短时间原理
费马最短时间原理，又称费马原理、最短时间原理，是物理学中的一个重要原理。
该原理由法国数学家和物理学家皮埃尔·德·费马于17世纪提出。
费马最短时间原理的核心思想是：光在介质中传播时，总是选择用时最短的路径。
换句话说，光在从一个点到另一个点的传播过程中，会选择一条路径，使得光在该路径上所花费的时间最短。
这个原理可以通过折射和反射来解释。
假设有一个光线从一个介质射入另一个介质中，当光线经过折射或者反射后到达另一个点，光线会选择使得总用时最短的路径。
这可以用以下实例来说明：
想象一个光线从空气中射入水中，光线将发生折射。
现在我们需要找到光线经过的路径，使得从起点到终点的总用时最短。
根据费马最短时间原理，光线在空气和水之间的界面上会以使得折射定律（即斯涅耳定律）成立的角度入射和折射，进而选择使得总用时最短的路径。
此外，费马最短时间原理还可以应用于其他领域，如声波、电磁波等的传播。
原理的基本思想是找到一条路径，使得传播过程中所花费的时间最少。
总之，费马最短时间原理是基于光在介质中传播的最短时间选
择性来构建的原理。
它在物理学中有着广泛的应用，帮助我们理解光和其他波动现象的传播过程。
费马定理
费马原理定义：最小光程原理。
光波在两点之间传递时，自动选取费时最少的路径。
应用学科：费马原理是几何光学中的一条重要原理，由此原理可证明光在均匀介质中传播时遵从的直线传播定律、反射和折射定律，以及傍轴条件下透镜的等光程性等。
光的可逆性原理是几何光学中的一条普遍原理，该原理说，若光线在介质中沿某一路径传播，当光线反向时，必沿同一路径逆向传播。
费马原理规定了光线传播的唯一可实现的路径，不论光线正向传播还是逆向传播，必沿同一路径。
因而借助于费马原理可说明光的可逆性原理的正确性。
光在任意介质中从一点传播到另一点时，沿所需时间最短的路径传播。
地震学中的费马原理地震波沿射线传播的旅行时和沿其他路径传播的旅行时相比为最小，亦是波沿旅行时最小的路径传播。
光学中的费马原理光线在两点间的实际路径是使所需的传播时间为极值的路径[1]。
在大部分情况下，此极值为最小值，但有时为最大值，有时为恒定值。
费马原理详解光在任意介质中从一点传播到另一点时，沿所需时间最短的路径传播。
又称最小时间原理或极短光程原理，法国数学家费马于1657年首先提出。
设介质折射率n在空间作连续变化，光传播路程ds 所需时间为式中c为真空中的光速。
光沿ACB曲线从A点传播到B点所需时间为费马原理指出了光传播的实际路径，这是一条所需时间τ为极小值的路径。
实际上τ除取极小值外，还可取极大值或稳定值，总之，τ应取极值。
光在介质中传播时，光传播的几何路程与介质折射率之乘积称为光程。
上式中的积分就是光沿ACB曲线从A点传到B点的总光程。
故费马原理也可表述为：光传播的实际路径是使光程取极值（极小值、极大值或稳定值）。
光程取极值的条件为光程的一级变分等于零，即此即费马原理的数学表达式。
费马原理是几何光学中的一条重要原理，由此原理可证明光在均匀介质中传播时遵从的直线传播定律、反射和折射定律，以及傍轴条件下透镜的等光程性等。
光的可逆性原理是几何光学中的一条普遍原理，该原理说，若光线在介质中沿某一路径传播，当光线反向时，必沿同一路径逆向传播。
费马定理
三.费马原理的应用
光程最小即为路程最短,根据直线是两点间最短距 离这一几何公理,对于真空或均匀介质,费马原理 可直接得到光线的直线传播定律. 费马原理只涉及光线传播路径,并未涉及到光线的
传播方向.若路径AB的光程取极值,则其逆路径BA
的光程也取极值——包含了光的可逆性.
11
光程为极值的例子
6
1.均匀介质中光程
l nl
2.如果光从A点出发,经过 k 种不同的均匀介质
而到达B点,则总光程为：
l1
A v1
l2 v 2
l3 v 3
li v i
lk v k
B
l ni li
i 1
k
7
3.若由A到B充满着折射律连续变化的介质, 则光由A到B的总光程为
[ L]
B
A
实像和虚像
1.单心光束：凡具有单个顶点的光束.
发散单 心光束
会聚单 心光束
16
光线经反射或折射后,如果光束的单心性没有 2.像：
被破坏,即虽然光线的方向改变了,但光束中仍
能找到一个顶点,这个顶点就叫做发光点的像.
实像
反射和折射后实际光线的汇聚点.
虚像
反射和折射后实际光线的反向延长线的汇聚点.
17
复 习
几何光学的基本实验定律
1.光在均匀介质中的直线传播定律 2.光在两种介质分解面的反射定律和折射定律 3.光的独立传播定律和光路可逆原理
1
§1.2 费马原理
费马原理是一个描述光线传播行为的原理.
光
程
费马原理的表述 费马原理的应用
2
一. 光 程
定义：
l nl
fermat原理
fermat原理费马原理是由法国数学家皮埃尔·德·费马在17世纪提出的一条重要定理，它在数学领域中具有广泛的应用。
费马原理从数学的角度解释了很多实际问题，并且对于现代科学的发展也起到了积极的推动作用。
本文将从费马原理的基本概念、应用领域和研究意义等方面进行阐述。
我们来介绍一下费马原理的基本概念。
费马原理是指当存在一个最小值点或最大值点时，该点的导数为零。
简单来说，就是在一条曲线上寻找极值点时，可以通过求导数并令导数为零来找到这些点。
费马原理可以用公式的形式表示，但在本文中我们不输出公式，而是通过文字来进行描述。
费马原理在几何光学、力学、最优化问题等领域中有着广泛的应用。
在几何光学中，费马原理可以用来解释光的传播路径。
光线在两个介质之间传播时，会选择一条路径使得传播时间最短。
这就是费马原理在光的传播中的应用。
在力学中，费马原理可以用来求解物体的最速下降路径。
当物体从一点出发，受重力作用滑动到另一点时，其滑动路径应该使得滑动时间最短。
这也是费马原理在力学中的应用之一。
在最优化问题中，费马原理可以用来求解函数的极值点。
通过费马原理，可以找到函数的极值点从而得到函数的最优解。
费马原理在科学研究中具有重要的意义。
首先，费马原理为解决实际问题提供了一种数学工具。
通过费马原理，可以将实际问题转化为数学问题，从而进行求解。
其次，费马原理提供了一种优化方法。
通过费马原理，可以求解函数的极值点，从而得到函数的最优解。
这对于现代科学研究和工程设计都具有重要的意义。
此外，费马原理的提出也推动了数学研究的发展。
费马原理是微积分的重要应用之一，而微积分又是现代数学的重要分支之一。
因此，费马原理的提出对于数学的发展起到了积极的推动作用。
费马原理是一条重要的数学定理，它在数学领域中具有广泛的应用。
费马原理的基本概念是当存在一个最小值点或最大值点时，该点的导数为零。
费马原理在几何光学、力学、最优化问题等领域中有着广泛的应用。
简述费马原理的内容
简述费马原理的内容
费马原理是光的传播路径的最小时间理论，描述了光线在两点之间传播时所采取的最经济路线。
该原理由法国数学家皮埃尔·德·费马于17世纪提出，被认为是光的最速传播原理。
费马原理的核心思想是：光在传播过程中通常会选择用时最短的路径。
这意味着光线在空间中传播时会遵循一定的规律，使得从发光点到达接收点的传播路径总是使光程取得极小值。
这一原则被认为能够解释光的折射、反射、衍射等现象，并用于研究光学器件的设计与光的传播途径的确定。
费马原理可以通过尺度变分方法进行推导。
在具体推导中，以两个不同介质的分界面上的光线为例，光线的折射原理（即斯涅尔定律）可以描绘为光线在两个介质中行进时路径的变化。
费马原理通过选择最短时间路径，以精确推导光线在界面上的折射、透镜的成像和光的传输等光学过程。
需要注意的是，费马原理是一个原则性的假设，不一定在所有情况下都成立。
在一些特殊情况下，如存在反射、多次折射或衍射等现象时，费马原理的应用可能会有所限制。
此外，费马原理的应用也不仅限于光学领域，还可以用于其他物理学和工程领域中光的传播问题的分析和设计。
综上所述，费马原理描述了光的最小时间传播路径，指导了光学器件的设计和光的传播路径的确定。
通过优化光线的路径，费马原理为光学领域的研究和应用提供了重要的理论基础。
最速降线原理
最速降线原理最速降线原理，又称费马原理，是数学中的一个重要原理，它描述了两点之间最短路径的特性。
这个原理在物理学、工程学、经济学等领域都有着广泛的应用。
在本文中，我们将深入探讨最速降线原理的相关概念、应用以及其在实际生活中的意义。
首先，我们来了解一下最速降线原理的基本概念。
最速降线原理指的是，两点之间的最短路径是一条曲线，其切线方向与两点之间的连线方向相同。
这条曲线被称为最速降线，因为在重力场中，物体沿着这条曲线下落的时间最短。
费马原理可以通过变分法来证明，它是微积分中的一个重要定理。
最速降线原理在物理学中有着广泛的应用。
例如，在光的传播中，光线在两点之间传播的路径也是一条最速降线，这就解释了光的折射定律。
在天体运动中，行星绕太阳运动的轨迹也是一条最速降线，这就是开普勒定律的基础。
此外，在工程学中，最速降线原理也被应用于优化问题的求解中，比如最短路径问题、最优控制问题等。
最速降线原理在实际生活中也有着重要的意义。
我们在日常生活中常常需要求解最短路径问题，比如规划最佳的出行路线、设计最有效的物流配送方案等。
而最速降线原理提供了一个重要的数学工具，帮助我们解决这些实际问题。
另外，最速降线原理也启发了人们对于优化问题的思考，促进了科学技术的发展。
总的来说，最速降线原理是数学中的一个重要概念，它描述了两点之间最短路径的特性。
这个原理在物理学、工程学、经济学等领域都有着广泛的应用，并在实际生活中发挥着重要的作用。
通过对最速降线原理的深入理解，我们可以更好地应用它解决实际问题，推动科学技术的发展。
希望本文对读者对最速降线原理有所帮助，谢谢阅读。
费马原理证明
费马原理证明
费马原理是数学中的一条重要原理，用来证明某些问题的解不存在。
这条原理被称为"费马原理"是因为它是由法国数学家费马首先提出的。
费马原理的基本思想是对某个问题的假设进行推导，然后通过推导的过程来证明问题的解不存在。
费马原理的具体内容如下：
假设存在一个问题的解，并设这个解为S；
利用这个解S来推导出一系列的逻辑关系和性质；
通过分析这些逻辑关系和性质，发现其中的矛盾和不可能的情况；
由于存在矛盾和不可能的情况，推出假设的解S不存在。
费马原理的应用范围非常广泛，在数学和其他学科中都有所应用。
它可以用来证明质数的存在性，也可以用来证明某些几何问题的解不存在。
费马原理的证明过程需要严格的逻辑推理和数学推导，在证明过程中需要排除其他因素的干扰，确保证明的正确性。
总之，费马原理是一条重要的数学原理，可以用来证明某些问题的解不存在。
通过对问题的假设进行推导，发现其中的矛盾和不可能的情况，从而推出问题的解不存在。
在使用费马原理证明问题时，应保证证明的逻辑严谨性和正确性。
费马原理(共5张PPT)
① 直线传播定律 ② 反射定律
③ 折射定律
Q 介质1 介质2 介质 P
n1
n2 3 n3
§4 费马原理
第一章 光和光的传播
• 〔1〕光的直线传播定律
•
在均匀介质中，两点间光程最短的
途径是直线。
§4 费马原理
第一章 光和光的传播
那么易知当i’=i时，QO+OP为光程最短的途径。 常数值(物—象等光程性) 在均匀介质中，两点间光程最短的途径是直线。 过Q、P点作与Σ面垂直的平面Π 在一样时间内光在真空中传播的间隔 常数值(物—象等光程性) P’是P点关于Σ面的对称点。 过Q、P点作与Σ面垂直的平面Π
§4 费马原理
第一章 光和光的传播
§4 费马原理
一 光程
在一样时间内光在真空中传播的间隔
折射率和路程的乘积
m
(QP) ni li i1
l1 N l2 M l3
Q 介质1 介质2 介质 P
n1
n2 3 n3
物理意义:可以经过比较两个振动的光程来调查两个振 动的步伐〔相位〕差别。
位相差 2 l
Q点发出的光经反 射面Σ到达P点
P’是P点关于Σ 面的对称点。
直线QP’与反射面 Σ交于O点。
P，Q，O三点 确定平面Π。
那么易知当i’=i时，QO+OP为光程最短的途径。
§4 费马原理
第一章 光和光的传播
Q
h1 i1 x
px n1
Q’
O P’
折射定律
过Q、P点作与Σ面垂直 的平面Π
光程差 l n2l2n1l1
§4 费马原理
第一章 光和光的传播
二 费马原理的表述
〔1〕定义：两点间的实践途径就是光程(或所需传播时
费马定理介绍
费马定理费马原理是光学中最为基础的原理,它在物理学发展的历程中有着至关重要的作用。
它用一种新的看法将几何光学的三个基本实验定律（光的反射定律和折射定律、光的独立传播定律光的直线传播定律直线传播）进行统一,并表述了三者的联系。
通过研究几何光学问题，能彰显出费马定理的重要性，能更加系统化光学理论.可见通过费马原理推导上述三个基本实验定律,能使我们更加系统的理解光学理论，这对广大学者都有着不可或缺的意义。
费马原理的直观表达：光从空间的一点到另一点的实际路径是沿着光程为极值的路径传播的。
或者说， 光沿着光程为极大、极小或者常量的路径传播。
光线从Q 点传播到P 点所需的总时间：⎰∑∑=∆=∆===ndl c t l n c v l t PQ i i i i i i 1111费马原理：在所有可能的光传播路径中，实际路径所需的时间 取极值。
⎰==01ndl ct P Q δδ 在光传播的所有可能存在的路径中，其实际路径所对应的光程取极致。
⎰==0ndl L P Q δδ① 直线传播定律:两点间的所有可能连线中，线段最短-—光程取极小值。
② 内椭球面的反射： 椭球面上任一点到两个焦点连线的角平分线即过该点的面法线，且两线段长度之和相等。
用费马原理导出反射定律如下图， PQ 为两个介质间的平面反射镜,从A 点发射出的光线照射到PQ 平面上的O 点，经过反射到达B 点。
假设光线所处的介质为均匀介质。
光线的透射点O 到A 点与反射平面垂足P 的长度为x 。
那么点A 到点B 的光程为：()⎥⎦⎤⎢⎣⎡-+++=222221x a H x H n OBn AO n L +=()22222211x a H n x H n -+++=OBn AO n L 21+=很明显，光程L 是关于变量x 的函数,由费马原理分析，真实的光程是固定的,在均匀介质中的一阶导数是0，即()()0222221=-+--+=x a H x a n x H nx dx dL即有()I n I n -sin sin =即I I -=反射定律由上面推导出来了.进一步可以证明22dxL d >0 ， 这说明满足反射定律的光线具有最短光程. 从费马原理导出折射定律下图中，两个介质均为均匀介质，它们的折射率分别为1n 、2n ，光线从1n 介质投射到折射面的O 点，光线折射后进入2n 介质，然后通过B 点。
费马原理
根据δ方向的任意性：
(na − n ' a') • δ = 0
E( x0 , y0 , z0 )
(na − n ' a') • δ = 0
P'( x ', y ', z ')
P( x, y, z )
n n'
n ' a '− na = ΓN
当G靠近E时，δ趋近于E点处的切向方向 N为E点处的法向方向。
[PP'] = ∫ ndl 的一阶变分等于0
P
P'
δ ∫ ndl Байду номын сангаас 0
P
P'
回转椭球面
光程取极小值
光程取稳定值
内切于回转椭球 面的凹面反射镜
费马原理：光从空间一点传播到另一点是沿着 光程为极值的路径传播的。
光程取极大值
光路可逆：若光线在空间中沿某一路径传播， 当光线反向时，必沿同一路径逆向传播 。
由费马原理导出折射定律
P( x, y, z )
n n' PEP′是实际路径
E( x0 , y0 , z0 )
P'( x ', y ', z ')
G是E邻域某点
PE= ( x0 − x) 2 + ( y0 − y ) 2 + ( z0 − z ) 2 = d
E( x0 , y0 , z0 )
P'E= ( x0 − x ') 2 + ( y0 − y ') 2 + ( z0 − z ') 2 = d '
• 两矢量的点积
光程差：
Δ[PP'] = [PP']− [PP']
费马原理解释
费马原理解释
费马原理(Fermat"s Last Theorem)是指数学家费马在1637年提出的一个猜想,即对于任何大于2的正整数n,方程a^n + b^n = c^n没有正整数解。
这个猜想在当时引起了广泛的讨论和猜测,直到1994年,数学家安德鲁·怀尔斯(Andrew Wiles)通过长期的努力,最终证明了费马原理。
怀尔斯的证明使用了现代数学中的多项式逼近论和证明技巧,这是数学中一个重要的分支。
费马原理本身是一个具有挑战性的问题,涉及到了代数几何、数论、分析等多个数学领域。
费马原理的提出是数学史上的一个里程碑,它推动了数学领域的发展,并为其他领域提供了新的思路和工具。
今天,费马原理仍然是数学中一个著名的问题,吸引着大量的数学家和学者进行探究和研究。
除了怀尔斯的证明外,还有许多其他数学家对费马原理进行了研究和探究。
例如,欧拉、拉格朗日、布洛赫等人都曾经提出过相关的猜想和理论,但都没有最终证明费马原理。
今天,费马原理仍然是数学中一个开放性的问题,吸引着众多的数学家和研究学者进行探究和研究。
拓展:
费马原理的提出是数学史上的一个里程碑,它推动了数学领域的发展,并为其他领域提供了新的思路和工具。
今天,费马原理仍然是数学中一个开放性的问题,吸引着众多的数学家和研究学者进行探究和研究。
除了怀尔斯的证明外,还有许多其他数学家对费马原理进行了研究和探究。
例如,欧拉、拉格朗日、布洛赫等人都曾经提出过相关的猜想和理论,但都没有最终证明费马原理。
今天,费马原理仍然是数学中一个开放性的问题,吸引着众多的数学家和研究学者进行探究和
研究。
费马定理介绍
费马定理费马原理是光学中最为基础的原理，它在物理学发展的历程中有着至关重要的作用。
它用一种新的看法将几何光学的三个基本实验定律（光的反射定律和折射定律、光的独立传播定律光的直线传播定律直线传播）进行统一，并表述了三者的联系。
通过研究几何光学问题，能彰显出费马定理的重要性，能更加系统化光学理论。
可见通过费马原理推导上述三个基本实验定律，能使我们更加系统的理解光学理论，这对广大学者都有着不可或缺的意义。
费马原理的直观表达:光从空间的一点到另一点的实际路径是沿着光程为极值的路径传播的。
或者说, 光沿着光程为极大、极小或者常量的路径传播。
光线从Q 点传播到P 点所需的总时间：⎰∑∑=∆=∆===ndl ct l n c v l t PQ i i i i i i 1111费马原理：在所有可能的光传播路径中，实际路径所需的时间 取极值。
⎰==01ndl ct P Q δδ 在光传播的所有可能存在的路径中，其实际路径所对应的光程取极致。
⎰==0ndl L P Qδδ① 直线传播定律：两点间的所有可能连线中，线段最短——光程取极小值。
② 内椭球面的反射： 椭球面上任一点到两个焦点连线的角平分线即过该点()⎥⎦⎤⎢⎣⎡-+++=222221x a H x H n OBn AO n L +=的面法线，且两线段长度之和相等。
用费马原理导出反射定律如下图， PQ 为两个介质间的平面反射镜,从A 点发射出的光线照射到PQ 平面上的O 点，经过反射到达B 点。
假设光线所处的介质为均匀介质。
光线的透射点O 到A 点与反射平面垂足P 的长度为x 。
那么点A 到点B 的光程为：很明显，光程L 是关于变量x 的函数，由费马原理分析，真实的光程是固定的，在均匀介质中的一阶导数是0，即()()0222221=-+--+=x a H x a n xH nx dxdL即有()I n I n -sin sin =即I I -=反射定律由上面推导出来了。
光线通过透镜后的光程差 费马原理
光线通过透镜后的光程差费马原理
费马原理是光学中的基本原理之一，它指出光总是沿着所需时间为最小的路径传播。
因此，光通过透镜后的光程差与透镜的折射率、光在透镜中行进的距离以及光入射的角度有关。
在透镜上，光线的入射角和折射角之间的差异会影响光程。
由于光在透镜中行进的距离和折射率也会影响光程，因此透镜的不同部分会有不同的光程。
当光线通过透镜后，如果从一个位置反射到另一个位置，则存在光程差。
这个光程差是由于光线在透镜中传播的速度不同而产生的。
因此，透镜的形状和折射率会直接影响光通过透镜后的光程差。
在设计透镜时，需要仔细考虑光程差的影响，以确保透镜的性能和光学质量。
费马原理的发现过程
费马原理的发现过程及基本原理解释1. 引言费马原理是一个重要的物理学原理，用于描述光的传播路径。
这个原理最早由法国数学家皮埃尔·德·费马（Pierre de Fermat）在17世纪提出，并被称为费马最小时间原理或费马法则。
费马原理对于光的折射、反射以及干涉等现象都有重要的应用。
2. 发现过程费马最早提出这个原理是在解决一道几何问题时。
他考虑了一种情况：如果一个光线从一个点A出发，经过一个介质，在另一个点B折射出来，那么光线所经过的路径是怎样的呢？费马通过研究这个问题，得出了一个结论：光线所经过的路径是使得从A到B所需时间最短的路径。
简单来说，当光传播时，它会选择花费最少时间的路径。
3. 基本原理解释费马原理可以通过以下几个方面来解释和说明：3.1 光程首先，我们需要了解什么是光程。
在空间中，从点A到点B沿着某条路径传播的光线，所经过的路径长度就是光程。
光程可以用符号S表示。
3.2 光程最小费马原理认为，当光从一个点A出发，经过介质传播到另一个点B时，光线所经过的路径是使得光程最小的路径。
也就是说，在所有可能的路径中，光会选择那条使得光程最小的路径。
3.3 光速不变费马原理还假设了一个重要的条件：在同一介质中，光的传播速度是不变的。
也就是说，在同一介质中，无论光线传播的方向如何，它都会以相同的速度进行传播。
3.4 反射和折射定律费马原理还可以用来推导反射和折射定律。
根据费马原理，我们可以得出以下结论：•反射定律：当一束光线从一个介质射入另一个介质时，在界面上反射出去的角度等于入射角。
•折射定律：当一束光线从一个介质射入另一个介质时，在界面上折射出去的角度满足斯涅尔定律。
这些定律都可以通过费马原理推导得出。
3.5 光的传播路径费马原理还可以用来解释光的传播路径。
根据费马原理，当光传播时，它会选择一条使得光程最小的路径。
这就解释了为什么光在直线上传播、折射时会遵循特定的规律。
4. 应用费马原理在物理学和光学中有广泛的应用，包括但不限于以下几个方面：4.1 光的反射和折射费马原理可以用来推导反射和折射定律。
费马原理的应用
费马原理的应用一、费马原理简介费马原理是法国数学家皮埃尔·德·费马在17世纪提出的著名原理之一。
该原理描述了光线在两个介质之间传播时的路径选择，在光学领域有着广泛的应用。
费马原理的核心思想是光线在两个介质中传播时，总是选择耗时最短的路径。
二、光的折射光的折射是费马原理的重要应用之一，可用于解释光线在不同介质中的传播规律。
根据费马原理，光线经过两个介质界面时，会选择一条使得传播时间最短的路径。
具体来说，当光从一个光疏介质（例如空气）入射到光密介质（例如玻璃）时，由于两种介质的光速不同，光线会发生折射。
根据费马原理，光线在折射发生时会选择一条路径，使得光线经过折射后的路径和光线在折射之前的路径之间的传播时间差最小。
三、光的反射费马原理也可以用于解释光的反射现象。
当光线在光滑的表面上发生反射时，根据费马原理，选择一条使得光线在反射前后的路径传播时间差最小的路径。
在镜面反射中，光线入射到反射面上后，会选择一条使得入射角和反射角相等的路径。
这条路径使得入射和反射之间的传播时间差最小。
四、光的聚焦费马原理在光学中还有一个重要应用是光的聚焦。
光聚焦是将光线聚集到一个点上，形成明亮的光斑。
在光学系统中，例如透镜系统，通过选择适当的透镜形状和位置，可以使得光线在透镜中传播的时间最短，从而实现光的聚焦。
五、其他应用领域费马原理除了在光学领域有广泛应用外，还可以在其他领域中找到应用。
1. 电磁场理论费马原理在电磁场理论中有重要意义。
在计算电磁场中的路径积分时，费马原理可以用于确定电磁波的传播路径。
2. 交通路径规划费马原理在交通路径规划中也有应用。
例如，在城市中规划交通路线时，可使用费马原理确定两点间的最短路径，以减少行车时间。
3. 其他物理学领域费马原理还可以应用于其他物理学领域，如波动力学、量子力学等。
在这些领域中，费马原理提供了一种优化路径选择的方法。
六、总结费马原理是现代物理学中的一个重要原理，描述了光线在介质中传播时的路径选择规律。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
费马原理的运用
王瑞林（03010425）
（东南大学能源与环境学院，南京 210010）
摘要：本文介绍了几何光学的基本定理——费马原理的定义、传统表述及运用波动光学对其本质的介绍。
并且运用费马原理证明了几何光学的三大定律，并求出了最速降线。
关键词：费马原理；折射定律；圆锥曲线光学性质；最速降线；最小作用量原理
The use of Fermat’s principle
Wangruilin
(The college of environment and energy , Southeast University, Nanjing 210096 )
Abstract: We introduced the Fundamental theorem of geometrical optics- Fermat’s principle. We introduced the definition and presentation of Fermat's principle, analysis its essemce . we also got the three basic laws of geometrical optics, and find the brachistochrone with proof of Fermat's principle.
key words: Fermat’s principle；Law of ref raction；Optical properties of coni c；Brachistochrone；Principle of least action
我们之前在初高中就已经学习过几何光学，并了解了其中的一些重要定律，但是都只是一些经验的描述和一些实验的简单验证，本文我们运用几何光学的基础原理——费马原理对已学过的几何定律做一个简单的梳理并简单介绍一下运用费马原理对最速降线问题的求解。
费马原理简介
一、费马定理的表述
关于费马原理的定义，教科书上的表述如下：“过空间中两定点的光，实际路径总是光程最短、最长或恒定值的路径。
”其实表述并不足够准确，因为对于某些路程，不能简单的以光程极值来加以限定，最为准确而精炼的表述要利用到数学上的泛函知识，具体描述为：“过两个定点的光走且仅走光程的一阶变分为零的路径。
”其中光程的定义为光通过的介质对光的折射率与光通过的路程的乘积。
费马原理的数学表述形式为
其中，δ是变分符号，p1、p2表示空间中两个固定点，n为介质的折射率，s表示路程。
我们将路径视为一个函数，而变分则是对泛函求导，其结果类似于我们函数求导，我们可以用函数求导来类似理解变分的求解。
费马定理还有另外一种表述：“过空间中两定点的光，实际路径总是时间最短、最长或恒定值的路径。
”其实就是把光程换成了时间t
这两种表述其实具有等价性，因为
费马原理被认为是物理学基本定律——最小作用量原理在几何光学中的特例，被誉为是几何光学的基础，更有人说有了费马定理便有了几何光学的全部，下面，我们将运用费马定理对几个几何定理重新进行梳理。
二、波动光学角度对费马定理的解释
费恩曼在他的物理学讲义中从波动光学的角度上对费马定理的正确性进行了论证：“要是他遵循一条需要不同时间的路径，则当它到达时就有不同相位。
而在某一点上的总振幅等于光能到达的所有不同路径振幅贡献的总和。
所有那些提供相位差异很大的路径将不会合成任何东西。
但如果你能找出一整序列路径，他们都具有几乎相同的相位，则小小的贡献便将加在一起而在到达之处得到一个可观测的总振幅。
因此，重要路径就成为许多能给出相同相位彼此靠近的路径。
”而只有时间取极值的那条路径，才能保证路径有微小变化时时间保持不变（再次与导数类比，函数取极值的那个点，当x有微小变化Δx时，Δy=Δx*y’=0，其余的点Δy都是一个不为0的数）。
因此，时间取极值的路径被叠加了，成为了实际路径，而其余的任何可能路径都被不同的相位给抵消没了。
”
其实就是光在每一条路程中都进行了传播，而真正形成“路径”的只有最短的一条，那一条便是费马原理中变分为零的那一条。
费马原理的运用
由费马原理我们可以推到出几何光学中的三大定律：（1）光在均与介质中沿直线传播（2）光在介质间传播的折射定律（3）光在介质界面的反射定律。
定律一非常直观我们不予证明，定律二我们给出直接证明，定律三我们将以圆锥曲线的光学性质证明替代。
同时我们还会对费马定理的一些推论和其他运用进行介绍。
1.1光线的折射定律
如图所示，假设光从介质1以速度V1进入介质2且速度变为V2，路径为从A至P再到B，按照图中记号，经过整个路程所用时间为
若要用时最小，则dt/dx=0, 得出
由此，我们的由费马定理推出了我们一般所说的折射定律，即光在两种介质之间传播时，入射角与折射角之比等与一个常数，等于光在两种介质中传播速度大小之比。
1.2圆锥曲线的光学性质
(1)从椭圆一个焦点发出的光，经过椭圆的反射，会汇集到另一个焦点上。
证明：根据椭圆的定义，F1P+PF2=定值，根据费马原理，光的实际路径是光程极小、极大或定值的路径，所以F1到圆锥曲线上任意一点再到F2是光走的实际路径，所以从F1发出的光经过圆锥曲线反射会汇集到F2
（2)从抛物线的焦点发出的光，经过抛物线反射会形成平行光束。
证明：做出抛物线的准线，F1P 等于P到准线的距离，即这两段光程相等。
光的实际路径至于光程的取值有关，所以从F1发出的经过抛物线反射的光和直接从准线向右发出的光完全等效，因此从F1发出的光，经过抛物线反射会形成平行光束。
(3)从双曲线的一个焦点发出的经过双曲线反射形成的光，好像是从双曲线的另一个焦点直接发出的。
证明：因为F1P-F2P=定值，所以对极值的取得没有影响，即从F2发出的经过P反射的光与从F1直接发出的经过P的光取极值的路径相同，即路径是一样的。
故证明了双曲线的光学性质。
我们知道，从数学角度上证明圆锥曲线的光学性质即为繁琐，然而运用费马定理来证明则即为简洁，这不单体现了费马定理在几何光学中的普适性，同时也体现了他在概括及检验物理规律上的简洁性。
1.3 费马原理解释光的衍射
从费尔曼物理学讲义上从波动光学角度对费马原理的解释上来看，我们甚至可以试着用费马定理来理解光的衍射现象：当我们用一个很细的狭缝来挡住一部分光时，时间不取极值的
某些路径也因为有一部分光被挡住
而不能很好的叠加为零，因此这种
情况下光并不是总衍直线传播，而
是产生了光可以绕到障碍物后面的
的现象，即衍射现象
1.4 利用费马原理求解最速降线
利用费马原理，我们得到了折射定律，即
如果光线穿越多重介质，在交界处无疑是满足折射定律的，即
当层数越变越多，厚度越来越厚时，在极限情况下，速度大小及方向自然会联系变化，且变化满足：
由费马原理，遵循这一规律的路径是行走最快最简洁的路径，若以小球沿此路径无摩擦的从A至B，用时无疑是最小的。
而这样的一条路径便是我们所求的最速降线，假设小球在A处速度大小为零，以A为原点建立直角坐标系，
则小球在不同高度的速度大小满足
利用几何关系，我们可知：
综合上述公式，我们可知
变换该式，得
记,我们得
此即摆线的标准方程，由此我们了解了无摩擦的最速降线为摆线，与其他方法所得结果相合。
总结
费马定理是法国业余数学家发现的一条十分重要的定理，是最小作用量原理在几何光学上的体现，是几何光学的基本定理，几乎概括了几何光学的全部内容，而已然学习过几何光学的我们对此则知之甚少，本文介绍了费马原理的科学表述及其在几何光学三大定律证明上的运用，并且运用波动光学对费马原理的正确性做出论证还介绍了利用费马原理解最速降线的巧妙解法。
从中我们看到了费马原理的普适性、简洁性与正确性。
同时对于最小作用量原理有了一些感悟。
参考文献：
[1]最小作用量原理与物理之美3——费马原理
/archives/124
[2]《最小作用量原理与物理学的发展》（许良著）
[3]《费恩曼物理学讲义第二卷》（R·P·费恩曼著
[4]《可怕的对称》（阿·热著）
[5]献给业余数学之王：澄清对费马原理的误解.
/article/59377/
[6] 尤明庆《最速降线和摩擦力影响的研究》。