天然气管道运输模型
管道运输与订购优化模型(CAI)
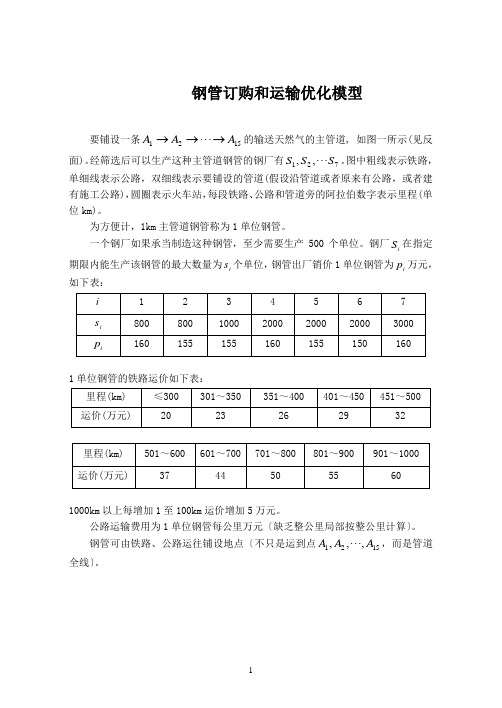
钢管订购和运输优化模型要铺设一条1521A A A →→→ 的输送天然气的主管道, 如图一所示(见反面)。
经筛选后可以生产这种主管道钢管的钢厂有721,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。
为方便计,1km 主管道钢管称为1单位钢管。
一个钢厂如果承当制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大数量为i s 个单位,钢管出厂销价1单位钢管为i p 万元,如下表:i1 2 3 4 5 6 7 i s800 800 1000 2000 2000 2000 3000 i p1601551551601551501601单位钢管的铁路运价如下表:里程(km) ≤300 301~350 351~400 401~450 451~500 运价(万元) 2023262932里程(km) 501~600 601~700 701~800 801~900 901~1000运价(万元) 37445055601000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位钢管每公里万元〔缺乏整公里局部按整公里计算〕。
钢管可由铁路、公路运往铺设地点〔不只是运到点1521,,,A A A ,而是管道全线〕。
问题:〔1〕请制定一个主管道钢管的订购和运输方案,使总费用最小〔给出总费用)。
思考题:〔2〕请就〔1〕的模型分析:哪个钢厂钢管的销价的变化对购运方案和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运方案和总费用的影响最大,并给出相应的数字结果。
〔3〕如果要铺设的管道不是一条线,而是一个树形图,铁路、公路和管道构成网络,请就这种更一般的情形给出一种解决方法,并对图二按〔1〕的要求给出模型和结果。
7一. 根本假设:1. 沿铺设的主管道以有公路或者有施工公路。
管道输运模型优化研究与实践

管道输运模型优化研究与实践第一章管道输运模型的基本概念和应用管道输运是一种重要的物流方式,在石油、天然气、化工等领域有广泛的应用。
管道输运模型优化可以提高输运效率、降低成本、减少资源浪费,因此受到了广泛的研究与实践。
1.1 管道输运模型的基本原理管道输运模型是通过建立数学模型来描述管道输送流体的运动、物质平衡、能量平衡、动量平衡等基本原理。
在建立模型时,需要考虑管道的几何结构、流体的性质、运输条件等因素。
1.2 管道输运模型的应用领域管道输运模型广泛应用于石油、天然气、化工等领域。
在石油行业,通过优化管道输送方案,可以提高油品的供应效率;在天然气行业,可以通过优化管道网络设计,提高天然气的输送能力;在化工行业,可以通过优化管道运输过程,降低能源消耗和环境污染。
第二章管道输运模型的优化方法和算法管道输运模型的优化是一个复杂的问题,需要综合考虑多个因素和约束条件。
本章将介绍常用的管道输运模型优化方法和算法。
2.1 数学规划方法数学规划方法是目前广泛应用于管道输运模型优化的一种方法。
它通过建立数学模型和运用优化算法,寻找最优的输送方案。
常用的数学规划方法包括线性规划、整数规划、多目标规划等。
2.2 启发式算法启发式算法是一种通过模拟人类的启发式搜索策略来求解问题的方法。
在管道输运模型优化中,可以采用启发式算法来搜索最优的方案。
常用的启发式算法包括遗传算法、蚁群算法、模拟退火算法等。
第三章管道输运模型优化的实践案例本章将结合实际案例,介绍管道输运模型优化在实践中的应用。
3.1 石油管道输送模型优化案例以某石油公司的管道输送为例,介绍如何通过优化输送方案,提高输送效率,降低成本和减少资源浪费。
3.2 天然气管道网络设计优化案例以某天然气公司的管道网络设计为例,介绍如何通过优化网络结构和输送方案,提高天然气的输送能力,并满足用户需求。
3.3 化工管道运输过程优化案例以某化工企业的管道运输过程为例,介绍如何通过优化运输路径、控制运输条件,降低能源消耗和环境污染。
管道钢管订购运输最优化模型

=
li
j=1
m , m (l ) ( r)
ji
ji
≥
0
其中
( j = 1...7) (i = 1...n)
n
∑(
m(l ji
)
+
m(r ji
)
)为钢厂S
的钢管产量
j
i =1
称之为产量约束
li为第i段管道所需钢管数量
称之为销量约束
2
作者 雷波 98109 董斐 98406 王双红 98404
设沿管道或者原来有公路 或者建有施工公路) 圆圈表示火车站 每段铁路 公路和管道旁的阿拉伯数 字表示里程(单位 km)
为方便计 1km 主管道钢管称为 1 单位钢管
一个钢厂如果承担制造这种钢管 至少需要生产 500 个单位 钢厂 Si 在指定期限内能生产该钢管的 最大数量为 si 个单位 钢管出厂销价 1 单位钢管为 pi 万元 如下表
m
(r ji
)
(1
+
m
(r ji
)
)
m(j
l i
)
(1
+
m
(l) ji
)
∑ ∑ ∑ (w m (l ) (l ) ji ji
+
w(r ji
)
m(r ji
)
)
+
g( j=1
j =1 i =1
i=1
j=1
2
+ j=1
j =1
)
2
决策变量 S.T.
( (
m( l ) 11
m( l ) 21
, ,
m( r ) 11
管道运输的种类(二)

管道运输的种类(二)
3.天然气管道
天然气管道是输送气天然气和油田伴生气的输气管道,由开采地或处理厂输送到城市配气中心,是陆地上大量运输天然气的唯一方式。
目前,我国天然气田主要在四川,全国现有天然气管道7000多公里,其中近5000公里在四川;伴生气主要产于辽河、中原等东部油田,管道约有2000多公里。
我国最长的输气管道为中原油田濮阳柳屯至沧州化肥厂的伴生气管道,管径426毫米、长362公里。
西气东输是我国目前天然气管道运输的主要项目,如图3-11、图3-12所示。
西气东输工程管线以新疆塔里木轮南油田为起点,经库尔勒、库米什、南湖戈璧,甘肃柳园、张掖、武威,宁夏甘塘、中卫,陕西靖边,三系临汾,河南郑州,安徽定远,江苏南
京,最后抵达上海,管线全长约4000公里,首期每年输气120亿立方米,投资规模1200亿元。
4.煤装、矿浆管道
煤裝、矿浆管道是将煤、矿石粉碎后加水成浆状通过管道运输。
世界上第一条煤浆管道于1970年在美国建成投入使用,年输送能力为450万吨。
目前,我国仅在厂矿内部短距离少量使用或试用煤装、矿浆管道,煤浆等使用管道外运尚处于研究阶段。
管道作为一种新型的现代化运输方式将逐步扩大其使用范围。
在建设方面,不仅地区成网、国内成网,国际间跨国管道的发展也有相当的势头;在运输货种方面,由现有原油、成
品油、天然气扩大到重油、二氧化碳气、沙石等建筑材料等。
由于各种性能的货种増加,相应的管道驱动方式多样,输送工艺将会更加复杂等。
天然气管道输送技术及优化模型设计

2016年9月天然气管道输送技术及优化模型设计王洪宇(新地能源工程技术有限公司燃气技术分公司,河北廊坊065000)摘要:天然气属于清洁、优质能源,具有环保的作用。
随着社会、经济的快速发展,我国在天然气方面的需求量也不断增加。
因此,在后续的工作中,必须采取针对性的办法,不断完善、优化天然气管道。
当前,我国天然气管道技术得到了进一步发展,进而建立了管线费用最小的优化设计模型,并得到了普遍应用。
其中,在西气东输二线管线优化中,创作了较高的价值,已经得到了证实。
关键词:天然气管道;输送技术;优化模型;设计作为一种清洁的优质能源,天然气在国外的能源结构中,比国内的比例更大。
当前,我国将天然气能源已经提高了战略高度。
并带动了相关技术的不断完善。
管道是连接生产气田与用户的枢纽,为了满足人们的生活需求,必须保证输送的稳定性。
从国外天然气管道发展上来看,管道技术的优化非常重要,关系到天然气工业的健康发展。
然而,由于我国天然气技术的研究比较晚,特别是在大口径管道设计,复杂大口径试压,自己管道系统维护方面,技术与经验还很不足。
鉴于此,要求引入国外的先进技术,然后加快天然气管道技术的优化,以此来促进天然气的高速发展。
1天然气管道输送技术现状1.1国内天然气管道输送技术我国天然气管道每年持续增长,并呈现出不断上升的趋势。
据相关数据统计,我国每年建设的管道任务为7000公里。
在十一五期间,我国单管年输量得到了很大程度的提升。
然而,与国外国家相比,输送效率依然比较低。
因此,在后期的天然气管道设计中,必须将提高输送效率作为重点工作来抓,力求实现质的飞跃。
在西气东输工程中,成功建立了西一线、西二线、西三线。
同时,积累了大量经验。
从实际建设的情况来看,要进一步提高压力或者扩大口径尺寸,面临很大困难。
主要是在钢管设计、制造、运行方面,存在很大难题。
因此,为了实现以上目标,必须加大天然气管道技术的研究力度。
只有这样,才能提高天然气管道的输送效率,最终保证天然气管道的快速发展。
第三章 天然气管输系统

2) 在T、d、G、P1 、P2 不变时,管线长度的影响 Q1/Q2=(L2/L1)1/2 即输气量与管长的0.5次方成反比,若管长缩小一半, 即:L2=0.5L1,则Q2=1.41Q1,如在原有两加压站间再增设一个加压站,输
天然气管输系统示意图
矿场 集气 支线 集气 站 加压站 配气 站 输 气 干 线 输配气 站 配气管 线
矿场 集气 集气 干线 净化 站 厂 首站 集气 站 集气 站 加压站
配气 站
1、矿场集气
气田集气从井口开始,经分离、计量、调压、净化和集中等一 系列过程,到向干线输气为止。包括井场、集气管网、集气站、天 然气处理厂、外输总站等。
2、干线输气
输气干线从矿场附近的输气首站开始,到终点配气站为止。长 距离管线管径大,压力高,距离长。
3、城市配气
城市配气从配气站开始,通过各级配气管网和气 体调压站根据用户的要求供气。 储气库以调节输气和供气之间的不平衡。
第二节 输气干线的工艺计算
一、一般输气管道通过能力公式及分析
1. 通过能力公式(潘汉德公式) 1)一般输气管指管线敷设在平坦地区,管线沿线地形起 伏的高差在200米以内。 Q=11500Ed2.53〔 (P12-P22)/(ZTLG0.961) 〕0.51
2 2
l输气管线运行的几项基本技术指标 运行操作参数
表征输气管线内气流状况的基本指标是压力、流 量、温度等,用以表明严密性、管内有无积液、污物、 水化物的堵塞。
天然气管道输送系统分析与建模
天然气管道输送系统分析与建模天然气作为清洁能源之一,在现代工业生产和居民生活中的应用越来越广泛。
而天然气在运输过程中则需要借助于天然气管道输送系统来完成。
本文将对天然气管道输送系统进行分析与建模,包括管道系统架构、管道输送流体模型、管道输送系统优化控制策略等几个方面进行阐述。
一、管道系统架构天然气管道输送系统主要由以下几部分组成:气源、气管、调压站、计量站、末端用户等。
其中气源指的是天然气采集站或者天然气井,将采集到的天然气压缩成高压气体并输送到气管中。
而气管是连接气源与调压站的管道。
调压站主要负责将高压天然气降低到所需要的压力,并完成流量的控制与调整。
计量站用于对天然气的质量和流量进行测量以及计量。
末端用户则是指使用天然气的生产、生活、供暖等方面的客户。
上述的各个环节,都需要通过管道系统进行联通,形成一个完整的输送系统。
在管道系统的设计和运行过程中,需要考虑到输送流量、压力、温度等因素的控制,以确保管道系统稳定、高效地运行。
二、管道输送流体模型天然气在运输过程中需要借助于管道进行输送,而管道内的气体流动是在一定的流动状态下进行的。
因此,有效地建立管道内流体的模型,是保证管道系统稳定运行的重要前提。
对于管道内气体流动的模型而言,需要考虑到气体的流动速度、压力、密度、温度等参数。
而更加重要的是,需要考虑到气体流动状态的物理性质以及热力学特性,以便用科学的方式来模拟和预测管道系统内的气体流动。
在气体流动模型中,流量、速度、压力和温度这些参数是相互关联的,因此需要建立起连续性方程、牛顿-莱布尼茨方程、热平衡方程等多个物理学方程。
这些方程通过数值计算的方法进行求解,预测和分析气体在管道内的流动情况,为管道系统的优化和调控提供了重要的依据。
三、管道输送系统优化控制策略针对天然气管道输送系统的相关问题,例如管道内压力梯度、夹层气体及管道内流体摩擦等,需要建立一套完整的控制策略,以满足运行和用户需求的要求。
为了保证管道系统的安全运行,需要对其进行定期检测和维修。
管道订购与运输模型
管道订购与运输模型信息学院 电子信息科学与技术专业摘要:本文针对主管道的订购和运输的实际问题,在详细分析的基础上,利用数学软件LINGO 的简单合理的算法,得出了快速制定并满足可行性和经济性的订购运输模型。
首先,对题中所给的一系列的数据进行了分析并提取得出从每个主管道钢管的钢厂i S 到各个运到点j A 的运输费用ij c (万元),而且从运输费用尽量小的原则出发,每个钢厂到运到点的运输路线也是唯一确定的(比如:从1S 到7A 直接通过公路即可)。
其次,模型认为将题中的“管道不只是运到点1521,,,A A A ,而是管道全线”可以这样理解:先将管道运到各点1521,,,A A A ,然后铺设的过程是各相邻两点之间实行双向铺设的方法,然后总费用可以认为是由钢管本身的价格、钢管的运费和铺设时的运费(1521,,,A A A 各铺设点之间按公路费用处理)三部分构成。
,也就不难得出总运输费用的计算关系式∑∑∑===+++=1412271151)(21.0)(k yk xk i ij i ij j p p c p xf ,由于仅我们目前的水平,只能将此问题当作是一个非线性规划问题求解,而且这样的算法符合简明性的要求,避免了要考虑图的出入度问题和博弈论提出的复杂的算法。
然后,根据钢管的供应和需求的双方的实际,不难发现该目标函数的约束条件有以下几个:①、1521,,,A A A (除了起始两点)中各点向左和向右铺设的钢管和应该等于721,,S S S 七个钢厂输送给该点钢管的总量;②、各点在铺设过程中所需要的运费(k b )是其向左和向右铺设所需要的运费之和;③、721,,S S S 每个钢厂向15个运到点所能供应的钢管总量应小于其生产总量i s 。
根据以上条件由LINGO 软件计算可以得出第一问的最小总费用为1326385万元;针对LINGO 的计算结果分析也可以得到第二问的答案,第一个钢厂产量的上限的变化对购运计划和总费用的影响最大,当其产量上限减少1单位时,总费用会增加171.0万元。
复杂系统建模与仿真——以天然气输送管道为例
复杂系统建模与仿真——以天然气输送管道为例天然气输送管道是现代社会能源供应的主要途径之一,其运行涉及到复杂的物理、化学、机械和控制问题。
为了保证天然气输送管道的安全和可靠性,需要对其进行建模和仿真分析。
本文将从天然气输送管道的特点入手,介绍复杂系统建模和仿真的相关方法,并结合具体案例进行讲解。
一、天然气输送管道的特点天然气输送管道的运行涉及到多个因素,诸如气流速度、温度、压力、湿度等等,这些因素在管道内发生的物理、化学和机械作用使其成为一个典型的复杂系统。
天然气输送管道还存在以下特点:1. 高压、高温、高速:输送管道内的天然气压力、温度和流速都很高,这就会导致管道的热膨胀、应力集中、材料疲劳等问题,这些问题对管道的安全和可靠性有很大的影响。
2. 长距离、大规模:天然气输送管道通常跨越多个城市、甚至多个国家,其长度和管径都非常大,这会导致输送管道的能耗、泄漏、管道损坏等问题,同时还会影响其运行的可持续性。
3. 多元化:天然气输送管道的运行还涉及到多个系统之间的耦合,例如天然气输送系统、防腐系统、安全系统等等,这些系统之间的相互作用会对天然气输送管道的整个运行过程产生影响。
二、复杂系统建模与仿真的相关方法复杂系统的建模和仿真是研究该系统行为的有效方法。
通常,我们将系统按照其组成部分分别进行建模,并利用仿真技术模拟系统在不同条件下的运行情况,以分析系统运行状态,并对系统进行优化设计。
常用的复杂系统建模和仿真方法包括:1. 数学建模:数学建模可以将系统的各个因素表示为符号、函数或方程的形式。
通过建立数学模型,可以优化系统参数,预测系统行为,分析系统的故障和瓶颈等问题。
数学建模通常包括模型选择、参数估计、模型检验等步骤。
2. 物理模拟:物理模拟是通过实验验证建立数学模型是否精确的有效方法。
通常采用实物模型或者根据系统特性建立模拟器,通过检测输出信号以及观察模型的行为方式,对数学模型进行验证,并优化其参数。
天然气管道运输模型
毕业论文论文题目天然气管道运输模型学院韩山师范学院专业数学与应用数学年级20111114学号2011111426学生姓名陈娴指导教师肖刚完成时间2014 年12 月韩山师范学院教务处制天然气管道运输模型陈 娴摘 要 通过对天然气供应商与居民区之间情况的分析,安排适当的管道运输方案,使管道运输费用最小,从而促使利润最大.根据具体情况,建立线性规划模型,利用约束条件和目标函数求解约束优化问题,并找出最佳的解决方案,在MATLAB 和LINGO 软件中证明该方法是可行的,以及管道运输的优化对城市燃气设计具有一定的指导意义. 关键词 天然气管道运输;线性规划;优化设计1 引言天然气作为燃料,有一个干净的,新的,高效,优质,无污染的特点,迅速成长为一个世界能源的三大支柱之一.我国各个城市天然气的使用也已经快速地发展起来.由于受到地理位置、本身造价和建设费用、管道维修和管理费用等因素的限制,如何安排管道运输方案,使运费最小或利润最大,这便需要建立适当的数学规划模型来解决此类问题.2 线性规划模型2.1线性规划问题的定义所谓线性规划,是指在一定条件下,为了使经济效果达到最好,怎样合理安排人力物力等资源,以求达到目标的过程.一般地,我们所求的线性规划问题,其实就是求线性目标函数在线性约束条件下如何求最大值或最小值的问题.其中,线性规划的最主要的三要素是决策变量、约束条件、目标函数.满足线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域[1]. 2.2线性规划问题的一般形式⎪⎪⎩⎪⎪⎨⎧=≥+==+++=≥+++++=n j m p i p i t s z x b x a x a x a b x a x a x a x c x c x c j n n in i i n n in i i n n ,,1,0,,1,1,..min 221122112211 ,,(2.1)其中,1,...,j x j n =为待定的决策变量,已知的系数ij a 组成的矩阵111212122212nn m m mn A a aa a a aa aa ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(2.2)称为约束矩阵.A 的列向量记为j A ,1,...,j n =;A 的行向量记为,1,...,T i A i m =(T 为转置符号),称1122n n c x c x c x ++为目标函数,记为x c j nj j z ∑==1,向量()Tnc c c ,,1=称为价值向量,j c (j=1,…,n )称为价值系数;向量()Tm b b b ,,1 =称为右端向量,条件0j x ≥称为非负约束;如果原问题是求目标函数x c j nj j ∑=1的最大值,可等价地转换为求)(1x c jnj j∑=-的最小值.因此,我们一般考虑的是求最小值的问题.一个满足所有约束条件的向量()Tn x x x ,1=称为线性规划问题(2.2.1)的可行解或可行点.所有的可行点组成的集合称为线性规划问题(2.2.1)的可行区域,记为D .给定一个线性规划问题,下列三种情况必居其一:(1)D=Φ,称该问题无解或不可行;(2)D ≠Φ,但目标函数在D 上无界,此时称该问题无界;(3)求解一个线性规划问题就是要判断该问题属于哪种情况,当问题有最优解时,还需要在可行区域中求出使目标函数达到最小值的点,也就是最优解,以及目标函数的最优值[1]. 2.3线性规划的发展有关线性规划这个概念的提出,分别由法国数学家 J.- B.- J.傅里叶和 C.瓦莱-普森分别于1832和1911年独立地提出,可惜当时并未引起人们的注意.接着,1939年在《生产组织与计划中的数学方法》一书中提出线性规划问题,这个作家就是苏联数学家Л.В.康托罗维奇,但也未引起大家的重视.1947年这门学科终于被奠定了基础,就是因为美国数学家G.B.丹齐克所提出线性规划的一般数学模型和求解线性规划问题的通用方法──单纯形法,大家终归初步懂得怎么求解线性规划问题.紧接着,终于在1947年,人们开创了线性规划的许多新的研究领域,就是因为美国数学家J.von 诺伊曼提出对偶理论,扩大了它的应用范围和解题能力.1951年,线性规划被应用到经济领域,美国经济学家T.C.库普曼斯为此与康托罗维奇一起获1975年诺贝尔经济学奖,取得了重大的成就.上世纪50年代的线性规划理论的研究中,一大批新算法的出现离不开科学家的贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天然气管道运输模型毕业论文论文题目天然气管道运输模型学院韩山师范学院专业数学与应用数学年级20111114学号2011111426学生姓名陈娴指导教师肖刚完成时间2014 年12 月韩山师范学院教务处制天然气管道运输模型陈娴摘要通过对天然气供应商与居民区之间情况的分析,安排适当的管道运输方案,使管道运输费用最小,从而促使利润最大.根据具体情况,建立线性规划模型,利用约束条件和目标函数求解约束优化问题,并找出最佳的解决方案,在MATLAB和LINGO 软件中证明该方法是可行的,以及管道运输的优化对城市燃气设计具有一定的指导意义.关键词天然气管道运输;线性规划;优化设计1 引言天然气作为燃料,有一个干净的,新的,高效,优质,无污染的特点,迅速成长为一个世界能源的三大支柱之一.我国各个城市天然气的使用也已经快速地发展起来.由于受到地理位置、本身造价和建设费用、管道维修和管理费用等因素的限制,如何安排管道运输方案,使运费最小或利润最大,这便需要建立适当的数学规划模型来解决此类问题.2 线性规划模型2.1线性规划问题的定义所谓线性规划,是指在一定条件下,为了使经济效果达到最好,怎样合理安排人力物力等资源,以求达到目标的过程.一般地,我们所求的线性规划问题,其实就是求线性目标函数在线性约束条件下如何求最大值或最小值的问题.其中,线性规划的最主要的三要素是决策变量、约束条件、目标函数.满足线性约束条件的解叫做可行解,由所有可行解组成的集合叫做可行域[1]. 2.2线性规划问题的一般形式⎪⎪⎩⎪⎪⎨⎧=≥+==+++=≥+++++=n j m p i p i t s z x b x a x a x a b x a x a x a x c x c x c j n n in i i n n in i i n n ,,1,0,,1,1,..min 221122112211 ,,(2.1)其中,1,...,j x j n =为待定的决策变量,已知的系数ij a 组成的矩阵111212122212nn m m mn A a aa a a aa aa ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦(2.2) 称为约束矩阵.A 的列向量记为j A ,1,...,j n =;A 的行向量记为,1,...,T i A i m =(T 为转置符号),称1122n n c x c x c x ++为目标函数,记为x c j nj j z ∑==1,向量()Tnc c c ,,1=称为价值向量,j c (j=1,…,n )称为价值系数;向量()Tm b b b ,,1 =称为右端向量,条件0j x ≥称为非负约束;如果原问题是求目标函数x c j nj j ∑=1的最大值,可等价地转换为求)(1x c jnj j∑=-的最小值.因此,我们一般考虑的是求最小值的问题.一个满足所有约束条件的向量()Tn x x x ,1=称为线性规划问题(2.2.1)的可行解或可行点.所有的可行点组成的集合称为线性规划问题(2.2.1)的可行区域,记为D .给定一个线性规划问题,下列三种情况必居其一:(1)D=Φ,称该问题无解或不可行;(2)D ≠Φ,但目标函数在D 上无界,此时称该问题无界;(3)求解一个线性规划问题就是要判断该问题属于哪种情况,当问题有最优解时,还需要在可行区域中求出使目标函数达到最小值的点,也就是最优解,以及目标函数的最优值[1].2.3线性规划的发展有关线性规划这个概念的提出,分别由法国数学家 J.- B.- J.傅里叶和 C.瓦莱-普森分别于1832和1911年独立地提出,可惜当时并未引起人们的注意.接着,1939年在《生产组织与计划中的数学方法》一书中提出线性规划问题,这个作家就是苏联数学家Л.В.康托罗维奇,但也未引起大家的重视.1947年这门学科终于被奠定了基础,就是因为美国数学家G.B.丹齐克所提出线性规划的一般数学模型和求解线性规划问题的通用方法──单纯形法,大家终归初步懂得怎么求解线性规划问题.紧接着,终于在1947年,人们开创了线性规划的许多新的研究领域,就是因为美国数学家J.von诺伊曼提出对偶理论,扩大了它的应用范围和解题能力.1951年,线性规划被应用到经济领域,美国经济学家T.C.库普曼斯为此与康托罗维奇一起获1975年诺贝尔经济学奖,取得了重大的成就.上世纪50年代的线性规划理论的研究中,一大批新算法的出现离不开科学家的贡献。
例如,1954年C.莱姆基提出对偶单纯形法,1954年S.加斯和T.萨迪等人解决了线性规划的灵敏度分析和参数规划问题,1956年A.塔克提出互补松弛定理,1960年G.B.丹齐克和P.沃尔夫提出分解算法等,把线性规划问题的发展推向高潮.其他数学规划问题包含整数规划、随机规划和非线性规划的算法钻研都是由于线性规划的研究成果高度发展和突破。
因为数字电子计算机的发展,出现了很多线性规划软件,如MPSX,OPHEIE,UMPIRE等,能够很方便地求解几千个变量的线性规划问题,这时线性规划的准确性得到机器的保障.在前人研究成果的基础上,1979年苏联数学家L. G. Khachian提出解线性规划问题的椭球算法,并证实它是多项式时间算法.1984年美国贝尔电话实验室的印度数学家N.卡马卡提出解线性规划问题的新的多项式时间算法,表明该方法是求解线性规划问题中变量个数为5000的时候比用单纯形法还要节省1/50的时间,大大提高了求解线性规划问题的效率.现已形成线性规划多项式算法理论.50年代后线性规划的应用范围不断扩大[2].2.4线性规划问题的实际应用在各种不同的工业,农业,商业,行政,军事,公用事业和其他领域,存在大量的线性规划问题.一些计划是非线性规划问题,但往往可以改变规模或利用分段线性的方法,转化为线性规划模型,并使用线性规划问题的专业解答软件轻易解决出来.用线性规划求解的典型问题有运输问题、生产计划问题、配套生产问题、下料和配料问题等,具体问题如下.①运输问题某产品有n个产地,m个销地.已知各产地的产量和各销地的销量,以及各产地到各销地的单位运价,问如何安排各产地到各销地的运量,使总的运费为最少?②生产计划问题用n种资源生产m种产品.已知各种产品每生产一单位可得的利润和所需的各种资源的数量,以及各种资源的限额.问如何计划各种产品的生产量,使总的利润为最大?③配套生产问题用若干台机床加工某种产品的各种零件.已知各机床加工不同零件的效率.问如何分配各机床的任务,在零件配套的前提下使一个生产周期内的产量最高?④下料问题将一批固定规格的条材或板材裁剪成具有规定尺寸的若干种毛坯,并已设计出若干种下料方式.问采用哪种下料方式,能使各种毛坯满足所需数量,又使总的用料最省?⑤混合配料问题用n种原料配制某些含有m种成分的产品.已知各种成分在各种原料中的单位含量,以及各种原料的单价和限额.问怎样混合调配,在满足产量要求和产品所含各种成分的要求下使成本为最低[2]?2.5用线性规划模型研究天然气管道运输的意义在实际生活中,常常会碰到在一定的人力、物力、财力等资源条件下,怎么精打细算高明安排,用最少的资本赢得最大的效益的问题,而这恰是线性规划研究的基本内容,它在实际生活中有着非常广泛的应用.随着计算技术的不断发展,使成千上万个约束条件和决策变量的线性规划问题能迅速地求解,更为线性规划在经济等各领域的广泛应用创造了极其有利的条件.天然气经过勘探开发到开采,使之成为一种能源投入到日常生产生活中,这本身便是一种经济效益规划活动.借此,天然气生产与经营部门与天然气用户之间便形成一种密切的关系,生产部门需要一定的投资(如铺设天然气管道)把天然气运输到用户,才能取得一定的经济效益.因此,我们所关注的如何取得利润最大化问题便成为我们所研究的对象.由于利润最大化又离不开对天然气开发、处理与运输和天然气管道维护的投资等成本问题,以及根据天然气用户的需气量和实际情况来决定天然气的价格,在这些限制条件下来考虑最大化问题,这便需要建立一个线性规划模型来研究和证明[3].3 天然气管道模型3.1模型引入:某市有甲、乙、丙、丁、戊五个居民小区,天然气有A、B、C三个燃气供应站供应.为了保证每个小区每天都能得到基本生活用气量(单位:4310m)分别为a1,a2,a3,a4,a5,三个供气站都进行了相应的调整,每天最多能分别供应天然气k1,k2,k3.但由于地理位置的差别,天然气公司从各供应点输气所需付出的管理费用不同(见下表),其他管理费用(单位:万元/4310m)都是m.根据公司规定,各区用户按照统一标准n收费.此外,五个小区都向天然气公司申请额外用气量(单位:4310m)b1,b2,b3,b4,b5.(1)该天然气公司应如何分配供气量,才能使获得的利润最大?(供气量能满足额外用气量)(2)为了预防供气量过分输出,造成不必要的浪费,天然气公司决定调整供气量,使三个供气站每天供气量(单位:4310m)调整为t1,t2,t3(供气量不能满足额外用气量),此时应该如何分配供气量,才能使获得的利润最大[4]?表1 从燃气供应点向各小区供气的输气管理费3.2模型分析:如何分配供气量,使得获得利润最大,这是本题的关键.根据题意可知,当能使获得的收入最大,而成本及管理费用等额外支出最小时,可获得利润最大.从题目所给的数据可知,A 、B 、C 三个供气站每天供气量(单位:4310m )分别为k 1、k 2、k 3。
超出五个小区所需的每天基本用气量和额外用气量之和为b bb b b a a a a a 5432154321+++++++++(单位:4310m ),所以供气站供气量不能全部输出.天然气公司所收取天然气费用为n 万元/4310m ,此外其他管理费用为m 万元/4310m ,还加上输气管理费如上表,所以可得实际三个供气站所得利润如下表2 从燃气供应点向各小区供气的纯利润纯利润/(万元) 甲乙 丙 丁 戊Ap m n 11--p m n 12--p m n 13--p m n 14--p m n 15--Bp m n 21--p m n 22--pm n 23--p m n 24--pm n 25--Cpm n 31--pm n 32--pm n 33--pm n 34--pm n 35--管理费/(万元) 甲乙丙丁戊Ap 11p 12p 13p 14p 15Bp 21p 22p 23p 24p 25Cp31p32p33p34p35再根据此表建立适当的线性规划模型,然后借助于解决线性规划的专业软件Lingo 或MATLAB 求解即可.至于问题(2),由于A 、B 、C 三个供气站供气量总和为t t t 321++(4310m ),不超过五个小区所需的每天基本用气量和额外用气量之和为b bb b b a a a a a 5432154321+++++++++(4310m ),所以供气站供气量能全部输出.所以每天天然气公司的总收入是)(321t t t n ++⋅(万元),每天其他管理费用为)(321t t t m ++⋅(万元),而这都与供气站分配的供气量无关.所以,要使利润最大,则要通过建立数学模型并求解使输气管理费最小便可. 3.3符号说明符号 意义单位 X 11供气站A 向甲区的日供气量 m3410X 12 供气站A 向乙区的日供气量 m 3410X 13 供气站A 向丙区的日供气量 m 3410X 14供气站A 向丁区的日供气量 m 3410X 15供气站A 向戊区的日供气量 m 3410X21供气站B 向甲区的日供气量 m 3410X22供气站B 向乙区的日供气量 m 3410X 23 供气站B 向丙区的日供气量 m 3410X 24 供气站B 向丁区的日供气量 m 3410X 25供气站B 向戊区的日供气量 m 3410X 31供气站C 向甲区的日供气量 m 3410X 32 供气站C 向乙区的日供气量 m 3410X33供气站C 向丙区的日供气量 m 3410X34供气站C 向丁区的日供气量 m 3410X 35供气站C 向戊区的日供气量m 3410Z 1问题一所获得的最大利润 万元Z 2问题二所获得的最大利润 万元Z 3问题二中的输气管理费用万元3.4模型建立3.4.1问题一模型建立决策变量:三个供气站A ,B ,C (i=1,2,3)分别向五个小区甲,乙,丙,丁,戊(j=1,2,3,4,5)供气.设ij X 表示供气站i 向j 小区的日供气量(i=1,2,3,j=1,2,3,4,5),即总共有15个决策变量.目标函数:设每天可获得利润为Z 1,则根据分析可知,当供气收入减去其他管理费和输气管理费后所得的纯利润,便是Z 1,即Xp X p X p Xp Xp X p X p X p X p X p Xp X p X p Xp X p Zm n m n m n m n m n m n m n m n m n m n m n m n m n m n m n 3535343433333232313125252424232322222121151514141313121211111)(--+--+--+--+--+--+--+--+--+--+--+--+--+--+--=)()()()()()()()()()()()()()(约束条件:由于供气站供气量不能全部输出,所以根据供气站供气量的限制,得kXXXXXk X X X X X k X X X X X 335343332312252423222111514131211,,≤++++≤++++≤++++此外,考虑到满足小区的基本用气量和额外用气量,决策变量可限制为:ba XXXab a XXX a b a X X X a b a X X X a b a X X X a 553525155443424144333323133223222122113121111,,,,+≤++≤+≤++≤+≤++≤+≤++≤+≤++≤综上可得线性规划为Xp X p X p X p X p X p X p X p X p X p Xp X p X p X p X p Zm n m n m n m n m n m n m n m n m n m n m n m n m n m n m n 3535343433333232313125252424232322222121151514141313121211111)(max --+--+--+--+--+--+--+--+--+--+--+--+--+--+--=)()()()()()()()()()()()()()(kXXXXXt s 11514131211..≤++++(3.1)kX XXXX 22524232221≤++++ (3.2)kXXXXX33534333231≤++++(3.3)b a X X X a 113121111+≤++≤ (3.4)b a X X X a 223222122+≤++≤ (3.5)b a XXXa 333323133+≤++≤ (3.6)b a X X X a 443424144+≤++≤ (3.7) b a X X X a 553525155+≤++≤ (3.8) 最后用Lingo 软件求得Z 1即可.3.4.2问题二模型建立决策变量:三个供气站A ,B ,C (i=1,2,3)分别向五个小区甲,乙,丙,丁,戊(j=1,2,3,4,5)供气.设ij X 表示供气站i 向j 小区的日供气量(i=1,2,3,j=1,2,3,4,5),即总共有15个决策变量.目标函数:设每天可获得利润为Z 2,由于三个供气站供气总量t t t 321++(4310m )不能满足五个小区的每日用气需求量和额外用气量b bb b b a a a a a 5432154321+++++++++(4310m ),故三个供气站的日供气量能全部输出,而根据收费标准天然气公司每天的总收入是)(321t t t n ++⋅(万元),每天其他管理费用是)(321t t t m ++⋅(万元),则目标函数是令输气管理费用最低,使得扣除两项收入后的利润最大,假设输气管理费用为Z 3,则Xp X p Xp Xp Xp X p X p X p X p X p X p X p X p X p Xp Z3535343433333232313125252424232322222121151514141313121211113++++++++++++++=.约束条件:由于供气站供气量能全部输出,所以根据供气站供气量的限制,得tX XXXXtXXXXX t X X X X X 335343332312252423222111514131211,,=++++=++++++++=此外,考虑到满足小区的基本用气量和额外用气量,决策变量可限制为:ba XXXa b a XXX a b a X X X a b a X X X a b a X X X a 553525155443424144333323133223222122113121111,,,,+≤++≤+≤++≤+≤++≤+≤++≤+≤++≤ 综上可得线性规划为Xp Xp Xp X p X p X p X p X p X p X p Xp Xp Xp X p X p Z 3535343433333232313125252424232322222121151514141313121211113m in ++++++++++++++=t X XXX X t s =++++11514131211.. (3.9)t XXXXX22524232221=++++(3.10)tXXXXX33534333231=++++(3.11)b a XXXa 113121111+≤++≤(3.12)ba XXXa 223222122+≤++≤ (3.13)b a X X X a 333323133+≤++≤ (3.14)b a X X X a 443424144+≤++≤(3.15)b a X X X a 553525155+≤++≤(3.16)用Lingo 软件求得Z 3,最后所求最大利润Zt t t t t tZ m n 33213212)()(-++-++=4 问题引入根据模型,假设甲、乙、丙、丁、戊五个小区每天的基本生活用气量分别为1.5,1.8,1.3,1.3,1.6(单位:4310m ),额外用气量分别为0.7,0.9,0.4,0.5,0.8(单位:4310m ),问题一中A 、B 、C 三个供气站每天的供气量分别为3.2,3.9,4.2(单位:4310m ),问题二中A 、B 、C 三个供气站每天的供气量分别调整为2.8,3.5,3.9(单位:4310m ),并假设B 点与乙区,C 点与丁区之间没有输气管道,其他管理费用都是1.5(单位:万元/4310m ),供气收费标准为4.8(单位:万元/4310m ),以及下表给出从燃气供应点向各小区供气的输气管理费.表3 从燃气供应点向各小区供气的输气管理费4.1模型建立4.1.1问题一模型建立由3.4.1可得,问题一中供气站向各小区供气所得利润如下表管理费/(万元)甲 乙 丙 丁 戊A 0.5 0.2 0.3 0.1 0.3 B0.3 / 0.4 0.3 0.5 C0.40.20.5/0.2表4 从燃气供应点向各小区供气的纯利润纯利润/(万元) 甲 乙丙 丁戊A2.83.1 33.2 3 B 3 / 2.9 3 2.8 C2.93.12.8/3.1故所建立线性规划模型如下X X X X X X X X X X X X X Z3533323125242321151413121111.38.21.39.28.239.2332.331.38.2max ++++++++++++=2.3..1514131211≤++++XXXXX t s (4.1)9.325242321≤+++X X X X (4.2) 2.435333231≤+++X X X X (4.3) 2.25.1312111≤++≤XXX(4.4)7.28.13212≤+≤XX(4.5)7.13.1332313≤++≤XXX(4.6)8.13.12414≤+≤X X (4.7)4.26.1352515≤++≤XXX(4.8)用Lingo 软件求解可得,A 供气站向丙区供气 1.4(4310m ),向丁区供气1.8(4310m );B 供气站向甲区供气2.2(4310m ),向丙区供气0.3(4310m );C 供气站向乙区供气2.7(4310m ),向戊区供气2.4(4310m ).最后获得的最大利润为33.24(万元).表5 问题一的结果列表供气量/(m3410)甲乙丙丁戊A 0 0 1.4 1.8 0B 2.2 / 0.3 0 0 C2.7/2.44.1.2问题二模型建立由3.4.2可得,问题二所建立的线性规划模型如下X X X X X X X X X X X X X Z3533323125242321151413121132.05.02.04.05.03.04.03.03.01.03.02.05.0min ++++++++++++=8.2..1514131211=++++XXXXX t s (4.9)5.325242321=+++X X X X (4.10)9.335333231=+++XXXX(4.11)2.25.1312111≤++≤XXX(4.12)7.28.13212≤+≤X X(4.13)7.13.1332313≤++≤X X X(4.14)8.13.12414≤+≤X X(4.15)4.26.1352515≤++≤X X X(4.16)用Lingo 软件求解可得,A 供气站向乙区供气1,向丁区供气1.8(4310m );B 供气站向甲区供气2.2(4310m ),向丙区供气1.3(4310m );C 供气站向乙区供气1.5(4310m ),向戊区供气2.4(4310m ).输气管理费用Z 3=2.34(万元).故最大利润Z 2=48.96-15.3- Z 3=48.96-15.3-2.34=31.32(万元).表6 问题二的结果列表供气量/(m3410)甲乙丙丁戊A 0 1 0 1.8 0B 2.2 / 1.3 0 0 C1.5/2.44.2结果分析4.2.1问题一结果分析(1)从结果上看,供气站不一定全部对所有小区提供供气,考虑到经济效益,某些供气站可以中断对该小区进行供气,只要满足该小区的日供气量,可以由其他供气站代为供气,而向经济利润大的小区提供更多支持.(2)由于供气站供气量超过小区所需的日用气量和额外需求量,所以小区每天基本用气量是能满足的,甚至连额外用气量也能满足,故以上约束条件④~⑧左边的约束可以去掉,把右边的 可以改成=,也不会影响最后的结果.(3)由于B 供气站直接向甲区提供所需的供气量,而不需要向其他小区供气,所以从经济角度上来说,考虑管道本身的造价问题,可以把B 供气站建立在甲区附近,尽可能减少因管道铺设所带来的额外支出,在减低成本的前提下实现利润最大化,其他供气站也可以此为借鉴. 4.2.2问题二结果分析(1)由于向乙区所需的供气量直接由A 供气站提供,所以从经济角度上来说,考虑管道本身的造价问题,可以把A 供气站建立在乙区附近,尽可能减少因管道铺设所带来的额外支出,在减低成本的前提下实现利润最大化.(2)若通过计算后实现利润的最大化,则可根据已知所求的结果,适当减少甚至关闭某小区和某供气站的输气管道,如本题中实现利润最大时,A 供气站不需要向甲区供气,则两点之间不必要铺设输气管道,也不用增加额外管理费用,也是在减低成本的前提下实现利润最大化.5 结论本文的研究重点,主要在已知其成本造价和额外支出的前提下,如何根据实际需求取得供气分配和利润的平衡,实现利润最大化.故应该根据已知条件分析模型,列出使利润最大的等式,建立适当的决策变量、目标函数和约束条件,并借助Lingo 软件求出答案,对结果进行探索和剖析.从结果上看,问题一中A 供气站向丙区供气1.4,向丁区供气1.8(4310m );B 供气站向甲区供气2.2(4310m ),向丙区供气0.3(4310m );C 供气站向乙区供气2.7(4310m ),向戊区供气2.4(4310m ).最后获得的最大利润为33.24万元;问题二中A供气站向乙区供气1(4310m);B10m),向丁区供气1.8(43供气站向甲区供气2.2(4310m),向丙区供气1.3(4310m);C供气站向乙区供气1.5(4310m).输气管理费用Z3=2.34万元.故最大利润Z2=31.32 10m),向戊区供气2.4(43万元.从经济与环境的可持续发展来说,天然气作为一种新型能源,具有洁净、高效、优质、无污染等特点,如何重点发展天然气产业,发展绿色环保经济,这是未来一个值得研究和摸索的话题.致谢:本次毕业论文是在我们的导师肖刚老师的悉心指导下完成的.在每次遇到问题时老师不辞辛苦地讲解才使得我的论文设计得以顺利地进行.从论文的选题到资料的搜集再到最后的修改整个过程中,花费了肖老师很多宝贵的时间和精力,再此向老师表示衷心地感谢!导师严谨的治学态度,开拓进取的精神和高度的责任心都将使学生终身受益!参考文献[1]刁在筠.运筹学(第三版)[M].北京:高等教育出版社,2007, 57-62.[2]张建中,许绍吉.线性规划[M].北京:科学出版社,2005.[3]王艳峰,沈祖培.输气管道优化设计新模型[J]. 油气储运. 2004.[4]姜启源.数学模型(第四版)[M].北京:高等教育出版社,2011, 85-95.The model of the transportation of natural gas pipelineChen XianAbstract:Through the analysis of gas suppliers and residential areas, we arrange the proper scheme of pipeline transport, make the pipeline transportation costs minimum, prompting the biggest profit. According to the specific circumstances, linear programming model is established, and the related constraints and objective function will be the constraint optimization problem.In the MATLAB and LINGO software we can find the optimalsolutions to prove that the method has its feasibility,and the optimization design of urban natural gas pipeline has a practical guiding significance.Key words: The transportation of natural gas pipeline; Linear programming; The optimization design6 附录6.1附录清单附录一:求解问题1的LINGO程序附录二:附录一的运行结果附录三:求解问题2的LINGO程序附录四:附录三的运行结果6.2附录正文附录一:求解问题1的LINGO程序max=2.8*x11+3.1*x12+3*x13+3.2*x14+3*x15+3*x21+2.9*x23+3*x24 +2.8*x25+2.9*x31+3.1*x32+2.8*x33+3.1*x35;x11+x12+x13+x14+x15<=3.2;x21+x23+x24+x25<=3.9;x31+x32+x33+x34<=4.2;x11+x21+x31>=1.5;x11+x21+x31<=2.2;x12+x32>=1.8;x12+x32<=2.7;x13+x23+x33>=1.3;x13+x23+x33<=1.7;x14+x24>=1.3;x14+x24<=1.8;x15+x25+x35>=1.6;x15+x25+x35<=2.4;end附录二:附录一的运行结果Global optimal solution found.Objective value: 33.24000Infeasibilities: 0.000000Total solver iterations: 8Variable Value Reduced Cost X11 0.000000 0.3000000 X12 0.000000 0.1000000 X13 1.400000 0.000000 X14 1.800000 0.000000 X15 0.000000 0.2000000 X21 2.200000 0.000000 X23 0.3000000 0.000000 X24 0.000000 0.1000000 X25 0.000000 0.3000000 X31 0.000000 0.1000000 X32 2.700000 0.000000 X33 0.000000 0.1000000 X35 2.400000 0.000000 X34 0.000000 0.000000 Row Slack or Surplus Dual Price1 33.24000 1.0000002 0.000000 0.10000003 1.400000 0.0000004 1.500000 0.0000005 0.7000000 0.0000006 0.000000 3.0000007 0.9000000 0.0000008 0.000000 3.1000009 0.4000000 0.00000010 0.000000 2.90000011 0.5000000 0.00000012 0.000000 3.10000013 0.8000000 0.00000014 0.000000 3.100000 附录三:求解问题2的LINGO程序min=0.5*x11+0.2*x12+0.3*x13+0.1*x14+0.3*x15+0.3*x21+0.4*x23 +0.3*x24+0.5*x25+0.4*x31+0.2*x32+0.5*x33+0.2*x35;x11+x12+x13+x14+x15=2.8;x21+x23+x24+x25=3.5;x31+x32+x33+x35=3.9;x11+x21+x31>=1.5;x11+x21+x31<=2.2;x12+x32>=1.8;x12+x32<=2.7;x13+x23+x33>=1.3;x13+x23+x33<=1.7;x14+x24>=1.3;x14+x24<=1.8;x15+x25+x35>=1.6;x15+x25+x35<=2.4;end附录四:附录三的运行结果Global optimal solution found.Objective value: 2.340000Infeasibilities: 0.000000Total solver iterations: 8Variable Value Reduced Cost X11 0.000000 0.3000000 X12 1.000000 0.000000 X13 0.000000 0.000000 X14 1.800000 0.000000 X15 0.000000 0.1000000 X21 2.200000 0.000000 X23 1.300000 0.000000 X24 0.000000 0.1000000 X25 0.000000 0.2000000 X31 0.000000 0.2000000X32 1.500000 0.000000 X33 0.000000 0.2000000 X35 2.400000 0.000000 Row Slack or Surplus Dual Price1 2.340000 -1.0000002 0.000000 -0.20000003 0.000000 -0.30000004 0.000000 -0.20000005 0.7000000 0.0000006 0.000000 0.0000007 0.7000000 0.0000008 0.2000000 0.0000009 0.000000 -0.100000010 0.4000000 0.00000011 0.5000000 0.00000012 0.000000 0.100000013 0.8000000 0.00000014 0.000000 0.000000。
