平面问题
合集下载
第7章平面问题
y xy
xz yz 0,则平面应变状态的
,且满足以下几何方程
u x x v y y
xy yx
1 u v ( ) 2 y x
(15-38 )
根据体积不变条件有 x y
平面变形状态下的应力状态特点: 1)由于平面变形时物体内与Z轴垂直的平面始终不会倾斜扭曲,所以z平面
上没有切应力分量,即 zx zy 0, z方向为主方向,该方向上的切应
力为零,z平面为主平面, z为中间主应力,在塑性状态下, z 等于平均应 力,即
z ( x y ) m
1 2
2)如果以应力主轴为坐标轴,平面塑性应变状态下的应力张量可 写成
1 ij 0 0
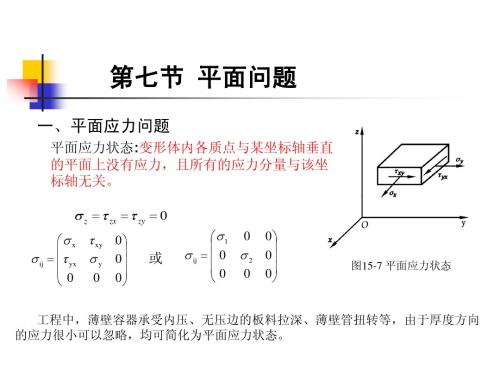
第七节 平面问题
一、平面应力问题
平面应力状态:变形体内各质点与某坐标轴垂直 的平面上没有应力,且所有的应力分量与该坐 标轴无关。
z zx zy 0
x xy ij yx y 0 0 0 0 0
或
1 0 ij 0 2 0 0
0
2
0
0 0 1 2-7 平面应力状态
工程中,薄壁容器承受内压、无压边的板料拉深、薄壁管扭转等,由于厚度方向 的应力很小可以忽略,均可简化为平面应力状态。
二、平面应变问题
平面变形(平面应变):物体内所有质点都只在同一坐标平面内发生变形,
而该平面的法线方向没有变形。 设没有变形的方向为 z方向,该方向上的位移分量为零,其余两个方向的 位移分量对z的偏导数必为零,所以 z = 三个应变分量为 x 、 、
xz yz 0,则平面应变状态的
,且满足以下几何方程
u x x v y y
xy yx
1 u v ( ) 2 y x
(15-38 )
根据体积不变条件有 x y
平面变形状态下的应力状态特点: 1)由于平面变形时物体内与Z轴垂直的平面始终不会倾斜扭曲,所以z平面
上没有切应力分量,即 zx zy 0, z方向为主方向,该方向上的切应
力为零,z平面为主平面, z为中间主应力,在塑性状态下, z 等于平均应 力,即
z ( x y ) m
1 2
2)如果以应力主轴为坐标轴,平面塑性应变状态下的应力张量可 写成
1 ij 0 0
第七节 平面问题
一、平面应力问题
平面应力状态:变形体内各质点与某坐标轴垂直 的平面上没有应力,且所有的应力分量与该坐 标轴无关。
z zx zy 0
x xy ij yx y 0 0 0 0 0
或
1 0 ij 0 2 0 0
0
2
0
0 0 1 2-7 平面应力状态
工程中,薄壁容器承受内压、无压边的板料拉深、薄壁管扭转等,由于厚度方向 的应力很小可以忽略,均可简化为平面应力状态。
二、平面应变问题
平面变形(平面应变):物体内所有质点都只在同一坐标平面内发生变形,
而该平面的法线方向没有变形。 设没有变形的方向为 z方向,该方向上的位移分量为零,其余两个方向的 位移分量对z的偏导数必为零,所以 z = 三个应变分量为 x 、 、
第六章-平面问题

2
就可得到平面应变 中的关系式:
x y xy
1 E 1 E
2 2
x y 1
y
1
1
x
2 (1 ) E
xy
由于这种相似性,在解平面应变问题时, 可把对应的平面问题的方程和解答中的弹性 常数进行上述代换,就可得到相应的平面应 变问题的解。
逆解法
逆解法,就是先设定满足相容方程的应力函数φf
2 x
2
f f 2 2 2 y x y
2 2 2
0
然后根据
x
f
2
y
2
2
Fb x x Fb y y
f x
2 2
y
xy
f
sin
m 1
m
x ( A m sh m y B m ch m y C m y sh m y
D m y ch m y )
' ' '
cos m x ( A m sh m y
' ' ' ' ' '
m 1
B m ch m y C m y sh m y D m y ch m y )
第三节 级数法
多项式形式的应力函数求解直角坐标平面 问题只对简单载荷或连续分布载荷的情况才适 用,如果载荷比较复杂,或者是间断载荷,一 般采用三角级数法求解。复杂载荷,或者是间 断载荷,通常可以展开为富氏级数。 为此,用逆解法,首先假设应力函数取如 下的形式:
就可得到平面应变 中的关系式:
x y xy
1 E 1 E
2 2
x y 1
y
1
1
x
2 (1 ) E
xy
由于这种相似性,在解平面应变问题时, 可把对应的平面问题的方程和解答中的弹性 常数进行上述代换,就可得到相应的平面应 变问题的解。
逆解法
逆解法,就是先设定满足相容方程的应力函数φf
2 x
2
f f 2 2 2 y x y
2 2 2
0
然后根据
x
f
2
y
2
2
Fb x x Fb y y
f x
2 2
y
xy
f
sin
m 1
m
x ( A m sh m y B m ch m y C m y sh m y
D m y ch m y )
' ' '
cos m x ( A m sh m y
' ' ' ' ' '
m 1
B m ch m y C m y sh m y D m y ch m y )
第三节 级数法
多项式形式的应力函数求解直角坐标平面 问题只对简单载荷或连续分布载荷的情况才适 用,如果载荷比较复杂,或者是间断载荷,一 般采用三角级数法求解。复杂载荷,或者是间 断载荷,通常可以展开为富氏级数。 为此,用逆解法,首先假设应力函数取如 下的形式:
2平面问题的基本理论(平面应力与应变,受力状态,圣维兰原理)

当面积 AB 无限减小而趋于 P 点时,平面 AB 上的 应力就是上述斜面上的应力。 现设斜面上的全应力p可以分解为沿坐标向的分 量( px , py ),或沿法向和切向的分量( σn , τn),如图 2-4b所示。
用n代表斜面AB的外法线方向,其方向余弦为:
cosn, x l, cosn, y m
c
0
,则有
F 0, F Mc 0
x
y
0
yx dy dy dx dx xy dy 1 ( yx dy)dx 1 yx dx 1 0 2 2 y 2 2
力矩方程化简后得到:
xy
1 xy 1 yx dx yx dy 2 x 2 y
x yx fx 0 y x xy y f 0 y x y
4.平衡微分方程适用的条件是,只要求符合连 续性和小变形假定。 5.对于平面应力问题和平面应变问题,平衡微 分方程相同。 6.由于τxy =τyx,以后只作为一个独立未知函数 处理。因此,2个独立的平衡微分方程(2-2) 中含有 3个应力未知函数。
由式(2-4)及(2-5)就可以求得经过P点的任意 斜面上的正应力 n 及切应力 n 。
3.然后,再求出主应力和应力主向
设经过P点的某一斜面上的切应力等于零,则该斜 面上的正应力称为在P点的一个主应力,而该斜面 称为在P点的一个应力主平面,该斜面的法线方向 称为在P点的一个应力主向。
(2)只在侧边上受有平行于板面且不沿厚度变化 的面力和体力,且不沿厚度变化,体力 f x , f y , o 和面 力 f x , f y , o ,只是x,y的函数,并构成平衡力系;
有限元分析——平面问题

Re=
NT
s
Pstds
江西五十铃发动机有限公司
技术中心 12 /33
4、整体分析 整体刚度矩阵 整体刚度矩阵组装的基本步骤:
先求出各个单元的单元刚度矩阵; 将单元刚度矩阵中的每个子块放在整体刚度矩阵中的对应位置上,得到单 元的扩大刚度矩阵; 将全部单元的扩大矩阵相加得到整体刚度矩阵。
不失一般性,仅考虑模型中有四个单元,如图所示,四个单元的整体节点位 移列阵为
τZX z= + t/2 =0
因板很薄,载荷又不沿厚度变化,应力沿板 的厚度方向是连续分布的,可以认为,在整
Z
个板内各点都有
σZ=0 τYZ=0 τZX=0
O
tX
图1 平面应力问题
根据剪应力的互等性、物理方程,可得描述平面应力问题的八个独立的基本变量 为
江西五十铃发动机有限公司
技术中心 4 /33
σ=[σX σY τXY]T ε=[εX εY γXY]T
x2 y2 ɑ1= x 3 y 3
1 y2 b1=- 1 y 3
1 c1= 1
x2 x3
(1,2,3)
上式表示下标轮换,即1 2,2 3,3 1同时更换。
江西五十铃发动机有限公司
技术中心 9 /33
重写位移函数,并以节点位移的形式进行表达,有
uv((xx,,yy))N(x,y)qe
其中形函数矩阵为
Y
江西五十铃发动机有限公司
图2 平面应变问题
技术中心 5 /33
根据几何方程、物理方程可得,描述平面应变问题的独立变量也是八个,且与 平面应力问题的一样。只是弹性矩阵变为
1
D=
E1
1 1 2 1
1
平面问题的基本理论

y
y
dy
说明: (1)两个平衡微分方程,三个未知量: x , y , xy yx
—— 超静定问题,需找补充方程才能求解。
(2)对于平面应变问题,x、y方向的平衡方程相同,z 方向自成平衡,上述方程两类平面问题均适用;
(3)平衡方程中不含E、μ,方程与材料性质无关 (钢、石料、混凝土等);
(4)平衡方程对整个弹性体内都满足,包括边界。
1) 2
时,τN为最大、最小值:
max 1 2
min
2
x A
N sN
由 l 1 得, τmax、 τmin 的方向与σ1 ( σ2 )成45°。 2
小结:
(1)斜面上的应力
px l x m yx py m y l xy
(2-3) (2-4)
N l 2 x m2 y 2lm xy (2-5) N lm( y x ) (l 2 m2 ) xy(2-6)
可近似为平面应变问题的例子:
—— 仅为 x y 的函数。
煤矿巷道的变形与破坏分析;挡土墙;重力坝等。
如图所示三种情形,是否都属平面问题?是平 面应力问题还是平面应变问题?
平面应力问题
平面应变问题
非平面问题
3. 平面问题的求解
问题: 已知:外力(体力、面力)、边界条件,
求: x , y , xy x , y , xy u, v
第二章 平面问题的基本理论
要点 —— 1)两类平面问题
2)建立平面问题的基本方程 3)一点应力状态的分析 包括:平衡微分方程;几何方程;物理方 程;变形协调方程;边界条件的描 述;方程的求解方法等
弹性力学是已知外力、物体的形状和大小(边界)、材料特性 (E、μ)、约束条件等,求解应力、应变、位移分量。
平面问题求解的三大方程

平面问题求解的三大方程
求解平面问题的三个主要方程是平面方程、直线方程和曲线方程。
1. 平面方程:平面的一般方程可以表示为Ax + By + Cz + D = 0,其中A、B、C为平面的法向量的三个分量,D是平面与原点的距离。
2. 直线方程:直线的一般方程可以表示为Ax + By + C = 0,其中A、B不同时为0,表示直线的斜率,C是直线与y轴的截距。
3. 曲线方程:曲线的方程通常是根据具体问题的几何特征而定。
常见的曲线方程有直角坐标方程、极坐标方程和参数方程等。
例如,直角坐标方程是x=f(t)和y=g(t)的函数关系式,极坐标
方程是r=f(θ)的关系式。
这三个方程是平面几何问题求解中最常用的工具,通过给定的条件和几何知识,可以将问题转化为方程求解的过程,从而得到解答。
第六章平面问题极坐标解3

G
2(1 E
v)
1 E
v
sin [2 A(1 3v) (1 v) 2B (1 v) D ]
E
3
1 E
v
sin
E
[2
A(3
v)
(1
v)
2B
3
(1
v)
D
]
21
E
v
21 v cos
E
2
A
2B
3
D
代入几何方程
u
sin
E
[2
A(1
3v)
(1
v)
2B
3
(1 v) D ]
f At Bte2t Ce2t D
1
df d
A
2
B(1 2ln ) 2C
d 2 f d 2
A
2
B(3 2ln ) 2C
0
(
d2
d 2
1
d
d
)(
d 2 f d 2
1
df ) 0 d
1
d
d
d
d
1
d
d
d f d
0
d
d
1
d
d
d f d
B1
1
d
d
d f d
B1 ln
u
1
u
sin [2 A(3 v)
E
(1
v
)
2B
3
(1 v) D ]
1
u
u
u
2
1
E
v
cos
2
A
2B
3
D
对第一式积分得
u
sin
《弹性力学》第五章平面问题的复变函数法

在非线性弹性力学中的应用
解决几何非线性问题
01
通过引入复变函数法,可以更精确地描述和分析材料
的几何非线性行为,如大变形、弯曲和扭转等。
分析材料非线性特性
02 复变函数法可用于研究材料的非线性本构关系,包括
弹性模量、泊松比和屈服强度等随应变变化的规律。
求解非线性弹性力学方程
03
利用复变函数法的数学工具,可以更有效地求解非线
03
典型应力集中问题的 复变函数解法
通过实例详细讲解复变函数法在求解 典型应力集中问题中的应用,如圆孔 、椭圆孔、矩形孔等孔边应力集中的 求解。
裂纹问题的复变函数解法
裂纹问题的定义和 分类
介绍裂纹的概念、分类以及裂 纹对材料和结构的影响,如疲 劳裂纹、脆性裂纹等。
复变函数法在裂纹 问题中的应用
阐述如何利用复变函数法求解 裂纹问题,包括裂纹尖端应力 场的求解、裂纹扩展的判据等 。
在迭代计算过程中,要判断 计算结果的收敛性。如果结 果不收敛,应调整计算参数 或改进算法。误差Fra bibliotek析程序实现
分析计算结果的误差来源, 如模型误差、离散化误差、 舍入误差等。尽量减小误差, 提高计算精度。
编写稳定、可靠的程序,实 现复变函数法的数值计算。 程序应具有良好的可读性和 可维护性。
06 复变函数法在弹性力学中 的拓展应用
04 复变函数法在平面问题中 的应用
应力集中问题的复变函数解法
01
应力集中问题的定义 和分类
阐述应力集中的概念,如孔边应力集 中、缺口应力集中等,以及不同类型 的应力集中对材料和结构的影响。
02
复变函数法在应力集 中问题中的应用
介绍如何利用复变函数法求解应力集 中问题,包括应力函数的构造、边界 条件的处理等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.定义单元类型 (1)确定选用solid平面单元(plane182或者plane183)
plane182
plane183
(2)plane182关键字的设置
K3:设置单元特性 Plane stress:不考虑厚度的平面应力(默认选项) Axisymmetric:轴对称 Plane strain :平面应变 Plane strs w/thk:考虑厚度的平面应力 Genrl plane strn:广义的平面应变
拉力为负
7.定义分析类型
8.求解
Von mises stress应力
实例:平面对称问题
实例[2]:如图平板,尺寸(mm)及载荷 如图所示。已知板厚t=2mm,材料弹性模 量E=2×105N/mm2,泊松比v=0.3,求平 板的最大应力及其位移。
解题思路:
1.该问题属于平面应力问题
2.根据平板结构的对称性,只需分析其中的四分之一即可。即如下简化模型:
(3)plane182实常数的设置
板的厚度
3.定义材料属性
4.建立几何模型
注意:平面问题,模型必须建立在总体坐标系下的xy平面
5.划分网格
5.施加载荷与约束
(1).施加约束
(2).施加载荷
q t 20 20 1N/mm2
注意:在平面问题和空间问题中,分布载荷均以压力为正,
平面问题的分析求解
Ansys求解基本步骤
1.确定问题的分析类型
2.定义单元类型
3.定义材料属性
4.建立几何模型 5.划分网格 6.定义约束与载荷 7.定义分析类型 8.求解 9.查看结果,分析结果的正确性。
实例
平面问题:板中圆孔的应力集中 如图所示板件,其中心位置有一个小圆孔,尺寸(mm)如图所示。 弹性模量E=2.1×105MPa, 泊松比v=0.3 拉伸载荷:q=20N/mm
简化分析模型
3. 几何边界、载荷、网格模型以及求解过程的有限元模型
边界、载荷、网格模型(映射网格)
有限元模型
4. 求解结果及其分析
(1)一般性分析
查计算结果可知,平板的最右侧中点位移最大,最大位移=0.519E-06mm; 孔顶部或底部的应力最大,最大等效应力=0.2889M/mm2
其变形图及应力云图如示整体效果 1.设置扩展模式:
Utility Menu>PlotCtrls>Style>Symmetry Expansion>Periodic/Cyclic Symmetry Expansion,即采用
部分循环对称扩展。选用默认值,其等效应力云图见下页,显示整体效果。
1/4两平面对称
几何模型如上图所示(单位为mm),平板厚度为2mm, 平板两边受均布拉力,P=5MPa。材料属性为弹性模量 E=2×1011Pa(钢材),泊松比为0.3。利用ANSYS软 件对该结构进行受力分析。
几何模型如上图所示(单位为mm),矩形平板厚度为3mm, 孔A固定,右侧边缘均布压力,P=1000Pa。材料属性为弹性 模量E=2×1011Pa(钢材),泊松比为0.3。利用ANSYS软件 对该结构进行受力分析。
平板的厚度:t=20mm
解题思路分析: 1.属于平面应力问题 2.中心带孔,应使用8节点四边形单元或三角形单元 3.注意单位:尺寸mm,力N,故应力N/mm2 4.最大变形约为0.001mm,最大应力在孔的顶部和底部,大小约为3.6N/mm2, 即3.6MPa。依次检验有限元的分析结果。
1.确定问题的分析类型 平面应力问题,静力学分析
