matlab生成各种常用序列
matlab中的rand用法
matlab中的rand用法随机数在计算机科学和数学领域中被广泛使用，其中MATLAB是一种常用的科学计算软件。
在MATLAB中，rand函数是生成随机数的一种常用方法。
本文将介绍MATLAB中rand函数的用法以及一些相关的概念。
一、rand函数的基本用法在MATLAB中，rand函数可用于生成一个0到1之间的均匀分布的随机数。
它的基本语法如下：rand这将生成一个0到1之间的随机数。
例如，运行以下代码：x = rand将会得到一个0到1之间的随机数，例如0.4572。
如果需要生成一个范围在a到b之间的随机数，可以使用如下语法：x = a + (b-a)*rand其中，a和b为给定的数值。
例如，如果想生成一个范围在10到20之间的随机数，可以运行以下代码：x = 10 + (20-10)*rand这将生成一个范围在10到20之间的随机数。
二、rand函数的应用举例1. 生成随机向量在MATLAB中，可以使用rand函数生成一个随机向量。
例如，如果想生成一个长度为n的随机向量，可以运行以下代码：x = rand(1, n)其中，n为给定的整数。
这将生成一个长度为n的随机向量。
2. 生成随机矩阵同样地，可以使用rand函数生成一个随机矩阵。
例如，如果想生成一个m行n 列的随机矩阵，可以运行以下代码：x = rand(m, n)这将生成一个m行n列的随机矩阵。
3. 生成服从正态分布的随机数除了生成均匀分布的随机数，还可以使用randn函数生成服从正态分布的随机数。
它的基本语法如下：x = mu + sigma*randn其中，mu和sigma为给定的数值。
例如，如果想生成一个均值为0，标准差为1的正态分布随机数，可以运行以下代码：x = randn这将生成一个服从标准正态分布的随机数。
4. 生成随机整数有时候，我们需要生成一个随机整数而不是小数。
可以使用randi函数来实现这个目的。
例如，如果想生成一个范围在a到b之间的随机整数，可以运行以下代码：x = randi([a,b])其中，a和b为给定的整数。
m序列产生要点
out1(k)=reg1(1);
end
reg2=ones(1,7); %寄存器初始状态
coeff2=[1 10 0 1 1 1]; %设置系数
N=2^length(reg2)-1;
for k=1:N
a_n=mod(sum(reg2.*coeff2(1:length(coeff2)-1)),2); %移位，反馈
[3]吴先用，邹学玉.一种m序列伪码发生器的产生方法[J].西安：西安电子科技大学出版社.2003
附录
clear;
reg1=ones(1,7); %寄存器初始状态
coeff1=[1 0 0 0 0 1 1]; %设置系数
N=2^length(reg1)-1;
%产生m序列
for k=1:N
a_n=mod(sum(reg1.*coeff1(1:length(coeff1)-1)),2);
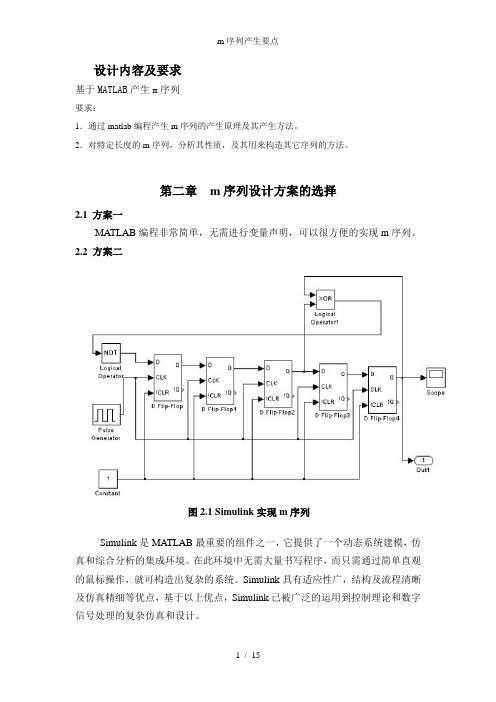
Simulink是MATLAB最重要的组件之一，它提供了一个动态系统建模，仿真和综合分析的集成环境。在此环境中无需大量书写程序，而只需通过简单直观的鼠标操作，就可构造出复杂的系统。Simulink具有适应性广，结构及流程清晰及仿真精细等优点，基于以上优点，Simulink已被广泛的运用到控制理论和数字信号处理的复杂仿真和设计。
m序列是最长线性反馈移位寄存器序列的简称，m序列是由带线性反馈的移位寄存器产生的。
由n级串联的移位寄存器和反馈逻辑线路可组成动态移位寄存器，如果反馈逻辑线路只由模2和构成，则称为线性反馈移位寄存器。
带线性反馈逻辑的移位寄存器设定初始状态后，在时钟触发下，每次移位后各级寄存器会发生变化，其中任何一级寄存器的输出，随着时钟节拍的推移都会产生一个序列，该序列称为移位寄存器序列。
MATLAB产生各种分布的随机数
M A T L A B产生各种分布的随机数The final revision was on November 23, 2020MATLAB产生各种分布的随机数1，均匀分布U（a,b）：产生m*n阶［a，b］均匀分布U（a，b）的随机数矩阵：unifrnd (a,b,m, n) 产生一个［a，b］均匀分布的随机数：unifrnd (a,b)2，0-1分布U（0,1）产生m*n阶［０，1］均匀分布的随机数矩阵：rand (m, n)产生一个［０，１］均匀分布的随机数：rand4，二类分布binornd(N,P,mm,nn)如binornd(10,,mm,nn)即产生mm*nn均值为N*P的矩阵binornd(N,p)则产生一个。
而binornd(10,,mm)则产生mm*mm的方阵，军阵为N*p。
5，产生m*n阶离散均匀分布的随机数矩阵：unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵6，产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd( ,mm, nn)此外，常用逆累积分布函数表函数名调用格式函数注释norminv X=norminv(P,mu,sigma) 正态逆累积分布函数expinv X=expinv(P,mu) 指数逆累积分布函数weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数Betainv X=betainv(P,A,B) β分布逆累积分布函数随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N，P的二项随机数据函数 binornd格式 R = binornd(N,P) %N、P为二项分布的两个参数，返回服从参数为N、P的二项分布的随机数，N、P大小相同。
R = binornd(N,P,m) %m指定随机数的个数，与R同维数。
matlab中xrange用法
matlab中xrange用法题目：Matlab中xrange的使用方法详解引言：Matlab是一种强大的数值计算与科学可视化工具，广泛应用于工程、科学、数据分析等领域。
而在Matlab中，xrange函数是一个非常常用和重要的函数之一。
本文将详细介绍xrange函数的概念、用法和示例，帮助读者全面了解和掌握该函数。
第一部分：概述1.1 函数定义：xrange函数用于生成一个整数序列。
1.2 函数语法：xrange(start, end, step)，其中start表示起始值，end表示结束值，step表示每一步的增量。
第二部分：使用方法2.1 基本用法：最简单的使用方法是在命令行中直接调用xrange函数。
比如，输入xrange(1, 10)将生成从1到10的整数序列(默认步长为1)。
2.2 参数解释：除了基本用法外，xrange函数还可以接收其他参数进行更灵活的使用。
其中，start参数指定序列的起始值，end参数指定序列的结束值，step 参数指定增量值(默认为1)。
2.3 步长设置：通过设置step参数，可以实现自定义的步长。
可以设置step为负数，实现逆序序列；可以设置step为小数，实现浮点数序列。
2.4 变量赋值：xrange函数返回一个生成器(generator)对象，可以将其赋值给一个变量，以便后续使用。
2.5 使用for循环：生成器对象可以直接用于for循环中遍历元素。
例如，for i in xrange(10)表示可以遍历从0到9的整数。
第三部分：示例演示3.1 默认步长示例：假设我们需要生成从1到10的整数序列，可以使用xrange(1, 11, 1)函数。
3.2 步长为负数示例：如果我们需要生成逆序的序列，可以使用xrange(10, 0, -1)函数。
3.3 步长为小数示例：有时候我们需要生成浮点数序列，可以使用xrange(1, 10, 0.5)函数。
第四部分：扩展应用4.1 使用xrange函数进行循环控制：通过遍历xrange函数的生成器对象，可以为循环提供更加灵活的控制条件和步长。
matlab生成m序列的方法
1 matlab生成m序列的方法
1 matlab生成m序列的方法
1.1 m序列基本知识点
1.2 matlab产生m序列
1.2.1 根据产生原理编写生成函数
1.2.1.1 生成m序列的函数：
1.2.1.2 调用已编写函数生成m序列
1.2.2 利用$idinput$函数
引言
m序列属于伪随机序列的一种。
在通信领域应用较为广泛。
由于其具有很好的伪噪声特性，因此在保密通信中，可以将其应用在高可靠性的保密通道中。
另外，雷达领域也有广泛应用，伪随机相位编码脉冲/连续波雷达中用到的调制信号正是m 序列。
1.1 m序列基本知识点
1. m序列的周期等于，N是m序列的级数，m序列由N级线性反馈移存
器产生。
2. m序列具有均衡性，序列中“1”和“0”的数目基本相等，“1”的个数比“0”多1。
3. m序列的循环自相关函数是双值电平。
4. m序列具有游程分布的规律。
1.2 matlab产生m序列
具体产生原理可参考相关资料（通信原理第七版，樊昌信、曹丽娜），这里只介绍matlab实现方法。
2. 生成其他阶数的m序列则只需要将 primpoly(7,'all') 命令中的数字‘7’更换到
函数
函数可以成成多种不同的序列。
也可以用来产生m序列：
序列的阶数等于7
Order_number)-1),'prbs')';%生成m序列。
如何使用Matlab技术进行时间序列分析
如何使用Matlab技术进行时间序列分析时间序列分析是一种用于统计和预测时间相关数据的方法。
它在各个领域都有广泛的应用，例如经济学、金融学、气象学等。
而Matlab作为一种功能强大的数值计算和数据可视化工具，能够帮助研究人员更加高效地进行时间序列分析。
一、时间序列的基本概念和特征时间序列是一组按时间顺序排列的随机变量值，通常用来描述某个变量在不同时间点上的观测结果。
它具有一些基本特征，比如趋势性、季节性和周期性。
为了更好地理解这些特征，我们可以通过Matlab对时间序列进行可视化分析。
在Matlab中，可以使用plot函数绘制时间序列的折线图。
例如，我们可以生成一个简单的时间序列数据并绘制其折线图。
代码如下：```matlabdata = [1, 3, 2, 4, 5, 7, 6, 8, 9, 10];plot(data)```通过运行上述代码，我们可以看到在Matlab的图形窗口中显示出了一条折线，它连接了数据中相邻观测点的值。
这条折线可以帮助我们观察时间序列的变化趋势。
二、时间序列的平稳性检验在进行时间序列分析之前，我们首先需要判断时间序列数据是否满足平稳性要求。
平稳性是指时间序列在统计特性上不随时间变化的性质。
如果时间序列数据是平稳的，那么我们就可以更加自信地进行后续的分析。
Matlab中有多种方法用于判断时间序列的平稳性。
其中一种常用的方法是ADF检验（Augmented Dickey-Fuller test）。
它的原假设是时间序列具有单位根（非平稳）的特性。
在Matlab中，可以使用adftest函数进行ADF检验。
例如，我们可以使用一个具有趋势的时间序列数据进行平稳性检验。
代码如下：```matlabdata = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];[h, pValue, stat, cValue] = adftest(data);```通过运行上述代码，我们可以得到h值，用来判断时间序列是否为平稳的。
MATLAB产生各种分布的随机数
MATLAB产生各种分布的随机数1,均匀分布Ua,b：产生mn阶a,b均匀分布Ua,b的随机数矩阵：unifrnd a,b,m, n产生一个a,b均匀分布的随机数：unifrnd a,b2,0-1分布U0,1产生mn阶０,1均匀分布的随机数矩阵：rand m, n产生一个０,１均匀分布的随机数：rand4,二类分布binorndN,P,mm,nn如binornd10,,mm,nn即产生mmnn均值为NP的矩阵binorndN,p则产生一个;而binornd10,,mm则产生mmmm的方阵,军阵为Np; 5,产生mn阶离散均匀分布的随机数矩阵：unidrndN,mm,nn产生一个数值在1-N区间的mmnn矩阵6,产生mm nn阶期望值为的指数分布的随机数矩阵：exprnd ,mm, nn此外,常用逆累积分布函数表函数名调用格式函数注释norminv X=norminvP,mu,sigma 正态逆累积分布函数expinv X=expinvP,mu 指数逆累积分布函数weibinv X=weibinvP,A,B 威布尔逆累积分布函数logninv X=logninvP,mu,sigma 对数正态逆累积分布函数Chi2inv X=chi2invP,A,B 卡方逆累积分布函数Betainv X=betainvP,A,B β分布逆累积分布函数随机数的产生4.1.1 二项分布的随机数据的产生命令参数为N,P的二项随机数据函数 binornd格式 R = binorndN,P %N、P为二项分布的两个参数,返回服从参数为N、P的二项分布的随机数,N、P大小相同;R = binorndN,P,m %m指定随机数的个数,与R同维数;R = binorndN,P,m,n %m,n分别表示R的行数和列数例4-1>> R=binornd10,R =3>> R=binornd10,,1,6R =8 1 3 7 6 4>> R=binornd10,,1,10R =6 8 4 67 5 3 5 6 2>> R=binornd10,,2,3R =7 5 86 5 6>>n = 10:10:60;>>r1 = binorndn,1./nr1 =2 1 0 1 1 2>>r2 = binorndn,1./n,1 6r2 =0 1 2 1 3 14.1.2 正态分布的随机数据的产生命令参数为μ、σ的正态分布的随机数据函数 normrnd格式 R = normrndMU,SIGMA %返回均值为MU,标准差为SIGMA的正态分布的随机数据,R可以是向量或矩阵;R = normrndMU,SIGMA,m %m指定随机数的个数,与R同维数;R = normrndMU,SIGMA,m,n %m,n分别表示R的行数和列数例4-2>>n1 = normrnd1:6,1./1:6n1 =>>n2 = normrnd0,1,1 5n2 =>>n3 = normrnd1 2 3;4 5 6,,2,3 %mu为均值矩阵n3 =>> R=normrnd10,,2,3 %mu为10,sigma为的2行3列个正态随机数R =4.1.3常见分布的随机数产生常见分布的随机数的使用格式与上面相同表4-1随机数产生函数表函数名调用形式注释UnifrndunifrndA,B,m,nA,B上均匀分布连续随机数UnidrndunidrndN,m,n均匀分布离散随机数Exprnd exprndLambda,m,n参数为Lambda的指数分布随机数NormrndnormrndMU,SIGMA,m,n参数为MU,SIGMA的正态分布随机数chi2rndchi2rndN,m,n自由度为N的卡方分布随机数TrndtrndN,m,n自由度为N 的t分布随机数Frnd frndN1, N2,m,n 第一自由度为N1,第二自由度为N2的F分布随机数gamrnd gamrndA, B,m,n 参数为A,B的分布随机数betarnd betarndA, B,m,n参数为A,B的分布随机数lognrndlognrndMU,SIGMA,m,n参数为MU,SIGMA的对数正态分布随机数nbinrndnbinrndR,P,m,n参数为R,P的负二项式分布随机数ncfrndncfrndN1,N2,delta,m,n参数为N1,N2,delta的非中心F分布随机数nctrndnctrndN,delta,m,n参数为N,delta的非中心t分布随机数ncx2rndncx2rndN,delta,m,n参数为N,delta的非中心卡方分布随机数raylrndraylrndB,m,n参数为B的瑞利分布随机数weibrndweibrndA,B,m,n参数为A,B的韦伯分布随机数binorndbinorndN,P,m,n参数为N,p的二项分布随机数georndgeorndP,m,n参数为p的几何分布随机数hygerndhygerndM,K,N,m,n参数为M,K,N的超几何分布随机数Poissrnd poissrndLambda,m,n参数为Lambda的泊松分布随机数4.1.4通用函数求各分布的随机数据命令求指定分布的随机数函数randomvar cpro_psid ="u2572954"; var cpro_pswidth =966; var cpro_psheight =120136格式y=random'name',A1,A2,A3,m,n%name的取值见表4-2；A1,A2,A3为分布的参数；m,n指定随机数的行和列例4-3产生123行4列个均值为2,标准差为的正态分布随机数>> y=random'norm',2,,3,4 y =随机变量的概率密度计算4.2.1 通用函数计算概率密度函数值命令通用函数计算概率密度函数值函数pdf格式Y=pdfname,K,AY=pdfname,K,A,B Y=pdfname,K,A,B,C说明返回在X=K处、参数为A、B、C的概率密度值,对于不同的分布,参数个数是不同；name为分布函数名,其取值如表4-2;表4-2 常见分布函数表name的取值函数说明'beta' 或'Beta' Beta分布'bino' 或'Binomial' 二项分布'chi2' 或'Chisquare' 卡方分布'exp' 或'Exponential' 指数分布'f' 或'F'F分布'gam' 或'Gamma' GAMMA分布'geo' 或'Geometric'几何分布'hyge' 或'Hypergeometric' 超几何分布'logn' 或'Lognormal'对数正态分布'nbin' 或'Negative Binomial' 负二项式分布'ncf' 或'Noncentral F' 非中心F分布'nct' 或'Noncentral t'非中心t分布'ncx2' 或'Noncentral Chi-square' 非中心卡方分布'norm' 或'Normal' 正态分布'poiss' 或'Poisson' 泊松分布'rayl' 或'Rayleigh' 瑞利分布't' 或'T'T分布'unif' 或'Uniform'均匀分布'unid' 或'Discrete Uniform' 离散均匀分布'weib'或'Weibull'Weibull分布例如二项分布：设一次试验,事件A发生的概率为p,那么,在n次独立重复试验中,事件A恰好发生K次的概率P_K为：P_K=P{X=K}=pdf'bino',K,n,p例4-4 计算正态分布N0,1的随机变量X在点的密度函数值;Matlab 的随机函数高斯分布均匀分布其它分布Matlab中随机数生成器主要有：betarnd 贝塔分布的随机数生成器binornd 二项分布的随机数生成器chi2rnd 卡方分布的随机数生成器exprnd 指数分布的随机数生成器frnd f分布的随机数生成器gamrnd 伽玛分布的随机数生成器geornd 几何分布的随机数生成器hygernd 超几何分布的随机数生成器lognrnd 对数正态分布的随机数生成器nbinrnd 负二项分布的随机数生成器ncfrnd 非中心f分布的随机数生成器nctrnd 非中心t分布的随机数生成器ncx2rnd 非中心卡方分布的随机数生成器normrnd 正态高斯分布的随机数生成器,normrnda,b,c,d：产生均值为a、方差为b大小为cXd的随机矩阵poissrnd 泊松分布的随机数生成器rand：产生均值为、幅度在0~1之间的伪随机数,randn：生成0到1之间的n阶随机数方阵,randm,n：生成0到1之间的m×n的随机数矩阵randn：产生均值为0、方差为1的高斯白噪声,使用方式同rand注：rand是0-1的均匀分布,randn是均值为0方差为1的正态分布randpermn:产生1到n的均匀分布随机序列raylrnd 瑞利分布的随机数生成器trnd 学生氏t分布的随机数生成器unidrnd 离散均匀分布的随机数生成器unifrnd 连续均匀分布的随机数生成器weibrnd 威布尔分布的随机数生成器以下介绍利用Matlab产生均值为0,方差为1的符合正态分布的高斯随机数;我们利用的函数为normrnda,b,c,d：产生均值为a、标准为b大小为cXd的随机矩阵,它有如下三种参数形式：R＝normrndμ,σR＝normrndμ,σ：生成服从正态分布μ参数代表均值,σ参数代表标准差的随机数;输入的向量或矩阵μ和σ必须形式相同,输出R也和它们形式相同;标量输入将被扩展成和其它输入具有相同维数的矩阵;R＝normrndμ,σ,mR＝norrmrndμ,σ,m：生成服从正态分布μ参数代表均值,σ参数代表标准差的随机数矩阵,矩阵的形式由m定义;m是一个1×2向量,其中的两个元素分别代表返回值R中行与列的维数;R＝normrndμ,σ,m,nR＝normrndμ,σ,m,n：生成m×n形式的正态分布的随机数矩阵;其中μ为均值,σ为标准方差,m、n为矩阵大小；----------------------------------------------------------------->> R = normrnd0,1,4,4 %产生4×4的标准正态分布矩阵R =>> varR %默认方差公式ans =>> varR,0 %默认方差公式N-1ans =>> varR,1 %方差公式Nans =>> varR,0,1 %列操作,第二参数为方差方式,第三参数为行、列标记ans =>> varR,0,2 %行操作,第二参数为方差方式,第三参数为行、列标记ans =>> varR' %check the ansans =>> varR: %矩阵所有元素的方差ans =。
matlab中冒号运算符
matlab中冒号运算符冒号运算符（:）是MATLAB中非常常用且强大的一种运算符，它可以广泛用于数组、矩阵的索引、切片、生成等操作。
本文将详细介绍冒号运算符的基本用法及其在MATLAB中的应用。
一、基本用法在MATLAB中，冒号运算符的基本用法是通过起始值、步长和结束值来生成一个序列。
具体的语法格式如下：[start:step:end]其中，start表示序列的起始值，step表示步长，end表示序列的结束值。
这三个参数都可以是数值型变量或常数。
1.1 生成等差数列冒号运算符常用于生成等差数列。
例如，生成从1到10的整数序列可以使用以下语句：1:10这将生成一个包含1到10的整数序列的行向量。
1.2 生成指定步长的序列冒号运算符还可以生成指定步长的序列。
例如，生成从1到10，步长为2的序列可以使用以下语句：1:2:10这将生成一个包含1、3、5、7、9的行向量。
1.3 生成逆序序列冒号运算符还可以用于生成逆序序列。
例如，生成从10到1的逆序序列可以使用以下语句：10:-1:1这将生成一个包含10到1的逆序序列的行向量。
二、应用场景冒号运算符在MATLAB中有着广泛的应用场景，以下介绍几个常见的应用案例。
2.1 数组索引与切片冒号运算符可以用于数组的索引和切片操作。
例如，对于一个二维数组A，可以使用以下语句获取第一行的所有元素：A(1,:)这将返回一个包含第一行所有元素的行向量。
2.2 矩阵的行列操作冒号运算符还可以用于矩阵的行列操作。
例如，对于一个二维矩阵B，可以使用以下语句获取第一列的所有元素：B(:,1)这将返回一个包含第一列所有元素的列向量。
2.3 生成矩阵冒号运算符可以用于生成矩阵。
例如，生成一个3行4列的矩阵，其中元素的值为1到12的连续整数，可以使用以下语句：reshape(1:12, 3, 4)这将生成一个3行4列的矩阵C。
2.4 循环迭代冒号运算符可以用于循环迭代。
例如，使用以下语句可以实现对一个向量D中的元素进行迭代操作：for i = 1:length(D)disp(D(i))end这将依次输出向量D中的每个元素。
数字信号处理相关MATLAB实验内容--第1章
实验1 离散时间信号的时域分析一、实验目的（1）了解MATLAB 语言的主要特点及作用；（2）熟悉MATLAB 主界面，初步掌握MATLAB 命令窗和编辑窗的操作方法；（3）学习简单的数组赋值、数组运算、绘图的程序编写；（4）了解常用时域离散信号及其特点；（5）掌握MATLAB 产生常用时域离散信号的方法。
二、知识点提示本章节的主要知识点是利用MATLAB 产生数字信号处理的几种常用典型序列、数字序列的基本运算；重点是单位脉冲、单位阶跃、正（余）弦信号的产生；难点是MATLAB 关系运算符“==、>=”的使用。
三、实验内容1. 在MATLAB 中利用逻辑关系式0==n 来实现()0n n -δ序列，显示范围21n n n ≤≤。
（函数命名为impseq(n0,n1,n2)）并利用该函数实现序列：()()()632-+-=n n n y δδ；103≤≤-nn 0212. 在MATLAB 中利用逻辑关系式0>=n 来实现()0n n u -序列，显示范围21n n n ≤≤。
（函数命名为stepseq(n0,n1,n2)）并利用该函数实现序列：()()()20522≤≤--++=n n u n u n y3. 在MATLAB 中利用数组运算符“.^”来实现一个实指数序列。
如： ()()5003.0≤≤=n n x n4. 在MATLAB 中用函数sin 或cos 产生正余弦序列，如：()()2003.0cos 553.0sin 11≤≤+⎪⎭⎫ ⎝⎛+=n n n n x πππ5. 已知()n n x 102cos 3π=，试显示()()()3,3,+-n x n x n x 在200≤≤n 区间的波形。
6. 参加运算的两个序列维数不同，已知()()6421≤≤-+=n n u n x ，()()8542≤≤--=n n u n x ，求()()()n x n x n x 21+=。
基于Matlab产生m序列
目录前言 (1)第一章设计任务 (2)1.2设计内容 (2)1.2设计要求 (2)1.3系统框图 (2)第二章m序列的分析 (4)2.1m序列的含义 (4)2.2m序列产生的原理 (5)2.2m序列的性质 (6)2.3自相关特性 (7)第三章m序列的设计 (8)3.1特征多项式确定 (8)3.2本原多项式的确定 (9)3.3m序列的发生 (10)第四章程序调试及结果分析 (11)4.1m序列的仿真结果及分析 (12)4.2该设计的序列相关性仿真结果及分析 (13)结论 (14)参考文献 (15)附录：程序代码 (16)前言扩频通信因其具有抗干扰、抗多径衰落、抗侦察等优点在通信领域中得到广泛应用。
扩频序列的设计和选择是扩频通信的关键技术，扩频序列性能的优劣在很大程度上决定了通信系统的多址干扰和符号间干扰的大小，从而直接影响到系统的性能。
因此，深入研究扩频序列的性质，构造设计具有良好相关性的扩频序列，来满足扩频系统的要求，是直接序列扩频系统的核心课题。
白噪声是一种随机过程，它有极其优良的相关特性。
但至今无法实现白噪声的放大、调制、检测、同步及控制等，而只能用类似于白噪声统计特性的伪随机序列来逼近它，并作为扩频系统的扩频码。
常见的伪随机序列有m 序列、GOLD 序列、M 序列、Walsh 序列等。
m 序列是目前研究最为彻底的伪随机序列，m 序列容易产生，有优良的自相关和互相关特性。
序列是伪随机序列的一种情况。
他可以在很多领域中都有重要应用。
由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n（n为移位寄存器的级数）。
通过对伪随机码中常用的m序列的结构和性质进行了分析，本文给出了基于MATLAB平台的m序列生成算法及代码伪随机序列分析。
第一章 设计任务1.2 设计内容掌握PN 序列的相关知识，掌握m 序列的产生原理及其在matlab 中的产生方法，对特定长度的m 序列，分析其性质，及其用来构造其它序列的方法；研究伪随机序列在跳频通信中的应用方法。
matlab高斯序列,如何用MATLAB产生高斯随机序列
matlab⾼斯序列,如何⽤MATLAB产⽣⾼斯随机序列MATLAB命令是normrnd功能：⽣成服从正态分布的随机数列，也就是你需要的⾼斯随机序列>> help normrndNORMRND Random arrays from the normal distribution.R = NORMRND(MU,SIGMA) returns an array of random numbers chosen from anormal distribution with mean MU and standard deviation SIGMA. The sizeof R is the common size of MU and SIGMA if both are arrays. If eitherparameter is a scalar, the size of R is the size of the otherparameter.R = NORMRND(MU,SIGMA,M,N,...) or R = NORMRND(MU,SIGMA,[M,N,...])returns an M-by-N-by-... array.语法：R＝normrnd(MU,SIGMA)R＝normrnd(MU,SIGMA,m)R＝normrnd(MU,SIGMA,m,n)说 明：R＝normrnd(MU,SIGMA)：⽣成服从正态分布(MU参数代表均值，DELTA参数代表标准差)的随机数。
输⼊的向量或矩阵MU和SIGMA必须形式相同，输出R也和它们形式相同。
标量输⼊将被扩展成和其它输⼊具有 相同维数的矩阵。
R＝norrmrnd(MU,SIGMA,m)：⽣成服从正态分布(MU参数代表均值，DELTA参数代表标准差)的 随机数矩阵，矩阵的形式由m定义。
m 是⼀个1×2向量，其中的两个元素分别代表返回值R中⾏与列的维数。
matlab中服从泊松过程的到达时间序列生成
Matlab中服从泊松过程的到达时间序列生成泊松过程是一种常见的随机过程，描述了事件在给定时间段内的到达规律。
在实际应用中，我们经常需要生成服从泊松过程的到达时间序列，以便进行仿真、建模和分析。
在Matlab中，我们可以通过一些方法来生成服从泊松过程的到达时间序列。
一、生成泊松过程到达时间序列的基本原理泊松过程的到达时间间隔服从指数分布，而指数分布可以通过指数分布的累积分布函数的逆函数来生成。
在Matlab中，我们可以使用rand函数生成服从均匀分布的随机数，再通过指数分布的累积分布函数的逆函数，即负指数分布的逆函数，来得到服从指数分布的随机数。
我们可以将这些随机数累积相加，即可得到泊松过程的到达时间序列。
二、Matlab代码实现以下是一段简单的Matlab代码，用于生成服从泊松过程的到达时间序列：```matlablambda = 10; % 泊松过程的到达率T = 100; % 时间段的长度N = poissrnd(lambda*T); % 生成总到达次数interarrival_times = exprnd(1/lambda, 1, N); % 生成到达时间间隔arrival_times = cumsum(interarrival_times); % 生成到达时间序列```在这段代码中，我们首先指定了泊松过程的到达率lambda和时间段的长度T。
我们使用poissrnd函数生成服从泊松分布的随机数N，表示在时间段内的总到达次数。
我们使用exprnd函数生成服从指数分布的随机数，表示到达时间间隔。
通过cumsum函数累积相加，得到服从泊松过程的到达时间序列。
三、代码分析和有效性验证这段代码的有效性可以通过对生成的到达时间序列进行统计分析来验证。
我们可以计算到达时间间隔的均值和方差，并与指数分布的理论均值和方差进行比较。
我们还可以绘制到达时间序列的直方图和间隔时间的概率密度函数，以直观地观察其分布特征。
randn在matlab中的用法
randn在matlab中的用法
randn是matlab中一个常用的函数，用于生成服从标准正态分布（均值为0，标准差为1）的随机数。
该函数的调用形式为randn(n)，其中n表示生成随机数的个数。
在matlab中使用randn函数生成随机数非常简单。
例如，如果我们希望生成10个服从标准正态分布的随机数，我们可以使用以下代码：
```matlab
random_numbers = randn(10);
```
上述代码将生成一个大小为1x10的矩阵，其中包含10个服从标准正态分布的随机数。
生成的随机数可以用于各种数值计算、模拟实验、随机信号生成等应用。
除了生成服从标准正态分布的随机数外，我们还可以使用randn函数生成服从不同均值和标准差的正态分布随机数。
例如，如果我们希望生成均值为3，标准差为2的正态分布随机数，我们可以使用以下代码：
```matlab
mean_val = 3;
std_dev = 2;
random_numbers = mean_val + std_dev * randn(10);
```
上述代码将生成服从均值为3，标准差为2的正态分布的随机数。
需要注意的是，randn函数生成的随机数是伪随机数，其生成结果可以通过设置随机数种子来重复。
如果想要生成不同的随机数序列，可以通过调用rng函数设置不同的随机数种子。
总之，randn函数是matlab中常用的生成服从标准正态分布的随机数的函数。
通过设置参数，我们还可以生成服从不同均值和标准差的正态分布随机数。
这个函数在各种数值计算和模拟实验中都有广泛的应用。
实验一 常见离散信号的MATLAB产生和图形显示
实验一 常见离散信号的MATLAB 产生和图形显示授课课时：2学时一、实验目的：（1）熟悉MATLAB 应用环境，常用窗口的功能和使用方法。
（2）掌握MATLAB 在时域内产生常用离散时间信号的方法。
（3）掌握离散信号的基本运算。
（4）掌握简单的绘图命令。
二、实验原理：（一）信号的表示和产生① 单位抽样序列⎩⎨⎧=01)(n δ 00≠=n n如果)(n δ在时间轴上延迟了k 个单位，得到)(k n -δ即：⎩⎨⎧=-01)(k n δ≠=n k n 参考程序：例1-1：)2010(()(<<-=n n n x ）δclear all n1=-10;n2=20;n0=0;%在起点为n1,终点为n2的范围内，于n0处产生冲激。
n=n1:n2;%生成离散信号的时间序列x=[n==n0];%生成离散信号x(n)stem(n,x);%绘制脉冲杆图xlabel(' n');ylabel('x(n)');%横坐标和纵坐标的标注说明。
title('Unit Sample Sequence');%图形上方标注图名axis([-10 20 0 1.2]);%确定横坐标和纵坐标的取值范围② 单位阶跃序列⎩⎨⎧=01)(n u 00<≥n n 例1-2：)202((u )(<<-=n n n x ）clear alln1=-2;n2=20;n0=0;n=n1:n2;%生成离散信号的时间序列x=[n>=n0];%生成离散信号x(n)stem(n,x,'filled');xlabel('n');ylabel('x(n)');title('Unit step Sequence');axis([-2 20 0 1.2]);③ 正弦序列)sin()(ϕ+=wn A n x例1-3：一正弦信号的频率为1HZ ，振幅值幅度A 为1V ，在窗口显示2个周期的信号波形，并对该信号的一个周期进行32点采样获得离散信号并显示该连续信号和离散信号的波形。
实验一常见离散信号的MATLAB产生及图形显示
Guangxi University of Science and Technology实验报告实验课程：数字信号处理实验内容：常见离散信号的MATLAB产生和图形显示院（系）：计算机科学与通信工程学院专业：通信工程班级：学生姓名：学号：指导教师：2016年 5 月 25 日实验一、常见离散信号的MATLAB 产生和图形显示一、实验目的：加深对常用离散信号的理解；二、实验原理：1.单位抽样序列实现: ⎩⎨⎧=01)(n δ 00≠=n n在MATLAB 中可以利用zeros()函数实现。
;1)1();,1(==x N zeros x如果)(n δ在时间轴上延迟了k 个单位，得到)(k n -δ即: ⎩⎨⎧=-01)(k n δ0≠=n k n2．单位阶跃序列实现: ⎩⎨⎧01)(n u 00<≥n n ;在MATLAB 中可以利用ones()函数实现。
);,1(N ones x =3．正弦序列实现: )/2sin()(ϕπ+=Fs fn A n x在MATLAB 中 )/***2sin(*1:0fai Fs n f pi A x N n +=-=4．复指数序列实现: n j e n x ϖ=)(在MATLAB 中 )**exp(1:0n w j x N n =-=5．实指数序列实现: n a n x =)(在MATLAB 中 n a x N n .^1:0=-=三、实验内容及步骤：1．单位抽样序列实现程序如下:n=n1:n2;x1=[zeros(1,5) 1 zeros(1,5)];%%n 为冲击位置x2=[zeros(1,7) 1 zeros(1,3)];%向右平移2个单位subplot(1,2,1);stem(n,x1,'filled');axis([n1,n2,0,1.1]);title('单位脉冲序列');xlabel('时间');ylabel('幅度x（n）');subplot(1,2,2);stem(n,x2,'filled');axis([n1,n2,0,1.1]);title('单位脉冲序列向右平移2个单位');xlabel('时间');ylabel('幅度x（n）');结果如下:图: 1-12. 单位阶跃序列程序如下:N=5;x=ones(1,N);xn=0:N-1;subplot(1,2,1);stem(xn,x,'filled')axis([-1 5 0 1.1])title('单位阶跃序列');xlabel('时间（n）');ylabel('幅度x(n)');x1=[0 0 ones(1,3)];subplot(1,2,2);stem(xn,x1,'filled')axis([-1 5 0 1.1])title('单位阶跃序列平移两个单位');xlabel('时间（n）');ylabel('幅度x(n)');结果如下:图: 1-2 3．正弦序列实现程序如下：n1=0;n2=15;n=n1:n2;x=3*sin(n*pi/4+pi/2);stem(n,x,'filled');axis([n1 n2 1.1*min(x) 1.1*max(x)]);axis([n1 n2 1.1*min(x) 1.1*max(x)]);title('正弦函数图');ylabel('时间x(n)');xlabel('幅度n');结果如下:图: 1-3 4.复指数序列实现程序如下：n1=30;a=-0.1;w=0.6;n=0:n1;x=exp((a+j*w)*n);subplot(1,2,1),stem(n,real(x),'filled');title('复指数原信号的实部');subplot(1,2,2),stem(n,imag(x),'filled');title('复指数原信号的虚部');结果如下:图: 1-4 5．实指数序列实现程序如下：n1=-10;n2=10;a1=0.5;a2=2;na1=n1:0;x1=a1.^na1;na2=0:n2;x2=a2.^na2;subplot(1,2,1),stem(na1,x1,'filled');title('实指数序列(a<1)');subplot(1,2,2),stem(na2,x2,'filled');title('实指数序列(a>1)');结果如下:图: 1-5四、实验总结与分析通过本实验，深入了解了MATLAB的运行环境，掌握了如何在该软件上编程、编译和运行一个MATLAB程序，通过运行简单的MATLAB程序，初步了解了MATLAB程序的特点，掌握了一些基本的MATLAB函数。
使用Matlab进行时间序列分析的方法
使用Matlab进行时间序列分析的方法时间序列分析是一种研究随时间变化的现象的方法。
在各个领域中，时间序列分析经常用于分析经济、金融、气象、交通等数据。
在本文中，我们将介绍使用Matlab进行时间序列分析的一些常用方法。
一、时间序列分析的基本概念和数据准备时间序列分析是根据一个或多个时间点上观测到的数值构成的数列来对未来或未来的数值进行预测和分析的一种技术方法。
在时间序列分析之前，我们首先需要对数据进行预处理和准备。
1. 数据读取和展示Matlab提供了多种读取数据的函数，例如xlsread、csvread等。
通过这些函数，我们可以将外部数据导入到Matlab工作环境中，并进行展示。
展示数据的常见方法是使用plot函数，该函数可以绘制时间序列的图形。
2. 数据平稳性检验在进行时间序列的分析之前，我们需要对数据的平稳性进行检验。
平稳性是指随时间变化，时间序列的均值和方差都不发生显著的变化。
常见的平稳性检验方法有ADF检验、KPSS检验等。
二、时间序列分析的方法在确定时间序列数据具有平稳性后，我们可以进行时间序列分析。
时间序列分析的方法主要包括时间序列模型、平滑方法、周期性分析、趋势分解等。
1. 时间序列模型时间序列模型是一种用来描述和预测时间序列的方法。
常见的时间序列模型有自回归移动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)、季节性自回归积分滑动平均模型(SARIMA)等。
使用Matlab中的arima函数可以方便地进行时间序列模型的建立和预测。
2. 平滑方法平滑方法是通过某种函数对时间序列数据进行平滑处理，以提取出数据的整体趋势和周期性成分。
常见的平滑方法有移动平均法、指数平滑法等。
3. 周期性分析周期性分析是对时间序列数据中存在的周期性成分进行分析和预测的方法。
常见的周期性分析方法有傅里叶分析、小波变换等。
在Matlab中，可以使用fft函数进行傅里叶分析，使用cwt函数进行小波变换。
matlab中的for循环
matlab中的for循环在MATLAB中，for循环是一种常用的控制结构，用于重复执行一段代码。
for循环的语法格式为：for variable = expressionstatementsend其中，variable是循环变量，expression是循环条件，statements 是要重复执行的代码块。
在每次循环中，循环变量会被赋值为expression中的一个元素，然后执行statements。
for循环的应用非常广泛，可以用于处理数组、矩阵、图像等各种数据类型。
下面以一个简单的例子来说明for循环的用法。
假设有一个长度为10的数组a，我们要将其中的每个元素都乘以2，然后输出结果。
可以使用如下代码：a = [1 2 3 4 5 6 7 8 9 10];for i = 1:length(a)a(i) = a(i) * 2;enddisp(a);在这个例子中，我们首先定义了一个长度为10的数组a，然后使用for循环遍历数组中的每个元素。
在每次循环中，将当前元素乘以2，然后将结果赋值回原数组。
最后使用disp函数输出结果。
除了遍历数组，for循环还可以用于生成一些特定的序列。
例如，我们可以使用for循环生成一个从1到10的整数序列，代码如下：for i = 1:10disp(i);end在这个例子中，我们使用了冒号运算符(:)来生成一个从1到10的整数序列，然后使用for循环遍历这个序列，并使用disp函数输出每个元素。
除了普通的for循环，MATLAB还提供了一些特殊的循环结构，如while循环、do-while循环等。
这些循环结构可以根据不同的需求选择使用。
for循环是MATLAB中非常重要的一个控制结构，掌握它的用法对于编写高效的MATLAB程序非常有帮助。
实验一MATLAB编程环境及常用信号的生成及波形仿真
实验⼀MATLAB编程环境及常⽤信号的⽣成及波形仿真实验⼀ MATLAB 编程环境及常⽤信号的⽣成及波形仿真⼀、实验⽬的1、学会运⽤Matlab 表⽰常⽤连续时间信号的⽅法2、观察并熟悉这些信号的波形和特性:3、实验内容：编程实现如下常⽤离散信号：单位脉冲序列，单位阶跃序列，矩形序列，实指数序列，正弦序列，复指数序列；⼆、实验原理及实例分析2、如何表⽰连续信号？从严格意义上讲，Matlab 数值计算的⽅法不能处理连续时间信号。
然⽽，可利⽤连续信号在等时间间隔点的取样值来近似表⽰连续信号，即当取样时间间隔⾜够⼩时，这些离散样值能被Matlab 处理，并且能较好地近似表⽰连续信号。
3、Matlab 提供了⼤量⽣成基本信号的函数。
如：（1）指数信号：K*exp(a*t)（2）正弦信号：K*sin(w*t+phi)和K*cos(w*t+phi)（3）复指数信号：K*exp((a+i*b)*t)（4）抽样信号：sin(t*pi)注意：在Matlab 中⽤与Sa(t)类似的sinc(t)函数表⽰，定义为：)t /()t (sin )t (sinc ππ=（5）矩形脉冲信号：rectpuls(t,width)（6）周期矩形脉冲信号：square(t,DUTY)，其中DUTY 参数表⽰信号的占空⽐DUTY%，即在⼀个周期脉冲宽度（正值部分）与脉冲周期的⽐值。
占空⽐默认为0.5。
（7）三⾓波脉冲信号：tripuls(t, width, skew)，其中skew 取值范围在-1~+1之间。
（8）周期三⾓波信号：sawtooth(t, width)（9）单位阶跃信号：y=(t>=0)常⽤的图形控制函数1）学习clc, dir(ls), help, clear, format,hold, clf控制命令的使⽤和M⽂件编辑/调试器使⽤操作；2）主函数函数的创建和⼦程序的调⽤；3）plot,subplot, grid on, figure, xlabel,ylabel,title,hold,title,Legend,绘图函数使⽤;axis([xmin,xmax,ymin,ymax])：图型显⽰区域控制函数，其中xmin为横轴的显⽰起点，xmax为横轴的显⽰终点，ymin为纵轴的显⽰起点，ymax为纵轴的显⽰终点。