大学物理练习册习题及答案4
大学物理练习册习题及答案4
习题及参考答案第3章 刚体力学 参考答案思考题3-1刚体角动量守恒的充分而必要的条件是(A )刚体不受外力矩的作用。
(B )刚体所受合外力矩为零。
(C)刚体所受的合外力和合外力矩均为零。
(D)刚体的转动惯量和角速度均保持不变。
答:(B )。
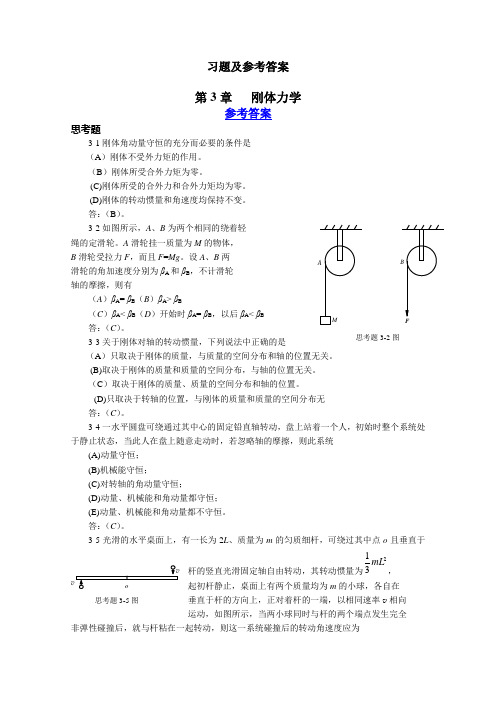
3-2如图所示,A 、B 为两个相同的绕着轻绳的定滑轮。
A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F =Mg 。
设A 、B 两滑轮的角加速度分别为βA 和βB ,不计滑轮轴的摩擦,则有(A )βA = βB (B )βA > βB(C )βA < βB (D )开始时βA = βB ,以后βA < βB答:(C )。
3-3关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无答:(C )。
3-4一水平圆盘可绕通过其中心的固定铅直轴转动,盘上站着一个人,初始时整个系统处于静止状态,当此人在盘上随意走动时,若忽略轴的摩擦,则此系统(A)动量守恒;(B)机械能守恒;(C)对转轴的角动量守恒;(D)动量、机械能和角动量都守恒;(E)动量、机械能和角动量都不守恒。
答:(C )。
3-5光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点o 且垂直于杆的竖直光滑固定轴自由转动,其转动惯量为213mL , 起初杆静止,桌面上有两个质量均为m 的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同速率v 相向运动,如图所示,当两小球同时与杆的两个端点发生完全 非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为 AM F 思考题3-2图 v思考题3-5图(A)23L v (B)45L v (C)67L v (D)89L v (E)127L v答:(C )。
大学物理练习册答案

练习一:1-3:D B D ;4、331ctv v +=,400121ctt v xx ++=5、s3;6、14rad, 15rad/s, 12rad/s27、解:(1)jt ti t r)4321()53(2-+++=; (2))/(73;)3(34s m j i v j t i dt rd v s t+=++===;(3))/(12s m j dtv d a == 68、解: ∵ xvvt x x v t v a d d d d d d d d === 分离变量: x x adx d )62(d 2+==υυ两边积分得c x x v ++=322221由题知,0=x 时,100=v ,∴50=c∴ 13sm 252-⋅++=x x v练习二:1、C ;2、B ;3、j8,ji 4+-,4412arctg arctg-+ππ或;4、32ct,ct 2,Rt c 42,R ct 2;5、212tt +,212t+;6、210θθθθtg tgtg tg ++7、解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 222s h l +=将上式对时间t 求导,得t s s t l l d d 2d d 2= 根据速度的定义,并注意到l ,s 是随t 减少的, ∴ tsv v tl v d d ,d d 0-==-=船绳即 θcos d d d d 00v v sl tl s l ts v==-=-=船或 sv s h slv v2/1220)(+==船将船v 再对t 求导,即得船的加速度32022222002)(d d d d d d sv h sv sls v slv s v v st s l tl s tv a =+-=+-=-==船船8、解:(1)由23RbtdtdRdtdsv-===θ得:Rbtdtdva6-==τ,4229tRbRvan==(2)nnnetRbeRbteaeaaˆ9ˆ6ˆˆ42+-=+=τττ练习三1、C,2、A,3、D,4、2121)(mmgmmF+-+,)2(1212gmFmmm++;5、0.41cm6、解:取弹簧原长时m2所在处为坐标原点,竖直向下为x轴,m1,m2的受力分析如上图所示。
大学物理学练习册参考答案全

大学物理学练习册参考答案单元一 质点运动学四、学生练习 (一)选择题1.B2.C3.B4.B5.B (二)填空题1. 0 02.2192x y -=, j i ρρ114+, j i ρρ82-3.16vi j =-+v v v ;14a i j =-+v vv;4. 020211V kt V -;5、16Rt 2 4 6 112M h h h =-v v(三)计算题1 解答(1)质点在第1s 末的位置为:x (1) = 6×12 - 2×13 = 4(m).在第2s 末的位置为:x (2) = 6×22 - 2×23 = 8(m). 在第2s 内的位移大小为:Δx = x (2) – x (1) = 4(m),经过的时间为Δt = 1s ,所以平均速度大小为:v =Δx /Δt = 4(m·s -1).(2)质点的瞬时速度大小为:v (t ) = d x /d t = 12t - 6t 2,因此v (1) = 12×1 - 6×12 = 6(m·s -1),v (2) = 12×2 - 6×22 = 0质点在第2s 内的路程等于其位移的大小,即Δs = Δx = 4m .(3)质点的瞬时加速度大小为:a (t ) = d v /d t = 12 - 12t ,因此1s 末的瞬时加速度为:a (1) = 12 - 12×1 = 0,第2s 内的平均加速度为:a = [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2).2.解答 1)由t y t x ππ6sin 86cos 5==消去t 得轨迹方程:1642522=+y x 2)tdt dy v t dtdx v y x ππππ6cos 486sin 30==-==当t=5得;πππππ4830cos 48030sin 30===-=y x v vt dt dv a t dtdv a y y xx ππππ6sin 2886cos 18022-==-==当t=5 030sin 28818030cos 180222=-==-=-=πππππdt dv a a yy x 3.解答:1)()t t dt t dt d t tvv 204240+=+==⎰⎰⎰则:t t )2(42++=2)()t t t dt t t dt d ttr )312(2)2(4322++=++==⎰⎰⎰t t t )312()22(32+++=4. [证明](1)分离变量得2d d vk t v=-, 故020d d v tv vk t v =-⎰⎰, 可得:011kt v v =+. (2)公式可化为001v v v kt=+,由于v = d x/d t ,所以:00001d d d(1)1(1)v x t v kt v kt k v kt ==+++ 积分00001d d(1)(1)x tx v kt k v kt =++⎰⎰.因此 01ln(1)x v kt k=+. 证毕.5.解答(1)角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1),法向加速度为 a n = rω2 = 230.4(m·s -2); 角加速度为 β = d ω/d t = 24t = 48(rad·s -2), 切向加速度为 a t = rβ = 4.8(m·s -2). (2)总加速度为a = (a t 2 + a n 2)1/2,当a t = a /2时,有4a t 2 = a t 2 + a n 2,即n a a =由此得2r r ω=22(12)24t =解得36t =.所以3242(13)t θ=+=+=3.154(rad).(3)当a t = a n 时,可得rβ = rω2, 即: 24t = (12t 2)2,解得 : t = (1/6)1/3 = 0.55(s).6.解答:当s 2=t 时,4.022.0=⨯==t βω 1s rad -⋅ 则16.04.04.0=⨯==ωR v 1s m -⋅064.0)4.0(4.022=⨯==ωR a n 2s m -⋅08.02.04.0=⨯==βτR a 2s m -⋅22222s m 102.0)08.0()064.0(-⋅=+=+=τa a a n单元二 牛顿运动定律(一)选择题 1.A 2.C 3.C 4.C 5 A 6.C (二)填空题 1. 022x F t COS F X ++-=ωωω2.略3. )13(35-4. 50N 1m/s5.21m m t f +∆ )()(212122221m m m t m t m t m f +∆+∆+∆6. 0 18J 17J 7J7. mr k rk (三)计算题1.解答:θμθcos )sin (f f mg =- ; θμθμsin cos +=mgf0cos sin =+=θμθθd df; 0tan =θ ; 037=θ θsin hl ==037sin 5.12. 解答;dtdvmkv F mg =--分离变量积分得 0ln(1)v tktm mdvmg F kvktmg F dt v e mg F kv mg F m k-----=??----蝌 3解答:烧断前 2221211();a L L a L w w =+=烧断后,弹簧瞬间的力不变,所以2a 不变。
大学物理(赵近芳)练习册答案

练习1 质点运动学(一)参考答案1. B ;2. D;3. 8m, 10m.4. 3, 3 6;5. 解:(1) 5.0/-==∆∆t x v m/s(2) v = d x /d t = 9t - 6t 2v (2) =-6 m/s(3) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m6. 答:矢径r是从坐标原点至质点所在位置的有向线段.而位移矢量是从某一个初始时刻质点所在位置到后一个时刻质点所在位置的有向线段.它们的一般关系为0r r r-=∆0r 为初始时刻的矢径, r 为末时刻的矢径,△r为位移矢量.若把坐标原点选在质点的初始位置,则0r =0,任意时刻质点对于此位置的位移为△r =r,即r既是矢径也是位移矢量.1. D ;2. -g /2 , ()g 3/322v3. 4t 3-3t 2 (rad/s), 12t 2-6t (m/s 2)4. 17.3 m/s, 20 m/s .5. 解: =a d v /d t 4=t , d v 4=t d t⎰⎰=vv 0d 4d tt tv 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰=x 2= t 3 /3+x 0 (SI)6. 解:根据已知条件确定常量k()222/rad 4//s Rt t k ===v ω24t =ω, 24Rt R ==ωvt=1s 时, v = 4Rt 2 = 8 m/s2s /168/m Rt dt d a t ===v 22s /32/m R a n ==v()8.352/122=+=nt a a a m/s 21.D2.C3.4. l/cos 2θ5.如图所示,A ,B ,C 三物体,质量分别为M=0.8kg, m= m 0=0.1kg ,当他们如图a 放置时,物体正好做匀速运动。
(1)求物体A 与水平桌面的摩擦系数;(2)若按图b 放置时,求系统的加速度及绳的张力。
大学物理练习册参考答案

大学物理练习册参考答案大学物理练习册是大学物理的重要教材之一,它的主要作用是为大学物理课程提供题目和习题,使学生能够更好地掌握和理解物理知识。
本文将为大家提供几个大学物理练习册的参考答案,供大家参考。
第一题:有一块长度为20cm,宽度为10cm,厚度为2cm的矩形金属板,重量为3N。
请问这块金属板的密度是多少?答案:首先我们需要知道密度的定义,密度是单位体积内物质的质量。
因此,我们可以根据这个公式计算出这块金属板的密度:密度=质量/体积其中,这块金属板的质量为3N,体积为20cm × 10cm × 2cm = 400cm³。
把质量和体积带入公式中,可以得到这块金属板的密度为:密度=3N/400cm³=0.0075N/cm³因此,这块金属板的密度为0.0075N/cm³。
第二题:有一个长度为4m的绳子,一个人沿着绳子向上爬,绳子的质量是忽略不计的。
如果人的体重为600N,他在绳子上爬行的过程中,绳子的张力是多少?答案:在求解这个问题之前,我们需要知道牛顿第二定律的公式:力=质量× 加速度根据牛顿第二定律,可以得到人在绳子上爬行时绳子所受的力等于绳子的张力减去重力。
因此,我们可以得到以下公式:绳子的张力=人的重力+绳子的重力其中,人的重力为600N,绳子的重力可以根据绳子的长度和重力加速度计算得出。
在地球上,物体的重力加速度大约为9.8m/s²。
因此,绳子的重力可以用下面的公式计算:绳子的重力=绳子的质量× 重力加速度因为绳子的质量可以根据绳子的长度和线密度计算得出,我们可以得到以下公式:绳子的质量=绳子的长度× 线密度假设绳子的线密度为ρ,绳子的质量可以表示为:绳子的质量=ρ × 面积× 长度根据绳子的面积和长度,可以得到:面积=长度× 直径/4因此,绳子的质量可以通过以下公式计算得出:绳子的质量=ρ × 直径² × 长度/16把绳子的质量和重力加速度带入公式中,可以得到绳子的重力为:绳子的重力=ρ × 直径² × 长度/16 × 重力加速度把人的重力和绳子的重力带入公式中,可以得到绳子的张力为:绳子的张力=人的重力+绳子的重力=600N+ρ × 直径² × 长度/16 × 重力加速度因此,如果已知绳子的线密度、直径、长度和重力加速度,就可以计算出绳子在负责人上爬行时所受的张力。
大学物理学 (第3版.修订版) 北京邮电大学出版社 上册 第四章习题4 答案

2 2 v v x v y 0.88 c
速度与 x 轴的夹角 为
tan
v y v x
1.07
46.8ο
题 4.10 图 4.11 静止在S系中的观测者测得一光子沿与 x 轴成 60 角的方向飞行.另一观测者静止于 S′系,S′系的 x 轴与 x 轴一致,并以0.6c的速度沿 x 方向运动.试问S′系中的观测者观 测到的光子运动方向如何? 解: S 系中光子运动速度的分量为
2
(D) c t 1 v / c
2
[答案:A ] (4)一宇航员要到离地球 5 光年的星球去旅行。如果宇航员希望把这路程缩短为 3 光年, 则他所乘的火箭相对于地球的速度 v 应为[ ]。 (A)0.5c (B)0.6c (C)0.8c (D)0.9c [答案:C ] (5) 某宇宙飞船以 0.8c 的速度离开地球, 若地球上测到它发出的两个信号之间的时间间隔 为 10s。则宇航员测出的相应的时间间隔为[ ]。 (A)6s (B)8s (C)10s (D)10/3s [答案:A ] 4.2 填空题 (1) 有一速度为u的宇宙飞船沿X轴正方向飞行,飞船头尾各有一个脉冲光源在工作,处 于船尾的观察者测得船头光源发出的光脉冲的传播速度大小为_________;处于船头的观察 者测得船尾光源发出的光脉冲的传播速度大小为__________。 [答案:c,c; ] ( 2 ) S 系相对 S 系沿 x 轴匀速运动的速度为 0.8c ,在 S 中观测,两个事件的时间间隔
习题 4 4.1 选择题 (1)在一惯性系中观测,两个事件同时不同地,则在其他惯性系中观测,他们[ (A)一定同时 (B)可能同时 (C)不可能同时,但可能同地 (D)不可能同时,也不可能同地 [答案:D ] (2)在一惯性系中观测,两个事件同地不同时,则在其他惯性系中观测,他们[ (A)一定同地 (B)可能同地 (C)不可能同地,但可能同时 (D)不可能同地,也不可能同时 [答案:D ]
大学物理练习册答案(DOC)

大学物理练习册答案(DOC)第十章练习一一、选择题1、下列四种运动(忽略阻力)中哪一种是简谐振动?()(A)小球在地面上作完全弹性的上下跳动(B)细线悬挂一小球在竖直平面上作大角度的来回摆动(C)浮在水里的一均匀矩形木块,将它部分按入水中,然后松开,使木块上下浮动(D)浮在水里的一均匀球形木块,将它部分按入水中,然后松开,使木块上下浮动2、质点作简谐振动,距平衡位置2.0cm时,加速度a=4.0cm/2,则该质点从一端运动到另一端的时间为()(A)1.2(B)2.4(C)2.2(D)4.43、如图下所示,以向右为正方向,用向左的力压缩一弹簧,然后松手任其振动,若从松手时开始计时,则该弹簧振子的初相位为()(A)0(B)(C)2kmFO某(D)24、一质量为m的物体与一个劲度系数为k 的轻弹簧组成弹簧振子,当其振幅为A时,该弹簧振子的总能量为E。
若将其弹簧分割成两等份,将两根弹簧并联组成新的弹簧振子,则新弹簧振子的振幅为多少时,其总能量与原先弹簧振子的总能量E相等()(A)AAA(B)(C)(D)A242T时的质点速度为,2二、填空题1、已知简谐振动某Aco(t0)的周期为T,在t加速度为2、已知月球上的重力加速度是地球的1/6,若一个单摆(只考虑小角度摆动)在地球上的振动周期为T,将该单摆拿到月球上去,其振动周期应为3、一质点作简谐振动,在同一周期内相继通过相距为11cm的A,B两点,历时2秒,速度大小与方向均相同,再经过2秒,从另一方向以相同速率反向通过B点。
该振动的振幅为,周期为4、简谐振动的总能量是E,当位移是振幅的一半时,当EkE,P,EE某时,EkEP。
A三、计算题1、一振动质点的振动曲线如右图所示,试求:(l)运动学方程;(2)点P对应的相位;(3)从振动开始到达点P相应位置所需的时间。
2、一质量为10g的物体作简谐运动,其振幅为24cm,周期为4.0,当t=0时,位移为+24cm。
武汉工程大学物理练习册练习四

M mol RT 8.31 300 0.24 2.0 10 3 kg / mol P 3.0 105
或 vP
2P
2 3.0 105 1581m / s 0.24
2 RT 2 8.31 300 vP 1579m / s 3 M mol 2.0 10
0.71 3.45107 m
9.今测得温度为t1=150C,压强为p1=0.76m汞柱高时,氩分子和 8 氖分子的平均自由程分别为:Ar 6.7 10 8 m 和 Ne 13.2 10 m ,求: (1) 氖分子和氩分子有效直径之比 d Ne / d Ar ; (2) 温度为t2=200C,压强为p2=0.15m汞柱高时,氩分子的平均自由 ' 程 Ar 。
23
7 3
1.04kg / m3
2.若某种理想气体分子的方均根速率 v
2
1/
450 m / s,气体压
强为P=7.00×104 Pa,则该气体的密度为 解:
=____。
1 1 2 2 p mnv v 3 3
3P 3P 3 7.00 104 v2 1.04kg / m3 2 2 4502 ( v )
8RT 8PV 8 50.7 103 3.0 102 v 440.2m / s 2 M mol M 3.14 2.0 10
100
f (v)dv N
100
f (v)dv
100
vf (v)dv /
100
f (v)dv
7.已知f(v)为麦克斯韦速率分布函数,N为总分子数,则(1)速 率v > 100 m·s-1的分子数占总分子数的百分比的表达式为 ; (2)速率v > 100 m·s-1的分子数的表达式为 。(3)速率v > 100 m·s-1的分子的平均速率表达式为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题及参考答案第3章 刚体力学参考答案思考题3-1刚体角动量守恒的充分而必要的条件是 (A )刚体不受外力矩的作用。
(B )刚体所受合外力矩为零。
(C)刚体所受的合外力和合外力矩均为零。
(D)刚体的转动惯量和角速度均保持不变。
答:(B )。
3-2如图所示,A 、B 为两个相同的绕着轻 绳的定滑轮。
A 滑轮挂一质量为M 的物体, B 滑轮受拉力F ,而且F =Mg 。
设A 、B 两 滑轮的角加速度分别为βA 和βB ,不计滑轮 轴的摩擦,则有(A )βA = βB (B )βA > βB(C )βA < βB (D )开始时βA = βB ,以后βA < βB 答:(C )。
3-3关于刚体对轴的转动惯量,下列说法中正确的是(A )只取决于刚体的质量,与质量的空间分布和轴的位置无关。
(B)取决于刚体的质量和质量的空间分布,与轴的位置无关。
(C )取决于刚体的质量、质量的空间分布和轴的位置。
(D)只取决于转轴的位置,与刚体的质量和质量的空间分布无 答:(C )。
3-4一水平圆盘可绕通过其中心的固定铅直轴转动,盘上站着一个人,初始时整个系统处于静止状态,当此人在盘上随意走动时,若忽略轴的摩擦,则此系统(A)动量守恒; (B)机械能守恒; (C)对转轴的角动量守恒;(D)动量、机械能和角动量都守恒; (E)动量、机械能和角动量都不守恒。
答:(C )。
3-5光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点o 且垂直于杆的竖直光滑固定轴自由转动,其转动惯量为213mL,起初杆静止,桌面上有两个质量均为m 的小球,各自在 垂直于杆的方向上,正对着杆的一端,以相同速率v 相向 运动,如图所示,当两小球同时与杆的两个端点发生完全非弹性碰撞后,就与杆粘在一起转动,则这一系统碰撞后的转动角速度应为AMF思考题3-2图v思考题3-5图(A)23L v (B)45L v (C)67L v (D)89L v (E)127L v答:(C )。
3-6一飞轮以600rev/min 的转速旋转,转动惯量为2. 5kg·m 2,现加一恒定的制动力矩使飞轮在1s 内停止转动,则该恒定制动力矩的大小M =___________答:157N ⋅m 。
3-7质量为m 的质点以速度v 沿一真线运动,则它对直线外垂直距离为d 的一点的角动量大小是_。
答:m v d 。
3-8哈雷慧星绕太阳的轨道是以太阳为一个焦点的椭圆。
它离太阳最近的距离是r 1 = 8.75×1010m ,此时它的速率是v 1= 5.46×104m·s -1。
它离太阳最远的速率是v 2= 9.08×102m·s -1,这时它离太阳的距离是r 2 =____________答:5.26×1012m 。
3-9两个滑冰运动员的质量各为70kg ,以6.5m·s -1的速率沿相反的方向滑行,滑行路线间的垂直距离为l0m,当彼此交错时各抓住一l0m 长的绳索的一端,然后相对旋转,则抓住绳索之后各自对绳中心的角动量L =_;它们各自收拢绳索,到绳长为5m 时,各自的速率v =__答:2275kg ⋅m 2⋅s -1;13m/s 。
三 习题3-1两个匀质圆盘,一大一小,同轴地粘贴在一起,构成组合轮。
小圆盘的半径为r ,质量为m ;大圆盘的半径r’ = 2r ,质量m '=2m 。
组合轮可绕通过其中心垂直于盘面的光滑水平固定轴o 转动,对o 轴的转动惯量J =9mr 2/2.两圆盘边缘上分别绕有轻质绳,细绳下端各悬挂质量为m 的物体A 和B ,如图所示,这一系统从静止开始运动,绳与盘无相对滑动,绳的长度不变。
已知r =10cm,求:(1)组合轮的角加速度β(2)当物体A 上升h =40cm 时,组合轮的角速度ω。
3-2电风扇在开启电源后,经过t 1,时间达到了额定转速,此时相应角速度为ω0。
当关闭电源后,经过t 2时间风扇停转。
已知风扇转子的转动惯量为J ,并假定摩擦阻力矩和电机的电磁力矩均为常数,试根据已知量推算电机的电磁力矩。
3-3一块宽L =0.60m 、质量M = 1kg 的均匀薄木板,可绕水平固定轴oo’无摩擦地自由转动。
当木板静止在平衡位置时,有一质量为m =10×10-3kg 的子弹垂直击中木板A 点,A 离转轴oo’距离l =0.36m ,子弹击中木板的速度为500m·s -1,穿出木板后的速度为200 m·s -1。
求:(1)子弹给予木板的冲量; (2)太板获得的角速度。
(已知木板绕oo’袖的转动惯量213J ML =)3-4一匀质细棒长为2L ,质量为m ,以与棒长方向相垂直的速度v 0在光滑水平面内平动时,与前方一固定的光滑支点o 发生完全非弹性碰撞。
碰撞点位于棒中心的一方L /2处,如图所示。
求棒在碰撞后的瞬时绕o 点转动的角速度ω。
(细棒绕通过其端点且与其垂直的轴转动时的转动惯量为mL 2/3,式中的m 和L 分别为棒习题3-3图的质量和长度。
)3-5有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦为μ的水平桌面上,它可绕通过其端点o 且与桌面垂直的固定光滑轴转动。
另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相碰撞,设碰撞时间极短。
已知小滑块在碰撞前后的速度分别为v 1和v 2,如图所示。
求碰撞后从细棒开始转动到停止转动的过程所需的时间。
(已知棒绕o 点的转动惯量J =m 1l 2/33-6飞轮的质量m =60kg,半径R =0.25m,绕其水平中心轴o 转动,转速为900rev/min.现利用一制动用的闸杆,在闸杆的一端加一竖直方向的制动力F ,可使飞轮减速。
已知闸杆的尺寸如图所示,闸瓦与飞轮之间的摩擦系数μ=0. 4,飞轮的转动惯量可按匀质圆盘计算,(1)设F =100N ,问可使飞轮在多长时间内停止转动?在这段时间里,飞轮转了几转?(2)如要在2s 内使飞轮转速减为一半,需加多大的制动力F ?3-7 一长L =0. 4m ,质量M =1.0kg 的均匀细木棒,由其上端的光滑水平轴o 吊起而处于静止,如图所示。
今有一质量m =8.0kg 的子弹以v =200m/s 的速率水平射人棒中,射人点在轴下d = 3L /4处。
求:(1)在子弹射人棒中的瞬时棒的角速度,(2)子弹射人棒的最大偏转角。
3-8 一个轻质弹簧的倔强系数K =2.0N/m ,它的一端固定,另一端通过一条细绳绕过一个定滑轮和一个质量为m =80g 的物体相连,如图所示。
定滑轮可看作均匀圆盘,它的质量M =100g ,半径r =0.05m 。
先用手托住物体m ,使弹簧处于其自然长度,然后松手。
求物体m习题3-4图 v 0oAv 0B 2121oAm 2m 1,l习题3-5图习题3-6图习题3-7图vm习题3-8图下降h =0. 5m 时的速度为多大?忽略滑轮轴上的摩擦,并认为绳在轮边缘上不打滑。
第3章 刚体力学参考答案思考题3-1 答:(B ) 3-2答:(C ) 3-3答:(C )。
3-4答:(C )。
3-5答:(C )。
3-6答:157N ⋅m 。
3-7答:m v d 。
3-8答:5.26×1012m 。
3-9答:2275kg ⋅m 2⋅s -1;13m/s 。
习题3 -1解:(1)各物体受力情况如图所示。
)2(9)2(''''r a r a Tr r T maT mg ma mg T ββ===-=-=-由上述方程组解得2/3.10)19/(2s rad r g ==β(2)设θ为组合轮转过的角度,则2/,2h r θωβθ==所以 rad /s 08.9)/2(2/1==r h βω3-2 解:假定电机产生得电磁力矩为M ,系统得阻力力矩为r M ,则根据转动定律得: 开启时 1r M M J β-= 关闭时 r M J β-= 则有 12()M J ββ=- 其中 011022,0t t ωβωβ=+= 故 101202/,/t t βωβω==-由此可得 )11(210t t J M +=ω3-3解:(1)子弹受到的冲量为0()I Fdt m ==-⎰v v习题3-1解图子弹对木块的冲量为''0()3N sI F dt Fdt m ==-=-=⋅⎰⎰v v方向与0v 相同(2)根据角动量定理'()Mdt l F dt lm ==-⎰⎰vv023()9rad/s lm mL ω-==v v3-4解:碰撞前瞬时,杆对o 点的角动量为3/2/220000012L L xdx xdx L m Lρρρ-==⎰⎰v v v v式中ρ为杆的线密度。
碰撞后瞬时,杆对o 的角动量为ωωω2221272141234331mL L m L m J =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=由角动量守恒2071122mL m Lω=v067L ω∴=v 3-5解:对棒和滑块系统,在碰撞过程中,由于碰撞时间很短,所以棒所受的摩擦力矩远小于滑块的冲力矩。
故可以认为合外力矩为零,系统角动量守恒,即22122113m l m l m l ω=-+v v (1)碰撞后棒在转动过程中所受的摩擦力矩为glm dx l m gx M lf 10121μμ-=-=⎰ (2) 由角动量定理 ω210310l m dt M t f -=⎰ (3)由式(1),(2),(3)可得12212t m m g μ+=v v 3-6解:(1)设杆与轮间的正压力为N ,120.5m,0.75l l ==m ,由杠杆平衡条件:121()F l l Nl +=又由摩擦力 N F r μ=,由转动定律21,2M I I mR β==,有340-=-=I R F r β停止转动时间s 06.70=-=βωt转过的角度 20153.12rad2t t θωβπ∆=+=⨯(2)s 2,300πω=内减半,知027.5rad/stωωβπ-==-则动力为112177N()mRlFl lβαμ-==+3-7解:(1)由角动量守恒22(/3)m d ML mdω=+v故2288.8rad/s13mvdML mdω==+(2)设棒的最大偏转角为θ,则由机械能守恒:22211()(1cos)(1cos)232Lmd ML Mg mgdωθθ+=-+-'1694o=θ3-8解:由于只有保守力作功,所以由弹簧、滑轮和物体组成的系统机械能守恒,故有:222111222mgh kh I mω=++vrω=v,221MrI=所以1.48m/s==v。
