实验十古典密码与破译
古典密码的设计与破译

8
讓Vigenère Cipher難以破解
所以當金鑰的長度與明文一樣長,甚至比明 文更長,將會增加其破譯的困難度,甚至無 法被敵人破譯。 而長度長的金鑰當然也能是約定好的某本書, 但是在發送接收訊息時也就必須要有金鑰本 在手邊,由於是有規則性地推移字母,即使 無密本也可逐字推算。
9
10
Enigma machine
16
3 movable rotors are sandwiched between 2 fixed wheels: the entry wheel on the right and the reflector (here marked "B") on the left.
17
連接板(Plug-board)
World War II 德國所使用 名稱源自希臘語,意指‚ 不可 思議的東西‛或‚謎‛ Enigma是突破性地結合機器來 進行加密,使得密碼更不易被 破解
11
基本元件與原理
其中最基本的三大部分為鍵盤、轉子和顯示器。 鍵盤共有26個鍵,分別為26個英文字母,其排 列接近我們現在所使用的計算機鍵盤。為了使 消息盡量簡短且更難破譯,空格和標點符號都 被省略。 鍵盤、轉子和顯示器由電線相連,轉子本身也 集成了26條線路,把鍵盤的信號對應到顯示器 不同的小燈上去,每一個字母都一一對應替換 為另一個字母 。
23
Enigma的破解(2)
雖然這些循環圈是由當日金鑰,也就是轉子 的位置,它們的初始方向以及連接版上字母 置換造成的,但是每組循環圈的個數和每個 循環圈的長度,卻僅僅是由轉子的位置和它 們的初始方向決定的,和連接版上字母交換 的情況無關﹗ 如果只考慮轉子的位置和它們的初始方向, 只有105456(6*263)種可能性。雖然這還 是一個很大的數字,但是把所有的可能性都 試驗一遍,已經是一件可以做到的事情了。
古典密码的实验报告

古典密码的实验报告古典密码的实验报告引言:密码学作为一门古老而又神秘的学科,一直以来都吸引着人们的兴趣。
在古代,人们用各种各样的密码来保护重要信息的安全性。
本实验旨在通过实际操作,探索古典密码的加密原理和破解方法,从而深入了解密码学的基本概念和应用。
一、凯撒密码凯撒密码,又称移位密码,是最简单的一种古典密码。
其原理是通过将明文中的每个字母按照一定的规则进行移位,得到密文。
在本实验中,我们选择了一个简单的凯撒密码进行破解。
首先,我们选择了一段明文:“HELLO WORLD”,并将其按照凯撒密码的规则进行移位,假设移位数为3,则得到密文:“KHOOR ZRUOG”。
接下来,我们尝试使用暴力破解的方法来还原明文。
通过尝试不同的移位数,我们发现当移位数为3时,得到的明文与原文完全一致。
这表明我们成功地破解了凯撒密码,并还原了原始的明文。
二、维吉尼亚密码维吉尼亚密码是一种基于多个凯撒密码组合而成的密码算法。
其原理是通过使用不同的移位数对明文进行加密,从而增加了密码的复杂度。
在本实验中,我们选择了一段明文:“CRYPTOGRAPHY”,并使用维吉尼亚密码进行加密。
我们选择了一个关键词“KEY”作为加密密钥。
首先,我们将关键词“KEY”重复至与明文长度相同,得到“KEYKEYKEYKEYK”。
然后,将明文中的每个字母与关键词中对应位置的字母进行凯撒密码的移位操作。
经过加密后,我们得到了密文:“LXFOPVEFRNHR”。
接下来,我们尝试使用破解方法来还原明文。
通过尝试不同的关键词和移位数的组合,我们发现当关键词为“KEY”且移位数为3时,得到的明文与原文完全一致。
这表明我们成功地破解了维吉尼亚密码,并还原了原始的明文。
三、栅栏密码栅栏密码是一种基于换位操作的密码算法。
其原理是通过将明文中的字母按照一定的规则进行重新排列,得到密文。
在本实验中,我们选择了一段明文:“HELLO WORLD”,并使用栅栏密码进行加密。
古典密码的加密和破译

古典密码的加密和破译组员:庄子元徐诚李金辰钱辰卢稼羿指导老师:王孙斌研究背景:现今网络安全越来越受人重视,密码是一个非常重要的环节。
现代密码是自从二战发展起来的,但由于难度较高,所以本小组研究它的前身古典密码,来对其有一个初步的了解。
研究目标及意义:了解古典密码的起源及发展,了解一些加密和解密过程,掌握一些基本的加密方法,和简单密码的破译,对古典密码有一个更深入的了解。
研究方案:通过网络途径和对图书馆有关书籍的查阅,并询问指导老师,获得一些基本了解后,组内自行设计密码并交换解密,加深了解。
即文献法和自主探究法。
研究成果:关于密码的起源:在人类历史上,对信息保护的需求与对信息本身的需求一样久远。
第一个用于加密和解密文本的编码方式是凯撒密码。
凯撒密码是一种移位密码。
密码加密方法密码的加密种类:密码一般加密方式分为移位和代换两种。
移位法换位法又称置换法或变位法。
换位法改变明文元素的相对位置,但保持其内容不变。
例如,把明文的字母重新排列组合,改变它们在明文中的位置,但字母本身不变。
这种换位可以是一维的,也可以是多维的。
最简单的换位密码是将明文的顺序颠倒过来,然后截成固定长度的字母组作密文。
例如,明文为this cryptosystem is not secure,用这种加密方法加密后以4位为一组,则得到密文ERUC、ESTO、NSIM、ETSY、SOTP、YRCS、IHT。
(为了清楚起见,这里用小写字母表示明文,而用大写字母表示密文。
)凯撒密码:移位密码的代表之一就是凯撒密码,当年恺撒曾用此方法与其将军们进行联系。
凯撒密码就是将字母按字母表顺序向后移动几个。
如cryptography——etarvqitcfja,所给的加密示例就是将字母向后移动两格。
但是此种加密方式易被破解,所以凯撒密码在不断的演变后成为了更复杂的加密方式的其中一个部分,如维吉尼亚密码。
维吉尼亚密码:人们在单一恺撒密码的基础上扩展出多表密码,称为“维吉尼亚”密码。
古典密码实验报告

实验报告一、实验室名称:SimpleSPC信息安全云实验系统二、实验项目名称:古典密码——置换密码三、实验学时:1学时四、实验原理:1) 算法原理a) 置换密码算法就是不改变明文字符,而就是按照某一规则重新排列消息中的比特或字符顺序,才而实现明文信息的加密。
将明文中的字母按照给定的顺序安排在一个矩阵中,然后用根据密钥提供的顺序重新组合矩阵中的字母,从而形成密文。
其解密过程就是根据密钥的字母数作为列数,将密文按照列、行的顺序写出,再根据密钥给出的矩阵置换产生新的矩阵,从而恢复明文。
b) 置换密码(Permutation Cipher),又称换位密码。
算法实施时,明文的字母保持相同,但顺序会被打乱。
置换只不过就是一个简单的换位,每个置换都可以用一个置换矩阵Ek来表示。
每个置换都有一个与之对应的逆置换Dk。
置换密码的特点就是仅有一个发送方与接受方知道的加密置换(用于加密)及对应的逆置换(用于解密)。
它就是对明文L长字母组中的字母位置进行重新排列,而每个字母本身并不改变。
c) 设n为一固定整数,P、C与K分别为明文空间、密文空间与密钥空间。
明/密文就是长度为n的字符序列,分别记为X(x1,x2,…,xn)属于P与Y(y1,y2,…,yn)属于C ,K就是定义在{1,2,…,n}的所有置换组成的集合。
对任何一个密钥(即一个置换),定义置换如下:加密置换为:解密置换为:上式中,就是的逆置换,密钥空间K的大小为n!2) 算法参数置换密码算法主要有c、m、k、n四个参数。
c为密文,m就是明文,k为密钥,n 为模数。
3) 算法流程算法流程。
如图所示五、实验目的:1)学习置换密码的原理2) 学习置换密码的算法实现六、实验内容:1、在虚拟机上运行置换密码、exe可执行文件,根据提示输入明文与密钥,同时检查输出的解密后的结果就是否与明文一致。
2、学习掌握置换密码的原理,并根据明文与密钥计算出对应的加密文,并与程序输出的结果进行比对,掌握其加密解密的过程。
现代密码学——古典密码算法(实验报告)
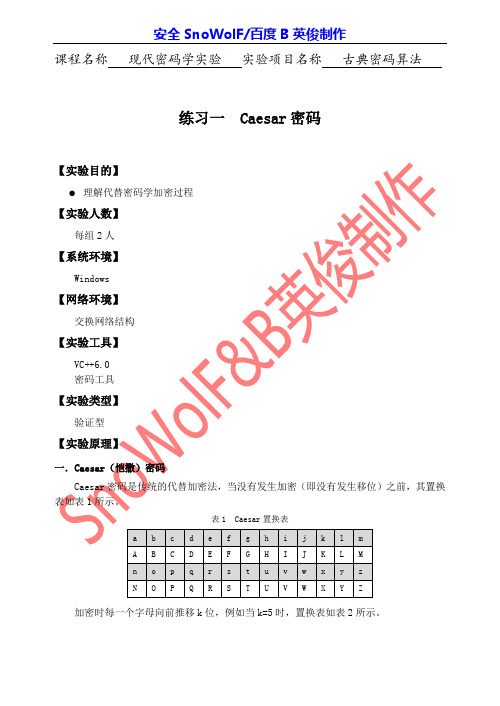
安全SnoWolF/百度B英俊制作课程名称现代密码学实验实验项目名称古典密码算法练习一 Caesar密码加密时每一个字母向前推移k位,例如当k=5时,置换表如表2所示。
表2 Caesar置换表于是对于明文:datasecurityhasevolvedrapidly经过加密后就可以得到密文:IFYFXJHZWNYDMFXJATQAJIWFUNIQD若令26个字母分别对应整数0~25,如表3所示。
表3 Caesar置换表则Caesar加密变换实际上是:c=(m+k)mod26其中m是明文对应的数据,c是与明文对应的密文数据,k是加密用的参数,也称为密钥。
很容易得到相应的Caesar解密变换是:m=D(c)=(c–k)mod26例如明文:datasecurity对应的数据序列:301901842201781924当k=5时经过加密变换得到密文序列:852452397252213243对应的密文为:IFYFXJHZWNYD【实验步骤】本练习主机A、B为一组,C、D为一组,E、F为一组。
首先使用“快照X”恢复Windows系统环境。
一.手动完成Caesar密码(1) 在实验原理部分我们已经了解了Caesar密码的基本原理,那么请同学们写出当密钥k=3时,对应明文:data security has evolved rapidly的密文: GDWD VHFXULWB KDV HYROYHG UDSLGOB 。
(2) 进入实验平台,单击工具栏中的“密码工具”按钮,启动密码工具,在向导区点击“Caesar密码”。
在明文输入区输入明文:data security has evolved rapidly。
将密钥k调节到3,查看相应的密文,并与你手动加密的密文进行比较。
请根据密钥验证密文与明文对应关系是否正确。
二.Caesar加密(1) 进入“加密解密”|“Caesar密码”视图,在明文输入区输入明文(明文应为英文),单击“加密”按钮进行加密。
实验吧_密码学实验报告(3篇)

第1篇一、实验背景密码学是一门研究信息加密与解密的学科,它广泛应用于信息安全领域。
为了更好地理解密码学的基本原理和算法,我们选择了实验吧平台上的密码学实验进行学习。
本次实验旨在通过实际操作,加深对古典密码、对称密码和不对称密码等密码学基本概念的理解,提高密码学应用能力。
二、实验目的1. 理解并掌握古典密码的基本原理和算法;2. 掌握对称密码和不对称密码的基本原理和算法;3. 通过实验操作,提高密码学应用能力;4. 培养团队协作和解决问题的能力。
三、实验内容1. 古典密码实验(1)仿射密码原理:仿射密码是一种单字母替换密码,加密公式为:C = (aP + b) mod 26,其中C为密文字母,P为明文字母,a和b为密钥。
操作步骤:1)编写加密函数encrypt,实现仿射密码加密;2)编写解密函数decrypt,实现仿射密码解密;3)测试加密和解密函数,验证其正确性。
(2)单表代替密码原理:单表代替密码是一种将明文字符映射到密文字符的替换密码。
操作步骤:1)编写加密函数subencrypt,实现单表代替密码加密;2)编写解密函数subdecrypt,实现单表代替密码解密;3)测试加密和解密函数,验证其正确性。
(3)维吉尼亚密码原理:维吉尼亚密码是一种多字母替换密码,加密公式为:C = (P + K[i]) mod 26,其中C为密文字母,P为明文字母,K为密钥,i为索引。
操作步骤:1)编写加密函数vigenereencrypt,实现维吉尼亚密码加密;2)编写解密函数vigeneredecrypt,实现维吉尼亚密码解密;3)测试加密和解密函数,验证其正确性。
2. 对称密码实验(1)DES加密算法原理:DES(Data Encryption Standard)是一种分组加密算法,采用56位密钥,64位分组。
操作步骤:1)编写DES加密函数desencrypt,实现DES加密;2)编写DES解密函数desdecrypt,实现DES解密;3)测试加密和解密函数,验证其正确性。
古典密码的实验报告

古典密码的实验报告1. 引言古典密码是一种古老的加密技术,用于在信息传递过程中保护敏感信息的安全性。
它通过将明文转换成密文,从而使未经授权的个体无法理解信息的内容。
本实验旨在介绍几种常见的古典密码算法,并通过实验验证其加密和解密的过程。
2. 凯撒密码凯撒密码是最简单的古典密码之一,它通过将明文中的每个字母向前或向后移动固定的位置来加密信息。
例如,当移动的位置为3时,明文中的字母A将被替换为D,字母B将被替换为E,以此类推。
2.1 加密过程1.输入明文。
2.设置移动的位置。
3.对于明文中的每个字母,按照移动的位置将其替换为对应的字母。
4.得到密文。
2.2 解密过程1.输入密文。
2.设置移动的位置。
3.对于密文中的每个字母,按照移动的位置将其替换为对应的字母。
4.得到明文。
3. 维吉尼亚密码维吉尼亚密码是一种多表密码,它通过使用一系列凯撒密码表来加密信息。
每个表中的移动位置逐个递增,这样可以更好地混淆明文的结构。
3.1 加密过程1.输入明文。
2.输入密钥。
3.对于明文中的每个字母,找到对应的凯撒密码表。
4.根据对应的表和密钥,将明文中的字母替换为密文。
5.得到密文。
3.2 解密过程1.输入密文。
2.输入密钥。
3.对于密文中的每个字母,找到对应的凯撒密码表。
4.根据对应的表和密钥,将密文中的字母替换为明文。
5.得到明文。
4. 培根密码培根密码是古典密码中的另一种类型,它使用一系列相同长度的字母组成的密钥来加密信息。
明文中的每个字母都将被替换为对应密钥中的字母。
4.1 加密过程1.输入明文。
2.输入密钥。
3.对于明文中的每个字母,将其对应到密钥中的相应字母。
4.得到密文。
4.2 解密过程1.输入密文。
2.输入密钥。
3.对于密文中的每个字母,将其对应到密钥中的相应字母。
4.得到明文。
5. 实验结果与讨论在本实验中,我们使用了凯撒密码、维吉尼亚密码和培根密码进行加密和解密实验。
通过对不同算法的测试,我们发现:1.凯撒密码是最简单的古典密码之一,但由于移动位置的确定性,易受到频率分析等攻击方式的威胁。
密码分析学实验报告

一、实验目的本次实验旨在让学生了解密码分析学的基本原理和方法,掌握密码分析的基本步骤,并能够运用所学知识对简单的加密算法进行破解。
通过实验,提高学生对密码分析学的认识和实际操作能力。
二、实验内容1. 实验背景密码分析学是研究密码的编制和破译的学科,其主要任务是分析密码系统的安全性,找出其弱点,从而提高密码系统的安全性。
本次实验将针对古典密码和现代密码进行分析。
2. 实验步骤(1)古典密码分析①移位密码分析:选取一组明文和密钥,通过编写程序实现移位密码的加密和解密操作,观察并分析加密结果。
②维吉尼亚密码分析:选取一组明文和密钥,通过编写程序实现维吉尼亚密码的加密和解密操作,观察并分析加密结果。
③周期置换密码分析:选取一组明文和密钥,通过编写程序实现周期置换密码的加密和解密操作,观察并分析加密结果。
(2)现代密码分析①公钥密码分析:选取一组公钥和私钥,通过编写程序实现公钥密码的加密和解密操作,观察并分析加密结果。
②对称密码分析:选取一组密钥,通过编写程序实现对称密码的加密和解密操作,观察并分析加密结果。
3. 实验结果与分析(1)古典密码分析结果①移位密码:通过编写程序,我们可以观察到当密钥正确时,加密后的密文与明文之间的差异较大;当密钥错误时,加密后的密文与明文之间的差异较小。
②维吉尼亚密码:通过编写程序,我们可以观察到当密钥正确时,加密后的密文与明文之间的差异较大;当密钥错误时,加密后的密文与明文之间的差异较小。
③周期置换密码:通过编写程序,我们可以观察到当密钥正确时,加密后的密文与明文之间的差异较大;当密钥错误时,加密后的密文与明文之间的差异较小。
(2)现代密码分析结果①公钥密码:通过编写程序,我们可以观察到当公钥和私钥正确时,加密后的密文与明文之间的差异较大;当公钥和私钥错误时,加密后的密文与明文之间的差异较小。
②对称密码:通过编写程序,我们可以观察到当密钥正确时,加密后的密文与明文之间的差异较大;当密钥错误时,加密后的密文与明文之间的差异较小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k | A |1 (mod 26)
本计算方法可推广到求矩阵 A 的 模 m 逆矩阵
Hill2 解密过程
1 2 设加密矩阵 A 0 3
1
3 2 | A | 3, A 0 1
1 3 2 A (mod 26) 3 (mod 26) (mod 26) 0 1
模 m 可逆
问题:是否 Zm 中所有的数都存在模 m 倒数?
a 存在唯一的模 m 倒数 a 与 m 无公共素数因子 命题:定义在集合 Zm 上的 n 阶方阵 A 模 m 可逆的充要条 件是:m 和 det(A) 无公共素数因子,即 m 与 det(A) 互素。
Hill2 密码的加密矩阵必须满足上述条件。 m=26 m 的素数因子只有 2 和 13
N O P Q R S T U V W X Y Z 14 15 16 17 18 19 20 21 22 23 24 25 0
Hill2 解密举例
① 将密文字母分组,通过查表列出每组字母对应的向量 ② 求出加密矩阵 A 的 模 26 逆矩阵
1 8 B 0 9
③ 用 B 左乘每组密文字母组成的向量,然后再反查字母
在模运算下解方程组: A =
A (mod 26) (mod 26)
1
问题:如何计算 A1 (mod 26) ?
模 m 逆矩阵的计算
1 A A | A|
1
A*为 A 的伴随矩阵
设 B=k A*为 A 的 模 26 逆,其中 k 为待定系数
BA k | A | E BA E (mod 26) k | A | 1(mod 26)
Hill2 解密过程
解密:加密的逆过程,将加密过程逆转回去即可。 例:怎么得到密文 “RBVWMDTT ” 的原文?
先查出密文字母 “RB VW MD TT” 所对应的向量:
18 22 13 20 , , , 2 23 4 20
Hill2 解密举例
序 分组 密文 明文 分组 号 密文 表值 表值 明文 13 L 12 2 B O 15 5 E 14 H 8 14 N D 4 10 J 15 K 11 9 I C 3 1 A 16 E 5 13 M A 1 9 I 17 F 6 4 D C 3 1 A 18 L 12 14 N W 23 25 Y 序 分组 密文 明文 分组 号 密文 表值 表值 明文 19 W 23 21 U C 3 1 A 20 V 22 14 N L 12 4 D 21 E 5 5 E M 13 13 M 22 I 9 9 I M 13 13 M 23 C 3 1 A C 3 1 A
① 通讯双方确定加密矩阵 ( 密钥) 和字母的表值对应表 ② 将明文字母分组,通过查表列出每组字母对应的向量
若明文只含奇数个字母,则补充一个哑元 ③ 令 = A mod(m) ,由 的分量反查字母表值表,
得到相应的密文字母
Hill2 解密过程总结
① 将密文字母分组,通过查表列出每组字母对应的向量 ② 求出加密矩阵 A 的 模 m 逆矩阵 B
定义在 Z26上的方阵 A 模 26 可逆的充要条件是:
det(A) 不能被 2 和 13 整除
模 26 可逆
Z26 中具有模 26 倒数的整数及其模 26 倒数表2
a a-1 1 1 3 5 7 9 11 15 17 19 21 23 25 9 21 15 3 19 7 23 11 5 17 25
定义 1:设 A 为定义在集合 Zm 上的 n 阶方阵,若存在一个定 义在 Zm 上的方阵 B,使得
AB BA E(mod m) 则称 A 模 m 可逆, B 为 A 的 模 m 逆矩阵,记为 B A1 (mod m)
定义 2:设 a Zm ,若存在 b Zm 使得 ab=1 (mod m) ,则 称 b 为 a 的 模 m 倒数 或乘法逆,记作 b = a-1 (mod m) 。 注: a , b 都是 Zm 中的数
1 2 3 4 5 6 7 8 9 10 11 12 13
8 24 19 24 , , , 18 25 10 24
Y
25
N
14
O
15
P
Q
R
18
S
19
T
20
U
21
V
22
W X
23 24
Z
0
16 17
Hill2 加密举例
Hill2 加密举例
例: 设明文为“HRXYSJX”(华锐学院数计系), 1 2 试给出这段明文的 Hill2 密文。 A
0 3
解:
将明文字母分组:
HR
XY
SJ
XX
最后的一个字母 X 为哑字母,无实际意义。 查表得每组字母的表值,得到 4 个二维列向量:
A B C D E F G H I J K L M
44 74 39 72 上面的向量是由 , , , 54 75 30 72
经过模 26 运算
得来的,现在的问题是怎样逆转回去?
在模运算下解方程组: A =
模 m 可逆
记 Zm {0,1, 2,..., m 1}
表值表,得到相应的明文字母
Hill2 解密举例
序 分组 密文 明文 分组 号 密文 表值 表值 明文 1 W 23 7 G K 11 21 U 2 V 22 4 D A 1 9 I 3 C 3 1 A P 16 14 N 4 E 5 13 M A 1 9 I 5 O 15 13 M C 3 1 A 6 I 9 19 S X 24 8 H 序 分组 密文 明文 分组 号 密文 表值 表值 明文 7 G 7 9 I W 23 25 Y 8 I 9 9 I Z 0 0 Z 9 U 21 9 I R 18 6 F 10 O 15 21 U Q 17 23 W 11 W 23 5 E A 1 9 I 12 B 2 10 J A 1 9 I
用 B 左乘密文对应的向量得:
18 34 B , 2 18 13 45 B , 4 36 22 206 B , 23 207 20 180 B 20 180
N O P Q R S T U V W X Y Z 14 15 16 17 18 19 20 21 22 23 24 25 0 注:这里假定明文中只使用 26 个大写字母
Hill2 密码的加密过程
② 选择一个 二阶可逆整数方阵 A,称为Hill2密码的 加 密矩阵,它是加密体制的 “密钥”,是加密的关键,仅 通讯双方掌握。
1 2 3 4 5 6 7 8 9 10 11 12 13 N O P Q R S T U V W X Y Z
14 15 16 17 18 19 20 21 22 23 24 25 0
Hill2 加密过程
明文字母 分组 查表值 左 乘 模运算 反查表值 一组向量 加 密 矩 阵
密文
一组新的向量
问题:怎样解密?
Hill2 解密过程
18 22 13 20 , , , 2 23 4 20
?
8 24 19 24 , , , 18 25 10 24
发送方
发 送
敌方截获 破译
明文(信息)
解密器
密文
接收方
Hill2 密码的加密过程
Hill2 密码中所用的数学手段是 矩阵运算。
加密过程: ① 将汉语拼音的 26 个字母 与 0 到 25 之间的整数建 立一一对应关系,称为字母的 表值,然后根据明文字 母的表值,将明文信息用数字表示。
设通讯双方所给出的 26 个字母的表值如下: A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8 I 9 J K L M 10 11 12 13
解密
明文
密文
明文
问题背景和实验目的
密码可分为古典密码和现代密码
古典密码:以字符为基本加密单元; 现代密码:以信息块为基本加密单元。
本实验主要介绍古典密码的加密与破译原理, 同时介绍如何用 Matlab 编程来实现加密、解密和 破译过程。Fra bibliotek 加密信息传递过程
明文(信息)
加密器
密文 普 通 信 道
B A1 (mod 26)
3 2 1 8 9 (mod 26) 0 1 0 9
18 22 13 20 , , , 2 23 4 20
?
8 24 19 24 , , , 18 25 10 24
模 26 运算后得:
8 24 , , 18 25 查表后得明文分别为: HR XY 19 24 , 10 24
SJ
XX
Matlab 的 Hill2 加密程序见 附录 2,相应解密程序见 附录 3。
Hill2 加密过程总结
数学实验
实验十
密码加密,解密与破译
问题背景和实验目的
