长郡中学理科实验班招生考试—数学试题

合集下载

长郡理科实验班招生考试数学试卷(四)

长郡理科实验班招生考试数学试卷（四）时量：60分钟满分：100分一、选择题（每题5分，共30分）1.已知<COSA<Sin80°，则锐角A 的取值范围是（） A.6080A ︒<<︒ B.3080A ︒<<︒ C.1060A ︒<<︒D.1030A ︒<<︒2.设1x 、2x 是方程20x x k ++=的两个实根，若恰有22211222x x x x k ++=成立，则k 的值为（） A.1-B.12或1-C.12D.12-或13.一名考生步行前往考场，10分钟走了总路程的14，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如右图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了.（）A.20分钟B.22分钟C.24分钟D.26分钟4.内角的度数为整数的正n 边形的个数是（） A.24B.22C.20D.185.如图，已知E 、F 点分别是正方形ABCD 的边AB 、BC 的中点，BD 、DF 分别交EC 于点C 、H ，若正方形ABCD 的面积是240，则四边形BFHG 的面积等于（）A.26B.28C.24D.306.张阿姨准备在某商场购买一件衣服、一双鞋和一套化妆品，这三件物品的原价和优惠方式如下表所示：请帮张阿姨分析一下，选择一个最省钱的购买方案.此时，张阿姨购买这三件物品实际所付出的钱的总数为（） A.500元 B.600元 C.700元 D.800元二、填空题（每题5分，共30分）7.若14x x-=，则2421x x x =++ .8.如右图，圆锥的母线长是3，底面半径是1，A 是底面圆周上一点，从4点出发绕侧面一周，再回到A 点的最短的路线长是 .9.若化简1x -25x -，则x 的取值范围是 .10.方程20x ax b ++=的两根为1x ，2x ，且3322121212x x x x x x +=+=+，则有序实数对(),a b 共有对.11.如右图，直角坐标系中直线AB 交x 轴，y 轴于点()4,0A 与()0,3B -，现有一半径为1的动圆的圆心位于原点处，以每秒1个单位的速度向右作平移运动，则经过秒后动圆与直线AB 相切.12.二次函数22y x ax a =++在12x -≤≤上有最小值4-，则a 的值为 .三、解答题（每题10分，共40分）13.已知,x y 均为实数，且满足17xy x y ++=，2266x y xy +=，求：代数式432234x x y x y xy xy ++++的值.14.在Rt ABC ∆中，90C ∠=︒，直角边BC 与直角坐标系中的x 轴重合，其内切圆的圆心坐标为()0,1P ，若抛物线221y kx kx =++的顶点为A .求：（1）求抛物线的对称轴、顶点坐标和开口方向；（2）用k 表示B 点的坐标；（3）当k 取何值时，60ABC ∠=︒.15.如图，在△ABC 中，AC BC =，CD 是AB 边上的高线，且有23CD AB =，又E ，F 为CD 的三等分点，求证：180ACB AEB AFB ∠+∠+∠=︒.16.已知二次函数2224y x mx m =-+-的图象与x 轴交于A B 、两点（点A 在点B 的左边），且与y 轴交于点D.（1）当点D 在y 轴正半轴时，是否存在实数m ，使得△BOD 为等腰三角形？若存.在，求出m 的值；若不存在，请说明理由；（2）当1m =-时，将函数2224y x mx m =-+-的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象Ω.当直线12y x b =+与图象Ω有两个公共点时，求实数b的取值范围.数学试卷（四）参考答案一、选择题（每题5分，共30分） 1.D 2.A 3.C 4.B. 5.B 6.B 二、填空题（每题5分，共30分）7.1198. 9.14x ≤≤ 10.311.73或17312.5三、解答题（每题10分，共40分）13.解：由已知条件可知xy 和()x y +是方程217660t t -+=的两个实数根， 16t =，261111xy t x y =⎧=⇒⎨+=⎩或116x y xy +=⎧⎨=⎩当11xy =，6x y +=时，x 、y 是方程26110y y -+=的两个根 ∵36440t ∆=-<，∴此方程没有实数根.当6xy =，11x y +=时，x ，y 是方程21160u u -+=的两个根 ∴2121240∆=->，∴此方程有实数根，这时()2222109x y x y xy +=+-= ∴432224x x y x y xy y ++++()()44222222x y x y xy x y xy x y =+++++ ()()2222222x y x y xy x y =+-++12499=14.（1）∵221y kx kx =++，∴.对称轴1x =-，易见抛物线是以Rt △ABC 的直角边AC 所在直线为对称轴，由题易得()1,1A k --，又当0x =时，1y =，则抛物线过()0,1P ，故开口向下.（2）如图，1AC k =-，1BC CO OB OB =+=+，AB AD BD AE OB AC CE OB OB k =+=+=-+=-，由勾股定理得()()()22211111,0111k k k k OB OB k OB OB B k k k ---⎛⎫-++=-⇒=⇒=⇒ ⎪+++⎝⎭（3）∵60ABC ∠=︒，∴tan ABC ∠=又21tan 2k ABC k-∠==210k +-=.∴12k =，22k =-.又∵0k <，∴2k =.15.证明：∵23CD AB =，且,E F 为CD 三等分点，D 为AB 中点， ∴1132CD AB =，即AD DF =，∴45AFD ∠=︒ ∴22222AF AD DF DF FE FC =+==⋅. ∴AFE CFA ∆∆:，∴CAF AEF ∠=∠. 即∴45ACD AED AFD ∠+∠=∠=︒.∴90ACD AED AFD ∠+∠+∠=︒，所以得证.16.解：令0y =得22240x mx m -+-=，解得12x m =-，22x m =+， ∴()2,0A m -，()2,0B m +，()20,4D m -. （1）∵点D 在y 轴正半轴，∴240m ->，设存在实数m ，使得BOD ∆为等腰三角形，则BO OD =，则224m m +=-， ①当20m +>时，242m m -=+，解得3x =或2x =-（舍去）； ②当20m +<时，2420m m -++=，解得1x =或2x =-（都舍去）； ③当20m +=时，点,,O B D 重合，不合题意，舍去；综上所述，3m =，（2）当1m =-时，223y x x =+-，则()3,0A -，()1,0B 顶点为()1,4--. 因为直线12y x b =+与图象Ω由两个公共点，则当直线12y x b =+过A 点准时32b =，当直线12y x b =+过()1,0B 时，12b =-，当直线12y x b =+与223y x x =--+只有一个公共点时，7316b =，根据图像，可得1322b -<<或7316b >.“最湖南的网课”，胡哥与他的朋友们，联合出品。

湖南省长沙市长郡中学高三实验班选拔考试理数试题

湖南省长沙市长郡中学高三实验班选拔考试理数试题比知识你海纳百川，比能力你无人能及，比心理你处变不惊，比信心你自信满满，比体力你精力充沛，综上所述，高考这场比赛你想不赢都难，祝高考好运，考试顺利。

绝密★启用前长郡中学2022～2022学年新高三实验班选拔考试理科数学试卷本试卷分第I卷和第Ⅱ卷两部分，时量120分钟，满分150分第Ⅰ卷（60分）一、选择题（本大题共12小题，毎小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.若复数（其中，为虚数单位）的虚部为1，则A.1B.2C.D.【答案】C【解析】,的虚部为，，故选C.2.已知集合，集合，则A.B.C.D.【答案】B【解析】,,故选B.3.长郡中学要从师生推荐的参加说课比赛的3位男教师和2名女教师中，任选2人参加说课比赛，则选取的2人恰为一男一女的概率为A.B.C.D.【答案】B【解析】由古典概型概率公式，可得选取的人恰为一男一女的概率为，故选B.4.已知等差数列的前项和为，若，则A.23B.96C.224D.276【答案】D【解析】是等差数列，可设首项为，公差为，由，可得，，故选D.5.已知为双曲线的一个焦点，其关于双曲线的一条渐近线的对称点在另一条渐近线上，则双曲线的离心率为A.B.C.2D.【答案】C【解析】设右焦点关于渐近线：的对称点为，则在上交于，由点到直线距离公式可得，为直角三角形，三边分别为，由对称性知，，，故选C.6.下列函数在其定义域上既是增函数又是奇函数的是A.B.C.D.【答案】C【解析】对于.函数是奇函数，在为整数）上递增，则不满足；对于.函数为奇函数，由于，则在上递增，则满足；对于.函数为偶函数，则不满足；对于.函数既不是奇函数，也不是偶函数，则不满足，故选C.7.执行如图所示的程序框图，若输入，则输出的结果为A.7B.9C.10D.11【答案】B【解析】执行程序框图，第一次循环，；第二次循环，；第三次循环，；第四次循环，；结束循环，输出，故选B.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题.解决程序框图问题时一定注意以下几点：(1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构；(3)注意区分当型循环结构和直到型循环结构；(4)处理循环结构的问题时一定要正确控制循环次数；(5)要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.8.若二项式展开式的各项系数之和为，则含项的系数为A.560B.C.280D.【答案】A【解析】因为二项式展开式的各项系数之和为，所以，的通项为，令项的系数为，故选A.9.某几何体的三视图如图，其俯视图中的曲线部分为半圆，则该几何体的体积是A.B.C.D.【答案】C【解析】依题意，由几何体的三视图可知，此几何体为一个直三棱柱和一个半圆柱组成的组合体，且直三棱柱底面为两直角边为和的直角三角形，高为，半圆柱的底面半径为，高为，所以该几何体的体积为，故选C.10.已知椭圆，若直线经过，与椭圆交于两点，且，则直线的方程为A.B.C.D.【答案】B【解析】设直线斜率为，，，由与联立可得，，则，解得，故选B.11.已知三棱锥的每个顶点都在球的表面上，底面，且二面角的正切值为4，则球的表面积为A.B.C.D.【答案】D【解析】设中点为，可得，则是“二面角”的平面角，由于“二面角”的正切值为，，由余弦定理知，，由正弦定理知，外接圆直径，设外接球半径为，则，球的表面积为，故选D.【方法点睛】本题主要考查三棱锥外接球表面积的求法，属于难题.要求外接球的表面积和体积，关键是求出求的半径，求外接球半径的常见方法有：①若三条棱两垂直则用（为三棱的长）；②若面（），则（为外接圆半径）；③可以转化为长方体的外接球；④特殊几何体可以直接找出球心和半径.12.已知函数在区间上有两个零点，则实数的取值范围为A.B.C.D.【答案】A【解析】函数在区间上有两个零点，等价于与的图象有两个交点，设与的图象相切，切点为，则，解得，因为关于的方程，与有两个交点，，故选A.【方法点睛】判断方程零点个数的常用方法：①直接法：可利用判别式的正负直接判定一元二次方程根的个数；②转化法：函数零点个数就是方程根的个数，结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)可确定函数的零点个数；③数形结合法：一是转化为两个函数的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为的交点个数的图象的交点个数问题.本题的解答就利用了方法③.第Ⅱ卷（90分）二、填空题（本大题共4小题，每小题5分，共20分）13.若实数满足，则的最小值为__________．【答案】【解析】画出表示的可行域如图，由图知，直线平移经过点时，有最小值为，故答案为.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.14.设，，且，则__________．【答案】【解析】由，可得，故答案为.15.已知，，则__________．【答案】【解析】，，故答案为.16.在数列中，首项不为零，且，为的前项和．令，则的最大值为__________．【答案】【解析】数列首项，所以数列是公比为的等比数列，，，，所以，设，令,当且时取等号，，即的最大值为，故答案为.三、解答题（本大题共7小题，共70分.解答应写出文字说明、证明过程或演算步骤）17.在锐角中，分别为角的对边，且．（Ⅰ）求的大小；（Ⅱ）若，求面积的取值范围．【答案】(1)；（2）.【解析】试题分析：（Ⅰ）由，根据二倍角的正弦、余弦公式以及辅助角公式化简可得，从而可得结果；（Ⅱ）在中，由正弦定理得，又，∴，∴，又∵，从而可得结果.试题解析：（Ⅰ）∵，∴①，又∵，∴②，又③，将①，②，③代入已知得：，整理得，即，又∵，∴，即．（Ⅱ）由（Ⅰ）得，∴，∵为锐角三角形，∴且，解得，在中，由正弦定理得：，∴，又，∴，∴，又∵，∴．18.如图，在直三棱柱中，，为线段的中点．（Ⅰ）求证：；（Ⅱ）若直线与平面所成角的正弦值为，求的长．【答案】(1)证明见解析；（2）或.【解析】试题分析：（Ⅰ）由直棱柱的性质可得，由等腰三角形的性质可得，由线面垂直的判定定理可得平面，进而由面面垂直的判定定理可得结论；（Ⅱ）以为原点，为轴，为轴，过点平行于的直线为轴建立空间直角坐标系，设，求出平面的一个法向量及，利用空间向量夹角余弦公式可得结果.试题解析：（Ⅰ）∵三棱柱是直三棱柱，∴平面，又平面∴，∵，是的中点，∴，又平面平面，∴平面，又平面，∴．（Ⅱ）由（Ⅰ）知平面，故以为原点，为轴，为轴，过点平行于的直线为轴建立空间直角坐标系（如图所示），设，则，∴，·设平面的一个法向量，则，即，则，令可得，，故，设直线与平面所成角为，则，解得或，即或．。

长郡理科实验班招生考试数学试卷(三)

长郡理科实验班招生考试数学试卷（三）时量：60分钟满分：100分一、选择题（每题5分，共30分）1.下列图中阴影部分面积与算式2131242-⎛⎫-++ ⎪⎝⎭的结果相同的是（）2.对于两个数，200820092009M =⨯，200920082008N =⨯.则（） A.M N = B.M N > C.M N < D.无法确定3.已知1sin cos 8αα⋅=，且4590α︒<<︒，则cos sin αα-的值为（）B. C.34D. 4.如果关于x 的方程2230x ax a -+-=至少有一个正根，则实数a 的取值范围是（）A.22a -<< 2a <≤ C.2a ≤D.2a ≤≤5.向高为H 的永瓶中注水，注满为止，如果注水量V 与水深h 的函数关系的图象如左图所示，那么水瓶的形状是（）6.如图，张三同学把一个直角边长分别为3cm ，4cm 的直角三角形硬纸板，在桌面上翻滚（顺时针方向），顶点A 的位置变化为12A A A →→，其中第二次翻滚时被桌面上一小木块挡住，使纸板一边21A C 与桌面所成的角恰好等于BAC ∠，则A 翻滚到2A 位置时共走过的路程为（）A.B.8πcmC.D.4πcm二、填空题（每题5分，共30分）7.若1x =，则((3221x x x -++的值是 .8.已知⊙O 的半径1OA =，弦AB 、AC 的长分别是、，则BAC ∠的度数是 .9.如图，在Rt ABC ∆中，90BCA ∠=︒，30BAC ∠=︒，6AB =，将ABC ∆以点B 为中心逆时针旋转，使点C 旋转至AB 边延长线上的点C '处，那么AC 边转过的图形（图中阴影部分）的面积是 .10.如图，两个反比例函数1k y x =和2ky x=在第一象限内的图象依次是1C 和2C ，设点P 在1C 上，PC x ⊥轴于点C ，交2C 于点A ，PD y ⊥轴于点D ，交2C 于点B ，则四边形PAOB 的面积为 .11.已知,,a b c 为实数且13ab a b =+，14bc b c =+，15ac a c =+，则abcab bc ca=++ . 12.设1C ，2C ，3C ……为一群圆，其作法如下：1C 是半径为a 的圆，在1C 的圆内作四个相等的圆2C （如图），每个圆2C 和圆1C 都内切，且相邻的两个圆2C 均外切，再在每一个圆2C 中，用同样的方法作四个相等的圆3C ，依此类推作出4C ，5C ，6C …….则（1）圆2C 的半径长等于（用a 表示）；（2）圆k C 的半径为（k 为正整数，用a 表示，不必证明）.三、解答题（13题12分、14题14分、15题14分，共40分）13.设m 是不小于1-的实数，关于x 的方程()2222330x m x m m +-+-+=有两个不相等的实数根1x 、2x ，（1）若22126x x +=，求m 值；（2）求22121211mx mx x x +--的最大值.14.某商场将进价为2600元的彩电以3000元售出，平均每天能销售出6台。

湖南长沙长郡中学初一实验班招生考试数学试题

( )＇ ()( 3 - 2 ) cm ，⊙O 与这两个圆都相切，3 + 2 cm 和12、以 O 为圆心的两个同心圆的半径分别为长郡中学初一理科实验班招生试卷(时量： 60 分钟；满分：100 分注意合理分配时间 )一、选择题：（每个题目只有一个正确答案，每题 6 分，共 36 分）１、平面内有 4 条相交直线，它们的交点最多有 m 个，最少有 n 个，则 m －n=（）A ．7B ．5C ．4D ．3 2、若（x －1）2的算术平方根是x －1，则x 的取值范围是（） A ．x ＜1 B ．x≤1 C ．x ＞1 D ．x≥13、直角三角形纸片的两直角边长分别为 6，8，现将 △ A BC 如图那样折叠，使点 A 与点 B 重合，折痕为 DE ，则 CE 的长为（）CA ．1B ． 2C ．74 D ．32 68E4、下列五个命题：（第 3 题）BA（1）若直角三角形的两条边长为 3 和 4，则第三边长是 5； D（2） a 2 ＝a （a ≥0）；（3）若点 P （a ，b ）在第三象限，则点 P （－a ，－b ＋1）在第一象限；（4）顺次连结对角线互相垂直且相等的四边形各边中点的四边形是正方形；（5）两边及第三边上的中线对应相等的两个三角形全等。

其中正确命题的个数是（） A ．2 个 B ．3 个 C ．4 个 D ．5 个5、已知抛物线 y = x 2 + bx + c 的系数满足 2b - c = 5 ，则这条抛物线一定经过点（)A ． (-2,-1)B ． (-1,-2)C ． (2,-1)D ． (-2,1) 6、关于 x 、y 的方程 x 2+xy+y 2=29 的整数解（x 、y ）的组数为（）A 、2组B 、3组C 、4组D 、无穷多组二.填空题：(每题 5 分，共 30 分)7、观察分析下列数据，寻找规律：已知一列实数１、 5 、3、 13 、 17 、……，则第n 个数是__________； 8、如图所示，菱形 A BCD 边长为 a ，点 O 在对角线 AC 上一点，且 OA=a ，OB=OC=OD=1,则 a 等于（） 9、如图，在 Rt ∆ABC 中，D 为斜边 AB 上一点，AD ＝5，BD ＝4，四边形 CEDF 为正方形，则图中阴影部分的面积为；第 8 题图第 9 题图第 10 题图10、如图 1 所示，在直角梯形 ABCD 中，AB ∥CD ，∠B=90°，动点 P 从点 B 出发，沿梯形的边由 B→C→D→A 运动，设点 P 运动的路程为 △x ， ABP 的面积为 y ，把 y 看作 x 的函数，函数图象如图 2 所示，则△ABC 的面积为111、若不论 x 取何值时，分式总有意义，则 m 的取值范围是_________x 2 - 2 x + m - 32 21则⊙O 1 的半径是（仔细想想）三、解答题（本大题共3题，13、14题11分，15每题12分，共34分）13、某仪器厂计划制造A、B两种型号的仪器共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于制造仪器，两种型号的制造成本和售价如下表：成本（万元/套）售价（万元/套）A2530B2834（1）该厂对这两种型号仪器有哪几种制造方案？（2）该厂应该选用哪种方案制造可获得利润最大？（3）根据市场调查，每套B型仪器的售价不会改变，每套A型仪器的售价将会提高a万元（a>0），且所制造的两种仪器可全部售出，问该厂又将如何制造才能获得最大利润？14、一自行车轮胎，若把它安装在前轮，则自行车行驶5000千米后该轮胎报废；若把它安装在后轮，则自行车行驶3000千米后该轮胎报废，行驶一定路程后可以交换前、后轮胎。

长郡理科实验班招生考试数学试卷(一)

最全长郡理科实验班招生考试数学试卷（一）时量：60分钟满分：100分一选择题（每题5分，共30分）l.已知α为实数，则代数式27−12α＋2a2的最小值为（）A.0B.3C.33D.92.若n为整数，则能使n+1n−1也为整数的n的个数有（）A.1个B.2个C.3个D.4个·3.已知α，b为实数，且αb=1，设M=a a+1+b b+1,N=1a+1+1b+1,则M、N的大小关系是A..M>NB.M=NC.M<N.D.无法确定4.一张圆桌旁有四个座位如图，A,B,C,D四人随机坐在四个座位上，则A与D相邻的概率是（）A.23B12C14 D.295.如图，∠ACB=60°，半径为2的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为（）A.2πB.πC.23D.46.如图，平面中两条直线l1，和l2相交子点0，对于平面上任意一点M，若P,q分别是M到直线l1和l2的距离，则称有序非负实数对（p1,q）是点M的“距离坐标”，根据上述定义，有以下几个结论：①“距离坐标”是（0,1)的点有1个；②“距离坐标”是（5，的的点有4个；③“距离坐标”是（α，α），（α为非负实数）的点有4个．其中正确的有其中正确的有（）A.0个B.1个C.2个D.3个二、填空题（每题5分，共30分）7.已知α，b,C是实数，且α2+6b＝-17,b2+8c=-23,c2+2α＝14，则α＋b+c=.8.已知关于的不等式（2α-b）＞b的解集是棨−12，则a b b+-36a3=.9.对正实数α，b作定义a∗b=ab−a+b，若4*x=44，则x的值是.10.在△ABC中，AB=4C,∠A=45°，AC的垂直平分线分别交AB、AC于D、E 两点，连结CD，如果AD=l，则tan∠BCD的值为.11.已知：如图，在直角△ABC中，AD=DE=EB，且CD2+CE2=1，则斜边AB的长为12.小明、小林和小颖共解出100道数学题，每人都解出了其中的60道，如果将其中只有1人解出的题叫做难题，2人解出的是基叫做中裆题，3人都解出的题叫做容易题，那么难题比容易题多道．三、解答题（每题10分，共40分）13.某商场将进价为2600元的彩电以3000元售出，平均每天能销售出6台．为丁配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种彩电的售价每降低50元，平均每天就能多售出3台．(1）商场要想在这种彩电销售中每天盈利3600元，同时又要使百姓得到最卢大实惠，每台彩电应降价多少元？(2）每告彩电降价多少元时，商场每天销售这种彩电的利润最高？最高利润是多少？14.已知点M,N的坐标分别为（0,1),(0,-1），点P是抛物线y=14x2上的一个动点．（1）求证：以点P为圆心，PM为半径的圆与直线y=-1的相切；（2）设直线PM与抛物线y=14x2的另一个交点为点Q，连接NP、NQ，求证：∠PNM=∠QNM.15、已知关于x的方程（m2−1）x2−33m−1+18=0有两个正整数根（m是整数），△ABC的三边a、b、c满足c=23，m2+a2m−8a=0，m2+b2m−8b=0，求：（1）m的值；（2）△ABC的面积；16.直线y=x−10与x轴交于A点，点B在第一象限，且AB=35，以cos∠OAB=25 (1）若点C是点B关于x轴的对称点，求过0、C、A三点的抛物线的表达式(2）在(1）中的抛物线上是否存在点P(P点在第一象限），使得以点P、0、C、A为顶点的囚边形是梯形？若存在，求出点O的坐标；若不存在，请说明理由．(3）若将点O、A分别变换为点Q(-4m,0),R(6m,0）（m 0且为常数）），设过Q、R两点且以QR的垂直平分线为对称轴的抛物线（开口向上）与y轴的交点为N，其顶点为M，记△QNM的面积为S∆QNM，△QNR的面积为S∆QNR，求S∆QNM:S∆QNR的数学试卷（一）参考答案一、选择题（每题5分，共30分）1.B2.D3.B4.A5.C6.B二、填空题（每题5分，共30分）7.-88.-39.3610.12 11.55312.20三、解答题（每题10分，共40分）13.解：设每台彩电降价x 元（0<x<400），商场销售这种彩电平均每天的利润为y 元，则有y =3000−2600−x 6+=350（x 2−−4000）……………………4分(1）因为要每天盈利3600元，则y=36002−300x −4000=3600所以x 2−300x +2000=0，解得x=100或俨200,又因为要使百姓得到最大实惠，则每台要降价200元．…………………………7分(2)∵y =350x 2−300x −4000=350（x −150）2+3750∴当x=150时，y 取得最大值为3750,所以每台彩电降价150元时，商场的利润最高为3750元．………………10分14.解：（1）设点P 的坐标为（x 0，14x 02），则PM===14x02+1；……………………4分（2）如图，分别过点P，Q作直线y=-1的垂线，垂足分别为H、R，由（1）知PH=PM,MN、QR都垂直于直线y=-1，所以PH//MH//QR，于是QM EN=MP NH,所以QR RN=PH HN,因此，Rt∆PHN∽Rt∆QNM.………………………………9分于是∠HNP=∠RNQ，从而∠PNM=∠QNM。

长郡理科实验班招生考试数学试卷13

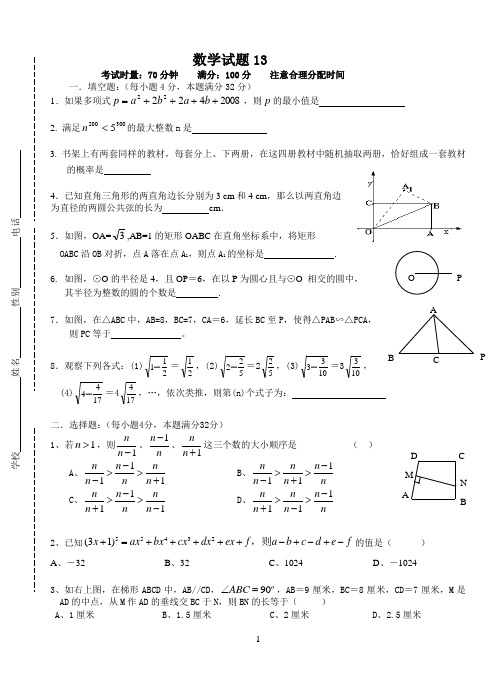
数学试题13考试时量：70分钟满分：100分注意合理分配时间一．填空题：（每小题4分，本题满分32分） 1．如果多项式200842222++++=b a b a p ，则p 的最小值是2. 满足3002005<n的最大整数n 是3. 书架上有两套同样的教材，每套分上、下两册，在这四册教材中随机抽取两册，恰好组成一套教材的概率是4．已知直角三角形的两直角边长分别为3 cm 和4 cm ，那么以两直角边为直径的两圆公共弦的长为 cm ．5．如图，OA=3,AB=1的矩形OABC 在直角坐标系中，将矩形OABC 沿OB 对折，点A 落在点A 1，则点A 1的坐标是 .6. 如图，⊙O 的半径是4，且OP ＝6，在以P 为圆心且与⊙O 相交的圆中，其半径为整数的圆的个数是 .7．如图，在△ABC 中，AB=8，BC=7，CA ＝6，延长BC 至P ，使得△PAB ∽△PCA ，则PC 等于。

8．观察下列各式：(1)21－1＝21，(2)52－2＝252，(3)103－3＝3103，(4)174－4＝4174，…，依次类推，则第(n)个式子为：二．选择题：（每小题4分，本题满分32分） 1、若1n >，则1n n -、1n n -、1nn +这三个数的大小顺序是（）A 、111n n n n n n ->>-+B 、111n n n n n n ->>-+C 、111n n n n n n ->>+-D 、111n n n n n n->>+-2、已知55432(31)x ax bx cx dx ex f a b c d e f +=+++++-+-+-，则的值是（） A 、－32 B 、32 C 、1024 D 、－10243、如右上图，在梯形ABCD 中，AB//CD ，90oABC ∠=，AB ＝9厘米，BC ＝8厘米，CD ＝7厘米，M 是AD 的中点，从M 作AD 的垂线交BC 于N ，则BN 的长等于（） A 、1厘米 B 、1.5厘米 C 、2厘米 D 、2.5厘米 ABC D MN PABCP学校姓名性别电话小朋友，本来你用10元钱买一盒饼干是有多的，但要再买一袋牛奶就不够了！今天是儿童节，我给你买的饼干打9折，两样东西请拿好！还有找你的8角钱. 阿姨，我买一盒饼干和一袋牛奶（递上10元钱）.4、如图，D 是△ABC 的BC 边延长线上一点，且CD ＝BC ，E 是AC 的中点，DE 的延长线交AB 于F ，则DE:EF 等于（）A 、2B 、3C 、32D 、235、已知：在ΔABC 中，∠ACB=90º，∠ABC=15º，AC=1，则BC 的长为（） A 、、2 C 、3 D6、若两个方程20x ax b ++=和20x bx a ++=，则（）A 、 a b =B 、 0a b +=C 、 1a b +=D 、 1a b +=-7、下列说法正确的是（）A 、全等三角形的中线相等；B 有两边对应相等的两个等腰三角形全等；C 、有两边和一角对应相等的两个三角形全等；D 、周长相等的两个等边三角形全等。

长郡理科实验班招生考试数学试卷27

数学试题27时间：75分钟满分：100分一．填空题：（每小题4分，本题满分32分）1．化简：22193m m m -=-+ ;2．人民公园的侧门口有9级台阶，小聪一步只能上１级台阶或２级台阶，小聪发现当台阶数分别为１级、２级、３级、４级、５级、６级、７级……逐渐增加时，上台阶的不同方法的种数依次为１、２、３、５、８、13、21……这就是著名的斐波那契数列．那么小聪上这９级台阶共有种不同方法．3．在△ABC 中，AB 边上的中线CD=3，AB=6，BC+AC=8，则△ABC 的面积为________________ 4．若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .5. 如图，直线PAPB ，是O 的两条切线，A B ，分别为切点，120APB =︒∠，10OP = 厘米，则弦AB 的长为厘米6.一青蛙在如图8×8的正方形（每个小正方形的边长为1）网格的格点（小正方形的顶点）上跳跃，青蛙从点A 开始连续跳六次正好跳回到点A ，则所构成的封闭图形的面积的最大值是________。

7.如图，△ABC 内接于⊙O ，∠A 所对弧的度数为120°.∠ABC 、∠ACB 的角平分线分别交于AC 、AB 于点D 、E ，CE 、BD 相交于点F.以下四个结论：①1cos 2BFE ∠=；②BC BD =；③EF FD =； ④2BF DF =.其中结论一定正确的序号数是8．在直角坐标系中，已知A （1，1），在x 轴上确定点P ，使△AOP 为等腰三角形，则符合条件的点P 共有个二．选择题：（每小题4分，本题满分32分）9. 初三的几位同学拍了一张合影作留念，已知冲一张底片需要0.80元，洗一张相片需要0.35元．在每位同学得到一张相片、共用一张底片的前提下，平均每人分摊的钱不足0.5元，那么参加合影的同学人数( )Ａ．至多６人Ｂ．至少６人Ｃ．至多５人Ｄ．至少５人 10．已知点I 为△ABC 的内心，∠BIC=130°，则∠BAC 的度数是（）。

长郡理科实验班招生考试数学试卷28

数学试卷28时间：75分钟满分：100分一、选择题（每小题4分，共32分）1、当3=x 时，代数式332)1()2(x x -+-的值是（） A 、3B 、321-C 、323-D 、132-2、已知一直角三角形的三边长为a 、b 、c 、∠B ＝90°，那么关于x 的方程0)1(2)1(22=++--x b cx x a 的根的情况是（）A 、有两个相等的实根B 、有两个不相等的实根C 、没有实数根D 、无法确定3、两年期定期储蓄的年利率为2.25％，按国家规定，所得利息要缴纳20％的利息税，王大爷于2002年6月存入银行一笔钱，两年到期时，共得税后利息540元，则王大爷2002年6月的存款为（）A 、20000元B 、18000元C 、15000元D 、12800元4、如图，MN 是⊙O 的直径，若∠A ＝20°，∠PMQ ＝50°，以PM 为边作圆的内接正多边形，则这个正多边形是（）A 、正七边形B 、正八边形C 、正六边形D 、正十边形5、如图，AB=AC ，EA=ED ，∠BAD ＝20°， ∠EDC ＝10°，则∠B 的度数为（）A 、45°B 、50°C 、55°D 、不能确定6、已知非零实数a 、b 满足0122=+-+++b a b ab a ，则ba 11+的值等于（） A 、－1 B 、0C 、1D 、27、若函数|)196100|196100(2122+-++-=x x x x y ，则自变量x 取1,2,3,4,…99,100这100个自然数时，函数值的和为（）AB DCE学校姓名性别联系电话考场号A 、540B 、390C 、194D 、978、设x 1、x 2是方程020*******=+-x x 的两个实根，实数a 、b 满足：2004,200320042200412003220031=+=+bx ax bx ax ，则2005220051bx ax +的值为（）A 、2005B 、2003C 、－2005D 、－2003二、填空题（每小题4分，共32分）9、已知实数a 满足a a-a||=+-20032002，则22002-a 的值为。

长郡中学理科实验班招生考试数学试卷

长郡中学理科实验班招生考试数学试卷满分：100 时量：70min一、选择题（本题有8小题，每小题4分，共32分） 1．函数y ＝1x -图象的大致形状是（）A B C D2．小明随机地在如图所示的正三角形及其内部区域投针，则针扎到其内切圆(阴影)区域的概率为（）A 、21B 、π63C 、π93D 、π33 3．满足不等式3002005<n的最大整数n 等于（）（A ）8 （B ）9 （C ）10 （D ）11 4．甲、乙两车分别从A ，B 两车站同时开出相向而行，相遇后甲驶1小时到达B 站，乙再驶4小时到达A 站. 那么，甲车速是乙车速的（A ）4倍（B ）3倍（C ）2倍（D ）1.5倍 5．图中的矩形被分成四部分，其中三部分面积分别为2，3，4，那么，阴影三角形的面积为（）（A ）5 （B ）6 （C ）7 （D ）86．如图，AB ，CD 分别是⊙O 的直径和弦，AD ，BC 相交于点E ，∠AEC=α，则△CDE 与△ABE 的面积比为（）（A ）cos α （B ）sin α （C ）cos 2α （D ）sin 2α7．两杯等量的液体，一杯是咖啡，一杯是奶油. 舀一勺奶油到咖啡杯里，搅匀后舀一勺混合液注入到奶油杯里. 这时，设咖啡杯里的奶油量为a ，奶油杯里的咖啡量为b ，那么a 和 b 的大小为（）（A ）b a > （B ）b a < （C ）b a = （D ）与勺子大小有关8．设A ，B ，C 是三角形的三个内角，满足B C B A 23,53<>，这个三角形是（）（A ）锐角三角形（B ）钝角三角形（C ）直角三角形（D ）都有可能二、填空题（本题有6小题，每小题5分，共30分）9．用数字1，2，3，4，5，6，7，8不重复地填写在下面连等式的方框中，使这个连等式成立：1＋□＋□=9＋□＋□=8＋□＋□=6＋□＋□10．如图，正三角形与正六边形的边长分别为2和1，正六边形的顶点O 是正三角形的中心，则四边形OABC 的面积等于 ______ . 11．计算：622633++++= ________ .yxOy xOy xOyxO……………..………….密………………..…………….封……………………………..线…………………….12．五支篮球队举行单循坏赛（就是每两队必须比赛1场，并且只比赛一场），当赛程进行到某天时，A 队已赛了4场，B 队已赛了3场，C 队已赛了2场，D 队已赛了1场，那么到这天为止一共已经赛了 __ 场，E 队比赛了 ___ 场.13．已知∠AOB=30°,C 是射线OB 上的一点，且OC=4，若以C 为圆心，半径为r 的圆与射线OA 有两个不同的交点，则r 的取值范围是_____________ 14．如图，△ABC 为等腰直角三角形，若AD=31AC ，CE=31BC ，则∠1 __ ∠2 （填“>”、“<”或“=”）三．解答题（共38分） 15. （１２分）今年长沙市筹备60周年国庆，园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A B ，两种园艺造型共50个摆放在五一大道两侧，已知搭配一个A 种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B 种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A 种造型的成本是800元，搭配一个B 种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？１６．（１２分）如图，ABC △是O 的内接三角形，AC BC =，D 为O 中AB 上一点，延长DA 至点E ，使CE CD =．（1）求证：AE BD =；（2）若AC BC ⊥，求证：2AD BD CD +=．（第14题）ＥＡＯＢ１７．（１４分）如图，在等腰梯形ABCD中，AD∥BC，AB=DC=50，AD=75，BC=135．点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动，过点Q向上作射线QK⊥BC，交折线段CD-DA-AB于点E．点P、Q同时开始运动，当点P与点C重合时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒（t＞0）．（1）当点P到达终点C时，求t的值，并指出此时BQ的长；（2）当点P运动到AD上时，t为何值能使PQ∥DC ？（3）设射线QK扫过梯形ABCD的面积为S，分别求出点E运动到CD、DA上时，S与t的函数关系式；（不必写出t的取值范围）（4）△PQE能否成为直角三角形？若能，写出t的取值范围；若不能，请说明理由．参考答案选择题 D C D C C C C B 9． 110．33 11． 26 12． 6场，2场 13．2r <≤ 14．＝1５．（１）解：设搭配A 种造型x 个，则B 种造型为(50)x -个，依题意，得：8050(50)34904090(50)2950x x x x +-⎧⎨+-⎩≤≤ ，解这个不等式组，得：3331x x ⎧⎨⎩≤≥，3133x ∴≤≤ x 是整数，x ∴可取313233，，，∴可设计三种搭配方案： ①A 种园艺造型31个 B 种园艺造型19个 ②A 种园艺造型32个 B 种园艺造型18个 ③A 种园艺造型33个 B 种园艺造型17个．（2）应选择方案③，成本最低，最低成本为42720元１６．证明：（1）在ABC △中，CAB CBA ∠=∠．在ECD △中，CAB CBA ∠=∠．CBA CDE ∠=∠，（同弧上的圆周角相等），ACB ECD ∴∠=∠． ACB ACD ECD ADE ∴∠-∠=∠-∠．ACE BCD∴∠=∠．在ACE △和BCD △中，ACE BCD CE CD AC BC ∠=∠==；； ACE BCD ∴△≌△．AE BD ∴=．（2）若AC BC ACB ECD ∠=∠⊥，．9045ECD CED CDE ∴∠=∴∠=∠=，． DE ∴=，又AD BD AD EA ED +=+=AD BD ∴+=１７．解：（1）t =（50＋75＋50）÷5=35（秒）时，点P 到达终点C ．此时，QC=35×3=105，∴BQ 的长为135－105=30．（2）如图8，若PQ ∥DC ，又AD∥BC ，则四边形PQCD 为平行四边形，从而PD=QC ，由QC=3t ，BA+AP=5t 得50＋75－5t=3t，解得t=1258．经检验，当t=1258时，有PQ ∥DC ．（3）①当点E 在CD 上运动时，如图9．分别过点A 、D 作AF ⊥BC 于点F ，DH ⊥BC 于点H ，则四边形 ADHF 为矩形，且△ABF ≌△DCH ，从而FH= AD=75，于是BF=CH=30．∴DH=AF=40．Q CDH=4t．又QC=3t，从而QE=QC·tanC=3t·CH（注：用相似三角形求解亦可）QE·QC=6t2；∴S=S⊿QCE =12②当点E在DA上运动时，如图8．过点D作DH⊥BC于点H，由①知DH=40，CH=30，又QC=3t，从而ED=QH=QC－CH=3t－30．(ED＋QC)DH =120 t－600．∴S= S梯形QCDE =12（4）△PQE能成为直角三角形．。

2022年湖南省长沙市长郡实验中学初升高理科实验班数学训练题(原启航杯)

英语试卷满分：100分时量：50分钟一、单项选择（每题2分，共60分）1.—Is dictionary on the desk yours?—No,I don’t have English—Chines dictionary.A.the;anB.an;theC.an;anD.the; the2.—How many friends will come to your birthday?—About.A.fifteen;fifteenB.fifteenth;fifteenthC.fifteenth;fifteenD.fifteen;fifteenth3.The old man used to in the countryside,but now he is used to in the big city.A.living;liveB.live;liveC.live;livingD. living;living4.—Simon,do you fell like basketball or football?—is OK.I heave a lot of homework to do.A.to play;NetherB.playing;BothC.to play;BothD.playing;Neither5.I listened to a CD Heart Strings.sB.callingC.calledD.of the name6.The problem is so difficult that students can work it out.A.a fewB.a littleC.fewD.little7.Lingling has gone to England for a English course.A.six monthB.six monthsC.six—mothD.six —month8.The weather in Beijing is colder than.A.GuangzhouB.in GuangzhouC.that in GuangzhouD.it in Guangzhou9.The teacher asked the boys on the wall.A.to not drawB.don’t drawC.not draw toD.not to draw10.Did you know in the past?A.which subject did Ted like bestB.which subject Ted likes bestC.which subject Ted liked bestD.which subject does Ted liked best11.—How about going hiking this weekend?—Sorry,I prefer rather than.A.to stay at home,go outB.to go out,stay at homeC.staying at home,go outD.going out,stay at home12.Can you provide us some information the computer?A.for,withB.with,aboutC.about,withD.with, with13.—I hope play soccer with us tomorrow.—Yes,I hope.A.him not to,not tooB.he won’t,it tooC.him not to,that tooD.he won’t,so too14.The two men walked the forest and got to a small house.A.acrossB.throughC.crossingD.over15.It took people the work.A.hundreds of,finishingB.hundred of,to finishC.hundreds of,to finishD.hundred of,finishing16.They were when they heard the news.A.excited,excitingB.exciting,excitedC.excited,excitedD.exciting,exciting17.Not only I but also he helpful to others.A.amB.isC.areD.be18.—I’m sorry to keep you waiting.—Oh,not at all.I here for only a few minutes.A.wasB.isC.have beenD.had been19.Now I spend time what I have to do.A.to doB.doingC.doD.did20.—Didn’t he go home last Sunday?—.A.Yes,he didB.No,he didC.Yes,he didn’tD.No,he doesn’t21.on real ice is very exciting.A.SkateB.SkatesC.SkatedD.Skating22.the students in the primary school is about three thousand,and of them are girls.A.A number of,two thirdB.The number of,two thirdsC.A number of,two thirdD.The number of,two third23.All the books will to the children who live in the small village.A.be sentB.sentC.be sendD.send24.Jack leave his teacher comes back.A.doesn’t,untilB./,untilC.won’t,.D.won’t,until25.I study math by lots of exercises.A.didB.doingC.doD.to do26.September10th is the.A.Children’s DayB.Children DayC.Teachers’DayD.Teacher’s Day27.—Jim enjoys listening to pop music.—.A.So does HelenB.Also is HelenC.Helen likes alsoD.So Helen does28.He doesn’t do his homework,though he has.A.careful enough,enough timeB.enough carelessly,time enoughC.carefully enough,enough timeD.enough carefully,enough time29.—May I go swimming now?—No,you.You must finish your homework first.A.mustn’tB.may notC.couldn’tD.needn’t30.—What’s the matter?—They said I should not be allowed here.They don’t allow in the waiting room.A.smoking,to smokeB.to smoke,smokeC.to smoke,smokingD.smoking,smoking二、完型填空（每题2分，共40分）(A)Mary did not31such sentences as“She is blue today.”,“You are yellow.”,“He has a32thumb(大拇指).”,“He has told a little white lie.”,and so on.And she went to her teacher33help.“Mrs.Smith,there is a34in each of these sentences.What do they mean?”she asked.“In35English,Mary,blue36means sad.Yellow—afraid.A person37a green thumb grows plants well and a white lie is not a bad one,”the teacher said.“Would you give me an38for a white lie,teacher?”“Certainly.Now I give you a cake.In fact you don’t like it,but you won’t say it. 39you say,‘No,thanks,I’m not40.’That’s a white lie.”()31.A.know B.understand C.read D.see()32.A.blue B.yellow C.white D.green()33.A.for B.to C.with D.by()34.A.word B.color C.mistake D.question ()35.A.today mon C.everyday ual()36.A.sometimes B.some times C.sometime D.some time ()37.A.to B.with C.of D.at()38.A.answer B.book C.question D.example ()39.A.And B.Instead C.But D.Also()40.A.ill B.happy C.full D.hungry(B)Han Meimei is a hard—working student.She can41English very well because she works hard at it.One day,her teacher,Mr Wu,asked her to come to the office.“Meimei,there42a story—telling contest next week.”He says.“Would you like to take part in it?”“What shall I have to do do,Mr Wu?”asks Meimei.“You’ll have to tell an English story in front of the whole school.If you tryyour best,43you’ll win,”said her teacher.“All right.I’ll try,”said Meimei.On Sunday night she went to bed late to get her story ready for the contest.It was 44interesting story.Meimei didn’t go to bed until midnight.On45morning she got up late.When she46it was already seven o’clock.She washed quickly.Then she had a quick breakfast.After that she ran all the way to school.When she got to school,Mr Wu47for her outside of the school building, and he looked48.“Why are you so49?”he asked.“Sorry,Mr Wu.I woke up late.”Meimei said.“The contest will begin in a minute.Remember to speak slowly and clearly.”Mr Wu said.Meimei kept his words.She told her story very well.In the end she came in first.“You’ve done very well.50!”said Mr Wu.()41.A.say B.talk C.tell D.speak()42.A.will have B.will be C.is D.has()43.A.I’m sorry B.I’m afraid C.I’m glad D.I’m sure ()44.A.an B.a C.the D./()45.A.Sunday B.Monday C.Tuesday D.Wednesday ()46.A.got up B.wakes C.woke up D.goes up()47.A.waits B.is waiting C.was waiting D.wait ()48.A.worried B.worry C.happy D.tired ()49.A.early te ter D.earlier ()50.A.Bad luck B.Congratulation C.OK D.Well答案1-5ACCCC6-10CCCDC11-15ABDBC16-20ABCBA21-25DBADB26-30CACAC31-35BDABC36-40ABDBD41-45DBDAB46-50CCABB。