机械动力学
机械动力学

…………………② …………………③ 阻力(矩)不变。
M r0 r M d d
0 Md Md
=
不计摩擦驱动力(矩)
计摩擦驱动力(矩) 计摩擦阻力(矩)
Mr = 0 Mr
不计摩擦阻力(矩)
驱动力(矩)不变。
第四节 刚性转子的平衡设计
1.静平衡设计(D/b5)
o表征几何形状对摩擦力的影响。
θ
Q
θ
N 21 2
②
N 21 2
①
3)o 总汇 (1) 简单平面移动副
o =
N21
v12 P
f21 1 2 Q
3)o 总汇
(2) V形槽移动副
Q
o=/sin
θ
θ
N 21 2
②
N 21 2
①
3)o 总汇
比较槽面摩擦:o=/sin
(3) 三角螺旋副 Q
34
FR R32
1 4
2
R41
R43
R12
21 23
Md R41
2
R43
FR
1
4
3 V34
R32
【教师例7-2】图示平底摆动从动件盘状凸轮机构的 凸轮为圆盘,摩擦圆、摩擦角、驱动力矩Md、阻力FR 如图所示。试画出图示机构的静力分析图。
【解】 R12 2 R32 FR
1、Md
二、单自由度系统等效力学模型的建立 1.建立系统运动方程 建立依据: dE dW Ndt
1 1 1 1 2 2 2 2 J J m m E S1 1 S2 2 2 S2 3 S3 2 2 2 2 N M d 1 m2 g S 2 cos Fr S 3
机械动力学课程教学大纲

机械动力学课程教学大纲一、课程简介机械动力学是机械工程中的重要基础课程之一,主要研究物体的运动规律和动力学原理。
本课程旨在培养学生对物体运动的分析和动力学理论的理解能力,为学生提供运动学和动力学的基础知识,为他们今后的学习和研究奠定牢固基础。
二、教学目标1. 培养学生对物体运动的观察和分析能力;2. 熟悉运动学和动力学的基本概念和原理;3. 掌握常见的力学定律和公式;4. 培养学生的问题解决能力和实践能力;5. 培养学生的团队合作能力和沟通能力。
三、教学内容1. 运动学基础1.1 位置、位移和速度1.2 加速度和曲线运动 1.3 圆周运动和角速度1.4 相对运动2. 动力学基础2.1 牛顿运动定律2.2 动量和动量守恒2.3 力和加速度2.4 动能和功2.5 能量守恒和机械能3. 静力学3.1 弹簧力和弹性势能 3.2 引力和万有引力定律3.3 惯性力和离心力4. 动力学4.1 圆周运动的力学分析4.2 非惯性系和转动惯量4.3 力矩和角动量4.4 角动量守恒和刚体转动4.5 飞行器的运动学和动力学四、教学方法1. 讲授理论知识:通过课堂讲解、示范等方式,向学生介绍理论知识和基本概念。
2. 实验教学:设计相关实验,让学生进行实验操作和数据分析,提高他们的实践能力。
3. 小组讨论:设置小组活动,让学生在团队中合作解决问题,培养团队合作和沟通能力。
4. 课堂练习:布置课后作业和练习题,加强对知识的巩固和运用能力。
五、考核方式1. 平时表现(20%):包括课堂参与、作业完成情况等。
2. 实验报告(30%):根据实验要求撰写实验报告并提交。
3. 期中考试(20%):考察对课程内容的理解和掌握程度。
4. 期末考试(30%):综合考察整个课程的学习成果。
六、参考教材1. 赵凤岐,机械动力学,高等教育出版社,2015年。
2. 谢振波,机械力学基础,清华大学出版社,2013年。
七、参考网址无。
八、备注本课程的教学大纲可根据实际教学需求进行调整和补充,以确保教学内容的连贯性和可操作性。
机械动力学分析

机械动力学分析机械动力学是研究物体受到外力作用时的运动规律和力学性质的学科。
它对于机械设计和工程分析非常重要。
本文将对机械动力学的基本概念、分析方法和实际应用进行详细探讨。
第一部分:机械动力学基础1.运动和力学运动是物体的位置随时间变化的过程。
力学是研究物体运动和力之间关系的学科。
在机械动力学中,重要的概念包括位移、速度、加速度和质量等。
2.牛顿定律牛顿定律是机械动力学的基石。
根据牛顿定律,物体受到的合力等于物体质量乘以加速度。
这个定律适用于解决物体在恒力作用下的运动问题。
3.动力学原理动力学原理描述了物体在受到外力作用时的运动规律。
其中,动量守恒原理和能量守恒原理是常用的分析工具。
动量守恒原理指出,在没有外力作用的情况下,物体的动量保持不变。
能量守恒原理指出,在封闭系统中,能量的总量保持不变。
第二部分:机械动力学分析方法1.静力学分析静力学是机械动力学的基础。
它研究物体在平衡状态下的受力和受力转矩。
静力学分析常使用受力图和受力平衡方程来求解。
2.运动学分析运动学研究物体的运动状态,包括位置、速度和加速度等。
运动学分析常使用位移、速度和加速度的关系式进行计算。
3.动力学分析动力学分析研究物体在受力作用下的运动规律。
它涉及物体的质量、力、加速度和位移等参数的计算。
常见的动力学分析方法包括牛顿第二定律、动量守恒和能量守恒的应用。
第三部分:机械动力学的实际应用1.机械设计机械动力学分析在机械设计中起着重要的作用。
通过对机械系统的动力学分析,可以评估机械的工作性能和可靠性,优化设计方案,减少能量消耗和材料使用等。
2.工程分析机械动力学分析在工程领域中广泛应用。
例如,在桥梁设计中,需要对桥梁受力和振动进行动力学分析,以保证结构的安全性和可靠性。
在汽车工程中,需要对汽车的运动性能和悬挂系统进行动力学分析,以提高驾驶舒适性和行驶稳定性。
3.故障诊断与维修机械动力学分析可以用于故障诊断和设备维修。
通过对受损机械的动力学分析,可以确定故障原因,并采取相应的维修措施。
第7章机械动力学
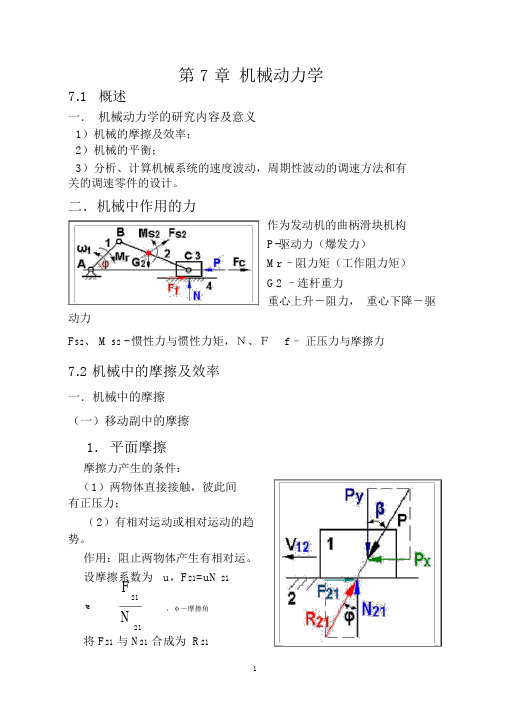
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
机械动力学

机械动力学Copyright @ 2009 HRBEU 702All Rights Reserved绪论一、机械动力学性质1.机械:机构、机器的总称。
(机械原理)2.动力学:研究刚体运动及受力关系的学科。
动力学正问题—已知力(力矩)求运动;动力学反(逆)问题—已知运动求力(力矩)。
机械动力学:是研究机械在力作用下的运动、机械在运动中产生的力(力矩)的科学。
F ma=例:机构组成性质:曲柄、急回。
若已知力(力矩),当机构处于平衡状态时,求力矩(力)--机械静力学问题。
若已知M、F,求ω、v 时—机械动力学。
ωM Fv二、机械动力学研究内容1. 描述机械有那些基本参数1)机构参数:几何参数(杆长);物理参数(质量m,转动惯量J)。
2)运动参数:转角θ、ω、α、s、v、a。
3)力矩M、力F。
2. 内容1)已知机械的物理、几何参数进行动力学分析。
a、已知力求运动;b、已知力求运动。
可表示为:2)已知运动、受力求结构这是机械设计研究问题,一般实际做法是先设计后校核,少数情况是直接求设计参数。
例:(,)(,,,,,,)f F Mg l m J v a ωαZZ X YZ Z q求支点最佳位置。
如果梁静止为静力学问题;如果梁有惯性运动为动力学问题。
3)具体章节内容单自由度运动学方程的建立二自由度运动学方程的建立,如差动轮系、五杆机构多自由度运动学方程的建立,如机械手臂、机器人等理想情况下(无摩擦变形等)考虑摩擦,如铰链、关节处摩擦考虑弹性变形,如杆变形、并联柔性机器人变质量问题,如推土机工作过程、火箭发射过程有间隙情况下动力学研究,不详讲述三、研究对象--以机械为研究对象三大典型机构连杆机构凸轮机构齿轮机构组合机构四、其它1.学习机械动力学目的、意义学习动力学分析问题的思想和基本方法,能够解决一般动力学问题。
2.教材(见前言)3.考核方式开卷。
§1-1 利用动态静力法进行动力学分析一、思路动静法:根据达朗贝尔原理将惯性力计入静力平衡方程,求出为平衡静载荷和动载荷而需在原动件上施加的力(力矩)。
机械动力学动力分析原理

机械动力学动力分析原理机械动力学是力学的一个重要分支,研究机械系统在外力作用下的运动规律。
在机械系统的设计、制造和优化过程中,动力分析起着重要的作用。
动力分析主要是指通过计算和分析力学参数,来研究机械系统的运动学特性、力学特性和动力学特性。
本文将介绍机械动力学动力分析的基本原理。
一、动力学基本概念在进行机械动力学动力分析之前,我们首先要了解一些基本概念。
1. 动力学:研究物体的运动是如何受到力的作用而改变状态的学科。
2. 动力学分析:通过对机械系统的力学参数进行计算和分析,以研究机械系统的运动规律和力学特性。
3. 动力:物体改变其状态所受到的力。
4. 动力学平衡:在机械系统中,当物体的运动状态不发生变化时,称为动力学平衡。
5. 力矩:力在力臂上的作用产生的力矩。
6. 动力矩:力矩与角速度的乘积,反映了物体绕固定轴旋转的难易程度。
二、动力分析的原理机械动力学动力分析的原理主要基于牛顿第二定律和动量定理。
1. 牛顿第二定律牛顿第二定律是机械动力学的基础,表明物体的加速度与作用力成正比,与物体的质量成反比。
在直线运动中,牛顿第二定律可以表达为F=ma,其中F是物体所受的合外力,m是物体的质量,a是物体的加速度。
在旋转运动中,牛顿第二定律可以表达为τ=Iα,其中τ是物体所受的合外力矩,I是物体的转动惯量,α是物体的角加速度。
2. 动量定理动量定理表明,当物体所受的合外力矩为零时,物体的角动量守恒。
动量定理可以表达为Στ=0,其中Στ是物体所受的合外力矩。
三、动力分析的应用机械动力学动力分析的应用非常广泛,涉及到各种机械系统的设计和优化。
1. 运动学分析通过对机械系统的运动学参数进行计算和分析,可以了解机械系统的运动规律和运动状态。
例如,可以计算机械系统的速度、加速度和位移等参数。
2. 力学分析通过对机械系统的力学参数进行计算和分析,可以了解机械系统所受的各种力和力矩的大小和方向,从而为机械系统的设计提供依据。
机械动力学

机械动力学
机械动力学是一种力学分支,用来研究物体的运动规律。
机械力学的基本原理是,物体受力时要考虑它的动量、势能和力学运动状态。
机械力学研究物体受力后,如何协调运动以实现力学系统的最终目标。
机械动力学的基本方程是力学平衡方程,它描述了物体在力学运动中,受力的情况下,动能、势能和运动状态变化的情况。
力学平衡方程主要由三个部分组成:力学定制、力学规律和力学流形。
力学定制是机械动力学的基本原理,它涉及物体的力学变化,包括物体的运动状态、势能和动能。
力学定制可以用来计算物体受力时,各变量的变化速率。
力学规律是机械动力学的第二个基本原理,它涉及物体在力学运动中受力所产生的力学变化。
力学规律具体表示为:物体受力时,质量、动量、势能和动能会发生变化。
力学流形是机械动力学的第三个基本原理,它涉及物体在力学运动中受力的情况下,力学参数的变化。
力学流形是由力学规律的积累,它可以提供物体在各种力学变化状态下的精确的运动状态。
机械动力学是一种比较复杂的力学,研究不仅仅限于物体受力时的运动状态,还可以涉及力学设计与分析、力学模拟、力学断裂以及力学仿真等方面。
它可以帮助科学家们深入了解物体运动规律,为人们在有限工作环境中分析残缺机械参数提供技术支持,实现更加省力、精确且有效的力学分析。
在当今社会,机械动力学已成为一门重要的科学,广泛应用于工
程设计、航天技术、发动机技术、精密仪器等领域。
未来,机械动力学将继续发挥重要作用,在复杂的工程设计及技术开发过程中,与其他科学形成有机结合,以实现精确、有效的力学应用。
机械工程中的机械动力学分析

机械工程中的机械动力学分析机械动力学是机械工程中的一门重要课程,它主要研究机械系统的运动规律、力学特性和动力学特性等问题。
从广义上讲,机械动力学可以分为静力学和动力学两部分,其中静力学研究机械系统在静止状态下的受力情况和平衡条件,而动力学则研究机械系统在运动状态下的运动规律和动力学特性。
本文将针对机械动力学中的动力学部分进行分析和讨论。
一、机械系统的运动规律机械系统的运动规律可以通过牛顿第二定律和角动量定理来描述。
牛顿第二定律表明,机械系统受到的合外力等于其质量乘以加速度,即F=ma。
对于刚性物体,牛顿第二定律可以表示为:ΣF=ma其中ΣF表示作用在物体上的合力,m表示物体的质量,a表示物体的加速度。
在运用牛顿第二定律求解机械系统运动规律时,需要根据实际情况选择适当的坐标系,并建立相应的运动方程。
角动量定理则是描述旋转运动的重要定律。
对于刚性物体的旋转运动,它的角动量可以通过以下公式来计算:L=Iω其中,L表示角动量,I表示物体的转动惯量,ω表示角速度。
根据角动量定理,系统中的合外力矩等于角动量的导数,即M=dL/dt通过角动量定理可以求解物体在旋转运动中的角加速度和角速度等参数。
二、力学特性的分析在机械动力学中,机械系统的力学特性包括弹性变形、破坏和能耗等方面。
弹性变形是机械系统在受到外力作用时,发生一定程度的形变而能够恢复原状的特性。
破坏是机械系统在受到过大的外力作用时,无法再恢复原状的特性。
能耗则是机械系统在运动或变形过程中所消耗的能量。
机械系统的弹性变形特性可以采用胡克定律来描述。
根据胡克定律,弹性形变发生时的应变与应力成线性关系。
对于一维弹性形变的情况,胡克定律可表示为:σ=Eε其中,σ表示应力,E表示弹性模量,ε表示应变。
胡克定律可以用来计算机械系统的弹性变形量。
机械系统的破坏特性可以采用强度学说来描述。
强度学说认为,在机械系统被外力破坏之前,其受到的最大应力应小于其材料的屈服强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现状:
对特征值和特征向量灵敏度的计算方法日趋成熟,采 用约束变尺度法和信赖域法求解复杂结构固有特性设计 引出的优化问题取得一系列成功,解决了有多阶固有频 率和振型要求的复杂结构设计问题,并应用于飞机颤振 模型、体育馆风洞模型等复杂结构的设计。
动响应设计
设计目标: 谋求给定激励下系统的最优动响应。 线性时不变系统
3.1.3 动力学设计
动力学设计的任务
在机械产品的设计阶段,根据给定的动 力学环境,按照功能、强度等方面的要求设 计产品,使其有良好的动态特性,达到控制 振动水平的目的。在研究内容上,动力学设 计可分为系统固有特性设计和动响应设计。
固有特性设计
(线性时不变系统) 方法:
从数学角度看,这是一逆特征值问题,只有在Jacobi 矩阵等特殊情况下可直接求解。对于实际工程问题,通 常将逆特征值问题表述为优化问题,求取某种范数下的 最优解。如果采用基于目标函数梯度的优化方法,还需 解决特征值和特征向量灵敏度的计算问题。
3.1.2 动力学分析
复杂机械系统动力学的数值模拟 非线性系统动力学 周期时变系统动力学
复杂机械系统动力学的数值模拟
描述复杂机械系统的最普适模型是多柔体系统, 其动力学方程可以是常微分方程,也可以是微分 代数方程。系统动力学数值模拟归结为高效、高 精度地求解这两类方程。近年来,有不少研究致 力于改进已有的数值计算方法,提高其计算效率、 鲁棒性等。此外,发展了一系列数值方法直接计 算系统平衡点、周期运动,分析其稳定性、分叉 和混沌特征。
已可导出了任意确定性激励和平稳随机激励下系统响应 关于设计变量的灵敏度,可采用优化方法解决动响应设计问 题。对于弹性连杆机构,引入KED分析中的瞬时结构假设, 也可采用灵敏度分析方法对其进行动态设计。
快时变线性系统和非线性系统
这方面的研究还非常初步。以非线性系统的动力学设计为 例,现有研究多基于正问题近似解对参数的依赖关系,通过 奇异性理论来定性找出所需的系统参数。
多刚体系统动力学建模
多柔体系统的建模
3.1.1 动力学建模
由于机械系统中普遍存在间隙、单侧约束, 近年来许多研究集中在数值模拟多体间的接触 与碰撞。
对于多柔体系统碰撞问题,一般沿用处理刚体碰撞 对于多刚体系统的二维接触/碰撞问题,基于互补 问题的方法,利用动量平衡法或引入等效弹簧和阻 约束条件的算法已经成熟。近期研究主要针对三维 尼描述柔体碰撞时的变形和能耗。由于对柔体碰撞 接触和计入摩擦的碰撞问题。 进行精细建模需要计入应力波在柔体中的传播,目 前尚限于对个案进行研究。
3.2
若干重要分支
转子动力学 齿轮传动系统动力学 弹性机构动力学 车辆动力学 微机电系统动力学 机械故障诊断
转子动力学存在的主要问题
轴承动力学 转子系统稳定性 转子动力学的主动转子动力学
齿轮传动系统动力学主要问题
周期时变系统动力学
现状: 新进展: 问题:
许多机械系统的动力学模型归结 为周期时变系统,并可简化为线 近年来,基于移动 上述各种近似方法虽各有 Chebyshev多 性周期时变系统。尽管线性周期 项式拟合成为一种引人注目的有 所长,但在对高维周期时 时变系统的稳定性理论早已成熟, 效计算方法。此外,还有学者基 变系统的处理上仍存在着 但真正解决实际问题却困难重重, 于 Poincaré映射理论提出了分析 相当大困难,因而对实际 其根本原因是只有极少数简单特 周期时变系统稳定性与分叉的新 具有周期运动特征的机械 殊的系统能求得解析的单值矩阵。 方法,提出了周期时变系统的广 系统动态分析和设计仍缺 其方法有: Hill法、摄动法、分 乏强有力的理论指导。 义频响函数法。 段常值法。
系统建模
各种耦合振动问题
非线性动力学分析 振动与噪声控制
弹性机构动力学主要问题
动力学建模与数值模拟
动力学设计
间隙问题 振动控制
车辆动力学主要问题
高速列车的动力学设计 高速受流系统动力学
汽车动力学的综合
微机电系统动力学主要问题
多学科耦合的大规模动力学模拟 尺度效应分析 非线性动力学分析 纳米机械的动力学模拟
机械故障诊断主要问题
特征提取方法
有针对性的故障诊断方法 专家系统 远程诊断系统
4.机械动力学学会 (中国)
几十位曾参加从"文革"末期开始到1980年基本结束的全 国三十九所重点院校机制专业教材联编工作的中年教师,为 了推进当时刚刚兴起的机床动力学学科的教学和科研工作, 发起筹建《全国高校机床动力学研究会》。1981年4月在昆 明召开了《全国高校机床动力学研究会》成立大会,推选出 研究会的第一届领导机构,由全国著名的机械振动专家屈维 德教授出任领导小组组长。一年半后,随即在杭州召开了 《全国高校机床动力学研究会》第二次代表大会暨第一年学 术年会,与会代表达200多名。1985年10月在屯溪举行了第 三次代表大会暨第二届学术年会,经代表讨论决定,研究会 正式改名为《中国机械动力学研究会》。到1986年5月,中 国振动工程学会成立后,机械动力学研究会集体加入中国振 动工程学会,成为她的一个分会,即《中国振动工程学会机 械动力学学会》,一直至今,已整整走过了二十年的历程。
机械动力学
绪论
1. 概念 运动学(kinematic)
动力学(dynamic)
2. 研究的意义
现代机械发展呈:
高速化、轻量化、精密化趋势
振动与噪声 机械弹性 动力学 机械动态特性 动态定位精度
3.研究的现状及存在的问题
3.1 一般性理论和方法的进展
3.2 若干重要分支的进展与问题
3.1一般性理论和方法的进展
实验建模
目的: 现状: 发展:
线性时不变系统的实验建模已比 较成熟,研究重点已转向线性时 非线性动力学的发展不断为非 确定机械系统中一些难 变系统和非线性系统。过去,一 线性系统的实验建模技术提供 以由理论分析得到的复 般通过对实验数据进行曲线或曲 新概念和新方法。例如,相空 杂因素,如系统阻尼、 面拟合来确定间隙、摩擦等非线 间重构、分维数、时间序列的 约束和支撑处的间隙和 性因素。近年来,则将动力学反 Lyapunov 算法使得有可能从实 摩擦、一些作动器的输 问题表述为优化问题,采基因算 验数据提取出描述无限维系统 入输出关系、控制环节 法、模拟退火算法等全局优化技 非线性动力学的最低维数和降 的时间滞后等,是典型 术来解决,或采用各种神经网络 阶模型 . 的动力学反问题。 来逼近原系统的动力学模型。
3.1.4 振动控制
现状及进展:
振动主动控制技术最引人注目的进展是集传感器、控 制器、作动器与结构为一体的智能结构。研究的热点是 基于压电传感器和作动器的智能结构,控制策略则来自 自适应控制、神经网络控制、非线性控制、混合控制等 控制理论的新成果。非线性控制和时滞控制正日益引起 人们的注意。由于振动半主动控制技术具有能耗低、勿 需对原系统作大修改等优点,近年来日益得到人们关注。
5. 动力学分析方法
功 能
动力学正问题(Forward Dynamics) 动力学反问题 (Inverse Dynamics)
静力分析(Static Analysis) 水 平 动态静力分析(Kineto-Static Analysis)
动力分析(Dynamic Analysis)
弹性动力分析(Elasto-Dynamic Analysis)
6. 学习方法
机械动力学
机械动力学是一门基于Newton力学,研究机械系统 宏观动态行为的学科。该学科的研究对象包括几乎所 有具有机械功能的系统,其研究范围涵盖了这类系统 的建模与仿真、动力学分析与设计、动力学控制、运 行状态监测和故障诊断等。该学科的主要任务是采用 尽可能低的代价使产品在设计、研制、运行各阶段具 有最佳的动力学品质。 新型飞行器、高速车辆、机器人、大型动力机械的 发展不断向机械工程师提出新的动力学与控制问题, 极大地促进了复杂机械系统和多体系统的动力学建模 与仿真、非线性动力学分析与计算、动力学分析与设 计、振动控制、状态监测和故障诊断等方面的发展。
3.1.1 动力学建模 3.1.2 动力学分析 3.1.3 动力学设计
3.1.4 振动控制
3.1.1 动力学建模
机械零部件动力学
技术已比较成熟,可在 有限元方法已比较成熟, 其基本思路是:采用有限 ADAMS 可在ANSYS 等商品化软件上来 、NASTRAN等 元、假设模态、校正模态、 完成。存在的主要问题问 商品化软件平台上完成 奇异扰动等方法获得柔性 题 动力学建模和各种分析。 :具有奇异性和冗余自 体动力学有限维逼近的坐 由度的多刚体系统建模, 相比之下,处理含运动 标基,联同关节变量作为 机电耦联系统的统一建模 部件的机械系统的多体 广义坐标,通过 Lagrange 等。 动力学方法和软件要落 方程或变分原理导出动力 后许多。 学方程组。这方面的研究 很多,但远远未达到工程 化水平。
非线性系统动力学
随着弱非线性系统近似解法、低余维分叉分析、 数值模拟方法等日趋成熟,人们对1~2个自由度 的非线性系统在简谐外激励或参数激励下的动力 学行为已有比较充分的认识。一些解析和近似分 析方法正被推广到高维系统、非光滑系统、受非 简谐激励的系统,并试图揭示新的非线性动力学 现象。近年来,对弹性结构等无限维系统的非线 性振动分析仍以Galerkin方法降维为主,在具体 结构分析上有许多进展。
机械动力学
近年来,随着信息科学和非线性科学的发展,机械动 力学的研究内涵更加深入,其特征是:在系统的建模阶 段计入各种重要而又复杂的非线性因素、柔性因素、边 界与结合部效应,应用非线性动力学分析与仿真技术研 究系统的大范围动力学特性,基于对系统动力学的深刻 理解和采用最新的优化方法实现系统的动力学设计,对 系统实施各种主动控制乃至智能控制来获得所需的运动, 在研究机电一体化的受控系统时考虑动力学和控制的相 互耦合问题,采用各种最新的信息提取和分析方法诊断 系统的故障等。
